The Structure of the Milky Way's Bar outside the Bulge

　アブストラクト

　１．イントロダクション　

　２．等級分布　

　２．１．H-, Ks データ　

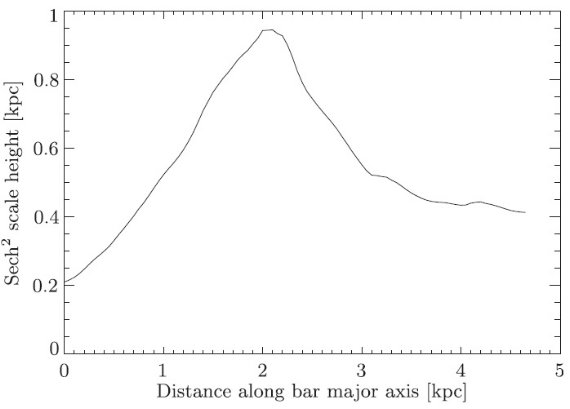
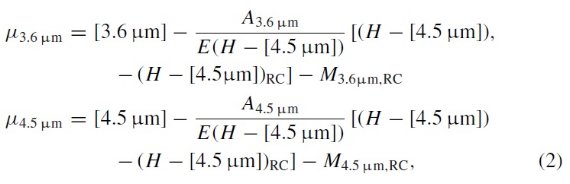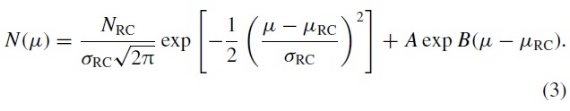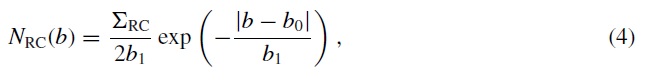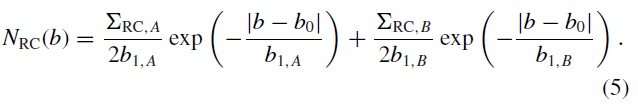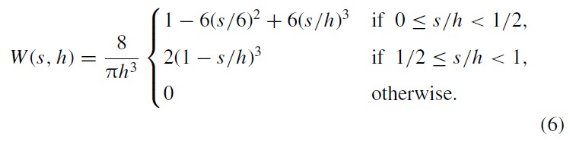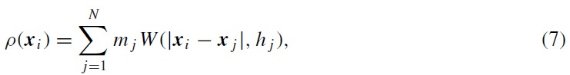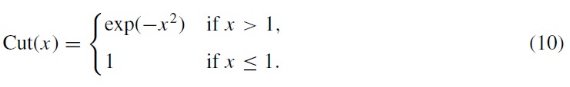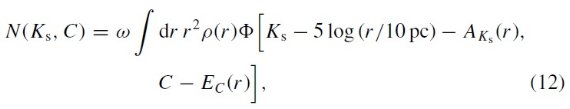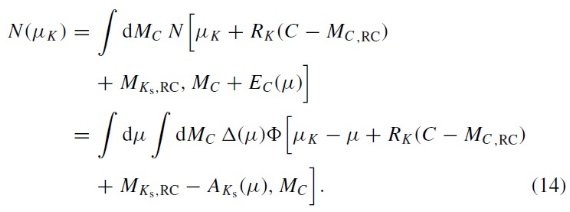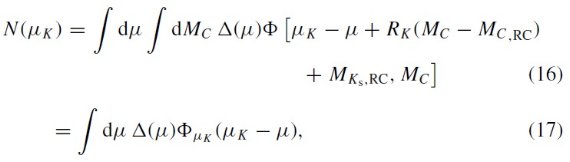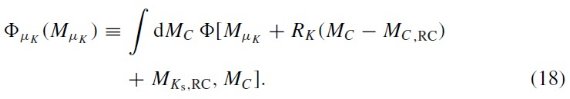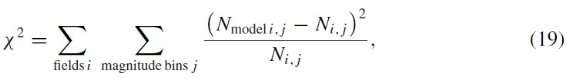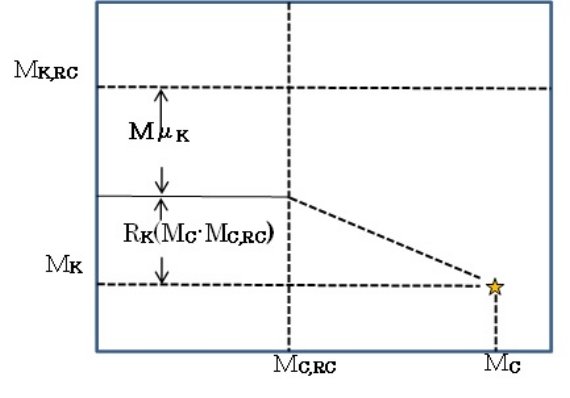
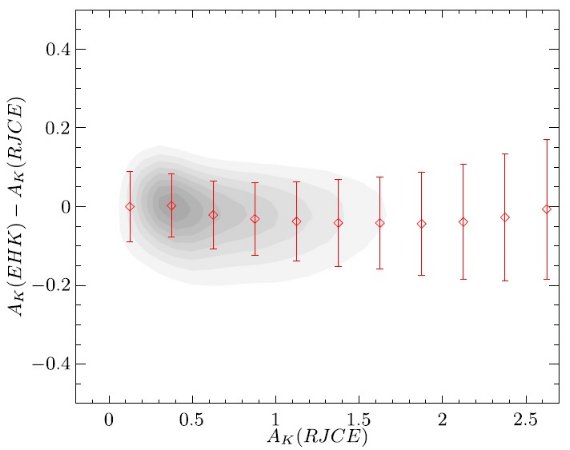
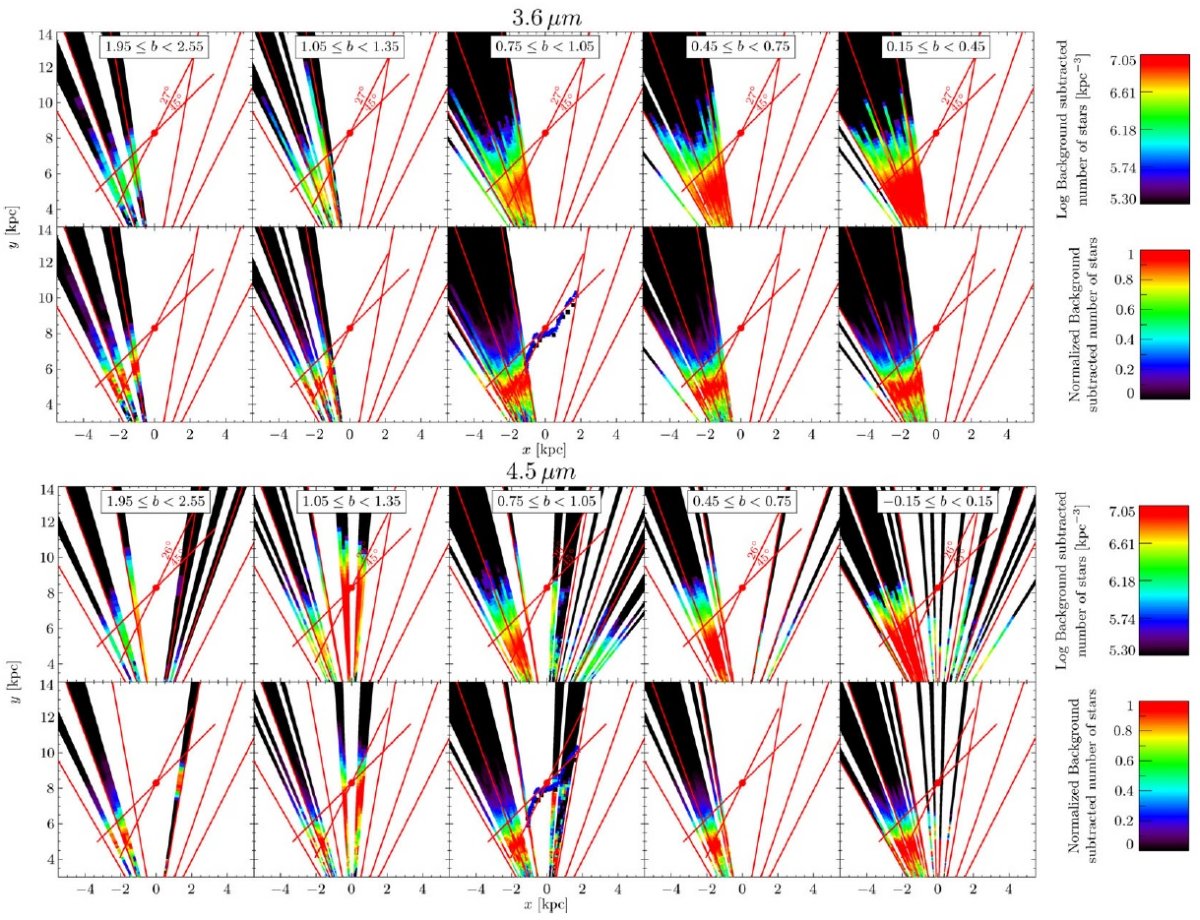
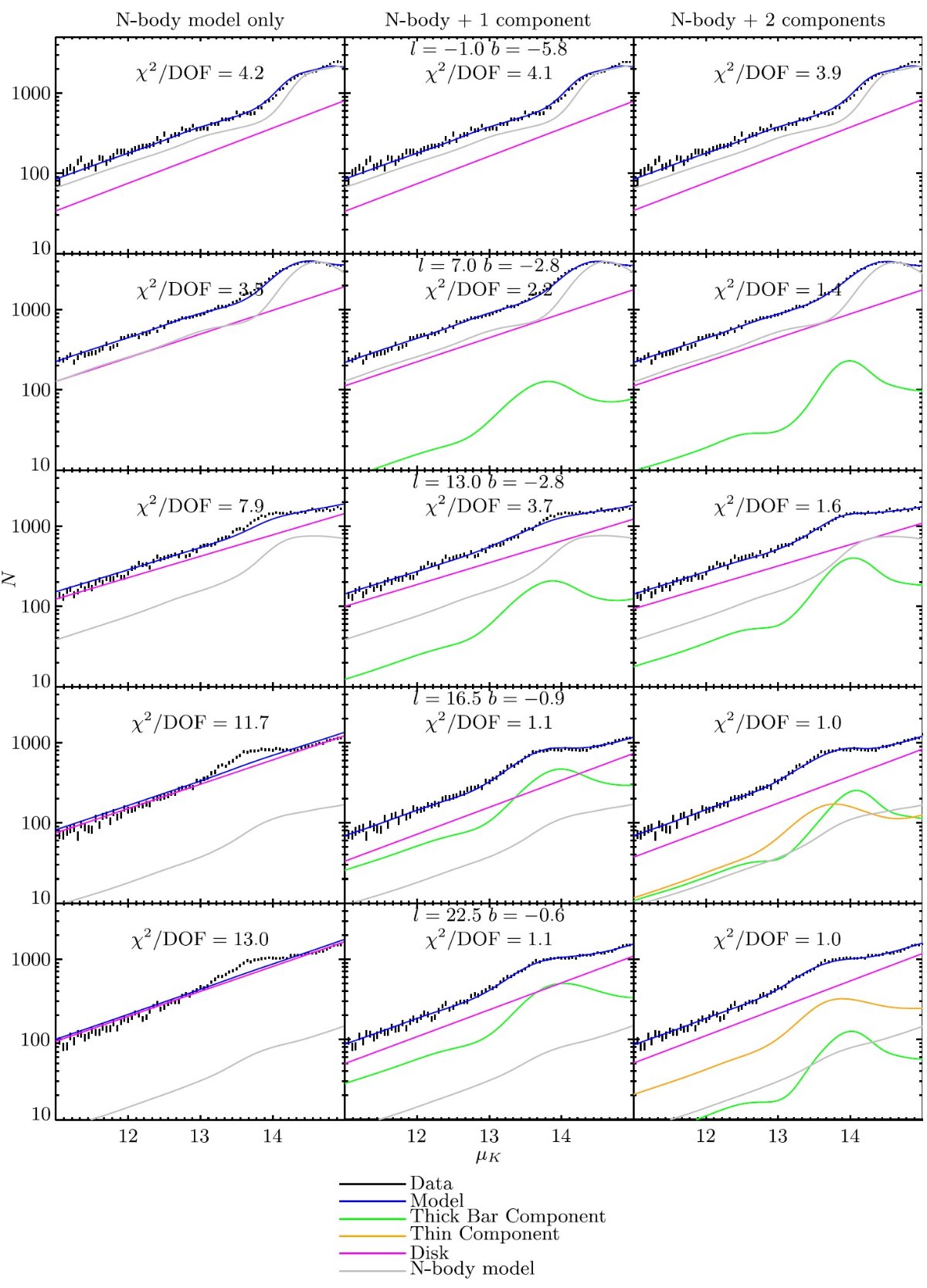
２．１．１．減光補正　 　測光システム　 　UKIDSS と VVV システムを 2MASS システムに変換した。付録Ａを見よ。 　バルジと違う減光状況　 　全ての星がレッドクランプ星であると仮定して次の式で減光を補正する。 ここに、(H-Ks)RC = レッドクランプ星の固有カラー、 MKs,RC = 絶対等級、AKs/E(H-Ks) = 減光則による。 μK = Ks 距離指数。 (μK は星がレッドクランプ の絶対等級、固有カラーを持つとして出した時に μ と区別して使って いるらしい。) 個別星毎に減光を決める方法は Cabrera-Lavers et al (2008) と同じである。バルジの場合にはダストの大部分は前面スクリーンに分布する と考え、２次元減光マップを適用すればよかった。しかし、銀河面上天体の 場合これは正しくないので、式１を用いる必要がある。 (全ての星をレッドクランプと考える という明らかに無茶な仮定をなぜ立てるのか？この後もこの仮定が貫徹されて いるのかどうかがよく分からない。)

近赤外減光則　 　近赤外では星のスペクトルはレーリージーンズ型に近いので, Lada et al (1994) の NICE 法が比較的正確に減光を与える。レッドクランプは、カラーが揃って いるだけでなく、絶対等級も一様である。減光補正の定数として、 西山その他 (2009) の AH = 1.73 （AKs/E(H-Ks) = 1.37）を採用する。 　MKs　 （１）レッドクランプのカラーをパドヴァ等時線から評価する。太陽メタル 10 Gyr 等時線に Kroupa IMF を使用してレッドクランプにガウシャンフィット してレッドクランプカラーとして H-Ks = 0.09 を得た。このカラーは年齢、 メタル量の影響が小さい。年齢を 1 - 15 Gyr, [Fe/H] = -0.7 to 0.17 の範囲 で H-Ks カラーの変動は 0.03 以下である。 （２）MKs = -1.72 を採用する。この値は Wegg, Gerhard (2013) でも使われ、バルジレッドクランプ星を Ro = 8.3 kpc の周りに分布させた。 ( この Ro = 8.3 Kpc を他の方法 例えば S2 を使った 7.94 Kpc と比較して MKs を確定し使用 した方がいい？その場合、L(-1.72)/8.32 = L(?)/7.942, L(?) = L(-1.72)(7.94/8.3)2, M(?) = -1.72 -5 log(7.94/8.3) = -1.72 + 0.096 = -1.62) 　２．１．２．カタログ作成　 　星毎に減光補正を行うには "band matched catalogue" が必要である。 UKIDSS と 2MASS はそれを提供しているが、VVV では、我々は H と Ks DR2 カタログの間で半径 1″ を用いてマッチを行う。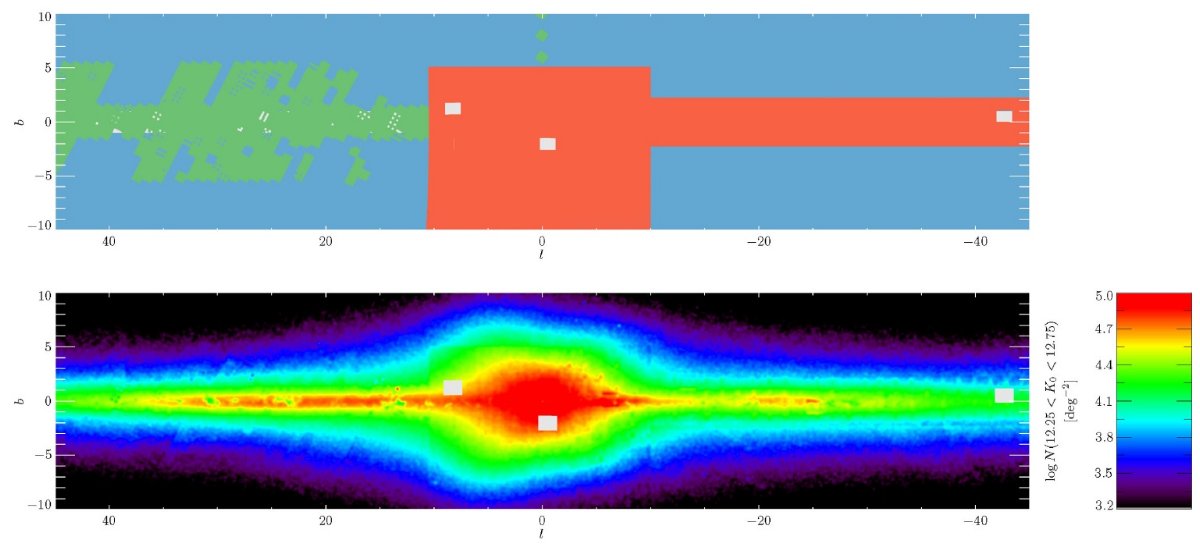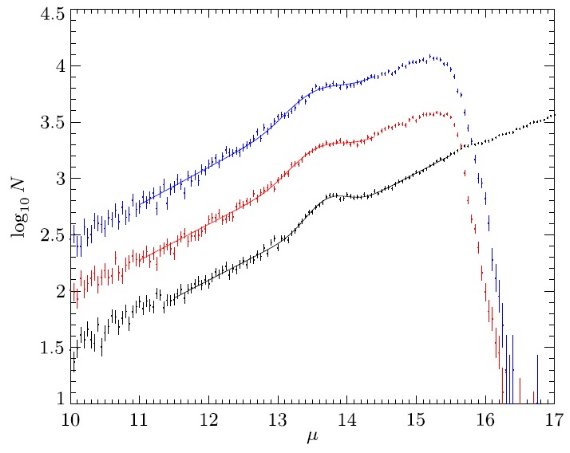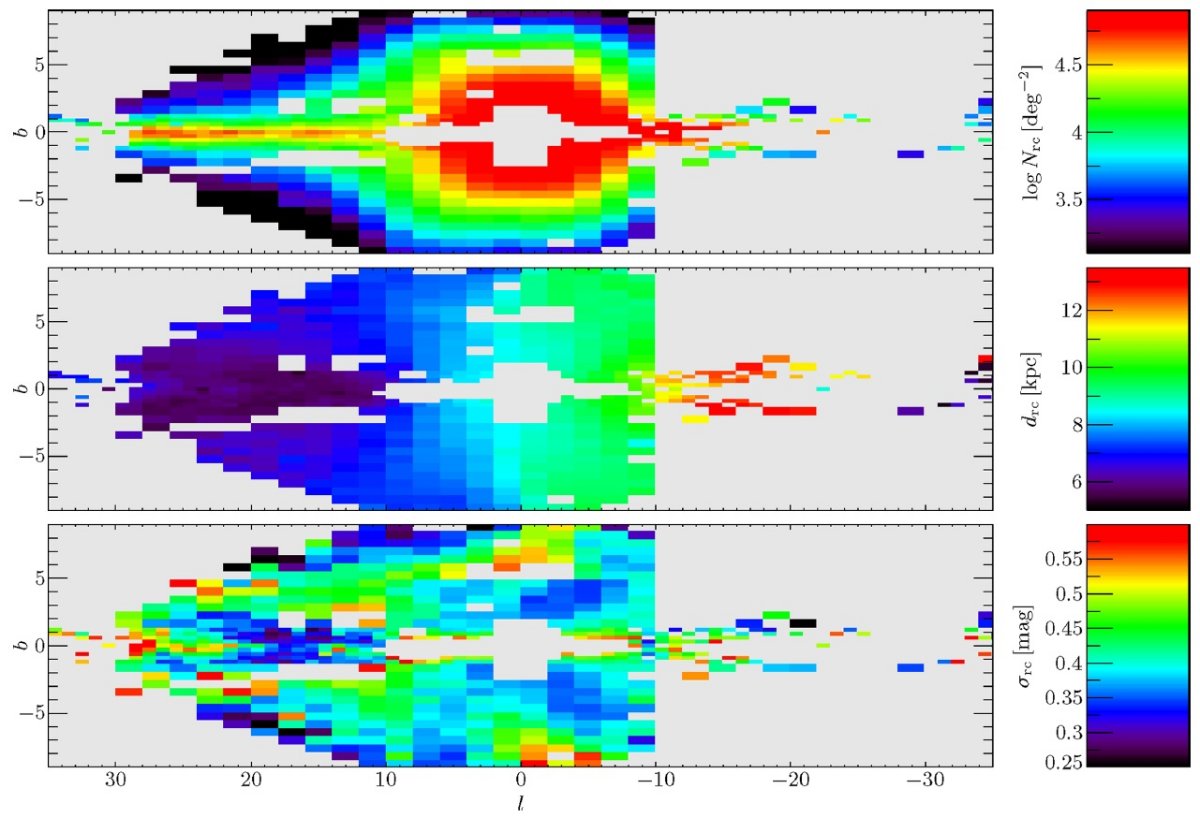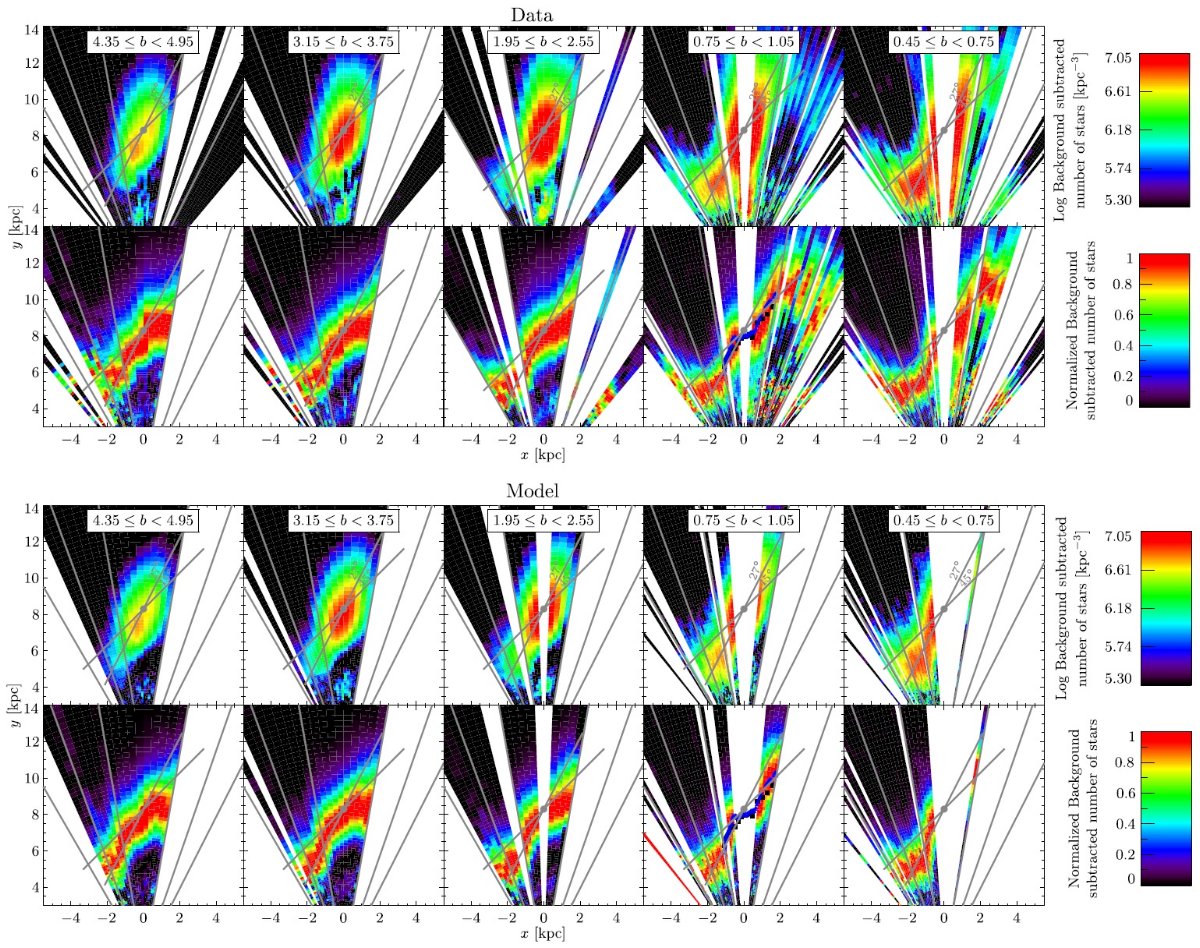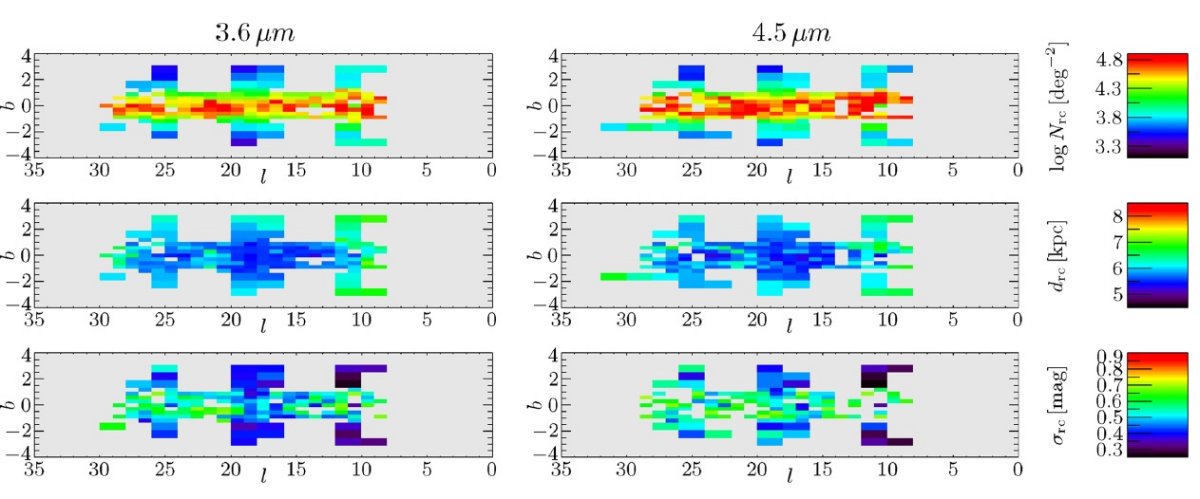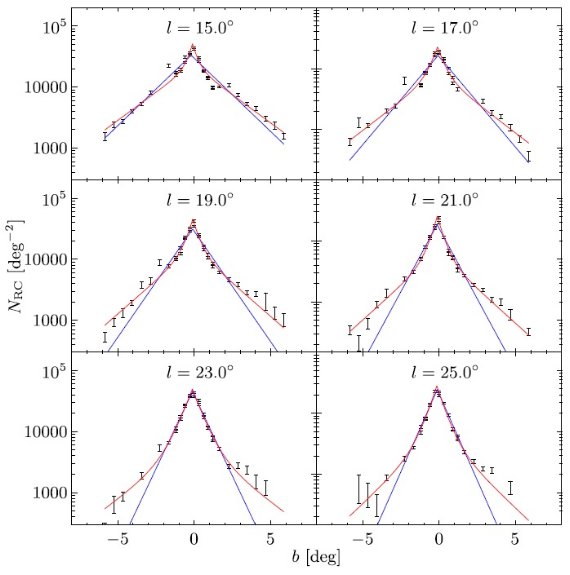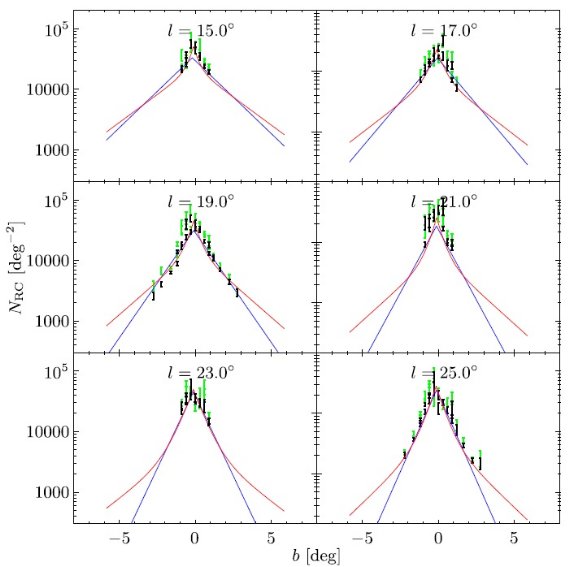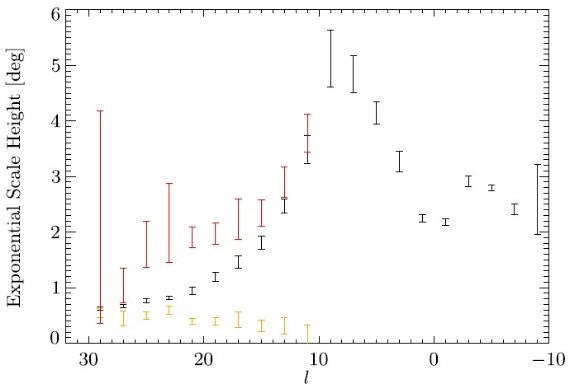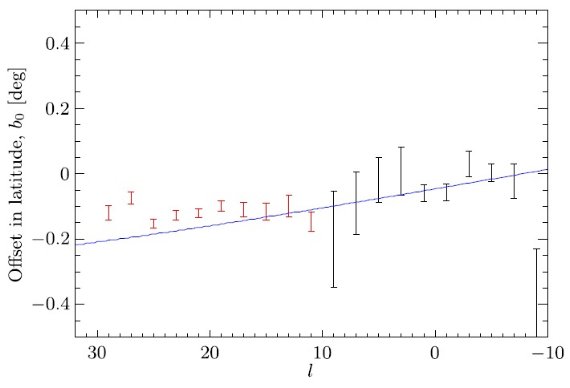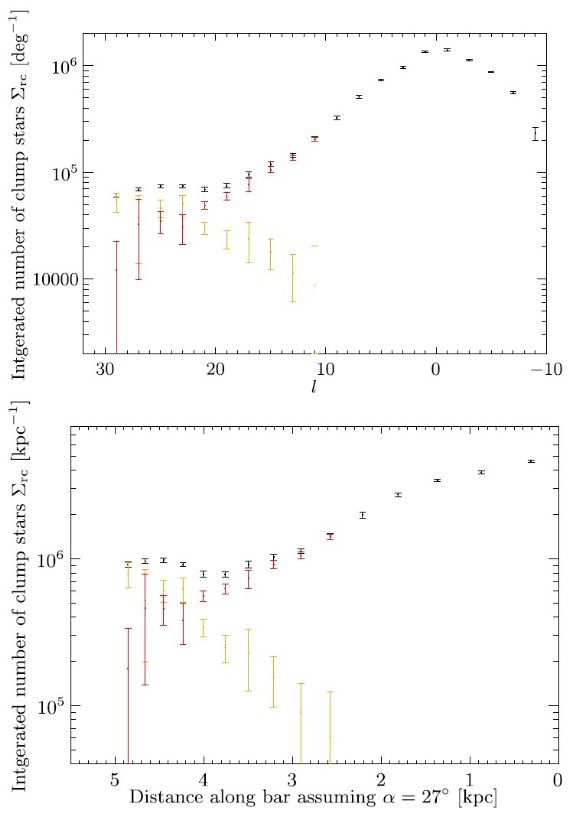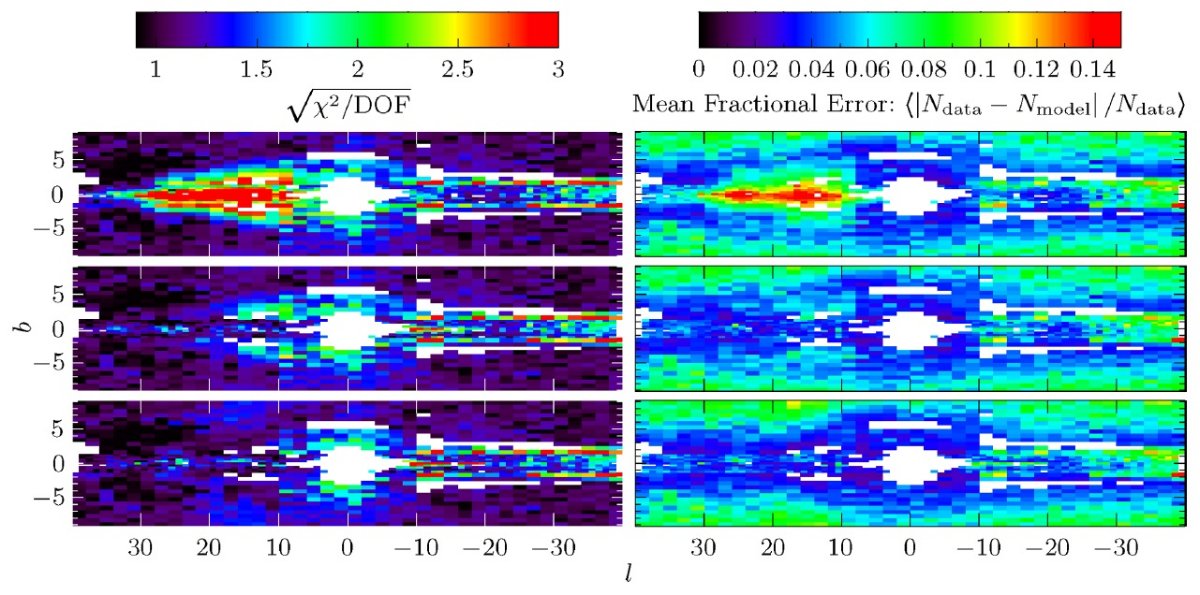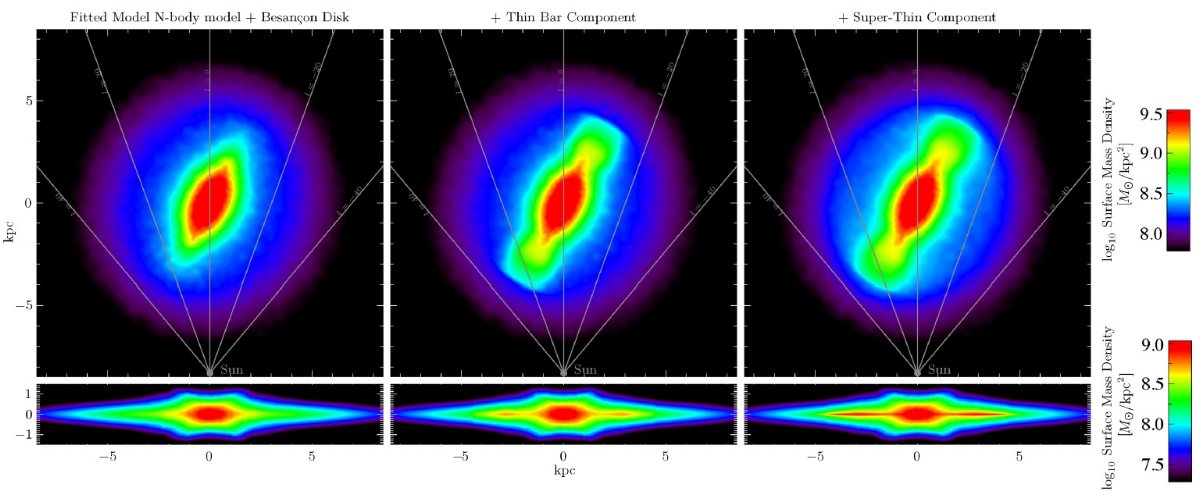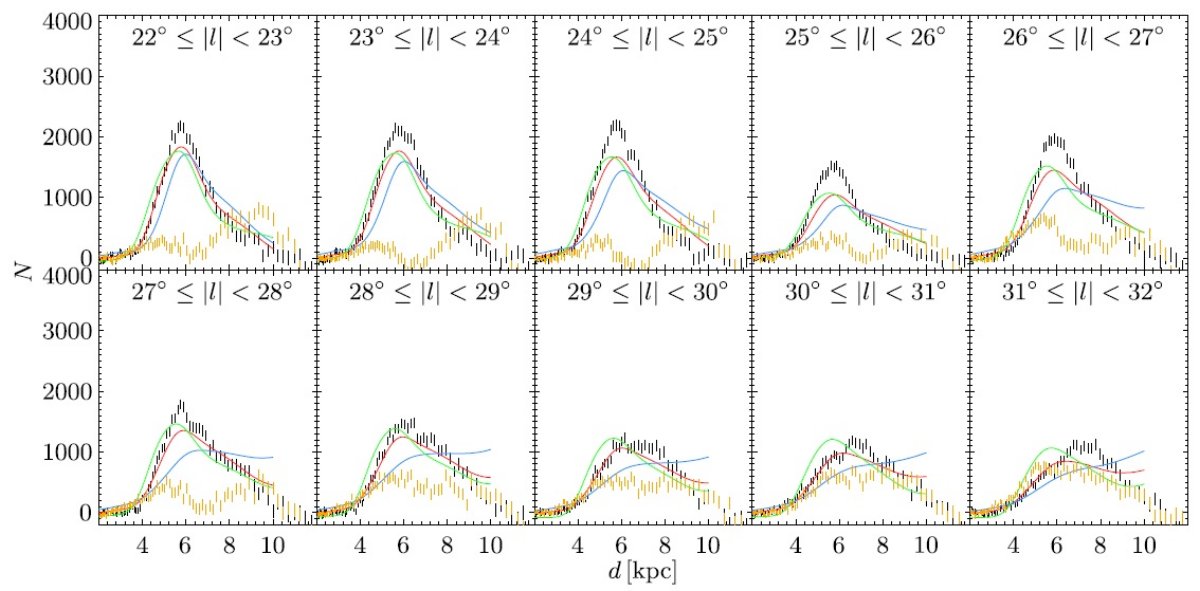 ( "match" の意味不明 ) カタログ優先度　 　サーベイを合体する際に、使用カタログは VVV, UKIDSS, 2MASS の順である。 サーベイの "footpeint" は図１に示した。図１の下段には、合体データの 減光補正 Ks バンドの星密度を示す。ロングバーは l 正側で星の数が多い ことに現れている。

　２．２．GLIMPSE データ　

RJCE 法の減光　 　GLIMPSE のデータは減光が小さいので Ks データのチェックに使用した。 Majewski et al (2011) の RJCE 法を用い、距離指数 μ を計算する。 A3.6/E(H-4.5) = 0.31, A4.5/E(H-4.5) = 0.23 は、 Zasowski et al (2009) の l = [15, 20] 測定値を用いた。彼らは AH/AKs = 1.73 を得ている。２．１．１．節のパドヴァ等時線を用いてレッドクランプ のカラーを測ると、 [3.6-Ks] = -0.05, [4.5-Ks] = 0.04 なので、 M3.6 = -1.72 - 0.05 = -1.75, M4.5 = -1.72 + 0.04 = -1.68 である。 図２．二つの方法で決めた AKs の比較。 AKs(EHK) = E(H-Ks) + 式１から。 AKs(RJCE) = E(H-4.5) + 式２から。μK = [12.5, 14] の星全てを含む。等高線はピークの 10, 20,...90 %.

バンドマッチ　 　E(H-4.5) を減光補正に用いるには GLIMPSE データを H-バンドデータの サーベイ観測とバンドマッチする必要がある。我々は UKIDSS と VVV H-バンド データにバンドマッチした。GLIMPSE は 2MASS へのマッチは既に提供している。 二つの AKs の比較　 　図２には、RJCE 法と E(H-Ks) 法の二つで決めた AKs を比較した。 差の平均は 0.05 mag 以下である。エラーの原因の多くは 4.5 μ の測光誤差 である。同様の比較を他の銀経 l でも行ったが大きな差はなかった。これは 減光則があまり大きくは変化しないことを意味する。 　等級分布　 　最後に |l| < 40, |b| < 9 における等級分布を作成した。グリッドは ２種類で、|b| < 1.2 では、(Δl, Δb) = (1, 0.3), |b| > 1.2 では、(Δl, Δb) = (2, 0.6) とする。 図３には、式１と式２を用いて計算した、サンプル区域での等級分布を示した。 このフィールドではバーのレッドクランプ星が μ = 13.5 付近のコブとして 現れる。背景は滑らかな非レッドクランプ星である。　 ( 繰り返すが、レッドクランプ星と 仮定して求めた μ の分布なのか？実際は Ks 分布だとしても、固有カラー 一定の仮定の精度は？) 図３．黒＝μ(Ks), 赤＝μ(3.6), 青＝μ(4.5) ヒストグラム。 すべての星をレッドクランプ星と仮定して μ を計算した。 (本当に明らかにレッドクランプ でない星もそうやって μ を計算してヒストグラムに含めている？) 見易さのため 0.5 ずつずらした。このサンプルフィールドの中心は (l, b) = (18.5, 0.9), 大きさは Δl = 1, Δb = 0.3 である。

　３．ガウシャンによるレッドクランプのフィット　

ガウシャンフィット　 　各領域の等級分布＝レッドクランプ（ガウシャン）＋背景（指数関数） (Stanek 1995, Nataf et al 2013) でフィットした。エラーはポアソンと仮定 し、χ2 最小とした。 　UKIDSS, 2MASS 使用領域では Ks = [11.5, 15.5] mag., VVV バルジ領域では Ks = [12, 16] mag. を使用した。GLIMPSE は浅いので明るい側は 10.5 mag., 暗い端は領域毎に変わる。フィットの例を図３に示す。フィットの結果は図４ に示す。このプロットでは Ncr > 3σ、つまりレッドクランプ数が 少なくともエラーの３倍以上あり、かつ背景の勾配 B > 0.55 の領域のみを 使用した。この第２の B 基準は暗い方の背景星の数が大幅に減ることと同等 である。さらにまた、フィットしたレッドクランプ等級がフィット範囲内に おさまり、レッドクランプの巾が σRC < 0.6 である ことを要請する。最後に、l < -10 の VVV データのない領域を撥ねる。 なぜなら、2MASS はそこではレッドクランプに届かないからである。 図５には B のヒストグラムを載せた。 　フィットへの特徴　 　図４の幾つかの特徴を述べる。 (i)　伝統的なバルジの外側で、レッドクランプが l = [10, 20], |b| = 5 で検出フィットされた。この領域では同じ l でのフィット距離は銀河面で 決めた距離と近い。 (ii)　l ≥ 30 ではよく定義されたレッドクランプのフィットはない。 この銀経は Lopez-Corredoira et al 2006, Cabrera-Lavers et al (2007) がロングバーの終点と主張している地点に近い。 (iii)　図１で l = [-20, -25] の表面密度に現れた密度超過はここでは見え ない。星の多くがレッドクランプ以外であったか、視線方向に長く伸びすぎ ていてレッドクランプの集中が検出されなかったか？ (iv)　バルジの短軸に沿い、|b| ≥ 5 では、分散が他より大きい。これ は１成分ガウシャンで二分レッドクランプをフィットしたためと考えられる。 (v)　銀河面内 l > 10 ではフィット距離の散乱は Cabrera-Lavers et al (2008) に較べはるかに小さい。

図５．式３でフィットした際の背景星の勾配。灰色：B < 0.55 であるために 撥ねた領域。その多くは混んだバルジ中心領域である。もし全てが巨星なら、 巨星枝の光度関数がべき乗型なために B = [0.6, 0.78] になる。 (Mendez et al 2002) 　上から見た分布　 　図６には背景を引いた後の生データを銀極方向から見た表示でのヒスト グラムで示す。加えて、ビンの数をその体積で割った値をヒストグラムにした。 このプロットからバーの方向が α = 45° Cabrera-Lavers et al (2008) より 27° Wegg, Gerhard (2013) の方が近いことは明らかである。低銀緯では曲がりの兆候が見える。

　同じ操作を GLIMPSE 3.6/4.5 で行った結果。

　４．ロングバーの垂直構造：銀経方向スライス　

図７．幾つかの銀経における、Ks 垂直分布。青＝単一指数関数によるベスト フィット。赤＝二重指数関数によるベストフィット。 図８．GLIMPSE 3.6/4.5 μm データによる垂直分布。 黒＝ 3.6 μm 分布。緑＝ 4.5 μm 分布。青＝ Ks 単一指数関数フィット。 赤＝ Ks 二重指数関数フィット。 　垂直分布を指数関数でフィット　 　各銀経毎に垂直分布を指数関数でフィットした。 ここに b0 はオフセットで、 b1 はスケール高で ある。l = [15, 25] では単一指数関数のフィットは悪い。従って、 二重指数関数のフィットを行った。 図７では Ks データ、図８では GLIMPSE データを用いてのフィットを 示す。 　フィット結果　 　図７(Ks)，図８(GLIMPSE)にはフィットの例を示す。GLIMPSE データは 銀河面から離れた所にはないが、近くでの結果はチェックとして重要である。 それはそこが減光が大きいからである。 　スケール高　 　スケール高の変化は図９に示す。スケール高はバルジ短軸付近で最小で あり、箱/ピーナッツバルジ領域で最大になり、ロングバー領域で次第に 低下して行く。二重指数関数の方が良く合うことが判った、ロングバー領域 ではスケール高は 0.5° と 2° であった。l = 20 ではバーは 距離 5.2 kpc の所にあり、そこでのスケール高は 45 pc と 180 pc となる。 180 pc は太陽近傍での薄い円盤のスケール高に近い。したがってこの成分 を薄いバーと呼ぶ。45 pc 成分は超薄いバーと呼ぶ。 オフセット　 　図１０にオフセット値の変化を示す。ほぼ b0 = -0.1 である。 これは 6 kpc で 14 pc に相当する。比較のために、銀河中央面の銀緯 オフセットを距離と銀経の関数として示した。その際太陽は中央面から 25 pc 上方にあり、 Sgr A* は銀河面上にあり、b = -0.046 であると仮定 した。図１０には α = 27 の仮定でオフセットの予想をプロットした。 l < 15 では良く合う。その先では少し過大評価になる。

図９．スケール高の銀経による変化。黒＝単一指数関数。赤とオレンジ＝二重 指数関数。 図１０．オフセットの銀経による変化。黒＝単一指数関数。赤＝二重指数関数。 青＝太陽が銀河面の 25 pc 上にあると仮定し、ロングバーの方向を 27° とした時の予想。銀河面中心を b = -0.046 (Goodman et al 2014) とする。 図１１．上：レッドクランプ星表面密度 ΣRC の銀経 l に よる変化。 ΣRC は式４と式５で定義される。 黒＝単一指数関数フィット（式４）の予想。赤とオレンジ＝二重指数関数 フィット（式５）の予想。 下：上の結果をバーが幾何学的に薄く α = 27° の仮定で、バー 主軸に沿った表面密度に変換。 　星数の変化　 　図１１には b 積分したレッドクランプ星の数を銀経に対してプロットした。 またそれを α = 27 の面に投影した図も示す。薄いバーの星は 指数関数的な変化を示す。スケール長は 1.5 kpc である。長薄いバー の星数は外側ほど大きくなる。これはバーの端で最近できた星が支配的な ためと考える。 　スケール高とレッドクランプ星数の双方は |l| < 10 のバルジ領域から l = [10, 30] のロングバー領域へ滑らかに移行している。これは二つの 構造がつながっていることの更なる証拠である。

　５．密度分布モデル　

パラメタ―モデル法を採用する　　 　本章では バー/バルジモデルを等級分布と合うように決め、その結果得られる バー角度、バー長、バー質量を述べる。その手法は、恒星分布モデルを作り、 それと光度関数で畳み込み、見かけ等級分布を作るというものである。 恒星分布が Ks-等級分布とフィットするまで修正する。対象等級範囲は Ks = [11, 15] で、これはレッドクランプ r = [1.6, 10] kpc に対応する。 ロングバー領域ではレッドクランプと非レッドクランプ星との比がバルジに較べ 低いので、残念ながら Wegg, Gerhard (2013) で行ったノンパラメトリックなモデル化は難しい。パラメタ―モデルを使用 する理由である。ここで作ったモデルは統計的にはデータと完全に合った とは言えないが、将来の有用なステップであると考える。 　モデル化の第１段　 　Portail et al 2015 の N-体モデルを採用する。それらは |l| < 10 の バルジを再現するよう調節されている。バー角度 α = 27° である。 　平滑化　 　N-体モデルを３次元スプライン法で平滑な密度分布に変換する。 　３次元スプラインカーネルは以下の形を採る。

すると平滑密度分布は次式で与えられる。 ここに mj = 粒子質量、hj = 粒子の平滑長である。 η = 3 とする。式７と８は逐次近似的に解かれる。 　ロングバーの追加　 　ロングバー成分として、Freudenreich 1998, Picaud, Robin 2004, Robin et al (2012) から、次の密度分布を仮定する。 ここに、x はバーの主軸、y は中間軸、z は北銀極方向に延びる右手系である。 R = sqrt(x2 + y2) は銀河中心軸からの半径である。

バーの内側縁 Rin と外側縁 Rout にはガウシャンカット を付ける。 このカットのためにバーの質量は式９のパラメタ―質量 Mbar より 小さくなる。Rin を必要としたのは N 体モデルが既に中心領域の等級分布を 再現済みだからである。 円盤スケール長　 　N-体モデルの円盤スケール長は 1.1 - 1.2 kpc で、銀河系円盤の スケール長 2 - 3 kpc に較べ短い。これは不安定円盤からバルジを形成する N-体モデル一般に共通で、バーの長さは円盤スケール長の数倍となる。 N-体モデルのロングバーがデータより不明瞭なのもこの円盤スケール長が短い ことと関連している。というのは、バーに沿って外側に行くと星の数が銀河系 よりも少なくなるからである。ここでは円盤モデルをデータに合うように直す ことはしないで、次式の埋め草を足す。 　　　Ndisk = N0,diskexp[b(μK - 13.5)]　　　（１１） もしも円盤に中心部ホールがあるならレッドクランプ星の不足は等級分布の 窪みとして現れるはずだが、それは見られない。それで式１１でよいと 考える。

星計数の基本式　 　各フィールドでの見かけ等級分布を合わせるために、我々は密度分布 (i) と (ii) に光度関数を畳み込み、(iii) を足す前に、μK の関数として星の数を予想する。 ( i, ii, iii は 式７、９、１１ の間違い？) 次の量を定義する。 　　　C = H - Ks, Mc = (H-Ks) - E(H-Ks) = (H-Ks)o（固有カラー）, 　　　Ec = E(H-Ks), RK = AKs/E(H-Ks) Φ(MK, MC)dMKdMC = 単位質量当たり、絶対等級dMK、固有カラーdMC 内にある星の数。与えられた種族構成の等時線から得られる。 N(Ks, C) dKsdC = 立体角 &omega: 内で観測された dKsdC の星の数。 この式を距離指数を使って書くと、 　N(Ks, C) = ∫dμΔ(μ)Φ[Ks-μ-AKs, C-EC(μ)]　　　　(13) ここに、Δ(μ) = (ln10/5)ωρr3 である。

( 式１３までは一般論で、全て の星がレッドクランプと言う仮定は使わない定式化である。ここからが チンプンカンプン。) 変数を (Ks, C) から (μK, Mc) へと変換することで、 　　　N(μK)dμK = 距離指数 dμK 内の星の数 が得られる。式１を使うと、 式１：Ks = μK + RK(C-MC,RC) + MK, RC と C = MC + (C-MC) が 式１４上段の N(Ks, C)の引数にそのまま入っている。μK は式１で定義される名目的な μ であることに注意。式１４下段は 式１４上段の N に式１３を代入した形式的変換。N(μK) = 観測 色等級図の星を右図のように赤化線に沿って MC,RC まで戻して作 った等級関数で、ただし引数は μK = 0 が 減光フリー等級 MEF = MK,RC に相当する。 　AKs(r) = RKsEc = RKs(C-Mc) より、

ここに、ΦμK(MμK) は Φ(MK, Mc) から次の式で得られる。 　 式１８を図解すると、 従って、ΦμK(MμK) は MC-MK 面上の点を、赤化線に沿って Mc = MC,RC 線上に投影した ものである。減光フリーな光度関数と名付けてよい。MμK = 0 は減光フリー等級 MEF = MK - RK(MC - MC,RC) が, MEF = MK,RC に相当する。 だから、式１７は色々な距離指数 μ における減光フリー光度関数 ΦμK(MμK) からの、減光フリー等級関数 N(μK) への寄与の和を表す。

ΦμK(MμK) の計算　 　式１７は減光フリー光度関数で書かれていることに注意せよ。この式の 畳み込み積分には高速フーリエ変換を用いた。この式の解に円盤成分 (iii) (多分式１１のこと)を足して最終解とする。 ΦμK(MμK) の計算には BaSTI = Bag of Stellar Tracks and Isochrones (Pietrinferni et al 2004) 等時線を用いる。 α 増強　10 Gyr, Kroupa 2001 IMF, に Zoccali et al 2009 の バーデの窓メタル量分布を適用した。レッドクランプ等級の不確定性を考え、 フィットに際し減光光度関数を全体として ΔK ずらすことも許容した。 　フィッティング領域　 　フィッティングは の最小化で行う。１９式で等級巾は 0.05 等であり、背景勾配 B < 0.55 の領域は除いた。そのような所は暗い方で測光不完全度が高いからである。

幾何学的配置　 　太陽は銀河面の 25 pc 上方にあり、Ro = 8.3 kpc とする。 Sgr A* は銀河 面中央にあり b = -0.046° とする。この結果、b = 0 面は銀河中央面に 対し少し傾く Goodman et al (2014)。 しかしこの傾きは今回はエラーの範囲内である。 フィットのステップ　 　フィットは３段階に分かれて行われる。 (i)　N-体モデルを中央部にフィットする。（５．１．節） (ii)　ロングバーを記述する成分を追加する。（５．２．節） (iii)　長薄いバー成分を追加する。（５．３．節） 　ベストモデルのパラメタ―　 　ベストモデルと判断されたのは、二つのロングバー成分を持つものである。 表１にはフィットしたパラメタ―を載せた。表２にはその結果としての バーの物理量を載せた。

　５．１．バルジのフィット　

　５．２．一成分ロングバーモデル　

　５．３．２成分バーモデル　

　５．４．バー角度　

　５．５．バー長さ　

　６．議論　

　６．１．ボックス/ピーナッツバルジとロングバーの連続性　

バルジとロングバーの角度の一致　 　バーとバルジがつながっていることの証拠は、 (i)　バーとバルジの方向角が近い。 (ii)　スケール長が連続的に変化する。 ことである。ロングバーは角度 alpha; = 28 - 33 で ボックス/ピーナッツバルジに対し |l| < 10 で決めた Wegg, Gerhart (2013) による角度と合うことが判った。この角度の決定は等級分布をフィットすること により行った。しかし、図６を見れば l = [10, 20] のバー角度がバルジに 対して見出された α ≈ 27 に近いことは直接見て取れる。 　大きなバー角度を出した以前の研究　 　GLIMPSE を使った以前の研究、Lopez-Corredoira et al 2006, Cbrera-Lavers et al (2007), Cbrera-Lavers et al (2008), Benjamin et al (2005) ではロングバーの方向角を α = 44±10 としていた。 しかし、同じ GLIMPSE データを使った Zasowski 2012 は α = 38±6, Zasowski. Benjamin, Majewski 2012 では α = 35 が得られている。これ はレッドクランプの光度を下げたためである。光度を下げた結果、ロングバーまで の距離が小さくなり、同じ銀河中心距離を採用した場合にはバー角度を低下させる 事となった。我々の研究では探査範囲がバルジ領域まで伸びているのでレッドク ランプの光度を変化させて角度が変わることはない。 Gonzalez et al (2012) は VVV データを用いて、 Amores et al (2013) はバー終端位置からバー角度を導いた。しかし、投影効果が大きいので要注意 である。レッドクランプ星までの距離から大きなバー角度を求めた Cbrera-Lavers et al (2007), Cbrera-Lavers et al (2008) の結果を本研究とすり合わせることは困難である。恐らく選択基準が大きく 異なる結果と考えられる。彼らは、減光モデルから距離による減光変化を予想し、 色等級図からレッドクランプ星を選んだ。一方我々の研究ではレッドクランプ は滑らかな背景星の上の超過成分として統計的に選ばれた。 　バルジからバーへの遷移　 　さらに、我々は図９でスケール高はバルジからロングバーへ滑らかに 変わって行くことを示した。これは両成分が結合した構造であることを支持する。 この遷移は N-体モデルと似ている。それを示すために図１６に N-体モデル のスケール高変化を示した。軸方向がほぼ揃っていることを認めると、 ロングバーは内側の縦に伸びたバーの延長であることが自然に理解される。 図１４下部には側面から見た投影図を示す。

図１６．Portail et al 2015 のモデル M85 におけるバー長軸に沿ったスケー ル高の距離による変化。示したモデルはフィッティングに先立ち、スケール高 が中心部で小さく、バルジ部分で増大し、ロングバー部で再び低下することを 示している。

　６．２．薄いバーと超薄いバー　

　６．３．バーの長さ　

バー角度の影響　 　我々が決めたバーの半軸長 5.0±0.2 kpc は以前決められた値、 例えば Cbrera-Lavers et al (2008) の 4.5 kpc、より長い。その理由の一つは我々が得たバー角度が小さいため である。 　円盤成分の差引　 　もう一つの問題は、我々が使用したブザンソンモデルの精度である。 仮に円盤の表面密度を２倍に上げると、バーの長さは 5 kpc から 4.6 kpc に減少する。これは Lmod が安定している理由である。 この長さは主軸と短軸に沿った輪郭の差がそうでなければ滑らかでもっと 穏やかなバーに沿った減少の 1/e にある点から決まる。これは基盤の円盤 部の影響を受けない。 (主軸と短軸の差って中心でゼロ だと思う。そしたら 1/e の意味がない。何だろう？) 　パターン速度　 　バーの無次元回転速度を R = RCR/Lbar と定義する。 バーは共回転半径より先には伸びられないので R > 1 である。 (どんな理由でか？) 我々のバー長測定から共回転は 5 kpc より外側になる。平坦回転速度 vc = 218 km/s (Bovy et al 2012) を仮定すると、これはパターン 速度が 45 km/s/kpc 以下であることを意味する。この値は、ヘラクレス星流を バーの外側リンドブラッド共鳴によるとする考えとは一種の緊張関係にある。 Antoja et al 2014 は、バー角度 29, Ro 8.3 kpc, vc = 220 km/s の仮定に基づいて、パターン速度 48.2±0.5 km/s/kpc を導いた。 これらの値を我々の結果と摺り合わせるには、バー回転速度を R = 1 まで上げる か、ヘラクレス星流の起源を別物と考えるしかない。反対に、B/P バルジの 力学モデルから Portail et al 2015 は回転速度 25 - 30 km/s/kpc を得た。 この回転速度を我々のバー長と組み合わせると R = 1.4 - 1.9 となり、 したがって、銀河系は遅い回転系であることになる。 　運動学データ　 　将来は我々の研究からのデータを運動学データと組み合わせて、 モデルを改善していく。

図１７．我々の２成分バーモデルを銀河のように、バー角度 45, 傾き角 i = 60 で外から見たと仮定した場合の様子。円盤のノードは水平である。 Erwin, Debattista 2013 が示したように、この角度から見るとボクシーと バーの形が共に良く見える。この角度からだと、ボクシーバルジの軸はロング バーよりもノード線に近く見える。 ガイア　 　ロングバーの |b| ≥ 1 成分の観測はガイアでも可能である。 さらに、レッドクランプ星の性質を詳しく規定することも可能となる。 これはバー研究では重要である。と言うのは、例えばバー角度の決定で 重要なのはレッドクランプの絶対等級が種族効果でどのくらい変化する かである。

　７．結論