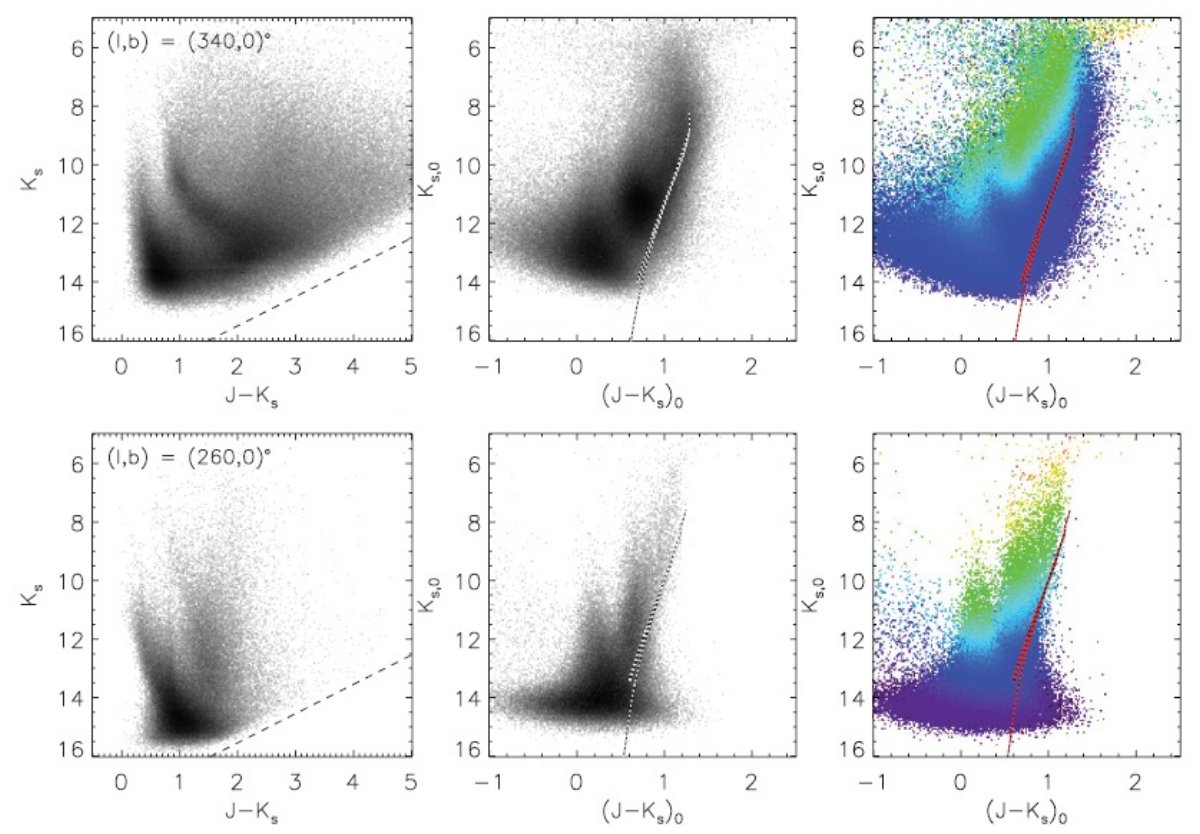
| 2MASS と IRAC 波長域は大部分の星ではレーリージーンズ波長帯にあたるので固有カラーは ほぼ一定である。したがって、NIR-MIR カラーの変化は赤化を表す。 そこで Rayleigh-Jeans Color Excess = RJCE = [H - 4.5] を赤化指数として調べた。 | その結果、銀河系の面における減光が IRAS/ISSA, COBE/DIRBE を用いて 100 μm 放射から導いた過去の結果と異なることが判った。われわれの結果は 13CO の マップと類似している。 |
1.1.銀河系構造研究に及ぼすダストの影響過去の研究論文が沢山あげてあるが省略する。 星間減光が障害になること 問題を整理すると、 (1)E(B-V) ≥ 0.5 では減光の変動スケールが現在の減光マップの分解能より小さい。 (2)現在の減光マップは2次元で、視線方向の総減光量を示し、ある星までの減光量は 与えない。 (3)減光の強い領域での可視減光則は「標準」減光則から外れる。 (4)減光により見かけ等級が暗くなる。 (5)赤化補正をすると、得られたスペクトルが縮退しがちである。 近赤外では問題のいくつかが解決する 近赤外では問題のいくつかが解決する。例えば近赤外では減光則の変動が小さい。 しかし、近赤外赤化ベクトルの方向は二色図上での進化の方向と重なるという新しい 問題も起きてくる。。 IRAC ばんどはさらにいい。 2MASS と IRAC を組み合わせると、個々の星までの減光量を出すことが可能になる。 減光則の変動は残るが小さく、さらに良いことに赤化ベクトルの方向は進化経路と 異なる。 |
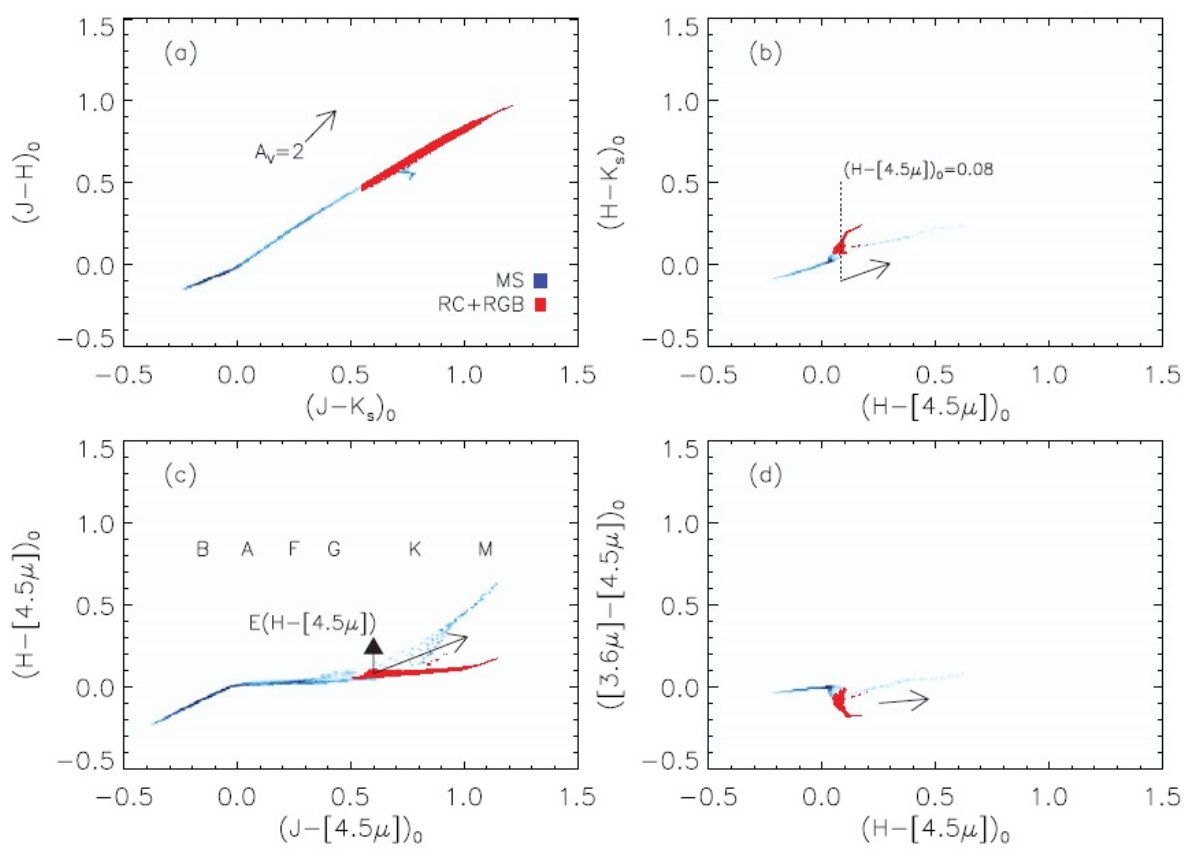
1.2.減光量を測る道具としての色超過Opikの説明Opik がいろいろな説明を考えたことが書いてあるが省略。 その後の減光則の歴史 これも文献が多数上がっているが省略 1.3.暗黒雲の星の近赤外色超過の研究の初期Jones et al 1980 の (J-H) - (H-K) 関係Jones et al 1980 は石炭袋方向の Bok グロビュールにある星の (J-H) - (H-K) を研究した。しかし、図1(a) を見ると分かるが、星の系列と赤化ベクトルの方向はパラレルなため、個々の星に対して、 固有カラーと赤化を分離するのは難しい。それにも拘らず、彼らは全ての星が M3 III であると 仮定して(E(J-K)o=1.1)、減光強度のグロビュール中心からの変化を導いた。しかし、この 方法の精度を上げるには、個々の星の分光観測を行ってスペクトル型を決めるという非常に 面倒な作業が必要となる。 Arce, Goodman 1999 による手法の評価 Arce, Goodman 1999 は減光マップの手法を比較検討した結果、「個々の星の スペクトル型を決めたうえで、色超過を測るのが最も信頼できる。」とした。 しかし、彼らはまた、「この方法の欠点はスペクトルを得るには膨大な時間がかかる。」 とのべている。測光のみでスペクトル型が決められると非常によいのだが。 |
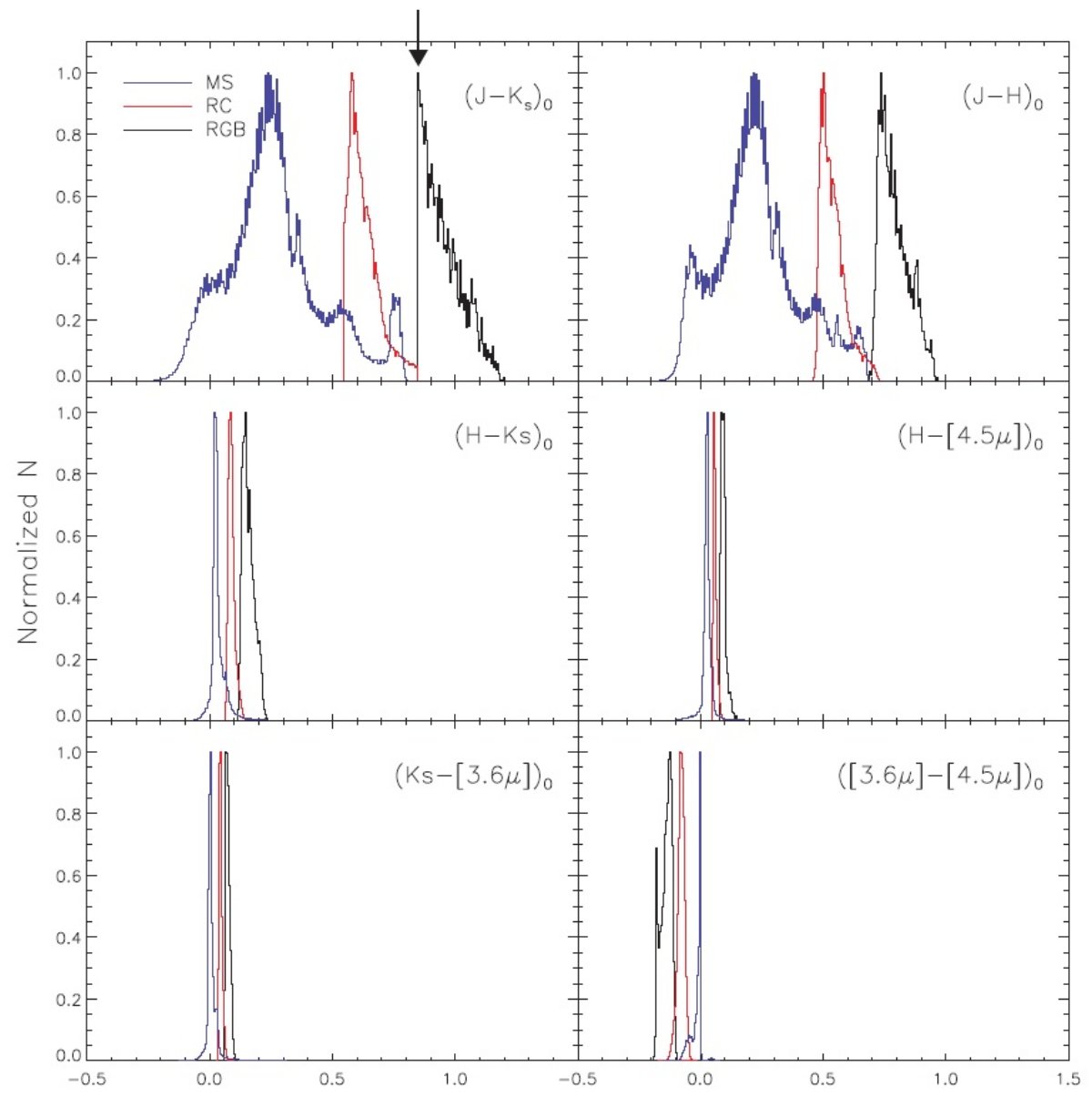
1.4.統計的近赤外色超過 (NICE) 法Lada et al 1994 の Near Infrared Color Excess (NICE) 法Lada et al 1994 は IC5146 の研究で、0 < (H-K)o < 0.3, つまり A0 - M 型の星 を選び、統計的に赤化を出した。 ( Lada たちは 1.4' x 1.5' のタイルで (H-K)-1.3 の平均をとった。1.3 はコントロールフィールドの (H-K) 平均。) NICE欠点は空間分解能と視線沿った減光分布が分からない しかし、NICE 法の統計誤差を小さくするには、サンプル区画の面積を大きくしてサンプル数を 増やすのがよい。しかし、引き換えに空間分解能が悪くなる。 NICER 法 Lombardi, Alves 2001 は Lada et al 1994 の方法を一般化して NICE-Revisited (NICER) 法を考案し, オリオン、Mon R2 領域 625 deg2 に適用した。NICER 法では (H-Ks) だけでなく、(J-H) も使用 する。しかし、(J-H)o は J が入る結果、固有分散が大きく (H-Ks) の 3 倍に達する。 Lombardi, Alves たちは、J の測光エラーは H, Ks より小さく、Av/E(J-H) は Av/E(J-Ks) より小さい( 9.35 と 15.87 Rieke, Lebofski 1985 ) ので E(J-H) 分散の効果を小さくする、と論じて E(J-H) の使用を正当化した。 |
しかし、NICER も依然として平均に依存し、固有カラーの平均値が一定という仮定
に依存ている。
その結果、 Lambardi-Alves マップでは NGC 2204 付近の青い星
が多いところでは減光がマイナスの区間が現れた。しかし、 NICER は (H-Ks) のみ
を使う NICE よりは減光が弱い領域までの感度が良いようである。
Gosling の V-NICE 法 Gosling et al 2009 は NICER 法に減光則が方向によって変化することを 認める改定を入れてバルジの減光を調べた。 1.5.レーリージーンズ色超過法(RJCE)(1).1930 年代に遡る色超過法をダスト量の推定に用いる。(2).NICE, RICER, V-NICE と同様に赤外カラーを用いる。 (3).大きな領域のマップに関心がある。 (4).終極の目標は星自体にあり、その性質、分布を知ることにある。ダストの分布も もちろん知りたい。 (5).個々の星の前面減光を知りたい。 (6).RJCE 法は中間赤外の導入でそれを可能にする。 (7).RJCE では個々の星のスペクトル型を求める。 |

2.1.レーリージーンズ色超過法の原理MIR を加える利点(1)図1の (c) と (d) を比べると分かるように、カラーと赤化の縮退は 中間赤外に移ると消えていく。 (2)IRAC 領域では星の SED がレーリージーンズ型になるので、その標準 カラーからのずれから直ちに赤化が出せる。 図1(c) での赤化 図1(c) では赤化を決める二つの例を示す。 (1)多くのカラーの組から脱赤化線が一つの星の固有カラーを通るようにすれば 赤化が決められる。図(c) ではそれが実際可能なことが判る。 (2)図(c)で分かるように、(H-4.5)o はスペクトル型による変化が小さく、0.1 以下である。これはつまり、(H-4.5) の観測値のみで個々の星の赤化を導けることを 意味する。 A(Ks) = 0.918[(H-4.5)-0.08] 銀河面方向で 2MASS CMD に乗っている星の大部分は F, G, K 巨星で、そのカラー は数 Gyr 主系列転向点と赤色巨星先端との中間値である。 |
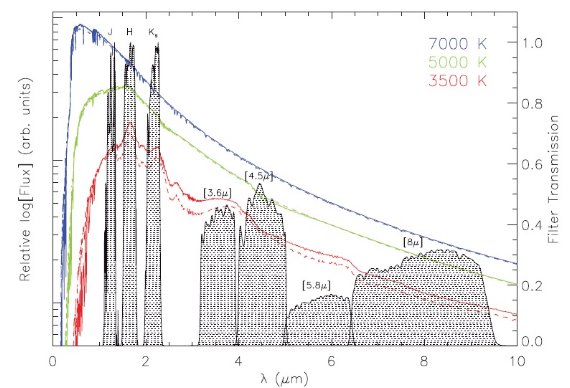 図2.Castelli, Kurucz 2004 モデルスペクトル(点線:[Fe/H]=-1, 実線 =0)と 2MASS, IRAC バンドパス。2MASS 波長帯に比べ、IRAC 波長帯でSED が 同じ形をしていることに注意。 |
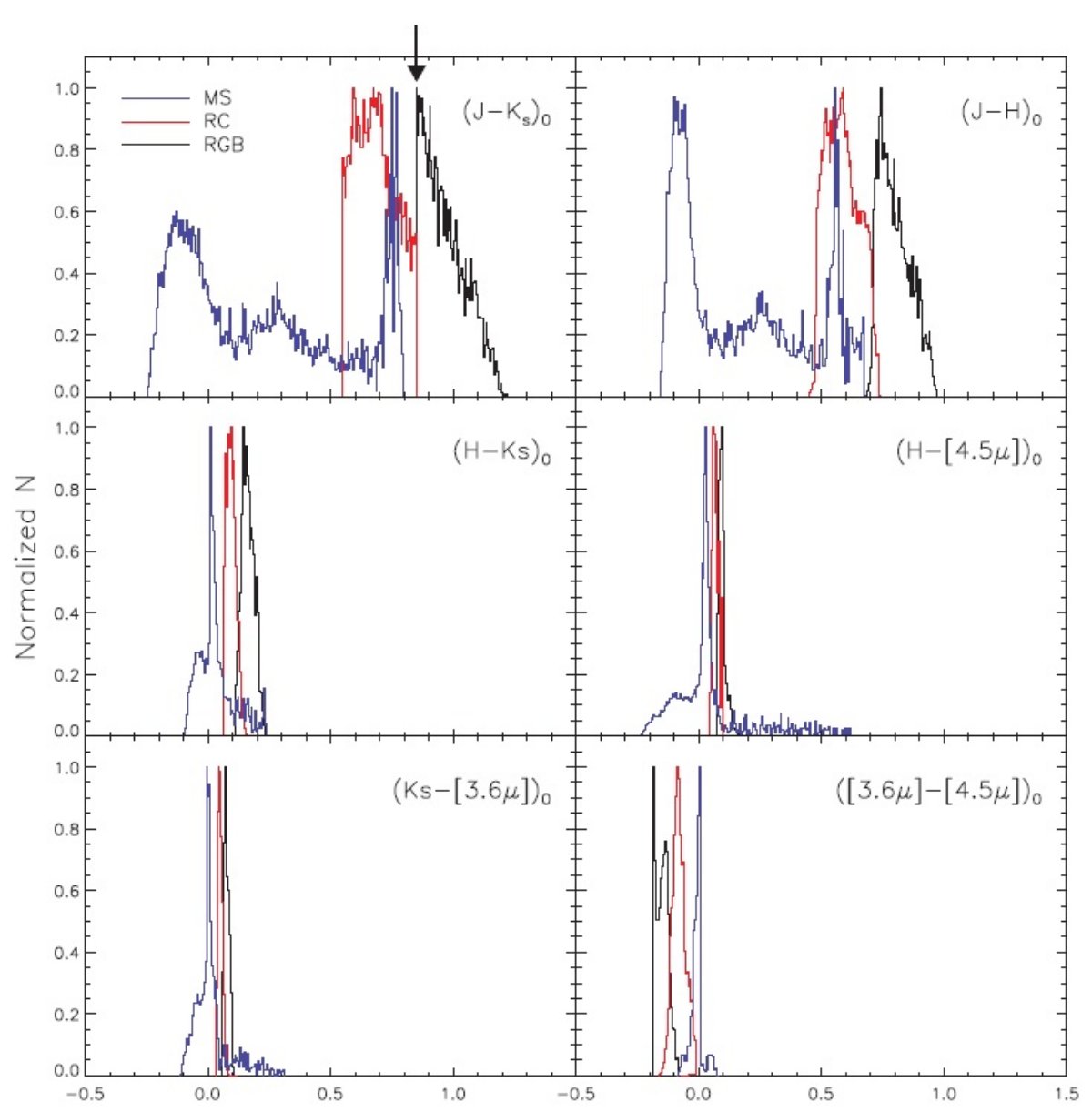
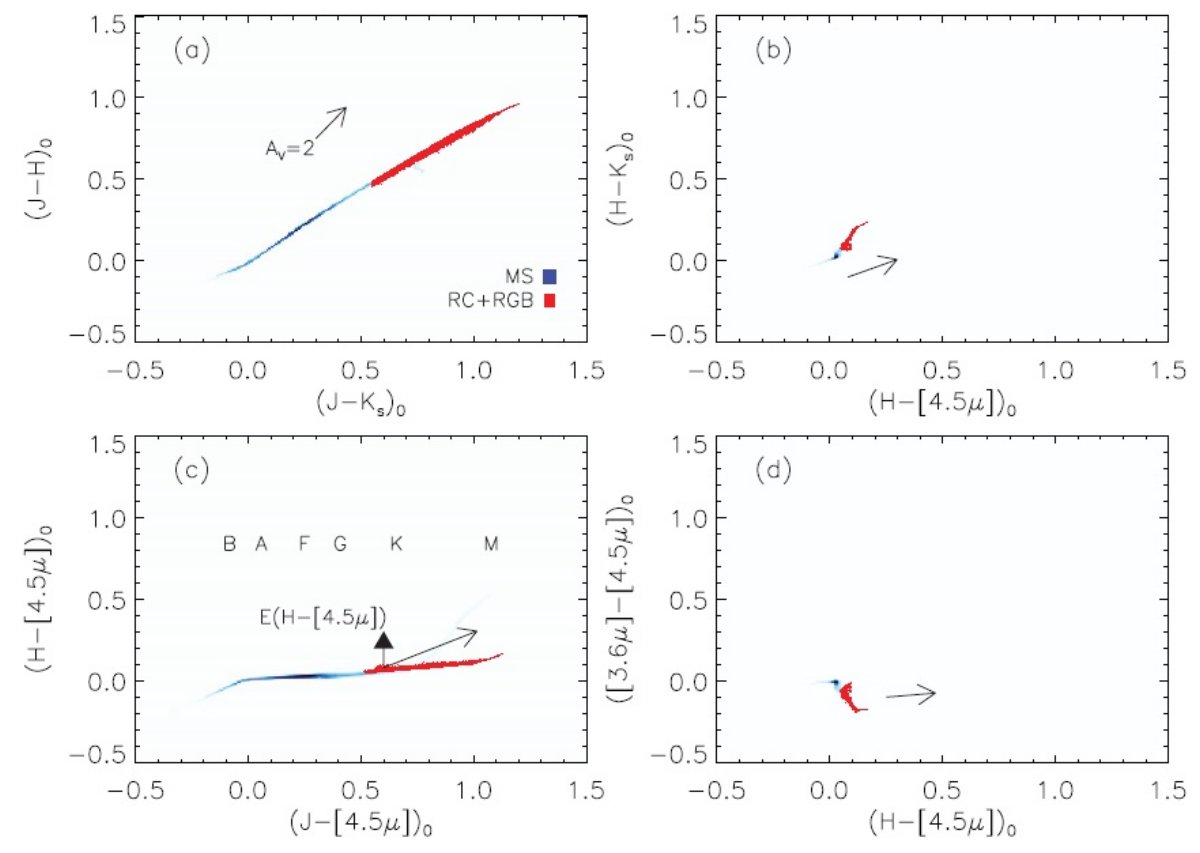
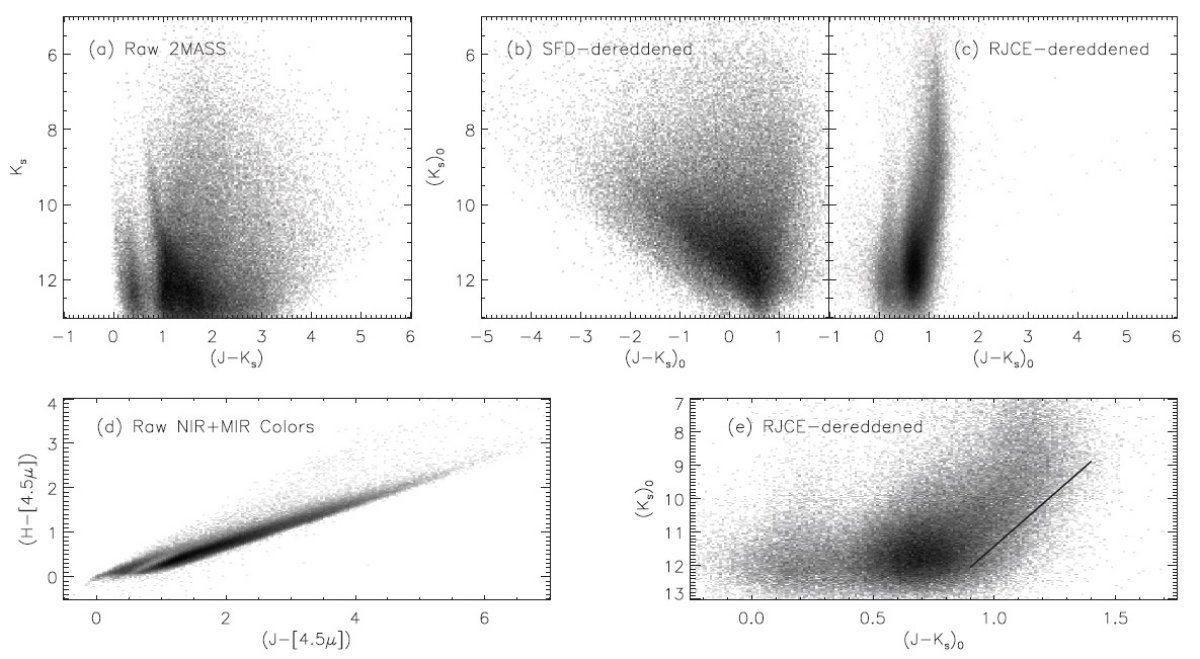
3.1.2MASS+IRAC データへの応用[4.5] は [5.8] よりいい。GLIMPSE サーベイ( Churchwell et al 2009 ) の GLIMPSE I をこの論文では使用する。[4.5] は [5.8] と違い、ダスト連続放射の 影響をあまり受けない。 最も簡単な RJCE 法の例 1: 図6(a) 図6には E(H-4.5)o = 0.08 を用いた最も単純な RJCE 法の結果を示した。6(a) 図は 2MASS ([J-Ks], Ks) 図を示す。RC フィンガーの下側が広がっているのは赤化がでこぼこ なためである。第3のフィンガー赤色巨星枝は最大の赤化を受けており、完全にぼやかされて しまった。 |
最も簡単な RJCE 法の例 2: 図6(b) 6 (b) は SFD 減光マップを使って赤化補正した例である。結果は明らかに悪化している。 最も簡単な RJCE 法の例 3: 図6(c) E(H-4.5)o = 0.08 を用いた最も単純な RJCE 法の結果を示した。星の分布が細くなった ばかりでなく、カラーも適切な値である。例えば、 RC は (J-Ks)o = 0.7 で円盤 RC 星の カラーと一致する。図6(e) には (c) の拡大図を載せたが、そこに示した 16 kpc RGB の 下側でサンプル数が落ちている。これはけんしゅつ不完全性によるものでなく、実際に 向こう側円盤の縁を見ているのであろう。 |
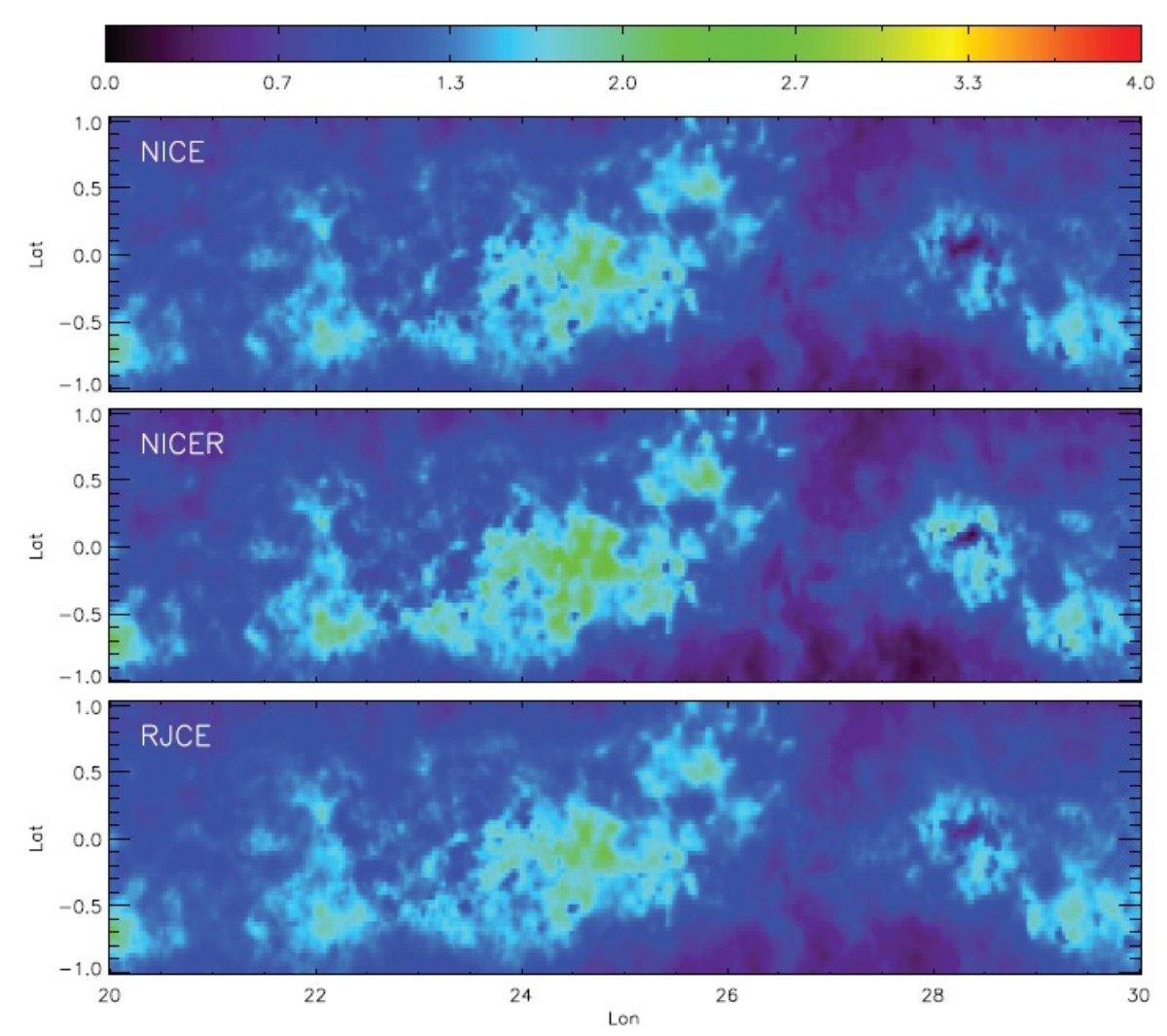
3.2.不定性の源(1).固有カラーの分散(2).測光エラー (3).減光則の視線に沿った、および方向による変化 それらを個々に評価すると、個々の星に対する A(Ks) の誤差は ≤ 0.11 mag である。 3.3.NICE, NICER, RJCE 法の比較図7= .NICE, NICER, RJCE 法の比較図7では.NICE, NICER, RJCE 法の比較を示した。各マップで、測光エラー < 0.5 mag. の星のみを使用した。また、ピクセルサイズは 2' × 2' である。NICE, NICER 法では Indebetouw et al 2005 の減光則を用いた。 A(Ks) = 1.05(J-H-0.76) A(Ks) = 1.82(H-Ks-0.13) 各マップはたがいによく似ている。ピクセル毎に比較するため、図8では ICE 対 RJCE と NICER 対 RJCE のピクセル比較を行った。 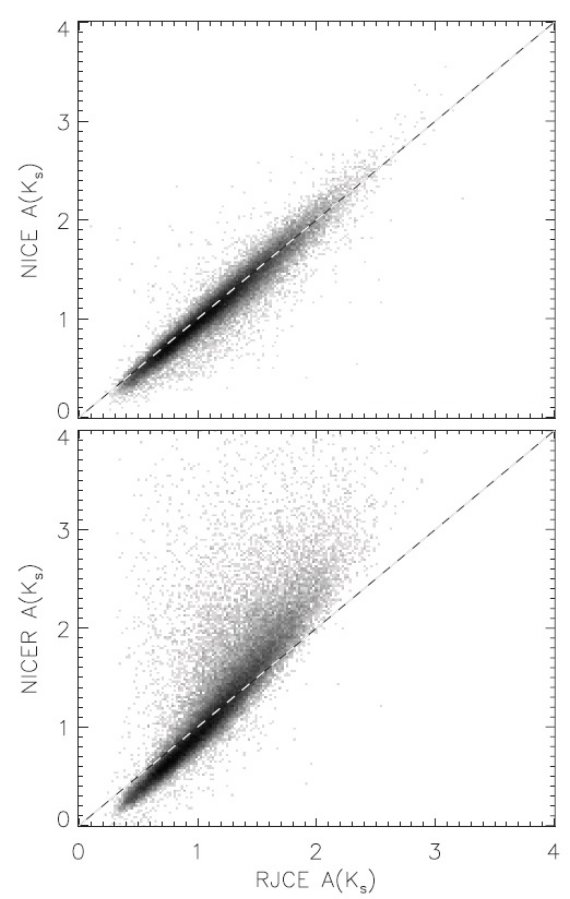 図8.NICE, NICER, RJCE 法間のピクセル比較。上:NICE 対 RJCE。下: NICER 対 RJCE。 |
減光が大きくなると
NICER 減光が RJCE 減光より大きくなる傾向が見られる。これは、NICER 法では
赤色巨星に対する A(Ks) を過大に評価する傾向があるためで、3.4.節で説明する。
同じ理由で、NICER 法では、また NICE でもある程度、A(Ks) ≤ 0.8 の弱い減光領域
では前景の矮星の A(Ks) を過小に評価する傾向がある。
図8の勾配が1でないのは減光則のため? 図8の勾配が1でないのは減光則のためかも知れない。もし NICE 法で A(Ks) = 1.59(H-Ks-0.05) を使うと、図8での NICE - RJCE 対応は改善される。 注意しておくとどの減光則を修正すべきかは未定であり、全て修正すべきかも知れない。 ピクセル内の A(Ks) 分散は微分減光を示す 図9にはピクセル内での A(Ks) 分散と A(Ks) の関係を示した。RJCE 法の分散が少し小さい のは (Ks-4.5) の固有分散が小さい結果であろう。しかし、どの図も想定される(3.2.節)より ずっと大きな分散を示している。これはピクセル内部にそれより小さなサイズの減光分布の 構造が存在することを意味する。 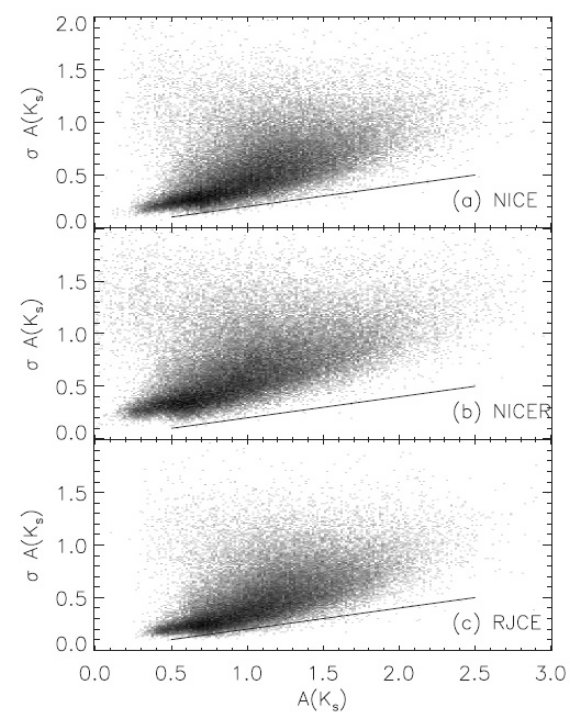 図9.ピクセル内での A(Ks) 分散と A(Ks) の関係。 上:NICE 中:NICER 下:RJCE。 |
|
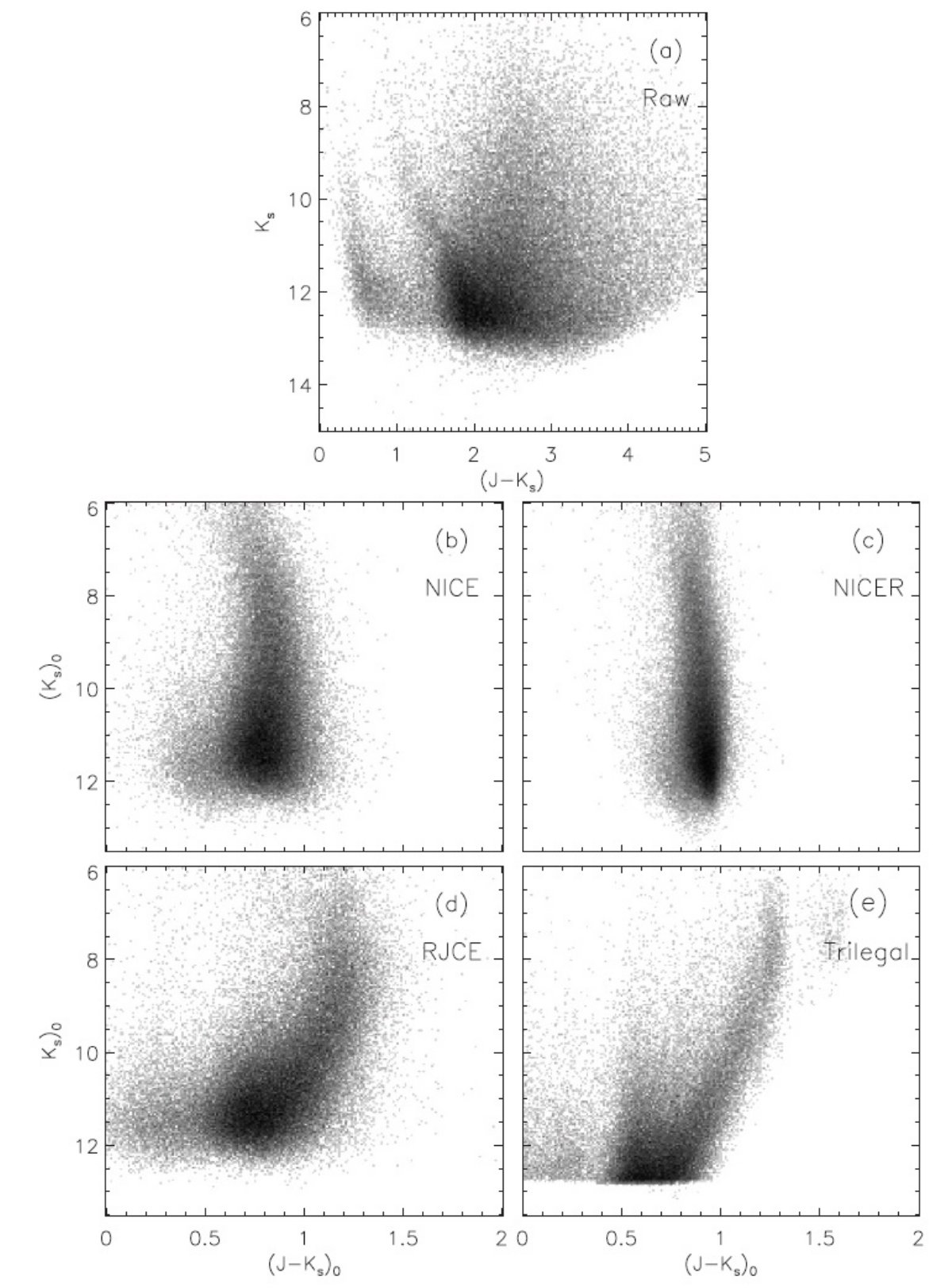
色超過法を CMD に応用する意義 これまで色超過法は減光マップの作成に用いられてきた。しかし、我々は色等級図 (CMD) にも関心がある。それは、視線に沿った種族を知り、ダストの距離分布を理解するのに 役立つ。 CMDを比較する 図10では (l, b) = (42°, 0°) 4 deg2 での赤化補正 色等級図の比較を行った。(a) は生データで、図6(a) と同様に赤くて暗い方向に弧を描いている。 (e) は TRILEGAL モデルの予想図で、MS, RC, RGB の3つの指が見える。(b) は NICE 赤化補正で あるが、全ての星に (H-Ks)o=0.13 を仮定した結果、導かれた (J-K)o に強い圧縮がかかった。特に、 もっとも赤くて明るかった巨星は、想定された平均カラーより赤いため、それを平均値 (H-Ks)o=0.13 まで戻すと、過補正されるからである。 |
(追加のくどい説明:NICE では個々の星の色超過を
E(H-Ks)=(H-Ks)-0.13 とみなす。そのため、(H-Ks)o > 0.13 の星は赤化補正が過剰になり、
(H-Ks)o ≤ 0.13 の星は赤化補正が不足する。図10を仮に Ks-(H-Ks) 図で並べた場合には
(b) は一本の縦線になってしまう。Ks-(H-4.5) 図を描いたら、今度は (d) が縦線になる番だが、
だからと言って、その時の (b) 図がよりリアルかどうかは保証できない。) RJCE 法 CMD はなかなかいい。 図10(d) は RJCE 法を用いている。(H-4,5) = 0.08 を全ての星に仮定しているが、 最も本物らしい CMD を回復できた。 回復 CMD の利用 きれいな CMD が得られると、星のタイプ毎に銀河系の構造を追跡することが可能になる。 例えば、RGB が選べると、最も明るく赤い星を用いて銀河系構造の深い探査が行える。 また、(J-Ks) = 0.55 - 0.80 の RC が選べると、メタル量依存の小さい標準光源が手に 入る。 |
|
減光ホール? 図7を見ると、減光の大きな領域の中央に穴が開いている。これは限界等級に より生じた人為的産物である。減光の強い雲があると、背後の星が見えなくなり、 (組み合わせでは主に 2MASS が原因。GLIMPSE は検出)手前の低減光の星が残る。 その結果、その方向は低減光領域となる。 ( 土橋マップの時と同じで、この論文も どこまでの減光をマップにしているのかという疑問が起きる。) それに対しての対策は、 (1)その領域を囲って無視。 (2)もっと深い測光 (3)吸収係数の低い波長での減光決定 RJCE 法の限界等級 RJCE 法では H = Ho + A(H) > 15 の星は脱落する。これが図7での制限の原因である。 と言うのは、図11(b), (c) で (Ks)o + A(Ks) ≤ 14.3 か、[4.5]o + A(4.5) ≤ 14.1 が検出領域だからである。 IRAC データのみなら深い減光領域まで達する しかし、図11(c) を見ると、 IRAC データのみを使えばもっと 深い減光領域まで達することが判る。それをはっきり示すのが図12である。特に図12(c) では E(3.6-4.5) を使った場合と E(H-4.5) の場合との A(Ks) の差がマップとして示されている。 この図には 図12(a) でホールとして現れていた部分が実は減光が強すぎたためであることが 明らかに示されている。 IRAC データのみの性質 しかし、(3.6-4.5) を使った場合に考慮すべき点がいくつかある。 (1)図3、5から分かるが、(3.6-4.5) の固有巾は (H-4.5) より大きい。長波長の 5.8, 8 μm データの使用が考えられるが、測光精度が落ち、ダスト放射の影響も大きい。また、論文2で 示すように Aλ/AKs は長波長では変動が激しい。 (2)(3.6-4.5) の巾が比較的小さいために星のタイプの情報が得られにくい。 (3)減光が弱いということは MIR からの減光マップは減光が弱い領域での精度が低い。 |
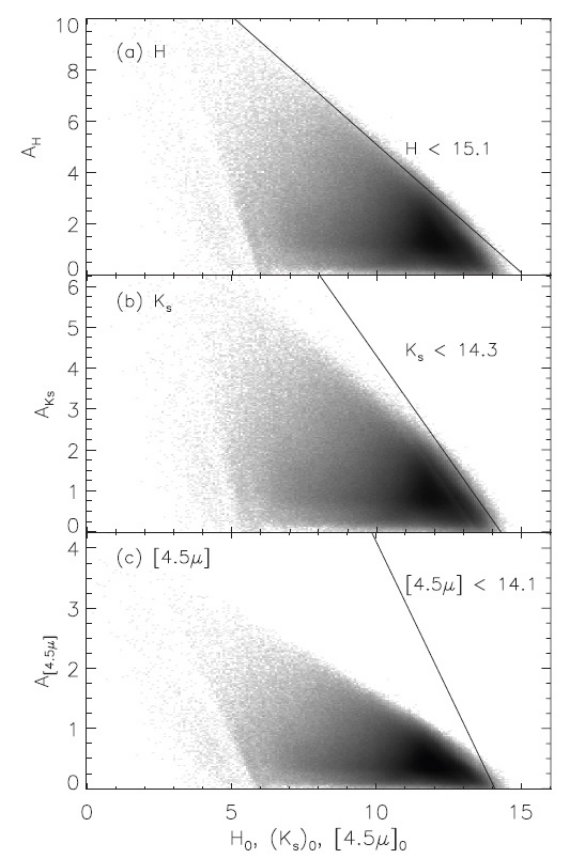 図11.上:[Ho, A(H)] 中:[Kso, A(Ks)] 下:[(4.5)o, A(4.5)] のプロット。実線は検出限界。図から分かるように、サンプルに含まれる限界は H で 制限されている。 |
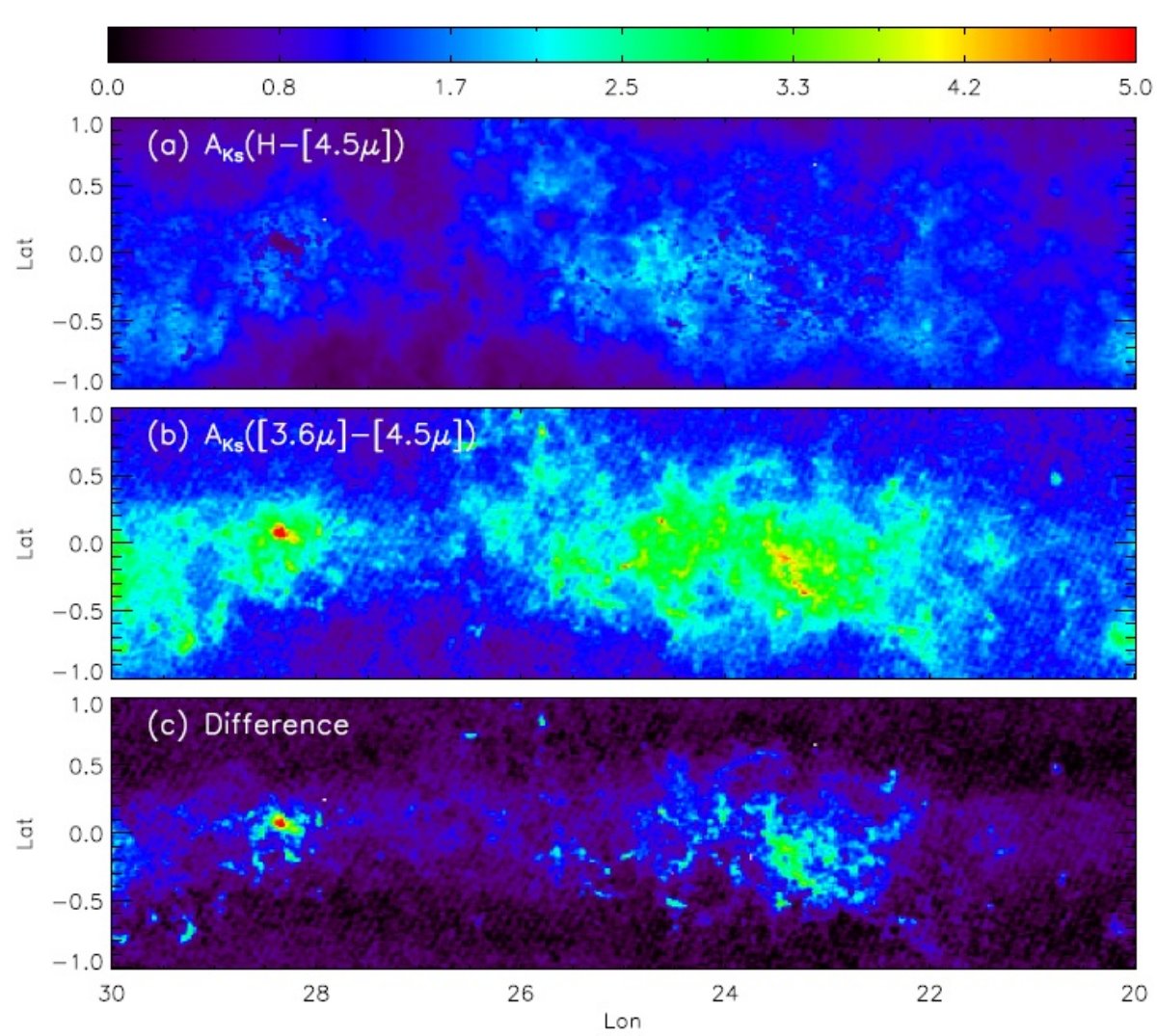
4.1.13CO図13(c) は、GRS サーベイ (Jackson et al 2006)による 13CO 積分強度。 黒はシグナルなし。白は Ta = 30 K. RJCE マップとの類似は著しい。大きな違いは CO のピーク付近が RJCE マップでは穴になっていることである。 13CO は厚い 分子雲でも光学的に薄いので雲の総質量を測るに適している。4.2.IRAC 8 μm図13(d) は、IRAC 8 μm 画像である。このバンドは熱いダストと PAH からの放射を示す。 加熱源が星形成域、SNR, HIIR からの UV 輻射なので、星間減光を追跡するには適していない と考えられていた。従って、 RJCE 減光マップとの類似性がないのは当然である。 |
4.3.星計数図13(e) は、2MASS/GLIMPSE サンプルの数密度マップである。この図が減光マップと 似ていることは、前景矮星の影響があまりないことを示している。また、この図は 背景星の欠如によって RJCE 法が適用できない領域がどこかをよく示している。4.4.SFD現在最もよく使われている減光マップは、 Schlegel et al. 1998 が COBE/DIRBE と IRAS/ISSA を用いて作った減光マップである。非常に広い意味では SFD マップは RJCE マップと似ているが、大きな相違がある個所も多い。 |

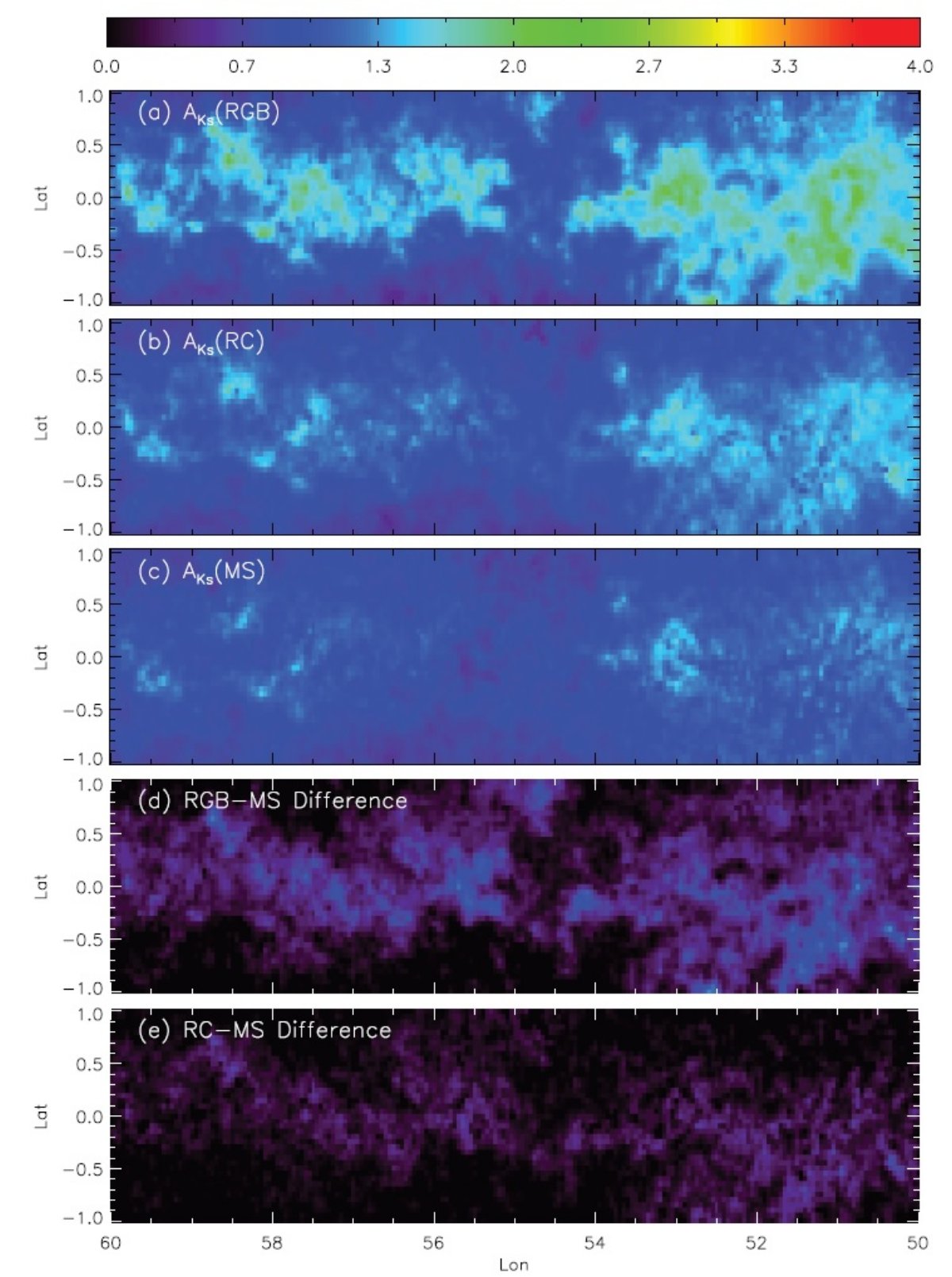
5.1.3次元減光分布星の種類による見通し距離の差3.3.節の2次元マップの比較では RJCE と NICE の差は大してなかった。 RJCE の真の価値は、個別星のスペクトル型と光度クラスを識別する能力にある。 赤化補正した CMD から MS, RC, RGB を分離して、様々な距離の星を探る能力を 示すため、図14では l = 50° - 60° で RGB, RC, MS に分けたそれぞれ のサンプルに対する RJCE A(Ks) マップを示した。3つのマップを比較すると RGB マップは 18 - 20 kpc, RC マップは 8 kpc, MS マップは 3 kpc 距離の星間雲 の構造を表していることが判る。 図14の図の違いの解説 RGB マップで (l, b) = (54.6, 0.8) にある雲は MS, RC マップには現れない。 (59.0, 0.5) の糸状の構造は RGB, RC にはあるが、 MS マップにはない。これは この構造が 3 - 8 kpc にあることを意味する。もっと近い例では (53.7, 0.5) はどれにも載っていて、 3 kpc 以内にあることを示す。 RGB で作った減光マップは銀河面を完全に貫いた減光を与える。 そのあと減光の分散に関してごちゃごちゃかいてあるが面倒くさいので略。必要なとき再読。 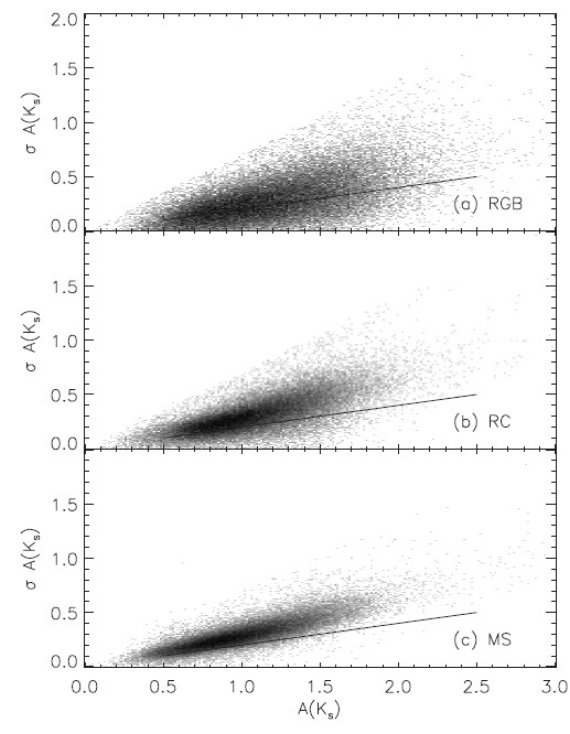 図15.図14の異なる星種族に対する、ピクセル毎の A(Ks) 分散と A(Ks) の関係。上:RGB. 中: RC. 下:MS. 実線=比較用の線 |
5.2.星種族の3次元分布測光視差個々の星の測光視差を得るには固有カラーと光度クラスが必要である。この問題は 論文 III で詳しく扱う。 銀河面の縁 あんまりよく分からない方法でフィットして縁を決めている。 図16にはこうして決めた銀河系の最も遠い星の位置が示されている。l = 45° - 315° ではもっともらしい位置にいる。しかし l = 315° - 45° の 垂直分布は 2MASS の限界等級、または混み合い限界を表している。 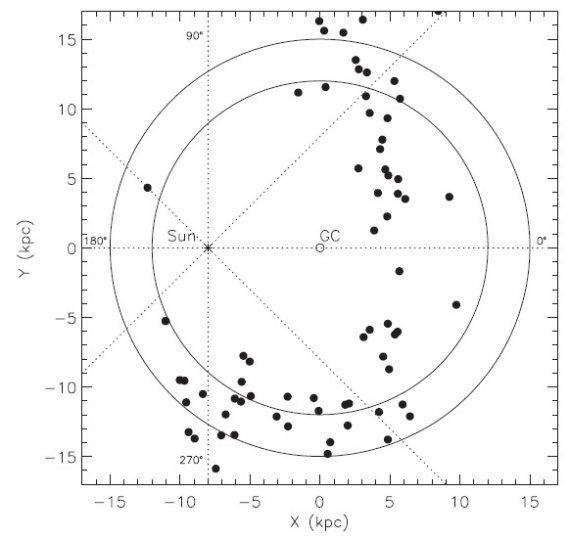 図16.NIR CMD の赤化補正 RGB 分布の下縁に等時線フィット して到達した最大距離。実線は銀河中心距離 = 12, 15 kpc. |