Stellar Populations in the Milky Way Bulge Region: towards Solving the Galactic Bulge and Bar Shapes Using 2MASS Data


Robin, Marshall, Shultheis, Reyle
2012 AA 538, 106 - 119



　アブストラクト

　バルジ領域の銀河系構造は非常に複雑である。バルジの方向は使用する星、 銀経、銀緯に応じて答えが変化する。そこで、ブザンソンモデルを用いた、 バルジ領域のパラメタ―フィットの仕組みを提案する。 　Ferrer の楕円体を用いて、バルジ種族の様々なパラメタ―と形態を探った。 内側円盤の形も同様の手段で調べた。その結果、バルジはボクシー構造で 主軸方向は 13° と分かった。しかし、フィットはより細長くて厚いバー を加えると大幅に改善された。 　第１の楕円体は主要ボクシーバーを表し、厚いバルジ種族は (i) バーの ポテンシャルにより少し平坦化した古典的バルジ、か又は (ii) 厚い円盤 の銀河系中心部対応物、であろう。 　Ferrer 楕円体を用いるとモデルは 2MASS データに対して 10 % レベルで 全バルジ領域のフィットを達成する。しかし、それだけではフタコブの特徴は 再現できない。中間銀緯で現れるフタコブ性はバーに僅かなフレアを加えると 作り出せる。 　種族をより良く特性付けるため、分光サーベイが行われてメタル分布が分か っている領域に対してシミュレイションを行った。 もし主要バーが太陽メタルで、より厚い種族は低メタルであると仮定するなら、 モデルは短軸に沿っての MDF と良く合う。この二つの種族を混ぜると、垂直 方向のメタル勾配も説明できる。 　薄い円盤のスケール長は 2.2 kpc で以前反中心方向で得られた値と一致する。 しかし、薄い円盤には中心部にホールが必要で、その勾配はスケール長 1.3 kpc, 円盤の密度は中心から 2.3 kpc で極大をとる。 　バルジの中心部にさらに新しい種族を発見した。銀経 2° 銀緯 1° で丁度中心分子帯と Alard 中心核バーに対応する。

　１．イントロ　

　２．バルジの種族合成モデル　

　２．１．薄い円盤種族　

　薄い円盤の種族構成　

　薄い円盤は銀河系中心領域では寄与が大きいので、バルジと同時にパラメタ―、 スケール長と中心ホールのサイズを決める必要がある。円盤種族は過去 10 Gyr 星形成率一定、IMF φ(M) = A M-α、α = 1.6 (M < 1 Mo), α = 3.0 (M > 1 Mo) で得られた。円盤種族を７つの 年齢成分に分け、それぞれの絶対等級と有効温度分布を計算した。

　薄い円盤の密度分布　

　各年齢成分は軸比が年齢で異なる回転楕円体で近似される。密度則は二つの 関数の差で以下のように表される。


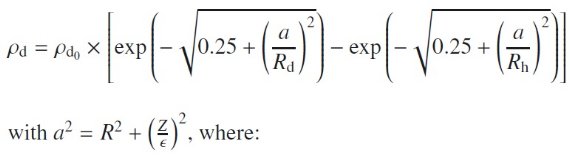
R, Z = 円筒座標
ε = 楕円軸比。値は Robin et al. 2003 を見よ。
Rd = 2.2 - 2.5 kpc = スケール長。
Rh = ホールのスケール高。円盤の密度極大は R = 2 kpc。
ρ,sub>do = 規格密度 = 近傍光度関数から Ro = 8 kpc, Zo = 15 pc を仮定して得た。

　２．２．外側バルジ　

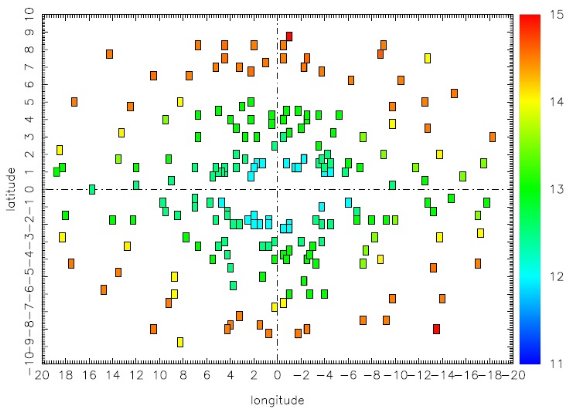
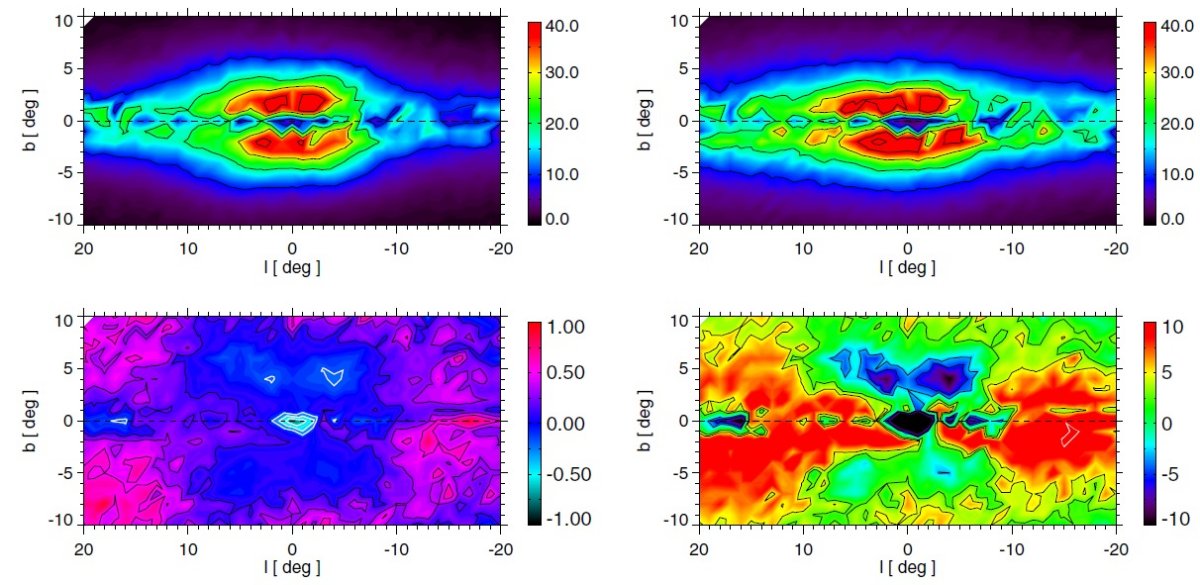
Picaud, Robin 2004 のバルジモデル　

　Picaud, Robin 2004 は DENIS データを使い、外側バルジ 94 箇所 l = [10, -8], b = [-4, 4] での密度分布を解析した。バルジと円盤の 11 次元 パラメタ―モデルをモンテカルロシミュレイションでフィットした。その結果 バルジはボクシー指数関数型またはボクシー sech2 型分布で あることが判った。これは Freudenreich 1998 が DIRBE 輝度分布をフィット した結果と同じである。これは Ferrers 楕円体 (Ferrers 1877) と呼ばれる。 軸の方向角は 10° であった。

　Freudenreich 1998 の S 関数

　 Freudenreich 1998 の S 関数は次のように表される。


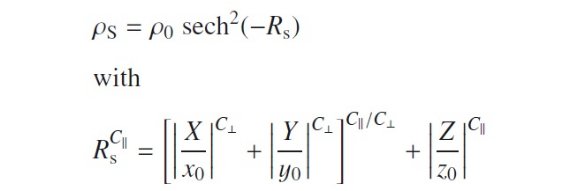
(X, Y, Z) はバルジ軸に沿ったデカルト座標で、 X は主軸、 Y は第２軸、 Z が短軸方向である。パラメタ― c⊥, c|| は ディスキーからボクシーまで様々な形態を表現する。

　他の表現　

　指数関数： ρE = ρ0 exp(-Rs)
　ガウシャン： ρG = ρ0 exp(-Rs2)


　カットオフ関数 fc 　

　密度関数には次にカットオフ関数 fc が掛かる。Rc = カットオフ半径。距離は kpc 単位。


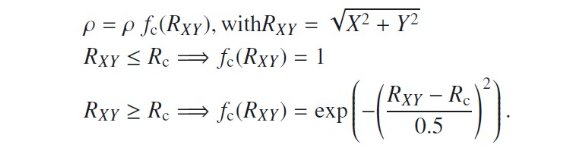
バルジの空間方向を決める次の三つの角度は、
φ = 主軸と銀河中心視線を銀河面に投影した角度
β = 主軸の銀河面に対するピッチ角
γ = 主軸周りの回転角
Picaud, Robin 2004 によると、β はゼロに近く、γ はよく決まら なかった。というのは Y と Z 方向の軸長が近いからである。従ってここでは β = γ = 0 と仮定する。

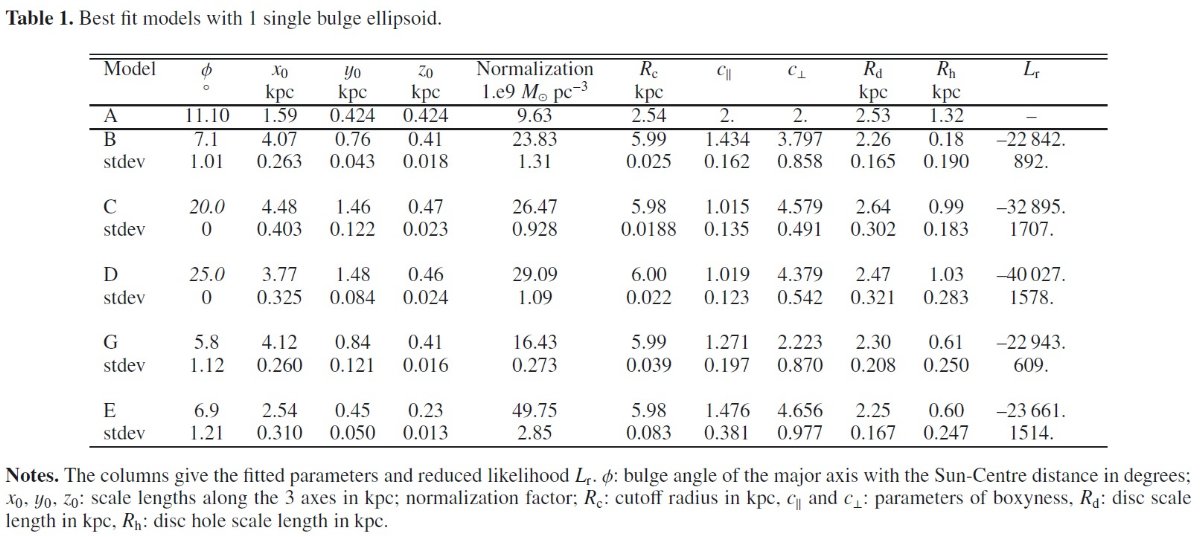
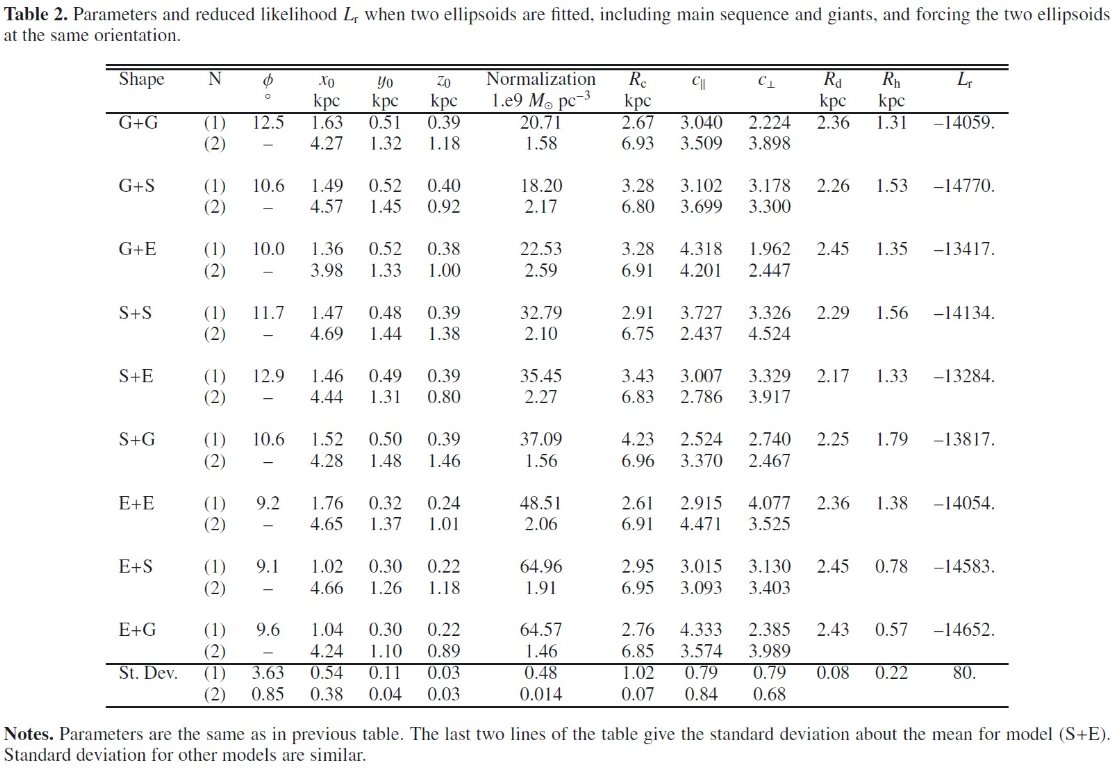
　モデルパラメタ―　

　残ったモデルパラメタ―は、φ, x0, y0, z0, ρ0, Rc, C&perp:, C|| である。

　星種族　

　Bruzual et al 1997 は 10 Gyr, Girardi et al 2002 は 7.94 Gyr (log t = 9.9) を推している。Ks 等級分布は年齢にあまり敏感でないので、ここでは log t =9.9 を採用する。

　３．データ記述と減光補正　

　３．１．2MASS データ　

　Picaud, Robin 2004 の解析は DENIS を使ったので、 l = [8, -12], b = [-4, 4] に限定された。また l = [-1, 1] のデータはあまり使えなかった。 そこで、ここでは 2MASS を使い、 l = [20, -20], b = [-10, 10] 領域を 解析する。データを使用して次の３つの作業を行う。

(i)　 Marshall et al 2006 の方法で減光を決める。

(ii)　選択領域でバルジパラメタ―を決める。

(iii)　バルジ全体でモデルと観測を比較する。

　３．２．減光　

　フィッティングの手順　

　 Marshall et al 2006 はブザンソンモデルからシミュレイトした色等級図を観測と比較して、領域 毎に減光の距離分布を決めた。 		しかし、バルジパラメタ―と減光を同時に決める ことは困難なので逐次近似の方法を採った。
(i)　Picaud, Robin 2004 のバルジモデルで減光分布を決める。
(ii)　その減光でバルジパラメタ―を決める。
(iii) 新しいバルジで決め直した減光が最初とあまり変わらないことを確認。
　"two binned distributions having different total number of elements" に対する χ2 フィット (Press et al 1992) を用いた。 このため、減光の決定はカラーの差に敏感で、観測とモデルの星数の差には 鈍感である。
( 意味不明)

　 Ks < 12 mag に限定　

　この研究では Ks と J-Ks の比較を用いる。Ks と J には完全度のカットを 適用した。さらに、モデルとデータとの比較を Ks < 12 mag に限定した。 その理由は、減光決定法が巨星のカラーに基づいていて、巨星カラーが矮星と 分離するのがこの等級までだからである。

　４．フィッティング手順　

　２００窓の位置　

　l = [20, -20], b = [-10, 10] 内に２００個の窓を設定した。その位置を 図１に示す。窓毎に完全度等級を定め、減光分布を決めた。

　色等級図の区分分け　

　色等級図を J-Ks で二分割、Ks を七分割、合計で１４分割する。尤度関数 は Picaud, Robin 2004 で用いられたのと同じである。モンテカルロシミュ レイションを 20 - 50 回繰り返して安定な極小を探す。

　モデルとデータとの比較　

　フィットしたモデルを l = [20, -20], b = [-10, 10] の 2MASS データ と 比較して、15′×15′ グリッド上 でデータとモデルとの相対差を計算する。目的は二つある。
(i)　バルジ領域全体でモデルが 2MASS データとフィットしているかの確認
(ii)　新モデルから計算した新しい減光と比較するための保存


　単一バルジ種族　

　最初は単一バルジ種族によるフィットを試みた。そこでのパラメタ―は、 φ, x0, y0, z0, Mbulge, Rc, C⊥, C||, hdisk, Rh である。


　第２成分が必要　

　　後に示すようにこのフィットは不十分であった。 第２成分を加え、垂直構造の表式を変えるなどのモデルを試した。ここでは Ghez et al 2008 に従い Ro = 8 kpc を採用する。Picaud, Robin 2004 では Ro = 8.5 kpc で あったことに注意せよ。

図１．フィッティングに使用した　２００個の窓の位置。カラーは限界 Ks 等級を表す。




表１．単成分モデルのパラメタ―

　４．１．単一楕円体によるフィット　

　Pocaud, Robin 2004 と異なる結果　

　単一楕円体を広い領域でフィットした結果は、l = [8, -12], b = [-4, 4] の 100 窓で合わせた Pocaud, Robin 2004 とはかなり異なる結果となった。 領域が広くなり、フィットに矮星も加え、減光をもっと現実的に扱ったことが 差の原因であろう。

　表１のモデルの説明　

　表１に結果を示す。モデルＡは Pocaud, Robin 2004 のフィットである。 その時には C⊥ = C|| = 2 に固定し、Ro = 8.5 kpc であった。フィットの際に固定されたパラメタ―はイタリックで示されている。 モデルＢは軸角度はフリーで垂直方向は sech2 型にした。モデルＣ は sech2 型だが、軸角度を 20° に固定した。モデルＤでは 角度を 25° である。モデルＧはモデルＢと同じく軸角度フリーだが、垂直 方向にガウシャンとした。モデルＥは指数関数型である。

　モデルＡと新しいモデルＢとの差　

　モデルＡと新しいモデルＢとの大きな差はバルジスケール長 x0 が 1.59 kpc (Picaud, Robin2004) から 4.0 kpc に伸びたことである。カット オフ半径も同じく 2.54 kpc から 6 kpc へと伸びた。第２軸のスケール長も 増加したが、第３軸はあまり変わらなかった。円盤とホールのスケール長は 少し減少した。 		モデルとデータの比較　

　図２にはモデルとデータの比較、モデルとデータの差を示す。図のモデルと してはモデルＢを取り上げた。残差分布を見ると、フィットしたバルジモデル の形が不適当であることが明らかである。銀河面付近では密度分布はデータと 良く合っている。しかし、銀河面から離れると X-型の残差が現れてくる。これは モデル密度が不足しているためである。銀河面付近と銀河面から離れた領域と の間でのフィットの調整がうまく行っていない可能性がある。左上図の 2MASS マップの等密度線は箱型であり、モデルでは再現できないことに注意せよ。

　中心核バー　

　残差マップは |l| < 2 に中心核構造が存在することを示す。これは Alard 2001 が発見した中心核バーであろう。この構造はモデルには組み込まれていない。



図２．左上：限界等級 Ks までの 2MASS 星計数。右上：モデル B の星計数。 左下： (Nmod - Nobs)/Nobs 右下： (Nmod - Nobs)/√Nmod. 残差マップでは等高線は、黒＝ 20 % 超過。白＝ 20 % 不足。一成分モデルは Ｘ型の残差を生み出す。中心付近ではモデルが中心核バーを欠いていることが 分かる。外側では差が小さいが星数が小さいためである。

　４．２．他のパラメタ―の影響　

　Ro

　Ro　はフィットからは決めず、 7, 7.5, 8, 8.5 kpc に固定してフィットを 行った。Ro = 8 kpc は大きな尤度を与えるがデータは距離をに対してあまり 鋭敏ではない。その上、Ro の値による C⊥, C|| への影響は小さい。

　年齢　

　バルジは 8 Gyr (log t = 9.9) と仮定した。t > 5 Gyr ではレッドク ランプへの影響は小さい。もしターンオフまで下がると光度関数に年齢の影響 が出るが、 2MASS はそこまで行っていない。若い種族ではターンオフの位置 が少し明るく、巨星枝は少し青くなる。しかし、これらは減光の強い領域での 広帯域測光では ２次的な効果しか持たない。Gyr レベルで種族を限定するには 補助データが必要である。そういう訳で、この研究では Girardi et al 2002 の 8 Gyr 等時線をバルジ種族に適用した。

　４．３．バルジ/バーの角度　

　

　多くのバルジモデルは我々がモデルＢで見出したバー角度 7.1° より 大きな値を得ている。大部分は 11 - 45 の範囲にある。そこで、バルジ角を 20, 25 に固定したモデルで良いフィットが得られるかどうか調べた。 これ等のモデルの尤度は

　

　

　

　

　




表２．２重楕円体でフィットした時のパラメタ―と reduced 尤度 Lr。 主系列星と巨星を含む。二つの楕円体の軸方向は同じとした。

　４．４．２重楕円体でフィット　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．

　　

　

　

　

　

　

　

　

　

　

　

　



図．


( )


Schlegel et al. 1998 先頭へ