The Long Bar in the Milky Way : Corroboration of an Old Hypothesis

　アブストラクト

　１．イントロダクション　

　２．星計数の非対称性　

ロングバー賛成　 　 Lopez-Corredoira et al. 2001 は星計数と負銀緯の減光マップを用いてロングバーの概像を確認した： |b| < 1.5, |l| < 30 では正銀経側が負銀経より多い。この 南北非対称は 　 Benjamin et al. 2005 によって、Galactic Legacy Infrared Mid-Plane Survey Extraordinaire (GLIMPSE) でも確認された。彼らは北側が南側に較べ 25 % 多い天体を 検出したが、その計数範囲には |l| < 10 も含まれていた。 Lopez-Corredoira et al. 2001 はまた、南側（負銀経）で減光が強いことを見出した。 　ロングバー反対　 　Babusiaux, Gilmore 2005 は減光分布に非対称性は見られないと主張した。 しかし、我々の考えでは彼らの測定点の数は少なすぎるし、彼らの l = -10 は Lopez-Corredoira et al. 2001 の図８を見ると極小を有して（？）いる。カラーを用いて、減光の効果を正し く補正して星計数を行うと、 Lopez-Corredoira et al. 2001 の図１０のような、南側銀河の明瞭な像が浮かび出てくる。それには、 Hammersley et al. 2000 が予想したように、l = -13 まで伸びる面内バーが明瞭に示されている。 Unavane, Gilmore 1998, Alard 2001 も星計数の非対称性を調べたが、 |l| < 4 に限られていた。 　2MASS データ　 　図１には 2MASS K < 9, |b| < 0.25° の星計数を示す。図は 明らかな非対称性を示す。この結果を Lopez-Corredoira et al. 2001 の TMGS データと合わせ、ロングバーは実際に存在し、その構造がバルジ 領域 (|l| < 15) を越えて l = 30 まで伸びていることを示した。

図１．2MASS K < 9 mag, |b| < 0.25° の星計数。l = [30, 0] と [0, -30] の非対称性に注目。カウントは l で５度で平均化した。

図２．MSX m(8.7μm) < 6.0, b = [-0.5, 0.5] の Δl = 1 星計数。 正銀経と負銀経の数の非対称を示す。 l = [-15, -18] の星の欠落に注意。 そこはロングバーの仮想的な端点とリングとの間にあたる。 　ＭＳＸデータ　 　図２には MSX にもやはり正銀経側に星計数の超過があることを示す。図は また l = [-15, -18] に星の欠落を示している。これは、負銀経側でのバー 先端が l = -14 にあることを示唆している。l = -22 の超過はおそらく 3 kpc リングによるものであろう。 　リングと星形成域　　 　Freudenreich 1998 は |l| < 30 の星計数超過をリングや腕の所々に起 きる星形成域のためと考えた。Picaud 2004 もリングに伴う星形成域を提唱し た。しかし、 Lopez-Corredoira et al. 2001 の図６に見えるように、リングによる星計数分布は図１と合わない。

図３．2MASS 減光補正等級 me = K - 1.77(H-K) < 7.0, |b| < 0.25 の星計数。 (ここで述べている"リング"は l = -22 の接線でなくて、|l| < 30 全体の超過である。 ) その上、図２ l = [-15, -18] の不足は l = [0, -22] にかけて連続した構造 が存在することを否定する。バーは星計数を完全に説明するが、リングは 失敗する。 (ここは、前段落の l = -22 をリングの 接線という見方まで否定しているのか？どうもはっきりしない。 ) 渦状腕が銀河中心の向こう側(d = 10 - 12 kpc) またはこちら側 (d = 5 kpc) という 解釈は Hammersley et al. 1994 により否定された。 減光　 　減光効果で南北非対称を説明する考えは、 Hammersley et al. 1994 および Lopez-Corredoira et al. 2001 により否定された。その上、減光補正計数は、 Lopez-Corredoira et al. 2001 の図１に示すように非対称をさらに増強したのである。 図３には Benjamin et al. 2005 の GLIMPSE データを用いた Lopez-Corredoira et al 2005 による me < 7.0 の星計数分布を示す。図２の MSX データと同様に GLIMPSE データも 非対称を示している。これらには減光の影響は非常に小さい。

　３．距離指標としてのレッドクランプ　

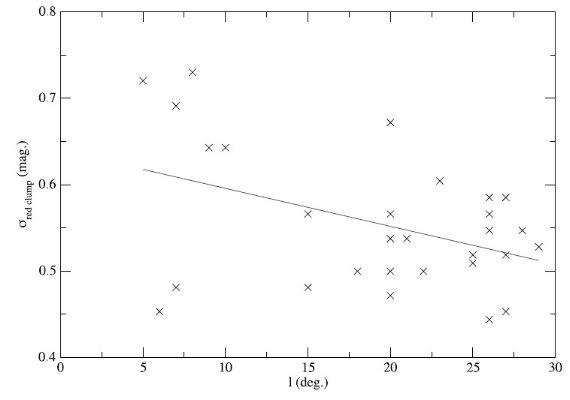
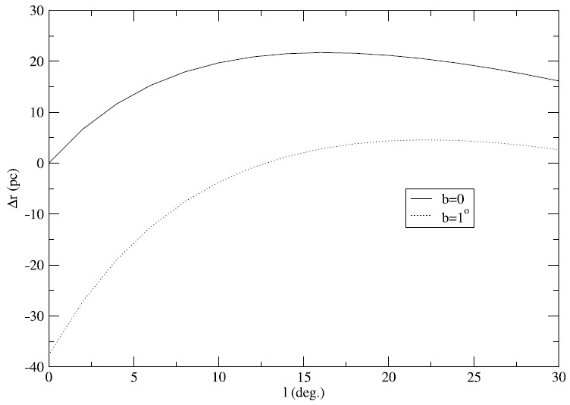
図４．|b| ≤ 1 レッドクランプの巾(Cabrera-Lavers et al 2006)。実線は フィット： y = 0.64 - 0.0044 l. 　視線上の密度極大と主軸とのズレは３軸バルジでは大きい　 　　ある視線方向で作った　CMD でレッドクランプの密度極大はバーの主軸に対応 すると一般には見なされる。それはバーの巾が狭い場合は正しい。狭いバー ではこのズレは 50 pc 程度である。しかし、３軸バルジのように太い場合、 密度極大は視線が等密度楕円体面と接する点になる。それは主軸位置とは 1 kpc も狂い得る。さらに、視線上の密度極大と視線に沿っての等級分布の極大とは 異なる。その差は薄いバーでは 25 - 50 pc 程度であるが、３軸バルジでは 100 - 300 pc となる。付録Ｂを参照。Babusiaux, Gilmore 2005 はこれらの 効果を考慮せずにバルジの主軸を決めており、不正確である。 　ロングバーの観測例を文献から集めた　 　文献から、銀河面上 |b| < 1 の距離を集めて、図５にプロットした。 それらは、 １． Hammersley et al. 2000 (l, b, d) = (0, 27, 5.7). ＣＭＤ法は混み合いで無理。 ２．Picaud et al 2003 (l, b, d) = (0, 26, 27, 5.9). ３．西山その他 2005 (l, b)= ([-10, 10], +1) l = [-4, +4] の位置角が [-10, 10] の位置角と 異なることから新しい構造を提唱。しかし、我々はそれはバルジとロングバー の複合効果と考える。図５には彼らのデータが我々の位置角 40 - 45 と合う ことを示す。 ４．Babusiaux, Gilmore 2005 (l, b) = (0, +1), (±5.7, 0), (±9.7, 0) での距離を レッドクランプ法で決定。l = -9.7 を除き、 φ = 22.5 に合う。l = -9.7 が選ばれたのはバー端末のリングまたは擬リングを含むと考えたからである。 l = +5.7 方向は距離が広く分散している。これはおそらくバーの向こう側の円盤 上レッドクランプを示しているのであろう。我々は図５のプロットから Babusiaux, Gilmore 2005 はロングバーを観測しており、その結果は φ = 40 - 45 と矛盾しないと考える。しかし彼らは、バルジ＋バーはレッドクランプ 距離に大きな距離分散を引き起こすだろうという理由でロングバーの存在を 否定した。しかし、（１）銀河面上ではバーが支配的である、（２）バーと バルジの位置角が近い、（３）分散は実際に存在するが低い、等の別説明が 可能である。

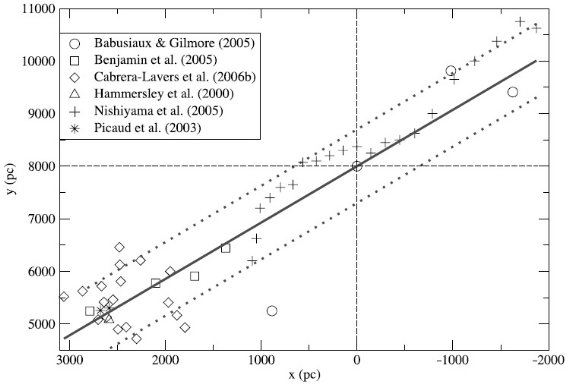
図５．レッドクランプ法により導いたロングバーの位置。銀河中心は (x, y) = (0, 8) kpc. Hammersley et al. 2000 バー、φ = 43、の位置を実線で示す。点線はバーの巾 1.4 kpc を示す。 ５． Benjamin et al. 2005 GLIMPSE データに基づく、彼らの図４から、彼らが用いた Ro = 8.5 kpc の代わりに 8.0 kpc を用いて等価距離（？）を計算した。 Ro = 8 kpc では M4.5 = -2.02, Ro = 8.5 kpc では M4.5 = -2.15 となる。これは、バーが銀河中心 Ro を通過する と仮定して、バーレッドクランプの絶対等級を GLIMPSE データから決めると いう構成だからである。前景減光には 0.05 mag/kpc を仮定した。 l = +12 から +28 まで Δl = 4 で観測した。 l = +24 は減光が高く、 レッドクランプのコブが見えない。これら GLIMPSE データを解析した Benjamin et al. 2005 によると、彼らの図２に示されるように、 |l| ≤ 30 には円盤の上に重なる コブ構造が見える。彼らはそれをロングバーのレッドクランプ星によるものと 解釈した。彼らが得た位置角は 44 ±10 である。彼らの図１は明瞭に 面内 l = [+30, -14] に構造が存在することを示している。 ６．Cabrera-Lavers et al 2006 新たな l = [18, 28], b = [-1, +1] データを加えた。 集めたデータ点は φ = 43±7 に合う　 　図５は上のデータが Hammersley et al. 2000 バー　φ = 43±7 によく合致するかを示している。データ点のエラー バーは、 l = 27, d = 5.7 kpc で 0.7 kpc である。文献の多くではもっと 小さなエラーを付けているが、我々の考えではそれは楽観的すぎる。しかし、 多くの点が点線の範囲内に入る。ｌ= +9.7, (x, y) = (887, 5247) pc は大き く外れているが、バルジの混入かも知れない。この点は Babusiaux, Gilmore 2005 によって、バーの位置角が 22.5 であると主張する根拠となった。しかし、 他の全てのデータを見渡すと、逆にこの点を捨てるべきであると思われる。 　昔の評価値　 　Peters 1975 は HI 分布を φ = 45 モデルで説明した。Weinberg 1992 は太陽円内での IRAS AGB 星分布を調べ、バーの位置角 36±10, 長軸 半径 5 kpc という値を出した。Sevenster et al 1999 は面内構造を調べて 位置角 45 を出した。彼らは３軸バルジを面から離れた銀緯でのみ検出した。 Van Loon et al 2003 は R > 1 kpc にロングバーを検出し、φ = 40 とした。Groenewegen, Blommaert 2005 は |l| < 12, b = [-5.8, -1.2] のミラ型星から φ = 47 ±17 とした。しかし、これはロングバー とバルジが混ざっているかも知れない。

　４．バーの他のパラメタ―　

バーのパラメタ―をまとめると　 　表１にバーのパラメタ―をまとめた。半軸長 3.9 kpc はバーの端点が l = 27 にあり、バーの角度が 43°, Ro = 8 kpc から出した。バーの巾はレッド クランプ星の散布度が 0.5 - 0.6 mag （ Hammersley et al. 2000, Benjamin et al. 2005, Cabrera-Lavers et al 2006) から導いた。特に |b| < 1° データ のフィット（Cabrera-Lavers et al 2006) は 　　　　　σRC = (0.640±0.037) - (0.0044±0.018) l mag. を与える。 　バーの巾はこう計算した　 　レッドクランプの固有散布度を 0.3±0.1 mag ( Lopez-Corredoira et al. 2002 ) とし、|b| ≤ 1 では視線に沿って高度変化は無視できるとする。 α = 視線方向 (l) とバーに垂直な線とのなす角 　　　= 90 - 43 - l 視線方向の厚みには cos α を掛ける必要がある。また、バーまでの距離 r(l) = Ro sin 43 /sin(43 + l) 以上をまとめると、 r=10**0.2[m-Mo-5], Δr/r = 0.2 ln10 Δm, σbar = r 0.2 ln10 sqrt(σbar2-0.32) cos α どういう計算をしてか、多分上の式を l = 0 の周りで展開してだろう。 　　　　　&sigma:bar = 1420±179 - (12.6±5.6) l pc ここに &sigma:bar はバーの巾である。垂直方向の厚みは Cabrera-Lavers et al 2006 のレッドクランプデータから 200 pc (スケール高 としては 100 pc)と決まった。 　バーの密度出す式はこれ　 　mK < 9 の超過星計数は ∼ ω[Δr(l)]r(l)2φ[MK<9 - 5log r(l) + 5 -AK(r(l),l)]⟨ρ⟩ で与えられる。図１を見ると、この超過計数は約、 1000 deg-2 で l にあまり依存しない。 Δr(l) = σbar/sin(43+l) で、ここに σbar はバーの巾である。AK(r(l),l) = 1.2 Lopez-Corredoira et al. 2001 ) とする。 　l = 20 での密度計算例　 　l = 20 では 視線と軸の角度が 43 + 20 = 63 だから、r(l) = Ro sin(43)/sin(63) = 8x0.68/0.89 = 6.1 kpc となる。星計数限界 K = 9 mag に対応する絶対等級は

表１．ロングバーのパラメタ― 　　　　　MK, max = 9 - 5 log r(l) + 5 - AK(r(l), l) 　　　　　　　　 = 9 - 5 log(6100) + 5 - 1.2 = -6.1 従って、前段落の式に代入すると、 　　　　　1000 = (π/180)2x[1170/sin(63)]x(6100)2x φ(MK < -6.1)ρ 　　　　　φ(MK < -6.1)ρ = (1000/1170) (180/3.14/6100)2 　　　　　　　　　　　　　　　　= 7 10-5 stars pc-3 バーの星総数は？　 　バーを 8x1x0.2 kpc3 の箱と考えると、星の総数は 1.6x109x7x10-5 = 1.1 105 星。 ( 論文では 2 105 星) Lopez-Corredoira et al. 2000 ) によるとこの明るさまでの星はバルジ全体で、600,000 個である。 　ロングバーの質量は？　 　簡単に言うと、ロングバーはバルジの　1/3 である。バルジ光度関数を使うと この光度までの星の数は全体の 2 × 10-5 である。 この値を適用すると、先に計算したバーの星数密度は 3.5 stars pc-3 Sevenster et al 1999 はバルジの総質量を 1.7 1010 Mo と見 積もった。その 1/3 とすると、ロングバーの総質量は 6 109 Mo 程度になる。 　バーの回転は？　 　バーの回転速度はまだ測られていない。将来の RAVE 観測が期待される。

　５．バルジの混入　

　６．結論　

　付録Ａ：３軸バルジの視線方向最高密度点と軸との交点との差　

座標系　 (r, l, b) ＝　銀河系座標 (x, y, z) ＝　銀河中心デカルト座標系。ｙ軸は太陽からGC方向 (x1, y1, z1) ＝　銀河中心デカルト座標系。 バルジの軸。 座標系変換　 　x1 = x sin α - y cos α 　y1 = x cos α + y sin α 　z1 = z 　x = r sin l cos b 　y = r cos l cis b - Ro 　z = r sin b 　楕円体面＝等密度面　　 　t2 = x12 + (y1/A)2 + (z1/B)2 　視線上の密度最大点　 rm = 視線上の密度最大点 ra = 視線と主軸との交点 Δr = rm - ra rm は視線上で t が極小となる点で定義されるから、 　　　　　(∂t/∂r) = 0 　　at r = rm 書き下すと、 x1(rm) ∂x1 | + y1(rm) ∂y1 | + z1(rm) ∂z1 | = 0 ∂r rm A2 ∂r rm B2 ∂r rm この式を解くと、 rm = Ro [ cos α + tan(l+α) sin α ] cos b A2 × [ cos(l+α) + sin(l+α) tan(l+α) A2 + ( tan b ) 2 1 ] -1 B cos(l+α) 一方、主軸との交点は、 ra = Ro sin α cos b sin(l+α) Δr はロングバーの場合 50 pc 以下で無視できる。しかし、３軸バルジの ように膨らむとこの差は考慮しなくてはいけない。

図６．密度最高点位置の説明図。四角＝視線に沿っての密度最高点。 丸＝視線が主軸を横切る点。

　付録Ｂ：　視線に沿った密度極大と等級星計数極大との差　

視線に沿った等級 m 分布の極大は密度極大とは違う。視野の立体角を ω とし、絶対等級 M = 一定の星のカウントを考える。 　　　　　A(m) dm = ω r2 ρ(r) dr　 　　　　　r = 10[m - M + 5 - E(r)]/5 dA/dm ω=1, ρ(r)=n とする。 A= r2n(dr/dm) dA/dm = [2rn+r2(dn/dm)](dr/dm)+r2n(dr/dm) (d2r/dm2) m = M + 5 log r -5 + E dm/dr = (5/ln10)(1/r) + dE/dr=(5/ln10)(1/r) + a(r) A(m)[(5/ln10)(1/r) + a(r)] = r2n(r) A(m) =n(r) r3/[(5/ln10) + r a(r)]　 (dA/dm)(dm/dr)=(dn/dr)r3/[(5/ln10) + r a(r)] +n(r) 3r2/[(5/ln10) + r a(r)] -n(r) r3[a(r)+r(da/dr)]/[(5/ln10) + r a(r)]2 =(dn/dr)r3/[(5/ln10) + r a(r)] +n(r) {[3(5/ln10)/r + 3 a(r)]-[a(r)+r(da/dr)]} r3/[(5/ln10) + r a(r)]2 =(dn/dr)r3/[(5/ln10) + r a(r)] +n(r) [3(5/ln10)/r + 2 a(r)-r(da/dr)] r3/[(5/ln10) + r a(r)]2 　 　計算ギブアップ 論文の方の結果は Δrm = 3ρ(rm) rmρ″(rm)

図７．視線に沿った等級 m 分布の極大と密度極大点との差。例は３軸比 1:0.11:0.04の楕円体。位置角＝43°.