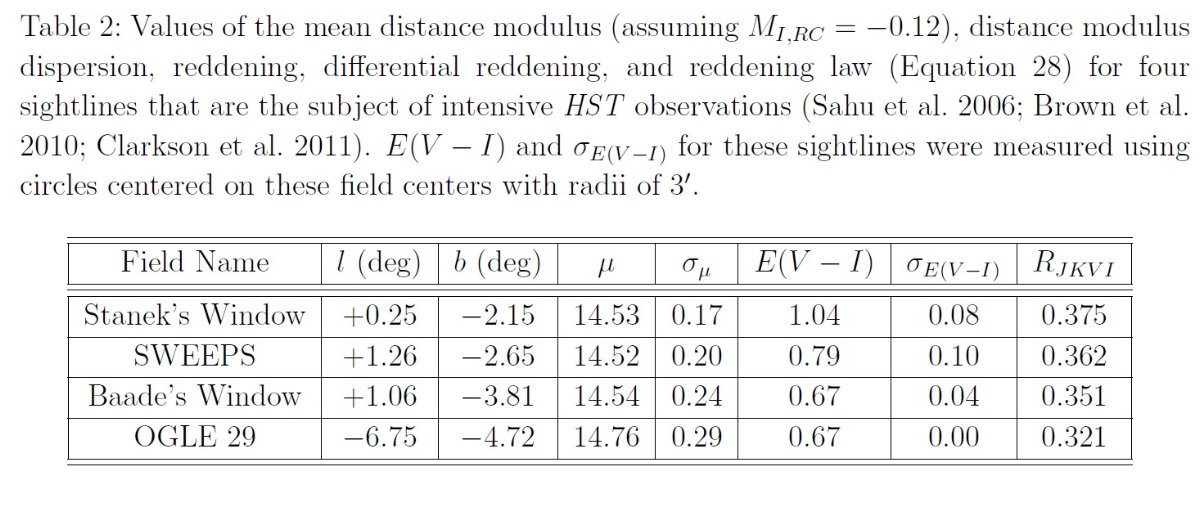
|
バルジ減光則 OGLE-III with VVV と 2MASS データの E(J-Ks) を結合して、長らく問題だった 銀河バルジ方向の非標準的可視域減光則の問題を解決した。減光は次の式でよく 表せる:AI = 0.7465E(V-I) + 1.3700E(J-Ks), または同等だが、 AI = 1.217 E(V-I)(1 + 1.126(E(J-Ks)/E(V-I) - 0.3433))。 内側銀河の可視と近赤外の減光則は Rv = 2.5 ±0.2 に従う。この値は タイプ Ia SN の起きた銀河での結果に一致する。我々の用いたフィールドの大きさ 6' という細かさでも場所による赤化の違いが検出された。 |
レッドクランプ バルジレッドクランプの固有パラメタ―は以下の通りに決まった: (MI,RC, σ(I)RC, (V-I)RC, σ(V-I)RC, (J-Ks)RC) = (-0.12, 0.09, 1.06, 0.121, 0.66) この値から、バルジ構造のパラメタ―を決めることが できた。われわれは銀河中心距離を 8.2 kpc と定めた。この結果、以前に 存在した I バンド観測から定めたバルジ距離の矛盾が解消した。軸の傾き 角度の上限 α = 40 deg である。見かけ等級のピークは N 体計算 からの予想値 25 deg と矛盾しない。RC星の数はバルジ星総質量として 2.0 × 1010 を示す。 |
|
内側銀河方向の減光則 バルジ RR Lyr (Stutz et al 1999), RC(Paczynski et al 1999) のカラーが 異常であることの説明として、 Popowski 2000 は内側銀河方向の減光則は 非標準的であると言った。Gould et al 2001, Udalski 2003 は内側銀河方向の R が小さいこと、つまりその方向では減光曲線の勾配が急で、小さなダスト サイズを示唆することを示した。Udalski 2003 は dAI/dE(V-I) = 1.1 (本論文では ΔAI/ΔE(V-I) と表記)をいくつかの バルジ領域で得た。この値は R = 3.1 から決まる dAI/dE(V-I) = 1.45 よりずっと小さい。Udalski 2003 はまた同じ 観測装置で求めた LMC では dAI/dE(V-I) = 1.44 となることを示した。 その上、バルジ内では視線方向により dAI/dE(V-I) が 0.94 から 1.16 まで急速に大きく変化することも分かった。減光則の勾配が内側銀河で急 であることは HST の観測(Revnivtsev et al 2010), OGLE-III による RR Lyr (Pietrukowicz et al 2012), NIR(Nishiyama et al 2008, Gosling et al 2009, Schodel et al 2010) などでも確認された。一方、Zasowsli et al 2009, Fritz et al 2011 は減光則が MIR で浅い(灰色)ことを見出した。 銀河中心距離 減光強度と減光則の双方が視線方向によって変化することはバルジの構造を調べる 際の大きな障害である(Majaess 2010)。Sumi 2004 はバルジの V-I 色等級図から VI 減光マップを作り、銀河中心距離を 9 kpc とした。これは幾何学的に求められた 7.94(Eisenhauer et al 2003, 8.27(Schonrich 2012, 8.4(Ghez et al 2008) に 比べると大きな値である。 |
我々の方法 われわれは OGLE-III V, I データと 2MASS から E(J-Ks) Gonzalez et al 2012 を 調べた。その結果、VI減光が内側銀河系で急勾配であることを再確認した。ただし、 その大きさは以前求められたほどではない。これは我々が「合成減光バイアス」と 名づけた効果によるものと考えられる。これを考慮すると dAI/dE(V-I) を E(V-I) = 0 まで外挿することは物理的に正しくない。我々の パラメタ―表式、AI = 0.7465E(V-I) + 1.3700E(J-Ks) は dAI/dE(V-I) の勾配を計算する方法に比べ、減光則の急激な 変動に対してより安定である。後者は 30'× 30' の大きな領域を必要とするが、 前者では 6' × 6' という小さな領域ごとに減光を決められる。 論文の構成 第2章:データの記述 第3章:RC パラメタ―の決定法 第4章:RC 固有光度 第5章:標準減光則から期待される赤化 第6章:赤化の測定 第7章:赤化から減光強度への変換 第8章:減光則の導出 第9章:MACHO データの解釈が間違えであること 第10章:銀河系中心距離 = 8.2 kpc バーの傾き = 41 deg 第11章:RC 星の計数 第12章:バルジ質量 M = 2.0 × 1010 Mo 第13章:データ構造 第14章:議論 |

観測はラスカンパナス 1.3 m ワルシャワ望遠鏡の 2Kx4k 8 CCD による 0.6°
×0.6° 視野の 263/267 OGLE-III フィールドから成る。
3.レッドクランプの測定視線方向2k x 4k CCD 画面、総計 8 x 263 = 2104、 を星密度に応じて 1, 2, 3, 6, 8, 10, 15, 21 に分割して 9,744 視線方向とした。実際には 9,014 方向を使用した。 各視線方向は平均して 6'×6' 角である。球状星団カタログ: http://gclusters.altervista.org/index.php にある星団(一つか複数か不明) の 7' または 3 ×半中心輝度半径 以内を省いたからである。測光の完全性は (V-I)RC ≤ 3.30 かつ IRC ≤ 17.70 で確認されている。 またこの領域には赤化変動が激しいというフラグや他の問題を示すフラグは立っていない。 RC 選択ボックス 図3の RC 選択ボックスは典型的には以下のように定義される: -0.30 < (V-I) - (V-I)RC -1.5 < I-IRC < 1.5 前景星は RC 等級では 0.6 mag 青く、RC の 2 mag 下で バルジ RGB に重なって くる(kiraga et al 1997)。 3.1.レッドクランプの平均等級、分散Paczynski, Stanek 1998 の光度関数 Paczynski, Stanek 1998 は RC の光度関数を次の形で表した。
この表式のフィットは σRC が大きい時に、逐次近似が発散して 非物理的な大きな σRC と負の RGB を出すことが知られている。 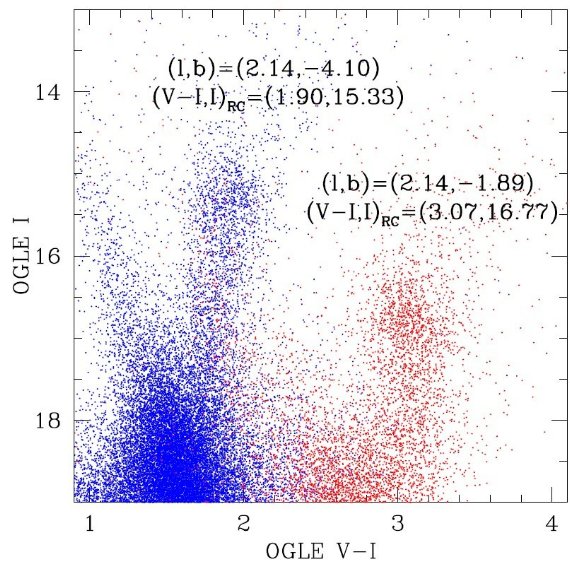 図2.赤: (l, b) = (2.14°, -1.80°)、青: (l, b) = (2.14°, -4.10°) 赤は青に比べ 1.17 mag. 赤く、1.44 mag. 暗いことが分かる。したがってカラー領域は 前景星とかぶらないよう視線方向毎に調整される。 |
Nataf et al 2011 の修正 そこで Nataf et al 2011 では、二次式を指数関数へ修正し、自由パラメタ― 数を3から2に減らしてフィットの安定化を図った。これはモデル計算の予想 (Castellani et al 1989) とも合っていて物理的にも意味のある近似である。 さらに red giant branch bump (RB) と Asymptotic giant branch bump (AB) も加えた。
ここに パラメタ-間には以下の関係を仮定した。 NRB = 0.201 NRC NAB = 0.028 NRC IRB = IRC + 0.737 IAB = IRC - 1.07 σRB = σAB = σRC ここにさらに ∫N(I)dI が一定という条件を加え、4つのパラメタ―、 IRC, σRC, B, NRC/A をフィットして決める。 図2と図3 図2には対照的な二つの CMD を、図3には典型的な CMD と、RC 選択ボックス、 光度関数とそのフィットを示した。 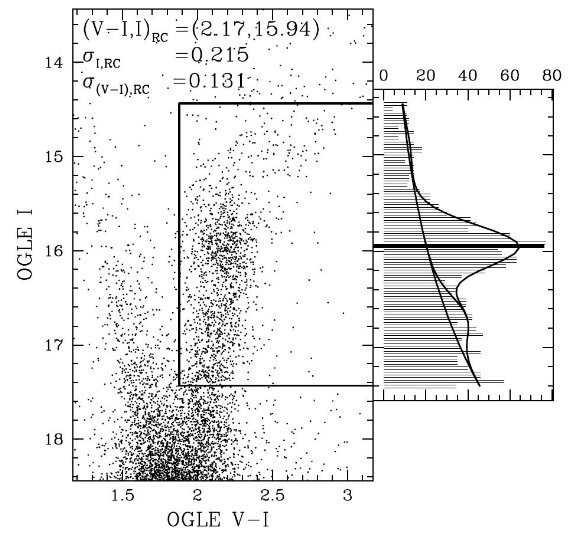 図3. 左:(l, b) = (-2.29°, -3.12°) 方向のCMD. 黒枠内が RC 選択域。右:選択域の光度関数。 |
3.2.レッドクランプの(V−I)カラーとカラー分散レッドクランプのカラーは当初 Nataf et al 2010 で測られた (V-I)RC 92,000 個を使っていたが、本論文では若干の修正を加えた。我々はまず古い値で出発し、 前節のフィット式で各視線方向毎にレッドクランプの平均 I 等級を定める。この値を 用いて、二つのカラーを得る。一つはレッドクランプカラー、もう一つは通常レッド クランプより 0.6 mag 青い円盤前景星のカラーである。それらは図2、3で容易に 見分けられる。色等級図上のすべての星は、どちらのカラーにより近いかによって 二分される。二つのカラーは星のカラーと近い方のカラーとの差の重み付き分散が 最少になるという条件で決まる。ここに重みは、Wi = RC/(RGB+RC)
RGB = A exp[B(I-IRC)] である。 3.3.レッドクランプの(J - Ks)カラーVVV サーベイGonzalez et al 2012 は -10 ≤ l ≤ +10.2, -10 ≤ b ≤ +5 で s¥Saito et al 2012 の VVV サーベイを用いて、 (J-Ks)RC を 測った。これらの結果は本論文で用いられ、OGLE-III の主領域をカバーしている。 2MASS サーベイ 残りの部分は 2MASS サーベイの結果を使用した。2MASS の限界等級は RC より上である。 その明るい RGB 星に対して、 (I-J), (I-Ks) = a + b [(V-I)RGB-(V-I)RC] で近似する。この二式の差は RC 星の (V-I) カラーにおける、 R GBR 星の (J-Ks) カラーを与える。この方法は Bennett et al 2010, Gould et al 2009 が開発した。 |
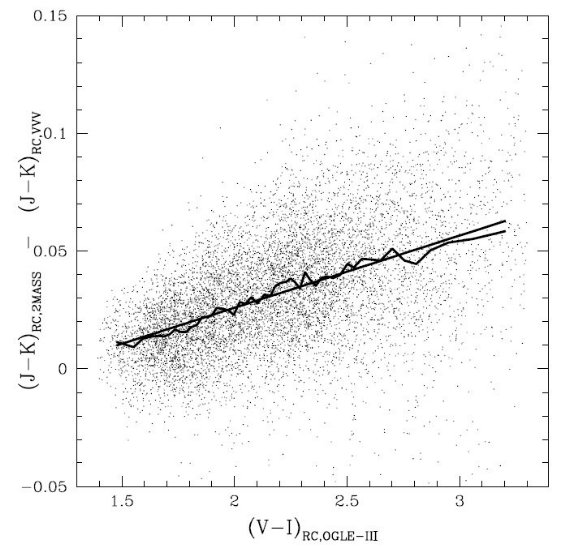 図4.2MASS と VVV 測光(Gonzalez et al 2012) との (J-Ks) カラーの差。 直線:(J-Ks)RC,2MASS-(J-Ks)RC,VVV=-0.035 + 0.031 (V-I)RC,OGLE-III。折れ線:ビンの中間値をつなぐ線。 |
4.1.重力レンズ効果を用いた (V-I)RC高倍率の重力レンズ効果を受けたバルジ主系列星、準巨星の分光観測から 組成と温度が決定された。これらの星の固有 (V-I) カラーが組成と温度、 それに観測的な [Fe/H] - カラー - Teff 関係 (Casagrande et al 2010) から 決まる。この固有カラーを観測から―と合わせ、赤化が決まる。この赤化が RC セントロイドの赤化と同じという仮定から、Bensby et al 2011 は(V-I)RC,0 = 1.06 を導いた。 4.2.47 Tuc と NGC 6791 からの (V-I)RC,0 MI,RC47 Tuc47 Tuc の HST F606W, F814W 測光を V, I に変換して、RC ボックス 546 星のデータを得た。その結果、 [(V-I)RC, IRC, σI,RC]47 Tuc =(0.913, 13.090, 0.062) を得た。 Thompson et al 2010 は食連星の観測から (m-M)V=13.35±0.08 を得た。E(B-V)=0.04 と標準減光則から [(V-I)RC,0, MI,RC, σI,RC,0]47 Tuc =(0.861, -0.208, 0.062) となる。星団メタル量には [Fe/H] = -0.76 を採用した。 NGC 6791 Stetson et al 2003 の測光カタログは Brogaad et al 2012 のために微分赤化の補正を 施されている。RC ボックスには 22 個の星が含まれている。そこから、 [(V-I)RC, IRC, σI,RC]NGC6791 =(1.326, 13.243, 0.050) を得た。Brogaad et al 2012 は3つの食連星を測り、E(V-I)=0.174, (m-M)V=13.51±0.06, [Fe/H]=+0.29 を得た。ここから我々は [(V-I)RC,0, MI,RC, σI,RC,0]NGC6791 =(1.152, -0.093, 0.050) を得た。 メタル効果の内挿式 上の二つを内挿して、以下の式を得た。 (V-I)RC,0 = 1.09 + 0.277([Fe/H]-0.005) MI,RC = -0.12 + 0.110([Fe/H]-0.005) バルジ RC 星は平均メタル量 ⟨[Fe/H]⟩ = +0.05 (Hill et al 2011) であり HB形態、年齢、α増加、ヘリウム、連星の効果を無視した場合、バルジ RC は (V-I)RC,0=1.09, MI,RC=-0.12 を意味する。 |
4.3.恒星モデル、ヒッパルコス、分光から求めた (V-I)RC,0, MI,RCGirardi,Salaris 2001, Salaris,Girardi 2002 のモデルGirardi,Salaris 2001, Salaris,Girardi 2002 は恒星種族パラメタ―を色々に 変えて、水平枝モデルのグリッドを作った。銀河系バルジに関しては、彼らは McWilliam, Rich 1994 の [Fe/H]=-0.22, [α/H]=+0.35 を採用し、年齢 の幅を 8 - 12 Gyr とした。これから彼らはバルジ RC は太陽近傍の RC に比べ、 (V-I) で 0.06 mag 赤く、0.01 mag 暗いとした。そして太陽近傍 RC はヒッパルコス の距離を用いて較正された。 新しいパラメタ―での RC モデル Hill et al 2011 は 219 のバルジ RC + RGB 星の分光組成を導いた。その結果は [Fe/H] = +0.05, [Mg/H] = +0.15 (Mg は α 元素の代表と考える。) [Fe/H] が +0.27 dex 増加し、[α/H] のシフトが半分にとどまった結果、バルジ RC は太陽 近傍 RC に比べ、 (V-I) で 0.20 mag 赤く、 I 等級で 0.10 mag 暗いことになった。 ヒッパルコス RC 星は Paczynski,Stanek 1998 によると、(V-I)RC,0 = 1.01, Groenewegen 2008 は MI,RC = -0.22±0.03 を得ている。両者を合わせると、 (V-I)RC,0=1.21, MI,RC=-0.12 モデルから得られるカラーが観測的に得られた値に比べ、なぜこんなに赤く なるのかは不明である。これは 4.1.に述べた Bensby et al 2011 と 4.3.で使った Hill et al 2011 とで異なる視線方向のため平均メタル量 に差が生じたのかも知れない。モデルが原因の可能性もある。 4.4.レッドクランプパラメタ―への種族不定性の影響レッドクランプの種族効果はどのくらいだろうか?それを調べるため、 Pietrinferni et al 2004, 2006 の BaSTI 恒星データベースを用いた。 合成水平枝を使って、メタル量、年齢、マスロス率を変えて計算した。 モデルが ΔY/ΔZ = 1.4 と仮定しているので、ヘリウム量は メタル量と結びついている。ヘリウムの効果だけを取り出すにはもっと間隔の 粗いモデルに頼ることになる。その結果MI,RC ∝ +0.20[Fe/H] + 0.015(t/Gyr) - 0.029(100Y-100Tss) +0.06(δΔM/0.1Mo) (9) (V-I)RC,0 ∝ 0.27[Fe/H] - 0.013(100Y-100Tss) (10) ここに Yss = scaled-solar helium abundance at metallicity [Fe/H] δΔM = BaSTI データベースに比べてのマスロス 式(10)に含まれる独立変数が式(9) に比べて少ないのことが不思議かも知れない: メタル量が十分に高いと、 RC 星のカラーは星の総質量にはあまり依存しなくなり、 その結果マスロスにも年齢にも影響されなくなるのである。 |
4.5.恒星モデルからの σI,RC.0 と分光メタル量分布σI,RC.0 = 距離指数の分散、 σA(I) = 減光の分散、σμ = 距離、微分減光効果がない場合の RC 等級の固有分散、 σ2I,RC,0 = σ2I,RC - σ2μ - σ2A(I) Nataf,Udalski 2011 は σI,RC.0 = 0.17 とした。しかし、 その時点では 6'×6' という小さいスケールでも微分減光が 0.10 を越える 場合があることが理解されていなかった。これまでに得られた値は (1)Girardi,Salaris 2001: McWilliam,Rich 1994 のメタル量分布、 8 Gyr ≤ t ≤ 12 Gyr で一定の星形成率を仮定して、恒星進化グリッドから σI,RC.0 = 0.107 mag (2)我々は BaSTI 恒星データベースの HB 計算を用い、古い高メタル種族に対し σI,RC.0 = 0.031 mag を得た。さらに Hill et al 2011 が 得たバルジ星のメタル分散 0.40 dex と、 BaSTI から求めた dMI/d[Fe/H] = 0.20 mag/dex から σI,RC.0 = 0.086 mag (3) 4.2.節で単純な古い高メタル種族に対し、 σI,RC.0 = 0.055 mag、 dMI/d[Fe/H] = 0.11 mag/dexを得た。この値を使うと σI,RC.0 = 0.071 mag 本論文ではこれらの平均 σI,RC.0 = 0.09 mag を用いる。 |
4.6. Red Giant Color-Color Relation から (J-Ks)RC.0 = 0.66Bessell,Brett 1988 には RG カラーの観測が載っている。ここから、Ks = K + 0.1×(H-K) で Ks を得て、彼らの表III(巨星のスペクトル型と固有カラー) 第5,6列から (J-Ks)0 = 0.620 + 0.625×[(V-I)0 - 1.00] を得る。この関係式に Bensby et al 2011 の(V-I)0 = 1.06 を組み合わせて (J-Ks)0 = 0.66 を得る。 この次に別の方法で同じ値を出す議論があるが、理解できないので省略。 |
|
Rv = Av/E(B-V) Cardelli et al 1989 はそれまでのデータをまとめて 0.125 μm ≤ λ ≤ 3.5 μm の減光則が一つの 量 Rv = Av/E(B-V) でパラメタ―化できることを示した。O'Donnell 1994 はデータを追加してこの結果を確認した。 有効波長 我々は V 0.546 μm, I 0.804 μm の有効波長を得た。 Gonzalez et al 2012, Indebetouw et al 2005 に従い J 1.240 μm, Ks 2.164 μm とした。 |
RI Schultz, Wiemer 1975, Sneden et al 1978 の標準 Rv = 3.1 を採用して Cardelli et al 1989 の減光則で計算すると、 RI = AI/E(V-I) = 1.481, RJKVI = E(J-Ks)/E(V-I) = 0.407 となる。一方、 O'Donnell 1994 のパラメタ―を使うと AI/E(V-I) = 1.424, RJKVI = 0.416 である。ここでは 平均をとって RI = 1.45, RJKVI = 0.41 を標準値とする。 |
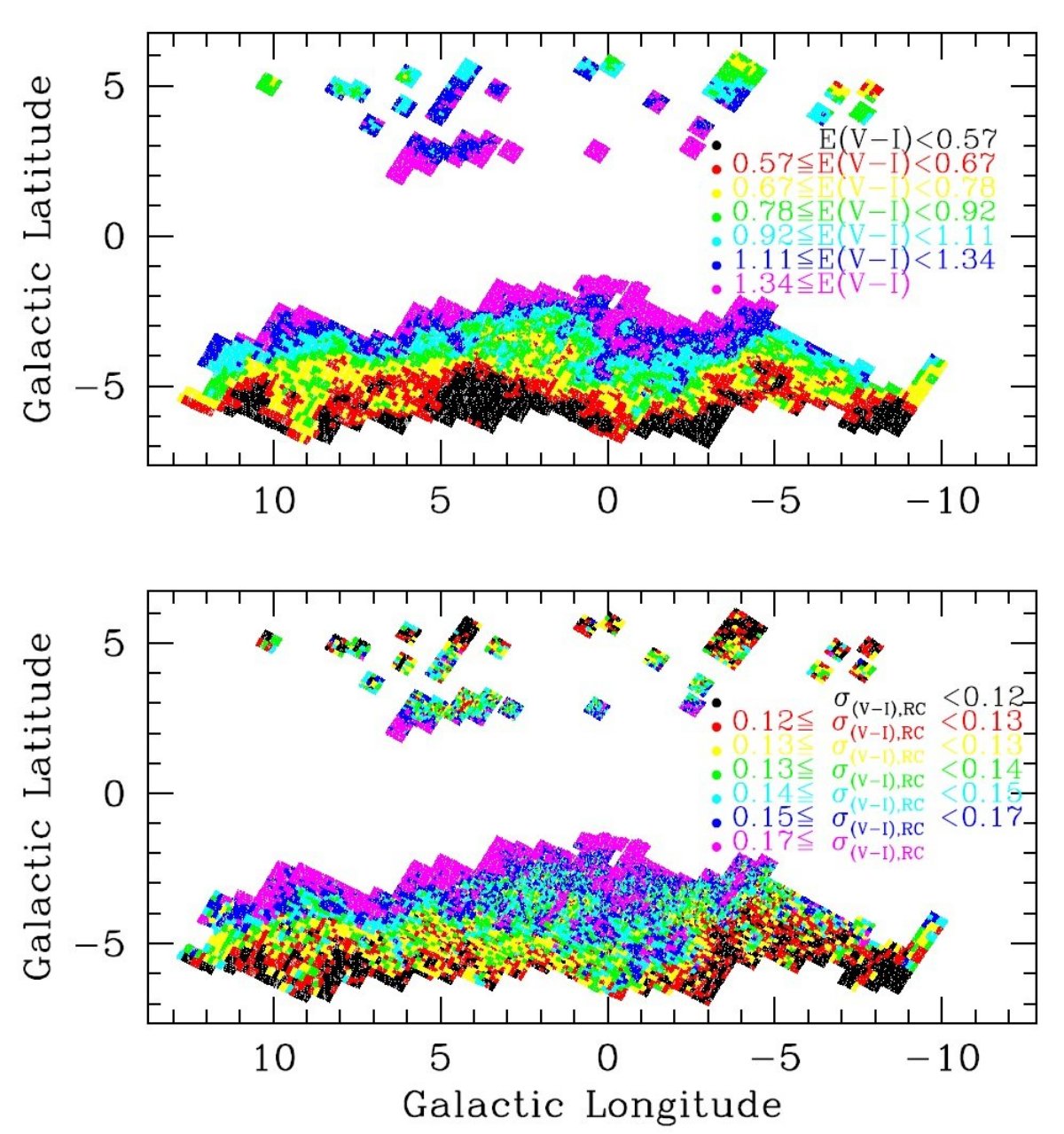
6.1.微分赤化のスケールE(V−I)E(V-I) = (V-I)RC - (V-I)RC,0 = (V-I)RC - 1.06 9014 視線方向での E(V-I) の分布を図5の上パネルに示した。 カラー分散 RC 光度における RG+RC のカラー分散 σ(V-I),RC を以下の式で定めた。 σ2(V-I),RC = σ2(V-I),RC,0 + σ2E(V-I) σ(V-I),RC の分布は E(B-V) とよく似ている。そこで、 以下の式を仮定した: σ2(V-I),RC = σ2(V-I),RC,0
|
ここに、ΔΩは視線方向が張る立体角、
CDR1 は減光量と減光分散との間の比例係数、
CDR2 は立体角による減光分散依存性を示すパラメタ―
である。 我々の得た値は、 σ(V-I),RC,0 = 0.121, CDR1 = 0.070, CDR2 = 0.017 であった。立体角の平均は 0.011 deg2 である。この結果は数 arcmin より小さいスケールで大きな微分赤化が生じていること を示す。 CDR1 と CDR2 の和は総赤化の 9 % が 微分赤化によることを示す。 |
6.2. 内側銀河系方向でのダスト分布簡単な2パラメタ―、ρD, HD モデル、E(V-I) = ∫0R(l,b)ρD exp[-r sin(|b|)/HD] dr ここに、R(l,b)=Ro sin(α)/[cos(b)sin(l+α)] で Ro=8.4 kpc(Ghez et al 2008), α=25° (Rattenbury et al 2007) を採用した。 フィットの結果は ρD = 0.427 mag/kpc, HD = 164 pc で Marshall et al 2006 の HD = 125 pc と大分違う。このモデルは 単純過ぎるのであろう。 |
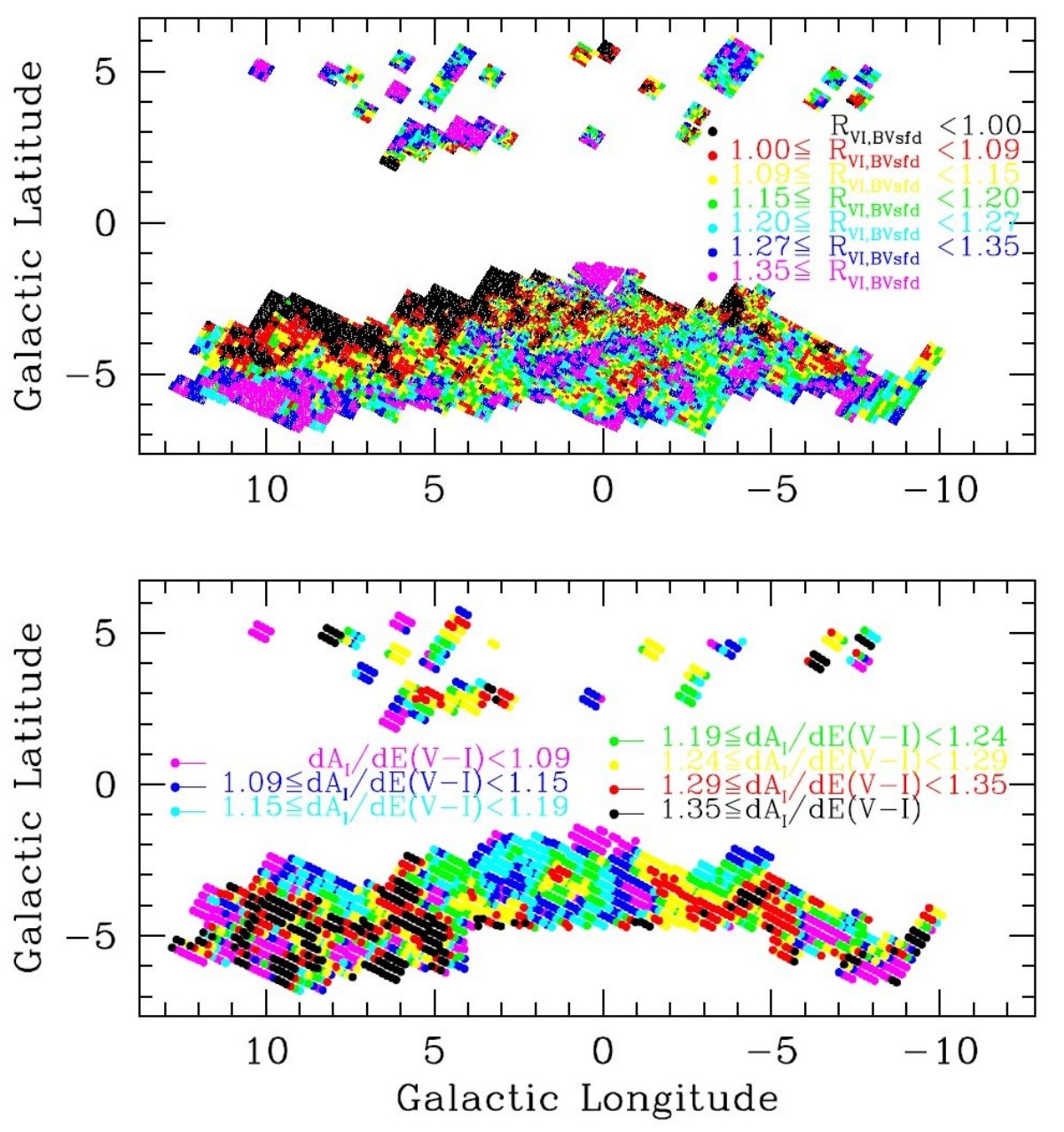
6.3. Schlegel et al 1989 マップとの比較各 E(V-I) 測定点に対し、隣の4つの Schlegel et al 1989 E(B-V) 値からの 内挿値を取って、それとの比 RVI, BVsfd を計算した。その平均値は RVI, BVsfd = 1.179 であった。図6にその分布を示す。O'Donnell 1994 は、RVI, BVsfd = 0.249 Rv + 0.562 という関係を予想している。 平均値 RVI, BVsfd = 1.179 をこの式に入れると、Rv = 2.47 となる。 この値はこの論文の後で得られる Rv = 2.5 と一致する。 |
|
減光を導く第1の方法 赤化から減光を導くには二つの方法がある。第1の方法は
標準減光則では RI = 1.45 として AI を求める。 減光を導く第2の方法 第2の方法はカラーと等級の変化を直線近似する。
この方法では固有光度の知識は必要ない。可視域では Udalski 2003, Sumi 2004, Rovvenivtsev et al 2010. Pietrukowicz et al 2012 がバルジ方向に応用、 バルジ近赤外に西山その他 2006, 2008, 2009 が、円盤の NIR, MIR 赤化の較正に Indebetouw et al 2005, Zasowski et al 2009, Gao et al 2009 が用いた。 第2法の手順 dAI/dE(V-I) を位置の関数として決める手順は以下のようである。 (1)9014 視線方向から、|l+0.5|≤4.5° and |b| ≥ 4.75° を除く。 ( "and" の意味がはっきりしない。除く理由 も書いていないが、NIR データがないからか?減光が弱すぎるからか?) (2)残った 1690 OGLE-III 視線各方向で, 中心座標の 30' 以内にある視線方向の RC 重心の等級とカラーをプロットして (IRC+0.03(l-lcentral ) 対 (V-I)RC 回帰直線を決める。0.03(l-lcentral はバーの傾きへの補正で実際には影響しない。図9にそのプロット4例を示す。 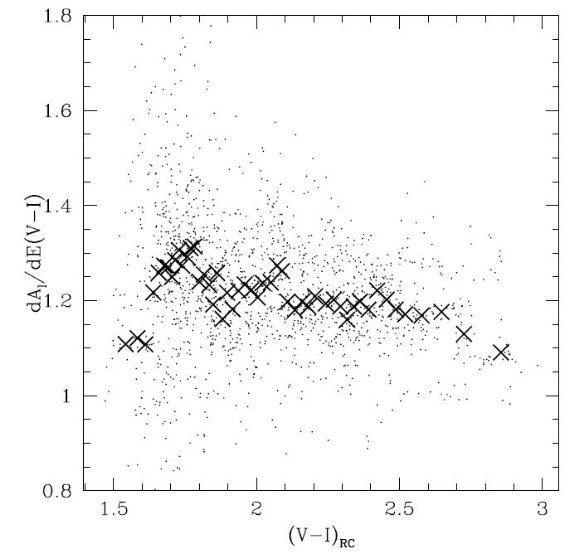 図8.dAI/dE(V-I) と 勾配を測るのに使ったセントロイドの 平均 (V-I)RC の関係。大きな X は 50 点毎の中間値。 |
dAI/dE(V-I)分布 図6下パネルには dAI/dE(V-I) 分布をプロットした。ただちに分かるのは、 (1)平均 dAI/dE(V-I) = 1.215 とバルジ方向では値が小さく、 (2)銀河系短軸から離れると dAI/dE(V-I) が標準値に近づく。 (2) の現象は Udalski 2003 や Sumi 2004 では見られなかったことで、l ≥ 5° ではかなりの視線方向で黒丸、すなわち dAI/dE(V-I) ≥ 1.35 である。 同様に Pietrukowizc et al 2012 の RR Lyr を用いた研究からも検出されなかった。 短軸から離れると OGLE-III の観測が少なくなるからである。Zasowski et al 2009 は MIR 減光則は銀河中心距離に依存し、内側では勾配が緩い灰色減光になるという結果を 示しているが、これは今回の短軸から離れると dAI/dE(V-I) が標準値に近 づくことと関連があるのかも知れない。 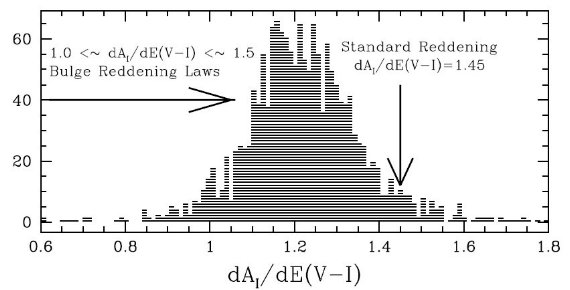 図7.dAI/dE(V-I)分布ヒストグラム。平均値は 1.215, 標準偏差は 0.18 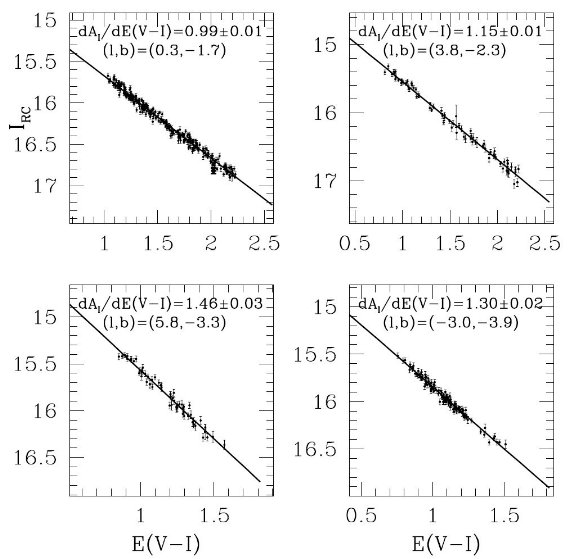 図9.4方向での IRC と E(V=I) のプロット例。 ( 視線方向から 30' 以内の視線方向で 決めた RC 重心というと、各視線方向は 6' 角平均だから 20 - 30 点くらいと思うが少し点数が多すぎる。ちょっとでも引っ掛かった方向は 加えているのか?) |
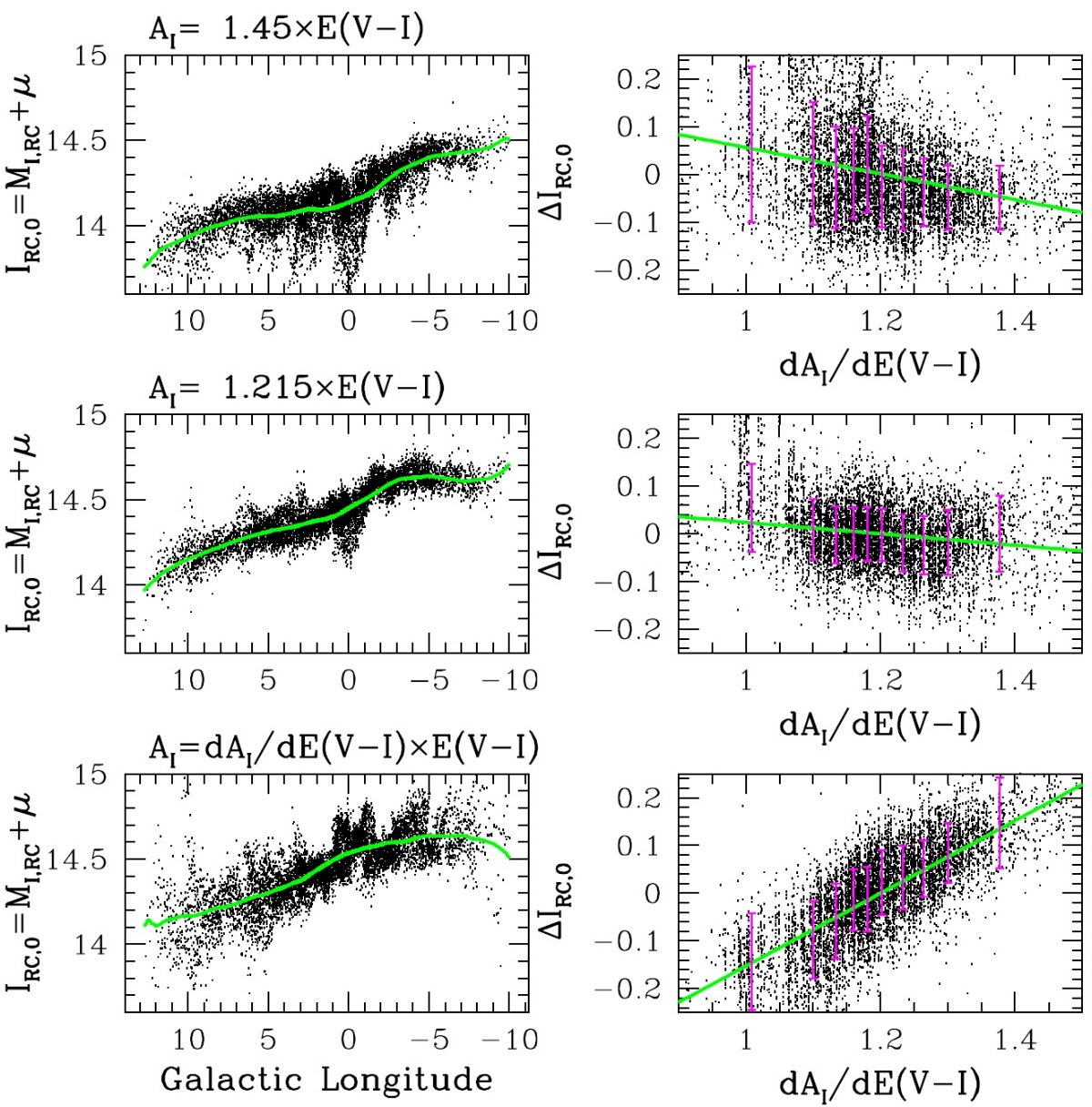
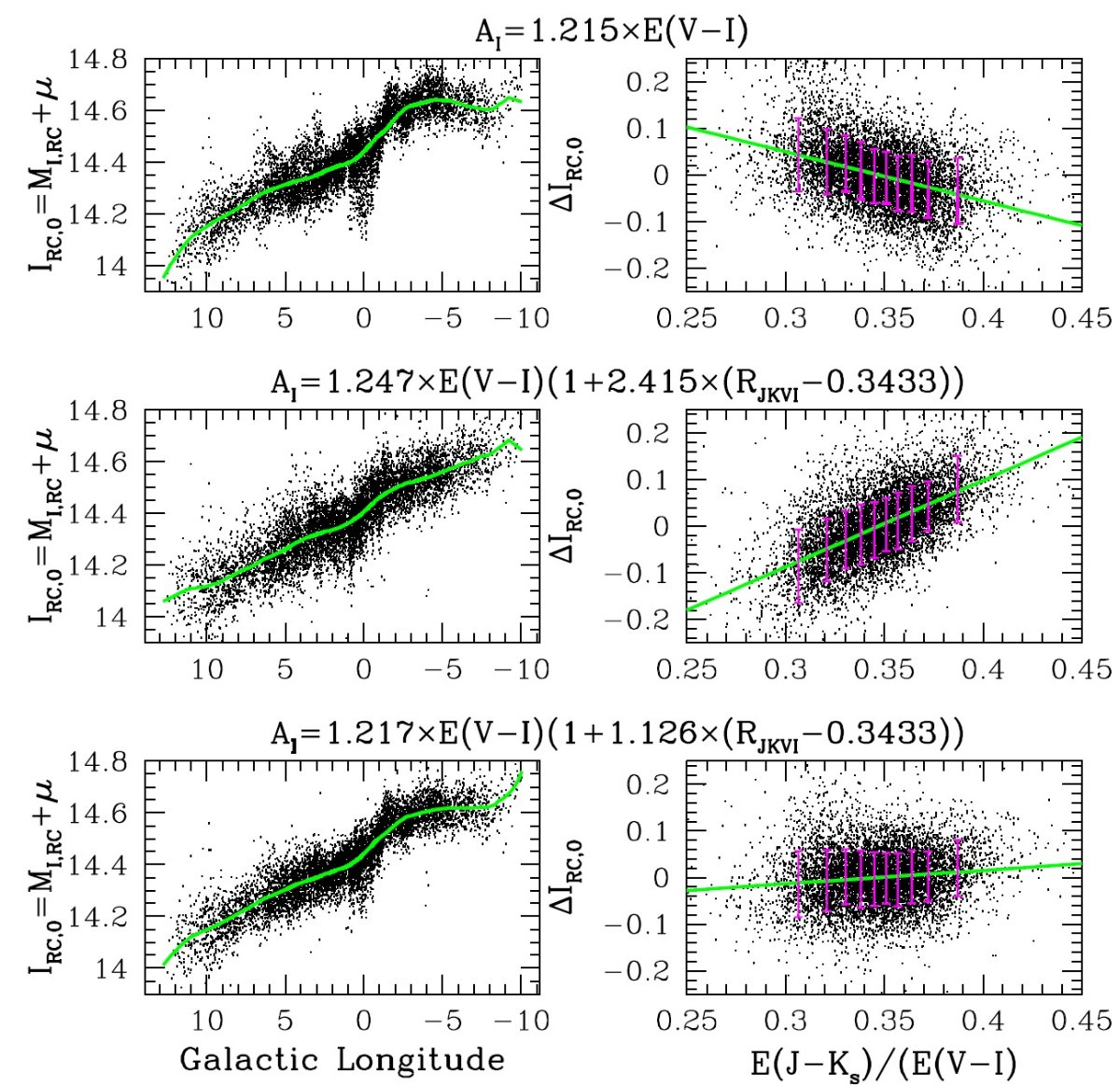
7.1.単一の赤化値から減光則を導く試みAI を求めるもっともらしい3つの方法がある。それらから求めた IRC,0 = MI,RC + μ を 図12に示した。どの図も同じ銀経で見て IRC,0 の変化が大きい。 のちに示すがこれは方法が間違っていることの表れである。 第1: RI = 1.45 標準 RI = 1.45 を使う。R = 3.1 に対応。図10を見ると 下向きの構造が多数見える。l = 0° でIRC,0 = 14.131 であり、 4.2節で求めた MI,RC = -0.12 を使うと、銀河系中心距離が 7 kpc になる。これは近すぎる値である。図10右側の IRC,0 と dAI/dE(V-I) との相関は ρ = -0.32 であり、dAI/dE(V-I) の中にまだ使われていない情報が残っていることを示す。バルジ方向への VI 減光 が非標準的であることは Gould et al 2001, Udalski 2003, Sumi 2004, Pietrukowicz et al 2012 で既に確立している。ここで再確認したのはこれが 新しい方向への出発だからである。 |
第2: RI = 1.215 この方法での分散は3つの内最少である。銀河系中心距離は 8.19 kpc で もっともらしい。しかし、相関係数は ρ = -0.23 でまだ大きい。プロットには 非物理的な特徴、例えば l = 0° 付近での下向きの筋、 l = +3° , +5° 付近での上向きの筋、が見える。 第3: AI/E(V-I) = dAI/dE(V-I) この方法が図10下段に見られるようにうまく働かなかったことは驚きである。 プロットはバー構造に大きなジグザグパターンが乗っていて、相関係数も ρ = +0.78 で最も大きい。 失敗の意味 AI/E(V-I) = dAI/dE(V-I) でないことは最もショッキングな 結果であった。この仮定はあまりに自然に見え、しばしば仮定であるとさえ述べられずに 用いられている。図9を見れば、この方法が自然に見えるのはもっともなのである。次節 ではこの問題を検討する。 |
7.2.視線に沿っての減光則の変化と合成減光バイアス減光の表式視線に沿っての減光の表式は、
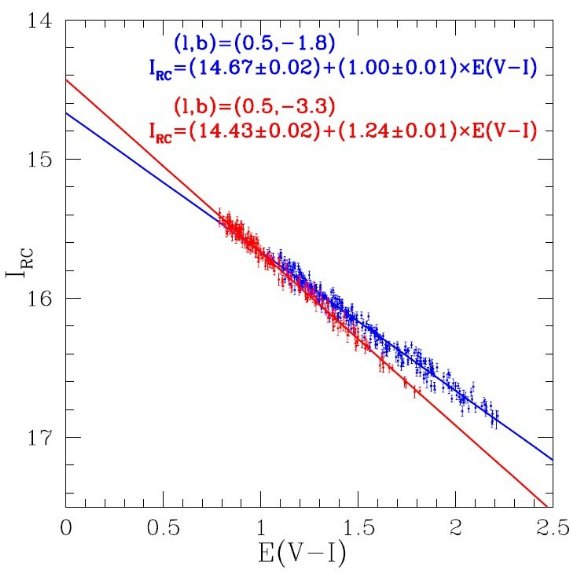
ここで、dAI/dE(V-I) = 減光則、dE(V-I)/dr = 赤化密度を距離の関数 として表したものである。 この式から分かるように、減光量は視線に沿っての減光則の寄与の総和になっている。 視線方向による減光則の違い 図11には同じ銀経での二つの視線方向に対する(IRC, (V-I)RC) の変化を示した。問題となるのは二本の回帰直線を E(V-I) = 0 まで伸ばした時の IRC が 0.24 mag 異なることである。この差は距離指数やメタルの違い では説明しきれない。太陽から距離が小さいところでは二つの視線の間隔は狭く、あまり 大きな減光則の差は期待できない。従っておそらく視線間の距離が大きくなったところで、 異なる減光則が影響してくると考えられる。 図11.二つの視線方向の各近傍における (IRC, (V-I)RC) の分散。それぞれの回帰直線の勾配 dAI/dE(V-I) は明らかに違う。 各直線を E(V-I) = 0 まで伸ばすと、異なる IRC,0 に辿りつくが 双方が同じ銀経 l = 5° を持つことからその差 0.24 mag は物理的に正しくない。 したがって、赤化 E(V-I) が小さいところでは勾配 dAI/dE(V-I) が 変化すると考えざるを得ない。 |
 |
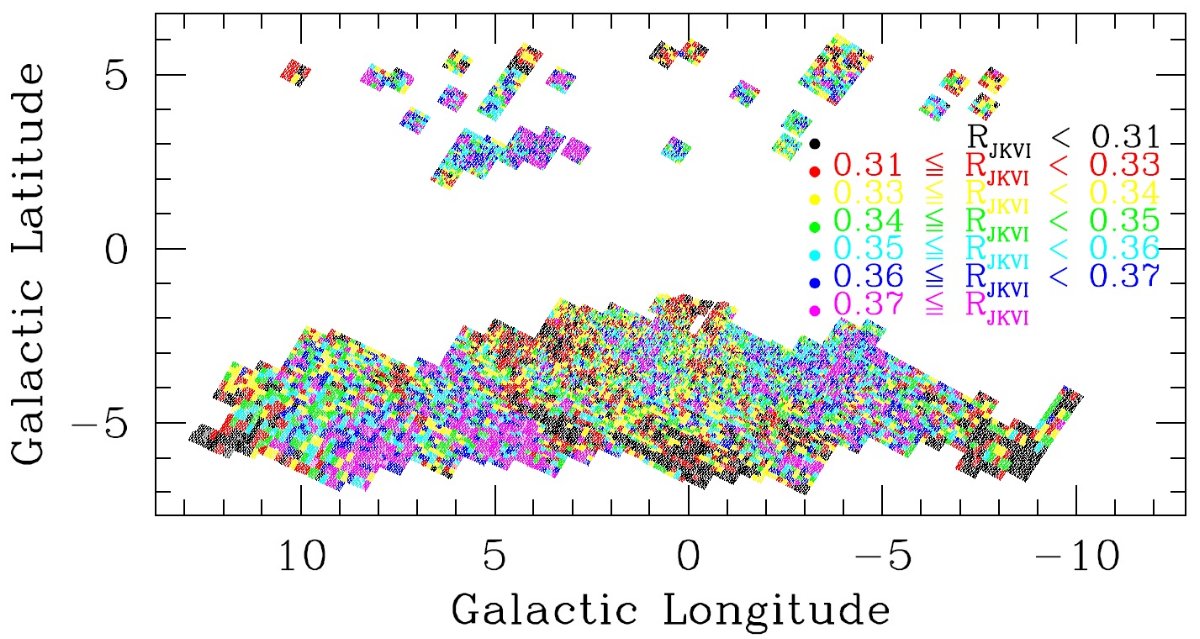
8.1.E(J-Ks)/E(V-I) の分布E(J-Ks)/E(V-I) の分布各視線方向で E(J-Ks) を加え、 (J-Ks)RC,0 = 0.66 として、 E(J-Ks) = (J-Ks) - (J-Ks)RC,0 を出すのか? それだと固有 カラーの分散が無視されるが? RJKVI = E(J-Ks)/E(V-I) の分布を図12に示した。平均値は 0.3433 で標準値 RJKVI = 0.41 より大分小さい。 RJKVI の利点 RJKVI の利用には二つの利点がある。 (1)二つの赤化の比は単一 RC と 二重 RC の双方で使える。(意味不明) (2)dAI/dE(V-I) は 30' 四方の広さが必要だが、 RJKVI は視線方向毎に決められる。 このため 減光則の変化に対し方向分解能が向上する。 8.2.E(J-Ks) と E(V-I) の関数として AI を決めるCardelli et al 1989 の減光則Cardelli et al 1989, O'Donnell 1994 は可視から赤外の減光則が Rv で決 まると仮定した。我々は B バンドデータがないので、Rv を求められない。しかし、 もしも減光則が単一パラメタ―ならば、RJKVI を知れば Rv は決まる。 Cardelli et al 1989, O'Donnell 1994 は減光則を次の形で表されると仮定した。 Aλ = Av[a(λ) + b(λ)/Rv] この結果、AI, E(V-I), E(J-Ks) の間に線形の関係が成立する。 AJ = AIaJ + E(V-I) bJ AKs = AIaKs + E(V-I) bKs E(J-Ks) = (aJ-aks)AI + (bJ-bks)E(V-I) AI = cVIE(V-I) + cJKsE(J-Ks) Cardelli et al 1989 の表式を引っくり返して次の式を得た。 AI = 0.1713 E(V-I) + 3.078 E(J-Ks) = 1.228 E(V-I) [1+2.507 (RJKVI-0.3433)] この係数は(多分)標準減光則を導いた時のもの? |
もし、O'Donnell 1994 の値を使うと下の式となる。
AI = 1.266 E(V-I) [1+2.323 (RJKVI-0.3433)] 上の2式には簡単な解釈が可能である:減光則を RJKVI について 一次まで展開した式。小さな RJKVI は急な減光則、恐らく小さな ダスト粒子、に対応する。 減光をフィットする第1の方法 図13には減光をフィットする3つの方法の結果が示されている。 上段では A が仮定された。E(J-Ks) 情報は 使用されない。この図右側は図10中段と同じである。移動平均の脱赤化見かけ 等級からの残差と RJKVI との相関は ρ = -0.39 で大きい。 この大きさが得られた情報を使いきっていないことを物語る。分散は 0.070 mag である。 第2の方法 中段には Cardelli et al 1989 と O'Donnell 1994 の表式の中間式、 AI = 1.247 E(V-I) [1+2.415 (RJKVI-0.3433)] を使用した。驚くべきことだが、この式は上の単純な表式より悪い。その分散は 0.078 mag で相関は ρ = +0.59 で約倍の大きさとなった。 第3の方法 下段では χ2 を最少にするよう最適化した係数を使った AI = 1.217 E(V-I) [1+1.126 (RJKVI-0.3433)] = -.7465 E(V-I) + 1.3700 E(J-Ks) を使用した。この式では分散 0.060 mag, 相関 ρ = +0.11 である。 相関の意味 第3の方法でもまだ相関が残ることは隠されたパラメタ―が残っていることを 意味する。しかし、I, (V-I), (J-Ks) の精度を考えると表式としては極めて高精度 と考えてよいだろう。 問題の解決 以上の結果、我々は長い間の問題であった非標準的 VI 減光の問題を解決したと 考える。 |
8.3.赤化則への注意注意1減光則が決定に使用された星のスペクトル型に依存している証拠がある。 本論文で求めた減光則は RR Lyr を用いた Pietrukowicz et al 2012 の 減光則より傾きが緩い。 注意2 メタル量勾配の影響。 |
注意3 減光則には銀経項があるのかもしれない。 注意4 我々の平均値は AI/E(V-I)=1.22, RJKVI=0.3433 で どちらの値も Rv = 2.5 を示唆する。しかし、これは B バンド観測なしでの 推測であり、推定に用いた定式化に依存する。Cardelli et al 1989 も O'Donnell 1994 も NIR では普遍的に A(λ) ∝ λ1.61 を仮定している。これは Rv に独立である。しかし 西山ら 2009 に よるとバルジでは A(λ) ∝ λ2.00 である。 恐らく NIR 指数が大きくなると Rv は低下するのであろう。しかし、 Cardelli et al 1989, O'Donnell 1994 の 51 視線方向では Rv がバルジのように 低い値は測っていない。図15では、 A(λ) ∝ λ2.00 を仮定して O'Donnell 1994 の式を訂正するとこの論文で得た E(J-Ks)/E(V-I) に 近づくことが示されている。これは偶然かもしれない。したがって、より多くのバンド の観測から NIR の指数が大きくなると Rv が下がるのかを確かめるべきである。 |
| Kunder et al 2008 が標準減光則と一致する結果を出した原因は、 Alcock et al 1999 の MACHO V, R バンドから Johson V, Kron-Cousins R への変換が正しく行われていると誤解したからである。 |
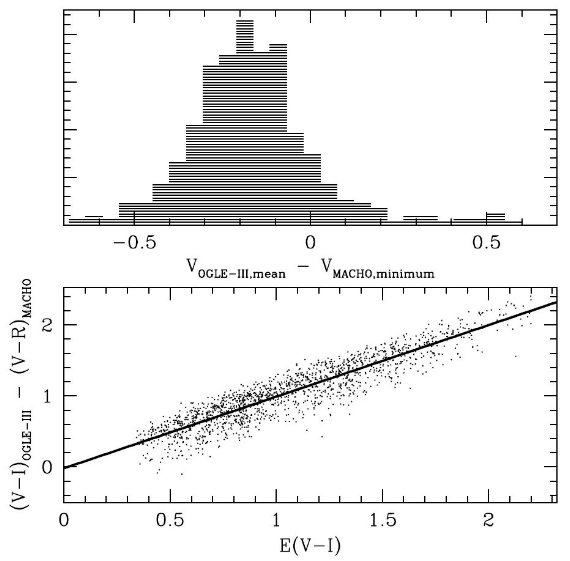 図16.MACHO と OGLE-III の RR Lyr 等級の差。 |
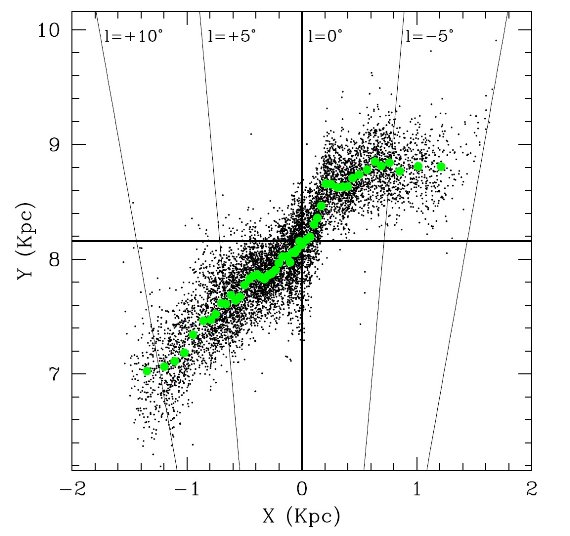 図17. |
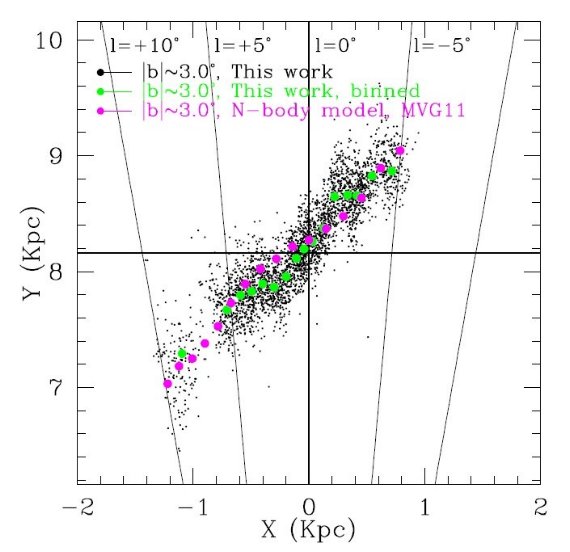 図18. |
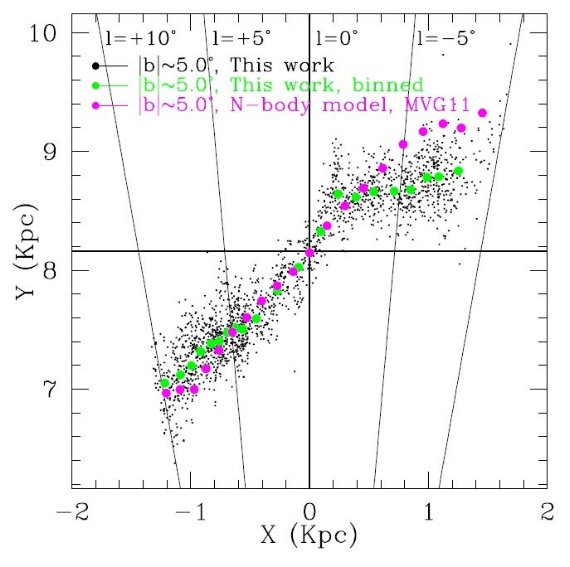 図19. |
|
|
|