The Effect of the Outer Lindblad Resonance of the Galactic Bar on the Local Stellar Velocity Distribution


Dehnen
2000 AJ 119, 800 - 812



　アブストラクト　

　内側銀河系の流体力学モデルから、銀河系バーの外側リンドブラッド共鳴 (OLR)半径は太陽付近であると予想される。この共鳴がバー円盤の外側部分に 影響するだろうか？また、太陽近傍で観測される速度分布関数にその影響を検 出できるだろうか？この疑問に答えるために、平坦回転曲線＋回転バーの指数 関数型円盤の外側における速度分布関数のシミュレイションを行った。古い恒 星円盤のモデルに対し、 OLR は外側円盤の相当部分で f(v) にはっきりした 特徴を残した。バー角度 0° - 70°, OLR 半径の 2 kpc 外側までの位 置では、速度分布関数は (1) LSR 中心の通常分布成分と (2) より低回転速度 で外側に向かう第２成分の二つに二分される。 　実際、太陽近傍の晩期型星に対するヒッパルコスデータからの速度分布関数 には、このような二分性が存在する。観測されるこの二分性が OLR により誘 引されたと解釈するなら、そして他の解釈は考えにくいが、OLR 半径は太陽 軌道半径 Ro より僅かに小さいことになる。その上、観測速度関数をシミュレ イションと較べると、バーのパターン速度は太陽近傍の回転周期の 1.85± 0.15 倍であると分かる。このエラーは主にバー角度と近傍回転速度の不定性 から来る。さらに、二分星ほど明らかではないが、しかしはっきり判別可能な 特徴は、外側 1 : 1 共鳴に補足された軌道による分布関数のさざ波である。

　１．イントロダクション　

　バー回転速度とバー角　

　Gerhard 1999, Weiner, Sellwood 1999 の流体計算や Fux (1999) の流体-,恒星-力学結合シミュレイションから、共回転半径は RCR ＝ 3.5 - 5 kpc (Ro = 8 kpc として) と推定された。バー先端の少し先と 考えられている。 バー角（バーの主軸に対する太陽の方位角）は 10° - 45° と考えら れる。

　バーとの共鳴　

　共回転共鳴のほかにあと二つ、内側 (ILR) と外側 (OLR) のリンドブラッド 共鳴が存在する。それは

 　Ωb = ωψ±(1/2) ωR

ここに、ωψ = 回転振動数、ωR = 動径振動数、Ωb = バーのパターン振動数である。 その時、 エピサイクリックな振動をする星から見ると、星振動の半分の振動数でバー が回るが、バーが中心対称なので星から見るとその振動数でバーが同じ配置 に戻る。つまりバーポテンシャルと共鳴する。

　OLR の位置　

　平坦回転曲線の場合、 ROLR = 1.7 RCR となる。 RCR = 3.5 - 5 kpc を入れると、ROLR = 6 - 9 koc となる。つまり、バーの OLR は我々の近くにある。

　１．１．OLR 付近の恒星力学　

　閉じた軌道の分類　

　Binney, Tremaine 1987 pp. 146 - 151 によると、バーポテンシャル中の 閉じた軌道は、ILR 内側＝x2軌道（バーに直行）、ILR と CR の 間＝x1軌道（バーに平行）、CR と OLR の間＝直交軌道、OLR 外 側＝平行軌道である。

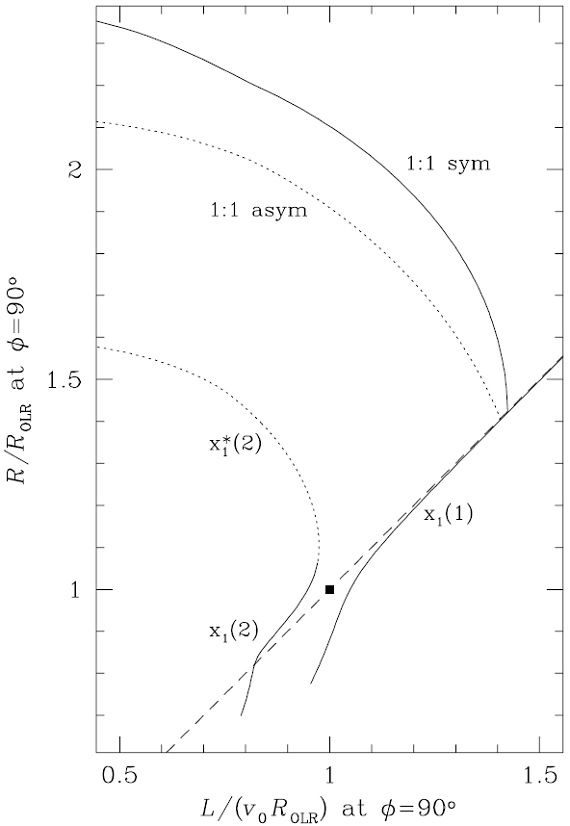
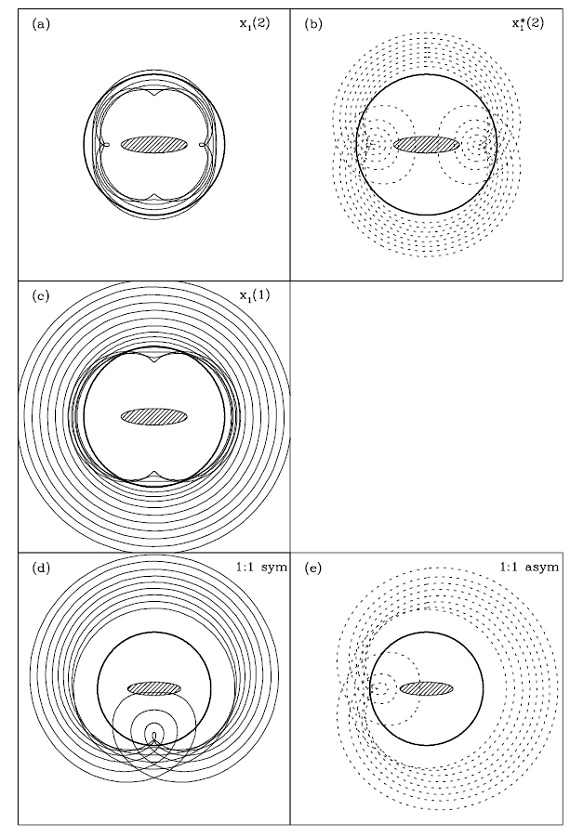
　図１＝OLR 付近の軌道　

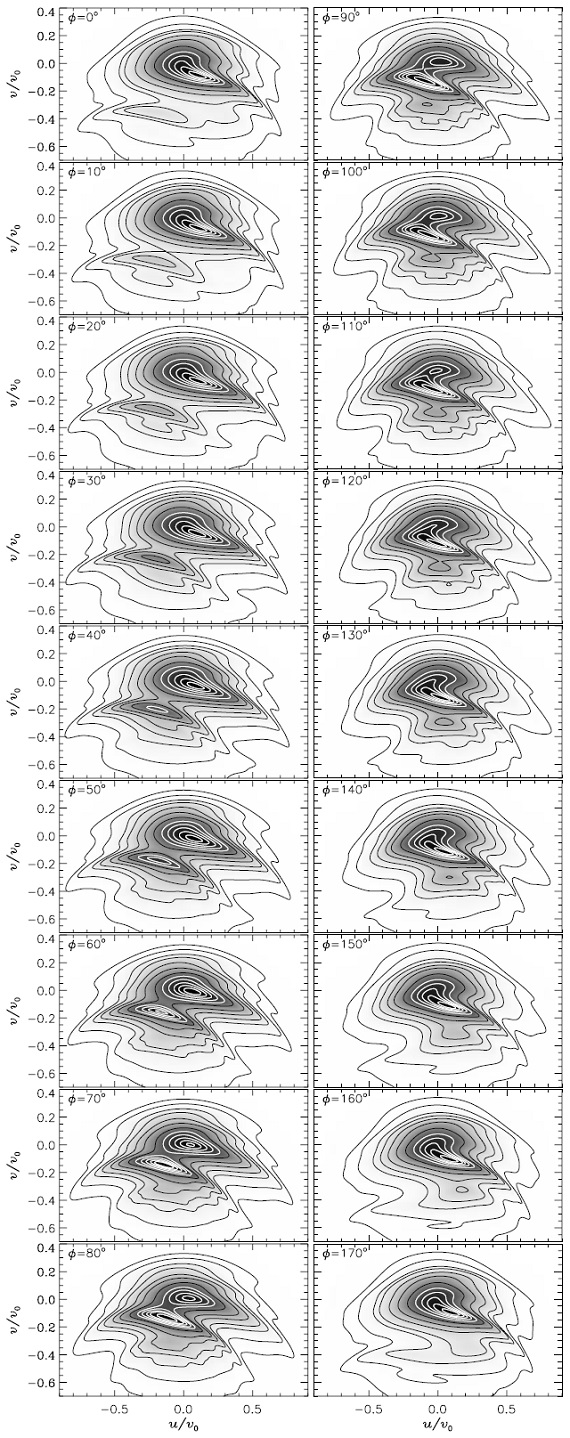
　図１に OLR 付近の様子をバーと同じ回転をする系で見た図を示す。この系 では、バーが時計回りとして、OLR 近くの軌道は反時計に回る。こうして、 図のようにバー角が φ = 0° - 90° の領域では OLR 内側の閉じた 軌道は僅かに外側に向かって反時計方向に動く。逆に OLR 外側の閉じた 軌道は僅かに内側に向かって反時計方向に動く。明らかに、もし全ての円盤星 が閉じた軌道上を動くなら、星の運動学がバー無しの円盤銀河の運動学からず れるのは閉じた著しく非線形となる ROLR の極く近くのみである。 特に、OLR 内側、外側双方の軌道が交わる特別な点付近では、内向きと外向き の二つの星流が見られる。

　OLR 内側からの近共鳴軌道星　

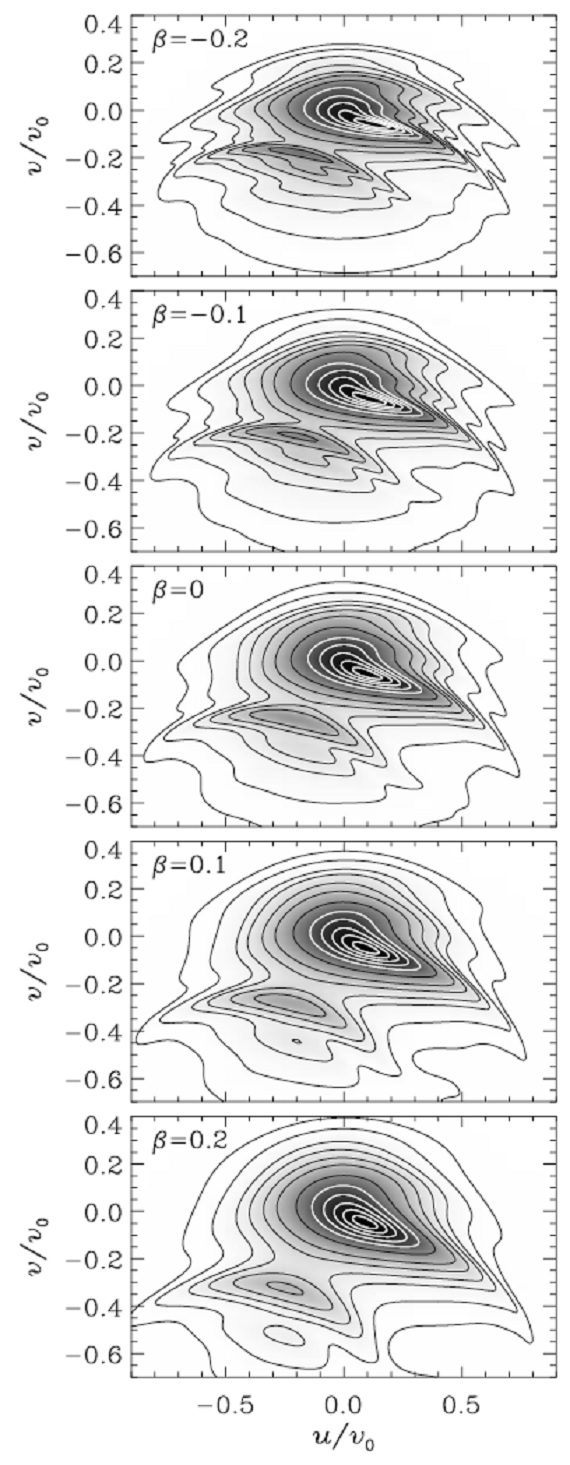
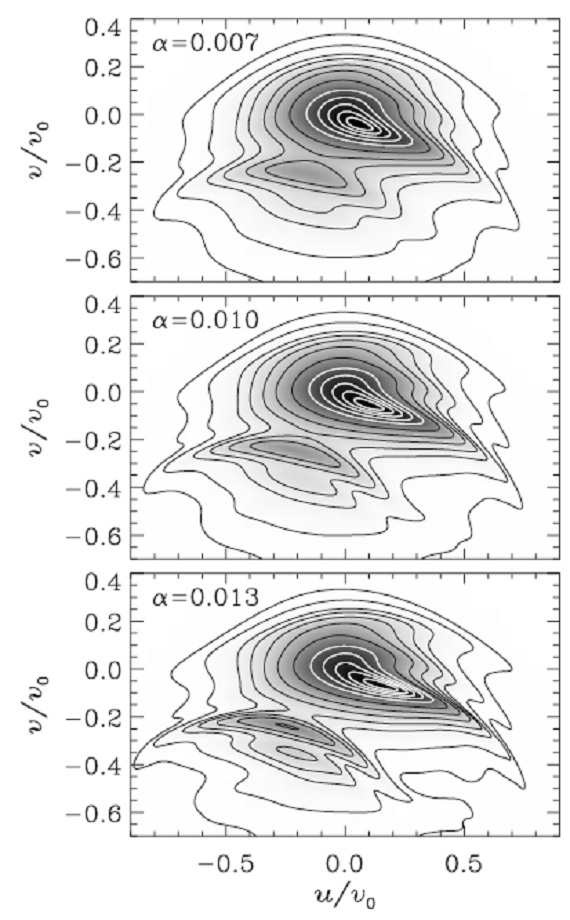
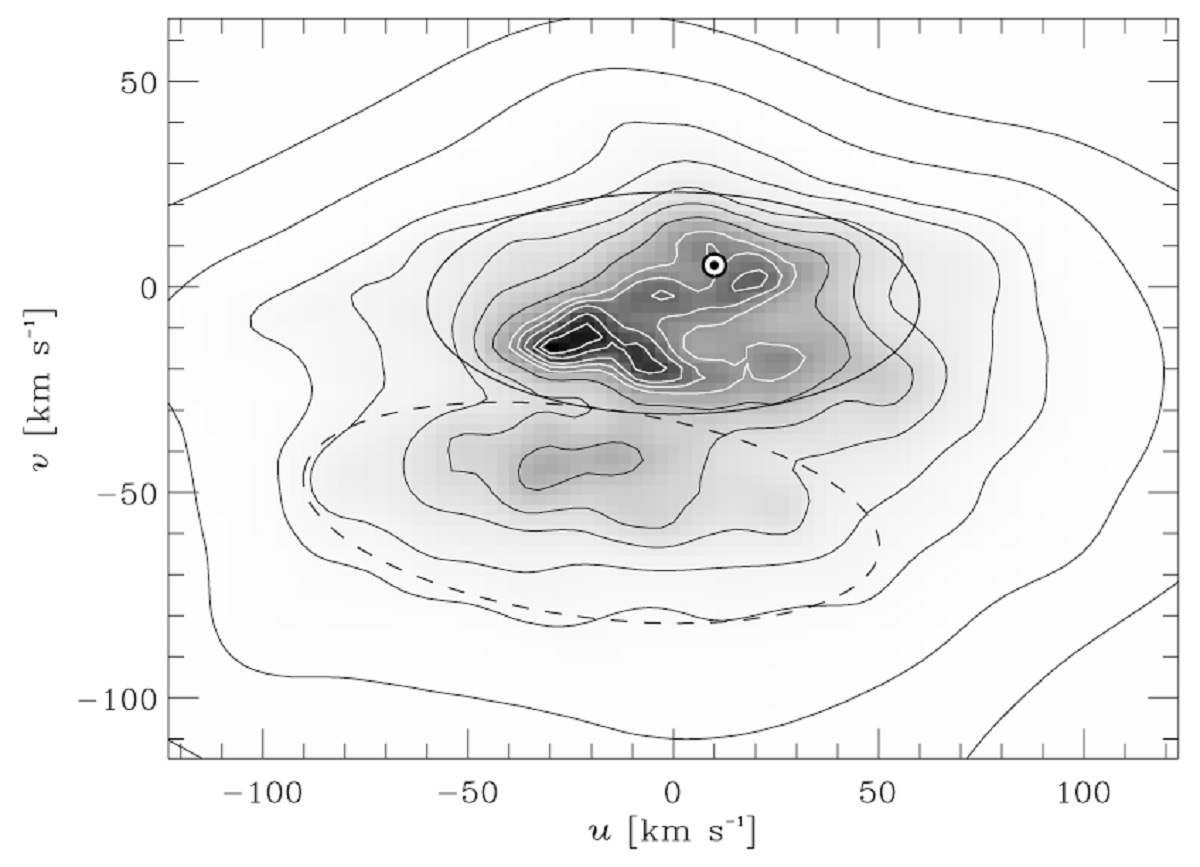
　しかし一般には星の軌道は閉じない。軌道の多くは共鳴に捕らわれ Weinberg 1994、閉軌道の周りにエピサイクリック振動を行う。これは、その 様に捕らわれた、OLR 内側からの離心軌道、つまり Ωb < ωψ+ωR/2 の星が ROLR の外側までやって来る可能性を意味する。近共鳴軌 道が太陽近くを通るなら、 OLR は太陽近傍の速度分布関数に影響するのであ る。

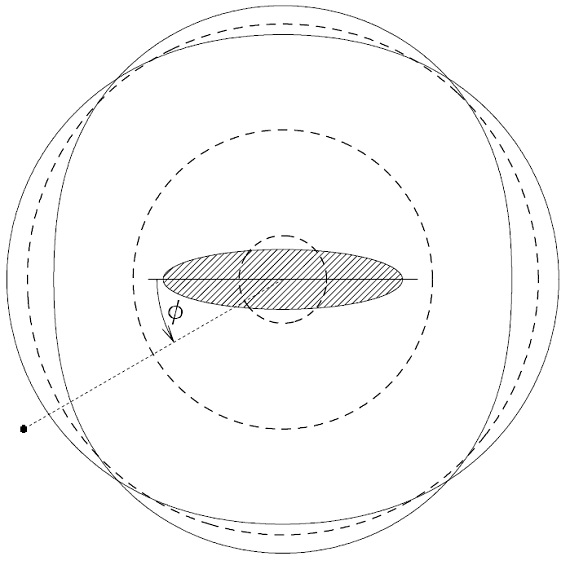
図１．実線＝バー（斜線楕円）の OLR のすぐ内側とすぐ外側の閉じた軌道。 破線円＝内側から ILR, CR, OLR. OLR のところで、軌道の方向角が変化することに注意せよ。 黒丸＝太陽の予想位置。

　２．シミュレイション　

　仮定　

　銀河系全体の N-体計算はまだ無理なので、次の仮定を置く。

（１）　バーの成長を与える。

（２）近傍密度に関係する二次元軌道のみを計算する。



　計算法　

　backward-integrating restricted N-body method を採用して、 ポアソンノイズを避ける。

　初期平衡状態　

回転曲線　　　vc = vo(R/Ro)β

ポテンシャル　Φo(R)= vo2(2β)-1(R/Ro)2β　　（β &ne: 0）
　　　　　　　　＝ vo2ln(R/Ro)　　　(β = 0)

平衡分布関数　f = F(E, Lz) 		　逆時間積分　

　無衝突ボルツマン方程式の解は軌跡に沿った位相空間密度が不変である。 w(x,v) = 位相空間内の点 は wo を t = 0 から t=t2 まで積分した結果とすると、f(wo,0)=f(w,t2).

N-体計算と違うのはポテンシャルは事前に与えられている点である。したがって、 時間 t2 に w を通る軌跡を逆時間方向に積分すれば wo に辿り着く。

　位相分布関数の計算　

　実際には、最終時間 t2 を設定し、次に実空間 (R,φ) にお いて、二次元速度 (u,v) のグリッドから位相空間中の点 w を選び、逆向き積 分を t = 0 まで実施して w を得る。出発点の初期エネルギーと角運動量 (E, Lz) は記録される。こうして、任意の軸対称初期平衡分布関数 F に対して, f(w,t2) = f(wo,0) = f(E, Lz) が計算できる。
(理解していない点：出発の平衡状 態が本当なら、なぜ時間変化するのか？ 逆時間方向に積分する理由は？)

図２．バー角の違いによる速度分布関数 fo(u, v) の変化。残りのパラメター は表１にある。 　

表１．シミュレイションのデフォルトパラメター

図３．積分時間 t2 による速度分布関数 fo(u, v) の変化。 Tb = バー回転時間。t1 = バーの成長時間は t1 = 2 t2 とする。


図４．ROLR/Ro による速度分布関数 fo(u, v) の変化。 　

図５．回転曲線の勾配 β による速度分布関数 fo(u, v) の変化。 　


図６．バー強度 α による速度分布関数 fo(u, v) の変化。 　

　３．閉軌道との関係　


図７．規格化した R と L 図上の実線＝安定と点線＝不安定閉軌道。破線＝ バー無し円盤の円周軌道。黒四角＝OLR.

図８．図７に示した閉軌道群。太丸＝ OLR. 実線＝安定軌道。破線＝不安定軌 道。




図９．B-V ≥ 0.6 の 3572 主系列及び 2491 非主系列 ヒッパルコス星の 速度分布 fo(u,v). 黒二重丸＝太陽。実線楕円（低速）＝早期型星領域。 破線楕円＝中間速度星＝晩期型星＝全体の 15 % がここ。 u = 中心方向。v = 回転方向。第２成分は円盤外向きに動く。

　６．結論　

　パラメタ―　

　速度分布関数への OLR による効果は４つのパラメターに依存することが 広範なパラメター空間を覆うシミュレイションで分かった：
（１）回転曲線の形（勾配）、（２）OLR と太陽の位置関係、（２） バー角、バー強度（？）は書いてない。

　第２成分　

　速度分布 f(u, v) は観測から実際に u, v < 0 領域に第２成分を 示すことが判った。それは、シミュレイションで現れる OLR モードに よく似ている。 		　他にも似ている　

　興味深いことに他にも観測とシミュレイションが一致する特徴がある。

（１）シミュレイションでは少し負の v (回転遅れ）で u 正方向に尾根が伸 びる。これは図９の v = -20 km/s に現れる尾根と似ている。この尾根は ヒアデス・プレアデス星流で u = 60 km/s まで伸びる。

（２）シミュレイションでは外側 1 : 1 共鳴に起因するさざ波が |u| 大で v > 0 に見える。図９では (u, v) = (-80, -5) と (40, 5) に超過が 観測される。

　Ωb/Ωo　

　近傍晩期型星の速度分布は内部円盤の情報なしに、バーの存在を予想する。 そのうえ、それから、太陽の位置は OLR 半径の少し外側であることが判る。 OLR 成分の LSR v 速度 vOLR からバーのパターン回転速度と 太陽近傍の回転速度の比 Ωb/Ωo = 1.75 - 2 である。