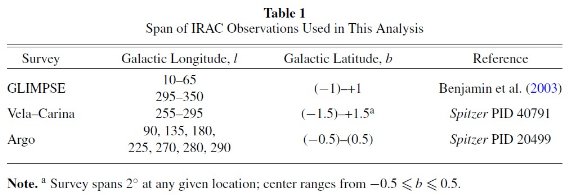
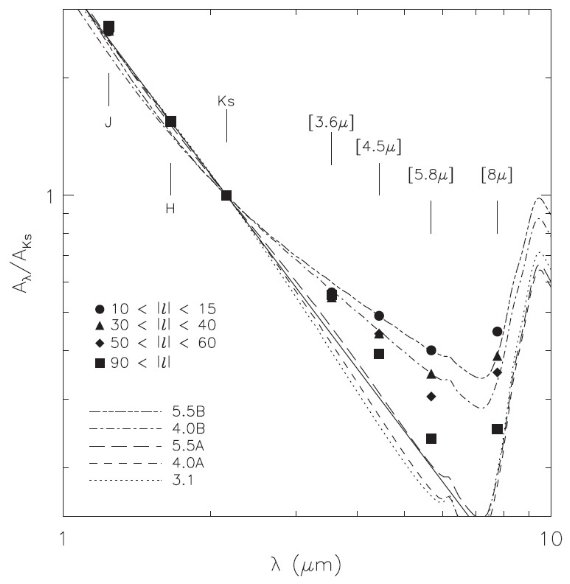
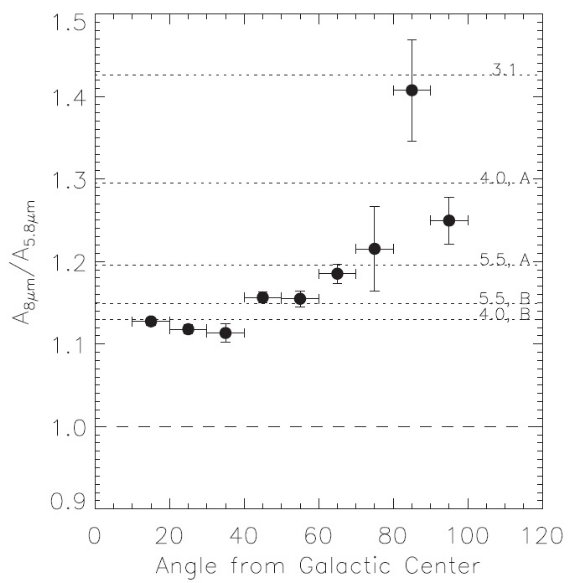
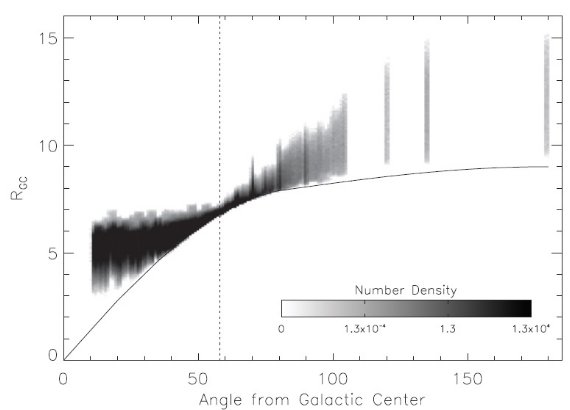
"13CO" 法のサンプル
FCRAO Galactic Ring Survey (GRS) l = 18° - 54° の
13CO データ, Jackson et al 2006 を濃い星間物質の指標に使った。
このマップは分解能 0.75' で中間距離にある雲の筋糸状構造を識別している。
最も安全な選択法として、我々は 13CO 放射が検出されない領域を
選んだ。GRS 実施領域内でこの非検出領域内にはレッドクランプ星の 55 % が
含まれている。 以前に述べたように、これは n(H) ≥ 1 - 5 cm-3
の雲が除去されていることを意味する。
"RPD" 法のサンプル
RPD法では、単位距離当たり赤化量(RPD) の最大値として、RPD ≥ 0.22 mag/kpc と
RPD ≥ 0.15 mag/kpc の二つを考察する。このカットはレッドクランプ星の
79 % と 57 % をそれぞれ残す。
サンプル数の比較
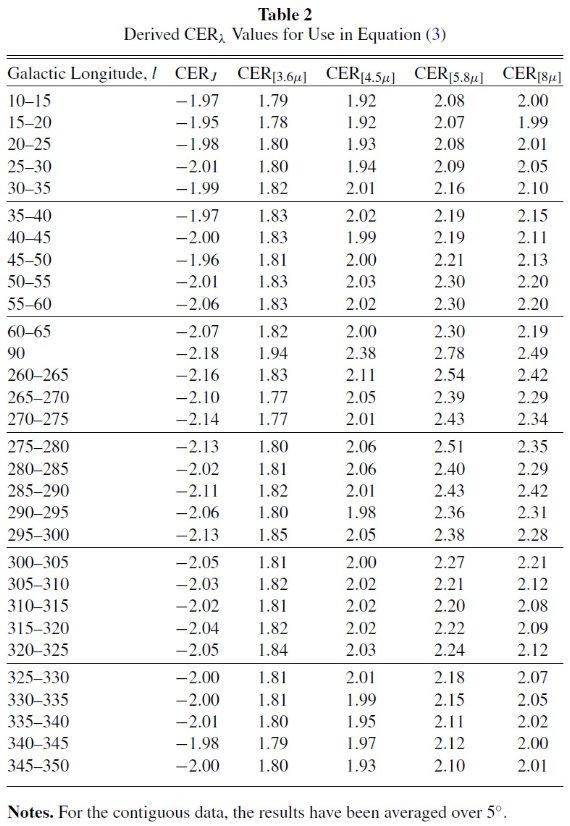
以上の様々な選択法によるサンプルに CERλ フィットを行った。
GRS サーヴェイの範囲が l = 18° - 54° なので、"13CO" 法のサンプル
はその範囲に限定される。それで、 RPD 法の結果も銀経の制限を付けた場合と制限なしの場合
の両方を示した。各区画でフィットに使用したサンプル星の最低数は、3.2.節での 820
から、RPD ≤ 0.22 mag/kpc での 14,000, RPD ≤ 0.15 mag/kpc での 5700, 13CO
法での 8000 である。初めの時より最低数が増加したのは l の範囲が 54° 以内になった
からである。図7のエラーバーが小さいのもそのためである。
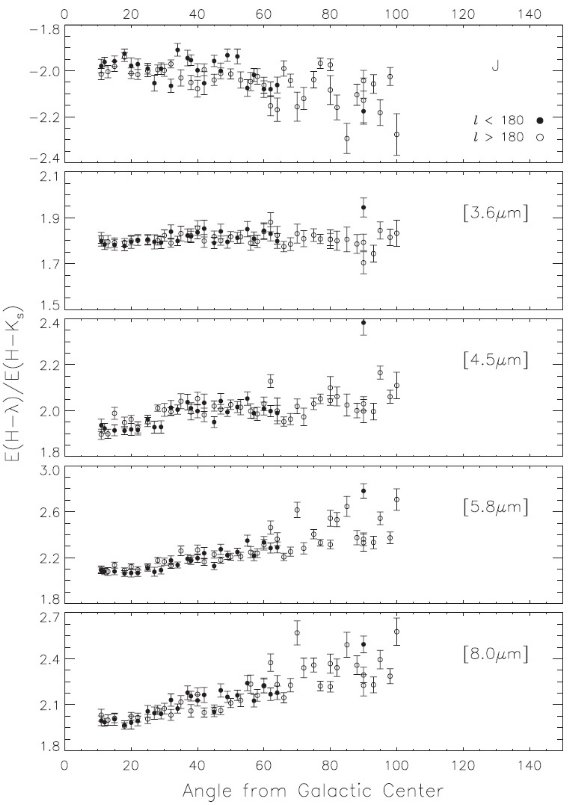
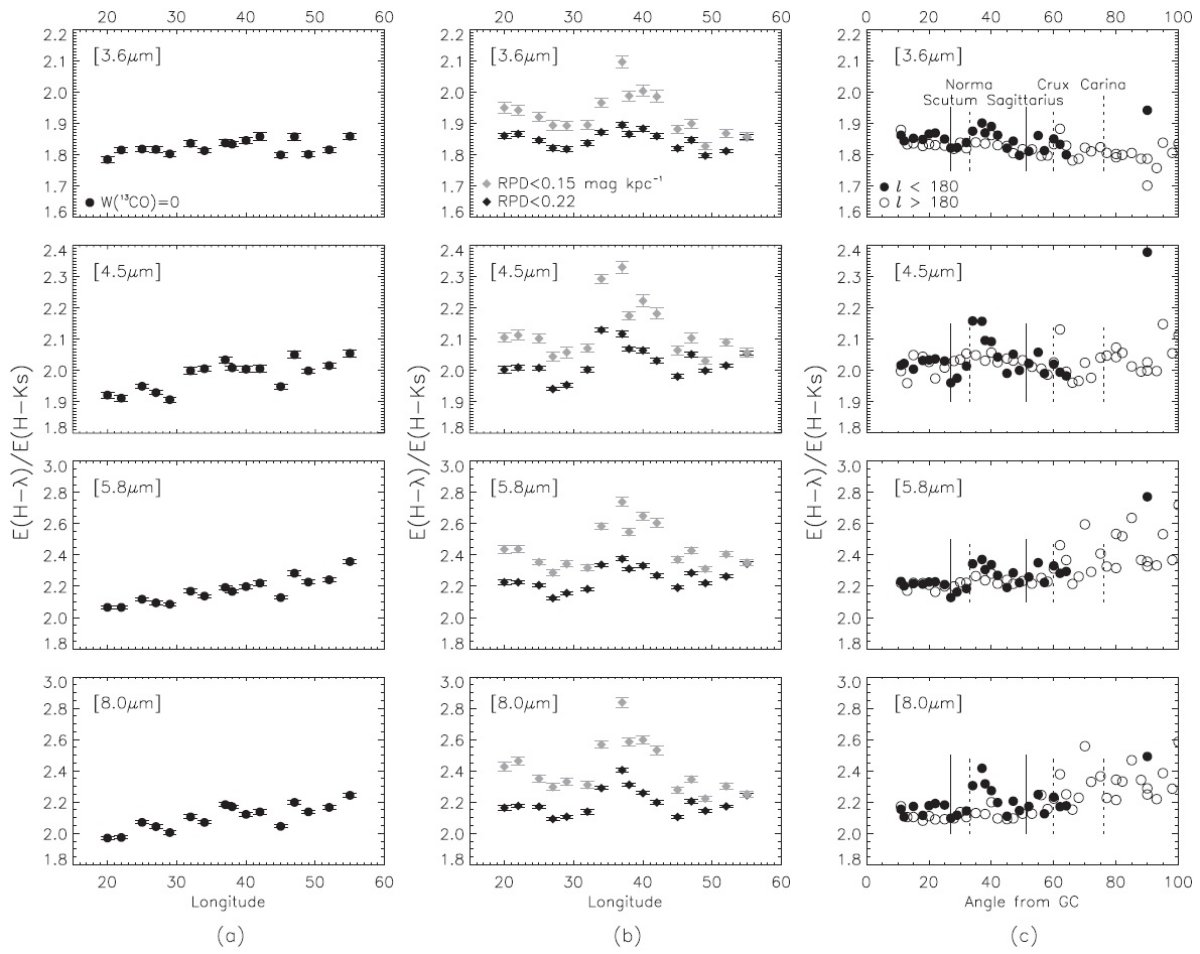
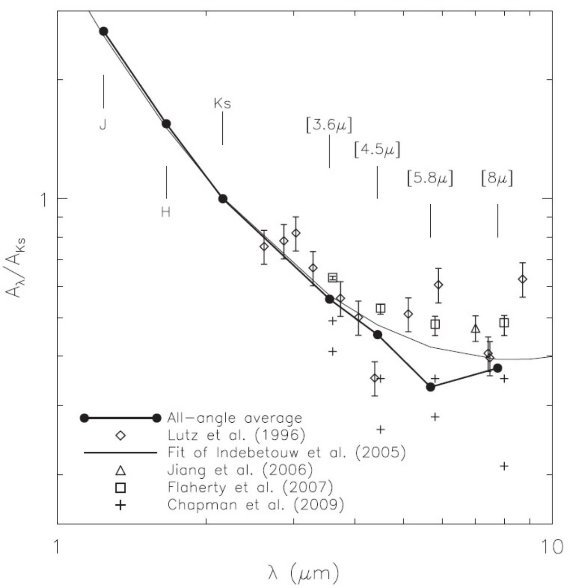
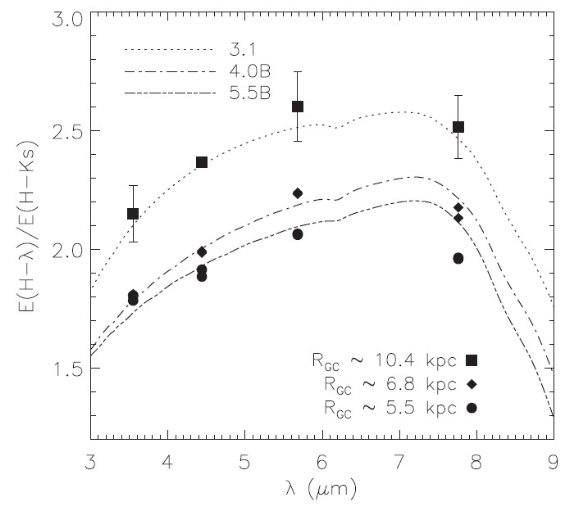
13CO 法の結果
13CO 法の結果は図7の左 (a) に示されている。驚くことに、図5の希薄、濃密
の区別をつけなかったフィットと全く同じで、銀河中心角度依存性が見られる。
RPD 法の結果
図7の中央 (b) には RPD 法の結果 を示した。今度は
銀経 l によって激しく CERλ が変動するが、大局的な変化傾向は
見られない。さらに、直観に反することだが、RPD 制限値を 0.22 から 0.15 に下げた時に、
Indebetouw et al 2005
の希薄星間空間減光則からの乖離は、 却って大きくなる。
希薄空間サンプルの減光則は不可解なことに急
その上、これらの希薄空間サンプルのみを選んで作った減光則は、単純なべき乗則
( JHKs での A(λ) ∝ λ
-α を指すのか?)、
や Rv = 3.1 ダストモデル(5.3.節参照) よりも急であることは理解が難しい。
( 希薄空間ではグレインサイズが小さくなるから
「理解が難しい。」と言うのか?
少なくとも CERλ の分散が大きい原因の一部は、高赤化星ほど優先的に
除去されてフィットが不確実になったためである。もし、l = 28°, 50° 付近の
低い CERλ を "trough" と考え、l = 37° の高みをピークとは
見なさないならば、これらの窪みは Scutum と Sarittarius 渦状腕の接線方向
(Englmaier, Gerhard 1999)にほぼ対応する。これは "trough" の説明となるかもしれない。
というのは、 CERλ が小さいことは減光曲線が浅くなることを意味し、
渦状腕が濃密であることと一致するからである。
| |
本当に腕が原因?
(1)RPD 大の星を除去しているので、RPD 限界を下げるほど分子雲原因の特徴が強まる
とは考えにくい。
(2)太陽から腕の接点までの距離はまだ確定していないが、最近の結果では、
我々のレッドクランプの存在距離よりも遠いらしい(Hou et al 2009)。すると、
RPD の低いサンプル星が腕の接点付近を見ている可能性は低い。
(3)第4象限での対応接点、l=284° (Carina) と l = 310° (Crux) で
RPD 法を適用してみた。RPD 法は 13CO サーベイの範囲に捕われない。
図7(c) を見ると、Crux, Carina に対応する窪みは見当たらない。
これらの点から l = 18° - 54° 間での CERλ の振る舞い
を銀河系構造に起因すると考えるのは難しい。
図7(b),(c) の特徴は本物か?
図7(b),(c) の特徴は本物かどうかに関しても、次のような疑問がある。
(1)RPD 限界を決める際の仮定が妥当だったか?
(2) RPD 限界値を下げると、現実的な CER 値から乖離する。
(3)RPD 計算は星までの距離に強く依存し、距離決定は仮定した減光則の影響が
大きい。
13CO 法の方が安全
これらの要因を考えると、13CO 法は完全ではないが、より安全と思われる。
「希薄」空間減光則と、「全サンプル」減光則が似ていることは、「全サンプル」レッド
クランプ星が探った星間空間環境は 13CO が存在するには希薄過ぎることを
意味する。
(「全サンプル」も分子雲減光は受けていない
と読める。分子雲も希薄空間も同じ減光則だが、何かの要因で同じ経度変化を被ると
考えるべきではないか? )
今後の解析は 13CO データがある区間に限定されず、可能な限り広い
銀経区間での減光則を扱う。希薄空間での減光則が、特に 5.8, 8 μm で、経度による
変化を示すことは、銀河系平均密度勾配の効果(ただし分子雲でのサイズ成長効果を
越えた何か)銀河円盤全般に渡る二次効果、例えば化学組成、サイズ、結晶の割合、を
指し示す。
希薄空間の意味
ここでは作業仮説として、「希薄空間物質」とは n(H) ≤ 1 - 5 cm-3
で 13CO が解離してしまうような星間物質を指す。この定義は普通に
「希薄空間物質」と言う場合に思い描かれるものに近いだけでなく、我々の結果を
実際かつ直接に赤化補正のために使用する場合に有用なものである。4成分星間空間
モデル(Whittet 2003) では「暖かい」と「冷たい(原子状)」成分が相当する。
この希薄成分は円盤全体で密度勾配を有する。と言うのは、この成分には分子雲の
周辺部が含まれていて、分子雲の空間占有率は円盤全域で変化するからである。
(ここも、なんで分子雲周辺部が密度勾配の
原因になるのか分からない。)
しかし、強調しなければいけないのは、我々の定義から、この星間空間物質は
「濃い星間雲」と考えてはならず、(prior to this study ?)一定で不変の減光則と結びつけてはいけないのである。
我々の結果では、この不変減光則は全ての視線方法の減光の振る舞いを正確に記述している
と言えない。希薄星間空間での減光則が変動することを考慮しない赤化補正は大きな系統誤差を
導入する危険がある。
|