The Long Galactic Bar as Seen by UKIDSS Galactic Plane Survey

　アブストラクト

　１．イントロダクション　

　２．データ：ＵＫＩＤＳＳ ＧＰＳ(Galactic Plane Survey)　

　３．レッドクランプ星の距離　

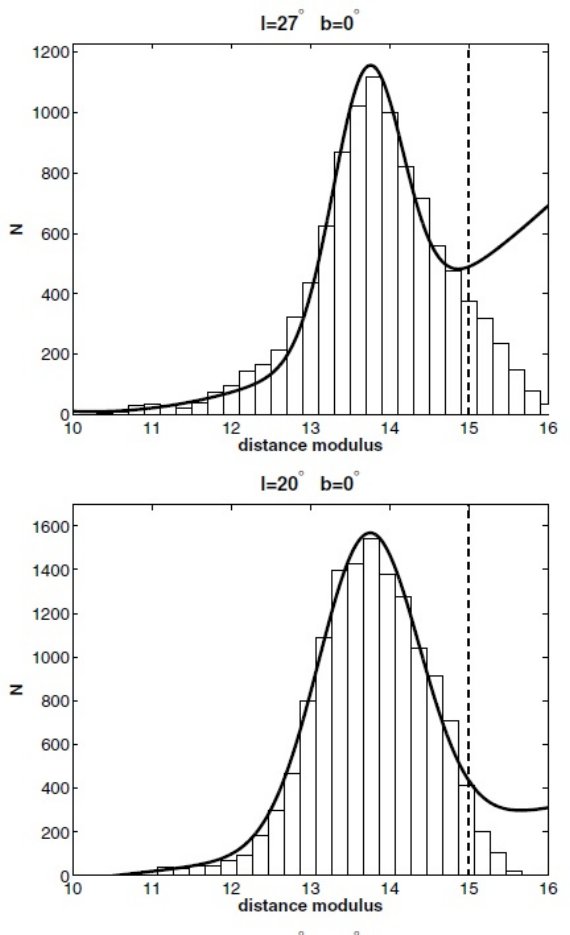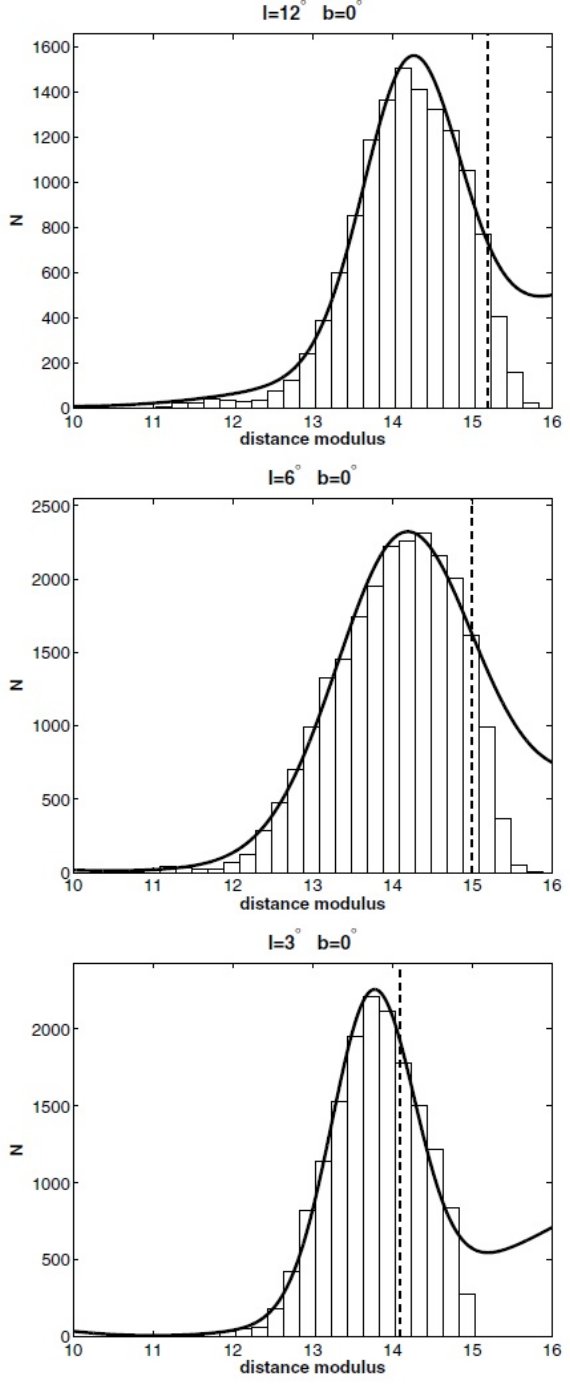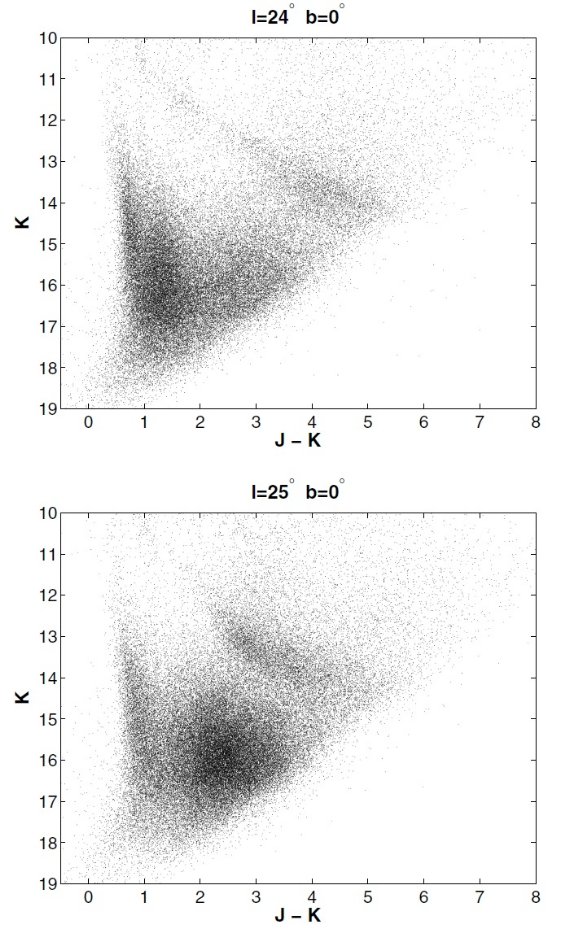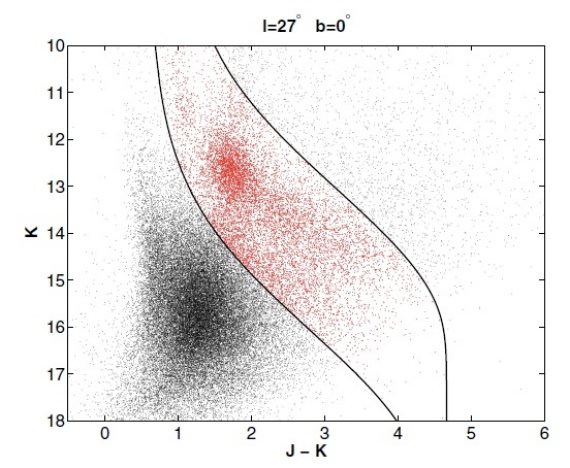
図１．SKY 減光モデルを使った巨星種族の理論的軌跡の利用例。 K0III と M0III, 二つの軌跡の間に挟まれた星はレッドクランプ星と考えられる。この図の場合、 (K, J-K) = (12.8, 1.8) にあるコブは視線方向に存在する細い構造を表す。 ( この図は K = 14 - 16 に下からの大きな 混入がある。間違えた構造を導かないか？) 　レッドクランプ星の抽出　 　 Cabrera et al. (2007) は Wainscoat et al 1992 の SKY 減光モデルを用いて、巨星種族の色等級図 上での理論軌跡を導いた。それらの軌跡を用いて、矮星を除去し、図１に示す ように、レッドクランプ星を抽出した。 　距離指数　 　距離指数は以下の式で定義される。 μ = Ks - AKs [(J-Ks) - (J-Ks)o] - MK AJ - AKs AKs/E(J-Ks) = 0.68 (Rieke, Lebofski 1985), MK = -1.62±0.03 (Alves 2000) を採用する。 　距離指数 m の分布　 　距離指数 m の分布を以下の式でフィットする。 N(m)=a+bm+cM2+ NRC exp [ - (m-MRC)2 ] σRC√(2π) 2σRC2

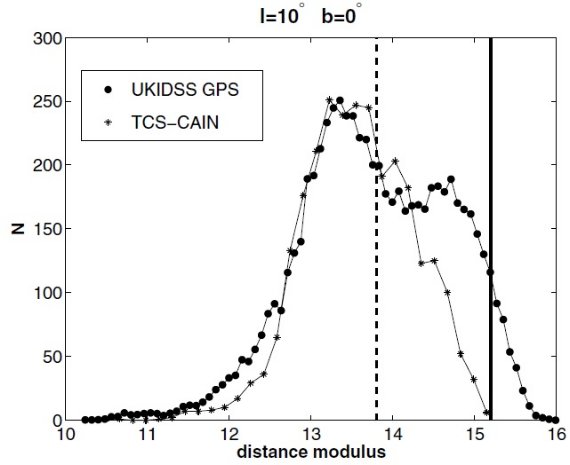
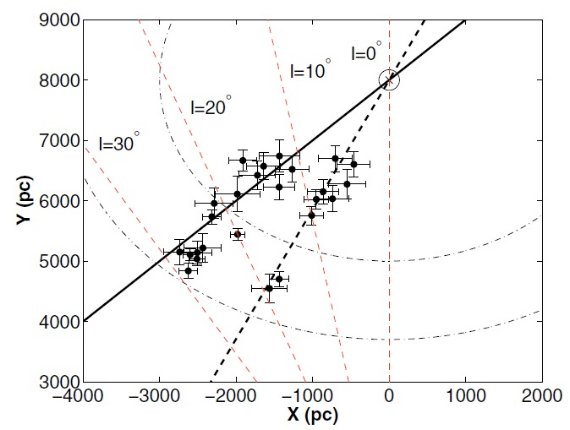
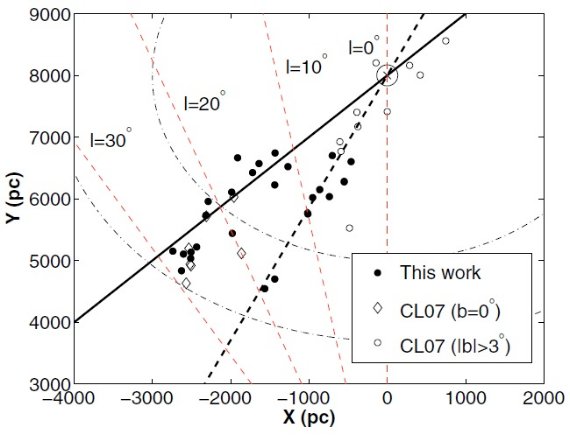
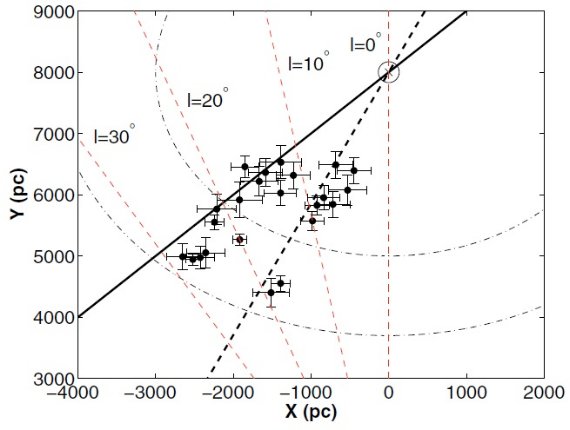
３．２．測光不完全性の影響　 図２．(l, b) = (10, 0) におけるレッドクランプ星分布の比較。 アステリスク＝ TCN-CAIN。黒点＝ UKIDSS。双方、最大値で規格化 した。 縦線はそれぞれの限界等級。TCN-CAIN の測光は浅いため、 限界線が分布ピークに近すぎ、暗い部分の表現が不完全になる。 TCS-CAIN サーベイの結果　 　 Cabrera et al. (2007) は TCS-CAIN サーベイを用いて l = [30, -30] データを解析した。その測光 は 2MASS より 1 - 2 mag 深い。しかしそれでも l = [-15, +15] の銀河面 を調べるには不十分である。彼らは |l| = [15, 30] では銀河面、 l = [5, -5] では銀河面外しデータを組み合わせて用いた。解析から、 銀河系最内側部に厚い構造＝バルジとより大きい薄い構造＝ロングバーが l = 27 まで伸びていることを明らかにした。 　データの比較　 　この論文では彼らの手法を用いて、 UKIDSS 銀河面データを解析する。 図２には二つのデータセットを比べた。UKIDSS の方が深いことが明らかであるが、 重なる部分では同じ密度分布を出していることも注意すべきである。

　４．結果：　レッドクランプ星の分布　

表１＝コブ位置と巾　 　表１には UKIDSS データから 銀河面沿い Δl = 1 間隔の、 Δl = Δb = 0.5 正方形領域 の星を用いたコブ位置と巾を示す。 　図３＝距離指数分布の例１．最内側　 　図３には銀河面上の５点における距離指数の分布を示す。全ての地点でコブ の存在は明らかである。コブ距離が銀経に従って変化すること、コブ幅が l = 27 で増大することに注意せよ。幾つかの点ではデータの不完全さのためフィットが 怪しい。l ≤ 1 の最内側では減光補正等級が浅すぎて、コブに届かない。 また、 l = 2, 3 の場合ピーク位置が限界等級に近いのでフィットの確実さが 保証されない。図３に l = 3 の場合を示す。なので、 l ≤ 3 の結果は以下 の議論では使わない。 　例２．l = 23, 24　 　l = 23, 24 ではコブが見えない。これは強い減光のためである。 Benjamin et al. (2005) の図１を見ても分かるが、この方向の減光は非常に強い。下の図４には l = 24 と l = 25 の CMD を比較した。すぐにわかるのは星の数の差である。また、 l = 25 では赤色巨星枝の構造が (J-K, K) = (2, 13) から (4.5, 14) へ伸び ているのがはっきり分かるが、これは l = 24 にも現れている。ただしこっち では (4, 14) に現れているが。明らかに 2 mag 深い観測が必要である。 (何のことか？　図で見ても分からない。 )

図３．銀河面内５領域での距離指数分布の例。ヒストグラム区間巾＝ 0.2 mag. 太線＝フィット。破線＝減光補正後の限界等級。

図４．上：l = 24 と下： l = 25 の CMD の比較。l = 24 では減光が強いために コブ構造に達していない。

図５：l = 10 で点列の角度に変化　 　図５には銀河面 X-Y 面上にレッドクランプのコブをプロットした。 l = 10 で点列に大きな変化が現れている。l < 10 では点列の傾き角は３軸 バルジとよく一致する。その軸角は 23.6±2.2 である。しかし、 l > 10 ではその角度は 42.4±2.1 に変わる。l > 28 では明白な コブは見られない。 　コブ位置の乱れ　 　l = 17, 19 のコブはロングバーから推定される場所から遠く離れた所に位置する。 表１を見るとそこはコブの巾が大きく、減光の強い方向であることが判る。この 方向には、G19.6-0.2 のような大きな星形成域がある。いずれにせよ、 Picaud et al. (2003) が l = 20, 21 について述べているように、密度超過は幾分か非一様である。 　軸角の不定性　 　注意すべきはレッドクランプフィットで決めた距離は視線方向の密度極大とは 同じでないことである。 Lopez-Corredoira et al. (2007), Cabrera Lavers et al. (2007), が述べているように、構造体の厚みが増すと軸角は実際の角度から離れていく。 ロングバーの場合は薄くて長いのでそのズレは小さい。バルジではズレの値が １０-１８度に及ぶので注意が必要である。 図５．銀河面 X-Y 上のレッドクランプコブ位置の分布。太陽は (0, 0), 銀河 中心は (0, 8kpc) である。図には可能な二つの配置を示した。実線＝バー角 45° と 破線＝バー角　25° である。一点鎖線は R = 3 kpc と 4.5 kpc の二つの円を定義する。銀経 10 おきの視線方向も示す。

　４．１．成分の厚み　

バルジの巾とバーの巾　 　距離指数分布に現れたコブの巾にも銀経依存性が現れる。図６を見よ。 l < 10 では幅が明らかに大きく、⟨σ⟩ = 0.75 である。 l < 10 での σ分布標準偏差は 0.128 である。l > 10 ではこれが、 ⟨σ⟩ = 0.496 で、標準偏差は 0.098 となる。図６のデータを 直線フィットすると、 　　　　　σ = 0.64 - 0.004 l となる。 Lopez-Corredoira et al. (2007), はロングバーの半巾値 0.6 kpc を得たが、図６とほぼ一致する。 　バルジ領域ではロングバー分離は無理　 　レッドクランプ星の数もバルジ領域では増加する。l < 10 の星数表面 密度は平均して l > 10 の３倍である。これは３軸バルジ領域ではロング バー成分を分離して取り出すことが不可能であることを意味する。

図６．レッドクランプコブの巾の銀経による変化。

　４．２．Cabrera-Labers et al 2007 との比較　

Cabrera Lavers et al. (2007)との比較　 　図７には TCN-CAIN を用いた Cabrera Lavers et al. (2007), の結果を図５と較べた。明らかに両者は一致する。 図７．図５と同じだが、Cabrera-Labers et al 2007 の銀河面外データから の結果も取り入れた。

TCN-CAIN と UKIDSS の測光を比べると、ΔJ = 0.015 mag, ΔH = 0.167 mag の違いがある。K バンドでの違いが大きいのは使用フィルターの差によるものである。 距離指数で 0.05 mag の違いは実距離で 150 pc の誤差である。 図８．この研究で得た距離指数と 、Cabrera-Labers et al 2007 の 同じ領域に対する距離指数との比較。実線＝１：１の場合。使用した K- フィルターの違いによる 0.05 mag のずれがある。

　４．３．レッドクランプ星の絶対等級における系統誤差　

レッドクランプが暗くなる影響　 　Groenewegen 2008 によるレッドクランプ星絶対等級の再計算はこの研究で 使用した値 MK = -1.62±0.03 と少し異なる値を与えた。 彼はヒッパルコスで決めた絶対等級は明るい方にバイアスがかかっていると 指摘し、真の値は MK = -1.54±0.04 とした。この結論は 我々の距離指数に系統誤差 0.08 mag を付け加える。これは最も近い対象点 D = 5 kpc に対して 0.15 kpc, 最も遠い D = 6.7 - 7 kpc 点では 0.2 kpc の誤差となる。 　 　しかし、図９を見ると分かるように、全体のスケールが縮むだけなので 大きな影響はない。 ( Ro 固定で、バーは中心通過とすると そうはいかない。 ) 　軸角の変化　 　Ro = 8 kpc を固定すると軸角は、ロングバーに対して 39.97±2.22, ３軸バルジに対して20.93±2.61 に変化する。

図９．図５と同じだが、絶対等級 MK = -1.54 を仮定した。

　５．結論