Unifying a Boxy Bulge and Planar Long Bar in the Milky Way

　アブストラクト

　１．イントロ　

　２．永年進化により形成されるバーとバルジ　

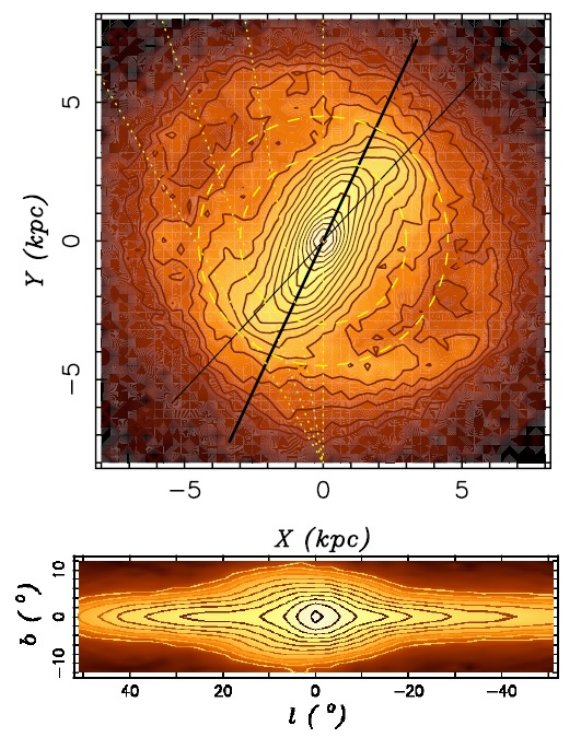
図１．上段： T = 1.9 Gyr でのシミュレーション画像。バーは時計回り で、その端が回転方向に折れ曲がり、渦状腕につながる。表示はバー軸 （太直線）を 25° に傾け、太陽位置を (0, -8) においた。細直線 は傾き 43° で、ロングバーの傾きとしてよく提案されている。 二つの円は半径 3 kpc と 4.5 kpc. 点線＝銀経 0, 10, 20, 30. 下段：太陽から見た側面図。 ボクシー構造が明らか。 　シミュレーション　 　計算コードは Heller, Shlosman 1994 の FTM4.4 を用いた。粒子数は１００ 万で、最初はダークマターハロー内部に指数関数型の円盤状に分布させた。 1.5 Gyr 後にバーが非常に強くなり、バックルして弱くなっていく。その後 バーは進化して再び強くなり、ボクシーバルジとバー構造を示すようになる。

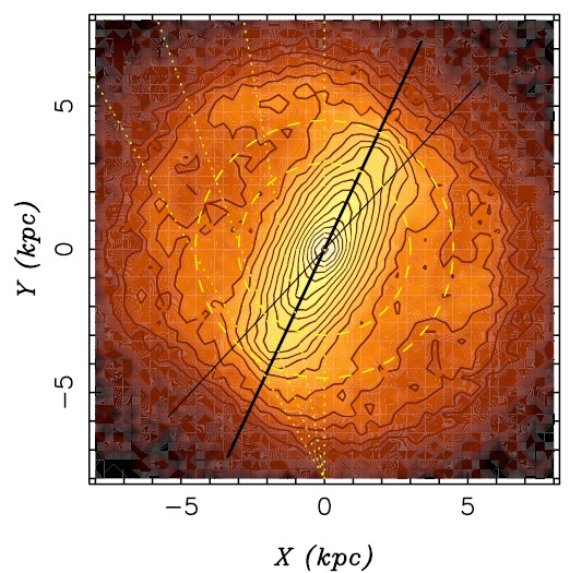
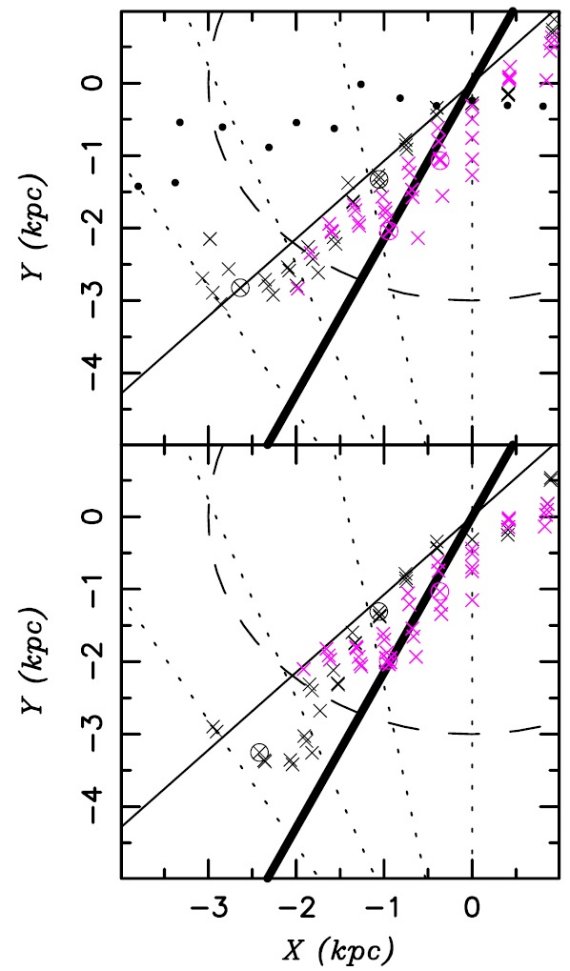
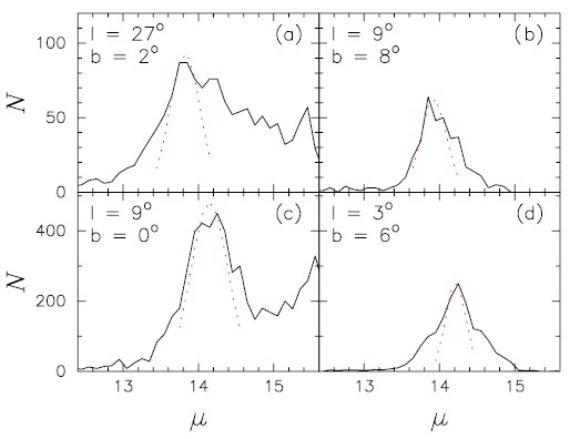
図２．同じシミュレイションからの別の時刻のスナップショット。ここでは バーの終端がバーの内側部と向きが揃っている。これは体積効果をはっきり 示すための例で、銀河系の表示としては図１ほど良くはない。 　1.9 Gyr のスナップショット　 　この時期 T = 1.9 Gyr のバルジが形成され、バーが再び成長した時期が 現在の銀河系に相当すると考える。図１はその正面図と側面図である。このモデルは Martinez-Valpuesta et al 2006 から採ったもので銀河系の再現を目的とはしていない。 このため、バーに較べバルジは実際より l で 20 % 大きく、バルジと円盤も厚い。 折れ曲がりの振動　 　図１上段を見るとバーの先端部が回転方向に曲がっていることが判る。1.2 Gyr の間、モデルは先端部が回転方向に折れ、真直ぐになり、逆側に折れという 振動を繰り返す。その間 40 % の時間はバーが回転方向に曲がった状態である。 そのような折れ曲がりは NGC3124 や NGC3450 (Buta et al 2007) で見える。 　真直ぐなバーの例　 　図２には比較のために真直ぐなバーの例を示す。

　２．１．定量解析：別の角度のロングバーは不必要　

図３．シミュレイション粒子の距離指数分布。左側：銀河面上での分布。 右側：ボクシーバルジ方向。 　図３にはシミュレイション粒子の距離 指数 μ の分布　 　図３にはシミュレイション粒子の距離指数 μ の分布をいくつかの視線 方向に対して示す。図３(a) はバー先端 l = 27 付近で、三つのピークが見 える。それらは、バー、背後の腕、円盤の端である。図３(b) は (l, b) = (9, 8) でボクシーバルジに当たる。極大値は図１の α = 25 ラインの 上に来る。この方向では円盤粒子の寄与は見えない。図３(c)は (9, 0) 方向 で (27, 2) に較べ粒子数の増加が見られる。また (9, 0) のピーク距離は (9, 8) より遠方になる。図３(d) (3, 6) はボクシーバルジの中心付近に当たる。 　図４＝距離変化　 　同様の操作を順次行い、 Cabrera-Labers et al. (2007) と同じようなプロットを作成する。図４にはその結果を図示する。図４(a) は 図１に、図４(b) は図２に対応している。いずれの場合もピンクバツ＝銀河面 から離れた所の星計数ピークは α = 25 の直線に乗っている。しかし、 黒バツ＝低銀緯になると点は遠方へと後退する。このため、 どちらのモデルでも銀河面上 l = [9, 0] の黒バツ点は α=43 の細線に 沿って並ぶ。これは N(μ) ∝ n(D)D2dD/dμ の 体積効果と密度分布の相乗から生じる。l = [20, 9] は中間領域で、 ボクシーバルジが薄くなり銀河メンバーへ移る途中である。l = [30, 20] では 銀河面上の粒子のみが見える。図４上段のバー先端が回転方向に曲がるケース では、銀河面上の黒バツ点が最後まで α = 43 ラインに追随する。 　単一構造による軸角の説明　 　従ってもしも我々がバーの構造について無知なまま図４のような観測結果を 見れば、二つの構造を見出すだろう。その一つは厚くて短く α 25 で、もう 一方は薄くて長く α = 43 となる。

図４．銀河面上での粒子計数極大点の位置。黒バツ＝銀河面上の領域。 ピンクバツ＝ボクシーバルジ方向。 |b| = [4, 8]。上段：バー先端が 回転方向に曲がっている場合。黒点＝当初の軸対称円盤の極大点。 下段：バー先端が真直ぐな場合。太い直線＝モデルの軸線で α25. 細い直線＝ α43. 破円＝半径 3 kpc.

　３．視線速度の予想　

図５＝視線速度プロファイル　 　幾つかの視線速度サーベイプログラムが走り出したので、モデルからの予想 を述べておく。我々は Clemens 1985 の CO サーベイデータに我々のモデルを R = 3 - 4.5 kpc で合わせ、銀経毎に平均視線速度を計算した。Vo = 250 km/s を仮定した。図５に、銀河面上２か所における、平均速度、速度散らばり、 星密度を示す。 　バーモデルの視線速度の特徴　 　バーモデルの非軸対称運動は μ = 13.0 - 13.6 ではっきり した特徴を示す。この領域ではバーの速度プロファイルが平坦になる。 バーの先行先端部に速度の μ = 13.7 に切断が起き、 次に軸対称型の速度プロファイルへ接近していく。真直ぐなバーモデルでは 切断が起きるのはもっと早く μ = 13.5 である。軸対称な場合とバーがあ る場合との差は 30 - 40 km/s である。

図５．上段＝平均視線速度、中段＝速度散らばり、下段＝星密度の距離依存性。 左： (l, b) = (27, 0). 右：　(l, b) = (24, 0).

　４．まとめ