2.1.VVV データ
VVV のサチュレーションは Ks = 10 - 12 である。2.2.GLIMPSE データ
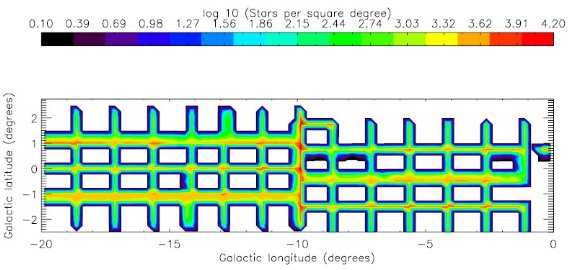
図1.観測タイル。星計数は Δl = Δb = 0.25 で区切られる。 色はduplication の回数。白は duplication がない箇所。
| 内側銀河系のロングバーに関しては未だにその存在や形状に関する論争が 残っている。我々は VVV サーベイを用いて、星計数を 2MASS より 3 等深く してロングバーの形状を探った。我々の探査はこれまであまり研究が及んでい なかった負銀経領域をカバーしている。 l = [0, -20] b = [-2, 2] 領域を VVV, 2MASS, GLIMPSE データで星計数を 行った。そこに平均星間減光を適用した。また銀緯プロファイルを用いて、 中心位置の変動とバーの厚みを調べた。 | ロングバーの構造を l = -14 の遠方端まで調べた。減光補正なしとありとで の星計数の差から粗い減光マップを作製し、星間減光の強い領域を同定した。そ れらは主に、銀河系バーの向こうである。銀緯プロファイルは中心が縦に変動し、 l = -13.8 で最小になることを示した。バーの軸角は α = 43±5 である。バーの厚み、長さ、星分布も調べた。 |
|
ロングバー 半軸長 4 kpc, 軸角 45 のロングバーが示唆されている。例えば、 Lopez-Corredoira et al. 2007, Cabrera-Lavers et al. (2007), Vallenari et al. (2008), Churchwell et al. (2009) このロングバー先端の正銀経は盾座腕が始まる銀経 Dame et al. 1986 と一致する。 Sevenster et al 1999 が述べているように、データから低銀緯部が除かれると軸角 25 付近、 銀河面 l = [30, -15] データからは軸角 40 - 45 が得られる。 中心バー Alard (2001), Nishiyama et al (2005), Gonzalez et al (2011) は第3の成分=中心バーが l = [4, -4] に存在する可能性を唱えた。 ただし、この部分ではバルジ、ロングバーが重なり合う複雑な領域であり、 Lopez-Corredoira et al. 2001b は中心核付近の星形成活動が影響する可能性を指摘した。 |
二本のバーという複雑な構造の代わりに Martinez-Valpuesta, Gerhard 2011 は一本の曲がった構造を考えた。純粋に形態上の観点からはこの構造は 受け入れ可能である。しかし、例えばロングバー先端の星形成域のような現象は 一本構造ではまだ説明されていないが、二本バー説では Lopez-Corredoira et al. 2011 がそれを説明している。 運動学 Minniti et al. (2006) はバルジの高メタル星と低メタル星とでは運動の特徴に 差があることを示した。高メタル成分はバー的な運動をして、低メタル成分は 高齢の楕円体又は厚い円盤的な運動をする。 研究 2MASS, VVV, GLIMPSE を組み合わせて、負銀経の構造を調べた。 |
2.1.VVV データVVV のサチュレーションは Ks = 10 - 12 である。2.2.GLIMPSE データ |
 図1.観測タイル。星計数は Δl = Δb = 0.25 で区切られる。 色はduplication の回数。白は duplication がない箇所。 |
3.VVV減光フリー等級解析法は Alard (2001), の方法に従う。 Robin et al. (2003), Marshall et al. (2006) によると、J-Ks < 0.5 の星は主に太陽近傍の矮星である。そこで、これらの 星は最初から除去する。J-Ks > 0.5 の円盤星もあるが、その比率は低いので ここでは無視する。減光フリー等級は以下の式で定める。
ここに、AKs/(AJ-AKs) = 3/5、(J-Ks)o = 1 とした。青い星は減光ゼロと看做される。 (J-Ks)o 一定のわけ バー/バルジと円盤の間に種族の違いがあるにも拘らず、(J-Ks)o に一定値を 採用する正当性は、平均カラーの変化が非常に小さいからである。星形成領域は 円盤に多く、超巨星や明るい巨星に飛んでいる。しかしそれらの明るい星たちは 数が非常に少ない。 レッドクランプ星の固有カラー実験 Sarajedini et al 1995 が述べているように(?)、レッドクランプ星は 年齢、メタル量変化に対し安定なカラーを有する。(J-Ks)o = 1.0 が妥当な値 であることを立証するために、我々は (J-Ks)o = 0.6 - 1.6 の範囲で、補正 Ks を求める実験を行った。0.25°×0.25° 区間内で 0.5 mag ステップの星計数(多分赤化補正後。)を実施する。 銀河面領域 ではこの 0.25° スケールで減光が大きく変化する。従って適切な固有 カラーによる補正が行われないと隣接区間同士で星計数の変動が大きくなる。 変動が最も小さい固有カラーが真の固有カラーであると考える。 (i, j) 区間の星計数分散を以下で定義する。
|
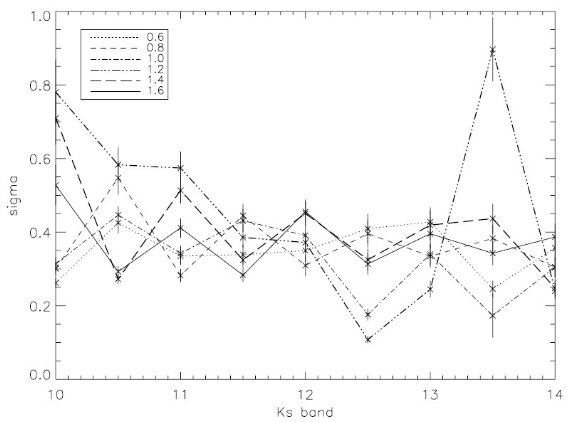 図2.式2で定義される σ の完全性限界による変化を (J-Ks)o 毎に示す。 全体の変動 σ は全区間の二乗平均として次の式で定義される。
図2には σ がカットオフ等級によりどう変化するかを、固有カラーの値 を変えて描いた。(J-Ks)o = 1.0 は、補正 Ks = 13.5 まで、安定して低い σ を維持している。 完全度限界 各区間で 0.5 等ビンの星計数ヒストグラムを作る。そのピーク等級を完全度 限界と定める。95 % の領域区間で完全度等級は Ks ≥ 13.5 であった。|l| ≤ 2 の幾つかの区間でそれより浅くなるが中心領域は今回の研究に重要な 個所ではない。 |
|
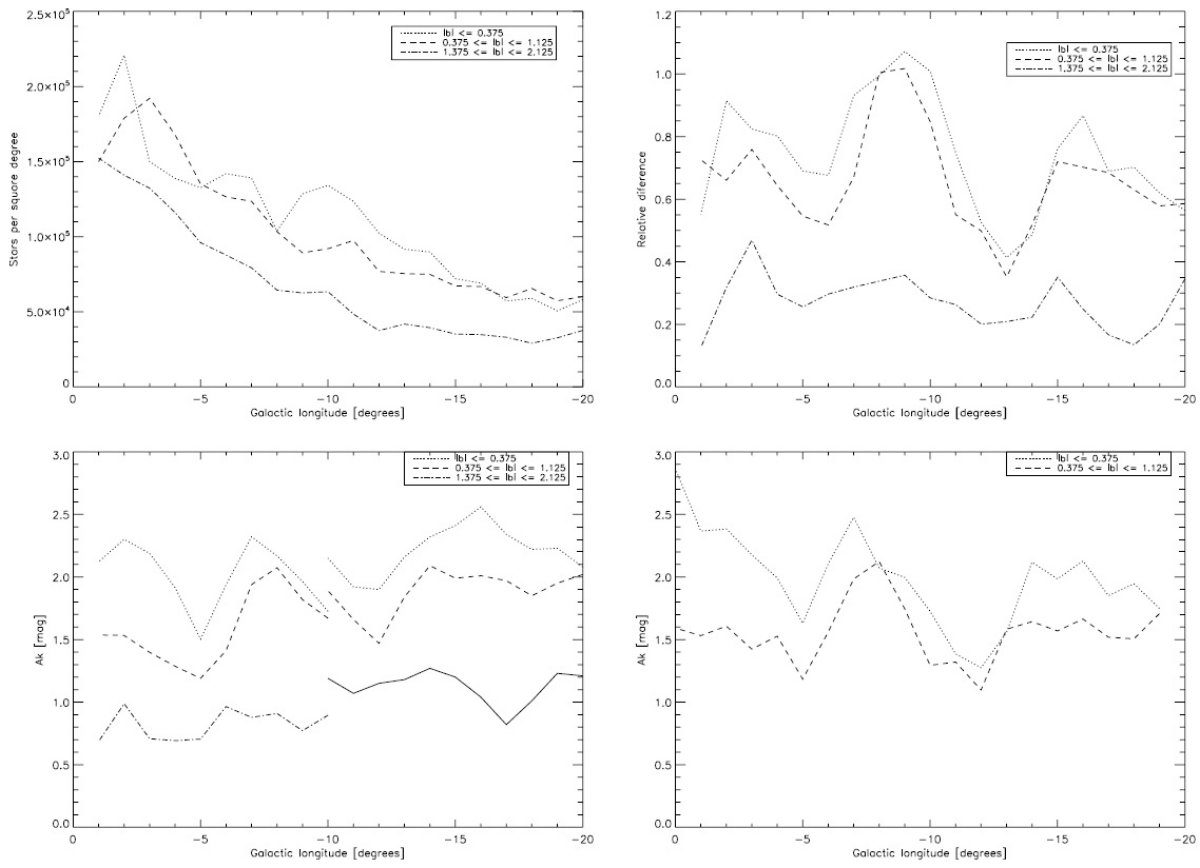
図3=星計数の銀経による変化 ここで考察する銀緯帯は、 i) |b| ≤ 0.356. (b = 0, ±0.25) ii) |b| = [0.375, 1.125] (b = ±0.5, 0.75, 1.0) iii) |b| = [1.375, 2.125] (b = ±1.5, 1.75, 2.0) 図3に減光補正後の Ks = 13.5 までの星計数の銀経による変化を示す。l = -14 まで明白な現象が見られる。 | その後グダグダ言っているが、不明瞭なので飛ばす。 |
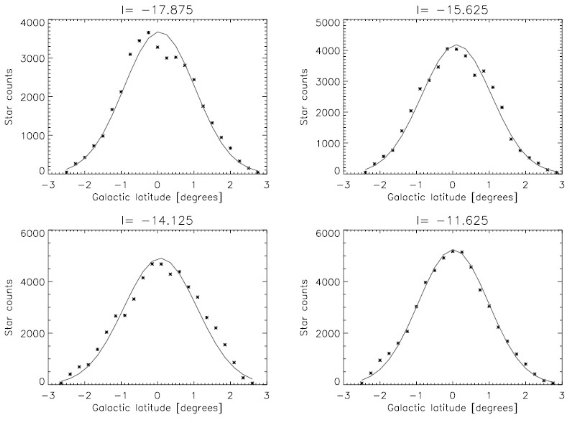 図4.減光補正 Ks 星計数銀緯プロファイルへのガウシャンフィット。 |
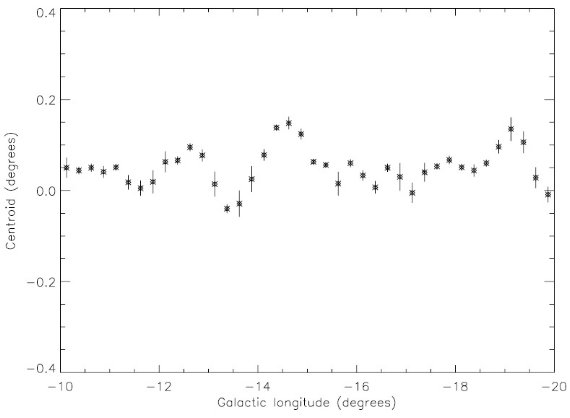 図5.銀緯プルファイル中心位置の銀経による変化。 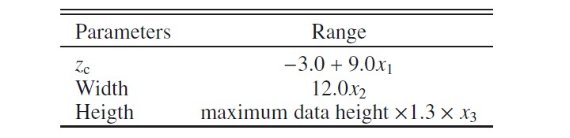 表2.式7でフィットに使用したパラメタ― |
|
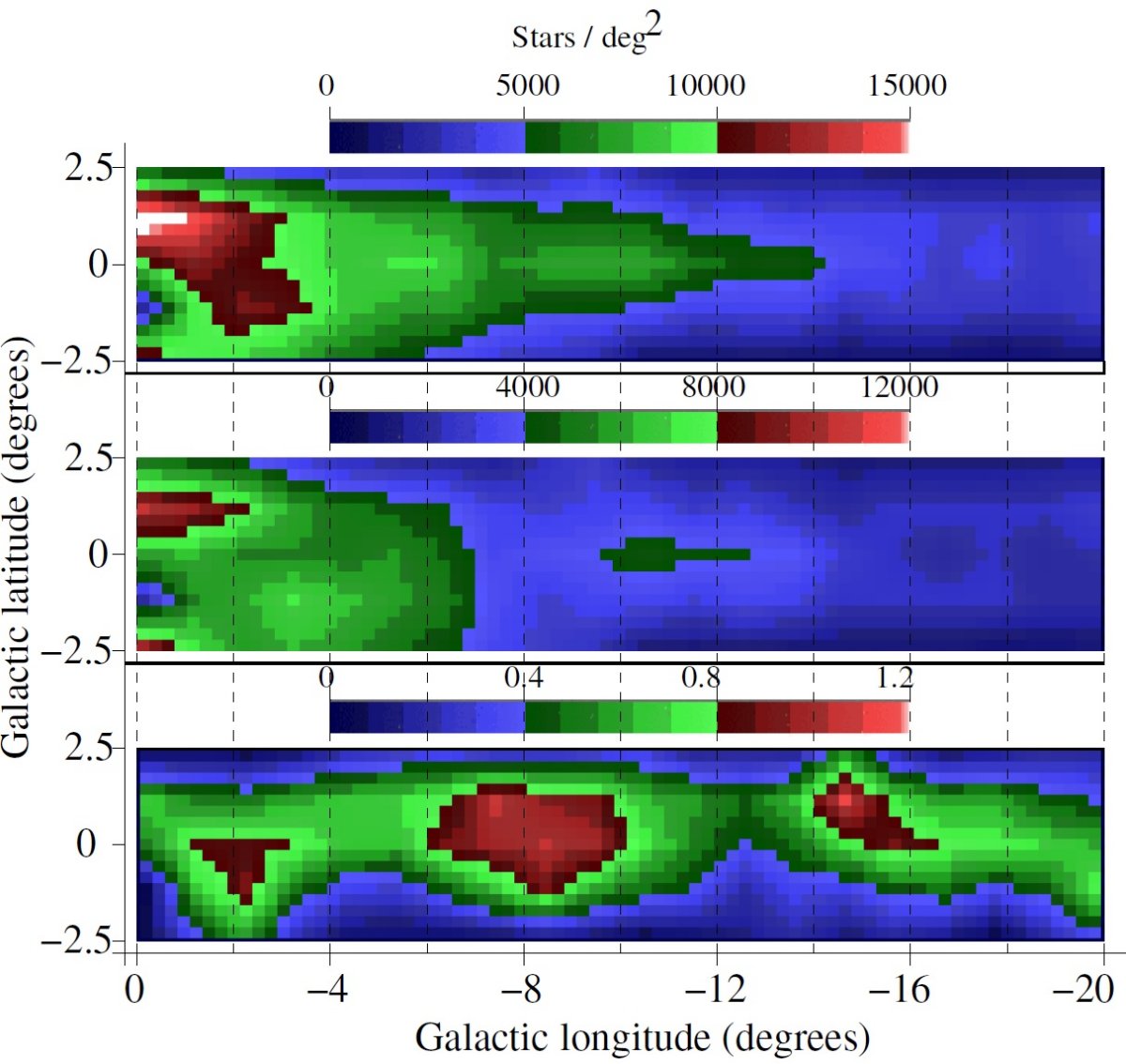
ロングバーの端 図6は減光補正を行った場合と行わなかった場合の Ks = 13.5 までの星計数 である。図6上段には l = -8 で終わるおそらくバルジの構造が見えている。 ロングバーの構造は l = -14 まで伸びる緑色の部分である。l = -15 の先では 星密度は薄青色に変わって減少していくがそこは円盤部分であろう。 共回転半径ではガス欠乏 力学共鳴モデルもバー終端領域が共回転の影響を受けることを示している。 渦状腕のポテンシャルが働き、共回転半径の内側では中心方向にネットの流れが 生じる。その結果、共回転領域からはガスが汲み出されて欠乏するのである。 減光補正の重要性 図6中段は減光補正の重要性を物語る。補正がないと l = -8 の構造は見え ない。星計数は l = -8 で急激に減少し、l > -8 の構造は厚くなりすぎ、 逆に l < -8 では薄くなり過ぎる。 減光の効果 図6下段では相対的な差を示す。この図ではバー端末部付近での高い減光が はっきり示される。これは図7の GLIMPSE データとの比較からも明らかであ る。K と Kcor との差は平均減光に比例する。したがって、図6 下段は平均減光のマップを表すと解釈できる。図の l = [-14, -16] に現れる 特徴は星間減光の非対称性であり、 Amores 2005 が指摘したように IRAS 100 μm マップでも見える。 Lopez-Corredoira et al. 2001a は l = [-8, -10] にも減光の高い領域を見出した。減光は l≈ -14 バー端末まで減少していく。 |
これは
Calbet et al. (1996)
Rodriguez-Fernandez et al. (2006)
Nagai et al. (2006)
Marshall et al. (2008)
が述べているダストレーンに関係するのであろう。
そこから高い減光域が l = -19、3kpc 腕の近くまで続く。この高減光構造は
図3右上に見られる星計数密度に対応する。
太陽側のバー 太陽側のバーに関しては、l = 27, D = 5.7 kpc の構造について Hammersley et al. (1994), Hammersley et al. (2000), Garzon et al. (1993), Cabrera-Labers et al. (2007), Picaud et al. (2003) の研究がある。 銀河中心向こう側のバーの距離 太陽から見て銀河中心向こう側のバーの距離は 11.1 kpc とした。この値は Lopez-Corredoira et al. 2001a も採用している。もしバーの半軸長 Lo を Hammersley et al. (1994), Hammersley et al. (2000), Lopez-Corredoira et al. 2001a に倣って 4.0±0.5 kpc とすると、銀河中心距離 Ro = 8 kpc として、 α = l + asin[(Ro/Lo)sin l] である。(負銀経 l を考えている)。これから α = 43±5 が得られる。 この値は銀経正の側で Hammersley et al. (2000), が得た値と同じである。 ( Lo の信頼性はどのくらい?) 銀経正の側の軸角 この値は Peters 1976 (α=45), Nakai 1992 (α=45), Hammersley et al. (2000), (α=45) と一致する。また、 Cabrera-Labers et al. (2007), Benjamin et al. (2005), Vallenari et al. (2008) は軸角 45 を得た。 |
|
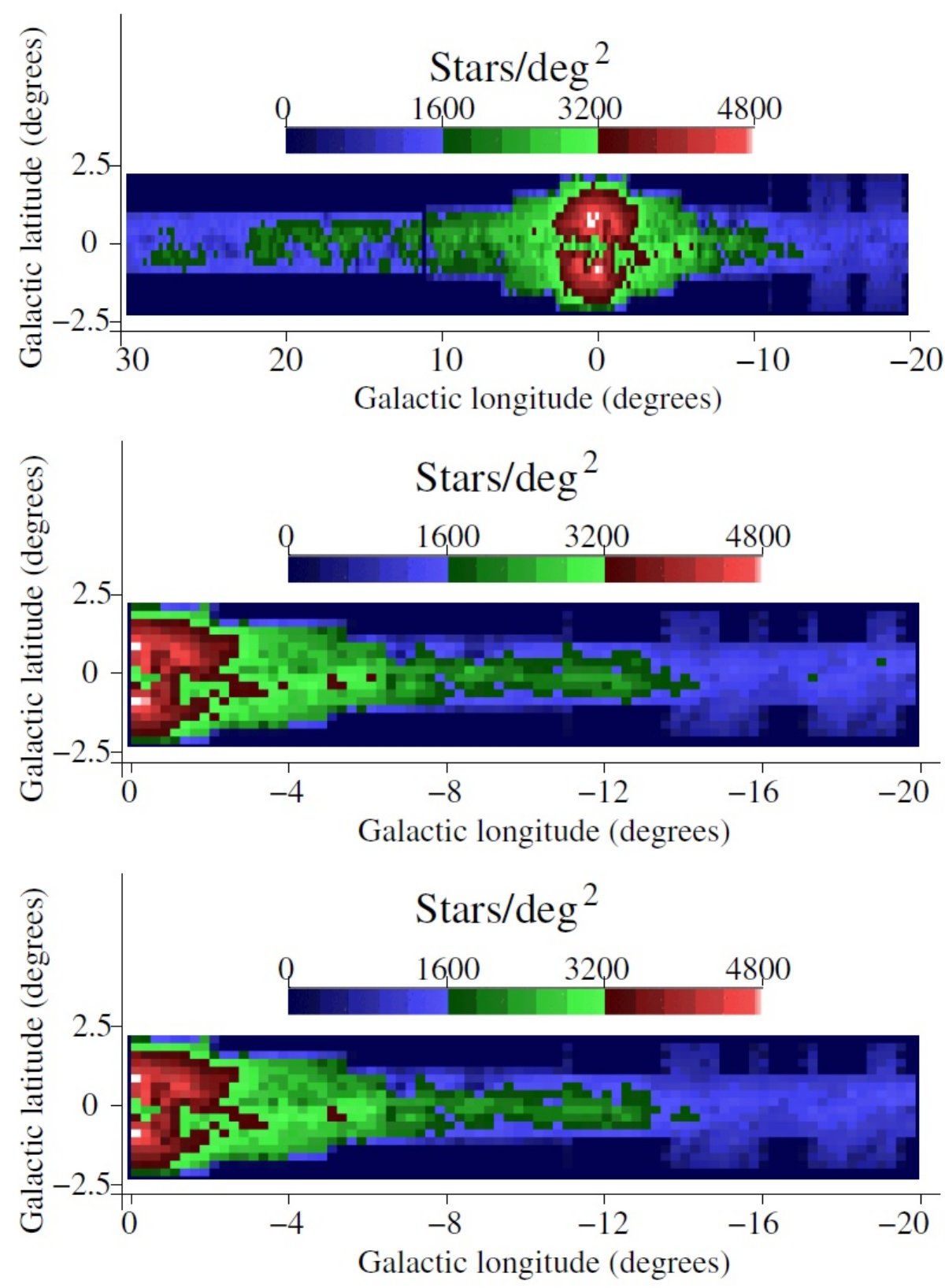
GLIMPSE [8.0] = 11.0 mag までの星計数 図7中段には [8.0] = 11.0 mag までの星計数を示す。図上ではロングバーに 対応する深緑の構造が l ≈ -13 まで伸びていることが判る。その先は 平坦で浅い係数値が続く。図6と同様にバルジははっきりと見え、 l ≈ -8 で終わる。図7上段には VVV を使わず GLIMPSE+2MASS で減光補正した結果 を示す。 GLIMPSE [4.5] の星計数との比較 Benjamin et al. (2005) は GLIMPSE [4.5] の星計数を用いて、軸角 44±10, Rbar = 4.5±0.5 kpc を得た。彼らの [4.5] 係数プロファイルは l ≈ -13 で減少を示す。ただし、彼らの図は我々の図7中段ほど明瞭ではない。 その原因は我々が深い J, Ks 測光とより良い減光補正、それに減光の浅い [8.0] 係数を適用したためであろう。両者の間での大きな違いは、 Benjamin et al. (2005) では、l = [-15, -17] で極めて少ない星計数を示していることである。 この領域は我々の図では大きな減光を受けている領域である。 ( その強い減光の原因は?) Nidever et al.(2012) との比較 Nidever et al.(2012) の図2には l ≈ -15 の先にギャップがある。特徴が不明瞭なのは 2MASS が浅いせいであろう。しかし、GLIMPSE は適切な等級帯、例えば [6.5, 14] の ような、を使えばバーの特徴を観測できるのである。例えば、 Benjamin et al. (2005), Churchwell et al. (2009) を見よ。 VVV 追加の効果 図8を見ると VVV 追加の効果がよりはっきり分かる。二つの差の原因は、 (i) VVV が深いので GLIMPSE とマッチする星の数が増加した。 (ii) 減光補正の精度が高いので l < -10 のプロファイルに差が生じた。 |
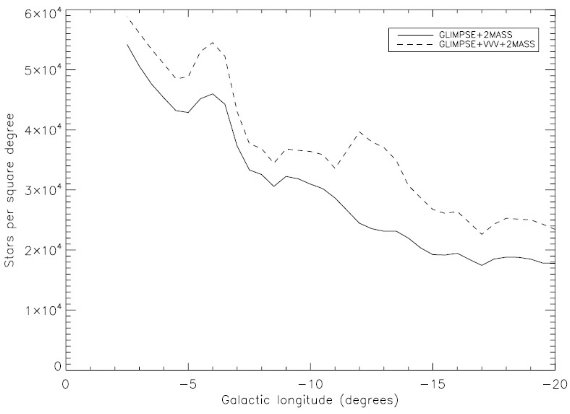 図8.GLIMPSE [8.0] 減光補正後の星計数プロファイル。 |