| 銀河中心方向の 1.2 - 8 μm 星間減光則を, IRSF/SIRIUS サーベイと, 2MASS, Spitzer/IRAC/GLIMPSE II カタログを用いて定めた。 IRSF/SIRIUS サーベイは |l| ≤ 3 deg, |b| ≤ 1 deg で行われた。この J, H, Ks バンドは MKO システムと似ている。GLIMPSE II カタログと同定 された天体に対して、 Ks - (Ks - λ) 色等級図を作った。ここに、 λ = 3.6, 4.5, 5.8, 8.0 μm である。バルジレッドクランプ星の Ks 等級と赤色巨星枝の (Ks - λ) カラーを赤化ベクトルのトレーサーに用い て、AKs/E(Ks-λ) を得た。 | 前論文で得た近赤外の結果とつないで、 AJ:AH:AKs:A3.6:A4.5 :A5.8:A8.0=3.02:1.73:1:0.50:0.39:0.36:0.43 を得た。 これは、λ > 3 μm での減光曲線の平坦化を確認するものである。 2MASS J, H, Ks に関しても減光を求め、 MKO システムとの一致を確かめた。 この結果、J, H, Ks 帯では銀河中心方向の減光則が λ-2.0 でよく近似されることが確立した。近傍分子雲や希薄星間空間では信頼できる 観測が不足していて減光則を決めることは困難である。しかし、それらの視線 方向の観測結果を一つの指数関数で表現することはできない。 |
|
Aλ の直接測定は極めて難しい。 減光 Aλ の直接測定は極めて難しい。そこで、通常は 次の式を用いて、推定する。
Rieke, Lebfsky 1985 Rieke, Lebfsky 1985 は銀河中心方向の超巨星５個と ο Sco の 観測から平均値として、E(V-K)/E(B-V)=2.744 を導いた。そして、 L, M, 8μm での減光の様子から、 AV/E(B-V) = 3.09 ±0.3 を仮定した。 問題は長波長での測光精度が悪いことである。 Lutz λ > 3 μm Lutz et al 1996, Lutz 1999 は銀河中心 Sgr A* の ISO/SWS により 水素再結合輝線の観測を行った。彼らは 14"×20" アパーチャで 行った HIIR 観測をケースＢモデルと比べ、減光曲線が Rieke, Lebofsky 1985 モデルよりずっと平坦であることを見出した。ただし、彼らは解析の際、 AK = 3.47 を仮定したことを注意しておく。 3 - 8 μm Indebetouw et al 2005 は銀河面の２方向で Spitzer/IRAC 観測から 平均色超過の比を導き、 3 - 8 μm で減光が平坦であることを見出した。 Flaherty et al 2007 は近傍星形成領域、Roman-Zuniga et al 2007 は Barnard 59 の観測から 3 - 8 μm でやはり平坦な減光を見出した。 |
これらの研究ではまず超過カラーの比 E(λ - Ks)/E(J - Ks) または
E(λ - Ks)/E(H - Ks) を求めた。
続いてそれらは次の式を用いて減光の比にと変換された。
レッドクランプ法のバルジへの応用 この論文では RC と RGB 距離分布の中心値は一定と仮定して、 AKs/E(Ks-λ) を求める。そしてその結果を以前に求められた 結果と比較する。 この方法は以前の中間赤外減光測定法に比べると、式 (1), (2) を使用していない 点が特色である。この方法では距離と絶対等級を共通と仮定している。 上部 RGB Frogel et al 1999 は上部 RGB (Ko = 8.0 - 12.5) のカラーをバーデ窓の赤色巨星 と比べて星間減光を得た。Schultheis et al 1999 は等時線モデルを基準に用いて、 減光マップを作成した。Dutra et al 2003 はバーデ窓の星を基準にして銀河中心から 10 deg 内の減光を定めた。強調しておきたいのは我々には SST/IRAC バンドで バーデ星のような赤化フリーの基準天体がないが、元来それは必要なく、等級と カラーの相対シフトのみを使用しているということである。 |
２．１．IRSF/SIRIUS詳細は Nishiyama et al. 2006 を見よ。２．２．GLMIICバルジは Galactic Legacy Infrared Mid-Plane Survey Extraordinaire (GLIMPSE) II として SST により観測された。各点で３回の 1.2 秒露出のIRAC [3.6], [4.5], [5.8], [8.6] バンド観測が行われた。GLIMPSE II には二つのカタログが 配布されている。一つは信頼度の高い Point Source Catalog (GLMIIC) で、もう一つはより完全な Point Source Archive (GLKIIA) である。本論文では GLMIIC を用いた。Meade et al 2008 に基準が述べてある。|l|≤1 deg, |b|≤0.75 deg 領域は別の観測となるので、GLMIIC には載っていない。 |
 図１．IRSF/SIRIUS と GLMIIC の同定天体の数密度。各ビンは 0.032 deg 角。 |
|
IRSF/SIRIUS と GLMIIC との同定 IRSF/SIRIUS と GLMIIC から 5.3 × 106 天体が同定された。 位置の rms 誤差は 0".2 であった。図１にそれらの分布を示す。 SST/IRAC にレッドクランプが見えない 図２に 0.2 deg 四方領域での星計数の結果を示す。レッドクランプのピークが IRSF/SIRIUS 観測には見られるが、他の観測では見えない。限界等級からは [3.6], [4.5] ではレッドクランプが見えるはずだが、おそらく混雑のために この領域では限界領域が変化しているのであろう。 RGB を使う SST/IRAC の色等級図ではレッドクランプがないので、代わりに赤色巨星枝を使う ことにする。 |
 図２．(l, b) = (+0.9 deg, -0.9 deg) 領域の光度関数。上： IRSF/SIRIUS 中： 2MASS 光度関数。 下：SST/IRAC |
|
１： Ks 光度関数 第１ステップとして、サーベイ領域を 0.2deg 四方の領域に分ける。次に、 その領域ごとに Ks 光度関数を作る。図３a にその一例を示した。Ks = 14 付近 にレッドクランプピークがあることが分かる。 ２：色等級図 第２に RGB のカラーを決めるために、領域ごとに Ks - (Ks - λ) 色等級図を作る。図３b には Ks - (Ks - [4.5]) 色等級図、図４には全 SST 波長に対しての色等級図を示す。 ３：RGB 勾配 第３に領域ごとに RGB 勾配を定める。そのために RGB を ΔKs = 0.5 mag の区間に分ける。そしてその区間の星の平均カラーを求める。図３b の丸印がその 平均カラーである。これらの丸印を直線フィットして RGB 勾配を定める。  図３a．(l, b) = (-0.3deg, -0.7deg) の Ks 光度関数。  図３c．13.0 < Ks < 13.5 の Ks-[4.5] カラー分布 |
４：平均 RGB 勾配 第４に領域ごとに定めた RGB 勾配の平均値を求める。図３d に勾配-1 のヒストグラムを示した。このヒストグラムをガウシアンフィットして求めた 勾配は 33.6([3.6]), 17.9([4.5]), -24.6([5.8]), -19.1([8.0]) であった。 ５： RGB カラー 第５に上で求めた平均勾配を固定して、各領域毎にもう一度直線フィットを行い、 RC 等級における直線のカラーを定める。固定勾配の仮定の結果、求められた値は RGB カラー等級分布セントロイドの中心値である。座標 (Ks-λ, K SRC) はレッドクランプが見えない場合でも、赤化と減光の指標である。  図３b．Ks - (Ks-[4.5]) 色等級図。丸＝破線枠の平均。RGB の傾きが決まる。  図３d．副領域ごとに決めた (RGB 勾配)-1 ヒストグラム |
|
Aλ/AKs 図５ a - d は、KsRC = RC ピークの Ks 等級対 (Ks - λ)RGB = RC ピークの Ks 等級まで RGB を伸ばした時のカラー、の分布図を示す。直線フィットから 求めた勾配 AKs/E(Ks - λ) を表１に示す。また、そこから求まる Aλ/AKs も同様に表１に示した。表２には全体を ４区分した領域ごとの星間減光を示す。しかし、有意な変化は認められないが N 側は 幾分 AKs/E(Ks - λ) が小さいようである。 |
 表１．IRSF/SIRIUS と SST/IPAC から求めた星間減光。 |
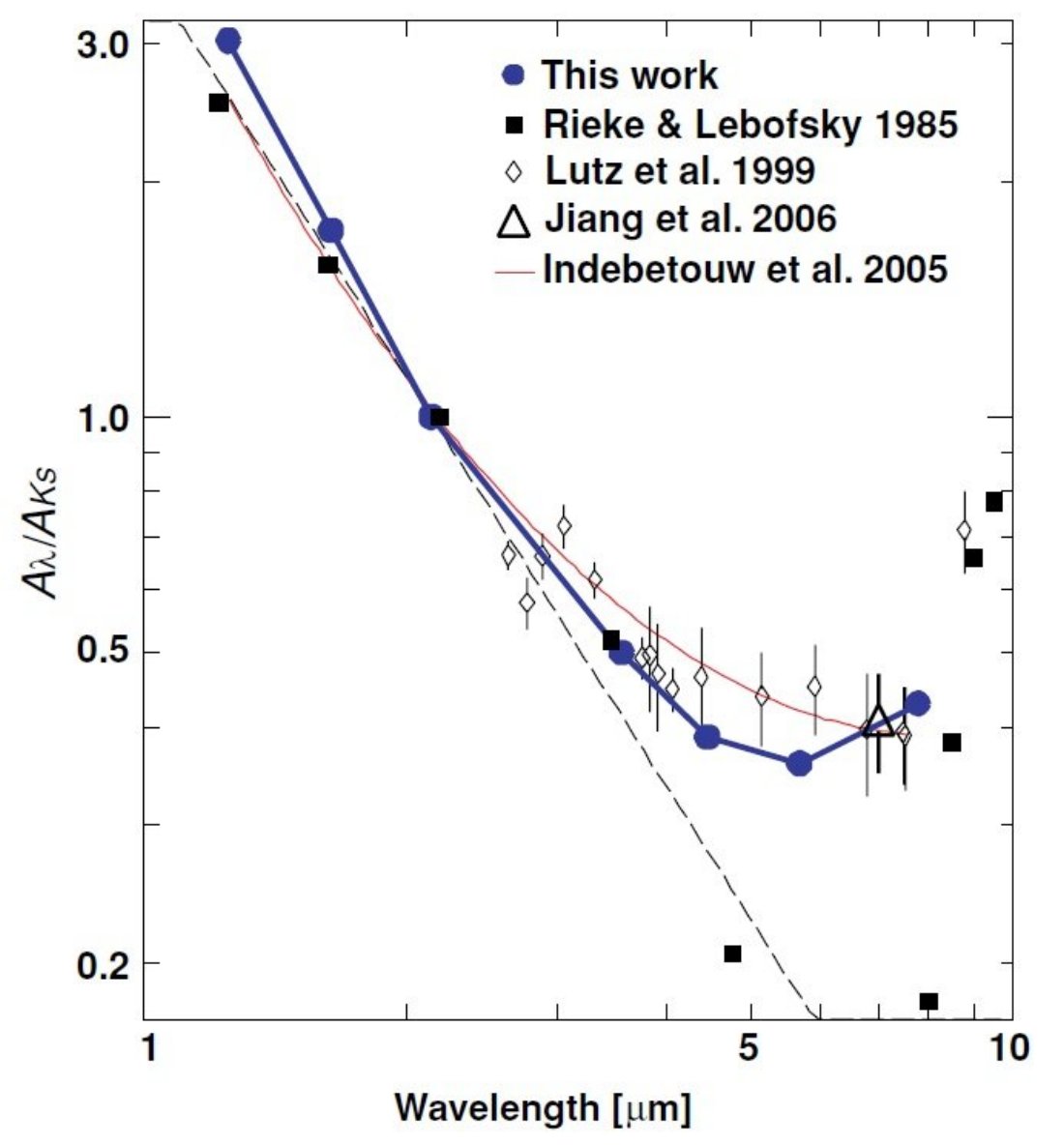
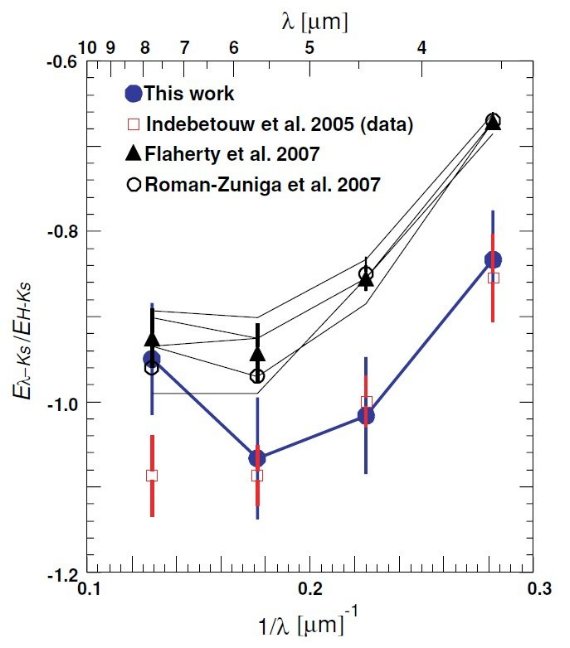
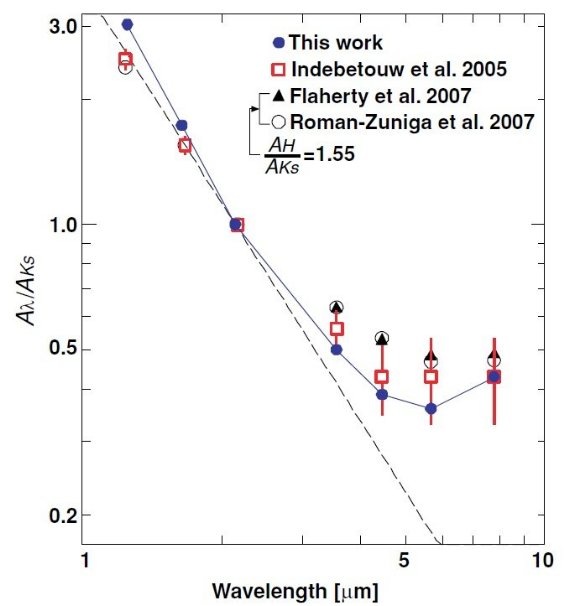
５．１．以前の研究結果との比較べき乗則からのかい離図７にはこれまで得られた銀河中心方向での減光比を示す。ISO/SWS 以前の 研究では 1 - 6 μm 帯の星間減光はべき乗則に従うと考えられていた。 しかし、ISO/SWS による Sgr A* 周囲 HIIR の観測はそれに疑いを投げかけた。 さらに最近の SST/IRAC による星形成域の観測はべき乗則からのかい離をはっきり させた。 3 - 6 μm の平坦な減光 ISO/SWS による GC スペクトルの解析 (Lutz et al 1996) は 3 - 6 μm の平坦な減光を明らかにした。この結果は Lutz 1999 によりさらに改善された。 図７では彼らの結果 Aλ/AV を Ks から彼らの &lambda: = 2.625 μm まで &lambda:-1.99 で伸ばして Aλ/AK に変換している。図７を見ると、 Lutz 1999 の減光は本論文とよく似ているが、[4.5], [5.8] で差がやや大きい ことが分かる。 氷吸収 この差の原因の一部は Sgr A* 方向で観測された大きな吸収帯 かも知れない。Chiar et al 2000 は Sgr* と Quintuplet 星団中の二つ の天体の 2.4 - 13 μm スペクトルを解析した。彼らは GC 方向のダスト成分 を論じ、6 μm 付近にある深くて幅広の吸収帯を H2O, NH3, CO2, HCOOH の 混成氷に依るとした。この方向では氷の 3 μm 吸収帯も検出されている。 Lutz 199 は同じスペクトルを用いており、彼の 3.0392, 3.2970, 5.9082 μm 減光が大きいのは視線上に存在した氷のためかも知れない。吸収の 幅や深さが視線に沿ってどのくらいかがはっきりしていないのだが、もし 3, 6 μm 吸収帯が Sgr A* 方向に特有な現象ならば、本論文とのずれ のいくらかはそれで説明される。 Rieke, Lebofsky 則 Rieke, Lebofsky 1985 は彼ら以前に決められた値とのとの一致に重みを 置いて Av/E(B-V) を決定した。そして、彼らの求めた ο Sco, Cyg OB2 No12, GC 付近の二つの星の J 等級は誤差の大きな 色超過を伴って測られた。これは固有カラーのエラーのためである。 彼らが定めた色超過 E(V-J)/E(B-V) = 2.19±0.04 と E(V-H)/E(B-V) = 2.55±0.02 は E(V-K)/E(B-V) = 2.744 という 仮定に基づいており、もし不定性を考慮するなら実際には我々の結果と矛盾 しない。 ( Rieke, Lebofsky 1985 に出ている シリケイト吸収帯の効果(8μm 付近)がこの論文では見えないのは 不思議。Rieke,Lebofsky のバンド幅が広くてシリケイト帯を引っかけている 可能性は？ ) |
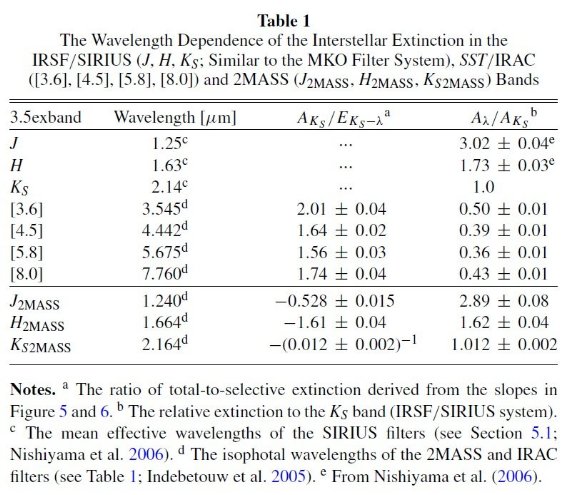
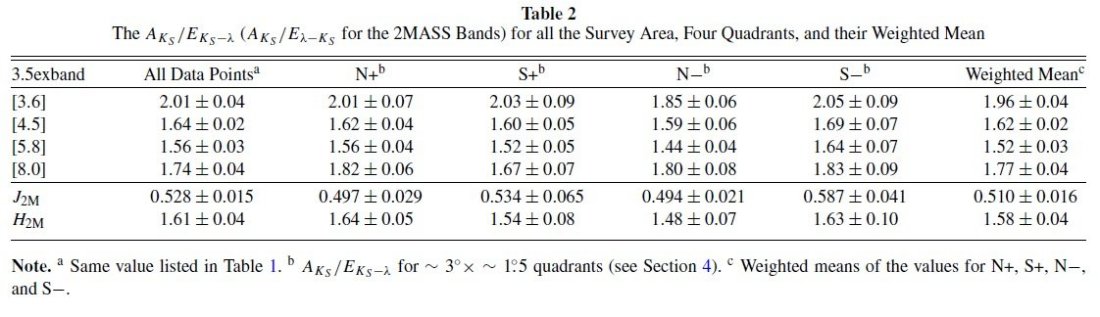
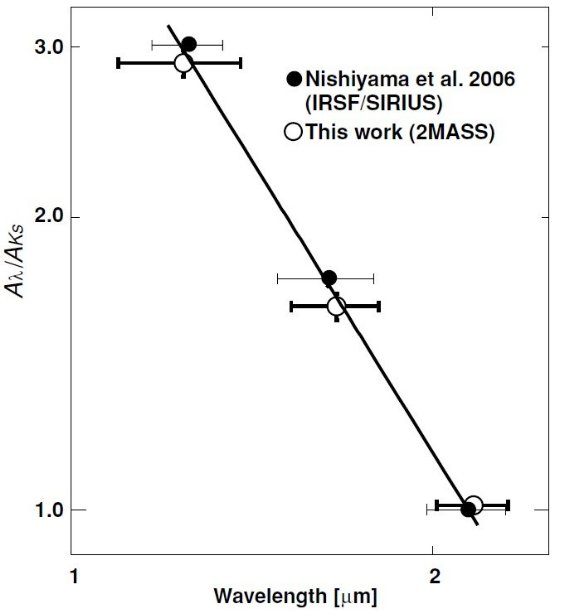
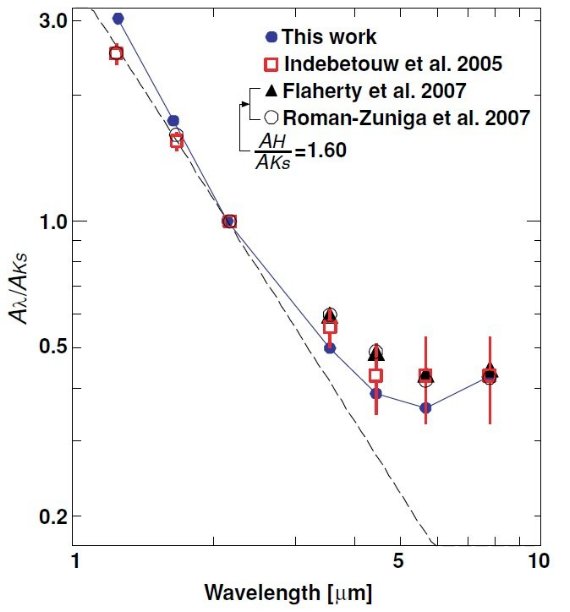
2MASS 同様の方法で 2MASS RGB を用いた結果を表１と図８に示す。我々の結果との一致 は極めてよく、J, H, Ks 帯での減光則は λ-2.0 であり λ-1.6 ではないことが確立した。  図８．J,H,K 帯での減光曲線。実線＝λ-2.0 |
５．２．色超過の比較E(λ-Ks)/E(H-Ks) は星形成領域で大きい図９には色超過の比 E(λ-Ks)/E(H-Ks) の波長変化を示す。星形成領域 と一般星間空間とでは差が存在する。星形成の濃いコア (Roman-Zuniga et al 2007) と近傍星形成領域 (Flaherty et al 2007) とは非常に似た値を出している。 Flaherty et al 2007 が述べているように、分子雲から離れた領域と雲を通る 視線方向とでは系統的にずれが存在するようだ。本論文の E(λ-Ks)/E(H-Ks) は星形成領域での値と比べ、8 μm を除いては、低い。GC 方向で [8.0] の比が Indebetouw et al 2005 の l = 284 deg に比べ大きいのは、他の視線方向と比べ Av の割にシリケイト吸収が大きい、τ9.7/Av 大、という Roche, Aitken 1985 の主張と一致する。 図９．色超過の比 E(λ-Ks)/E(H-Ks) の波長変化。 青丸＝本論文。白丸＝Roman-Zuniga et al 2007。実線＝Plaherty et al 2007 による星形成５領域。黒三角＝その重み付き平均。赤三角＝ Flaherty et al 2007 が Indebetouw et al 2005 データから求めた比。 |
 |
 図１０a．Aλ/AKs の波長変化。青丸＝ GC 方向(本論文)。 赤四角(Indebetouw et al 2007)＝分子雲を外れた視線方向。黒三角(Flaherty et al 2007), 白丸(Roman-Zuniga et al 2007) = 星形成域。破線(Draine 1989)＝ λ-1.75. 変換に AH/AKs を仮定した。 ５．３．異なる視線方向での減光曲線J, H, K 帯でべき乗指数 -2.0 の普遍性絶対減光強度は銀河中心方向のみで得られている。他の視線方向では少なくとも 一つの量、例えば AH/AKs を仮定しなければならない。 (ちょっと意味不明 ) ここではべき乗則を仮定してその指数を調べる。Flaherty et al 2007 は E(J-Ks)/E(H-Ks) を NGC2024/2023 と NGC2068/2071、Serpens で測り、それぞれ 3.00±0.04, 2.98±0.03, 3.05±0.04 を得た。彼らは また l = 284 deg 方向でも Indebetouw et al 2005 データから 3.07±0.04 を得た。これらの値は、これらの分子雲や希薄星間空間の間では、この比の変化が 小さいことを示している。 2MASS 有効波長を 1.240, 1.664, 2.164 μm (Indebetouw et al 2005) と仮定し、さらに減光則がべき乗式で近似されると仮定 して我々はこれらの方向でのべき乗指数を求めることができる。得られた指数は -2.04 から -2.18 の間であった。つまり、星間減光は全ての方向で Aλ ∝ λ-2.0 と考えてよい。 では、べき乗指数 -1.7 は？ しかし、Flaherty et al 2007 が示したように、Indebetouw et al 2005 は E(J-Ks)/E(H-Ks) = 3.07±0.04 という上と同じ値を使っているに拘わらず、 もっと緩やかな減光則 λ-1.7 を導いた。実は彼らの論文の表１ ではもっと小さな E(J-Ks)/E(H-Ks) を使っているがこれは選択効果のためであろう。 このように、色超過の比のみからは減光比に縮退が生じるのである。特に、しばしば 引用される JHKs 二色図はべき乗指数の変化に対し極めて感度が低い。したがって、 E(J-Ks)/E(H-Ks) から AH/Aks を一意に決めることはできない。 さらに、 E(J-Ks)/E(H-Ks) 自身が方向で変化することにも注意しなければならない。 例えば Naoi et al 2006 の ρ Oph、Cha I での値は GC と一致する。しかし、 Coalsack Globule 2 (Naoi et al 2007) はずっと大きい値を持つ。 |
 図１０b．Aλ/AKs ＝ 1.60 を仮定して 黒三角(Flaherty et al 2007), 白丸(Roman-Zuniga et al 2007) を導いた場合の変化。 Aλ/AKs の導出法 本論文では AKs/E(Ks-λ) が Aλ/AKs から直接求められている。 それに対して、式(2) を使って、Aλ/AKs を 求めるために, AH/AKs = 1.55 を仮定しなければ ならなかった。異なる AH/AKs は異なる Aλ/AKs に導く。 AH/AKs = 1.55 を用いた結果、 暗黒雲 や星形成域での減光は銀河中心や l = 284 deg での値よりずっと 大きくなった。一方、AH/AKs = 1.60 を用いると 分子雲データは銀河中心値に近づく。もっとも一致させるには 1.69 が 必要だが。 分子雲と希薄星間空間で減光則は同じか？ 分子雲と希薄星間空間で減光則は同じか、異なるのか、現在はっきりしない。主な 原因は銀河中心以外では減光対色超過比が求まっていないからである。しかしながら、 図９に見られるように、E(λ-Ks)/E(H-Ks) の差や、一致させるために必要な AH/AKs = 1.69 という極端な値を考えると、全てのデータを 単一のべき乗則でまとめることは難しい。 |
|
減光則 IRSF/SIRIUS, 2MAS, SST/IRAC を結んで、銀河中心方向で 1.2 - 8.0 μm の減光を求めることに成功した。 J, H, Ks 帯では λ-2.0 でよく近似できることが分かった。さらに、より長波長側では減光曲線が 緩やかになることが分かった。特に、減光は SST/IRAC 波長帯で浅くて幅広な 極小を示す。 A[4.5], A[5.8] は AKs の 0.4 倍より少し小さいだけである。 RC 法の特色 本論文の手法、 RC 法、はこれまでの手法と比べ、AKs/ E(Ks-λ) が直接求められる点が特色である。ただし、個々の天体の AKs は決まらない。 |
方向による変化 銀河中心方向、一般星間空間での減光は、星形成領域でのそれと異なっている。 ただしその差は観測誤差に比べそれほど大きいわけでもないが。 |