Reddening and Metallicity Maps of the Milky Way Bulge from VVV and 2MASS I. The Method and Minor Axis Maps


Gonzalez, Rejkuba, Zoccali, Valenti, Minniti
2011 AA 534, A3



　アブストラクト

背景　
　銀河系バルジの性質は複雑で数か所から外挿で導くわけにはいかない。

　目的　
　赤化マップを作る方法を示し、バルジ構造とメタル量勾配を測る。データには 最近始まった Vista Variables in the Via Lactea (VVV) を用いる。

　方法　
　b = [-8, -0.4], l = [0.2, 1.7] の 1835 サブフィールド内のレッドクランプ星の 平均 J - Ks カラーを求め、バーデの窓での値と比べる。バーデの窓に対しては、 E(B-V) = 0.55 を採用した。そこから微分赤化の影響がないほど小さい空間スケールで 赤化マップを作成する。赤化補正した等級を用いて 0.4° x 0.4° の大きさでバルジ光度関数を作る。それらから距離指標を求め、バルジ構造を探る。 		最後に、各サブフィールドごとに導いた距離と減光から測光金属量を、赤色巨星枝カラー の内挿値を使って、求める。測光金属量分布は分光から求めた分布と比較する。

結果　
　赤化の決定は作った図から見て取れるように小さなスケールの変動に鋭敏である。 エラーの範囲で我々の結果は他の方法で決めた文献値と合致した。我々のマップは それらより高分解能で範囲も広い。光度関数は最近 2MASS, OGLEIII で発見された 二重レッドクランプを示し、従って X 字型のバルジ形態を追尾する。最後に、 測光金属量は分光値と良く合った。

　結論　
　VVV サーベイはここで示した方法でバルジの性質を調べるのに優秀な道具である。 多の方法との一致はこの方法をもっと広げることの安全性を保証する。

　１．イントロダクション　

　バルジは一様でない　

　多くの研究から、バルジの組成、内部形状は複雑と分かった。BW のような 低減光域で得られた星種族構成をバルジ全体に適用することは危険である。 Zoccali et al 2003, Johnson et al 2011 はそれぞれ b = -6 と -8 で、上部 RGB 測光が測光メタル量の決定に使えることを示した。類似の手法で、 バルジ全体のメタル分布を導くなら、バルジ内の鉄の量を初めて与えることに なろう。

　減光マップ　

　しかし、その障害となるのは変動する減光である。|b| < 3 では、 Schlegel et al. 1998 の減光マップの信頼性が低くなることはよく知られている。 Schultheis et al. 1999 と Dutra et al 2003 は 2MASS を使い、RGB の測光特性から内側バルジのいく つかの領域で 2D 減光マップを得た。 Marshall et al. 2006 は内側銀河系を角分解能 15' で 3D 減光マップを得た。しかしながら、 外側および最内側を含めた一様なバルジ減光マップは依然として必要である。 		レッドクランプをトレーサーにできる　

　レッドクランプの測光解析からバルジ全体に亘る減光と構造が得られる。 バルジのように古くて比較的高メタルな種族では、K-等級の補正は 0.1 等 程度である。したがって、レッドクランプの等級を減光と距離のトレーサー に使うことが正当化される。

　VVV で赤化と距離、2MASS でメタル量　

　ここでは、 VVV データを用いてバルジを解析する初の試みを提示する。 我々は視線に沿って RC を調べ、赤化と平均距離を調べる。その上方を 次に上部 RGB 星の 2MASS データに移して、バルジのメタル量分布を調べる。

　次は 300 deg2 　

　次の論文では VVV の バルジ 300 deg2 観測データを解析する。

　２．VVV サーベイデータ　

　VVV は二つ　

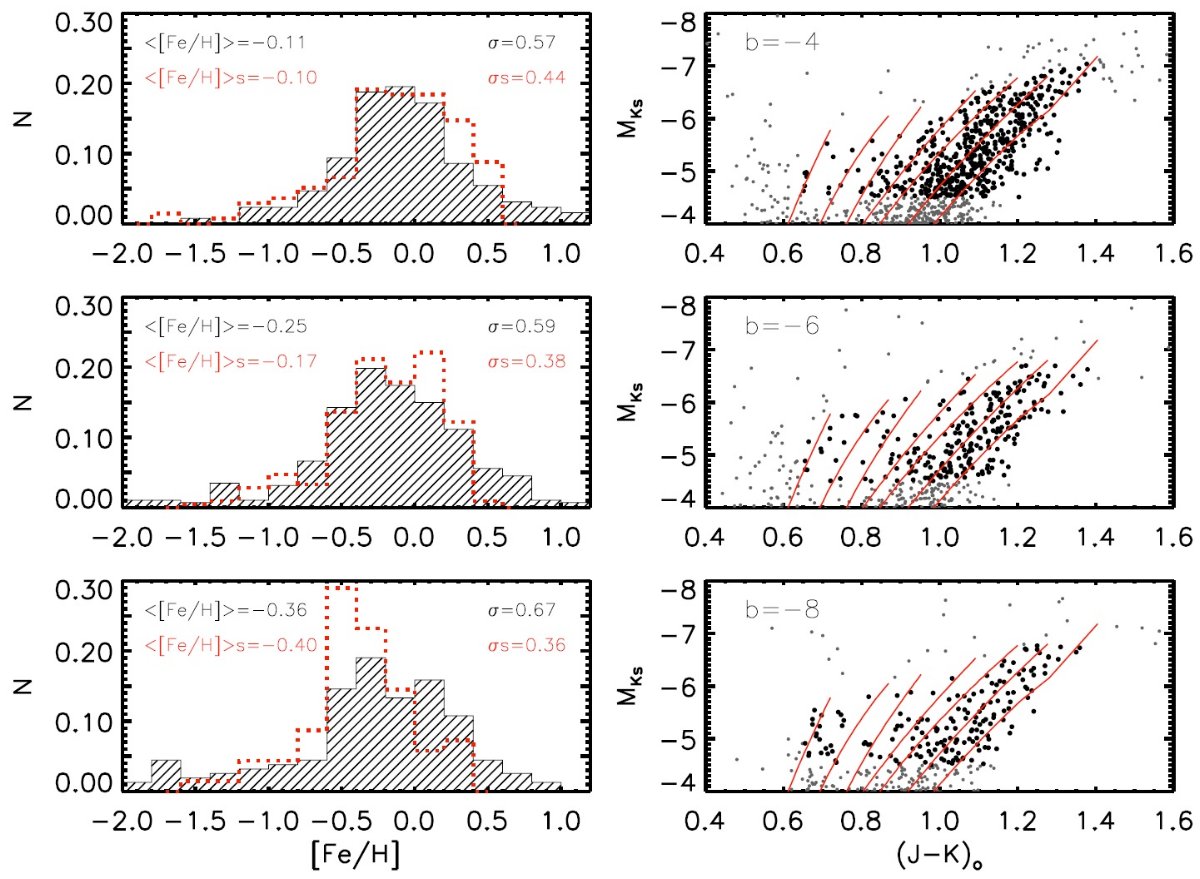
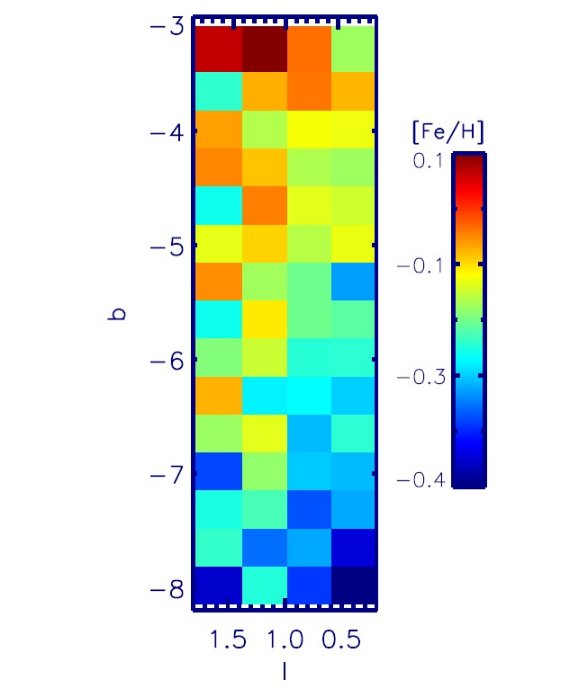
　VVV は 2010 年に開始され、520 deg2 で変光星を探すこと を目標にしている。そのため Ks で繰り返し観測を行い、 バルジの RR Lyr, 円盤内のセファイドや食連星を探す。また、 Z, Y, J, H, Ks の５バンド 測光も行う。観測は次の二つから成る。

（１）バルジサーベイ＝300 deg2 で l = [-10,10], b=[-10,5]

（２）銀河面サーベイ＝220 deg2 で l = [295,350], b=[-2,2]

2010 年の第１シーズンでは全領域の 95 % が　J, H, Ks で掃かれ、 円盤の 84 % と バルジの 40 % が YZ で掃かれた。繰り返し観測の大部分は 来季に持ち越された。

　タイル　

　タイル＝2 pawprints = 12 回露出から作る。各 H, Ks 画像は 4 秒露出、 J は 3 秒x2 回の露出であるので、結局最低でも H, Ks では 16 秒、J は 24 秒の総露出時間を掛けている。


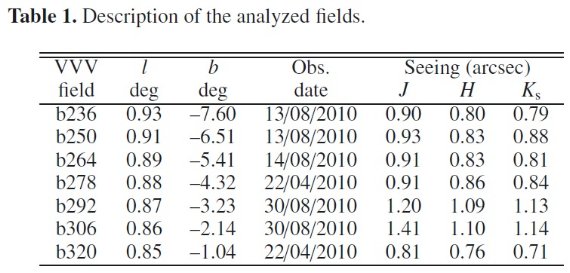
表１．解析したフィールド 		　VIRCAM

　VVV は VISTA 4.1 m 望遠鏡のサービスモードで行われる。バルジ領域は 各 1.48°x1.18° の 196 タイルで張られる。VIRCAM は 4x4 = 16 個 の 2048x2048 ピクセルアレイからなる。アレイ間には隙間があり、６回の 露出(pawprints) で 1.5 deg2 のタイル画像を撮る。0.34"/pixel で PSF の FWHM = 0.51" である。メディアン画質は Ks 0.8", J 0.9", Z 1.0" である。

　２．１．多バンドカタログ　


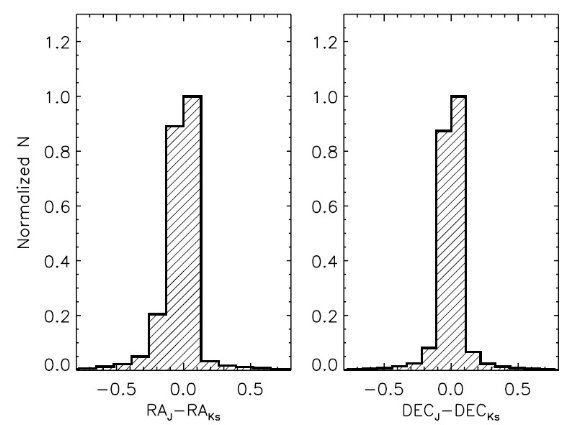
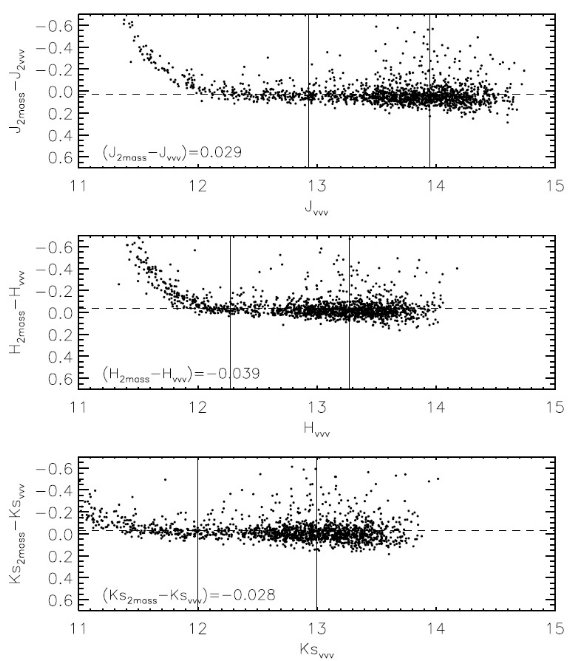
図１．フィールドｂ２７８における J と Ks の位置同定の誤差。

　２．２．測光較正　


図２．VVV カタログと 2MAS 間の J, H, Ks 等級差の分布。破線＝直線間での平均。

　２．３．バルジ短軸の色等級図　


図３．VVV による b278 区間 20′×20′ における (J-Ks, Ks) 図。


　図３には、フィールド b278 の Ks-(J-Ks) CMD を示す。RGB は高メタル星の 特徴で傾きが大きい。幅が広いのはメタル量、距離、減光の散らばりによる。 レッドクランプは Ks = 13 付近に見られ、 RGB バンプと　部分的に混ざり合っ ている。測光が深いのでサブジャイアントも見えているはずであるが、ほぼ 垂直の円盤前景星の青い系列がその同定を困難にしている。

　３．相対的赤化マップ　


図４．右：バーデの窓、10′×10′ 区間の色等級図。図内の箱をレッドクランプとする。左：そのレッドクランプ星の 色分布。実線＝ガウシャン近似

　図４＝ BW の CMD

　BW (l, b) = (1.14, -4.18) を中心とする 10'x10' 領域で CMD を得る。 その E(B-V) = 0.55 である。図４に BW の CMD を示す。図から (J-Ks) BWRC = 0.96 である。

　相対赤化　

　 Cardelli et al. 1989 の減光則を用いると、AJ = 0.87E(B-V), AKs = 0.35 E(B-V) である。したがって、

　　E(B-V) = E(B-V)BW + Δ(J-Ks)RC/(0.97-0.35)

ここに、Δ(J-Ks)RC = (J-Ks)RC-(J-Ks) BWRC である。 Nishiyama et al. 2008 は標準的な AK = 0.640 E(J-K) の代わりに異なる減光則 AK = 0.528 E(J-K) を使用して内側バルジの研究をしたこと を注意する。


図５．右： b306 区間の色等級図。左：赤化補正した色等級図。 星の一部のみをプロットした。等高線がクランプの位置を示している。 右図の矢印は E(B-V) = 0.5 の赤化ベクトル。

区画の大きさ　

　減光決定のため、b < -5 は 10'x10', b = [-5, -1.5] は 6'x6', b = [-1.5, 0] は 3'x3' の区画に分けられた。

　赤化補正した合成 CMD　

　図５に b306 領域における赤化補正の結果を示す。左図は赤化補正前、 右図は各サブ区間で補正した後に合成した CMD である。左図にあった、 ΔE(B-V) にして 0.5 等程度の内部赤化差が右図では消えて、 RC の巾が小さくなっていることが分かる。


　３．１．短軸の赤化マップ　

　図６、７＝減光マップの例　

　図６に l = [2, 0], b = [-8, -1.4](多分) の、 図７には l = [2, 0], b = [-1.4, -0.4] の減光マップを示す。 b が低くなると減光変化が激しくなり、細かい区分が必要になる。
(l 方向はもっと粗くても良さそう。 )


　他のマップ　

　 Schultheius et al. 1999 は Bertelli et al 1994 の 10 Gyr, Zo, R = 8 kpc の等時線 RGB を基準線として、 DENIS 2'x2'CMD の　RGB フィットとの比較から減光マップを作製した。 Dutra et al 2002 は, バルジ合成 CMD を基準とし、RGB の同様な比較から 減光を求めた。


図６．バルジ短軸に沿った赤化マップ。b < -5 の領域を 6&primel ボックスで平滑化した。 		図８＝減光の比較　

　図８には Schuletheis et al 1999、Dutra et al 2002 減光と我々の減光 との比較を示す。我々は Cardelli et ak 1989 減光曲線で A(K) を出して 比較に用いた。我々の値は系統的に彼らより大きく、ずれは減光と共に大きくなっていく。
(差でなく比を考えたら？ )


　差の原因　

　我々の減光は BW の Av が基準となっている。したがって Av(BW) の狂いは 系統的誤差を生む。さらに、バルジ全面で星種族が一様と言う仮定も置いている。 同様の仮定は他の研究にもある。 Schultheius et al. 1999 は、年齢、メタル量が全ての星で共通と仮定した。Dutra et al. 2002 も同様 である。バルジ種族が場所に寄らず一様と言う仮定は全ての研究に共通する 弱点であるが、我々の用いたレッドクランプ星はメタル量依存が小さいという 利点がある。


図７．短軸沿いのバルジ内側領域の赤化マップ。




図８．我々の AK を 黒＝ Schlutheis et al 1999 と赤＝ Dutra et al 2003 と比較。


　４．バルジ光度関数と距離　

　図９＝二つの銀緯での LF の違い　

　赤化補正後の CMD を調べるため、図９には 左： BW(b=-4) と右：ｂ＝６ での CMD を比較する。BW では Kso = 12.9 mag に単一ピークが存在する。 一方、 b = 6 では Kso = 13.2 と 12.6 の二つのピークが見える。また、 BW には Kso = 13.6 に RGB bump が見える。

　X-バルジ　

　McWilliams, Zoccali 2010, Nataf et al 2010 は高銀緯で RC LF がダブル ピークになることを見出した。これは、X-バルジの表れと解釈された。 Saito et al 2011 は 2MASS を用いて、X-型形状が低銀緯では単一バーに収斂 するとした。次の論文ではこの問題を扱う。

図９．下：バーデの窓と b = -6 での光度関数。背後の赤色巨星枝は ２次式で、レッドクランプは b = -6 の方は Ks = 12.9 と 13.2 の ２つのガウシャンで、バーデの窓は Ks = 12.9 の単ガウシャンで フィットした。上：対応する色等級図。




図１０．左：バルジ短軸沿い b = -4, -6, -8 での、斜線ヒストグラム＝測光金属量。 赤点ヒストグラム＝分光金属量分布。平均 [Fe/H] と σ も示す。 右：絶対等級　CMD.経験的 RGB テンプレートも示す。黒丸＝測光金属量 分布を出すのに使った星。

　５．バルジ測光金属量の分布　

　最終目標はメタル量勾配　

　ここまでに求めた減光と距離分布を用いて、研究の最終目標はバルジの メタル量勾配である。我々は、MKs - (J-Ks) 面上に球状星団の RGB 稜線を描き、バルジフィールドの CMDs と比べた。フィールド CMDs を 得るには，先章で導いた距離と減光量を用いた。球状星団の稜線は Valenti et al. 2004 の表３にある値を用いた。これはメタリシティー -2.16 から +0.35 までをカバーしている。特に NGC 6791 は t = 6-12 Gyr で [Fe/H] = 0.35 の銀河星団で貴重である。その上、それらの星団の α 元素超過 が NGC 6528 までは存在し、それより高メタルでは太陽と同じ α 元素 相対比、と言うパターンがバルジ星と同じなので、星団の稜線位置をフィール ド星の α 元素量に合うよう調整する必要がない。メタル量の研究には MKs = -4.5 より明るく、（J-Ks)o > 0.6 の星のみを使用する。

　距離の影響　

　銀緯 b で距離が変化するかも知れないが、メタル量による変化は大きいの で結果にあまり関係ない。

　X バルジのどっち？　

　RGB で X バルジを分離できないので、二つの RC の平均値を RGB の DM と して採用した。

　５．１．分光メタル量との比較　

図１１．バルジ短軸に沿った平均金属量マップ。

　６．結論　

　VVV を用いて、バルジ短軸に沿って性質を調べた。 レッドクランプ星のカラーから短軸沿い b = [-8, -0.5] の赤化を定めた。　 赤化補正した Ko 光度関数から、X-バルジの形状を確認した。

　

　また、 RGB 星を用いてメタル量勾配も調べた。 この研究は今後、 300 deg2 に広げる。