2.1.概説
2.2.薄い円盤
円盤は中央に穴が開いている。円盤は7つの恒星種族から構成され、それぞれが 下式のような異なる構造パラメタ―を持つ。表1を見よ。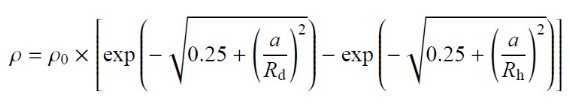
Rd = 2.37 kpc, Rh = 1.31.kpc である。
2.3.減光
ブザンソンモデルは独自の減光分布を備えているが、この研究では 視線毎に減光を決めていき、モデルの減光は使用しない。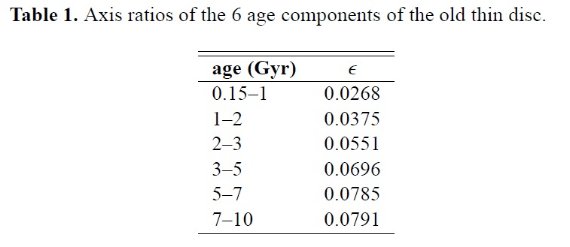
表1.6つの種族の扁平率
| Garzon et al 1997, Lopez-Corredoira et al 1999, Hammersley et al 2000 は TMGS と DENIS データを用い、 (l, b) = (27, 0) 領域で密度超過を見出した。 それは銀河面内のバーかも知れない。我々は銀河面上 l = 15 - 45 の 15 箇所で NIR CAIN 星計数を行い、それをブザンソン銀河系モデルと較べた。 | 比較の結果、 l < 27 で密度超過が確認された。モデルから予想される星数に較べ 超過率は 100 % を越えた。太陽からの距離は 6 kpc 以下と見積もられた。この密度超過 がバーの星種族に対応するならば、バーの半軸長は 3.9±0.4 kpc で、軸角は 45±9 である。 |
2.1.概説2.2.薄い円盤円盤は中央に穴が開いている。円盤は7つの恒星種族から構成され、それぞれが 下式のような異なる構造パラメタ―を持つ。表1を見よ。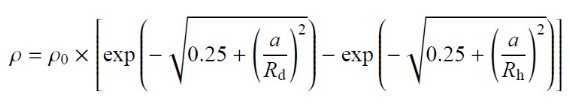 Rd = 2.37 kpc, Rh = 1.31.kpc である。 2.3.減光ブザンソンモデルは独自の減光分布を備えているが、この研究では 視線毎に減光を決めていき、モデルの減光は使用しない。 |
 表1.6つの種族の扁平率 |
|
サーベイ IAC グループは 1999 年から 1.5 m Telescopio Carlos Sanchez (TCS) に 赤外カメラ CAIN を搭載して銀河面サーベイを開始した。20′ × 12′ 領域を単位とした観測が連結されていく。 観測は l = [0, 220] にかけて行われる。 バンド 観測には J, H, Kshort が使用される。限界等級は J 17, H 16.5, Kshort 15.2 である。DENIS や 2MASS より 1 等深いので内側銀河系の研究には大変良い。 選択領域 表2には選択領域 15 個の位置を示す。 | 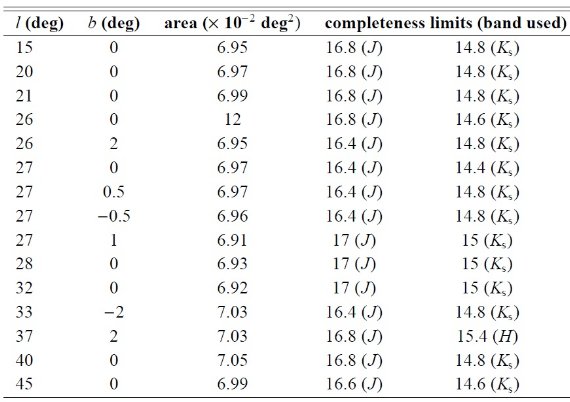
表2.CAIN サーベイの選択領域 |
Lopez-Corredoira et al. 2002
は赤外色等級図上で視線に沿って K2III 星を抽出して、星密度と減光を求める
方法を開発した。その方法では、K = 一定の星の J-K カラー分布を作り、
ガウシャンフィットで極大値を求める。減光 AK は
で定める。 距離 r は
で与えられる。 |
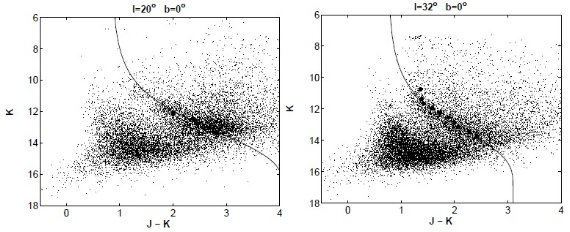 図1.二つの領域での CMD 上で、ガウシャンフィットにより決めた極大点 を示す。実線=極大線。 |
|
Lopez-Corredoira et al. 2002 の値
Lopez-Corredoira et al. 2002 では、レッドクランプ星は K2III とされた。これは Wainscoat et al 1992 の "SKY" モデルに従った結果である。彼が採用した値は、 MK = -1.65, (J-K)o = 0.75 で、 σMK = 0.3, σJ-K = 0.2 である。 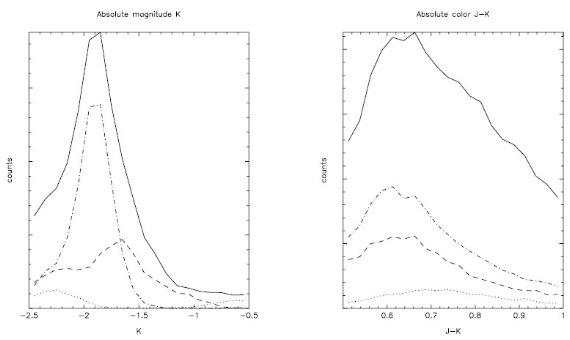 図2.ブザンソンモデルにおける MK と (J-K)o の分布。 点線= K0 星。一点破線= K1 星。破線= K2 星。実線= K0+K1+K2 星。 K1 星の極大=レッドクランプで MK = -1.85, (J-K)o = 0.64。 |
ブザンソンモデルの値 しかし、この論文ではブザンソンモデルの値を用いる。このモデルは 突出した K1 巨星数を予想している。その値は図2に示すように、 MK = -1.85, (J-K)o = 0.64 である。 差は小さい どちらの値を使ってもその差は小さい。AK で 7 % 以下、 距離 r で 9 % 以下である。 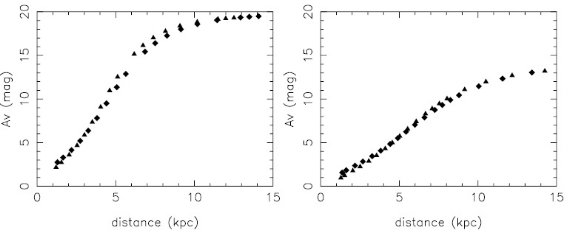 図3.視線に沿った減光分布。左:(l, b) = (20, 0). 右:(l, b) = (32, 0). 三角: MK = -1.65, (J-K)o = 0.75 (Lopez02). 菱形: MK = -1.85, (J-K)o = 0.64 (ブザンソンモデル). 両者の差は小さい。 |
|
H絶対等級 Ks データがないため、(l, b) = (37, -2) 方向では H バンドデータを使用 した。ブザンソンモデルのレッドクランプ星は MH = -1.65, (J-H)o = 0.5 を持つ。その分散は Ks より大きい。 |
H減光 我々は銀河面から少し離れた領域を扱うので、減光は小さく H バンドでも 十分である。 |
|
減光が強い領域では不十分 表2を見ると、減光が強い領域では J データが赤化が強く暗い星に対して 不完全であることが判る。星計数は Ks = 13.5 (l = 37 では H =14) まで、 J-Ks = 3 まで行われた。この限界では不十分な領域もあるが、密度超過は 検出できた。 矮星の混入 前景矮星の混入を減らすため、面内領域に対しては J-Ks ≥ 1.5, 面外領域 では J-Ks ≥ 0.75 の制限を設けた。しかし、ブザンソンモデルによると Ks で暗い、赤い面内星では 20 %、面外では青い J-Ks 星で 40 % の混入が ある。この混入は定量的研究に対しての障害になる。  表2.CAIN サーベイの選択領域。 |
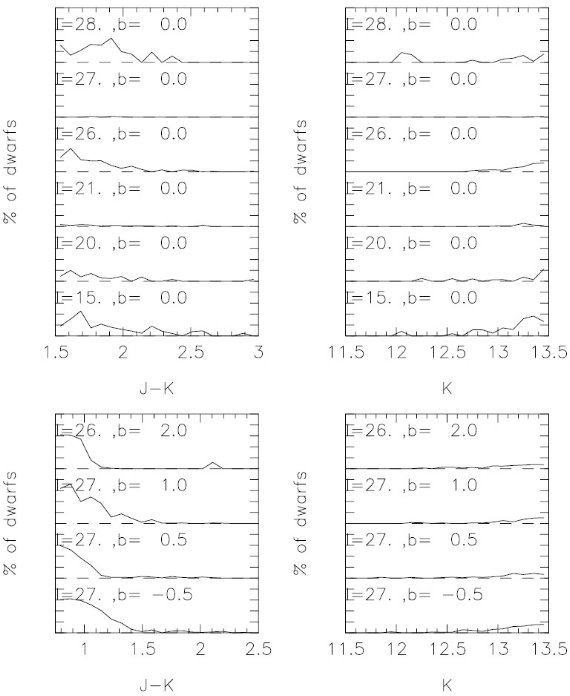 図4.ブザンソンモデルにおける矮星の割合。上:銀河面内。下:銀河面外。 左:(J-Ks). 右:Ks. 破線= 0 %. 破線間隔は 50 %. |
|
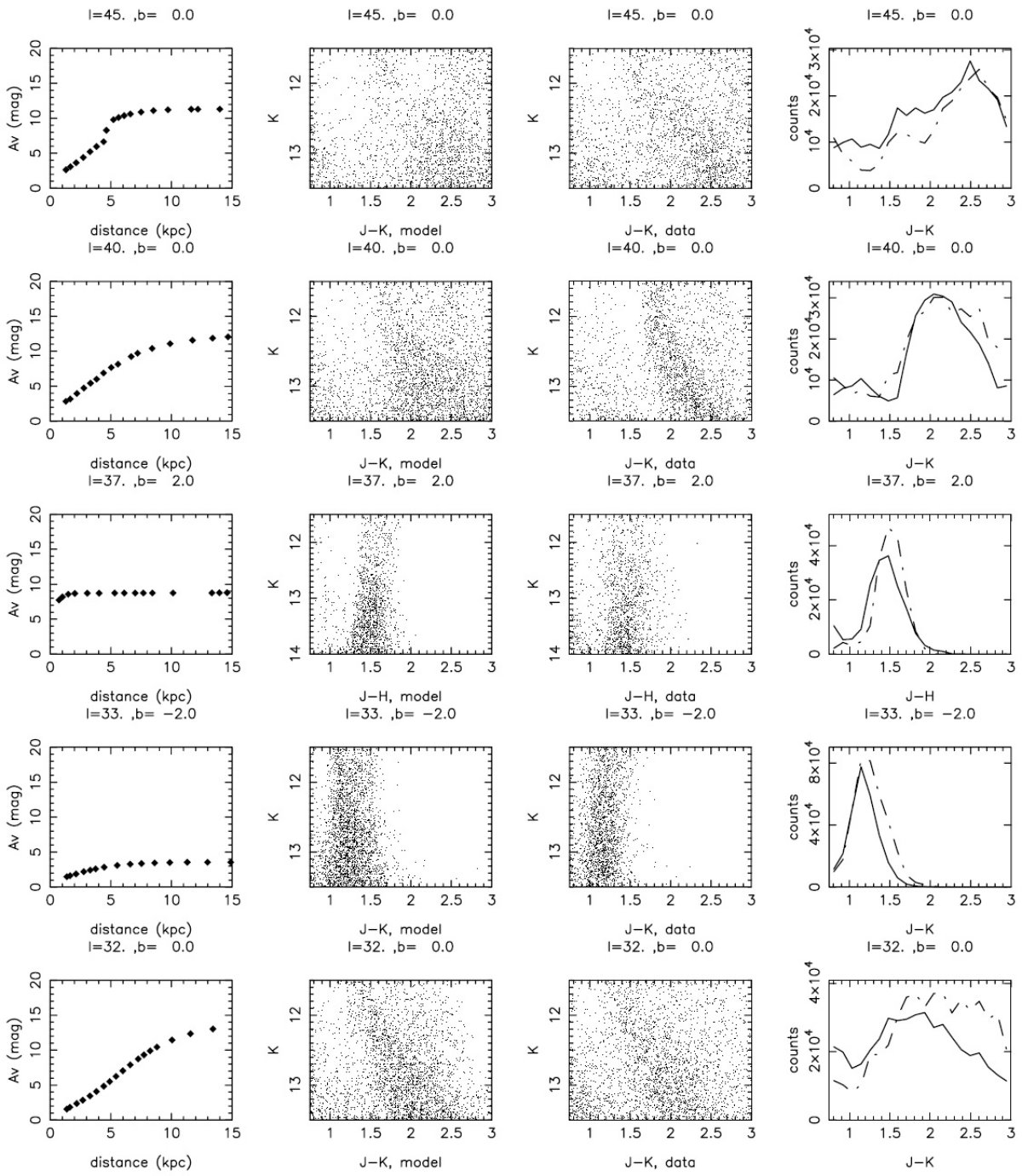
面内と面外領域 モデルと観測の星計数を比べたのは、面内3領域 b = 0, l = 45, 40, 32, 面外2領域 (l, b) = (37, 2) と (33, -2) である。図5にそれらの減光分布、 色等級図、カラー分布を示す。 色等級図でのモデルと観測の比較 色等級図を比べるとモデルと観測の結果は良く似ている。いくつかの領域で 非常に赤い星の数が超過している。モデルに使用した Haywood et al 1997 の 晩期型星寿命を少し長くとり過ぎ、実際にはそれらの多くが既に白色矮星や 惑星状星雲になっているのかも知れない。 |
巨星問題 K5 より晩期の巨星と 7 Gyr より高齢の星を除くことでモデルを補正した。 晩期型星問題は銀河面外領域ではさらに大きくなる。これらの領域では減光が 小さく、大部分は Ks ≤ 13.5, J-Ks ≤ 3 の制限を通過する。その上 赤化が小さいので前景矮星の混入が激しい。 しかし超過量は小さい しかし超過量は小さいので、ブザンソンモデルを使い続ける。 |
|
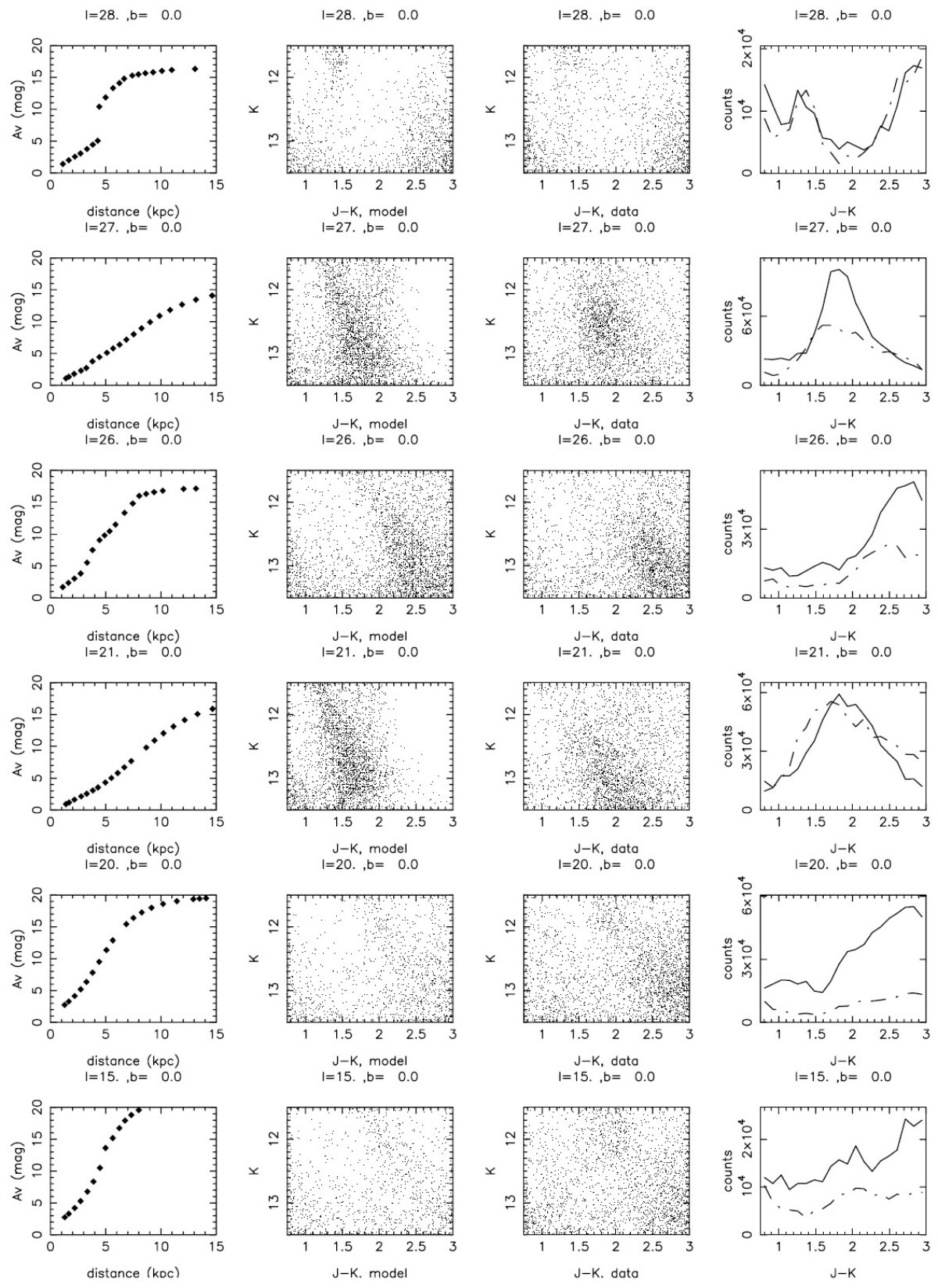
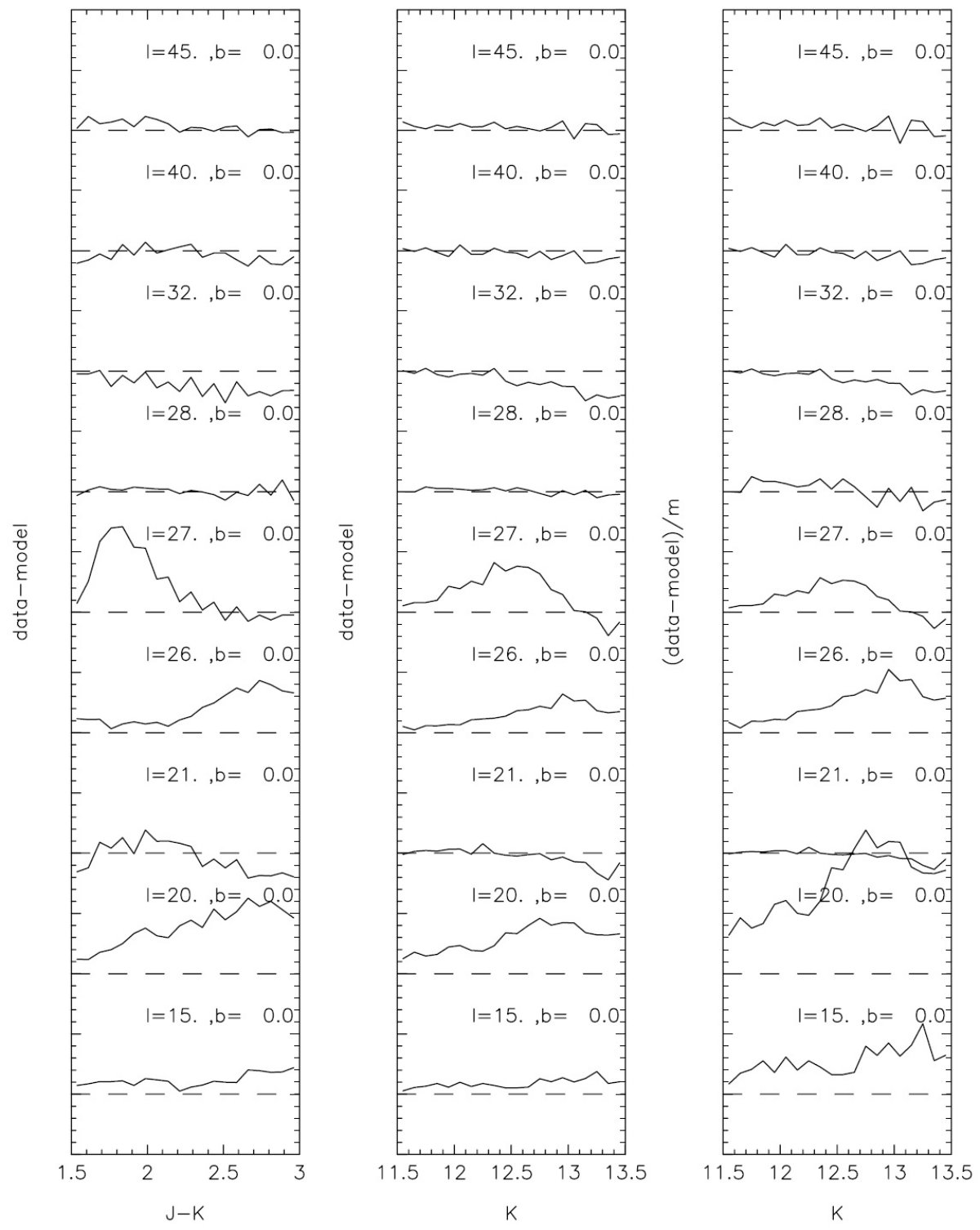
銀河面追加6領域 図5では銀河面に沿った b = 0, l = 45, 40, 32 の3領域と銀河面外 (l, b) = (37, 2), (33, -2) の2領域でモデルとデータを比べた。銀河面に 沿ってはさらに b &le, 28 の6領域 b = 0, l = 28, 27, 26, 21, 20 でも 比較を行った。それらは図6に示した。 密度超過 図7にはデータからモデルを引いた結果を示す。この図を見ると、 l ≤ 27 に明らかな超過が存在することが判る。l = 21 だけには超過が見えないが。 一方、 l ≥ 28 には超過が現れない。 盾座腕の混入 超過の原因として考えられる一つは盾座腕である。しかし、盾座の効果は 接点方向でしか現れないがそれは l = 33 で、それ以外では無視できる程度 ( Hammersley et al. 1994 )である。 モデルのため? CMDの非常に赤い部分を除くと、ブザンソンモデルはかなりよく l = [32, 45] の銀河円盤を表現していると言える。従って、モデルの悪いためにこ の超過が現れたとは考えにくい。 円盤中央ホール しかし、ホールのスケール長の効果は大きい。図8の (データ - モデル) 星計数を見ると、ホールスケール長が 0.5 kpc より小さい時には結果は変わらない。 また 1.5 kpc より大きいのは非現実的である。しかし、 その間ではスケール長 の値が超過に大きな影響を与えることが判る。しかし、その影響は銀経が大きく なると減少し、全ての超過を説明することはできない。 密度超過の始まりと終わり 従って図7の超過を解析した結果、薄い円盤モデルに対して密度超過が存在 することは確かである。それは l = 27 で始まり、少なくとも l = 15 までは 伸びている。その内側では非一様になり l = 21 では消滅する。 |
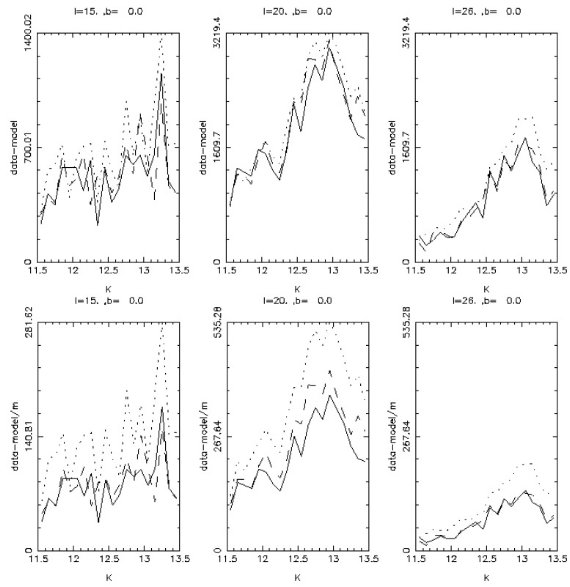 図8.b = 0, l = 15, 20, 25 における (データ - モデル) 星計数。 実線:穴のスケール長=0.5 kpc, 破線= 1 kpc, 点線= 1.5 kpc. 上:実数差(stars/mag/deg2)。下:相対差(%) |
|
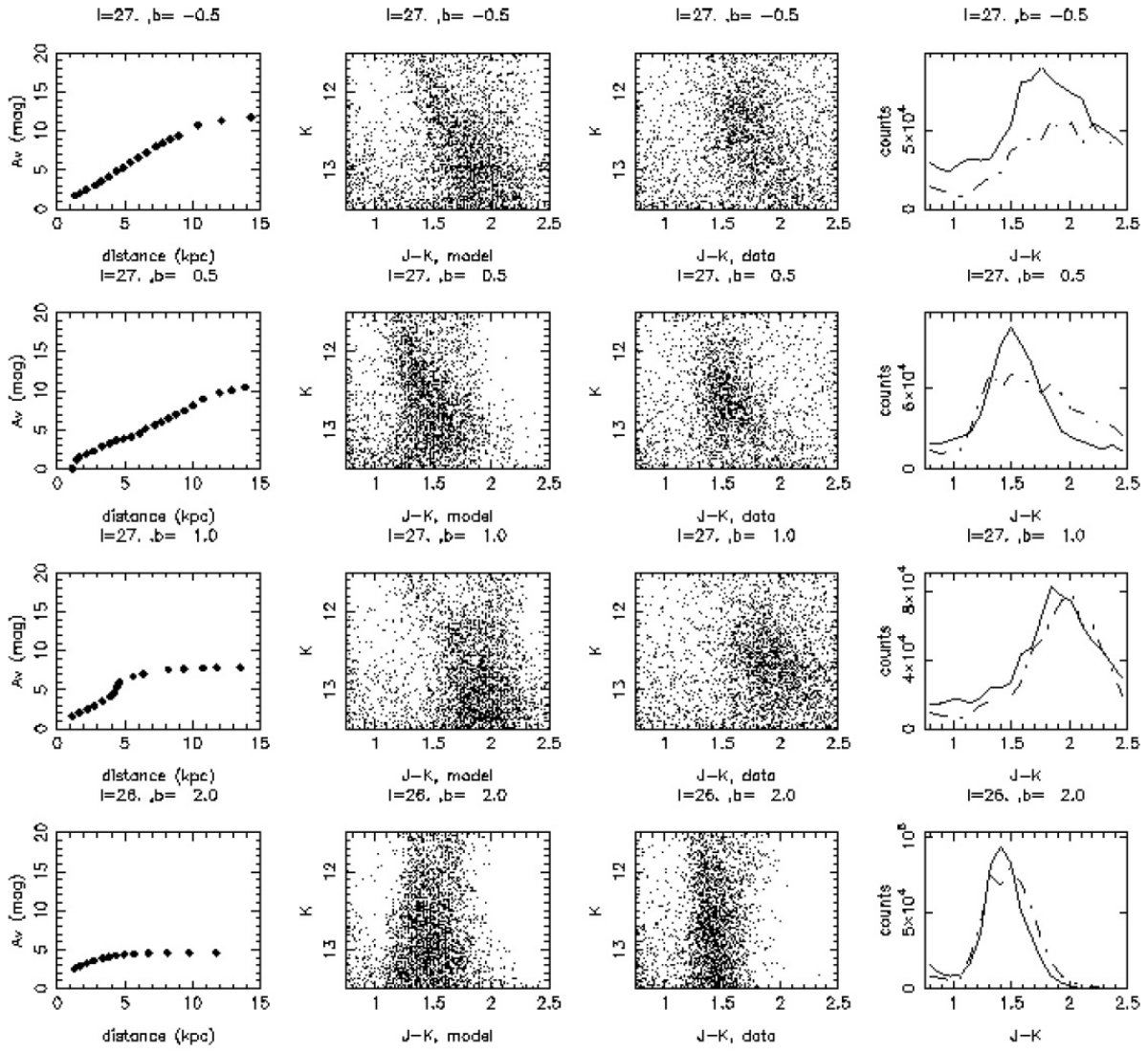
密度超過終端付近の銀河面外4領域 密度超過終端付近の銀河面外4領域 (l, b) = (27, -0.5), (27, 0.5), (27, 1), (26, 2) で星計数のデータとモデル比較を行った。図9には 色等級図、図10では (データ - モデル) ヒストグラムを示す。 比較が困難 しかし、面外では減光が低く、かつ星数も小さいので比較が困難である。 |
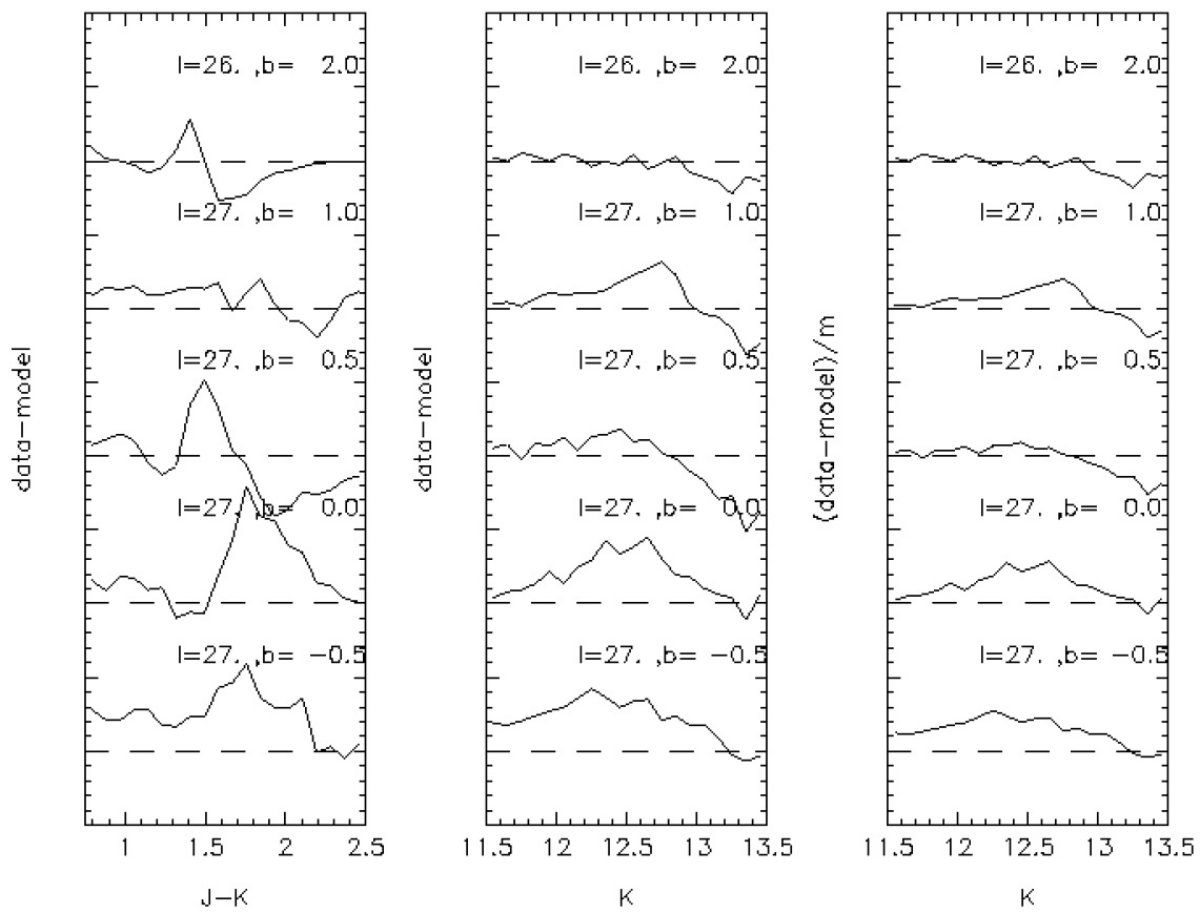
銀河面外では超過が消える しかし、図10は超過が銀緯と共に低下することを示している。実際、 (l, b) = (27, 0) に存在する超過は b = -0.5、+0.5 にも存在する. しかし、b = 1 では弱くなり、b = 2 では消滅する。 このように、少なくとも超過の端 l = 26 - 27 においては超過が 銀河面に貼り付いていることが確認された。 |
|
定量的な特性を得ることは困難 円盤モデルの欠陥、減光の不定性、測光不完全性などがあっても、密度超過 の検出は確実である。しかし、定量的な特性を得ることは困難である。 しかし、それにも拘わらず得られる限りの定量評価を行った。最も重要な 数値は K ヒストグラムのピークにおける星計数の超過量である。表3には6領域に おける、ピーク超過量を示す。数字の信頼性には注意が必要だが、ピークでは超過星 が円盤本体と同じくらいあることが判る。つまり2倍?いやもっと? |
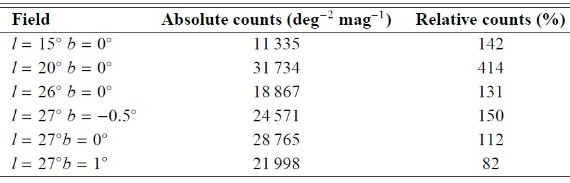 表3.K ヒストグラムのピークにおける星計数の差。第2列=( Ndata - Nmodel) (stars/deg |
|
Hammersley00 の手法を採用 Hammersley et al. (2000) は CAIN データの (J-H, H) CMD 解析から l = 27 において、超過極大が 太陽からの距離 5.7±0.7 kpc にあることを見出した。ここでは、 同様の手法を (J-K, K) CMD に対して行い、ピークまでの距離を定める。 系列端付近でのみ距離が決められる (l, b) = (26, 0), (27, 0), (27, -0.5) の3方向を距離決定に使用する。 そこでは超過極大がきれいに決まるからである。l = 15 と l = 20 は減光が 強すぎて極大を決めにくい。従って、距離がよく決まるのは超過系列の端の 方だけである。 距離決定手順 (1)超過星は円盤星と同じ絶対等級と固有カラーと仮定する。 (2)個々のカラー・等級区間に対する距離を計算する。 (3)距離ヒストグラムをモデルからの超過分に対して作成する。図11. 距離 ピーク距離は (27, 0) と (26, 0) に対し 5.9 kpc、(27, -0.5) で 5.5 kpc であった。 |
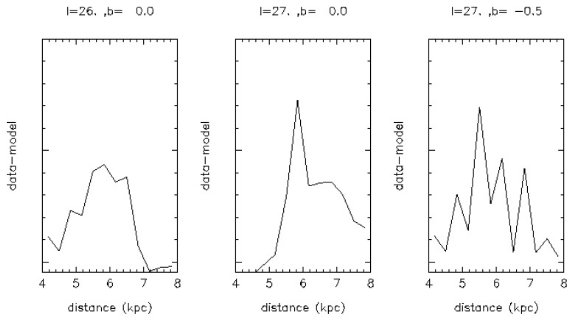 図11.(データ - モデル) 星計数の距離ヒストグラム。 (l, b) = (26, 0) 方向では、Ks = [12, 13.5], J-Ks = [1.6, 3]、(l, b) = (27, 0), (27, -0.5) 方向では、Ks = [11.7, 13.5], J-Ks = [1.3, 2.5] を 12 × 12 区間に 分けて計算した。 |
|
密度超過の系列と距離 密度超過が l = [20, 27] で検出され、 l = 26 - 27 でその距離が 6 kpc より少し小さいことが判った。 バーのパラメタ― 密度超過が銀河面に沿って検出されることは、銀河面バーの存在を示唆する。 この構造が銀河系中心を向くバーであるとし、 Ro = 8±0.5 kpc、 バー端末距離= 5.9±0.5 kpc とすると、図12のような配置から バーの軸半径 3.9±0.4 kpc, 軸角= 45±9 が導かれる。 この結果は以前の研究結果と大体一致する。 結果の不確実性 残念ながら研究は l ≥ 15 のデータに基づいている。 l = 15 領域でさえ、 赤化が強く、かつバルジ星の混入があり、注意深い解析が要求される。 その上、この付近ではホールのスケール長をどう取るかで結果が大きく変わる。 また、(l, b) = (21, 0) のように超過が消える箇所もあり、一様な構造ではない らしい。バーを負銀経側に対称に伸ばすと、 l = -14±2 まで見えるはず である。距離は 11±1 kpc なのでもっと深い観測が必要である。 |
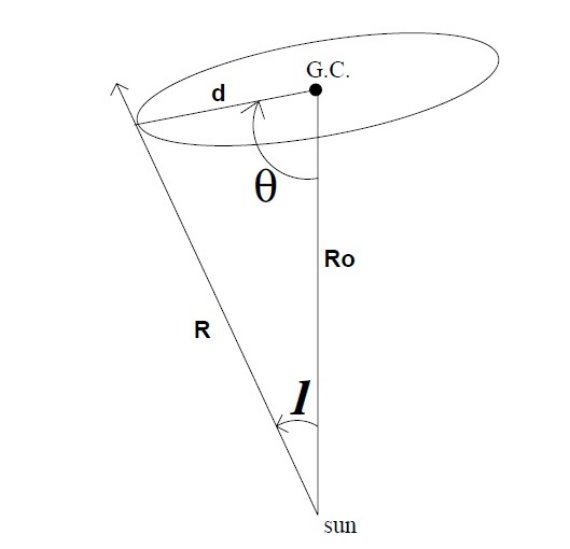 図12.銀河系円盤内バーの説明図。 |