Searching for the In-Plane Galactic Bar and Ring in DENIS

　アブストラクト

　１．イントロダクション　

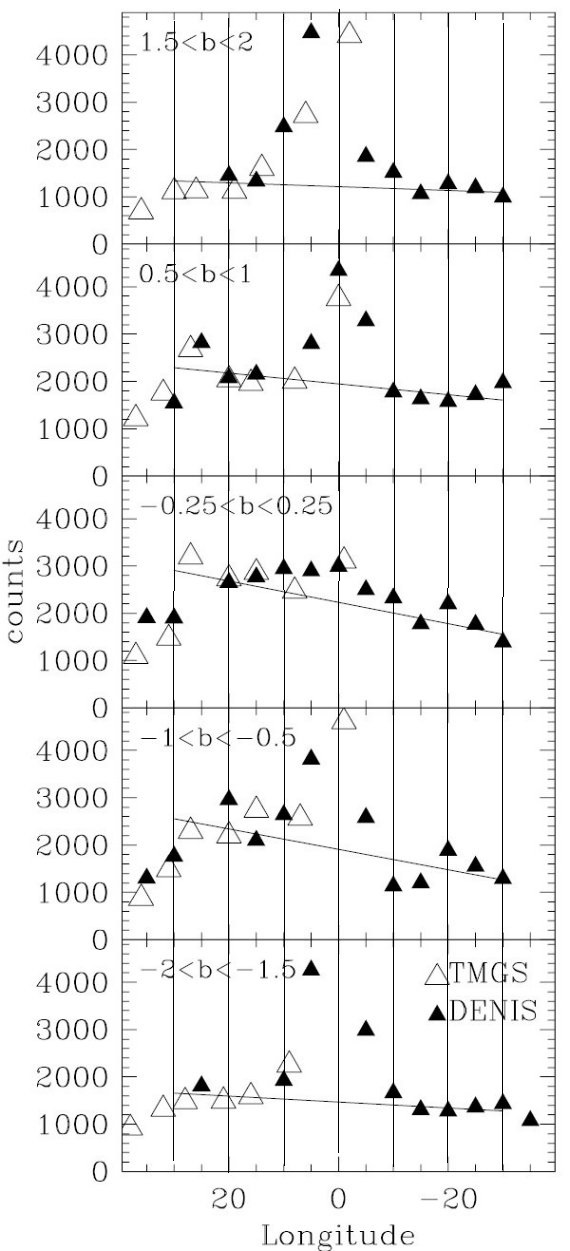
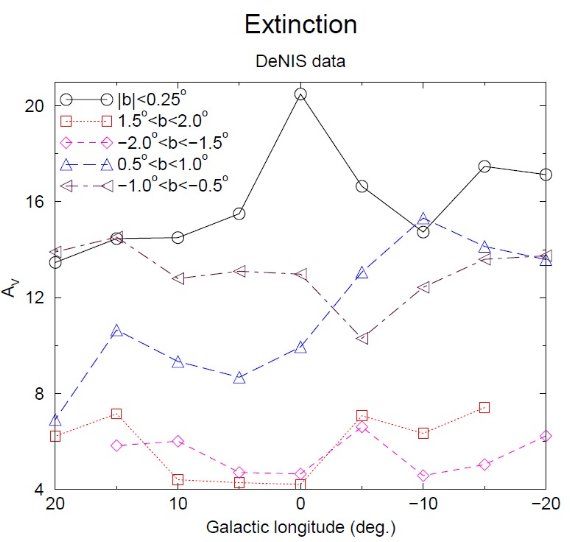
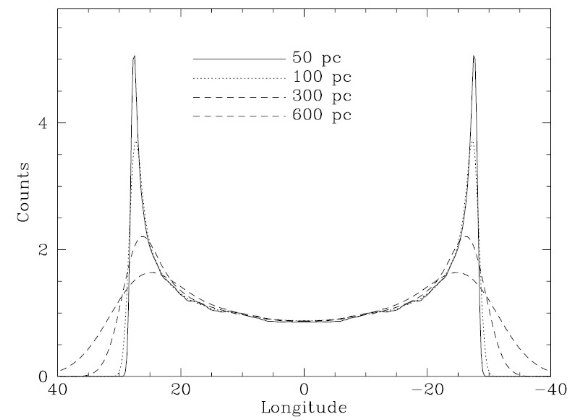
図１．渦状銀河 M 95 の POSS II (J-Blue) 画像。バー＋バルジの例。 　３軸バルジと面内バーの組み合わせ　 　観測では非対称の広がりと強さは銀緯と共に変化する。低銀緯部が除外され ３軸バルジのみを見ると通常の傾き角は　25° 程度である。銀河面が入る と Sevenster et al 1999 角度は 45° まで上がる。正銀経と負銀経の 間の差も銀河面近くになると増大する。それでもその差は銀緯 10° でも検出できる。この現象を矛盾なく説明するのに都合よいのは、傾き角 45 の３軸バルジと傾き角 20 かそれ以下の平面バーである。観測される 傾き角の銀緯による変化は両成分の混ざり具合による。両者の角度が異なる ことは銀河ではありふれたことである。 　バーとバルジの大きさ　 　どんな棒銀河でも重要なパラメタ―は共回転半径である。通常共回転は バーの長さの 1.1 - 1.2 倍位置にあり、バーは共回転半径を越えられない。 一方、３軸バルジは垂直内側リンドブラッド共鳴点(vertical ILR) の近く が終端であり、それは Rcr/2.2 (Friedli 1999) である。したがって、 薄いバーと３軸バルジのどちらも共回転位置を 4.5 - 5 kpc としている。 この値はCombes 1996 の結論と合致する。 　銀河系を正面から見たら？　 　内側銀河系を正面から見たら、SBb(r)II 銀河 M 95 (NGC 3351) か、 SBb(s) I-II 銀河 NGC 1433 のように見えるのではないか。 ここで、"r" はリング、 "s" は渦状腕がバーの端または中心から生じている ことを示す。 I, II は早期型、中間型を示す。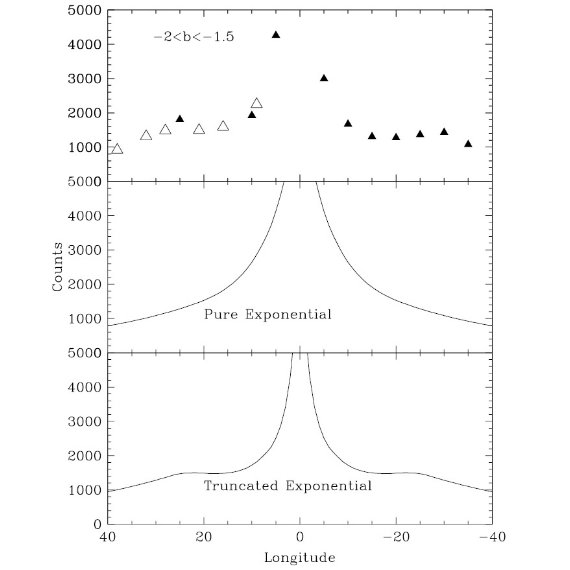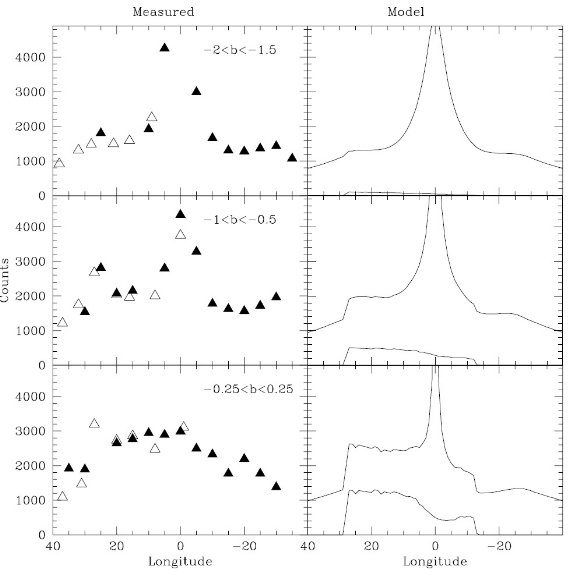 　配置模式図　 　図３はバーの配置模式図である。この論文の目的は、DENIS から 長くて平たいバーまたはリングを探すことである。

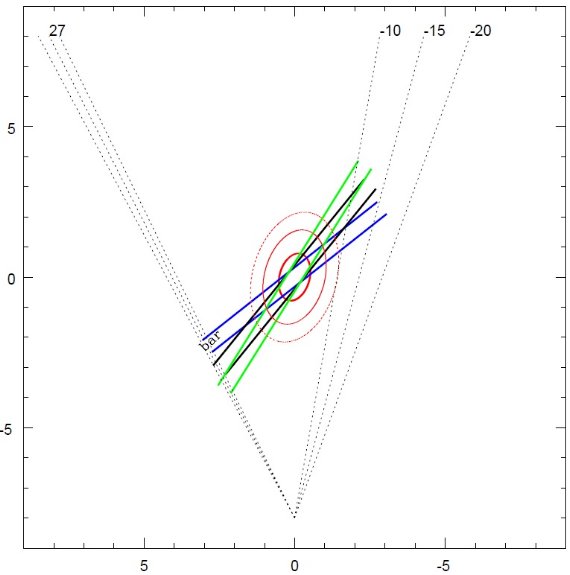
図２．渦状銀河 NGC 1433 の POSS II (R-Red) 画像。バー＋バルジの もう一つの例。 図３．我々が提案する「３軸バルジ＋バー」モデルの模式図。バーの巾 = 500 pc。 l = 27 をバー終端とした時の可能なバーの配置の例を３通りの位置角で示す。 視線の l = 28, 27, 26, -10, -15, -20. 太陽位置は (0, -8).

　２．ＤＥＮＩＳデータ　

　３．銀河面星計数の非対称　

面内非軸対称　 　バルジは銀河面から幾分か外れ、 |b| < 10, |l| < 15 で支配的である が、薄く長いバーは |b| < 2, 正銀経では　l < 27, 負銀経ではそれより 短い範囲に存在する。 バルジの非軸対称性は広く認められているが、銀河面内 での大規模な非軸対称性はまだ研究されていない。 　星計数の範囲　 　DENIS の Ks 限界等級は 14 mag だが、混んだ領域での完全度は数等悪化する。 今回は明るい星のみを扱うので、限界等級の問題は小さい。限界等級が暗くなる ほど良いと思われているが、内側銀河の研究では必ずしもそうでない。 それより重要なのは、内側銀河の星と太陽い近傍の星との比である。 Garzon et al 1993 によると、太陽近傍の星に対して内側銀河系の星の比率が最も高く なるのは K = 8 付近である。 ( 論文の表５のことだろうが、そうは言っていない。 逆に K = 7 付近でピークに見えるのは confusion の結果だろうと述べている。 さらに、彼らが内側銀河の成分としているのは中心から 1 kpc 以内で、 l = 23 の視線方向は一般円盤星としていて、近傍星とは言っていない。) そこで、K = 9 までの星計数を用いる。 　K = 9 までの星計数の結果　 　図４には K = 9 までの星計数の結果を示す。DENIS 計数は Δl = 5° の平均値である。DENIS で足りない個所は TMGS データで補った。両者のフィルター は差があるが、 Cohen 1997 はその差は 0.03 mag 以下である。図４では 5 つの帯が銀緯で分けられる。銀河中心距離を 8 kpc とすると、その距離での 銀河面からの高度は、0 pc, ±100 pc, ±240 pc である。 注意しなければならないのは、 （i）cuts furthest from the plane are substantially different from those in the plane （ii）計数は銀緯に関して対称に行われた。 （iii）太陽が銀河面から 14 pc 上にあるため、負銀緯星の数は増える。 （iv）銀緯正と負とで減光が異なる。

図４．様々な銀緯における K ≤ 9.0 星計数。十字＝DENIS のΔl = 5° 平均。丸＝ TMGS (Garzon et al 1993, 1996) 各領域内の星数は 数千あるのでポアソンエラーは無視できる。破線＝ |l| = [10, 25] の 一般的傾向を示す。

　３．１．銀河面外での星計数　

平坦部は何？　 　|b| = 1.75 切面は銀河面から高いので A(Ks) = 0.2 - 0.3 mag と 減光は小さい。その上、若い円盤種族の寄与が小さいのでスケール高が 数百パーセクの内側銀河種族が主な成分となる。図４を見ると、 |b| = 1.75 切面は銀経に関して幾分か対称的であることが分かる。 初め銀経が下がるとカウントは上がる。しかし、30 > |l| > 12 でカウントは平坦になり、その先 |l| < 10 ではバルジの寄与が大きく なって上がって行く。この平坦部は指数関数円盤では予期されていない。 　穴開き円盤？　 　図５上には図４一番下の b = -1.75 を再録した。図５中と下は Wainscoat, Cohen, Volk, Walker, Schwartz 1992 による単純円盤＋バルジモデルである。バルジは 軸対称を仮定しているがここでの議論には十分である。図５中は銀河系 中心まで詰った指数関数円盤であり、図５下は指数関数円盤は R = 3.5 kpc までで、その内側の密度は中心でゼロまで直線状に低下して行く。 これは、中心に穴の開いた フリーマン II 型円盤の近似となっている。 　切り詰め円盤は棒銀河では多い　 　図５中の中心まで詰まった指数関数型円盤は輝度勾配が中心に向かって どんどん急になっていく。しかし、観測ではそうなっていない。図５下の 切り詰め円盤(truncared disc) は輝度分布を上手く再現している。この 円盤の内側構造を詳しく議論はしないが、これは Freudenreich 1998 の円盤モデルと良く合っている。内側が切り詰められた円盤は棒渦状銀河 では極めて普通である。太田その他(1996) は６個の早期型渦状銀河を 調べて全てがフリーマン II 型円盤を有していることを見出した。Baggett et al 1996 は棒銀河は非棒銀河に較べ切り詰め円盤を持つ割合が２倍以上 になることを示した。

図５．上：K ≤ 9.0, b = [-2, -1.5] での星計数。中、下：二つの 簡単な円盤＋バルジモデルの予想。

　３．２．銀河面内での星計数　

銀河面に沿っての非対称性は極めて明瞭　 　銀河面に沿っての非対称性は極めて明瞭である。正銀経側のカウントは負銀経 より遥かに高い。その上、カウントの形が全く違う。これは内側銀河の形を 楕円形にしたくらいでは再現できない。l = [27, 0] ではカウントは平坦である が、 l = [0, -18] では半分になる。この非対称性は b = 0 の方が |b| = 0.75 より激しい。恐らくバーの相対的寄与が高いからであろう。l = 20 でのカウント の約半分が円盤の寄与であろう。円盤は軸対称であるので、円盤分を差し引くと 銀経正と負との対比は巨大なものとなる。 　銀河面にないバルジピークと非対称面内成分　 　バルジに伴う l = 0 のピークは銀河面沿いの切帯では全く見えない。 しかし銀河面から外れた切帯ではピークがはっきり表れる。これは一部には 銀河中心から数百パーセクでの強い減光がカウントを押し下げているせいでも ある。(l, b) = (7, 0) では GC 周囲の減光の影響を受けないので、 K ≤ 9 カウントの 50 % はバルジ星と考えられる。 l > 10 ではバルジは消失して 殆ど見えない。したがって、l = 27 まで伸びる他の成分が必要である。 この成分は検出天体の約 50 % に寄与し、おもに正銀経で見える。そして バルジから伸びて l = 27 まで達する。 　減光、リング？　 　勿論、この非対称性を減光で説明したくなる。しかし、正銀経側ではカウントの 減少ではなく増加成分が問題となっている。リングはどうだろう？図６には リングの厚さを変えた時のカウントの変化を示す。特にリングを楕円形にすると 非対称になって都合が良い。しかし、リング接線に現れるピークを消すことは 難しい。

図６．様々な厚みのリングに対する銀河面に沿った星計数の予想図。リング半径は 3.7 kpc で動径方向にはガウシャン分布とする。計数は l = 0 で同じ値になるように 規格化した。リングは円形とした。楕円形にすると、ピーク位置がずれて、 銀経に関して対称ではなくなる。 ( 厚みがなぜ影響するか分からない。)

バー？　 　　もう一つの説明はバーである。 Hammersley et al. 1994、 Hammersley et al. 2000 のモデルでは、近い側が l = 27, 距離 5.7 kpc, 遠い側は l = 12、 距離 11 kpc である。バーモデルを観測と比較する際、考慮すべき点が 幾つかある。 (i) 空の単位面積内の星の数は視線方向単位立体角がバーから切り取る体積 に依存する。視線とバー軸との角度を α とすると、これは距離の 二乗と sec α の積によるということである。バーの負銀経側は 距離が大きく、α が小さいのでこのファクターは大きくなる。 (ii) 同じ見かけ限界等級に対し、正銀経側では絶対等級でより暗い星まで 検出できる。Klimit = +9 に対し、l = -12 では MK = -7.5 より明るい星が、l = +27 では MK = -6.0 より明るい 星が受かる。光度関数の勾配が急なので、正銀経側ではより多数の星が 受かる。 (iii) バーのスケール高は重要である。 Hammersley et al. 1994 は 50 pc とした。これは l = 27 のバー近端では Δb = 0.5, l = -12 のバー遠端では Δb = 0.25 になる。したがって、|b| < 0.25 カウントを行うと、 l = -12 では区間の一辺はバースケール高 となり、l = 27 ではスケール高の半分となる。この結果、 "遠端/近短" 比は小さくなる。銀河面から離れた銀緯ではこの効果は一層 大きい。 (iv) 遠端距離が増加すると、減光が増加する。その上、バーの進行面側 にはダストレーンが付随しやすい。 　内側銀河系モデル　 　図７には星計数の観測値をモデルと較べた。モデルは切り詰め円盤+バルジ+バー。 ただし、バルジと減光には Waincoat et al 1992 を用いた。バーの厚みは 500 pc, 長軸半径 4 kpc, 位置角 43° を持つ。バーの密度分布は一定 だが、高度方向にはスケール高 50 pc （明示されていないが）の指数関数型 と仮定した。バーで観測される星は明るい若い星であると考えている。 バーの光度関数は円盤と同じものを採用した。密度は l = 27 で総カウントが 一致するように規格化した。 　観測とモデルの比較　 （i）モデルは l = 27 で銀河面表面密度の急変を予測している。 （ii）モデルは l = [27, -12] で銀河面表面密度が一定となることを予想している。 l = -12 で密度は急落する。 （iii）b = [-1, -0.5] プロットに関し、モデルは正銀経では追加天体が 多数あるが、負銀経ではそうではないと予測した。 (l, b) = (-10, -0.75) のカウントは大体円盤のレベルである。しかし、 (l, b) = (-10, 0) では追加分が多い。これはスケール高が小さなバーの影響 である。 （iv）予測できなかったのは l = -22 のピークである。これは後に論じる。

図７．Ks < 9 までの星計数。左：黒三角＝DENIS. 白三角＝TMGS. 右：モデル。内側切り詰め円盤＋バルジ＋ 3.9 kpc バー。バー方位角 40°. 画面下側実線＝バーのみの寄与。 Unavane らの L カウントとの違い　 　Unavane, Gilmore 1998, Unavane et al 1998 は銀河系中心周辺 の数か所で L バンドと DENIS の星計数を取り、そのデータを解析した。 本論文の結果と異なり、彼らは負銀経で正銀経より多数の星計数を得た。 彼らはそれを（多分）３軸バルジとして解釈した。彼らの測ったのは 銀河中心から数度以内で、バルジが支配的な領域である。それらは古い 種族の星である。 (結局、b = 0 ではバルジとバーのどちら が見えるのか？K = 8 ではバー、K = 10 ではバルジというなら納得だが、 そうなのか？ ) Hammersley et al. 2000 のモデルを彼らと比較するのは適当でない。

　４．銀河面上の減光分布の非対称　

図８．Δl = 2, Δb = 0.5 で平均した減光 AV の変化。この Av は視線方向最遠の星に対する減光である 　第四象限の追加減光　 　観測された銀経非対称を説明する別法は減光である。向こう側のバーは遠い ので減光も大きいだろう。その上、バー進行面側にはダストレーンが付随する 可能性がある。それらは、バルジが弱まる l = -8 からバーの終端 l = -12 にかけてであろう。 　減光の決め方　 　ＣＭＤを利用すると円盤矮星、円盤巨星、内側銀河巨星の簡単な分離が 可能である。( Hammersley et al 2000, Ruphy et al 1997 ) Schultheis et al 1999 は DENIS の (J-K, K) を使い l = [8, -8] の 内側銀河面の減光マップを作った。彼らは Bertelli et al 1994 のモデル 等時線, Z = 0.02, t = 10 Gyr, R = 8 kpc, を使い、フィットが最も良い Av を決めた。　Glass et al 1999 の減光則 AV : AJ : AK = 1 : 0.256 : 0.089 が用いられた。この同じ方法を l = [20, -20] につかって求めた減光マップ を図８、図９に示す。 (バルジ全体に距離 8 kpc でも問題 だが、円盤とバーでもそうしているのか？)

図９．Δl = 2, Δb = 0.5 で平均した減光マップ。データの 不足部分は内挿で補った。 　減光非対称性　 　図から b = [-0.25, 0.25] と b = [0.5, 1.0] での減光非対称性が 明らかである。銀河面上では負銀経の Av が 2 - 3 mag 大きい。銀河面から 外れた |b| = [1.5, 2] では減光の非対称は見当たらない。 内側銀河と円盤の星を分離できていない 　ここで示した減光は近似的なものである。と言うのは、内側銀河と 円盤の星を分離できていないからである。 　減光の傾き　 　図９は減光マップである。減光の銀経非対称と共に目立つのは、減光の傾き である。この傾きは l = [-8, 8] 区間で、b = -0.05 l と表される。この 傾きは CO, HI マップで既に知られている。減光マップに同じ傾きが見える ことは、この減光が銀河中心のガスとダストに起因することを示している。 (つまり、前面のサジタリウス腕や 盾座腕の分子雲ではないと？ ) この傾きの結果、図８では b = [-1.0, -0.5] では非対称が見えず、 b = [0.5, 1.0] では強い非対称が現れた。正銀経での減光は負銀経より Av で 5 mag 程度低い。ただし、 (l, b) = (15, -0.5) のようなおそらく分子リング に付随する分子雲起源の高減光域はある。 ( この論理はよく分からない。)

　５．l < 0 内側銀河面の解析　

マップは負銀経のみ。　 　図１０上には Ks ≤ 9.0 の星計数マップ、Δl = 2, Δb = 0.5 を示す。DENIS のデータが揃っている l ≤ 0 領域のみをマップ化した。正領域側は、 Hammersley et al. 1994 Kent et al. 1991 を見よ。 　星計数ピークに２種類ある　 　図１０のマップにはピークが (l, b) = (0, ±1.5), (-5, -1), (-12, 0), (-22, 0), (-30, -1) に見える。実際に星が集中して生まれた ピークと低減光の窓部分がその原因である。 　減光補正　 　減光補正は、 (J-K) > 1 の星に対して、 　　　　　Kcorrected = K -[AKs/(AJAKs)] [(J-Ks) - 1.0] で行った。つまり (J-Ks)o = 1.0 を仮定している。 AKs/(AJAKs = 3/5 とした。 固有カラーは早期 M-型巨星の値 1.1 から来ている。これは R = 8 kpc, K = 9.0 mag に対応した。 ( M(K) = 9 - 5log800 = -5.5. Ko = 9 の意味で、減光は考慮していない。変。 ) (J-K) ≤ 1 の星の減光補正は行わない。 こうして、個々星の減光補正を行ってから、(J-K)corrected > 0.5 の 星で作った星計数マップが図１０下である。 　減光補正の正当性　 　この方法で、内側銀河系の星の比率を高めた。注意すべきは高減光領域では J が DENIS の検出限界のため受からなくなっていることである。 この補正の結果、デコボコだったマップがかなり平滑になり、多くのピークが 消滅した。また星計数に減光と違い傾きが見られない。 これは円盤のワープを研究する際に気を付ける必要がある。 　谷と頂点の解説　 (i) (l, b) = (0, 0) 補正前は(l, b) = (0, ±0.5) のピークに挟まれた谷だった。補正すると ピークに代わった。 ( Kcorrected の星計数限界等級は減光大 領域では浅くなるのではないか？どうしてピークになり得たのか、不思議。) 　 (ii) (l, b) = (-5, -1) 補正前のピークは減光の窓に対応していた。補正後ピークは消失した。 　 (iii) (l, b) = ([-8,-10], 0) 補正前の星計数ではへこみがあった。高減光を補正すると凹みは消えた。 　 (iv) (l, b) = ([-12, -14], 0) 減光が周囲より低い。以前 Sevenster 1999 が述べた l = -10 付近の OH/IR 星のピークは若い星の l = -12 ピークと関係するかも知れない。 減光補正後、ピークはバルジの先に伸びる尾根に変わった。 この尾根は l = -14 で止まる。

図１０．Δl = 2, Δb = 0.5 の DENIS 星計数マップ l = [0, -32], b = [-1.5, 1.5]。上： K ≤ 9.0, 下： Kcorrected ≤ 9 かつ (J-Ks) > 0.5 　 (v) (l, b) = ([-15,-19], 0) 減光補正前も後も周囲より星計数レベルが低い。この領域の内側銀河 天体の数は本当に少ないのかも知れない。 　 (vi) (l, b) = ([-20,-24] ,0) 減光補正後も数度にわたるピークが残っている。 Hammersley et al. 1994 はこの領域をバーの遠端とした。しかし、それは COBE/DIRBE の表面輝度 分布に基づいた結論であった。今回の解析はバーの遠端は l = -12 付近 であると結論する。l = -22 ピークはリング、または腕の接線と考える べきであろう。次章でこのピークを議論する。 (vii) (l, b) = (-30, -1)　 減光補正前にあったピークは補正後は消失した。

　６．議論　

　７．結論