A Dust Lane Leading the Galctic Bar at Negative Galactic Longitudes

　アブストラクト

　１．イントロ　

　２．星計数からの証拠　

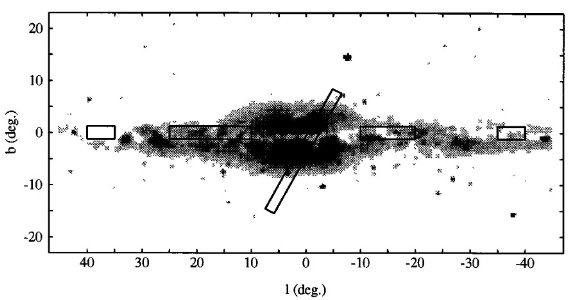
図１＝銀緯プロファイルと考える　 　図１には K = 8 までの星計数をプロットした。計数は赤緯一定のラインに 沿って行われた。我々は大規模な構造に興味があるので、この計数を l = -1 における銀緯プロファイルと看做すことにする。 　特徴１　 　銀河面への集中が K = +6 から開始される。これは集中する星の固有光度が高い ことを意味する。l = -1 から l = 171 まで様々な銀経でこのような星計数を 行ったが銀河中心付近でのみこのように明るい星の銀河面集中が観測された。 軸対称を仮定し、この特徴の銀経広がりから、銀河系中心から半径 0.5 kpc の 内部バルジを見ていると思われる。 　特徴２　 　銀河面では強い減光が内側バルジを隠している。この領域で見える TMGS 星が 同じフィールドの可視星と一致しないのでダストレーンは太陽から少なくとも 3 kpc は離れていると思われる。 　銀河中心減光もダストレーン？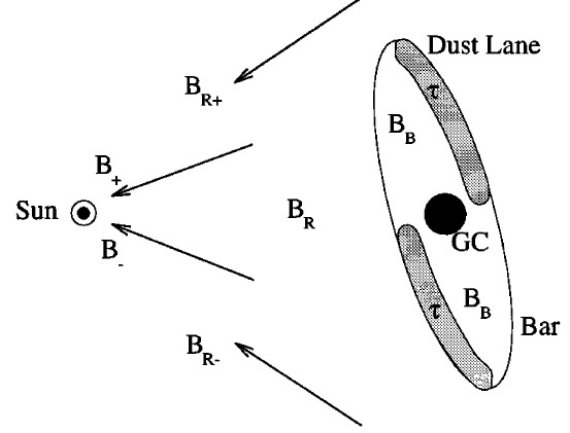　 　バー前面のダストレーン仮説が正しければ、銀河中心の強い減光は、実は銀河 中心付近でスタートしてバーの端 l = -22 まで伸びるダストレーンと考えられる。 残念ながら TMGS は l > -2 に限られている。DENIS, 2MASS が期待される。

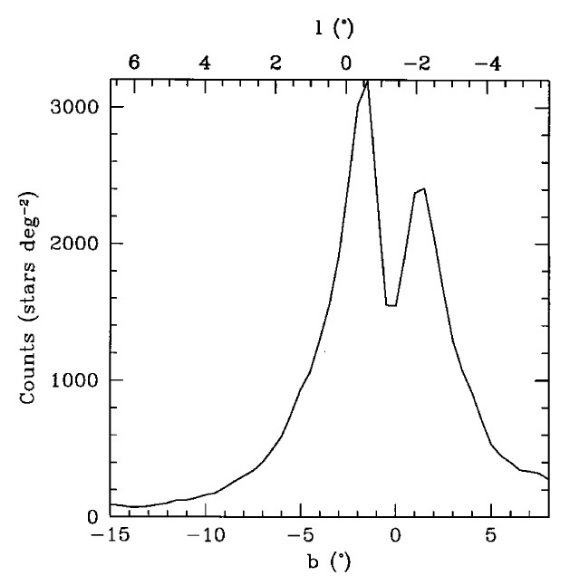
図１．TMGS 星計数、K = 8 mag まで。斜めの計数帯の銀経(上)と銀緯（下） は横軸の上下に示した。計数帯の位置は図２を見よ。

　３．フラックス・マップからの証拠　

非対称減光の再確認　 　ダストレーンの位置は l = 27 と l = -22 でのフラックスに反映されるだろう。 その対比は減光の効果が大きい短波長ほど大きいだろうが、波長が短くなり過ぎ ると、太陽近傍しか見えなくなる。この対比が最も大きいのは J バンドと思わ れる。図２にはこの非対称性が示されている。この図を見ると、強いダストレーン が銀河中心付近で始まり、 l = -20 で終わることが判る。またその厚みが b で 2° であることも分かる。ただし、この減光が太陽近傍で生じた可能性もある。 　そこで、ダストレーンモデルを作って観測と較べる。

図２．JDIRBE J バンドマップ。銀経正負の非対称性に注意。四角はこの論文で 扱う領域。傾いた四角は図１で星計数を求めた領域。水平の領域は平均フラックス が左から右へ BR+(λ), B+(λ), B-(λ), BR-(λ) が測定された領域。

　４．ダストレーンモデル　

ダストレーンモデル　 　モデルの漫画を図３に示す。バー自体は銀河中心に関して対称とする。 　　　　　αB = 隠されるバーの割合 　　　　　αN = 1 - αB = 透け透けバーの割合。 　　　　　B+(λ) = BR+(λ) + BB(λ) 　　　　　B-(λ) = BR-(λ) + αBBB(λ)e-τ(λ) + αNBB(λ) 我々は上のモデルから減光係数（？）を得て、それが通常の波長依存性を示すかどうか に興味がある。そのために、以下の式を計算する。 B-(λ) - BR-(λ) = αN + αBe-τ(λ) B+(λ) - BR+(λ) このモデルにはダスト放射が入っていない。この成分は長波長では重要なはず である。しかし、ダストレーンの減光を定めるという目的は達成できる。 　BR(λ) の測定　 　平均フラックス B+(λ) と B-(λ) は 表面輝度マップから容易に計算できる。より困難なのは、BR(λ) である。このために、バーに近いがバーではない銀経での測定が必要である。 これは、BR(λ) の銀経による変化や、特に遠方側の BR(λ) に対する減光の効果などを無視している。

図３．バーモデル。 B+＝バーがある正銀経領域からのフラックス。 B-＝バーがある負銀経領域からのフラックス。 BB＝ バーからのモデルフラックス。 BR＝バー以外からのモデルフラックス。 BR+＝バーが存在しない正銀経からの実際のフラックス。 BR-＝バーが存在しない負銀経からの実際のフラックス。 τ = ダストレーン光学的深さ。

　５．データとの比較　

平均フラックス　 　平均フラックスを計算するため、 b 方向には DIRBE 6 ピクセル = 2.11° 巾で採る。BR- は l = [-35, -40] の平均で決めた。 BR+ は l = [40, 35] の平均で決めた。 B- は l = [-10, -20] から決める。これはバルジとバー端末の 星形成域を外し、バー部分だけを選んでいる。同様に B+ は l = [25, 10] から決める。 　領域　 　図２に測定域を示す。測定結果は表１に載せた。 　結果　 　図４には A(λ)/A(J) をプロットした。負銀経ダストレーンの減光則 は標準減光則に良く合っている。

図４．相対減光 A(λ)/A(J). 四角：Mathis 1990 の減光則。 三角：αB=1 モデルの結果。星：αB=0.651 モデルの結果。

　６．結論