|
レーリージーンズ色超過法 (RJCE)減光マップ レーリージーンズ色超過法 (RJCE) を用いて、銀河面の高分解減光マップ を作った。この RJCE 法では近赤外と中間赤外の測光を組み合わせて、星ごとに 減光度を決める。RJCE マップは 2'×2' ピクセルで、256° - 65° 区間を GLIMPSE-I, -II, -3D と Vela-Carina サーベイデータからマップした。 赤化補正から星のマップ RJCE 減光測定に基づき、我々は赤化補正色等級図を作り、 そしてそれを用いて、今度は逆に主系列、レッドクランプ、 赤色巨星毎に異なった距離区間のマップを作った。こうして粗いダスト雲の 3次元分布を調べた。 |
赤色巨星から作った減光マップ 赤色巨星から作った減光マップは 18 - 20 kpc にまで達し、大抵の 方向で円盤減光のほとんどの向こう側まで探り、全円盤減光マップに 近いところまで行っている。最低でも A(Ks) の最小限度の高分解マップ を与える。 これはいいマップ このマップは、赤化の測定から直接描かれたものであり、間接的な 手法からの推測でない。このマップは銀河面に沿って入り乱れた減光の 詳細を図示した現在最も精密なものである。 |
|
過去の減光観測 Struve 1847 から始まる減光研究の紹介。 色超過を用いる方法 個々の星の赤化を知るには、スペクトルを撮って分光分類を行う のが伝統的な手法であった。これは非常に面倒な要求である。しかしここ 数十年、測光法が試みられてきた。星または銀河の色分布が一様であると 仮定し、観測された平均カラーからのズレを赤化と考えるのである。 ( 個々の星の平均カラーからのズレ という意味なら滅茶苦茶な論理だし、何を言っているのか?) 赤外カラーの表面温度依存性が小さいことと、赤外での減光強度が小さいこと が相まって、可視ー赤外カラー、赤外カラーを使った赤化の観測が特に 高減光域で多数行われた。 赤外色超過法の例 それらを挙げると、 Jones et al. 1980, Jones et al 1980, 1984, Smith 1987 が初期の試み。 Lada et al. 1994 は Near-Infrared Color Excess (NICE) 法を考案した。NICE は 大量測光と星計数を結びつけて小領域の平均減光を求める方法である。 この方法はその後著しい進化を遂げた。例えば、Lombardi,Alves 2001 の NICER, Gosling et al 2009 の V-NICE, Lombardi 2010 の NICEST など。Alves et al 1998, Lada et al 2009, Lombardi et al 2010 は これらの方法を暗黒雲の減光研究に用いた。色超過法は銀河にも 用いられた。銀河は天の川の全赤化を決めるのに適している。より 正確な減光量の決定には RR Lyr, 球状星団、レッドクランプ星のような カラー狭い範囲によく決まっている天体が用いられた。 巨大楕円銀河の積分スペクトルは驚くほど一様である。Burnstein et al 1988, Faber et al 1989 は Mg2 指数を 用いて(B-V)o を推定した。 |
Schlegel et al の減光マップは銀河面で不正確 Schlegel et al. 1998 の減光マップ (SFD マップ) は COBE/DIRBE+IRAS/ISSA データの 100 μm マップから 導かれた。これは低減光域では信頼できる。問題は分解能が 6' と低く、 これより小さいスケー ルで大きく変動する領域では使いにくいことと、 低銀緯帯になると A(V) の見積もりが超過しがちで、大きいところでは 50 % もずれていたことである。 Majewski et al. 2011 はその理由を SFD 真布の基となった 100 μm 放射を担うダストと 短波長減光に効くダストが異なることがその違いの原因であると論じた。 他の減光指標を使った結果と比べてみると、 SFD マップの高減光点は実は SNR や SFR をなぞっている。冷たい暗黒雲は減光で見ると、 SFD の遠赤外 放射を欠いていることが判った。 RJCE 法 RJCE 法は、通常星の長波長部 SED がレーリージーンズ型であることを 用いる。 Majewski et al. 2011 では、RJCE 法が銀河面付近で SFD 法より優れ、RICE 法及びその改良版に 較べると、採用カラーが星の種類によらず一様である点で優れていることを 示した。さらに良いのは、RJCE 法では赤化と固有カラーを綺麗に分離する ので、星のタイプ、主系列、レッドクランプ、赤色巨星、を決定できる のである。こうして、我々は最も遠くまで探れる天体、赤色巨星、を選り分け て、視線方向の総赤化量を定めることが可能となった。また別に、レッドクランプ を標準光源として用いると、距離決定の精度が各段に向上する。こうして、 様々な固有光度の星をつなげて、我々は視線に沿ったダストの距離分布を得る のである。 二次元減光マップを提示する。 この論文では、新しい二次元減光マップを提示する。第2章ではどうやって マップを作成したかを述べる。第3章では完全マップを示す。第4章はマップ使用に 際しての注意点、第5章は電子データへのアクセス法を述べる。 |

2.1.RJCE 法のまとめ近赤外カラーを色超過にする際の問題(1)固有カラー自体の広がりが A - K 型で、(J-H)o, (J-Ks)o で約 1 等、 (H-Ks) で 0.5 等の巾を持つ。 (2)赤化ベクトルの方向が星の固有経路と重なる。 RJCE 法の赤化 これらの問題は長波長に移ると解消する。そこでは SED の勾配が星の 表面温度によりほとんど変わらない。例えば、A - K 型での (H-4.5)o カラーは 0.1 等の巾しかない。その上、赤化ベクトルの方向は赤色巨星系列と 直交する。主系列は平行になるのだが、 2MASS/Spitzer サンプルに占める 割合は小さい。 色々と検討した結果、(H-4.5) カラーがベストという結論になった。 13CO マップとの類似性 Majewski et al 2011 で示されたのは、 RJCE マップと 13CO マップと NIR 星計数マップとの驚くほどの構造的な類似性である。それら二つは冷たくて 濃密な減光領域をなぞっていると考えられる。それに対して、SFD マップは [8.0] マップにより近い。 |
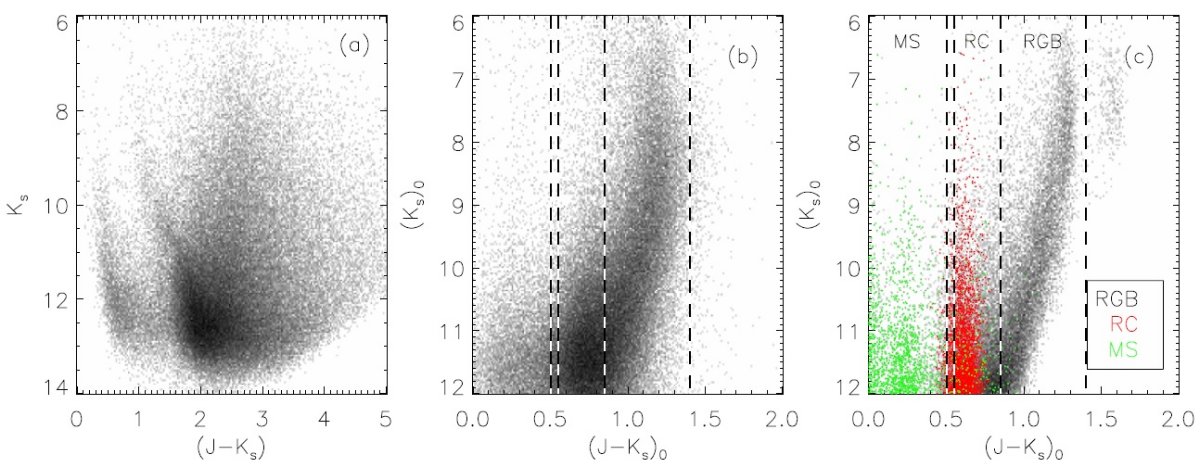
2.2.サンプルの選択星の分類RJCE 法の利点は赤化補正後、特に J バンドを含むカラーを使って、 星のスペクトル型を回復できることである。 赤化補正したカラーで、 0.0 ≤ (J-Ks)o ≤ 0.5 は主系列星、 0.55 ≤ (J-Ks)o ≤ 0.85 はレッドクランプ、 0.85 < (J-Ks)o ≤ 1.4 は赤色巨星である。NIR カラーの赤い方では確かに 矮星・巨星の縮退がある。しかし、 TRIEGAL モデルの示すところによれば 矮星の割合は無視できるほどに小さい。 赤化補正後の色等級図の例 図1には赤化補正した色等級図の例を示す。カラーによる星の区分も 示してある。それぞれを追跡子に使い、それぞれの距離分担のあたりの減光マップ を作ってそれを合わせると粗い3次元減光マップが作れる。 |
|
小区間に A(Ks) を与える 図2は減光マップバージョン1である。 作成手順は次のよう。 (1)J, H, Ks, [4.5] で測光エラーが 0.2 mag 以下の星をサンプルに 選ぶ。 (2) A(Ks) = 0.918 × (H - [4.5] - 0.08) (3)星ごとに赤化補正し、3種類に分類する。 (4)それぞれのサブサンプルは 2' 角の小区画に入れられる。 (5)小区画毎に減光 A(Ks) の中間値と 90th percentile 値を求める。 つまり、3(主系列、レッドクランプ、赤色巨星)x2(中間値、90th percentile) の6種の減光値が各小区間に与えられる。 (6)星の種類で分けない全サンプルを用いて同様に2種類の A(Ks) を決める。 (7)FWHM = 1.4' ガウシアンで平滑処理してノイズを減らす。 90th percentile マップ 90th percentile マップはビン内の星の大部分に影響する減光の主要部を 代表しているばかりか、冷たい前景矮星、測光エラーなどの混入から 生じるバイアスの影響を最も受けにくい。 星計数マップ 星計数を行い、A(Ks) 分散を与えた。これは A(Ks) の不確定性とは 異なる。星の数が1個かゼロの小区画は A(Ks) を与えていない。 総減光の下限マップ 最後に、総減光の下限マップも作った。これは [3.6], [4.5] で 測光エラー < 0.5 mag の全ての星の 90th percentile マップである。 ここで使用した減光は以下の通り。 A(Ks) = 9.188 × ([3.6] - [4.5] + 0.235) この式は、l = 20° - 30° の測光エラー 0.07 mag 以下の星全てに E(H-4.5) から導いた A(Ks) と (3.6 - 4.5) とを直線フィットして導いた。 [3.6] - [4.5] の固有分散と測光エラーは (H-4.5) より大きい。 ( この減光が前の3グループより 圧倒的に大きいのはどうしてか?) このマップを入れると全部で 18 種のマップが作られる。図2のその例を示す。 銀河系外周部 外部銀河系は低密度のために赤色巨星マップに空白ピクセルが多い。レッド クランプと主系列はそれほどひどくない。幸い、この領域では最遠レッド クランプ星が円盤の縁までの減光を与えるので、赤色巨星の代わりになる。 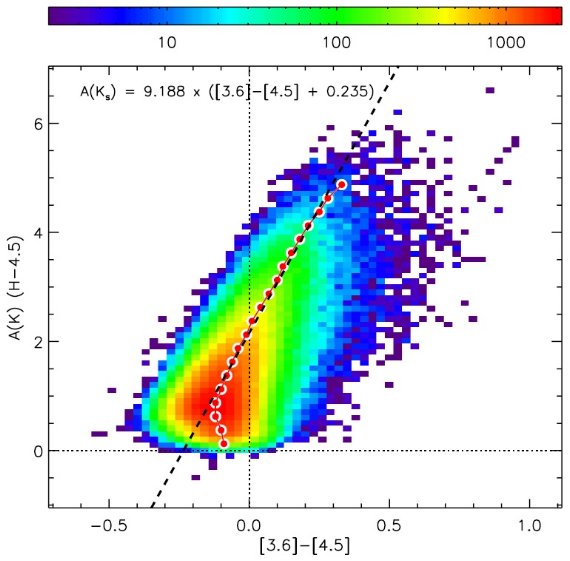 図3.E(H-4.5) から導いた A(Ks) と (3.6 - 4.5) プロット。サンプルの 測光精度は 0.07 mag 以下。ビンは A(Ks) で 0.25 mag., |
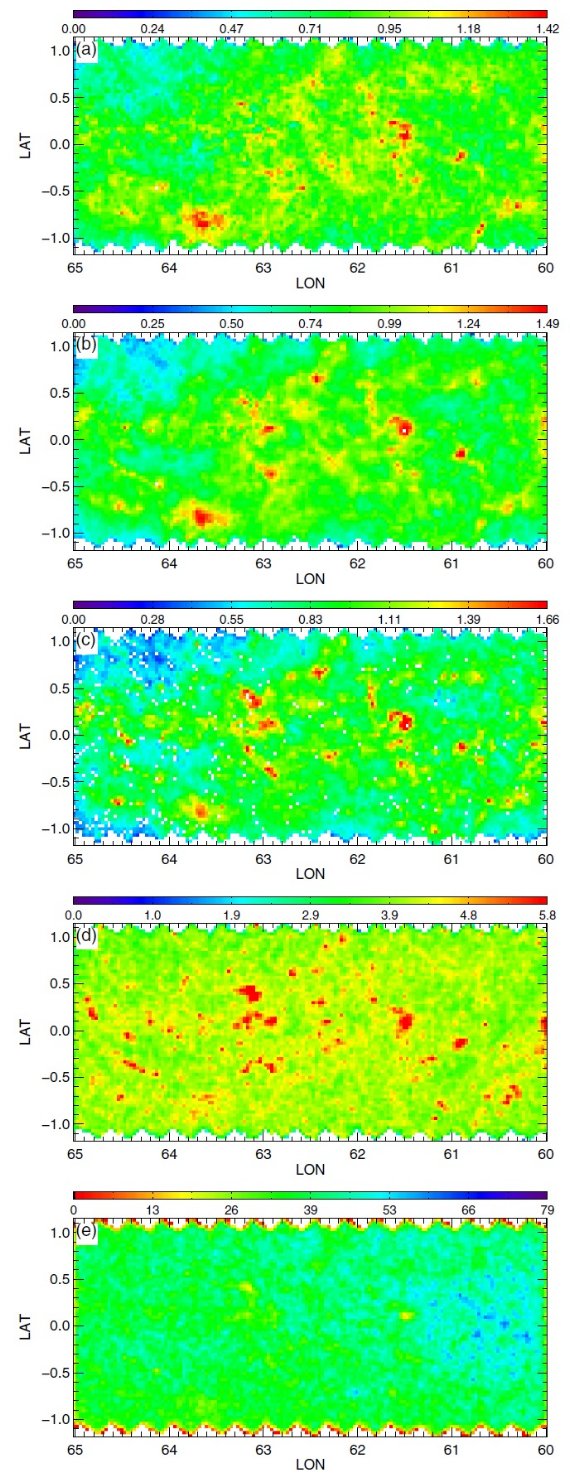 図2.公開マップ。初めの3列は 90th percentile A(Ks) での減光マップで、 (H-4.5) を使った RJCE 法で作った。第1列は主系列ターンオフ星、第2列は レッドクランプ星、第3列は赤色巨星を用いた。第4列は全ての星の (3.5-4.5) カラーを用いた 90th percentile A(Ks) での減光マップ。 第1−3列のカラーコードとスケールが異なる点に注意せよ。第5列は全ての星の計数マップ である。星がないピクセルは、第1−4列で白、第5列で黒。 |
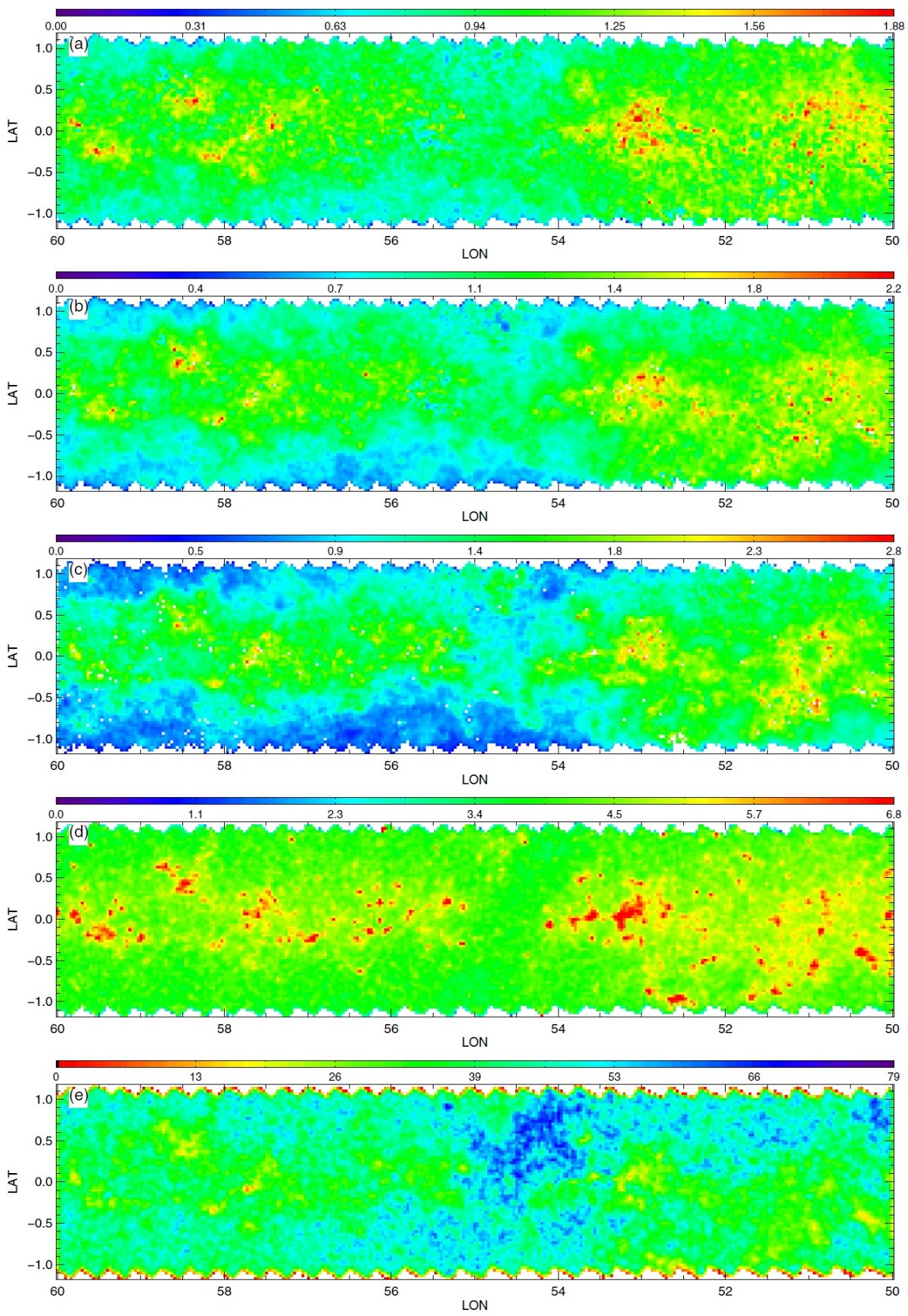
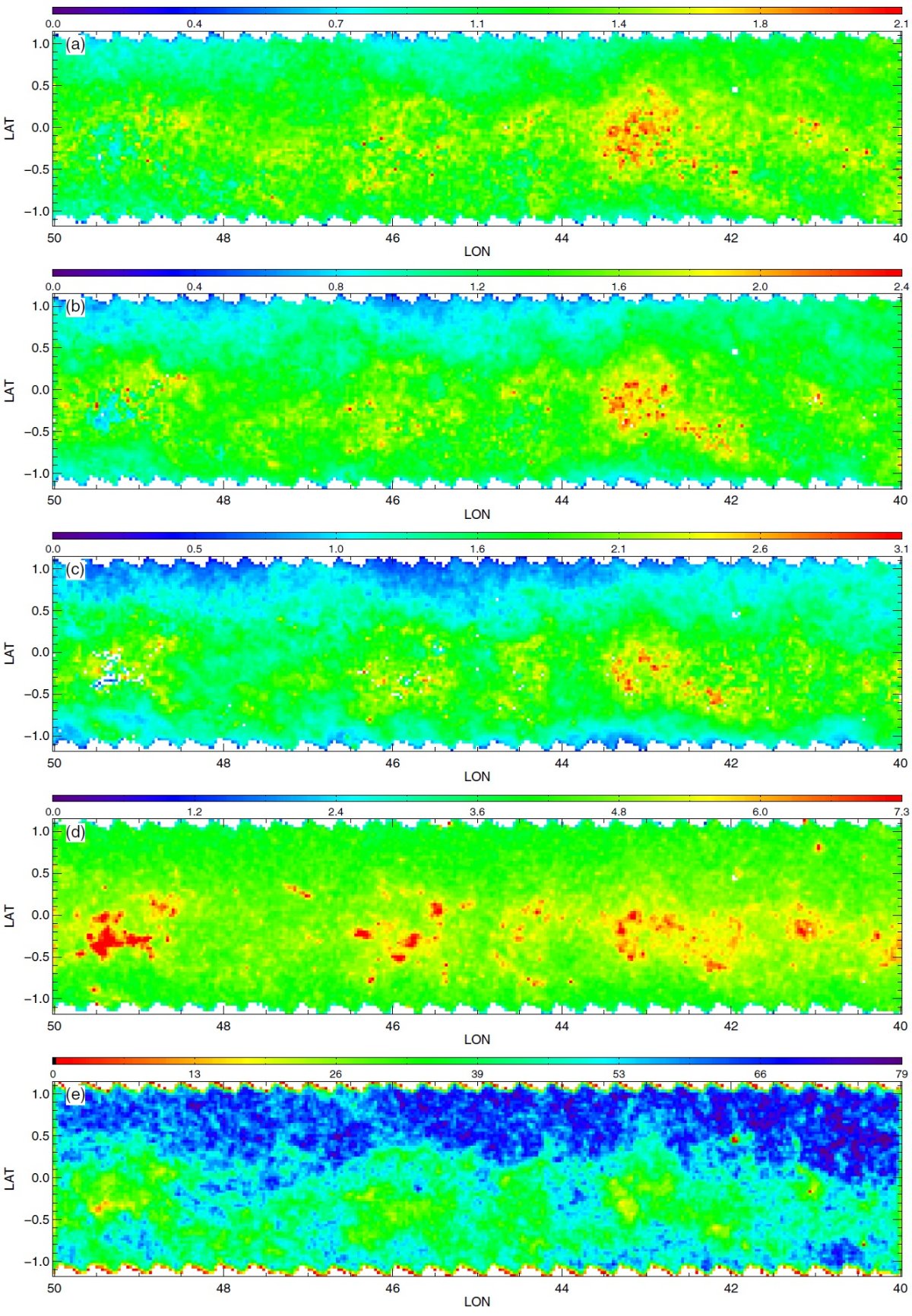
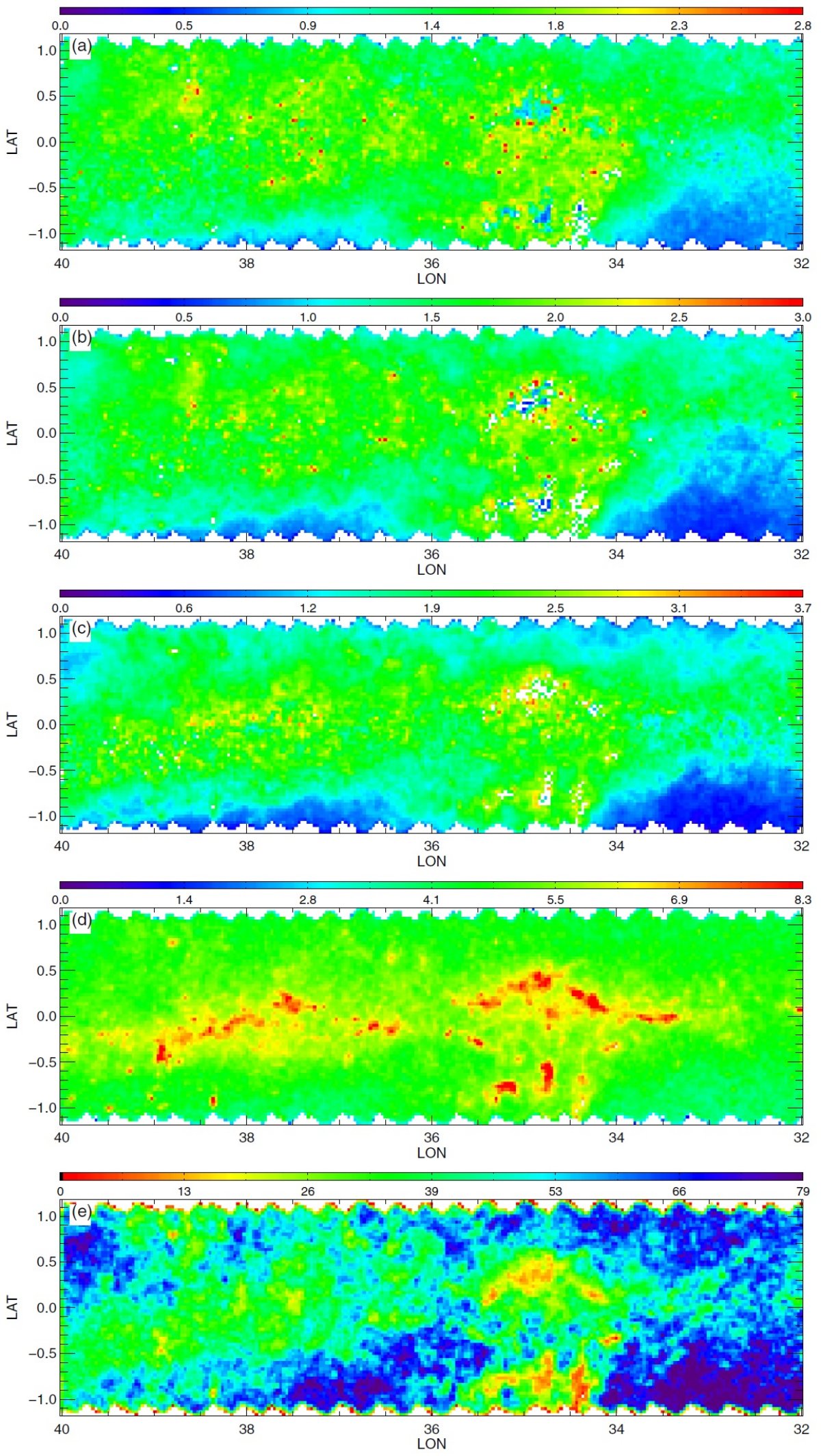
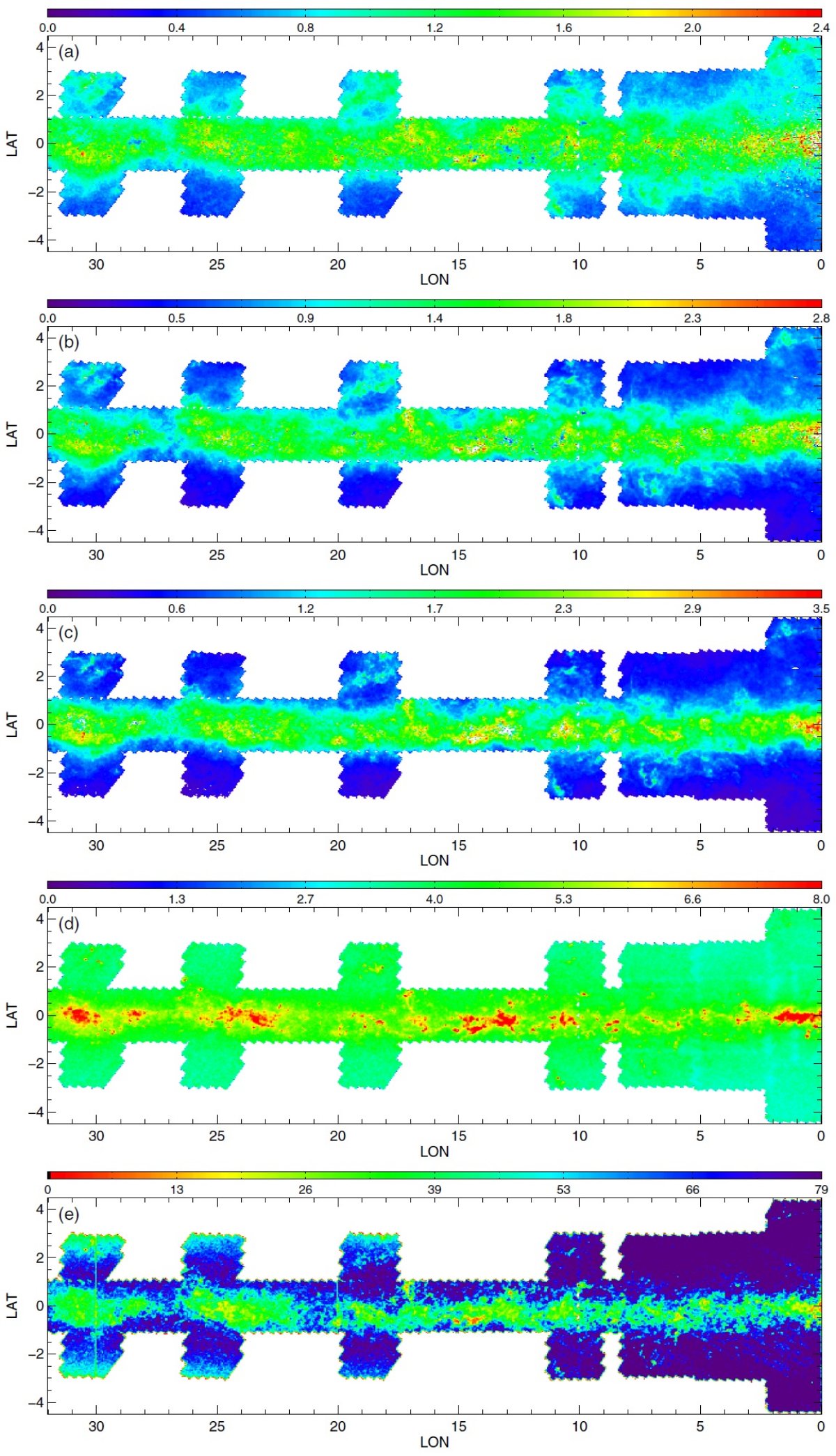
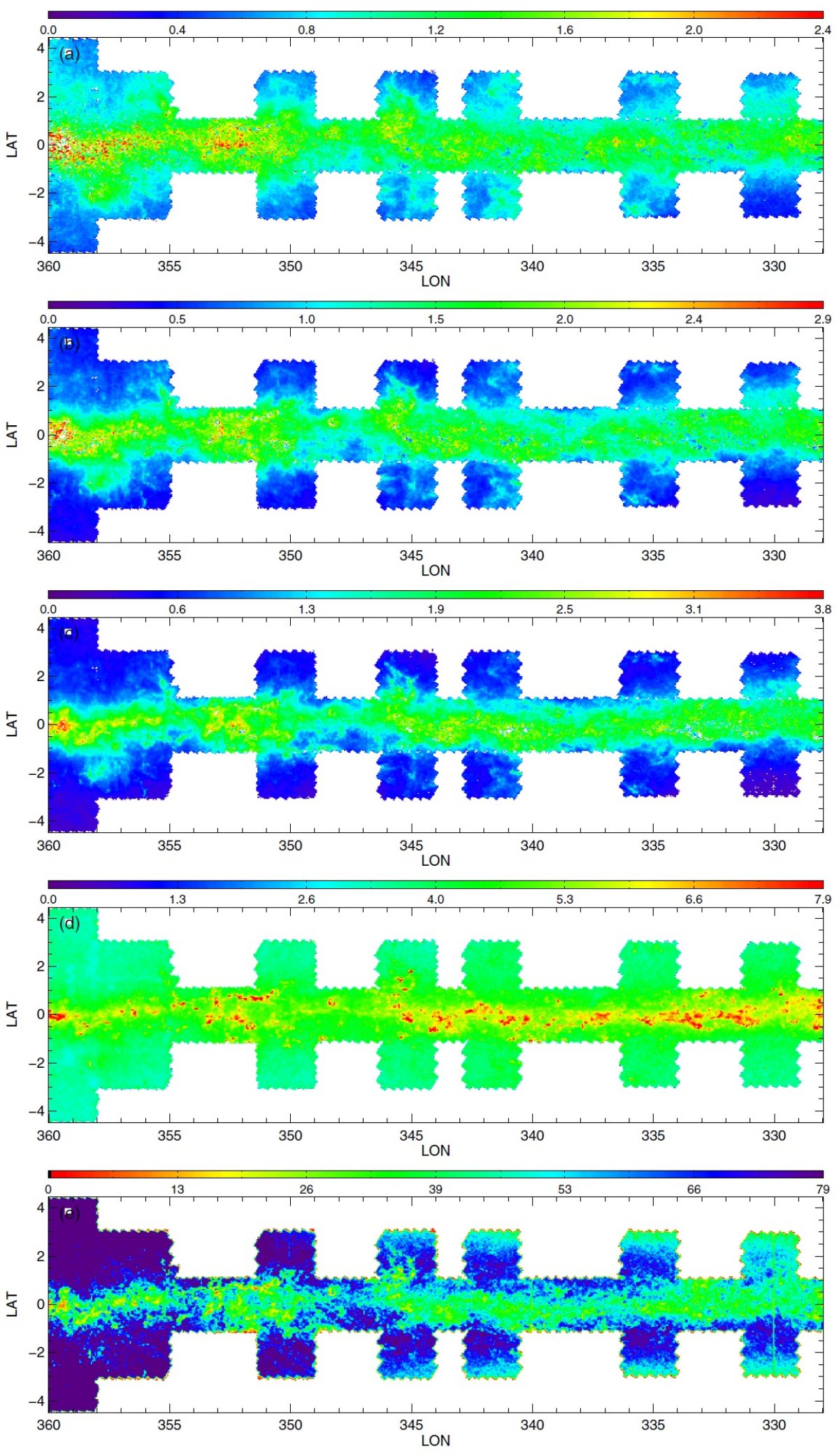
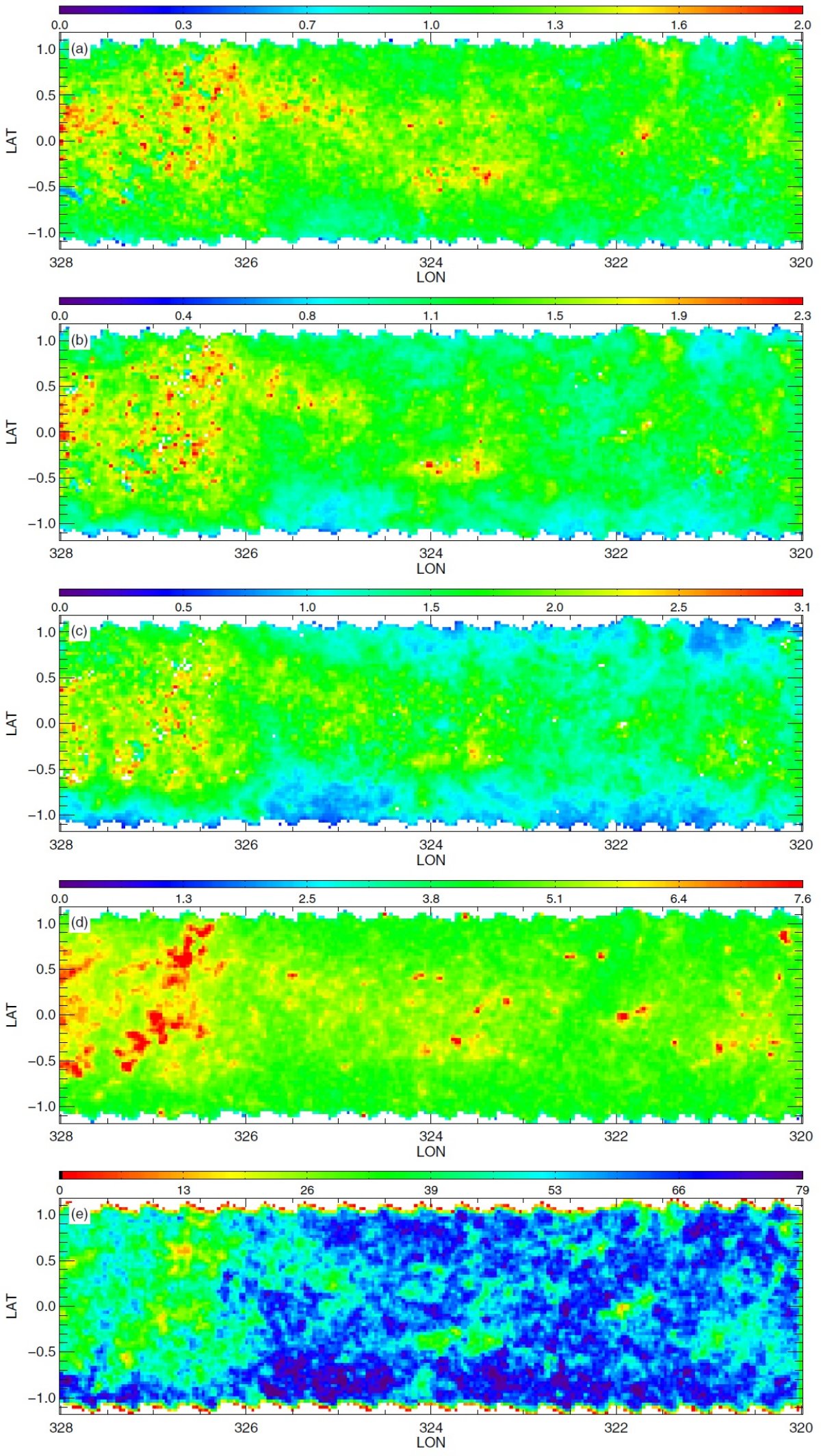
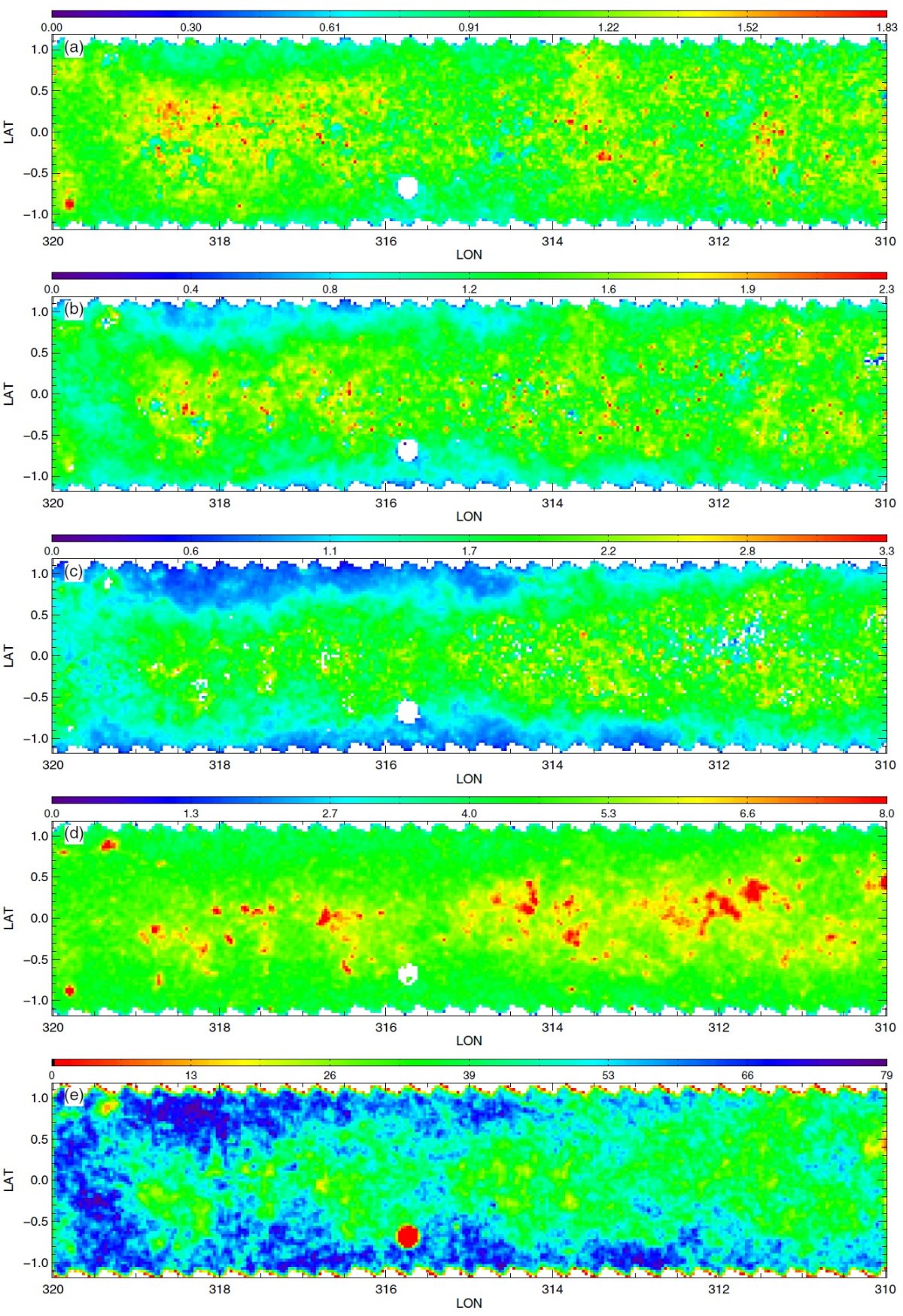
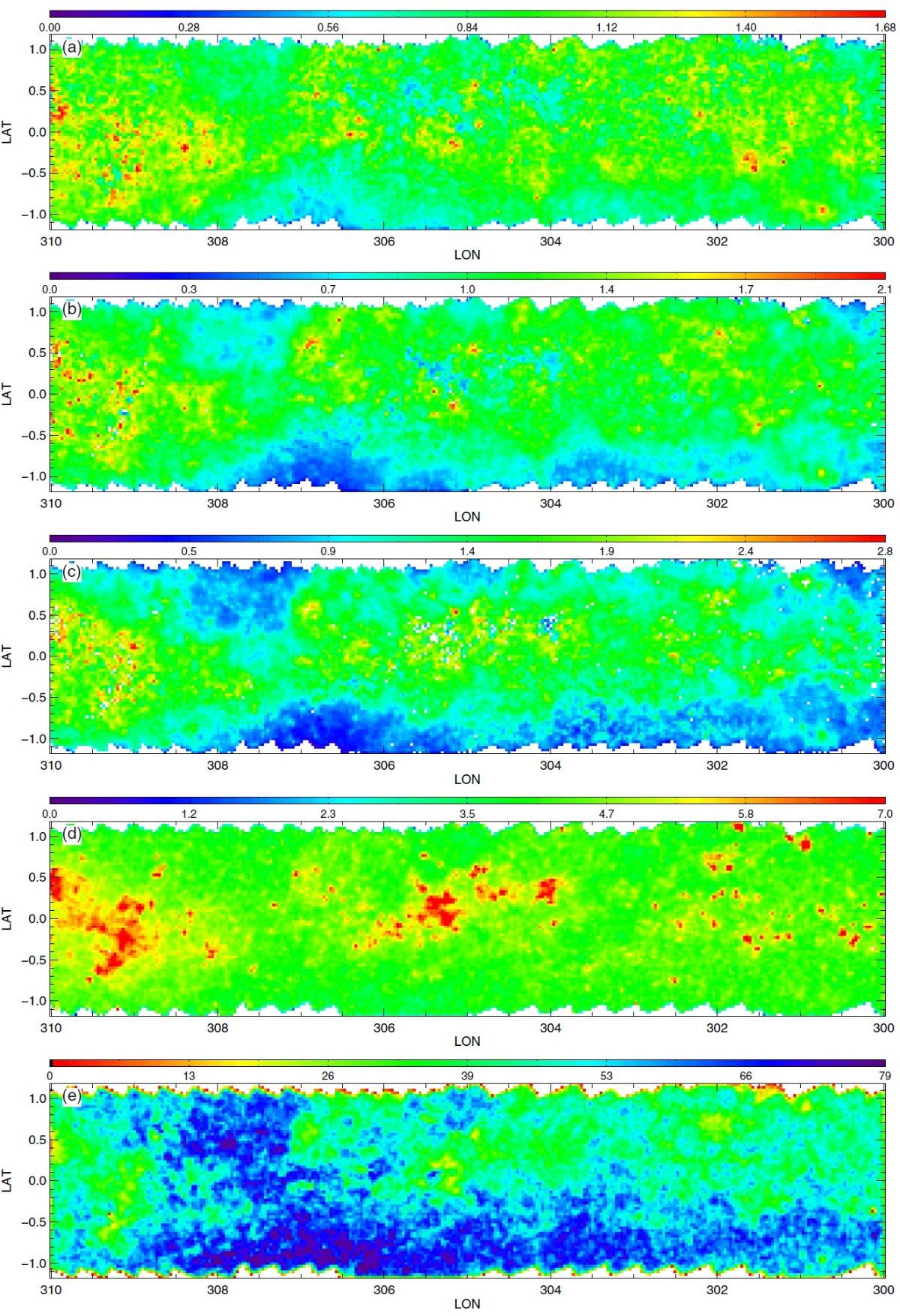
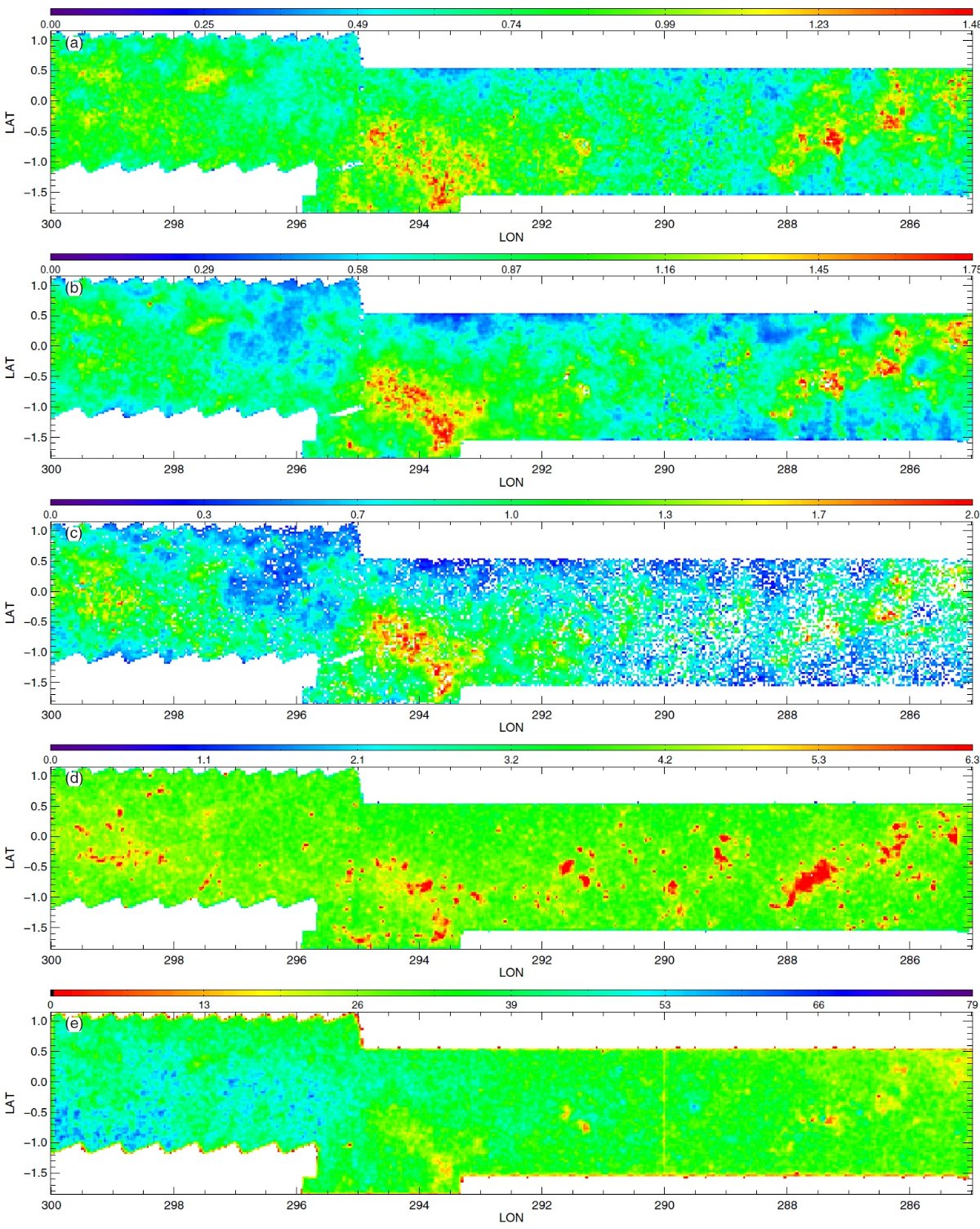
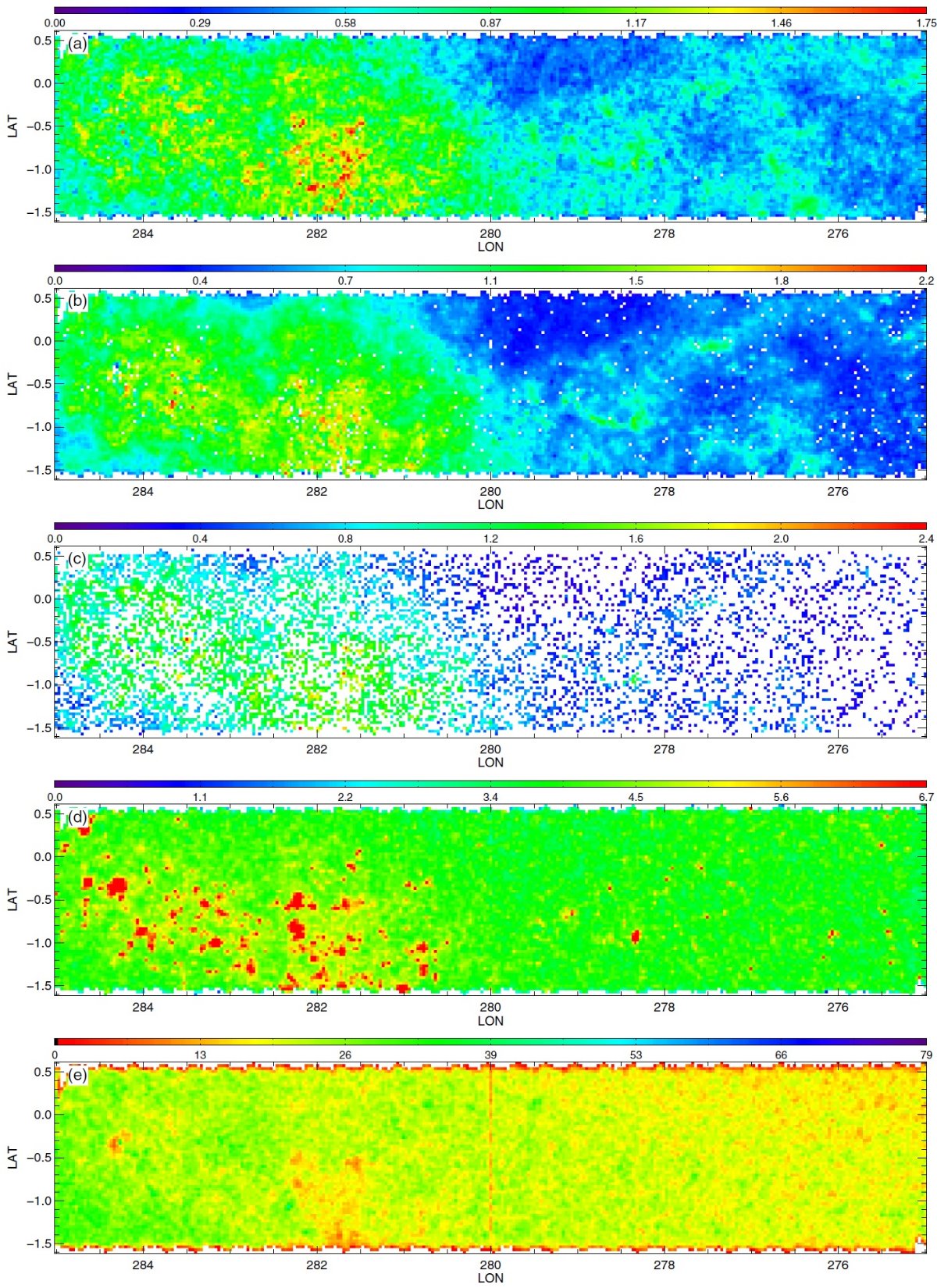
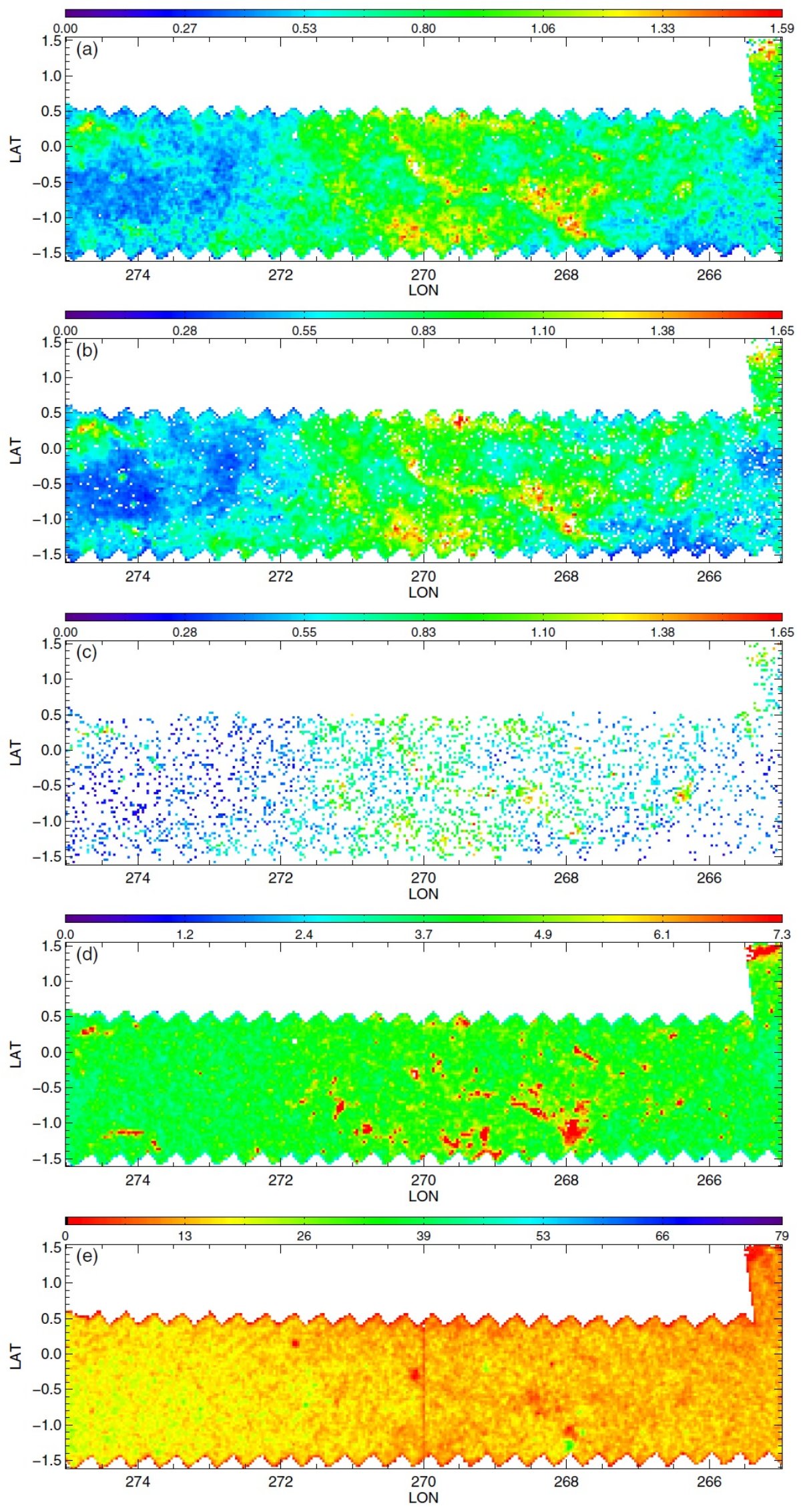
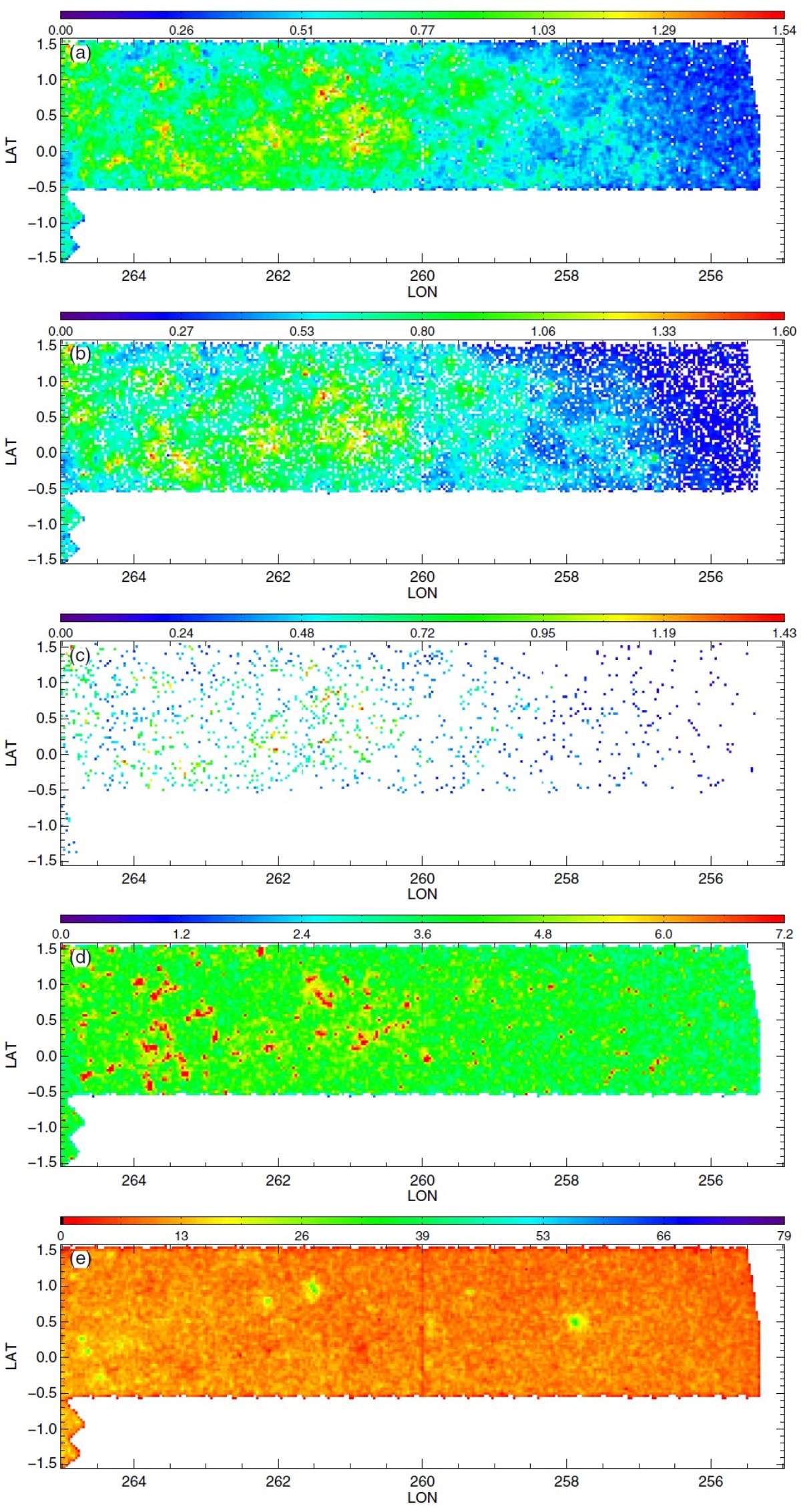
3.1.3次元情報減光マップはダストの3次元分布の粗い情報を与えるここに示した減光マップはダストの3次元分布の粗い情報を与える。3種類の 星サンプルはそれぞれが異なる距離範囲を探査しているので、マップを比較して 個々のダスト雲の距離と厚みの情報を得ることができる。 遠方の雲 図2B の l = 506deg; - 60° マップはその可能性をよく示している。 例えば、RGB マップの (l, b) = (54.8°, 0.8°) にある 0.5° 巾の雲は、 RC, MSTO マップのいずれにも 現れない。 RC の最大到達距離が 8 kpc であることを考えると、この雲はそれより 遠方に位置すると考えられる。 別の例 (l, b) = (59.0°, 0.5°) の糸状の特徴は RC, RGB マップで見えるが、 MSTO マップには現れない。これはこの構造が RC より近くにあることを示している。 もっと近い構造は (l, b) = (53.7°, 0.5°) にある。これは全てのマップ に現れており、距離が近いことを示している。 将来の精密化 将来、星の距離分布をより丁寧に計算して、雲の距離をより詳しく決められる ようになるだろう。 3.2.不定性の評価RJCE 減光測定に入り込む誤差については、 Majewski et al. 2011 で詳しく論じられた。それらは、(1)固有カラーの分散 (2)測光エラー (3)減光則の不定性 で合わせて、個々の星の A(Ks) に ≤ 0.11 mag の不定性を導く。小区画 での 90th percentile, 中間値を使うと誤差はさらに減少する。 |
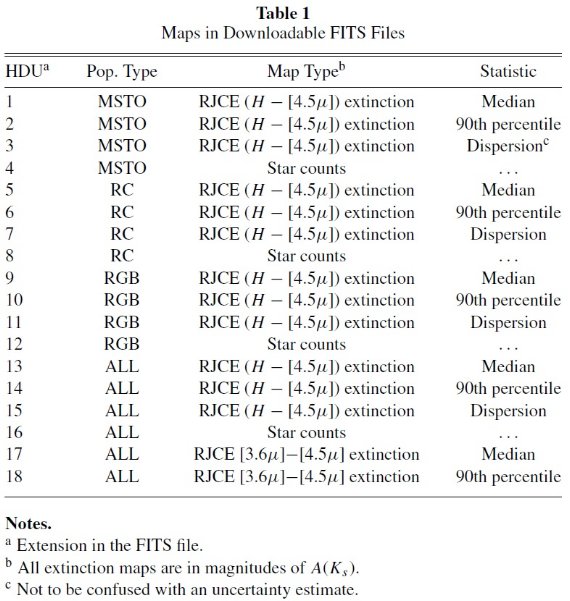 表1.FITS ファイルでダウンロード可能なマップ |
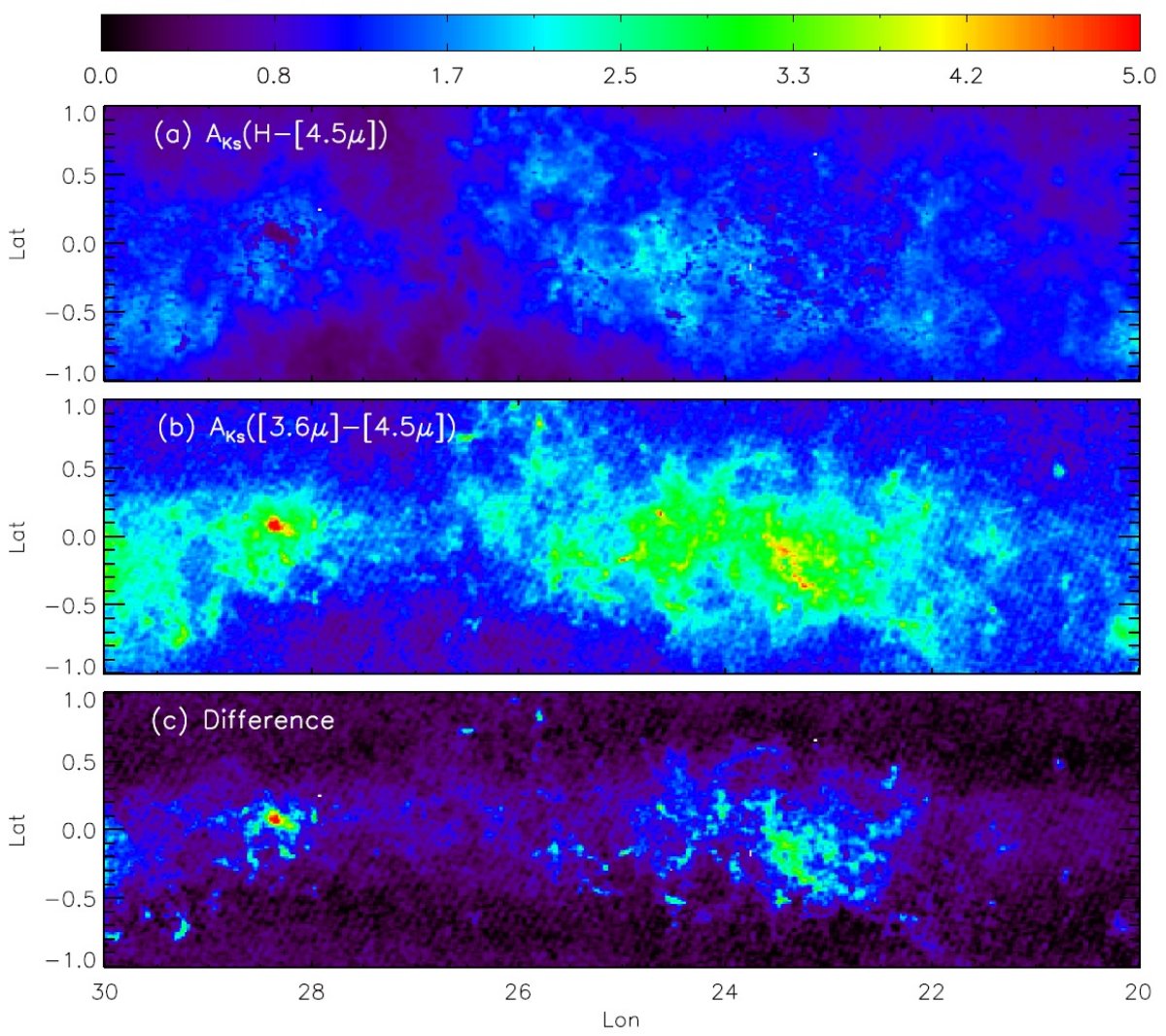
4.1.高減光領域での測光減光マップの「あな」図2、特に外側銀河系高銀緯部と銀河中心付近の高減光領域には、 くっきりした「穴」がいくつも見える。、が前者は低密度のため実際に星が欠けている 部分である。しかし、高減光部の「穴」はカタログの測光限界による見かけ の現象である。そのような雲が近くにあったら、結果としてその雲の領域では 星が殆ど消えてしまう。一方、雲が遠いと前景の浅い赤化を受けた星しか見えない。 このため、減光雲中央の減光「ピーク」は周辺より低くなる現象が起きる。 高減光による「あな」をどう扱うか? (1)より深い測光。大口径サーベイ望遠鏡の出現により今後可能になる。それまで は暗黒雲中心等の狭い領域に限られるだろう。 (2)そのようなピクセルを無視する。この論文の空白ピクセルがそれ。 (3)より減光の弱い波長を使って向こう側を見る。(3.6-4.5) はそのような 目的のための補助手段である。 中間赤外のみでの減光マップ Majewski et al. 2011 における限界等級の解析によれば、中間赤外データのみでなら最も厚い暗黒雲の向こう側 でさえ透して見ることが出来る。3.6, 4.5 μm での減光は ∼ 0.04×A(V) しかない。これに対し、A(H) ∼ 0.2×A(V) である。図4 中に示される通り、 E(3.6-4.5) のマップは(H-4.5)マップで「あな」だったところがピークである ことを示した。ただし、エラーも大きくなる。 |
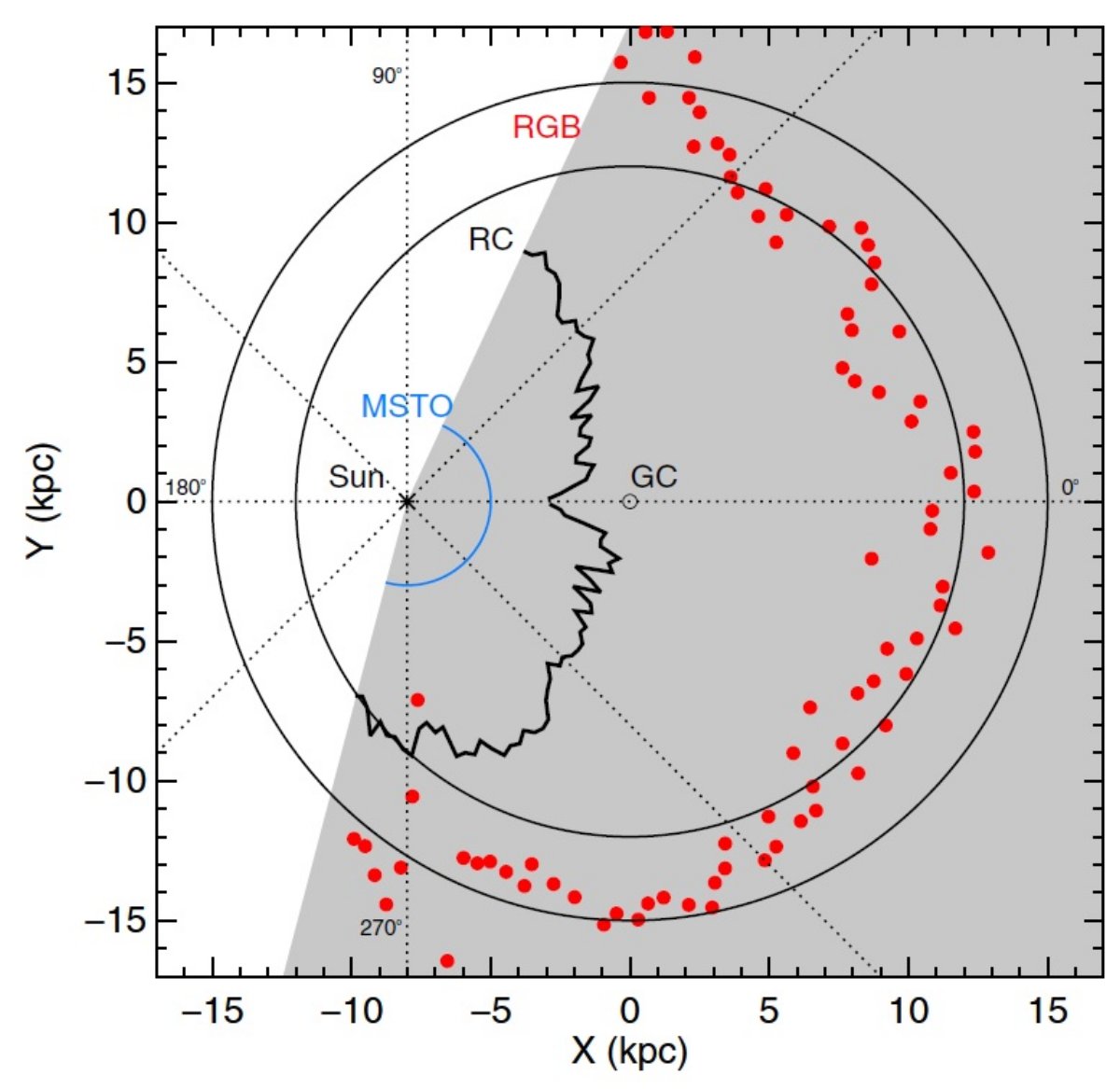
4.2.距離への制限赤色巨星枝のフィット赤化補正した色等級図上で赤色巨星枝の暗い側の縁を調べた。 -1.3 ≤ [Fe/H] ≤ +1.7, 9.0 ≤ log t ≤ 10.05 (Girardi et al 2002) 等時線で距離をフリーパラメタ―としてフィットした。その結果、各色等級図に対し 最遠距離を割り振れたのみでなく、それらの星がカタログの等級限界でどのように 見えるかも(円盤の縁でなく)教えてくれた。 (実際にはどんな差なのだろう? ) ここで用いられた手続きは Majewski et al. 2011 と非常によく似ている。主な差は、与えられたカラーでの円盤の縁は明るい方から 90 % のところの星の等級で決められたということである。ここで用いた改良版は RGB の暗い縁をフィットする信頼度を上げ、図5に示されている。 MSTO TRILEGAL モデルで (l, b) = (30°, 0°) 方向の色等級図 を (J-Ks)o = 0.0 - 0.4, Ks,o = 12.5 - 13.5 の星が存在する距離を 知らべた。ここは観測で MSTO クランプが見える部分である。そこ でのモデル星の距離の中間値は 2 kpc, 90th percentile は 4 kpc であった。 したがって、 MSTO は大体 2 - 4 kpc に存在すると言える。 RC Salaris, Girardi 2002 によれば、レッドクランプ星の明るさは [Fe/H] に ほとんどよらず一定であるので、M(Ks) = -1.54 ±0.04 Groewegen 2008 距離を決められる。レッドクランプ星は (J-Ks)o = 0.55 - 0.85 から選んだ。 各小区画で 90th percentile 減光を求めた。赤化補正した Ks,o と M(Ks) から 距離が決まる。2° 区間での中間値ラインを図5に示す。 RGB テスト領域 (l, b) = (30°, 0°) で TRILEGAL モデルと等時線から RGB 距離を決めた。(J-Ks)o = 0.85 - 1.4, Ks < 13.5 を赤色巨星として選んだ。 それらの中間距離は 15 kpc, 90th percentile は 19 kpc であった。さらに、 [Fe/H] = 0, t = 5 Gyr のパドヴァ等時線を用いて、l = [+29, +31], b = [-1, +1] (J-Ks)o = [0.85, 1.25] の観測にフィットした。その結果は、中間等時線距離 10 kpc, 90th percentile 24 kpc であった。これに対し、上に述べた「CMDの縁」距離は 平均 15 kpc であった。なので、 RGB 距離は 15 - 24 kpc である。 ( 2つの方法の距離の差は不定性と認めて いるということか?) |
|
恒星分類と減光マップ 赤化補正後のカラーから星を3グループに分け、それぞれの減光マップを 作った。その比較から雲の位置を推定した。濃い場所では (3.6-4.5) の 中間赤外カラーを用いた減光を与えた。 中間赤外カラーの利用可能性 近赤外測光が出来ない高減光域で中間赤外カラーの利用可能性があるかを探った。 中間赤外カラーは固有カラーが縮退していて星の分類に適していないが、高減光域 での減光を与えることが出来る。 |
RJCE 法の改良 APOGEE プログラムで得られる分光データは RJCE で得た星のスペクトル型 と比べることができる。 最終目標 最終的にはこの赤化補正を星とダストの3次元分布を求めるために使用すること である。既にこのデータを減光則を求めるために使用した。現在は 赤化補正した色等級図を中心バーや外側渦状腕、円盤の縁を調べるために使っている。 |