| ヒッパルコスやその他の大規模サーベイにより」銀河系の構造と進化には新たな 制約が課された。それらのデータを解釈し、銀河系の進化シナリオと較べるには 種族合成法が有効である。ここに、可視、赤外星計数の解析とブザンソン種族合成 モデルから得られる進化パラメタ―への新しい制約を述べる。 | ヒッパルコスの結果と回転曲線に合わせて、銀河系ポテンシャルを与える。外側 バルジ構造、ワープし、広がった円盤、厚い円盤、楕円体成分に対する整約が与え られる。モデルを調整して、 U から K バンドの信頼できる星計数が与えられるように した。最後に、シミュレイション、ベイジアン確率評価に基づく新しい分類、 などに関する応用を述べる。 |
| 他の種族合成モデルと較べ、ブザンソンモデルの特徴は、力学的 整合性である。ボルツマン方程式は等温の仮定の下で、速度散布度と銀河系 ポテンシャルの制約からスケール高を与える。 | このような力学的制約はフリー パラメタ―のセットを排除する。これにより、モデルの物理的信頼度が 向上した。 |

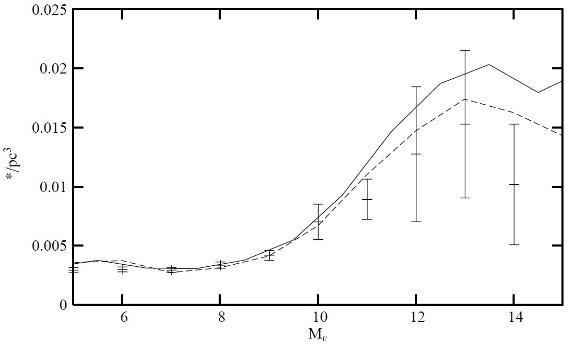 図1.太陽付近での V バンド光度関数。縦棒=近傍星カタログからの Jahreiss の推定値。実線=べき乗型IMFでの光度関数、m < 1 Mo で α1.7. 破線=α1.7. 種族合成モデルと恒星進化経路の結合 Bienayme et al 1987a,b は初めて銀河系の進化モデルに力学的整合性を取り入れた。 Heywood et al 1997 はより良い進化経路を使って、 IMF と SFR に制限を加えた。この 論文にはパラメタ―調整の詳細が述べられている。薄い円盤種族は過去 10 Gyr に渡り、 進化してきたと想定される。年齢は白色矮星の光度関数 Wood, Oswalt 1998 から 得られ、精度は 15 % である。 IMF 勾配と SFR の組を仮定し、星計数と比較される。 ヒッパルコスからの新情報 ヒッパルコスのお陰で、近傍密度とポテンシャル Creze et al 1998, 光度関数 Jahreiss, Wielen 1997, 運動学 Gomez et al 1997 の新しい情報が得られた。 (1)光度関数 ヒッパルコス光度関数は太陽近傍低質量星の IMF に制限を加えた。表1にあるように、 IMF は 二つのべき乗則の重ね合わせで表される。高質量側では Heywood et al 1997 が決めた α = 3 の勾配は、サルピータの値より少し大きい。高質量側では Heywood et al 1997 が決めた α = 1.7 の勾配は、本論文では 1.6 に訂正 された。これは、 Jahreib が Catalogue of Nearby stars から決めた新しい光度関数 と合うようにしたのである。図1を見ると分かるが、新しい IMF は 6 > Mv < 13 での近傍光度関数に良く合っている。この勾配は Kroupa 2000 が独立に定めた α = 1.3 ±0.5 (M = [0.08, 0.5]Mo) とも良く合っている。ただし、Kroupa 2000 は M = [0.5, 1.0] Mo でサルピータの α = 2.3 を採用している。我々の見解では 現在のデータで Kroupa 2000 のように質量を4区間に分けるのは無理がある。そこで 質量を二つに分けた。 |
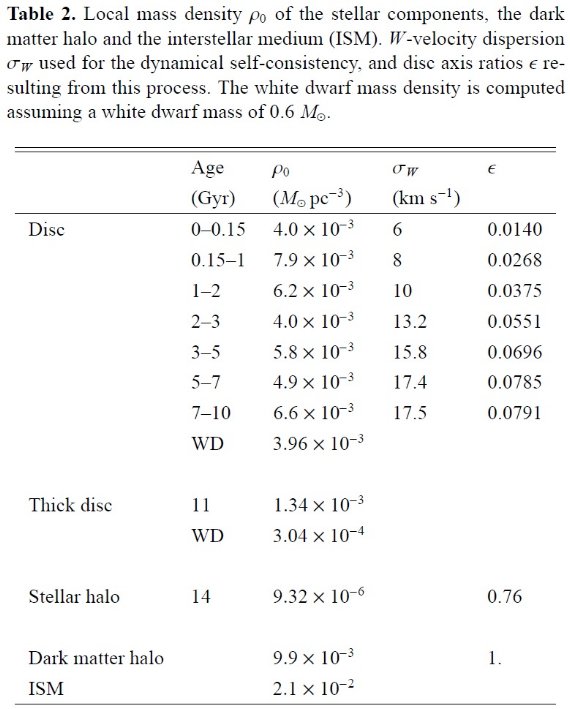 表2.種族ごとの太陽近傍質量密度。 σW = W-速度分散 は力学的整合性のために決めた。円盤軸比 ε はその過程で 決まる。白色矮星質量密度は mWD = 0.6 Mo を仮定して決めた。 (2)運動学 ヒッパルコスから得た Gomez et al 1997 の年齢ー散布度関係を導入した。 (3)星間物質 太陽近傍星間物質表面密度に Dame 1993 の 6 Mo pc-2 を採用した。 この不確定性はファクター 2 である。スケール高 = 140 pc とすると、銀河面上 での体積密度は 0.021 Mo pc-3 である。これは我々の前モデルで使った 値の約半分である。 |
|
近傍空間密度 星、ガス、ダークハロー(表2)を足すと、全物質密度は 0.0759 Mo pc-3 となる。これは Creze et al 1998 がヒッパルコス A-, F-型星への Kz 力から導いた 0.076 Mo pc-3 と一致する。 まだ軌道進化までは扱えていない 進化モデルは太陽近傍単位体積内にある星の数を、年齢、質量、有効温度、 重力、メタル量別に与える。進化モデルはまだ軌道進化までは扱えていない ので、我々は星をボルツマン方程式から道にかれる年齢厚み関係を用いて再配分 することにした。 Bienayme et al 1987 のポテンシャル Bienayme et al 1987 は力学的に整合なポテンシャルを与えた。彼らは銀河系 ポテンシャルが恒星、星間物質、ダークハローの和で与えられると仮定した。 我々はポアソン方程式を解いてポテンシャルを求めた。円盤は銀河面で特異点を生じ ないように、二重指数関数型ではなく、 Einasto 則 (1979、表3に表式あり) を採用した。 薄い円盤種族は 0 - 10 Gyr の7つの異なる年齢の等温種族に分けられた。7副種族の 夫々は、最も若い種族(力学的に緩和していない)を除いて、年齢ー速度散布度関係 による速度散布度を与えられる。その速度散布度に応じ、下の(1)式からスケール高 (回転楕円体なら軸比)が得られる。一方、回転曲線はダークハローの形と近傍密度に 制限(Bienayme et al 1987) を与える。
ポテンシャルと密度を整合させる 以上から新しい総質量密度が計算される。こうして、逐次近似が繰り返され、 ポテンシャル値と円盤の厚みの差を 1 % 以下に押さえる。表2にはこうして 得た円盤の軸比が載せてある。図2にはベストフィットモデルの回転曲線を 示す。 ダークハロー成分 ダークハローの近傍密度は 9.9 × 10-3 Mo pc-3 で、Bienayme et al 1987 が定めた値の 20 % 上である。一方、円盤の質量 密度は低めに出た。この差は彼らが「不可視の円盤」を考え、その近傍密度を 0.01 Mo pc-3 としたからである。ただし、その散在は Creze et al 1998 により明確に否定された。回転曲線を合わせるには、円盤からの力の不足を ダークハローで補う必要があった。その力は R > 5 kpc では引力の主成分 である。 |
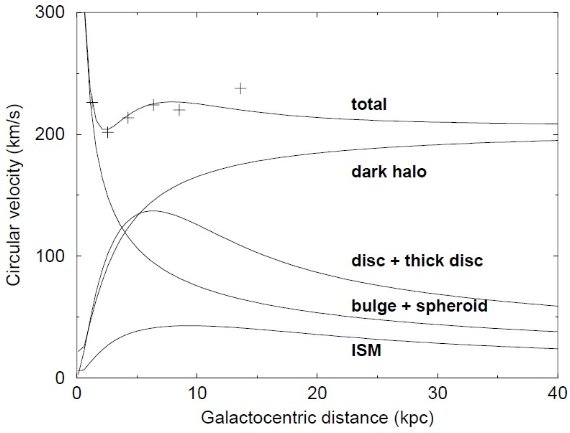 図2.自己整合的な回転速度。十字= Caldwell, Ostriker 1981 による 制約。銀河系各成分の寄与も示す。 各成分の質量
|

2.1.2.大気モデルとカラー評価年齢メタル量関係メタル量は年齢・メタル量関係とそのガウシアン散布度を仮定して決める。 薄い円盤には、 Twarog 1980 の関係式 表1 を用いた。Haywood 2001 のより 太陽組成に重点をおいた年齢・メタル量関係も使える。Twarog と Heywood の 関係式の差は広帯測光データを扱う限り殆ど問題にならない。 |
モデルのカラー BaSel データ Lejeune et al 1997, 1998. 大気モデルを観測データに合うように 修正して、色々な測光システムのカラーを与えた。 Baraffe et al 1998. 低メタル星の近赤外カラーに使用した。 Guglielmo 1993. ≥ M7 星の赤外等級とカラーの観測値。これら晩期 M 型巨星と AGB 星の中間赤外モデルは不正確かも知れない。将来修正されるであろう。 |
2.1.3.外側円盤円盤の縁とワープRobin et al 1992, Ruphy et al 1996 は R = 14 kpc に円盤の縁があると主張した。 しかし、 DENIS データから Derriere, Robin 2001 は近赤外星計数にはワープと フレアがはっきりと現れていることを示した。 o これまでのワープ検出
ワープの起源説 (1)円盤とダークハローの相互作用;軸の向きが違うため。 (2)サジタリウス矮小銀河やマゼラン雲との作用。 (3)落下する銀河間ガス。 星ワープのパラメタ― 起源に関わらず、我々は 電波観測に合うワープのパラメタ―をまず選び、 DENIS データと照合して、パラメタ―の調整を行う。 ワープに対しては Porcel et al 1997 の傾斜円環モデルを採用した。 ワープした円盤の密度則を計算する時には、銀河中心距離が Rwarp より遠くでは 銀河中心座標 (R, θ, z) は銀河面より、 zwarp = zc cos (θ - θmax) だけ上に移動する。ここに、θmax = ワープが最高になる方向、 zc は与えられた R に対するワープの最大高度である。 我々は線形のワープ振幅を仮定した。 zc = γwarp(R - Rwarp) Burton 1988 に習い、太陽はワープのノード線上にある, θmax = 90, とする。また、振幅の増加率は Gyuk et al. 1999 と大体同じ γwarp = 0.18 を採用した。DENIS を使った予備研究 Derriere, Robin 2001, Derriere 2001 は、 Rwarp = 8.4 kpc で Ro に近い。 Ro の値が論文に見当たらない。 星フレアのパラメタ― Gyuk et al. 1999 と同様、フレアのスケール高は相対比で、次の式で与えられる。 kflare = 1 + γflare(R - Rflare) フレア円盤の表面密度は正常円盤と同じとする。γflare = 5.4 10 -4 kpc-1、 Rflare = 9.5 kpc とする。 pc-1 の間違い? |
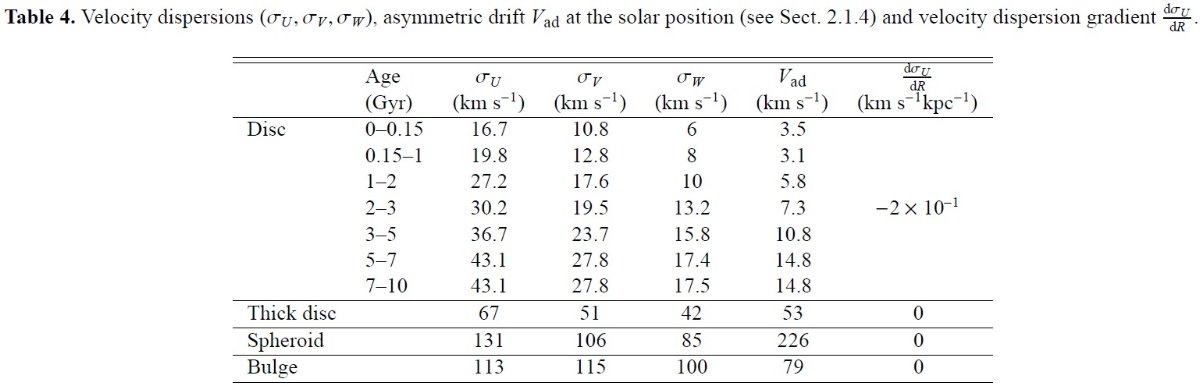
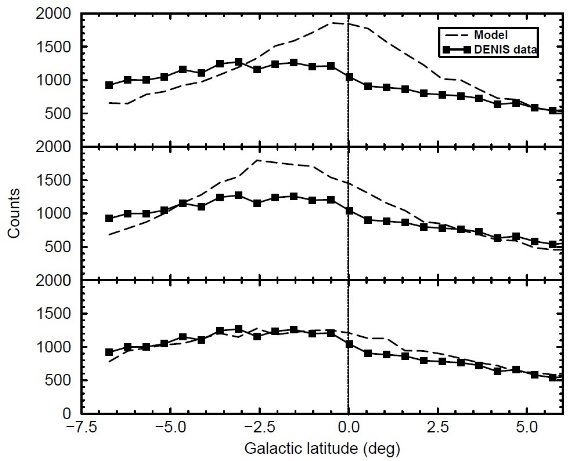 図3.DENIS ストリップに沿った星計数。ストリップは銀河面を l = 266.1 で横断する。実線=データ。破線=モデル。上:真直ぐに平らな銀河面。 中:ワープした円盤。下:ワープして広がった円盤。 モデルフィット 図3には、ワープとフレアが近赤外星計数に与える影響の例を示す。四角= l 266.1 を通過する DENIS 帯での DENIS K-星計数。破線=モデル。上図はワープもフレアもない モデルの予測で、ピーク位置がデータと大きくずれている。中図はワープだけ入れたので ピーク位置は合うが、ピーク値が大きすぎる。下図は両方を含むモデルで、観測と 良く合う。 2.1.4.円盤運動学円盤の速度楕円体は Gomez et al 1997 のヒッパルコスデータ解析からとった。 年齢と銀河中心距離勾配による速度散布度の変化は表4に示す。非対称ドリフトは以下の 式から求めた。
ここに、 dρdR は密度勾配である。Uo = 10.3 km s-1, Vo = 6.3 km s-1, Wo = 5.9 km s-1, VLSR = 226 km s-1 とした。VLSR は質量モデルを観測 回転曲線にフィットして得た。 |
|
形成モデル 厚い円盤の形成シナリオとしてマージャーがある。降着天体により円盤種族が加熱されて 大きな速度散布度を持つ厚い円盤を形成した。この降着が起きた時期の結果、厚い円盤の 元素量はハローと薄い円盤の中間になった。化学組成観測から厚い円盤の星形成期間は 1 Gyr を越えないことが判っている。円盤形成の時期は、 8 Gyr から 13 Gyr に渡って 諸説がある。我々は 11 Gyr とした。 厚い円盤の星形成モデル 一回性の星形成を仮定する。つまり、星形成期間は銀河年齢に較べ非常に短い。厚い円盤の メタル量は -0.78 dex とする。メタル量の散布度は 0.3 dex とし、低メタル側のテールは 考えない。 |
厚い円盤の密度分布 星までの距離の不定性が主な理由で、厚い円盤の密度分布は不確定である。そこで、 銀河面から高い所では指数関数型、低いところは二次関数型という妥協案を採用した。 係数は表3を見よ。密度則パラメタ―は、スケール長 hR = 2.5±0.5 kpc, スケール高 hz = 0.8±0.05 kpc, xl = 0.4 kpc. 太陽近傍密度 ρ0 = 1.03 10-3 星 pc-3, または 7.6 10-4 Mo pc-3 (Mv ≤ 8). この密度は薄い円盤の 近傍密度の 6.8 % に相当する。IMF は dN/dm ∝ m-0.5 で、勾配は 大規模データセットで制限を受けている。すると、総密度は 2.83 10-3 星 pc-3, または 1.34 10-3 Mo pc-3 (Mv ≤ 8). Mv 範囲をどこまでにしてるのか? |
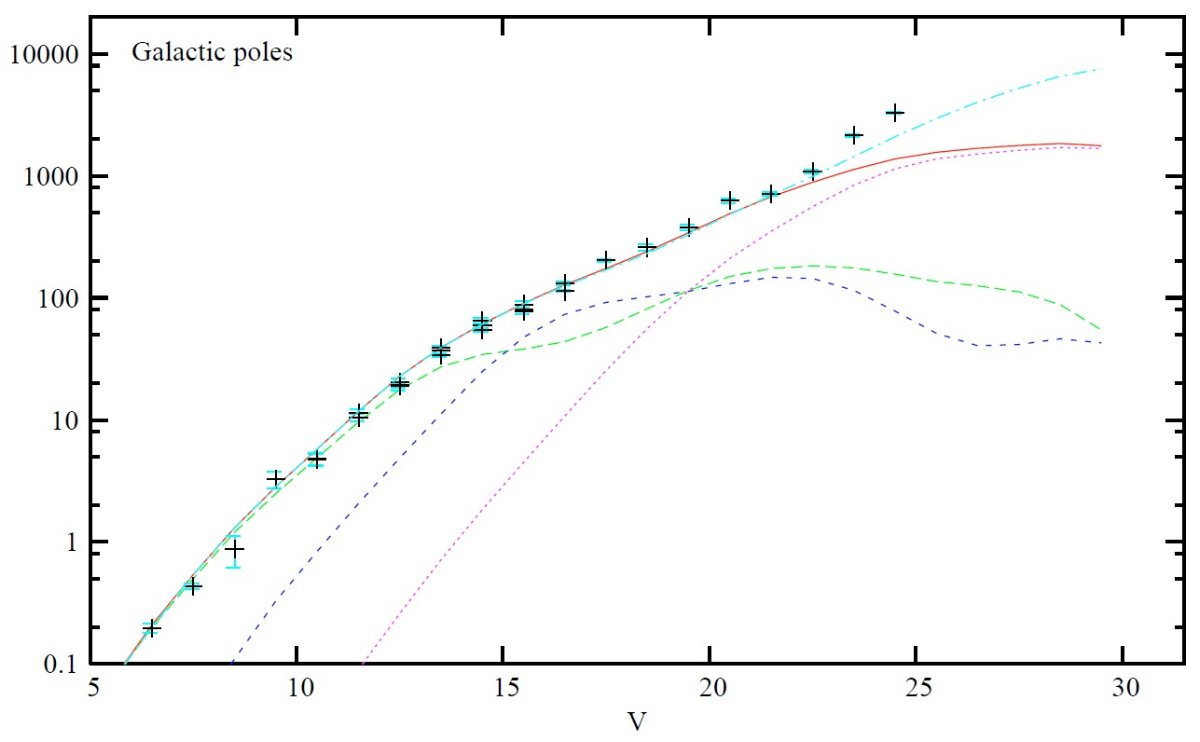
| 一様な種族とし、年齢 14 Gyr, 平均メタル量 [M/H] = -1.78, 散布度 0.5 dex, とする。密度分布は指数 n = 2.44 のべき乗則、平坦度 ε = 0.76, 太陽 近傍密度 ρ0 = 2.185 10-5 星 pc-3, または 0.932 10-5 Mo pc-3 である。星には下限質量まで含むが、白色矮星は入っていない。この密度は IMF dN/dm ∝ m-0.5 を仮定している。これは球状星団、 厚い円盤と同じ形である。 | 総密度は低質量星からの寄与、従って IMF の傾きに依存する。IMF dN/dm ∝ m-2 を仮定すると、近傍総密度は 8.19 10-5 星 pc-3 である。IMF 勾配の差は銀極方向星計数で、 V = 22 より暗い 所で効いてくる。図4の実線と一点鎖線の差を見よ。 |
|
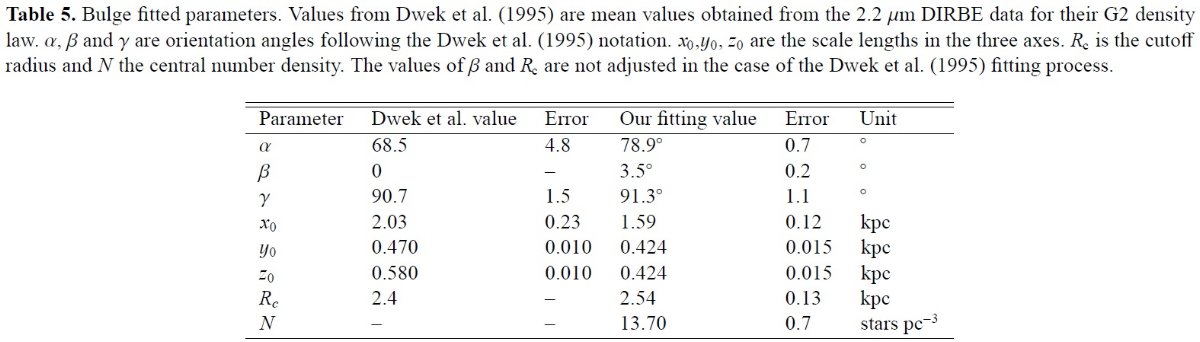
バルジ形成シナリオ バルジ形成シナリオは幾つかある。 (1)原始崩落。Eggen et al 1962 (2)階層的銀河形成(早期マージャー)。 Kauffmann et al 1994 (3)衛星銀河の落下(後期マージャー)。 (4)円盤の永年進化 Bouwens et al 1999 は上の全てが銀河進化史の間に作動したと述べている。 中里、野本 2003 は N-体計算から、バルジ星の 60 % は準銀河マージャー起源で、 40 % は内側円盤の星であると結論した。この二つのグループは元素組成の点で はっきり異なる。彼らのモデルはメタル量及び速度分散・メタル量関係を再現 するのに成功した。 バルジの特徴 バルジの観測的特徴は以下のようである。 (1)3軸不等形状。 非対称性は COBE/DIRBE 近赤外データに現れている。 Dwek et al 1995, Freudenreich 1998 は DIRBE データにモデルフィットを 行った。 Binney et al. 1997, Bissantz, Gerhard 2002 は同じデータからノンパラメトリックモデルを得た。 (2)メタル量分布。 K-型巨星のメタル量分布は [Fe/H] = [-1.2, +0.9] という広い範囲に渡っている。 McWilliam, Rich 1994. Minniti 1996 と Tiede, Terndrop 1999 は速度分散と メタル量の間の明白な関係を示した。この結果は彼が観測した範囲 b = [-8, -6] にハロー、バルジ、厚い円盤の種族が混じり合った結果かも知れない。 (3)回転 バルジは回転運動で支持されていて、投影回転速度は 53.3±0.3 km/s/kpc Tiede, Terndrop 1999 である。 内側バルジ ここでは l = [-1, +1], b = [-1, +1] の内側バルジを除いた、外側バルジを 扱う。もっとも差がはっきり決まっているわけではない。 スタート密度則 第1近似は Dwek et al 1995 の G2 密度則を採用する。それを基に DENIS 星計数をフィットしてバルジ分布パラメターを決めた。詳しい説明は Picaud et al 準備中で述べる。 円盤スケール長もバルジパラメターと並行して決められる。内側銀河方向の データは明らかに両種族が共存していることを示す。しかし、Einasto モデルは 円盤の中央に穴が開いている可能性を示唆する。そこで、この論文では、バルジ種族と 円盤種族が共存しているのか、それともある半径で置き換わるのか、二つの可能性を 調べた。 密度則 表3に密度則のパラメタ―を示す。バルジのパラメタ―は Dwek に従って8つある。 それらは、 |
α = 傾斜角(バルジ主軸と太陽・銀河中心線に直交する線との角度。
だから、完全横向きの時が0°)。
β = バルジ面と銀河面との間の角度。
γ = バルジ主軸の回転角。 x0 = 主軸上のスケール長。y0、z0 = 副軸上のスケール長。 N = 中心数密度。 Rc = カットオフ半径。 LF と IMF モンテカルロシミュレイションに使うバルジ光度関数は Bruzual et al 1997 の太陽メタル、年齢 10 Gyr モデルを用いた。別の関数として、パドヴァ等時線 も将来は考える。サルピータ― IMF (表1)を考えるが、これは大質量、 中間質量星では観測から確認されている。しかし、低質量では確かでない。 Holtzman et al 1998 は HST から M > 0.7 Mo で 勾配 -2.2 を出しているが、 それより低質量では M = 0.5 - 0.7 Mo で折れ曲がりの兆候を見出している。 DENIS データ Schultheis et al. 1999 のバルジ減光マップを用いて、15′×15′ の低減光 100 領域を l = [-8, +12], b = [-4, +4] ないに選択した。完全度 限界等級は注意深く決められた。DENIS の特別なバルジサーベイから、J, J-K 星計数、 K = 8.5 - 11.5 を選び、シミュレーション結果と比較した。 ベストフィットパラメタ― 表5にベストフィットパラメタ―を示す。形状はオブレートで、時にはバーと呼ばれる。 その方向は太陽ー銀河中心線とほぼ 10° の角度を成す。これは Lopez-Corredoira et al 2000 が独立なデータから出した 12° とよく一致する。軸比は Dwek et al 1995 の値と合っている。我々の得た結果の精度が高いのは比較的低光度の星に感度の 高い星計数を用い、バルジの奥深くまでカバーしたからである。積分表面輝度を使うと 最高光度の星が支配的となり、脱投影でバイアスがかかるのである。(?) 質量 外側バルジの総質量は 2.03 1010 Mo で、白色矮星はその 26 % を占める。 内側バルジと中心ブラックホールは含まない。 円盤の穴 中心領域を合わせると、薄い円盤の中心部には穴が開く。これは棒状銀河では 普通に見られる現象である。円盤のスケール長は hR+ = 2.53 ±0.11 kpc, 穴のスケール長は hR- = 1.32 ±0.14 kpc である。 イメージが浮かばない。LP レコード盤じゃないのか? バー バーはバルジとは別個の種族と考えられる。それはバルジより遠方、Lopez- Corredoira et al 2000 に見られるように、l = 27 まで伸びている。その性質は 別途 Picaud et al 2003 で述べる。 |
白色矮星の進化経路には Bergeron et al 1995 の DA 白色矮星進化
モデルを用いた。これは観測的チェックを受けて信頼できる。ハロー
白色矮星には Chabrier 1999 を適用するがこれはまだ不確定性が
大きい。
2.5.1.薄い円盤の白色矮星太陽近傍でのはくしょく矮星 LF は良く調べられている。その太陽近傍 空間密度は低温の白色矮星が見つかるにつれ増大しつつあるが、 最近の Holberg et al 2002 の結果では 5.5 10-3 星 pc-3 である。Mv > 16 の暗い白色矮星の数は 空間密度の値を左右するが、それは現在わずか 3 個である。我々は Wood 1992 の年齢 10 Gyr 円盤の一定星形成モデルを採用し、6.6 10-3 星 を得た。 |
2.5.2.厚い円盤の白色矮星厚い円盤の白色矮星種族は Garcia-Berro et al 1999 がサルピータ IMF を仮定して計算した。しかし、観測で同定された厚い円盤の白色矮星は 殆どない。そこで、太陽近傍の高速度白色矮星を厚い円盤種族と看做して、 密度を計算した。その値は 5 10-4 星 pc-3 である。 |
2.5.3.ハローの白色矮星マゼラン雲 MACHO 観測から Freese, Graff 1997 は MACHO が赤色矮星や 褐色矮星である可能性は低いとした。残された可能性はハロー白色矮星で ある。これまで、 Oppenheimer et al 2001 や Goldman et al 2002 の ハロー白色矮星の見積もりは低かった。 | 最近 Mendes 2002 は NGC 6397 付近 で7個のハロー白色矮星と6個の厚い円盤白色矮星を見出したと述べた。 固有運動が大きな星のサーベイ VIRMOS から、 Le Fevre et al 1998 は 0.94 deg2 に高固有運動天体が検出されなかった。 |
|
FIR 放射からダスト分布決定 星間物質の大局分布は若い星と同様に、二重指数関数または Einasto 則で 表現される。しかし、平均減光の表現はそれでよいが、より小スケールの変動 を表す必要がある。Drimmel, Spergel 2001 は 3D 減光モデルを作った。 そこでは円盤や腕にある減光雲の分布はダスト遠赤外放射で決められる。 (距離は? ) Schlegel et al. 1998 が COBE で同様のことをしている。 |
減光則 減光則は Mathis 1990 のものを使う。 Cardelli et al. 1989 はこの減光則が λ = [0.125, 3.5] μm で妥当であり、 かつ希薄星間雲でも分子雲でも適用可能であることを示した。 我々は Rv = 3.1 を採用する。 |
|
銀河内の星の分布 上述の入力を用い、銀河のどの場所でも、与えられた年齢、タイプ、有効 温度、絶対等級を持つ星の数を計算できる。太陽位置は Ro = 8.5 kpc、 銀河面から 15 pc 上と仮定した。 |
見かけ等級 見かけ等級とカラーは減光を考慮して計算する。測光バンドとしては、 Johnson-Cousins システム UBVRIJHKL と GAIA G バンドである。 カタログ 表4の運動学パラメタ―に則り、位置、速度を計算した。こうして、 任意の方向の擬似カタログを作成する。 |
|
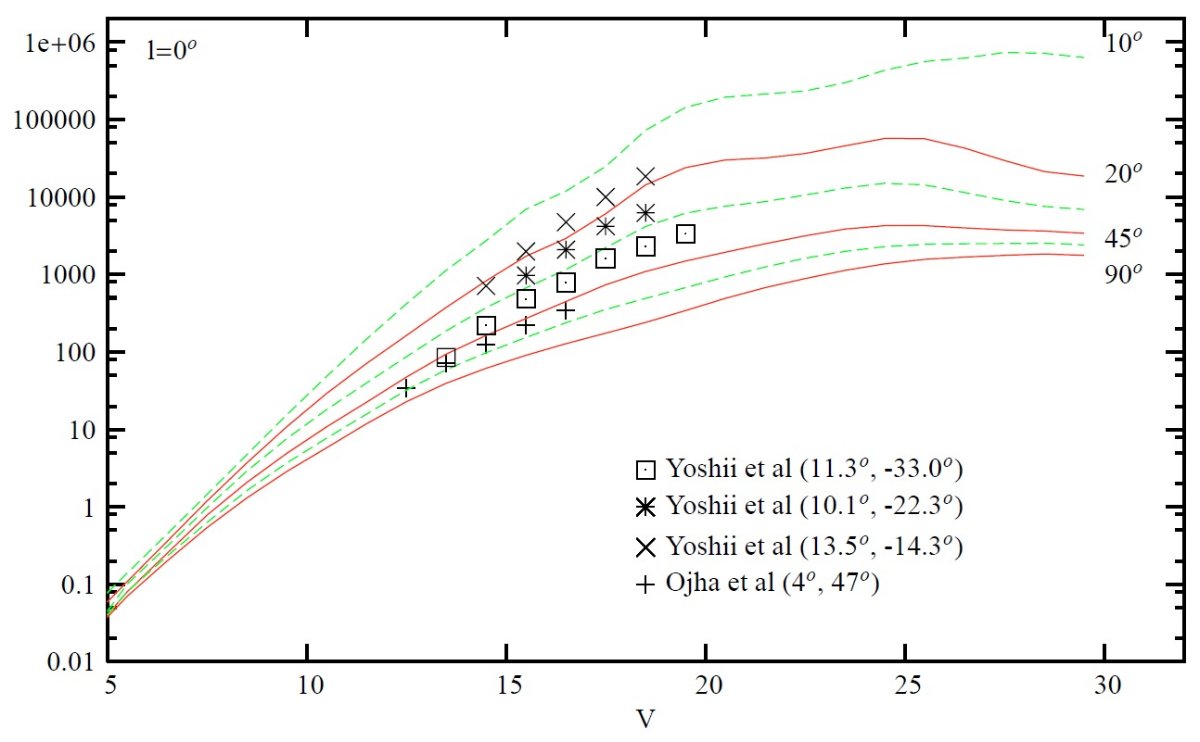
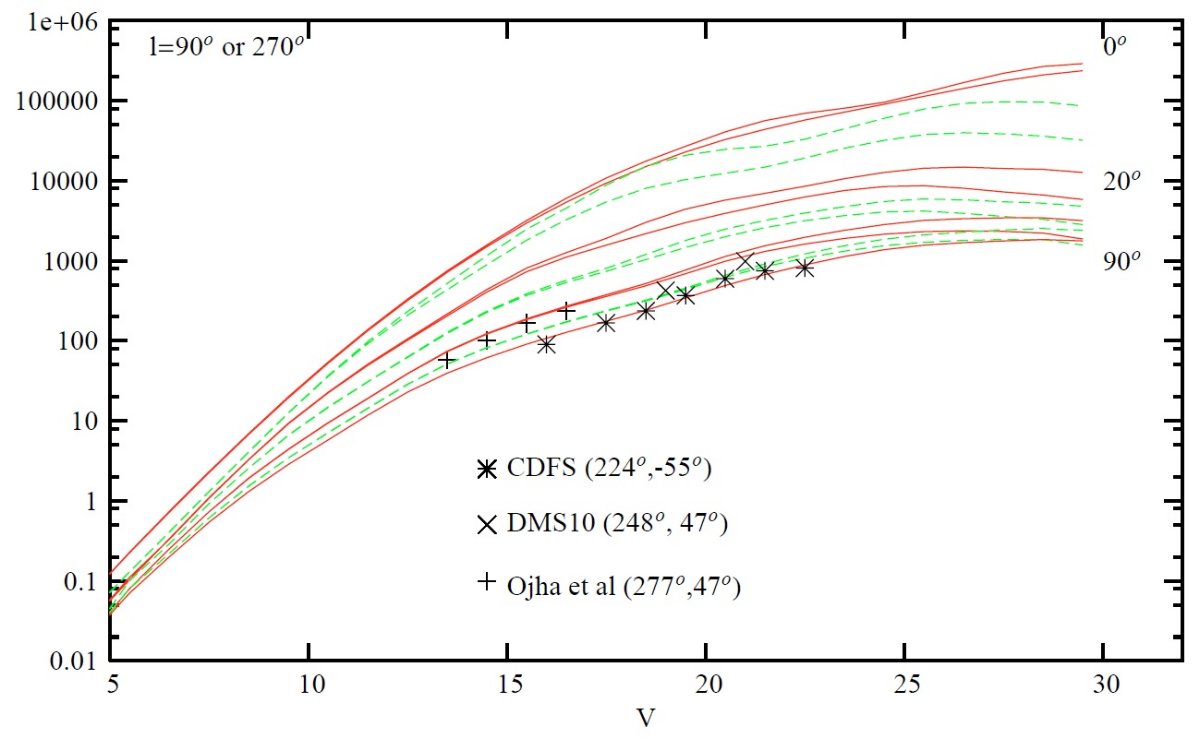
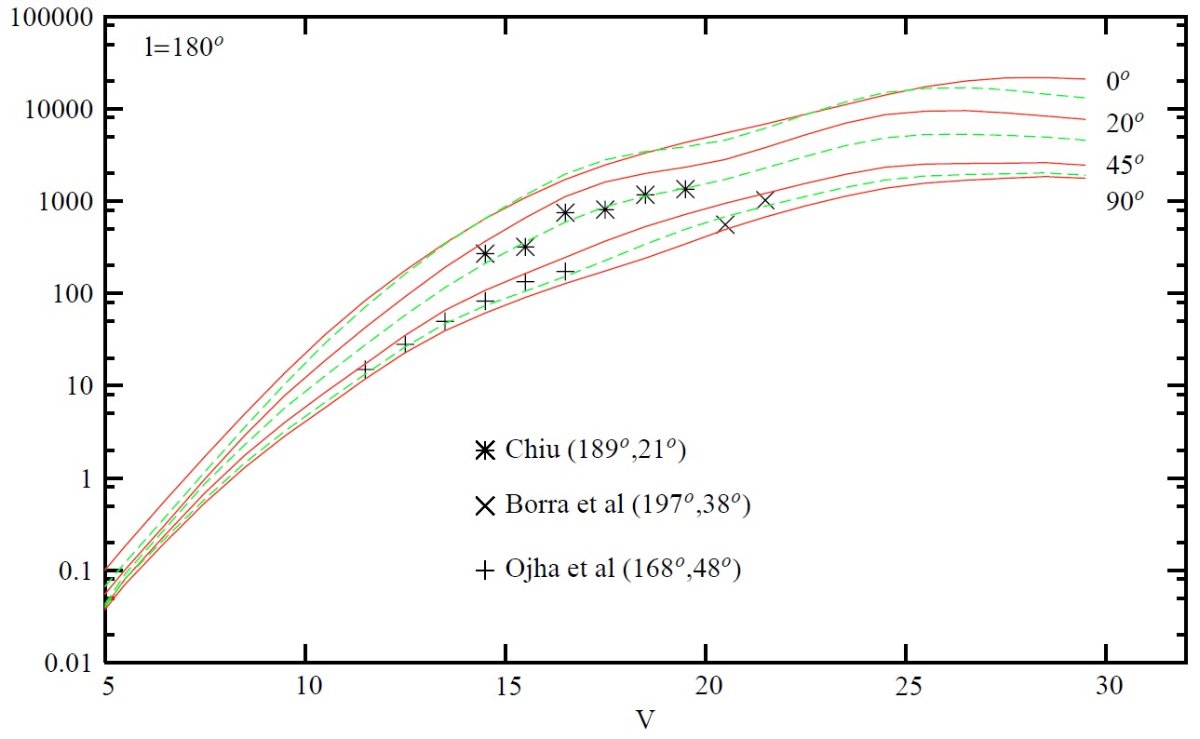
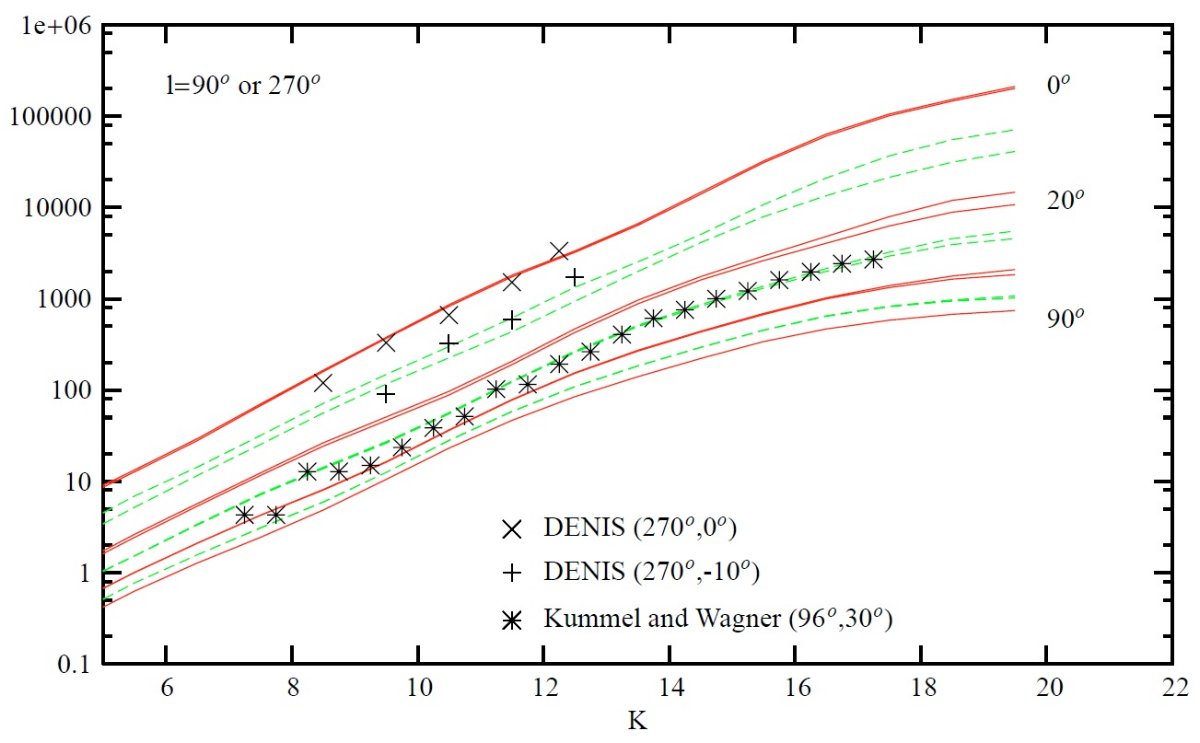
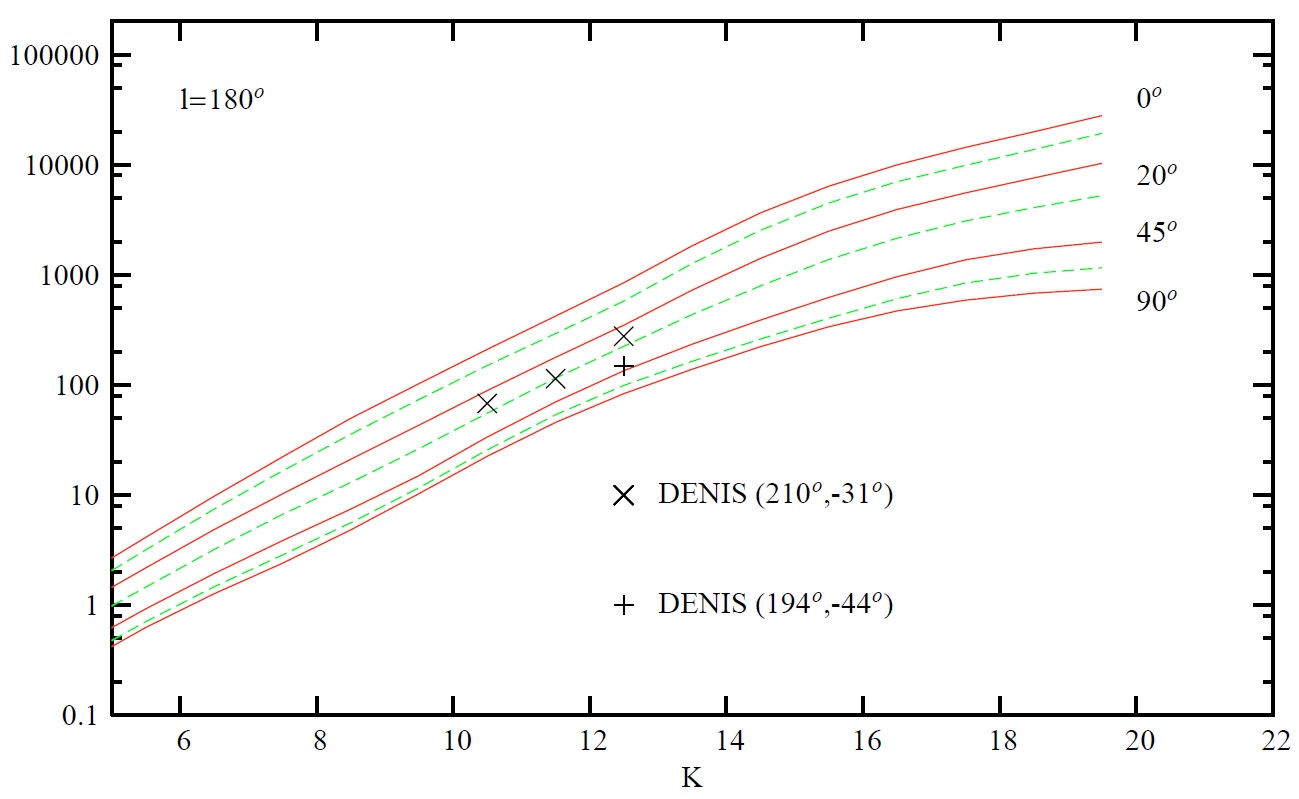
星計数 (1)可視バンド Goldman et al. 2002, Ojha 2001, Robin et al 2000, Reyle, Robin 2001a, Castellani 2001 (2)I バンド: Krause 2003 (2)近赤外 Ruphy et al 1996, Persi et al 1999, Persi et al 2001, Reyle, Robin 2001a 拡散 X 線 Guillout et al 1996 は ROSAT バンドをへの拡張モデルを拡散背景 X 線と比較した。 運動 Bienayme et al 1992, Chareton et al 1993, Ojha et al 1999, Rapaport et al 2001, Soubiran et al 2003 星間減光 Zagury et al 1999. 将来3次元減光分布を決定する助けとなるだろう。 V-バンド 図4 - 7は V-バンド星計数の予想カーブを観測と比較した。一致はよい。 注意しておくと、 l = 0 付近の赤化は未調整なので、 l = 0 予想曲線は 不十分の可能性がある。また、図5では銀河系中心方向の予想曲線は示さ なかった。モデルに内側バルジを含めていないからである。図6では l = 90 と 270 とではワープの影響が V > 12, |b| > 45 で現れる。 図7の反中心方向のフレアの効果は、 b = ± 10 での星計数 が b = 0 とほぼ等しいという形で現れている。 (図には l = 10 なし。) |
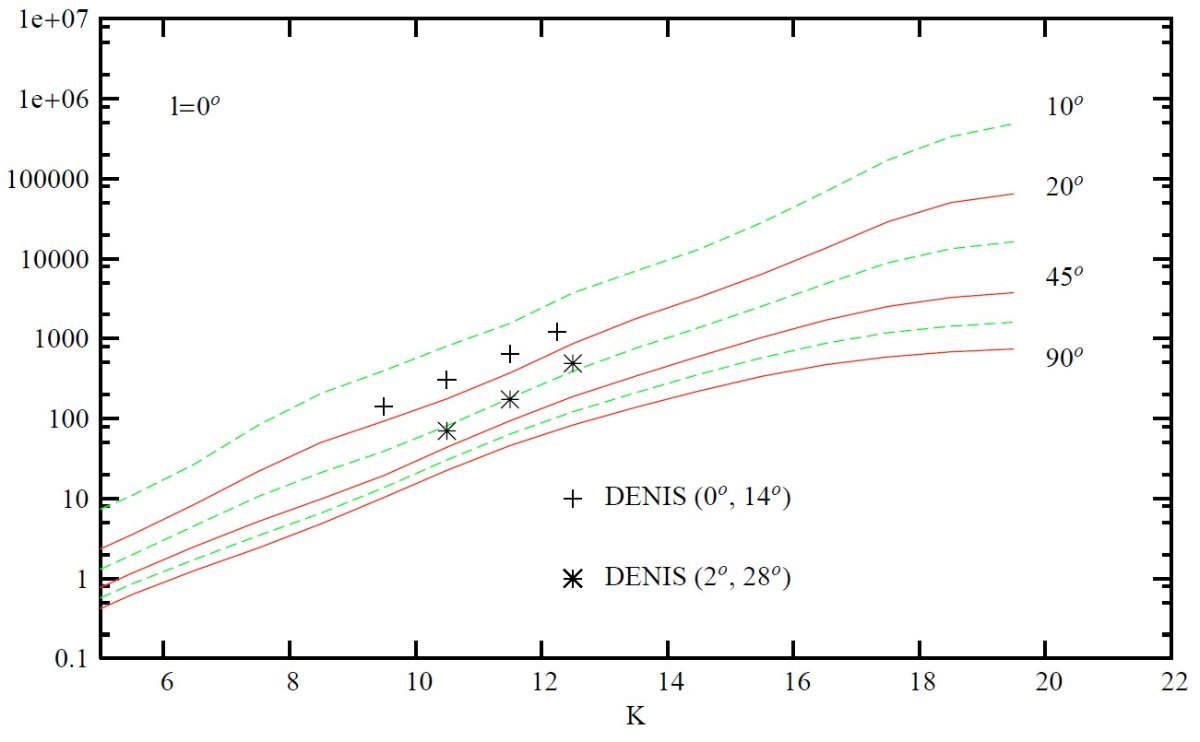
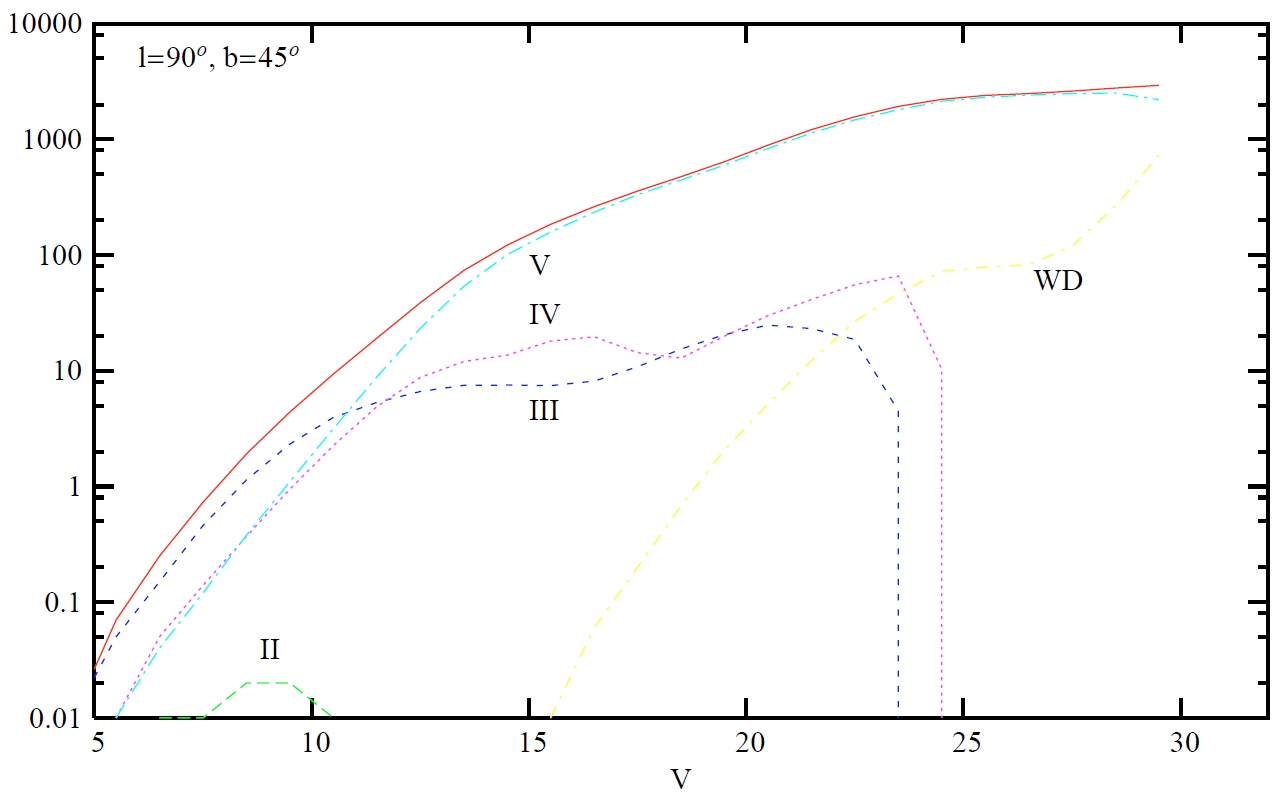
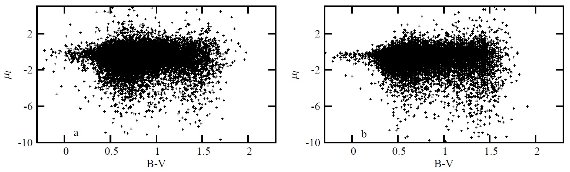 図12.(l, b) = (44, 474?) 方向の (B-V) 対 固有運動 μ,sub>l. 星は V = [12, 18]. 左: Ojha et al 1996. 右:シミュレイション。 K-バンド 図 8 - 10は K-バンド星計数予想を DENIS と較べた。図5と同じく、 銀河系中心は含めていない。図9では l = 90 と 270 とではワープの影響が V > 12, |b| > 45 で現れる。 スペクトル型別の寄与 図11には V-バンドでのスペクトル型別の寄与を (l, b) = (90, 45) で 示した。V < 11 までは巨星の寄与が大きい。そこより暗くなると主系列星 が支配的となる。境界等級は低銀緯になると暗い方へ移る。 カラーと固有運動の関係 図12は、(l, b) = (3, 47), V = [12, 18] でのカラーと固有運動の関係 を示す。データは Ojha et al 1996 である。モデルは観測をよく再現してい る。図の赤い星は円盤種族、青い星は厚い円盤と楕円体種族の星である。 |
| Reyle et al 2002 がベイジアン統計で分類を行った。 |
|
銀河面の減光 このモデルは銀河面上の減光モデルが粗いために、フィットの信頼度 が低い。我々は Drimmel, Spergel 2001 がやったような減光 3D モデル を信頼できる形で作りたい。 IMF 勾配 現在、観測との一致は V = [12, 24] で良い。より暗い方ではモデル は低質量星の IMF で限定されるが、現状では不定性が大きい。 図4は銀極方向でのモデルと観測の V 計数の対比を示す。V = 22 までは 全体として良く合っていることが判る。もっと暗い等級では、 楕円体成分に対し、標準モデルの勾配 α = 0.5 (実線)より急な IMF 勾配 α = 2 (点線)の方がフィットが良い。しかし、楕円体 IMF の低質量域のデータは少なく、銀河の混入もあり、将来の深い サーベイに期待している。 |
モデルの使用 ブザンソンモデルは銀河系の構造パラメタ―をテストするには現在 最適の道具である。 http://www.obs-besancon.fr/modele/model2003.html を見よ。 |