
|
追跡天体 銀河系渦状腕構造の研究には追跡天体の数と距離精度の向上が欠かせない。 HIIR, 巨大分子雲、6.7 GHz メタノールメーザーは良い追跡天体である。 それらの距離は三角法、測光法、運動学により決められ文献から得られる。 我々はそれらのカタログを新しくした。 データ 我々は HIIR 2500 個、巨大分子雲 1300 個、メタノールメーザー 900 個の データを集めた。測光距離または三角視差が得られない場合には運動距離を 求めた。銀河系回転曲線には Ro = 8.5 kpc、Θo = 220 km/s の IAU 値 を使用した。 |
また、追跡天体の速度を太陽運動で補正した後、最新の値、
Ro = 8.3 kpc、Θo = 239 km/s で運動距離を求めた。
HIIR の励起ファクター、または巨大分子雲の質量で重みをつけて、それら追跡子
の銀河面分布を求めた。
渦状腕 追跡子分布は第1象限に少なくとも4本の腕の一部を示し、第4象限には 3本見い出された。ペルセウス腕と局所腕は、また多くの明るい HIIR に よってもなぞられた。大質量星形成領域と巨大分子雲で追跡された腕部分は 外側銀河系の HI 観測と合わせられた。3本と4本の対数渦状腕モデルが大 部分の渦状腕追跡子をつなげることが分かった。 |
|
Hou et al. 2009 でのデータ 文献から、三角視差、測光距離、運動距離が既知の 815 HIIR, 963 GMC を 集めて、渦状腕を描いた Hou, Han, Shi 2009 。腕の多項対数式モデルが提案された。データは H110α and H2CO Downes, Wilson, Bieging, Wink 1980 "H110α and H2CO Survey of Galactic Radio Sources" H110α and H109α Caswell, Haynes 1987 "Southern HII Region: An Extensive Study of Radio Recombination Line Emission" CO Solomon, Rivolo, Barrett, Yahil 1987 "Mass, Luminosity, and Line Width Relations of Galactic Molecular Clouds" CO Grabelsky, Cohen, Bronfman, Thaddeus 1988 "Molecular Clouds in the Carina Arm: the Largest Objects; Associated Regions of Star Formation; and the Carina Arm in the Galaxy" H109α and H2CO Araya, Hofner, Churchwell, Kurtz 2002 "ARECIBO Observations of Formaldehyde and Radio Recombination Lines toward Ultracompact HII Regions" 多波長 Russeil 2003 "Star-Forming Complexes and the Spiral Structure of Our Galaxy" HIIR カタログ Paladini, Davies, DeZotti 2004 "Spatial Distribution of Galactic HII Regions" H110α and H2CO Sewilo, Watson, Araya, Churchwell, Hofner, Kurtz "Resolution of Distance Ambiguities of Inner Galaxy Massive Star Formation Regions II." 過去数年でのデータ増加 CO Rathborne et al 2009, "Molecular Clouds and Clumps in the Boston University-Five College Radio Astronomy Galactic Ring Survey " 9 GHz 再結合線 Anderson, Bania, Balser, Rood 2011 "The Green Bank Telescope HII Region Discovery Survey II. The Source Catalog" メタノールメーザー Green, McClure-Griffiths 2011 " Distances to Southern 6.7-GHz Methanol Masers through HI Self-Absorption" CO Garcia, Bronfman, Nyman, Dame 2014 "Giant Molecular Clouds and Massive Star Formation in the Southern Milky Way" |
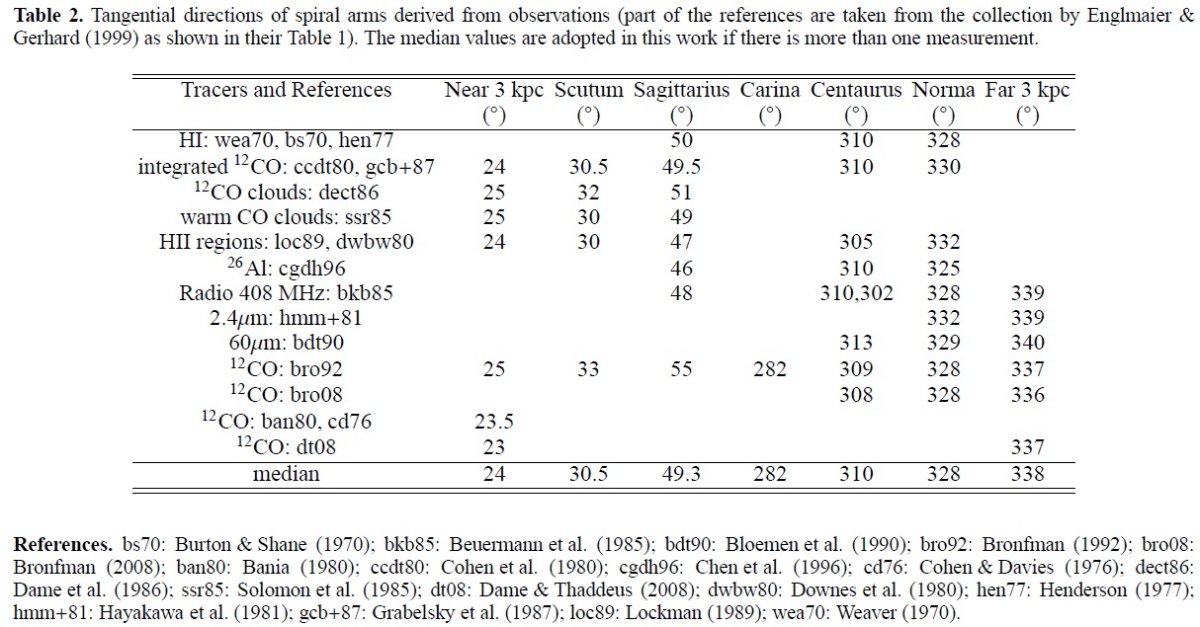
最近の進展 D ∼ 20 kpc の HIIR、分子雲複合体 Anderson, Bania, Balser, Rood 2011, Dame, Thaddeus 2011, が発見された。 HIIRs, GNCs, H2CO メーザー源の遠近距離の不定性が解消した: Roman-Duval, Jackson, Heyer 2009, Anderson, Bania, Balser, Rood 2012, Urquhart, Hoare, Lumsden et al 2012, Lepine et al. 2011, Green, McClure-Griffiths 2011, Jones, Dickey 2012。 さらに、信頼度の高い三角視差が幾つかの HIIR, メーザー源で得られるようになった。 Rygl et al. 2010: H2COで ON1,L1206,L1287,NGC281-W,S255 Sato et al. 2010: H2Oで G14.33-0.64 Moises et al 2011: Spitzer 測光と比較。 35 HIIR Xu et al 2013: H2Oで ON1,G074.03-01.71,G075.76+00.33 G075.78+00.34,G076.38-00.61,G079.87+01.17,G090.21+02.32, G092.67+03.07,G105.41+09.87 Russeil 2012 (?) Zhang et al 2014; W 43 Foster, Brunt 2014: (?) 銀河系の新しい基本パラメタ― LSR に対する太陽運動 (Schonrich et al 2010) Uo = 11.10 km/s (動径方向内側), Vo = 12.24 km/s (銀河回転方向), Wo = 7.25 km/s (上向き) 太陽位置 (Brunthaler et al 2011) Ro = 8.3 kpc. 銀河中心付近の星の運動(Ghez et al 2008, Gillessen et al 2009) Sgr B2、星形成域の視差 (Reid et al 2009,Brunthaler et al 2011) Θo = 239 km/s (Brunthaler et al 2011) Schonrich et al 2011, Reid et al 2014 もこの値を確認した。 そこで これらの最近の進歩を取り入れ、さらにメタノールメーザーのデータも加えて、 Hou et al 2009 を改定する。 |
2.1.1.HIIR の距離データこれまでの追跡結果可視で明るい約 100 個の HIIR の Hα, H109α 観測データから、 Georgelin, Georgelin 1976 は4つの部分腕を持つ天の川渦状腕構造を提唱した。 Downes, Wilson, Bieging, Wink 1980 と Caswell, Haynes 1987 は第1、第4象限の HIIR を多数発見し、Georgelin, Georgelin 1976 モデル を改善した。 Araya, Hofner, Churchwell, Kurtz 2002, Watson et al 2003, Sewilo, Watson, Araya, Churchwell, Hofner, Kurtz は H110α と H2CO ラインの観測を多数の UCHIIR に対して行い、かつ 遠近運動距離不定性を解消した。UCHIIR の分布は第1象限で3つの部分腕に 沿っていた。 Russeil 2003 は 400 個の星形成複合体のデータを集め、それを2、3、4本の対数 渦状腕モデルにフィットした。彼女の結論は4本腕のモデルが最もよく 合うというものであった。 Paladini, Davies, DeZotti 2004 は距離が既知の 180 個の HIIR データから、それらの分布は Georgelin, Georgelin 1976 モデルと良く合うとした。 HIIR 励起星の測光距離 Pinheiro, Copetti, Oliveira 2010 は 9 個の HIIR の励起星を同定し、測光距離を定めた。 Moises et al 2011: は 35 HIIR の近赤外カラーを用いて中心星を選び出して測光距離を 求めた。 Russeil 2012 (?) は、二つの星形成域 NGC 6334, NGC 6357 の OB 星を解析してそれらの測光 距離を改定した。 Foster, Brunt 2014: は第2、第3象限の 103 HIIR の測光距離を定めた。 |
最近の HIIR 電波運動距離 この数年で HIIR データは急増した。まず、 Bania, Anderson, Balser, Rood 2010, Anderson, Bania, Balser, Rood 2011, Anderson, Bania, Balser et al 2014 は、Green Bank Telescope HII Region Discovery Survey (HRDS) において、448 天体 から水素再結合線 603 成分を検出した。約 60 成分が、 第1象限で負速度 または第4象限で正速度を示し、それらが太陽円より外側の天体であるか、または 3-kpc 腕にある Dame, Thaddeus 2008 ことを示唆している。この観測で新たに見つかった 149 個の遠近運動距離の不定性 は Anderson et al 2012 により解かれた。Bania et al 2012 は Arecibo HII Region Discovery Survey (Arecibo HRDS) により新たに 37 個の新しい HIIR を発見し、その内 23 個の運動距離を定めた。 Du et al 2011 と Research in Astronomy and Astrophysics 11, 156 (2011) Han, Zhou, Esimbek, Wu, Gao は Urumqi 25 m 望遠鏡で、 200 個の UCHIIR 候補で H110α, H2CO 探査を行い、 20 HIIR の運動距離を得た。 Lepine et al. 2011 は UCHIIR (Wood, Churchwell 1989) に付随する 800 以上の CS 2-1 源 (Bronfman et al 1996) に対し 遠近運動距離の分離を行った。 Urquhart et al 2012 は Red MSX Source Survey から選んだ 105 CHIIR の HI 吸収データを解析 して遠近運動距離の分離を行った。 Jones, Dickey 2012 は 75 個の HIIR に対し似た処理を行った。 干渉計三角視差 HIIR に付随するメーザーの三角視差を測り、 Rygl et al. 2010, Oh, Kobayashi, Honma, Hirota, Ueno 2010, Sato et al. 2010, Niinuma et al. 2010, Shiozaki et al. 2010, Sanna et al. 2012, Xu et al 2013 Zhang et al 2014; Wu et al 2014 の研究から約 30 の HIIR の三角視差が高精度で求められた。 |


2.1.2.巨大分子雲CO サーベイCohen, Dame, Thaddeus 1986, Dame, Elmegreen, Cohen, Thaddeus 1986, Grabelsky, Cohen, Bronfman, Thaddeus 1988 は巨大分子雲が腕の良い追尾天体であることを証明した。有名なサジタリウスーカリーナ 腕 Grabelsky, Cohen, Bronfman, Thaddeus 1988 は、巨大分子雲によりきれいになぞられた。 Solomon, Rivolo, Barrett, Yahil 1987 は第1象限で 268 個の巨大分子雲を同定し、3本の部分腕を見出した。Efremov 1998 は既知の巨大分子雲データから4本腕モデルを唱えた。 Roman-Duval, Jackson, Heyer 2009, は 13CO Galactic Ring Survey (Jackson et al 2006, Rathborne et al 2009) データを用いて、750 個の巨大分子雲の遠近運動距離の不定性を解き、3本の 部分腕を見出した。 |
Dame, Thaddeus 2011
は第1象限に負速度の CO 成分を 10 個発見し、Outer Arm のさらに外側にある
腕であるとした。第4象限では、
Bronfman, Alvarez, Cohen, Thaddeus 1989
による予備的 CO サーベイにより分子雲が同定された。最近、
Garcia, Bronfman, Nyman, Dame 2014
は Columbia-U.de Chile Survy CO データを再解析し、92 個の巨大分子雲を
同定した。内 87 個にあった遠近不定性が解かれた。
Hou et al 2009 の改訂 Hou et al 2009 の巨大分子雲カタログはこれらの新しいデータを入れて改訂された。 M > 104 Mo の雲を巨大と呼ぶ。全部で 1300 個の巨大分子雲が集め られた。その一部を表A2に示す。 |

|
メタノールメーザー観測の例 6.7 GHz メタノールメーザーは多くの星形成領域から検出されている。初期の 結果は Pestalozzi et al 2005 に、その後の Arecibo での成果は Pandian et al 2007 にある。Ellingsen 2007 は Spitzer/Glimpse 天体 200 個の観測から 38 天体にメタノールメーザーを検出した。内 9 個が新発見だった。Xu et al 2008 は水メーザー天体を 100 m 望遠鏡で観測し、新しいメタノールメーザー を 10 個検出した。 中でも重要なのは、 Methanol Multibeam (MMB) Survey ( Green et al. 2009,2010,2012, Caswell et al 2011) による全銀河面メタノールメーザーサーベイである。 Fontani et al 2010 は 256 星形成域を観測し、55 検出、内新発見 12 という 結果を得た。Fontani et al 2010 は 296 個の大質量星形成領域を探査して、 55 天体、内 22 新発見、を得た。Olmi et al 2014 はハーシェルの銀河面サーベイ で見つかった 107 天体から 32 メーザー、内新発見 22, を検出した。 |
メーザー源の位置 Pandian et al 2009 は HI 自己吸収法により、 86 天体の遠近分離を果たした。 Green, McClure-Griffiths 2011 は文献から大量のメーザー源を集めた。彼らの データベースは l = [270, 358], l =[5, 67] で b = [-1.5, 1.5] の範囲である。 400 メタノールメーザーの遠近距離が分離された。 我々のデータベース 我々は以上の文献から 900 以上のメタノールメーザーを集めた。表A3にその 例を示す。その内 750 個の運動距離を定めた。いくつかは三角視差、測光距離 も求められている。大質量星形成領域方向のメーザーには通常幾つかの速度成分 がある。Green, McClure-Griffiths 2011 によると、その中間速度を代表させる のがよい。 |
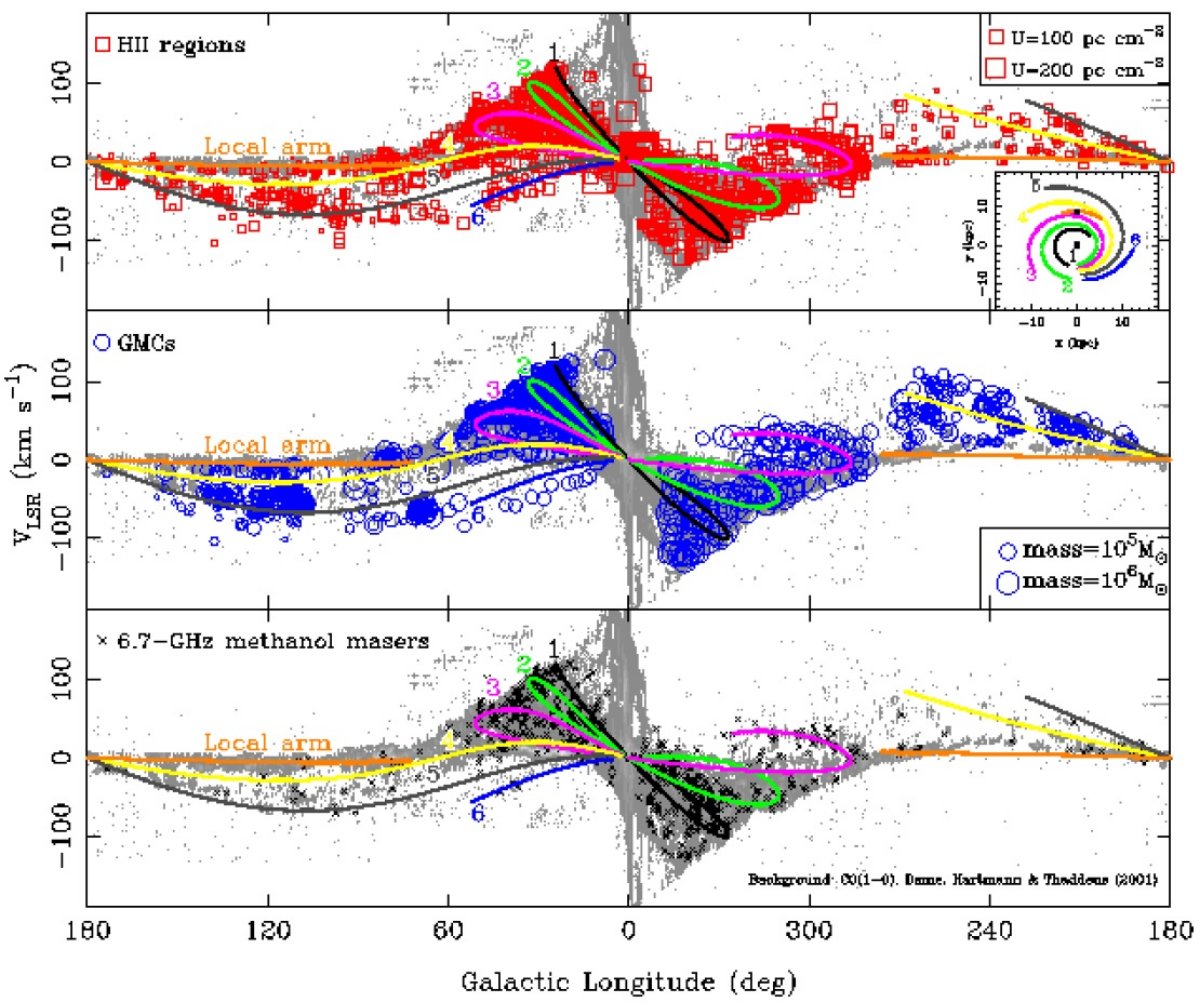
2.1.4.渦状腕追尾天体の (l, v) 図拡散ガス成分Dame, Hartman, Thaddeus 2001 には星間ガスの運動が示されている。ガス渦状腕をマップ化する第1歩は、 観測された (l, v) 図からガスの分布を再構成することである。 内側銀河のガス成分の距離を定めるのは極めて困難である。拡散 HI, CO の分布から導く渦状構造は現在のところ非常に不鮮明である。 Nakanishi, Sofue 2003, 2006 |
それに対し、 HIIRs, GMCs, メーザー源は渦状腕のよい追尾天体である。 それらの距離は三角視差、測光距離、運動距離等の方法で求められる。図2に 示すように、 Dame, Hartman, Thaddeus 2001 の (l, v) 図上の特徴のほぼ全てには HIIR やメーザーの対応天体が存在 する。距離が分かれば、未知の腕を明らかにすることも可能である。 |
|
Ro と Θo 1985 年の IAU 標準値は、 Ro = 8.5 kpc, Θo = 220 km/s である。 Ghez et al 2008 は Keck 望遠鏡を用い、銀河中心を周回する S-star の軌道解析から Ro = 8.4±0.4 kpc を得た。一方、Gillessen et al 2009 は NTT, VLT の観測から Ro = 8.33±0.35 kpc を得た。Reid et al. 2009 は Sgr B2 の三角視差を測り、 Ro = 7.9+0.8 -0.7 kpc を得た。Reid et al 2009b と Brunthaler et al 2011 は大質量星形成域の三角視差へのフィットから Ro = 8.4±0.6 kpc と Θo = 254±16 km/s を得た。これらの値の重み付き平均を 取って、Brunthaler et al 2011 は Ro = 8.3±0.23 kpc を導いた。 彼らは回転曲線の形により、 Θo = 223 - 280 km/s でフィットした。 Θo/Ro = 29.4±0.9 km/s/kpc である。 (223-280)/8.3 = 27 - 34 なんだけど。 ある回転曲線に対してだけど。 Schonrich 2012 は星の運動の解析から、 Ro = 8.27±0.29 kpc、 Θo = 238±9 km/s を導いた。 Honma et al 2012 は 52 メーザー源の VLBI データ解析から、 Ro = 8.05 ±0.45 kpc、Θo = 238±14 km/s を導いた。 Reid et al 2014 は 星形成領域の新しい三角視差データ解析から、 Ro = 8.34 ±0.16 kpc、Θo = 240±8 km/s を導いた。 Chatzopoulos et al 2014 は 星団運動と S-星軌道から、 Ro = 8.36 ±0.11 kpc を導いた。 |
太陽運動 LSR に対する太陽運動の IAU 標準値は、 Uo = 10.27 km/s, Vo = 15.32 km/s, Wo = 7.74 km/s であった。最近の研究でも Uo, Wo はあまり変化していないが、 Vo は係争中 である。 Dehne, Binney 1998 は、Uo = 10.00±0.36 km/s, Vo = 5.25±0.62 km/s, Wo = 7.17±0.38 km/s を得た。 Reid et al 2009 は 18 個の星形成域の三角視差観測を解析し、回転速度に 15 km/s の差を見出した。彼らはその原因を Vo の誤りにあると考えた。 大きな Vo の 12.24 - 14.6 km/s が、やはり、Francis, Anderson 2009, Schonrich et al 2010, Coskunoglu et al 2011, Reid et al 2014 により 提案されている。Schonrich et al 2010 の新しい Vo に基づき、 Brunthaler et al 2011 は大質量星形成域の三角視差データを再解析し、特異 回転速度(peculia rotation velocity) ∼ 8±2 km/s を見出した。 ( この言葉知らない。) 2種類の太陽運動 この先、この論文では2種類の太陽運動を用いる。一つは IAU 標準値で、 Ro = 8.5 kpc, Θo = 220 km/s、 Uo = 10.27 km/s, Vo = 15.32 km/s, Wo = 7.74 km/s である。もう一つは、 Ro = 8.3 kpc, Θo = 239 km/s (Brunthale et al 2011, Reid et al 2014) Uo = 11.10±1.2 km/s, Vo = 12.24±2.1 km/s, Wo = 7.25±0.6 km/s (Schonrich et al 2010) である。 回転曲線も 2 種類、平坦回転曲線 (reid et al 2009, Brunthaler et al 2011, Reid et al 2014)、もう一つは Brand , Blitz 1993 のものを運動距離の計算に使う。 |
|
複数速度成分 幾つかの HIIR では複数の速度成分がある。その場合は平均値を使う。 運動距離の計算に使う回転曲線は前節で述べた2種類を使用した。Fortran プログラムは Reid より提供された。 3 kpc 腕とバー l = [-15, +15] の天体に対しては、 3 kpc 腕 (Dame, Thaddeus 2008, Green et al 2011, Jones et al 2013) と バー (Hammersley et al 2000, Churchwell et al 2009) の影響があるので 慎重に計算する必要がある。まず最初に Dame, Thaddeus 2008 の与えた腕 パラメタ―に基づいて、3 kpc に帰属しているかどうかの判定を行う。次に 距離を計算する。 ( バーはどう考慮するのか?) |
随伴性 HIIR, GMC, メーザー源が同一天体の場合もある。それらの随伴度は次の基準 出判定した。 (1). 文献に随伴すると載っている。 (2). GMC のサイズ内に HIIR, メーザー源があり、速度差が 10 km/s 以内。 (3). HIIR とメーザー源位置が 2′ 以内で。速度差が 10 km/s 以内。 メタノールメーザーの速度から導く距離には不定性が大きいので、随伴が認め られた場合は、 HIIR か GMC を優先する。 |
|
HIIR の重み HIIR の重みとして我々は励起パラメタ― (Schraml,Mezger 1969) U を使う: U = 4.5526{α(ν,Te)-1ν0.1 Te0.35SνD2}1/3 ここに、Te = 電子温度、Sν = 電波フラックス(Jy)、 単純のためパラメタ― α(ν,Te) = 1 とする。Te が文献に与えられて いる場合はそれを採用したが、ない場合は Te = 6500 K とした。Te と U の 分布を図3,4に示す。表A1の HIIR カタログには UCHIIR も含まれている。 それらは実サイズが小さく、電波フラックスも小さいがある領域においては 渦状構造を追尾するのに重要である。 HIIR の重みは WHII = U/Uo とした。ここに Uo = 100 pc cm-2 である。図4から分かるように WHII = [0.0, 3.0] である。Sν データのない場合は WHII = 0.1 とした。 GMCの重み GMC にはその質量を使った。文献で得られた質量は表2Aで採用した距離に よって再計算された。その分布は図4(下)にある。その重みには、 log(MGMC/104Mo) を採用した。メタノールメーザーには 単純に WM = 0.1 とした。 重みファクター 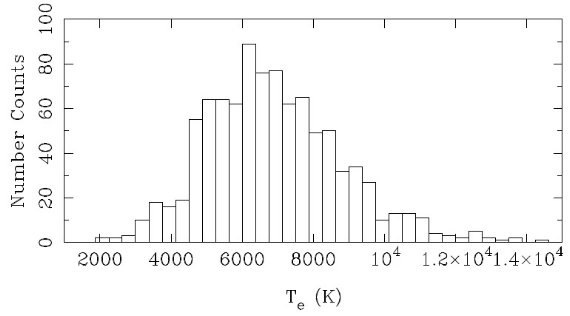 図3.HIIR の Te 分布。 | 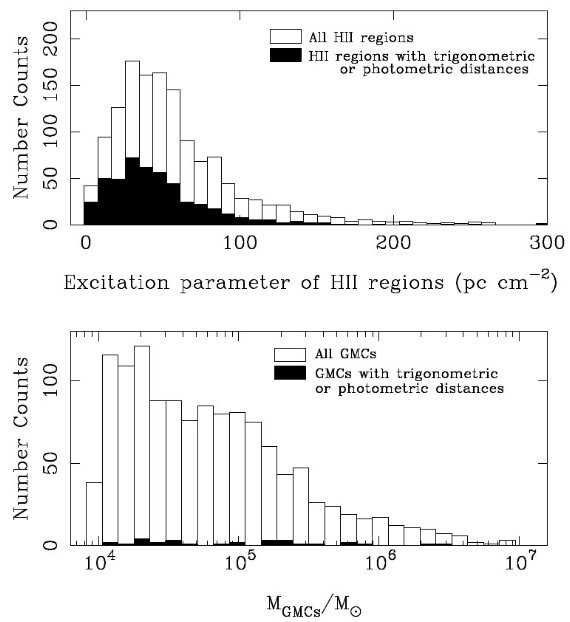 図4.上:HIIR の励起パラメタ― U の分布。下:GMC の質量分布。 三角視差、測光距離が無い天体の 計算には IAU 標準セットに平坦回転曲線を用いた。 |
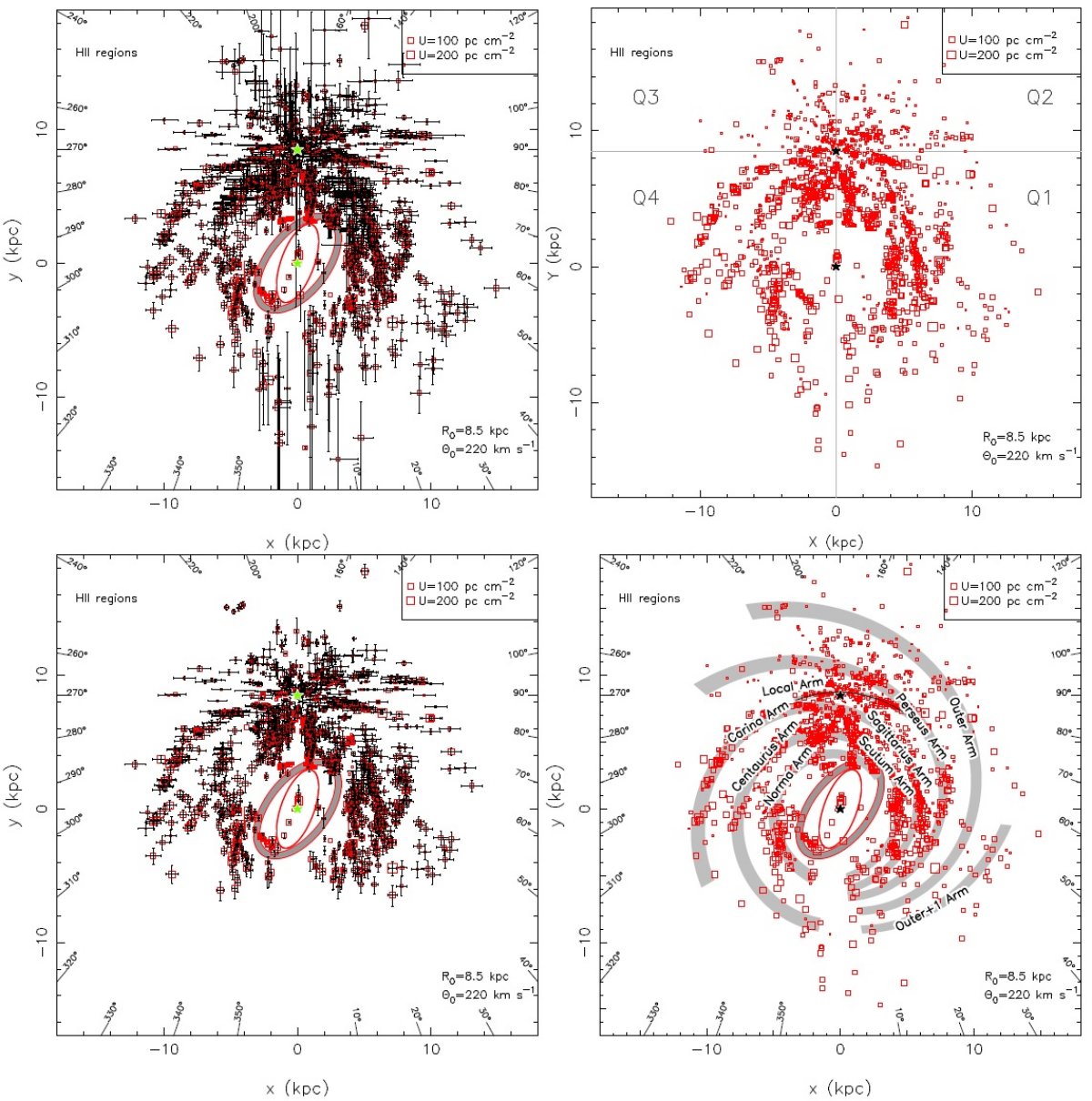
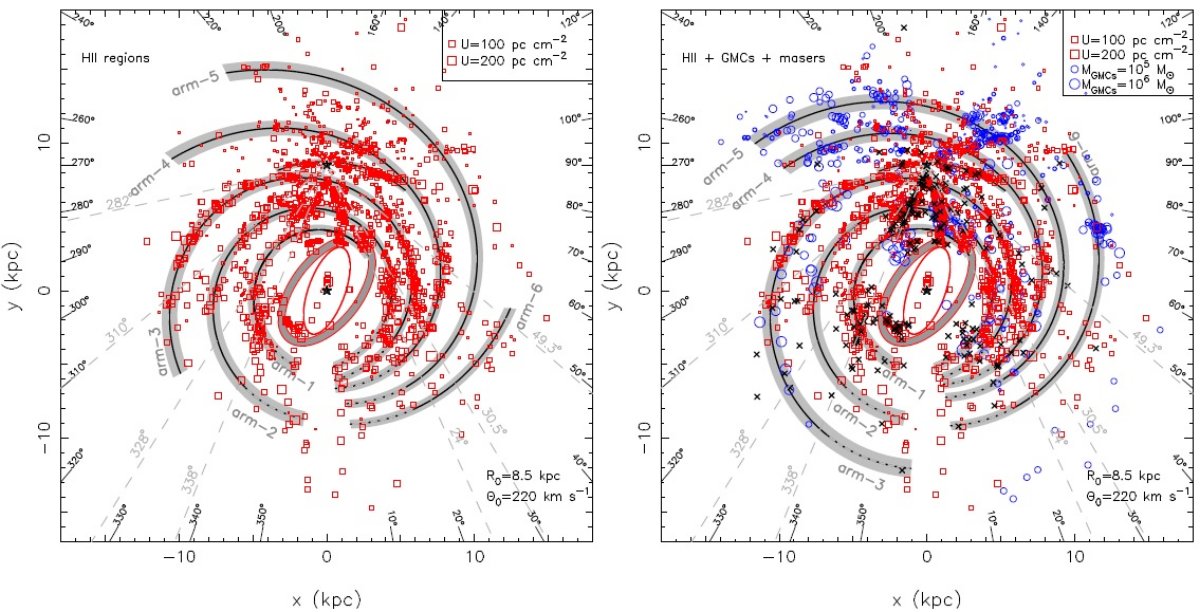
3.1.1.HIIR からの渦構造局所腕図5に HIIR 分布を示す。その右下図で黒の実線で局所腕が描かれている。 それはペルセウス腕 x = 5 kpc, y = 7.5 kpc から始まり、太陽付近では二本 に枝分かれするようである。その一本はペルセウス腕の近く、(-1, 9) へ、 もう一本は (-1.5, 8.5) のカリーナ腕近くへと。 Xu et al 2013 は局所腕はサジタリウス腕よりもペルセウス腕に近く、ペルセウス腕の分枝と 看做すべきであると述べている。 第1象限(Q1) 第1象限(Q1) には3本の部分腕がある。それらは内側から順に、 盾座腕、サジタリウス腕、ペルセウス腕である。外側銀河系領域、 x = 7 から 14 kpc, y = -10 から -1 kpc、 には the Outer Arm らしきもの、またさらには the Outer+1 Arm の兆候のようなものが見える。内側銀河、(x, y) = (2, 3) kpc 付近の HIIR の集合は銀河バーの近端、と/あるいは、 3 kpc 腕と関連するもので あろう。 |
第2,3象限 第2,3象限で目立つのは x = [-4, 4] kpc, y ∼ 10 kpx のペルセウス 腕である。そのそとがわには the Outer Arm の続きと the Outer+1 Arm さえも 見える。第2,3象限の運動距離異常( Roberts 1972) による図5の構造への 影響は小さい。というのは、この象限では明るい HIIR の大部分は測光距離また は三角視差が求まっているからである。 第4象限 (Q4) 第4象限 (Q4) には3本の部分腕が認められる。外側から、カリーナ腕、 ケンタウルス腕、それに 定規座腕(the Norm Arm) である。(x,y) = (-2, -3) 付近に HIIR が集まっているバーの遠端、と/あるいは、 3 kpc 腕であろう。 運動距離不定性の影響 運動距離不定性の影響は構造の表現にある程度のボケをもたらす。図5の左下図 には位置精度が 1 kpc 以下の HIIR のみをプロットした。この図では隣り合う 腕間の分離がよりはっきりと現れている。分離間隔の大きさは位置精度より大きい。 この結果は上に述べた腕の存在を指示する。 |
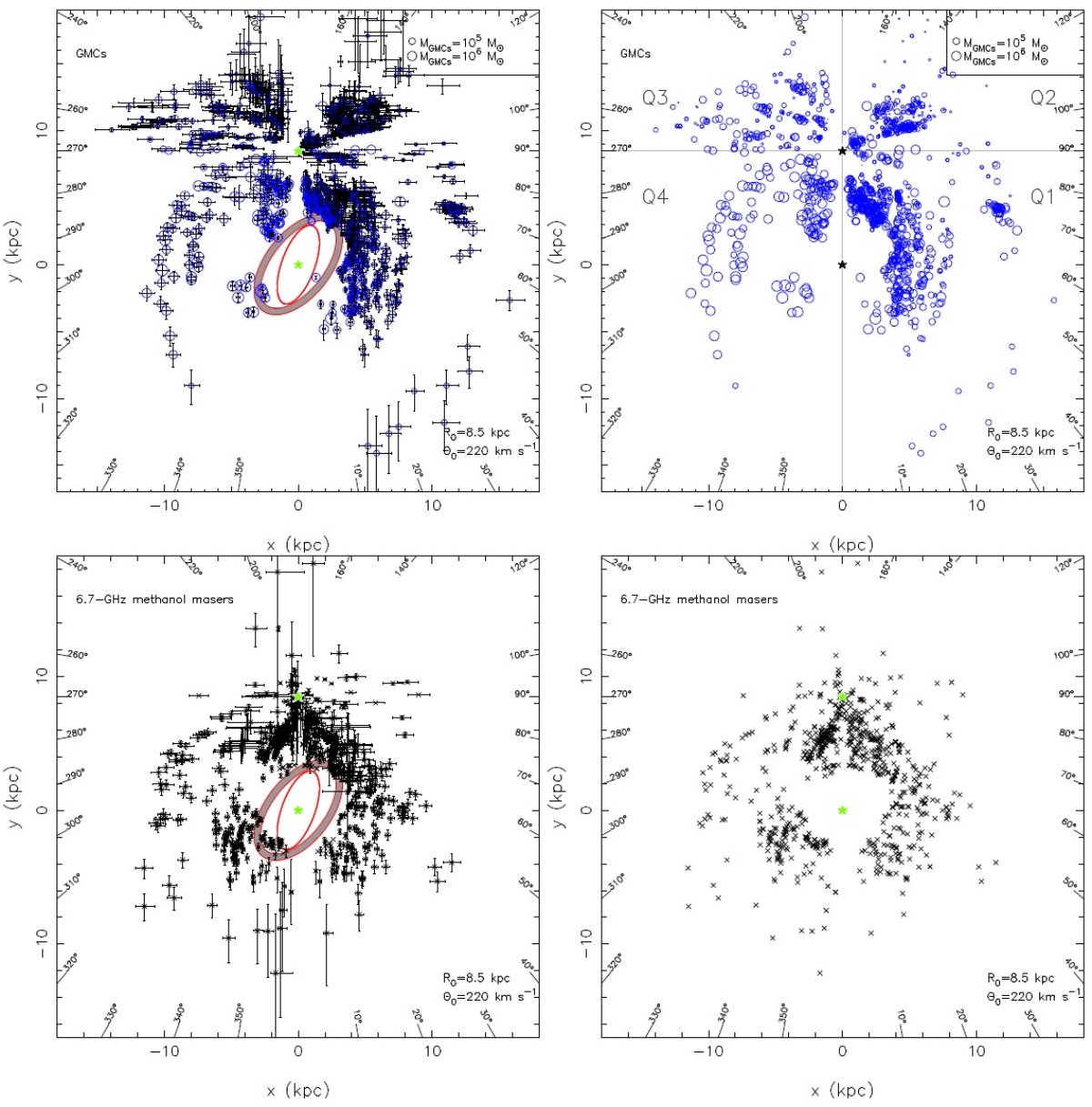
3.1.2.巨大分子雲巨大分子雲と HIIR の対応図6に示された巨大分子雲配列の殆どには HIIR が対応している。 第1象限 第1象限には3本の部分腕、盾座腕、サジタリウス腕、ペルセウス腕、が見える。 第1象限の遠方、 l = [20, 60], D ≥ 20 kpc、にはいくつかの CO 放射体が 存在することを Dame, Thaddeus 2011 が明らかにした。 完全にマップされた CO 放射の一つは質量 5 × 104 Mo であった。他の CO 放射体は まだ完全なマップが済んでいないが、多分巨大分子雲であろう。これらの巨大 分子雲は the Outer Arm のさらに外側にある腕の存在を暗示する。 Digel et al 1990 が発見した (x, y) = (12, 4) の分子雲の幾つかはアウターアームか その外側の the Outer+1 Arm に属するのかも知れない。 |
第2、3象限 第2、第3象限には May et al 1997, Heyer et al 2001, Nakagawa et al 2005 が見出した多くの巨大分子雲が存在する。しかし、腕状構造は見いだせない。 多分、ほとんどの距離は運動距離なため、Roberts 1972 の言う運動距離異常が原因 でぼけているのだろう。 第4象限 第4象限には二本のはっきりした部分腕がある。それらは外側からカリーナ腕 とケンタウルス腕である。(x, y) = (-2, 3) に巨大分子雲が集まっているのは 定規座腕 (Norma Arm) の一部を追尾しているのかも知れない。(-3, -2) の 分子雲は定規座腕の延長か 3kpc 腕の手前側かも知れない。 3.1.3.6.7 GHz メタノールメーザーメタノールメーザーの分布は HIIR, GMC の分布と似ているが、ばらつきが もっと大きい。その距離の大部分は運動距離である。メーザースポットの非円周 運動が大きな距離不定性を招いている。 |
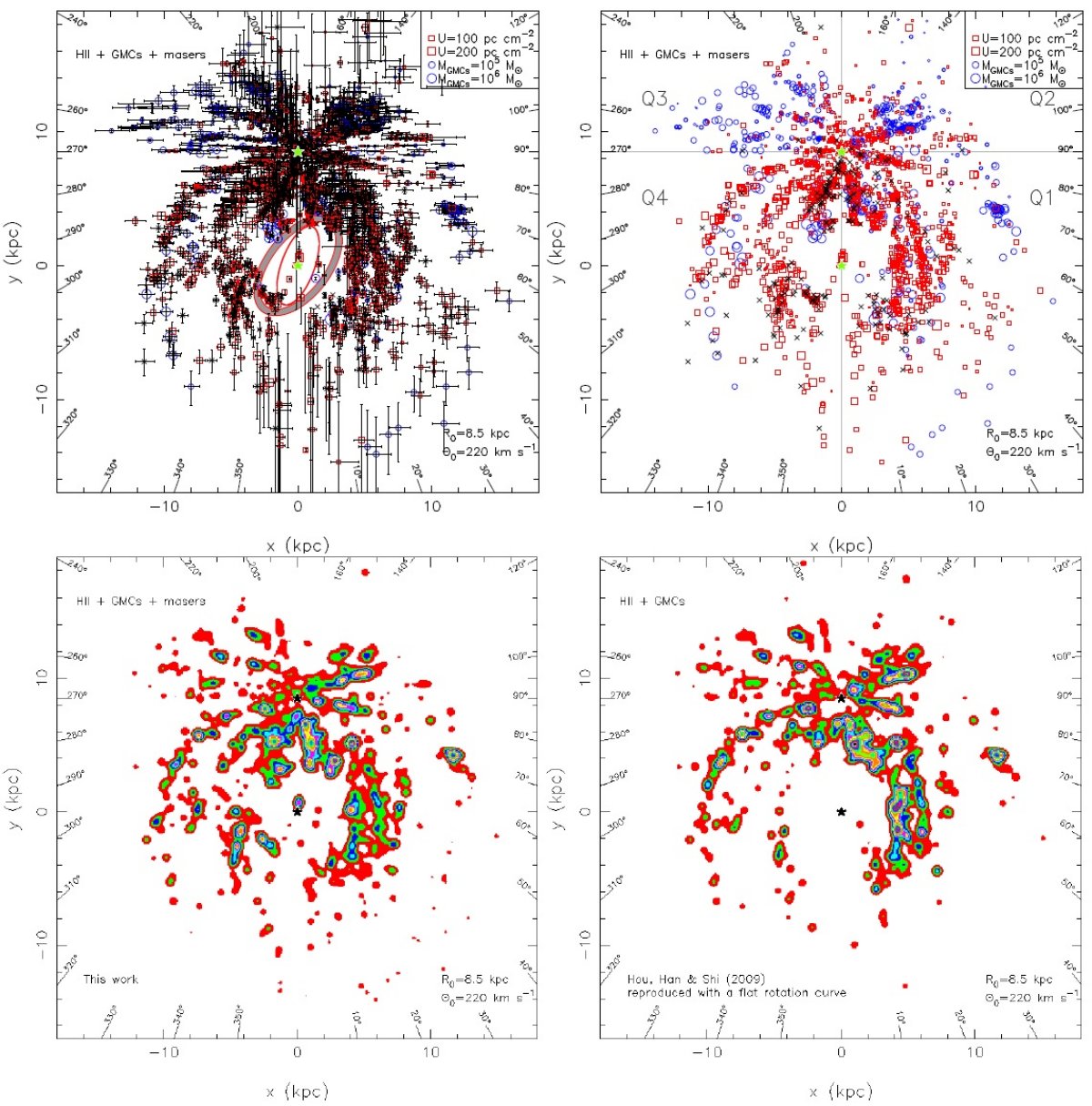
3.1.4.追尾天体から見た渦状腕図7=3種天体全部の分布図7には3種の天体の分布を示す。同一天体からの放射と判断されたものは 一つのシンボルで表した。Hou et al 2009 に倣い、腕を強調するために、 各天体を次の式でなました。
こうして得られたカラー強度マップが図7左下図である。ここでは σ = 0.2 とした。 σ = [0.05, 0.4] は類似する結果となった。Hou et al 2009 の 対応する図を図7右下図に示す。今回の方が、Outer Arm, Outer+1 Arm の一部、 局所腕、ケンタウルス腕、定規座腕の表示が改善された。 第1象限での HI との比較 HI ガスと追尾天体との比較が図8にある。この図から、同定された腕の範囲が どの程度のものかが分かる。第1象限、(x, y) = (12, -8) に Anderson, Bania, Balser, Rood 2011 が発見した数十の HIIR と Dame, Thaddeus 2011 が発見した巨大分子雲は HI の腕的な特徴と合致する。それらは (12, 4) にある 巨大分子雲の集団につながると考えられる。 第3、第4象限での HI との比較 第3、第4象限では外側から内側へ3本の HI 腕がある。それらは、アウター腕(x = [-13, -7], y = 12, l = [200, 270]、ペルセウス腕 (x = -7, y = 9, l = 235)、 カリーナ腕 x = -10 に対応する。特に HIIR と GMC で辿るカリーナ腕は HI 腕 との一致が素晴らしい。 まとめると まとめると、 HIIR と GMC の分布には明らかな部分腕構造が見られる。それは 外側銀河系で特によく HI 腕と一致する。しかし、異なる象限での部分腕をどう つなげるかはまだ intuitive でない。 |
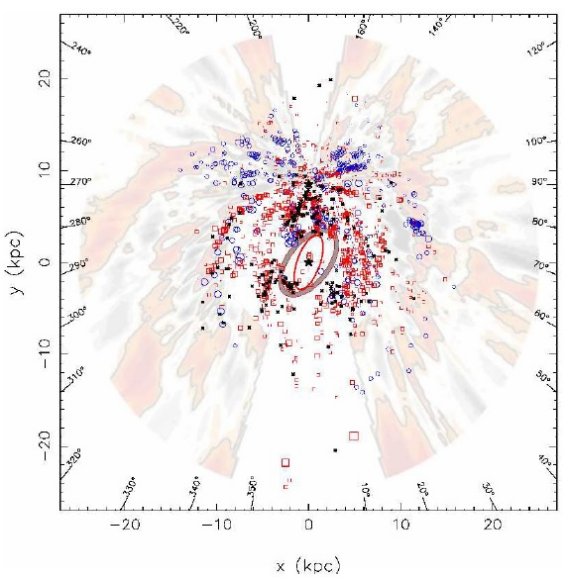 図8.Levine et al 2006 の HI 分布状に重ねた渦状腕追尾天体の分布。シンボルの 意味は図2と同じ。 |
|
腕の分離が困難な箇所 図9では log(r) - θ 面上で、各腕の領域を大体分割した。 θ ∼ 90° 付近で追尾天体が入り混じる。盾座ーケンタウルス腕 とサジタリウスーカリーナ腕はほとんど見分けられない。θ ∼ 320° 付近では、やはり腕が交じり合い、確信を持って分離するのは無理である。 その上、 r 大になると追尾天体の数が疎らになる。そのため、アウター腕と アウター+1腕の同定はギリギリとなっている。局所腕 θ = [50, 110], log (r) =2.1 は明らかに短く巻き込み角が他とはっきり違う。 腕構造モデル 様々な腕構造 (Vallee 2008, 2013) が提案されてきた。典型的なのは Georgelin, Georgelin 1976 が提唱した4つの部分腕を持つ天の川渦状腕構造である。 ここではまず伝統的な対数螺旋腕でデータを合わせてみよう。 3.2.1.対数螺旋腕モデル2本腕天の川銀河では2本腕は明らかに観測にフィットしない。3本腕と4本腕は 同じくらい良くフィットする。(Russeil 2003, Hou et al 2009). 本研究では巨大分子雲で追尾される渦状構造に集中する。銀河によっては、 (Grosbol, Patsis 1998) 星成分で辿られる渦構造とガスで辿られる渦が異なる。 天の川銀河では、星成分は通常2本腕(Drimmel, Spergel 2001, Benjamin et al 2005, Churchwell et al 2009, Francis, Anderson 2012) に支配されている と考えられている。 対数螺旋のフィット 対数螺旋は次の式で表される。
ここで、θ は x 正軸からスタートし、逆時計回りに測る。θi = 渦の出発角。Ri = スタート半径。Ψi = 巻き込み角 である。フィットを測る量は、
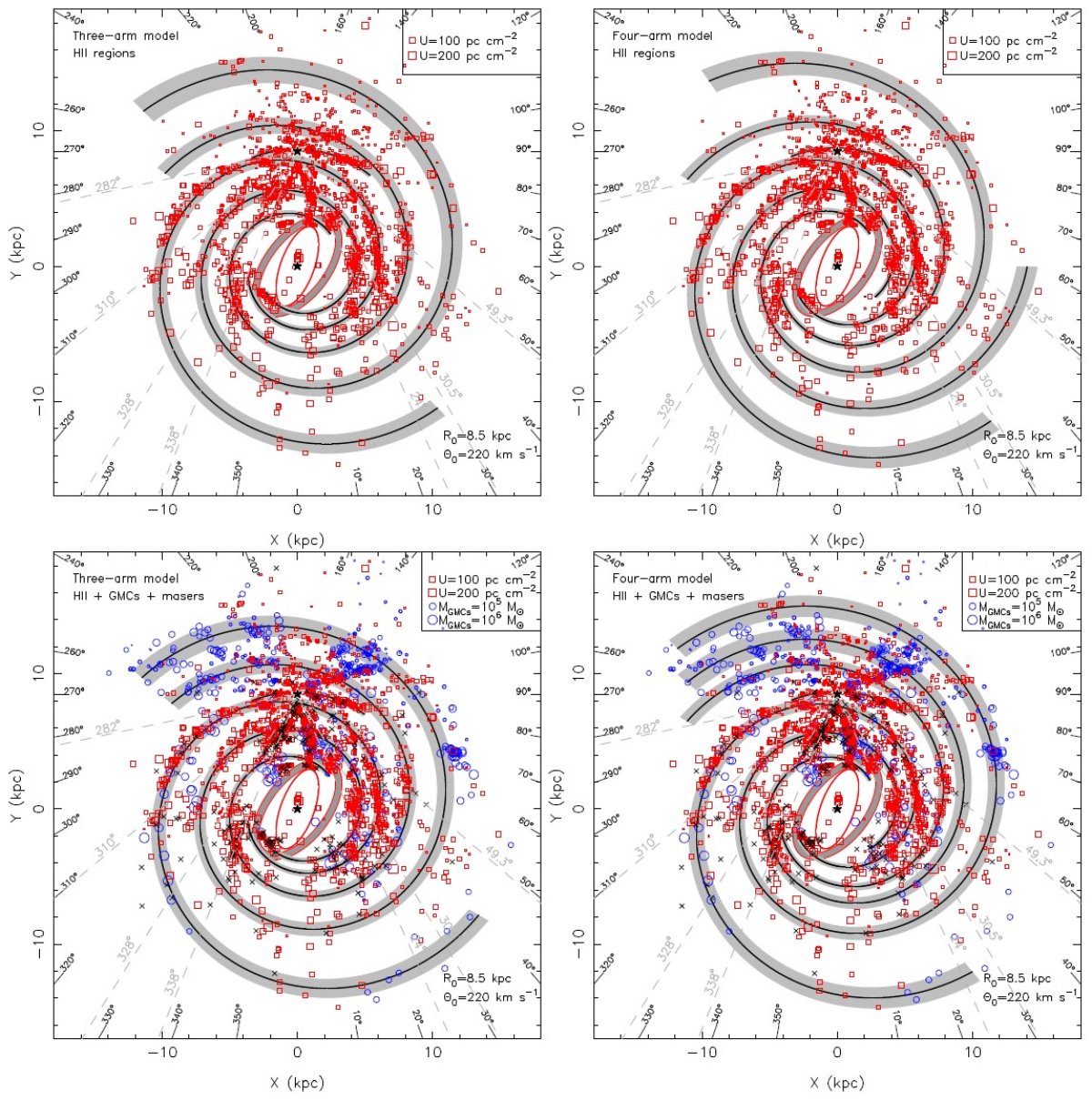
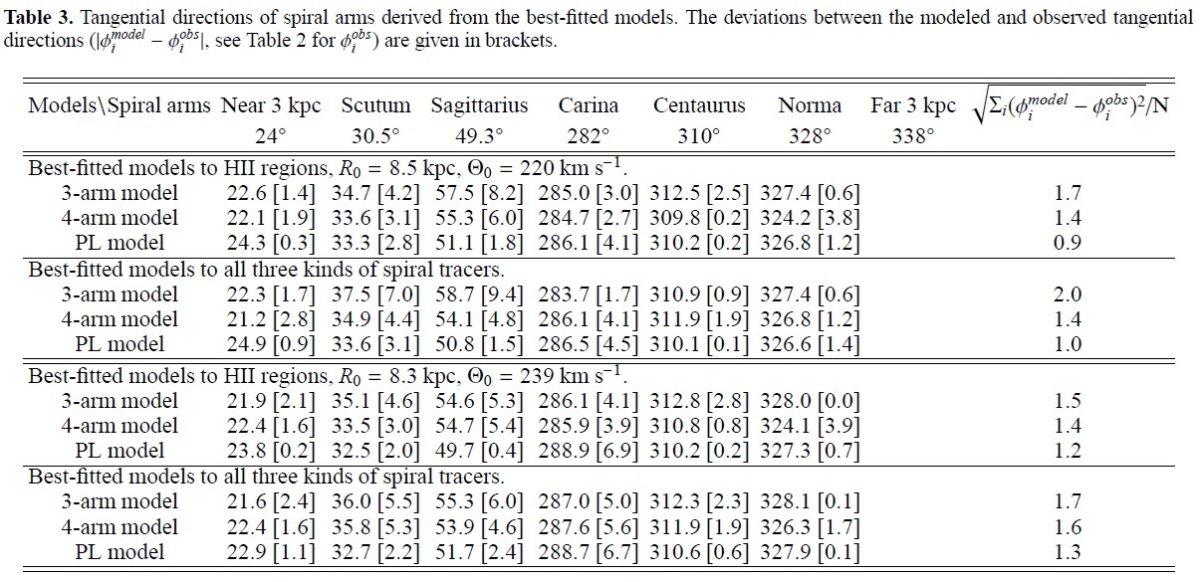
ここに、Wi=天体の重み、(xi,yi)=天体座標、 (xt,yt)=天体に最も近い腕上の点座標。 追尾天体の距離 HIIR の距離は三角視差、測光距離の方が運動距離よりも精度が高いことが分かった。 特に運動異常が見られる第2、第3象限ではそうである。 フィット結果 HIIR へのベストフィットを図10の上図に示す。表1には対応するモデル パラメタ―を載せた。3本腕(Z=0.17)も4本腕(Z=0.16)も両方とも大部分の 追尾天体をつないでいる。違いは部分腕の接続である。 4本モデル 定規座腕はバーの近端から出て、アウターアームにつながる。 ペルセウス腕は完結した腕 盾座腕は (x,y)=(4,0) HIIR 集団から、ケンタウルス腕に繋がる。 その後さらアウター+1アームへ伸びる。 3本腕モデル 定規座腕はペルセウス腕につながる。 盾座腕はバー遠端から、ケンタウルス腕、アウターアーム接続。 サジタリウスーカリーナ腕はどちらでもよく合っている。ただ、その延長は 異なる。局所腕はどちらでもペルセウス腕から第4象限でカリーナ腕近くへ伸びる。 接線方向 腕の接線方向に関しては4本腕の方が観測に良く合っている。表3の最終列が フィットの評価である。 |
2本腕説 最近 Dame 2013 は2本腕を提唱した。これは、以下の観測データの解析に基づいている。 Benjamin et al 2005 "First GLIMPSE Results on the Stellar Structure of the Galaxy", Dame, Thaddeus 2008 "A New Spiral Arm of the Galaxy: the Far 3 kpc Arm", Dame, Thaddeus 2011 "A Molecular Spiral arm in the Far Outer Galaxy" Anderson, Bania, Balser, Rood 2011 "The Green Bank Telescope H II Region Discovery Survey. II. The Source Catalog" 二本対称性は3本腕より4本腕と相性が良い。 (Dame 説と本研究で違うデータか? このデータで二本腕をフィットするとどうなるのか? ) 3種の追尾天体に同時フィット 図10の下2枚は3種天体全てへのベストフィットである。HIIR フィットの図とほぼ 同じであるが、外側銀河系、特に第2、第3象限で食い違いがある。そこには多数の 巨大分子雲が存在している。運動距離の不定性のため、それらの分布はかなり乱れて いる。正確な干渉計距離が分かるまで、第2、第3象限での腕の追跡は怪しいままであろう。 HIIRは頼りになる それに反して、第2、第3象限の明るい HIIR は測光距離、三角視差が得られている。 HIIR が描く腕の姿は信頼度が高い。従って、我々は図10右上の図が最も 信用できると考える。 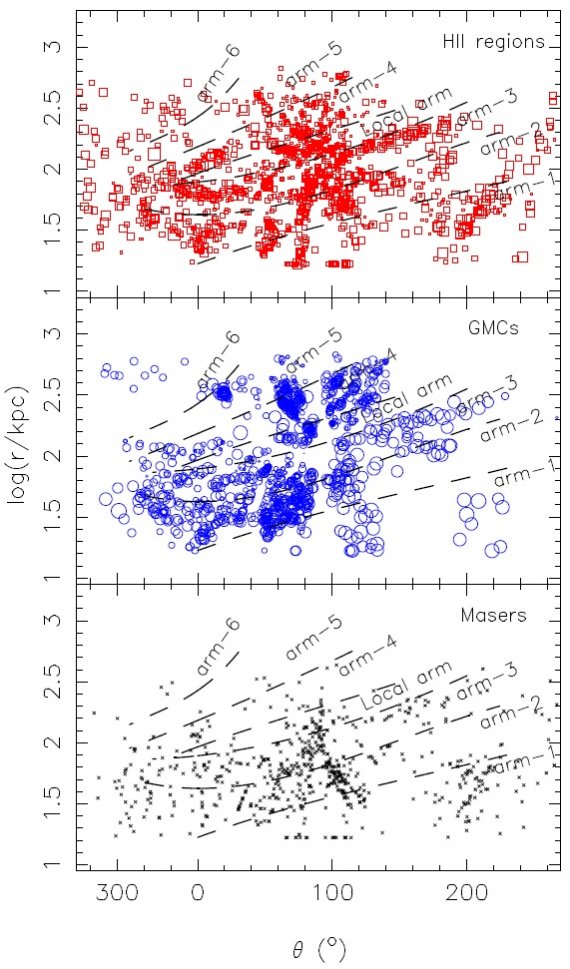 図9.上: HIIR、中: GMC、下:メーザー源の log r - θ 分布図。 θ は x 軸から始まり、逆時計回りに測る。破線は腕の大体の境界。 |
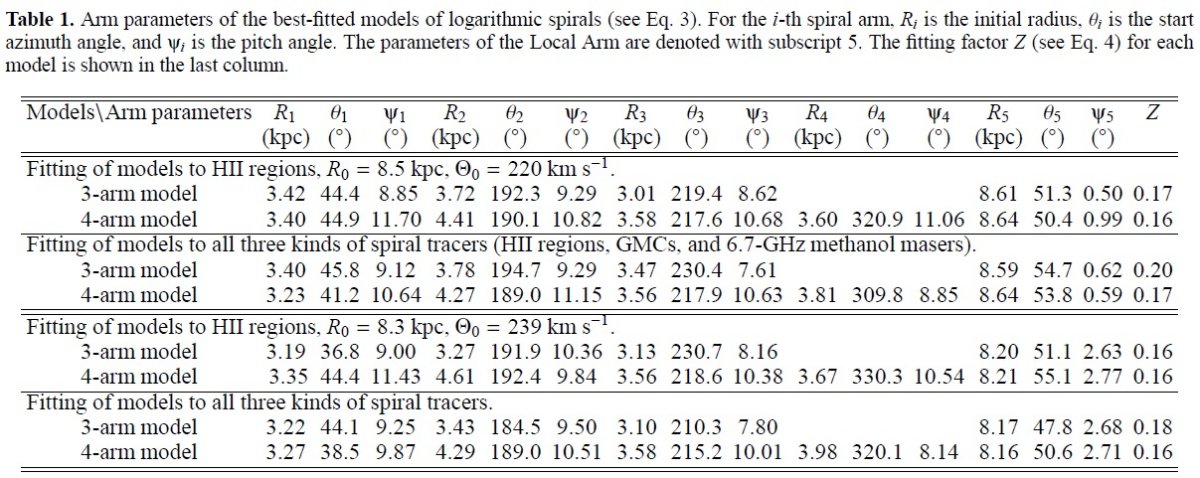
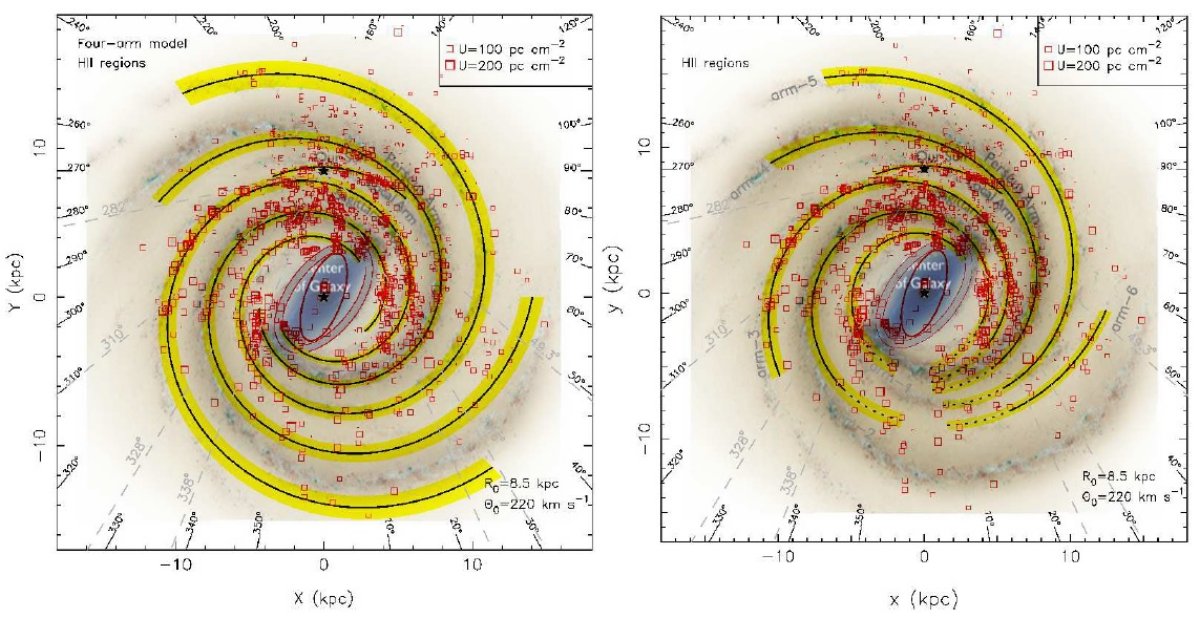
3.2.2.多項対数螺旋モデル多項対数螺旋モデル多くの銀河で渦の切り込み角度は一定でない。その変化は大きい時には 20° に達する。そこで、フィットの向上のため、対数螺旋モデル Hou, Han, Shi 2009 を提案した。モデル式は ln r = ai + biθ + ciθ2 + diθ3 フィットは Minuit パケッジを用いた。初めに、図9の r-θ 図に ある7つの部分腕をそれぞれ螺旋で表現して初期値とした。次に、6本の部分腕と 局所腕を同時にフィットしてベストモデルを求めた。局所腕は単純な 対数螺旋で十分である。 HIIR ベストフィット 図11に多項対数螺旋モデルを示し、表4にはそのパラメタ―を載せた。 このモデルでは、既知の部分腕がうまくフィットされている。 アーム1=定規座腕 アーム2=盾座ーケンタウルス座腕 アーム3=サジタリウスーカリーナ腕 アーム4=ペルセウス腕 アーム5=アウターアーム アーム6=アウター+1アーム 局所腕もよくフィットされている。 全3種追尾天体のベストフィット 図11右図には全3種追尾天体のベストフィットを示す。腕1−4と局所腕は HIIR モデルと一致するが、アウターアームとアウター+1アームの位置は異なる。 これは主に外側銀河では HIIR が少ないことと第2、第3象限で GMC の運動距離 エラーが大きいことが原因であろう。第1象限遠方では、Dame, Thaddeus 2011 が明らかにした CO 天体がアウター+1アームよりさらに遠方の腕を追跡する かも知れない。 巻き込み角 巻き込み角 Ψ は tan(Ψ) = b + 2 c θ + 3 d θ2 で計算される。図12にはその結果を示す。 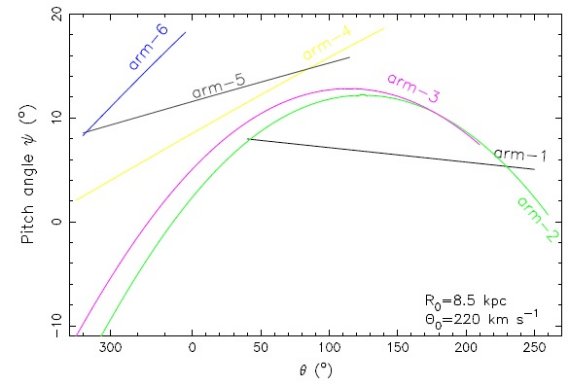 図12.多項螺旋ベストフィットモデルの渦の傾き角 Ψiの変化。 |
 表4.多項螺旋ベストフィットモデルのパラメタ―。フィットは HIIR と全部との 両方に行った。 |
|
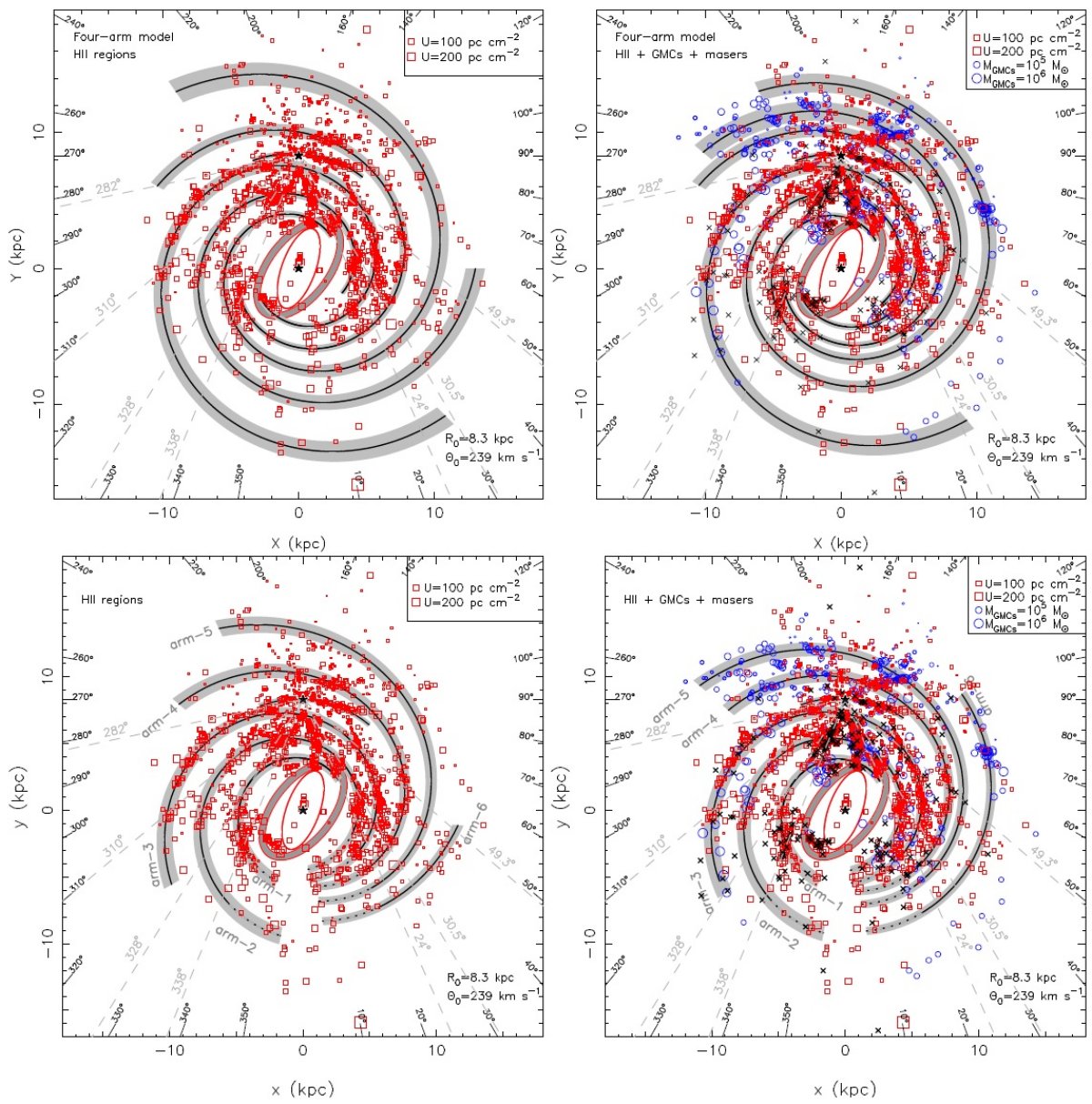
局所腕 NASA 画像では局所腕がペルセウス腕付近から発し、ペルセウス腕とサジタ リウスーカリーナ腕(x,y) = (-3,9) の間を伸びて行く。この構造は HIIR の 分布からは確認されなかった。図13では、局所腕はペルセウス腕付近で発し、 第4象限の方に延び、カリーナ腕 (x,y) = (-1.5, 8.3) に近づく。この腕は 太陽から遠くへは伸びない。 盾座腕の出発点 盾座腕はバーの近端から発すると考えられている。しかし、それは追尾天体 分布と矛盾する。ベストフィットモデルでは盾座腕は (x, y) = (4, 0) HIIR 集団と関連する。これは Georgelin, Georgelin 1976, Cordes, Lazio 2002 のモデルと一致する。 |
サジタリウスーカリーナ腕と盾座ーケンタウルス腕の分画 銀河中心方向 |x| < 2 kpc, y = [4, 7] kpc では サジタリウスーカリーナ腕と盾座ーケンタウルス腕の間のデータ分布に明瞭な 区分がない。 サジタリウスーカリーナ腕と 盾座ーケンタウルス座腕の延長 図13に見られるように、y < -6 kpc で、サジタリウスーカリーナ腕と 盾座ーケンタウルス座腕の延長に関しては、我々のベストフィットモデルと NASA 概念図との間には大きな違いがある。 |
3.4.銀河系基本パラメタ―の影響距離を再計算2.2. 節に述べたように最近の観測は銀河系基本パラメタ―が IAU 標準と異 なることを示す。その変化の影響を調べるため、追尾天体の距離を、平坦回転 曲線、 Ro = 8.3 kpc, Θo = 239 km/s (Brunthaler et al 2011) に Schonrich et al 2010 の太陽運動を組み合わせて、再計算した。 (その結果自体は表Aの第22−24列にある。) 分布図 その結果を図14に示す。腕の様子は IAU 標準値の場合とよく似ているが、 幾分小さくなっている。4本対数螺旋と多項対数螺旋のベストフィットも 示した。そのパラメタ―は表1と表4に載せた。モデルの接線方向は表3 にある。 |
3.5.銀河系回転曲線の影響Brand, Blitz 1993 銀河回転モデルは以前の研究で広く使われている。 Hou, Han, Shi 2009 で示したように、このモデルは Clemens 1985 や Fich et al 1989 より 合理的である。この回転曲線を使って距離を計算した結果を図15に 示す。腕の位置は平坦回転曲線の場合と非常に良く似ている。 Brand, Blitz 1993 回転曲線は R = [5, 15] kpc で殆ど平坦なのでこれは 当然である。 |
|
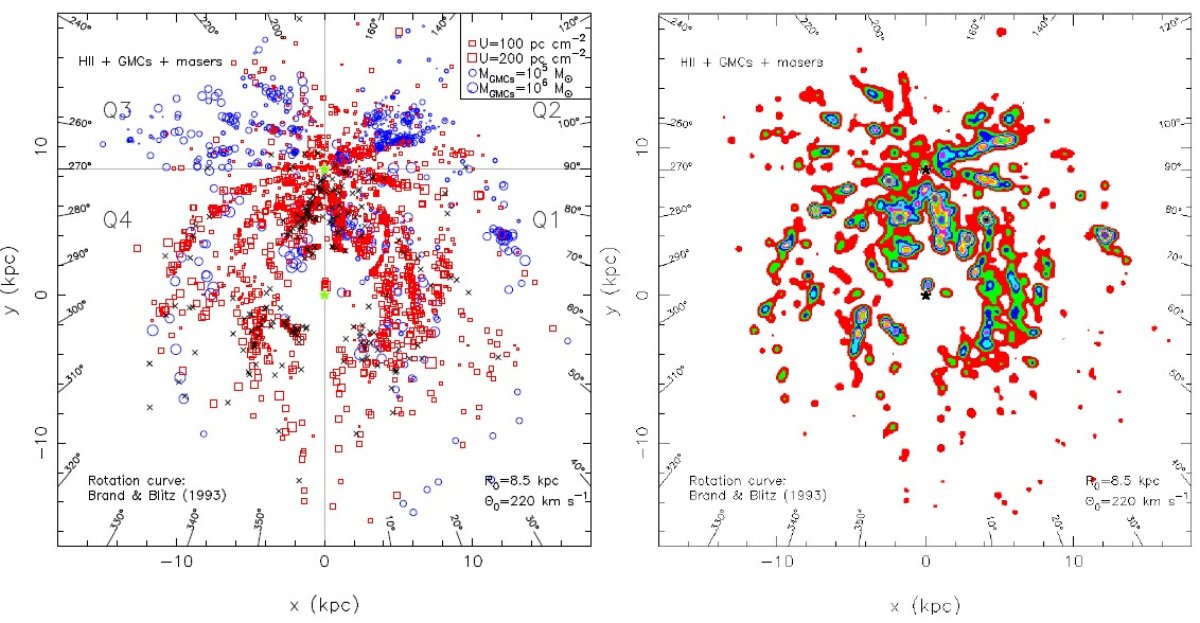
様々な天体のワープ 銀河系ワープは HI の初期サーベイで Kerr 1957, Burton 1988 により 発見された。これは銀河面から 3 kpc 以上もずれていた。銀河面のワープ は HI 吸収、レッドクランプ (Lopez-Corredoira et al 2010, Bobylev 2010, 低密度の温かい電離ガス Cersosimo et al 2009、 2MASS IR 星 Reyle et al 2009, 若い散開星団(Vazquez et al 2008), 分子ガス(Nakagawa et al 2004), HIIR(Paladini et al 2004)、 星形成 領域 (Russeil 2003) で見つかっている。 追尾天体のワープ HIIR, 巨大分子雲、メタノールのカタログから図16に示すように 明らかなワープの証拠が見出された。図を見ると、第1、第2象限では アウターアームとアウター+1アームが銀河面の上にあり、 第2第3象限では、アウターアーム、ペルセウス腕、カリーナ腕が 銀河面の下にあることが分かる。 ( l-b マップ上で各腕は b = 0 の上下に実際にずれて見える?) |
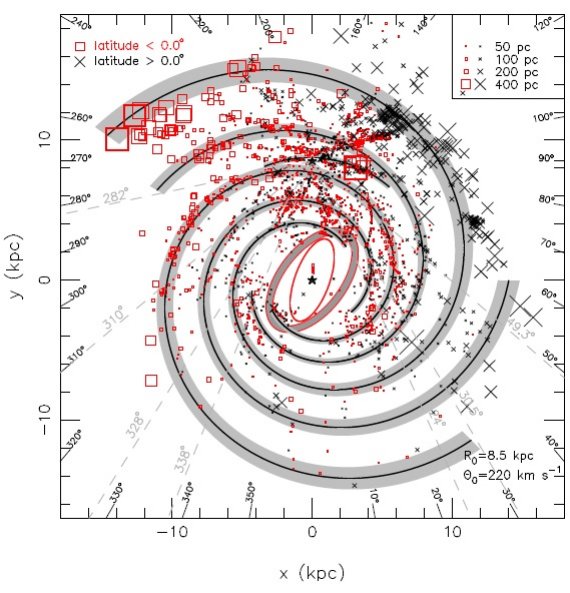 図16.HIIR, 巨大分子雲、メタノール(同じシンボルなので注意) で見出されたワープの証拠。四角= b<0 天体。×=b>0 天体。 シンボルの大きさは銀河面からの距離に比例する。腕は4本対数螺旋 モデル。 |
|
サンプル HIIR, GMC サンプルは前回より大幅に増えた。今回メタノール メーザーを加えたが、精度が悪くあまり助けにならなかった。 |
腕の同定 HIIR 分布はきれいに部分腕をなぞっている。内側から外へ、 定規座腕、盾座ーケンタウルス腕、サジタリウスーカリーナ腕、 ペルセウス腕、アウターアーム、アウター+1アームである。 局所腕は短い部分腕として同定された。巨大分子雲で 同定された部分腕は外側銀河系の HI 腕と一致し、天の川 銀河がグランドデザイン銀河であることを示唆する。 |