| VLBA による BeSSeL サーベイの一環としてサジタリウス腕の 10 大質量星 形成域の三角視差と固有運動を測った。これらのデータを文献から採った他の 8天体データと合わせて、銀河中心経度 β = [-2, 65] 区間での腕の構造 と運動を調べた。 | 腕のピッチ角= 7.3° ±1.5°, フィットした腕からのズレの rms 偏差として決めた腕の半巾=0.2 kpc, サジタリウス腕の太陽からの最短距離 = 1.4±0.2 kpc である。隣あう腕と異なり、サジタリウス腕の天体には 銀河回転に対し反対向きの大きな特異運動はない。 |

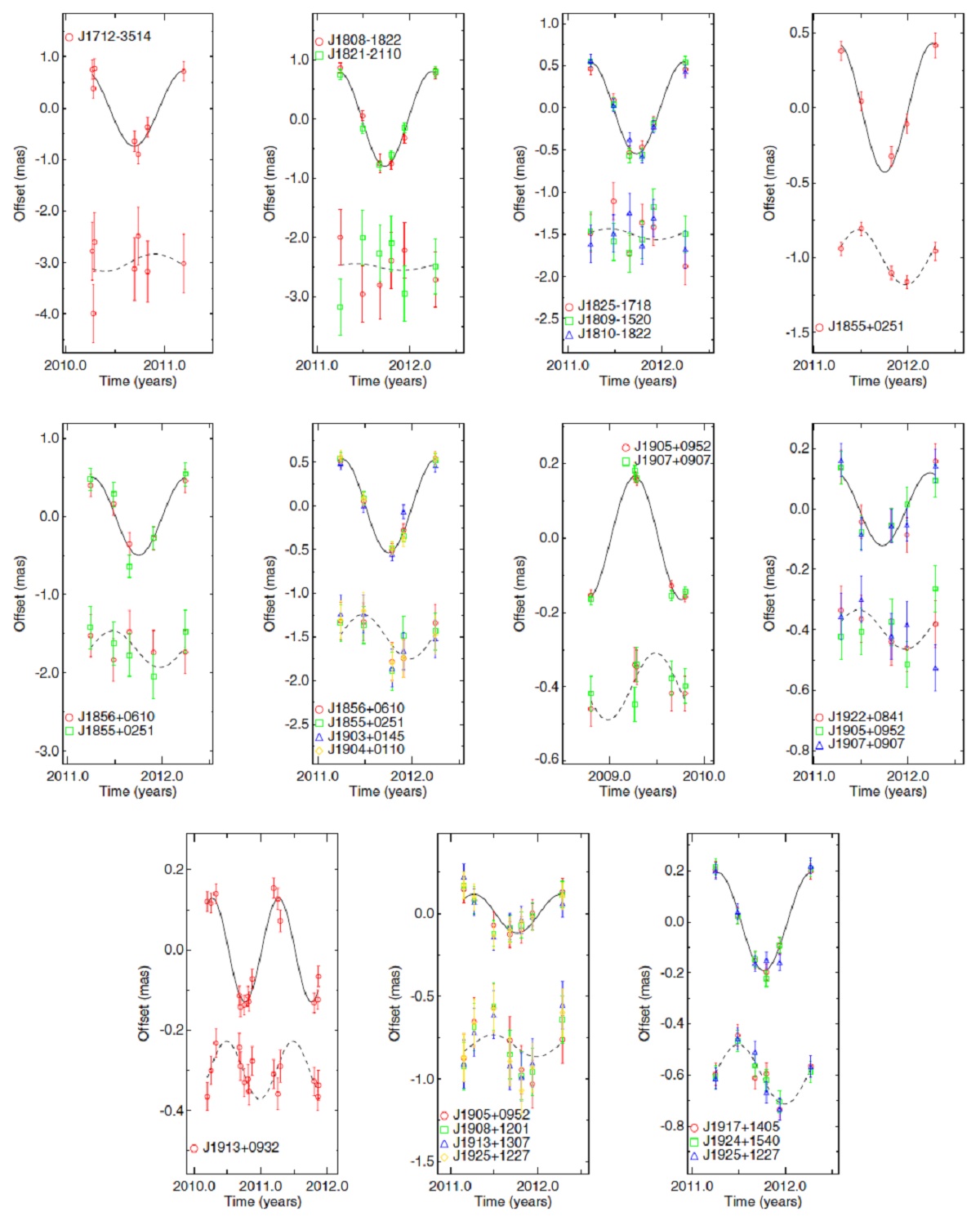
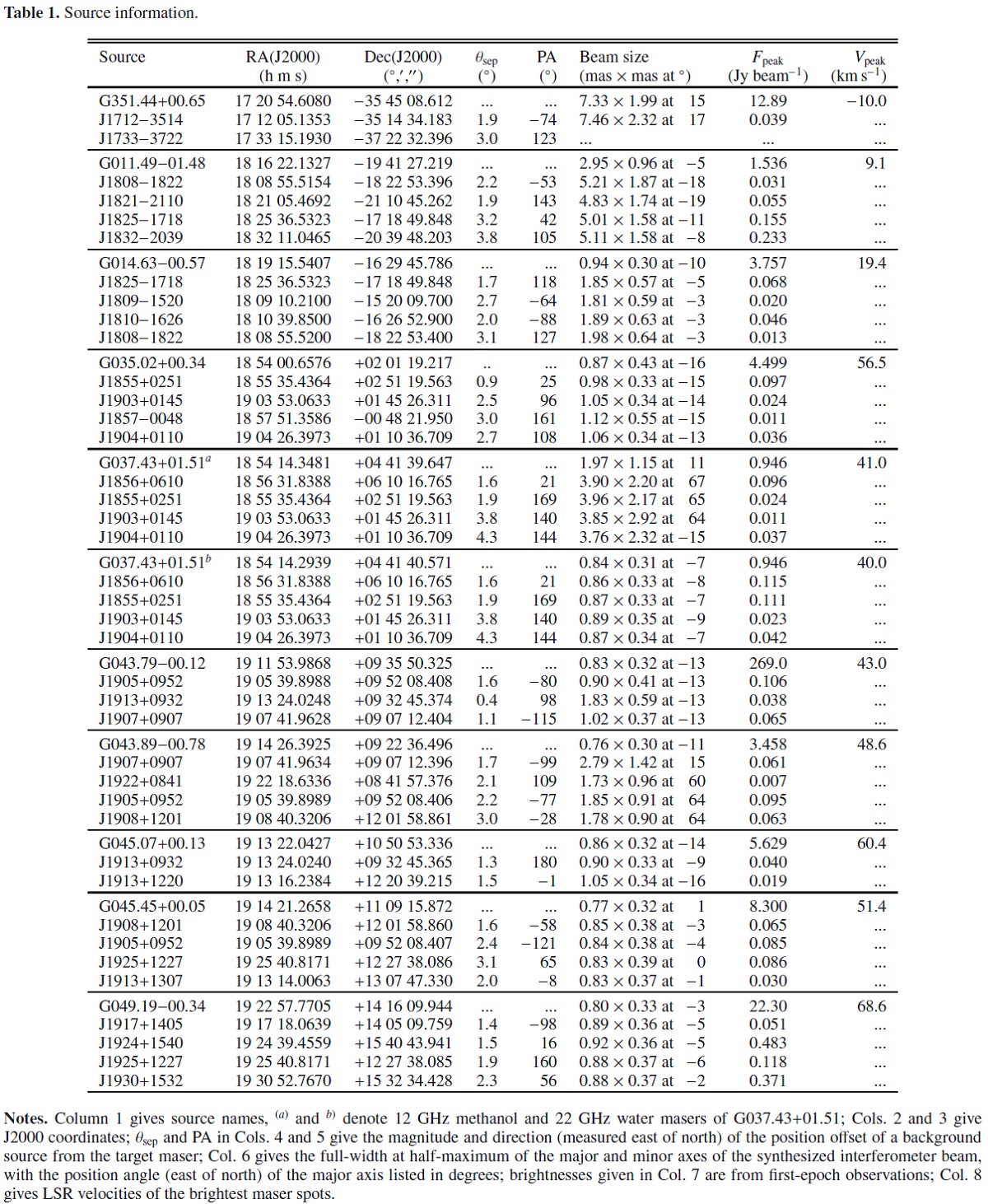

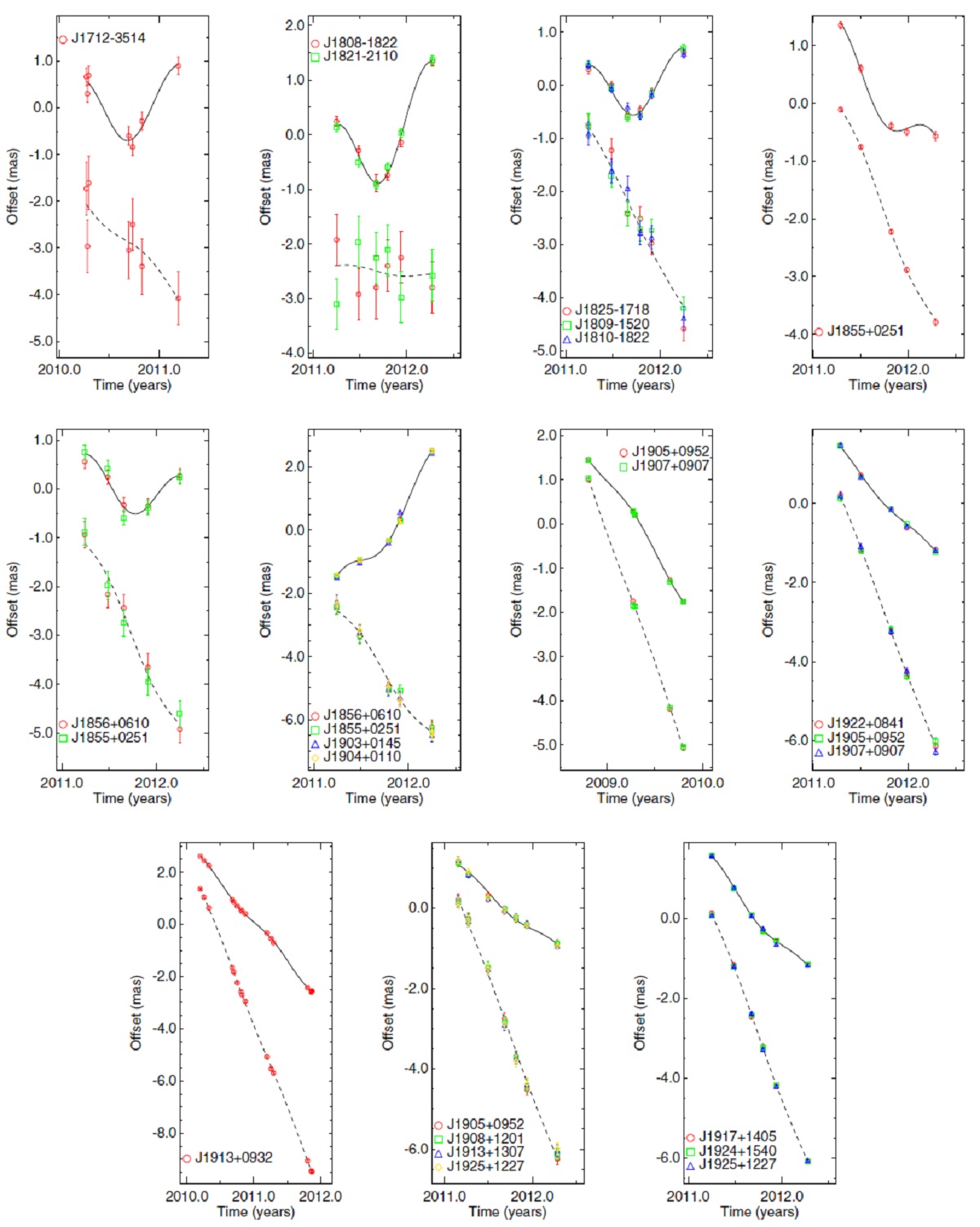
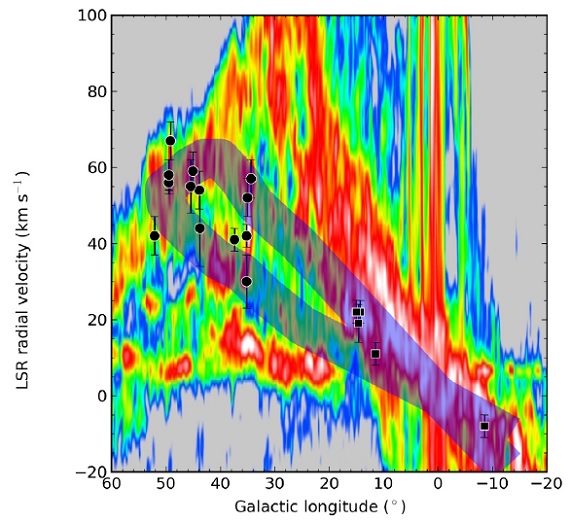 図3.サジタリウス腕 HMSFRs と CO ( Dame et al.2001 )の l-v 図。黒丸=l-v 図で判定されたサジタリウス腕 HMSFRs. 四角= 視差で判定された HMSFRs. 斜線= Burton, Shane 1970 によるサジタリウス腕。 斜線の巾は Δv = 5 km/s である。 CO l-v 図上のサジタリウス腕 図3では Dame et al.2001 による CO l−v図上に HMSFRs を描いた。13 の HMSFRs がサジタリウス腕に 配属された。それらは全て図3の腕経路に近いかその上に乗っている。次に それらの距離を調べ、それらが腕の形を成すことを確かめた。 腕の収束領域の HMSFRs l < 15° では l-v 図上で幾つかの腕が重なり合う。四角で示す 5 つの HMSFRs がその範囲にある。それらの距離が 1-2 kpc なのでサジタリウス腕 天体とした。 |
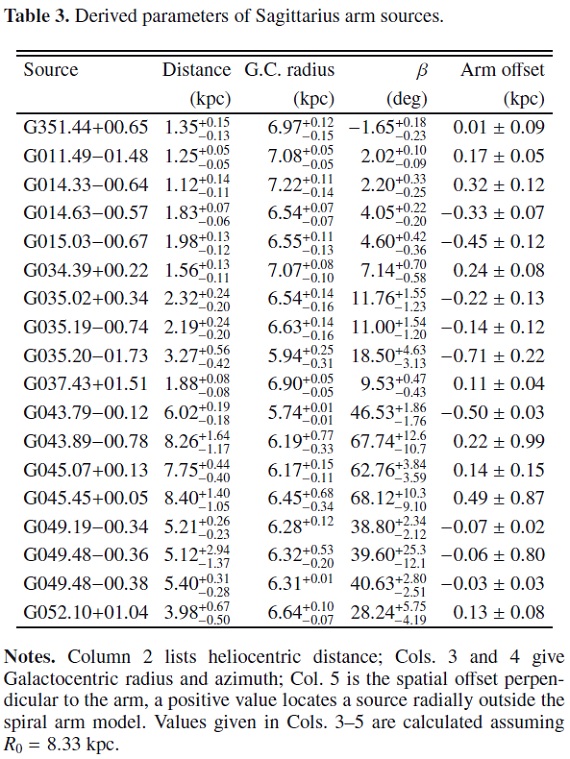 表3.サジタリウス腕天体の性質 |
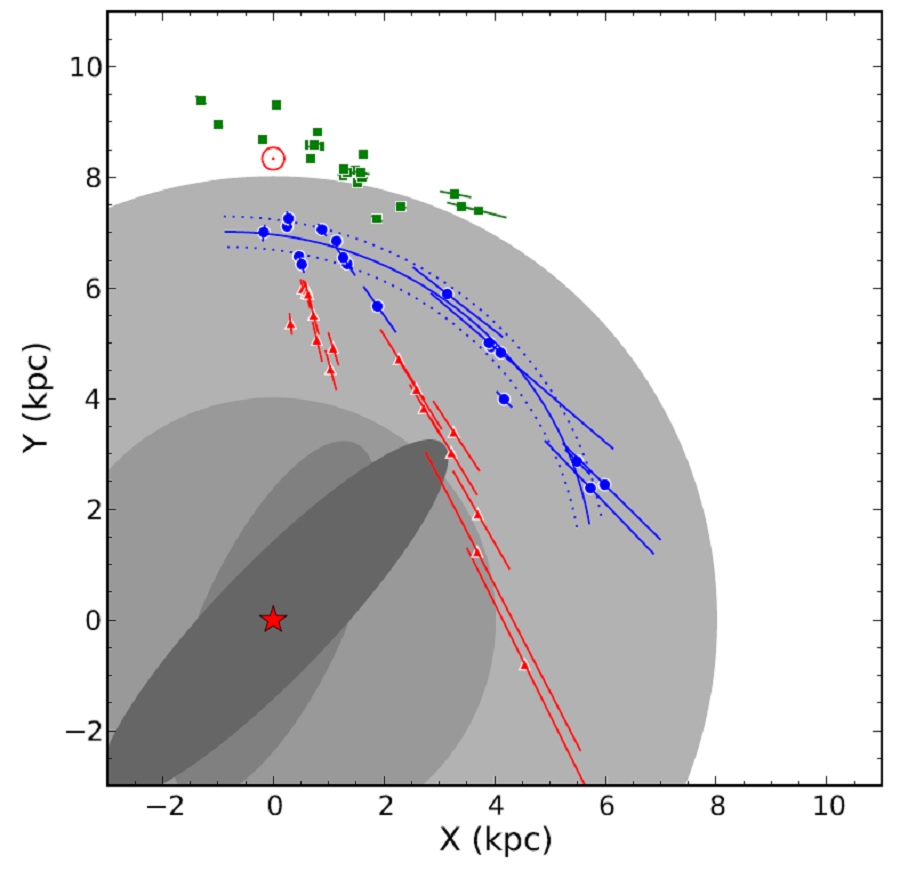
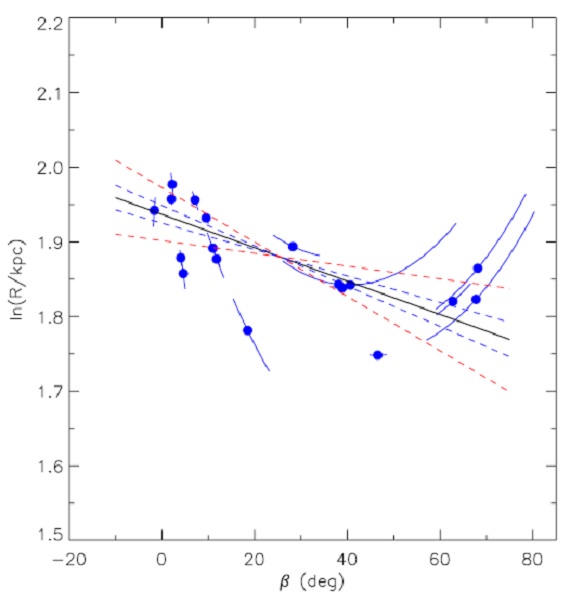 図5.R-β 図。実線=ピッチ角 ψSag 7.3° の対数 螺旋。青点線=±1σ, 赤点線=±3σ ピッチ角不定性 を示す。カーブする弧は三角視差の ±1σ 不定性の影響を示す。 HMSFRs の配置 図4では銀河面上に、銀河系中心座標で β = [-2, 65], R = [5.7, 7.2] の HMSFRs をプロットした。 Georgelin,Georgelin 1976 はサジタリウス腕の曲率が滑らかに変化すると述べ、Taylor-Cordes モデルは β = [-20, 65] で腕が平坦になるとした。しかし、図4を見ると、その ような平坦部は見えない。それは不正確な運動距離をスプライン曲線に合わせ たための見せかけ効果ではないか。 |
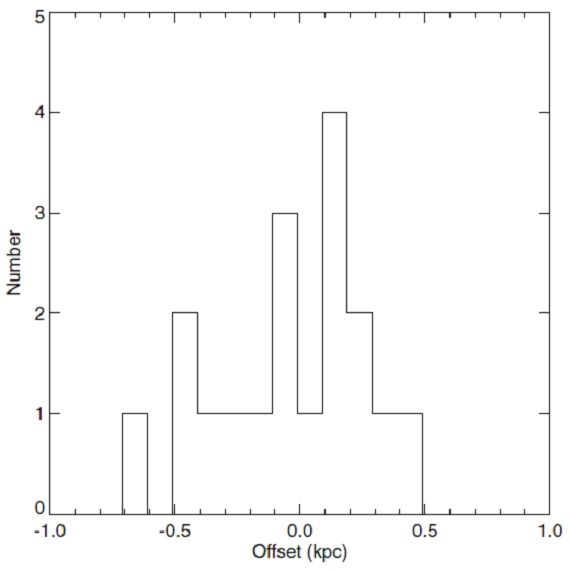 図6.HMSFRs 位置の対数螺旋腕に直交する方向のズレのヒストグラム。 ピッチ角 対数螺旋は ln(R/Rref) = βref-β で 表される。図5のベストフィットは lnRref= 1.88, βref =25.4°, ψ = 7.3°±1.5° を示す。この場合、 接線角は 51° である。太陽に最も近づくのは、 l = 0、 D=1.4 kpc である。 ここで得られたピッチ角はたの腕より少し小さいが、 HI や CO の観測から 決められた角度と合致する。距離誤差は 100 pc でこれは腕の巾を少し広げる。 |

|
3次元運動 太陽から見た HMSFRs 運動に、LSR 運動と太陽運動を加えて、銀河中心座標 系での運動が求まる。ここでは Ro=8.44 kpc, Θo=243 km/s, Uo=10.7, Vo=12.2, Wo=8.7 km/s を使用した。 特異運動 フラットな回転曲線を仮定すると、各天体の特異運動が決まる。ここで, Us = GC 方向の運動成分、Vs=銀河回転方向の成分、Ws=銀河系北極方向の 成分である。表4にそれらの運動を載せた。図7には図示した。 |
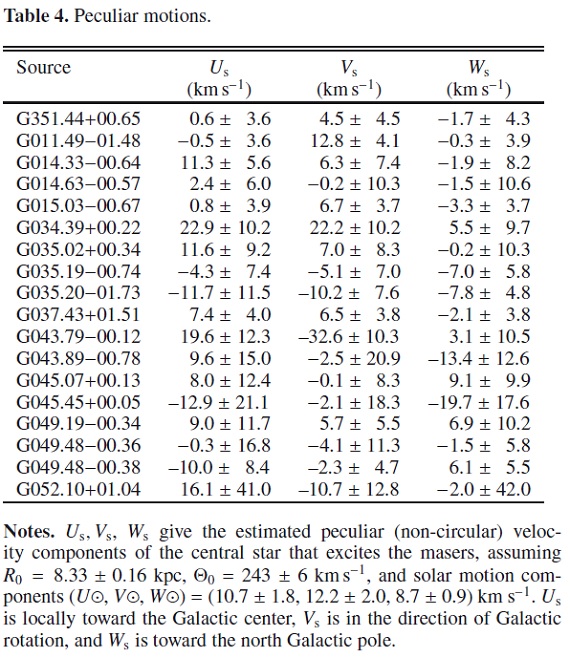 表4.特異運動 |
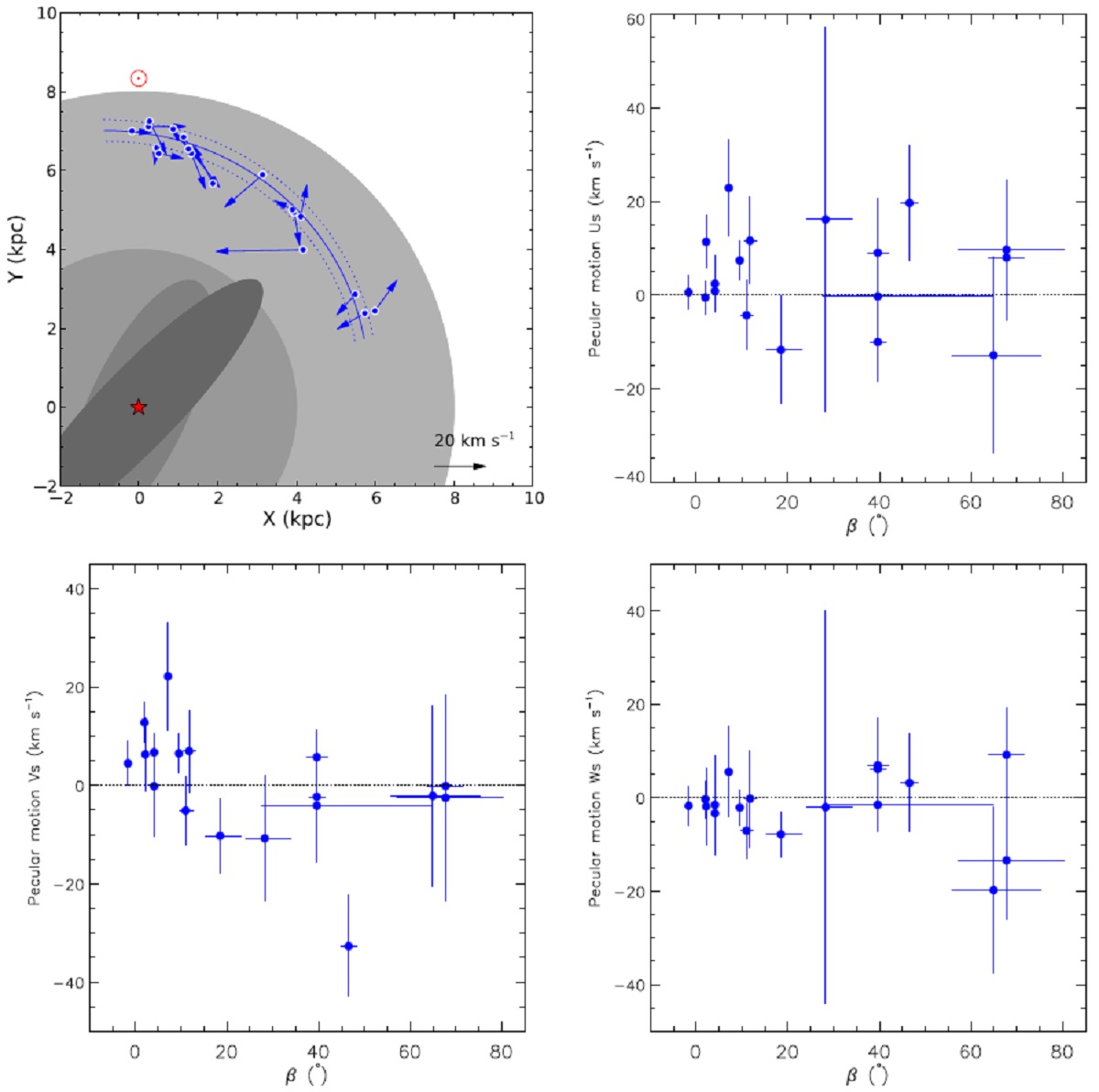
|
アームの決定 BeSSel 観測からサジタリウス腕を決定。 固有運動 他の腕と違い、回転運動と反対方向の平均固有運動は見られない。 逆に HMSFRsは銀河回転より 10 km 速い平均速度を持つ。 | 観測を南天とより遠方に拡張したい。 |