Red Clump Stars


Girardi
2016 ARAA 54, 95 - 133



　アブストラクト　

　ヘリウム中心核燃焼段階にある低質量星は近傍銀河の色等級図上に鋭い構造 ＝レッドクランプを作る。この構造は、特にマゼラン雲と銀河系バルジにおい て、恒星距離と減光の分布を探る幾つかの研究を生み出した。大規模分光および 振動サーベイで、レッドクランプは容易に識別可能である。そのため、これは 銀河系円盤上で星の密度、運動、元素組成を探る絶好の探索子となる。 　レッドクランプは明るいので、矮星よりも遠方まで届く。また他の巨星よりも 精度が高い。ここで、我々はなぜレッドクランプが観測データの狭い範囲に収 まるのか、その細かい構造を論じ、さらに、年齢、メタル量、観測バンドによる 系統的変化を議論する。これらは、いくつかあるレッドクランプ法の適用に 制限を加えるものである。

　１．イントロダクション　

　１．１．歴史　

　レッドクランプと水平枝　

　レッドクランプの外層
　　　＝十分の数太陽質量のやや高メタルのガスが対流層に必要。

　水平枝星
　　　＝どちらかが欠けると大きな対流外層が出来ない。

普通の銀河を十分深く測光すると、赤色巨星の大体 1/3 がレッドクランプで ある。銀河系内でも大規模赤外サーベイ、2MASS, UKIDSS, VVV, GLIMPSE, WISE などで同じく 1/3 はレッドクランプせいである。同様に、分光サーベイ、 RAVE, APOGEE, GES, GALAH, LAMOST でも大きな割合を占めている。 		　距離、赤化の指標天体としてのレッドクランプ　

　このように普遍的存在であるに拘わらず、レッドクランプは Cannon (1970) が "clump of red giants" という言葉を用いるまであまり意識されて来なかった。 この仕事でレッドクランプを距離と赤化の評価に用いる可能性が指摘された。

　ヒッパルコスの影響　

　距離指標としてのレッドクランプに関心が高まったのはヒッパルコスにより その絶対等級が確定してからである。特に Paczynski, Stanek (1998) による I 絶対等級の決定の影響は大きい。

　１．２．このレビューの目的　

　レッドクランプの一般的性質の無理解　

　レッドクランプ利用は最近爆発的に増えたが、レッドクランプの一般的性質 を理解して用いていない例が多い。ここではレッドクランプの特徴の 変化に重点を置いて解説する。

　恒星進化上の位置づけ　

　第２章では基本的恒星進化と恒星種族の解説を述べる。銀河系と近傍銀河に 関してのより深い議論は第３章で述べる。そこでは、さらに、レッドクランプ に関する最近の知見：(a) レッドクランプのさらに細かい構造、(b) Kepler, CoRoT 衛星の星震学によるレッドクランプ星と赤色巨星枝星との区別、につい て述べる。 		　ＲＣ法　

　第４章では距離、赤化、恒星密度、運動、化学進化を求めるための RC 法を 論ずる。第５章ではモデルの不定性を議論する。

　展望　

　第６章は GAIA, LSST, WFIRST による数百万のレッドクランプ星観測から 何が期待されるかを展望する。

　これまでのレビュー　

　これまでのレビューでは以上のテーマが良く論じられてこなかった。ただし、 Bland-Hawthorn, Gerhard (2016) は銀河系の構造、化学進化、運動に対するレビューの中で頻繁にレッドクランプ について言及している。

　２．基礎理論　

　２．１．ＨＲ図上のレッドクランプ　


図１．(a): M = 1.3 Mo, Z = 0.014, Y = 0.273 星のキッペンハーン図。PARSEC 経路図 (Bressan et al 2012) より。青＝水素燃焼領域。赤＝ヘリウム燃焼領域。 灰色＝対流層。実線＝水素欠乏及びヘリウム欠乏領域の境界線。右軸＝中心核 中のヘリウム、炭素、酸素の割合。
(b): 光度の時間変化。Lg = 重力収縮による光度。
(b):

　1.3 Mo の例　

　図１には、太陽メタル 1.3 Mo　の星のレッドクランプ進化段階の例を示す。 中心核ヘリウム燃焼段階の進化では、中心部においてヘリウムが次第に炭素、 酸素に変換されていき、同時に水素燃焼殻がゆっくりと外側に広がって行く。 この時期の最後、ヘリウム燃焼が中心核から殻に移る際にだけ、 Lg が無視 できない大きさになる。水素燃焼殻による光度は前半はヘリウム燃焼を上回 り、その後は下回る。全光度はゆっくり増加していく。

　ヘリウム燃焼の点火　Mcore0　

　ヘリウム点火時の中心核質量 Mcore0 は母星質量に 余りよらない。中心核は主に電子伝導、少しはプラズマニュートリノロスで、 により低温に保たれる。Mcore = 0.47 Mo まで成長すると、 中心から外れた位置で点火が起き、縮退が解ける。

　MHeF　

　図２(a) を見ると分かるように、Mi < MHeF の時、 Mcore0　はほぼ一定値を保つ。これが、中心核ヘリウム 燃焼星の明るさがほぼ一定になる理由である。

図２．いくつかのメタル量に対し、中心核ヘリウム燃焼開始時＝中心 He の 5 % が 3α 反応で既に燃えた時点、での物理量を星質量の関数として表し た。
(a): Mcore = H-欠乏核の質量。 (b): L = 星の光度。 (c): LH/LHe
(d): τHe = 中心核 He 燃焼時間。 　

　MHeF < M < MHeF+0.3Mo　

M = MHeF では Mcore = 0.33 Mo に急落する。このため、 MHeF < M < MHeF+0.3Mo では 光度がレッドク ランプ光度より落ちる。この質量範囲の星が混ざると、ＨＲ図上に第２レッドク ランプを形成する。その結果、レッドクランプ全体が 0.4 等下に伸びた形になる。

　MHeF+0.3Mo < M　

一方、MHeF より質量の大きい星では、収縮中心核の電子縮退が始まる前にヘリウム燃焼が 始まる。その中心核質量はそれ以前の対流核の大きさで決まり、恒星質量にほぼ 比例する。その光度はレッドクランプ光度より大きいので、ＨＲ図上では 垂直構造を形成する。MHeF < M の星の構造は低質量星とそう 変わるわけではないが、LH が LHe を上回っている点が 著しい違いである。




図３．(a): 中心核ヘリウム燃焼星の進化経路。PARSEC データベース (Bressan et al 2012) より。左：Z = 0.002 (SMC), 右：0.017 (太陽近傍)。 Mi = 0.6 - 2.6 Mo 経路を 0.1 Mo おきに表示。MHeF = 1.7 Mo (Z = 0.002), 1.9 Mo (Z = 0.017) である。 中心核ヘリウム燃焼期は LHe > 0 かつ |Lg|/L < 0.005 で定義し、黒バツ＝スタートである。進化経路上の黒丸＝ 107 yr 毎の位置。大きい丸＝中間年齢。
(b): 各経路の中間年齢の位置（図a の大きな丸）のみを表示。
(図a との対比から、Mi は分かる。例えば、 Z = 0.002 の 一番下が 0.7 Mo である。しかし、説明不足！)
破線＝バンド V, I, Ks での等級一定線。
(c) : （ｂ）と同じだが log g - log Teff 面上で示す。

　ZACHeB 後の進化　

　ヘリウム燃焼開始後は光度が緩やかに上昇し、有効温度は最初は上昇するが、 その後低下して行く。この進化がどのくらいかは、モデルに使用する対流モデル と 12C(α, γ)12O 反応率に掛かっている。 現在使われているモデルでは、低質量星の場合、L で 0.1 dex, Teff で 0.01 dex 程度である。しかし、MHeF を少し上回る質量の星では、 ヘリウム燃焼開始の時の中心核質量が小さいので、スタート時の光度も低い。 そして、L の変化も大きく、CHeB 期の寿命も低質量の場合の 2.5 - 3 倍に長い。 Girardi et al 2013 に示された通り、この傾向は、メッシュの粗さその他の 違いに拘わらず、ほぼ全ての計算コードで共有されている。

　図３b = 中間位置の変化　

　図３b には、様々なメタル量に対し、 CHeB 進化の中間年齢位置の Mi に よる HR 図 (L, Te) 上の変化を示す。典型的な重力値として log g = 2.5, それに、Castelli, Kurucz 2003 の合成スペクトルライブラリー [Fe/H] = -0.5 から導いた輻射補正を使い、HR-図上に V, I, Ks バンドでの一定等級 ラインを引いた。その傾きはバンド波長により変わって行くが、 Ks バンド より長い方ではほぼ一定値に収れんする。 		　図３c ＝ (log g, log Teff) 図　

　図３c では同じ中間年齢位置の変化を (log g, log Teff) 図上に示す。 分光データとの比較にはこちらの方が向いている。レッドクランプ主要部に対 する log g の変化巾は 0.5 dex 程度と分かる。特に低メタルではその幅が 0.2 - 0.3 dex 程度に狭まる。興味深いことに、高メタルではより広い範囲の 中間質量星がこの図上で、純粋のレッドクランプメンバーと看做されるほどに 近くに集まる。実際、第２レッドクランプは HR-図では MHeF - MHeF+0.3Mo の星で定義されるが、(log g, log Teff) 面では MHeF+1.3Mo の星でさえ低質量レッドクランプ星と同じ log g 領域に現れる。したがって、第２レッドクランプはこちらの方がはっきりと わかる。


( log g - log Te 面で近接 というのがどこを指しているのか分からない。最後の文も どういう論理なのか分からない。)




図４．(a): 赤太線＝ 0 - 12.5 Gyr の間一定星形成率銀河での中心核ヘリウム 燃焼星の質量分布。赤破線＝第１赤色巨星枝での質量放出の効果。ここでの M は実際の質量（初期質量でない）。ピンク斜線域＝ 8 Gyr 昔に星形成を停止 した場合の N(Mi)。
(b): 中心核ヘリウム燃焼星の年齢分布。点線＝比較用の t-0.6 関数

　２．２．種族合成の基礎：質量、年齢分布　

　質量、年齢分布の基本式　

　銀河の中心核ヘリウム燃焼星に対して、次の質量、年齢分布を仮定する。

　　　N(M) ∝ φ(Mi)ψ[t-τH(Mi)]τHe(M)

　　　N(t) ∝ φ(Mi) |dτH(Mi)/dMi|-1 ψ[t-τH(Mi)]τHe(M)

ここに、φ(Mi) = dN/dMi = 初期質量関数
(dN のかわりに dNi, Ni = 形成さ れた、質量 Mi 以下の星の総数、ならまあいいけど。)

τH(Mi) = 主系列寿命。τHe(Mi) = 中心核 ヘリウム燃焼期寿命。
ψ[t-τH(Mi)] = Mi の星が形成された時期の星形成率。
φ(Mi) |dτH(Mi)/dMi|-1 ψ[t-τH(Mi)] = 星が主系列を離れる割合。

(M と Mi がよく判らない。 Mi の星が 第１赤色巨星枝質量放出を経験して RC 時に M になっていると考えている？ 第１式を見ると t = 0 が星形成開始時、現時点が t = 12.5 Gyr と見える。 しかし、４(b) 図説明を読むと、 t = 0 が現在、t = 12.5 Gyr が最初時と 書いてある。そう看做す時、第１式は先ず、右辺に dMi/dM を掛ける。 次に、ψ[t-τH(Mi)] は ψ[τH(Mi)] にすると正しい式になる。
次に第２式だが、 dN = N(Mi)dMi = N(τ)dτ なので、N(τ) = N(Mi) (dMi/dτ) となる。したがって、右辺の ψ[t-τH(Mi)] を ψ[t] にし、さらに dMi/dM を掛ければ正しい。t = τH(Mi) が t と Mi とを繋げている。ひどくおかしいようだが本当か？)



　星形成率 ψ[t] = 一定の例　

　上式で 星形成率 ψ[t] = 一定（t = 0 - 12.5 Gyr), IMF φ ∝ Mi-2.35 と仮定した例を図４に示す。同じ仮定だが、星形成が古い 時期 (t = 8 - 12.5 Gyr) に限られた場合を赤ベタで示す。図４左の赤破線＝ 第１巨星枝質量放出をレーマーズ則 (η=0.35) で仮定した場合の Mi でなく レッドクランプ期の M 分布。 		　静謐銀河では N(t) ∝ t-0.6 　

　一定星形成と別のタイプの銀河が静謐(quiescent)銀河で、数 Gyr 以前に星 形成を停止している。そのような銀河では the function が t-0.6 で近似でき、レッドクランプの年齢分布は N(t) ∝ ψ(t-τH) t-0.6 で表される。年齢 t = 8 - 12.5 Gyr の間に t-0.6 は 30 % 程度しか変化しない。このケースはレッドクランプの観測数が銀河の 総星形成率を直接与える唯一の例である。
(しかし、規格化されていないから、 活動期の長さと、総質量とが縮退するのではないか。 )


　レッドクランプの質量分布と年齢分布　

　銀河が全期間星形成を続けるより一般の場合には、質量分布は (a) 最小質量 帯の星と、(b) Mi = MHeF 付近でのレッドクランプ期間が長い星の 二つのピークを持つ。しかし、年齢分布では Mi = MHeF に対応する 年齢付近の単一ピークとなる。重要なことは、 Gyr タイムスケールでは比較的 一定の星形成率を持つような銀河では、レッドクランプの平均年齢は比較的若く、 1- 4 Gyr 程度に落ち着く。
(赤色巨星全体ではこうはならない？ )


　NRC(t, Z) = レッドクランプ数　

　もう一つ注意すべきは、左ページの２式は τHe ≈ τH の場合は成立しない。じっさい、 Mi ≈ MHeF では、τHe/τH ≈ 0.3 となる。従って、 ここで用いている近似はあくまで全体的な傾向を調べるものであって、種族 合成の研究では等時線を用いなければならない。 Girardi, Salaris (2001) はレッドクランプの平均等級を年齢とメタル量の関数として表にした。それは 次の式で定義される：

⟨Mλ (t, Z)⟩ = -2.5 log [ 1 ∫ CHeB φ(Mi)10-0.4M λdMi ]
NRC


ここに、NRC はある (t, Z) の星形成で出来る単位質量当たりの レッドクランプ星の数
　　　　　NRC = ∫CHeBφ(Mi)dMi

である。φ(Mi)は 1Mo の星形成事象に規格化されている。NRC (t, Z) グリッドから、モデル銀河のレッドクランプの平均値は、例えば ⟨Mλ⟩ のような、単純に NRC と 星形成率を掛けて平均すればよい。図５(a) には NRC(t, Z) を 示す。



図５．PARSEC 等時線(Bressan et al 2003) と Kroupa 2002 初期質量関数、 第１巨星枝で質量放出ナシという仮定での中心核ヘリウム燃焼星の理論予測。
(a): N(RC) (b): ヒッパルコスによる観測値 Francis,Anderson 2014 と較べた I 平均等級。赤＝モデル値が明るい。青＝モデルが暗い。 (c): K 等級での比較。(d): 輻射等級の 1σ 散布度。

　２．３．副構造：第２レッドクランプ、垂直構造、水平枝　

　副構造の種類　

　通常の年齢・メタル量関係に従う銀河ではレッドクランプには、主要部、 はっきりした第２レッドクランプ、弱い垂直構造、それにもし古い星が低メタル なら水平枝を持つ。垂直構造と水平枝は τHe が短い、 IMF が低い、垂直構造では等級の広がりが大きい、水平枝では質量巾が小さい 等の理由で貧弱である。それに対し、第２レッドクランプはもっとはっきりした 構造である。それは、年齢 1 Gyr の種族に対してはほぼ確実に出現する。 		ただし、非常に低メタルの場合は除く。合成種族モデル CMD では質量分割が十分に 細かくないと第２レッドクランプはもれ落ちることに注意せよ。

　静謐銀河　

　静謐銀河は一般に副構造が見えない。レッドクランプと水平枝の分離は星形 成史の細部に係る問題である。

　３．レッドクランプの観測　

　３．１．銀河系の高メタル散開星団　

　サンプル　

　質量が小さいため、銀河系散開星団にはレッドクランプ星が少ない。 M67 （3.5 Gyr, Sandquist 2004) に７つ、Berkley 32 (6 Gyr, D'Orazi et al 2006) に４つ、NGC 188 (7 Gyr, Sarajedini et aal 1999) に多分３つ。 Mermilliod et al 2008 と Mermilliod, Mayor 1990 にはあと幾つかの レッドクランプが示されている。NGC 2477, NGC 2506, NGC 6819 のような 遠くて大きな星団には数十のレッドクランプ候補星があるが、そのメンバー シップが疑わしい。
　少数にせよ、存在する星団レッドクランプ星から、メタル量が分かっている 場合、距離と減光が決まる。すると、年齢が主系列フィットから決まる。

　モデルとの不一致　

　この方法は等時線上のレッドクランプが距離既知の星団中のレッドクランプを 再現できることが前提である。ヒッパルコスで視差が精度よく分かっている星団 は全て 1 Gyr より若い（van Leeuwen 2009）のでこのチェックはできない。 Percival, Salaris 2003 は主系列フィットで距離が判明した星団のレッドク ランプ等級をモデル予想値と比較し、それらが Girardi, Salaris 2001 モデル の予想と一致することを確認した。しかし、世間に流布しているモデルの全て が一致するわけではない。特に物理メカニズムとデータを最新のものにした モデルが系統的に観測値より 0.2 等明るいモデルを生み出すことは問題で、図 ６にその様子を示す。この不一致はレイマースの質量放出則 η = 0.35 を 適用すると 0.1 等にまで抑えられる。

　二重種族　

　もっとも良く調べられた散開星団の内、 NGC 472 と NGC 7789 ではレッド クランプ等級 (Mermilliod et al 1998) がモデル予想より広い範囲に散らば っている。現在これらの星団は二重種族ではないかと疑われている。二重種族 の問題は３．７節で議論する。

　レッドクランプと赤色巨星枝のカラー差と年齢　

　Hatzidimitriou 1991 はレッドクランプの B-R カラーと一定等級の RGB カラーとの差が星団年齢とよく相関することを見出した。この関係はモデルから も見出された。Girardi 1999. ただし、モデルは太陽メタルとスーパー太陽 メタルとの間で勾配に大きな差が生じることを予言した。

図６．銀河系散開星団中のレッドクランプ。距離と年齢は主系列フィットから 得た一様な手法 Percival, Salaris 2003 での値を用いた。古い球状星団 47 Tuc もサンプルに含む。[M/H] = 0, -0.5 のモデル予想値も示す。 実線＝第１赤色巨星枝での質量放出なし。点線＝ Reimers 1975 放出則 η = 0.35 を仮定。




図７．ヒッパルコスによる太陽近傍レッドクランプの色等級図。測光は Anderson, Francis 2012 の Extended Hipparcos Compilaation から 採った。視差は van Leeuwen 2007 の改訂版を使用。データ点の大きさは 視差のエラーに反比例する。σπ/π < 10 % データのみ使用。

　３．２．ヒッパルコスによる太陽近傍レッドクランプ　　

　ヒッパルコスレッドクランプ星　

　ヒッパルコスは V < 7 mag の星は殆ど観測した。視差のエラーの典型値 は 1 mas なので、σπ/π < 0.1 の制限では 100 pc 以内の Mv < 2 巨星が全て含まれる。ヒッパルコスが観測したそのような 巨星 844 個中、 508 個がレッドクランプ星、Mv = [0.5, 1.5], B-V > 0.8 であった。Girardi et al 2005 によるシミュレイションではこの体積中の中心 核ヘリウム燃焼星の数は 390 で全赤色巨星の 31 % を占める。

　MI 一定　

　図７にはヒッパルコス色等級図を示す。 Paczynski, Stanek (1998) は σπ/π < 0.1 のレッドクランプ星 約 600 個を 使い、MI が V-I に依存しないことを注意した。彼らは MI = -0.279±0.088, σ = 0.23 を得た。彼らの結果はレッドクラン プ星を距離指標に用いる途を切り開いた。

　第２レッドクランプ　

　一見すると図７には副構造があるように見えない。Girardi et al 1998 は 合成モデルとの対比から、その暗くて青い部分, Mv = 1, B-V = 0.9 - 1.0 が 第２レッドクランプに対応することを指摘した。ただし、現在第２レッドクランプ の証拠はケプラーの観測から来ている。

　３．３．銀河系広域測光サーベイにおけるレッドクランプ　

　バルジ　

　MACHO, OGLE, VVV はレッドクランプが減光により引き伸ばされる様子を示す。 赤化の弱い、バーデの窓のような領域では、レッドクランプが I = 14.4, K = 13 Paczynski, Stanek (1998)、 Saito, et al (2012) に見える。

　X-型バルジ　

　 McWilliam, Zoccali (2010), Nataf et al.(2010) は近赤外 CMD の解析からバルジの幾つかの方向ではレッドクランプが最大 0.3 等まで分裂することを示した。 Saito, et al (2011) は VVV 観測からこの分裂が銀河系中心方向にはなく、銀河面の上下で銀河面 から離れるほど広がって行くことを示した。最も単純な解釈はバルジ内に X 字 型の構造があると考えることである。

　　

　銀河系の一般フィールドではレッドクランプ星は視線上様々な距離にある。 このため CMD 上では垂直構造を成す。図８a では J-Ks = 0.75 mag にその 垂直構造がはっきり見える。方向によっては、強い減光の効果で広がり、斜め になって、 M ≤ 0.5 Mo の低温矮星 J-Ks = 0.85 mag と混ざり合う。この 効果は 4.3. 節で議論する。

　３．４．大規模分光サーベイにおけるレッドクランプ　

　分光から log g で選別　

　測光サーベイではレッドクランプに多数の紛れ込みが防げないが、分光サー ベイではレッドクランプは Teff - log g 面上でかたまるのでその心配はない。 図３a から分かるように、単一年齢のレッドクランプモデルでは固有散布度は log g で 0.1 dex である。銀河系円盤のように複合種族の系では Girardi et al 2005 モデルは log g の散布度 0.15 dex を示唆する。この値は分光観測 から導く log g のエラーより小さい。

　サンプルクリーニング　

　RAVE, ARGOS, APOGEE で多くのレッドクランプ星が同定された。 図８b には APOGEE からの例を示す。明らかに赤色巨星からの混入は避けられ ない。Bovy et al 2014 は、同じメタル量を持つレッドクランプ星と赤色巨星 の間に系統的な Teff 差があることを利用して選別を行った。彼らはまた、青い 第２レッドクランプ星もメタル量に応じたカットで切り捨てた。こうして得た "クリーンな" サンプルは運動、化学進化の探索子として有用である。

図８．(a) 外側銀河系低銀緯領域の 2MASS 色等級図。Zasowski et al 2013. レッドクランプ垂直構造が J-Ks = 0.75 にはっきり見える。内枠＝ Girardi et al 2005 TRILEGAL 銀河系種族モデルによる同方向のシミュレイション。 レッドクランプと他の混入天体を示す。このモデルではダスト分布をスケール高 110 pc の指数関数型層状構造で, 近傍の減光 Av/D = 0.75 mag/kpc とした。 (b) APOGEE データリリース 12 (DR12) の (log g, log Teff) プロット。 星の多くは H < 14, (J-Ks)o > 0.5 である。レッドクランプ星の大部分 が log g = 2.4 - 3.0 である。






図９．恒星振動から見たレッドクランプ星。(a) ケプラーからの APOKASC サンプル Pinsonneault et al 2014 の (log g, log Teff) プロット。 ただし g は分光からではなく、恒星振動学から決めた。星の色は質量を示す。 レッドクランプ構造、特に第２レッドクランプが、しっかり辿れるのは驚き である。Mosser et al 2014 の ΔΠ1 がある星については、 レッドクランプは星印、第１巨星枝星は三角印で示した。星質量は色で示す。
(b): Mosser et al 2014 が調べたケプラー巨星の ΔΠ1 - Δν プロット。星質量は色で示す。ΔΠ1 で綺麗に 分かれた星は中心核ヘリウム燃焼星 ΔΠ1 > 120 s と 第１赤色巨星枝星 ΔΠ1 < 100 s である。さらに 第２レッドクランプ星は δν > 5 μHz として分離して見える。 これらは 1.8 Mo より重い星である。

　３．５．大規模音響振動サーベイにおけるレッドクランプ　

　Δν と νmax の分布　

　Δν = 振動数間隔
　νmax = 最大パワー振動数
とすると、以下の関係がある。

　Δν ∝ ⟨ρ⟩1/2 ∝ M1/2 R-3/2

　νmax ∝ g T-1/2 ∝ (M/R2) Teff-1/2

観測した Δν と νmax の分布はレッドクランプに対応 するピークを明らかにした。CoRot では νmax = 30.2 ± 0.2 μHz, Δν = 3.96 ±0.33 μHz である。ピーク値は R = 10 Ro に相当するがこれはレッドクランプ星の典型値である。重要なことは 天体振動学から導く log g は分光観測からの価より精度が高い。その結果、 図９a では、第２レッドクランプの存在が明確に示された。

　赤色巨星枝上端での質量放出量　

　CoRot, Kepler が観測した銀河星団においては、観測から導かれた星パラ メタ―とモデル等時線との比較からレッドクランプ星にたいしてきつい制約が 課せられた。例えば、 NGC 6791 の場合、Miglio et al 2012 はレッドクランプ と赤色巨星枝の星の質量を較べて、赤色巨星枝上端で起きると想定される質量 放出量はレイマース則からの予想をかなり下回るとした。

　レッドクランプと赤色巨星の分離　

　天体振動学に関し、もう一つの重要な成果は赤色巨星において、高密度輻射核 の重力波と外層部での音波との相互作用が発見されたことである。これら混合 モードの所謂周期間隔、ΔP は半径の似たレッドクランプと赤色巨星が がはっきりと分かれることを示した。 		　ΔΠ1 - Δν 図　

今や、ΔΠ1 - Δν は巨星の診断に有望な方法 である。最初に Bedding et al 2011, 最近では Mosser et al 2014 が示すように、小質量中心核ヘリウム燃焼星は Δν < 5 μHz, ΔΠ1 > 200 s に固まる。 この塊りは赤色巨星と分離している。さらに、この天体振動データはこれらの 星の質量差さえも分解し、さらに各質量別に進化経路、次第に ΔΠ1 が大きくなり、その後 Δν が小さくなる、 も示している。第２レッドクランプにある、 1.9 - 2.4 Mo の星はレッドクラ ンプから Δν = 9 μHz, ΔΠ1 = 100 s へと 伸びている。ケプラーデータには少ないが、それより質量の大きい星では同じ 経路を逆向きに戻る。Montablan et al 2013 は第２レッドクランプ系列に沿っ て ΔΠ1 がヘリウム点火時の核質量を追っていることを 示した。こうして、我々は観測的に MHeF の丁度始まる質量を 定めることが出来る。これは、主系列に沿って対流オーバーシューティングの 効率を測ることに相当する。

　ヘリウム量の決定　

　さらに困難な課題は赤色巨星、レッドクランプ星のヘリウム量を決定する ことである。原理的には可能であるので、近い将来実現するであろう。

　展望　

　ΔΠ1 の測定は直接的ではなく、少数の星でしか得ら れていない。しかしその数は増加しつつある。図９に示す log g - Teff 図 が APOKASC カタログなどから作られ、そこに周期間隔、高分解能分光からの 回転速度、化学組成などの情報が加わることで恒星進化モデルに対する制約が 強められる。




図１０．(a) 南黄極(South Ecliptic Pole) 1.6 deg2 の VISTA サーベイ (VMC). LMC 中心から 4.5 kpc 北東に当たる。 (b) 30 Dor の 1.6 deg2 VMC データ。Tatton et al 2013. (a), (b) 共に Y-Ks > 0.5, Ks < 20 mag = 第１赤色巨星枝基部 の星の 1/3 はレッドクランプである。 (c) PARSEC 経路と TRILEGAL コード, Holtzman et al 1997 SFH で、減光ゼロ、 距離 50 kpc, 測光エラー　0.01 mag の仮定で作成した LMC モデル。 (d) M 31 円盤、 Panchromatic Hubble Andromeda Treasury (PHAT) カタログ(Williams et al 2014) より.

　３．６．局所群銀河のレッドクランプ　

　局所群銀河　

　レッドクランプ星はスカルプターや M 81 銀河群で既に検出されている。 しかし、その CMD の詳細が HST 測光で分かっているのは M 31 とその周辺 銀河である。局所群では中間年齢種族を含む全ての矮小銀河にレッドクランプ が存在する。良い例はカリーナ、レオＩ、フェニックス矮小楕円銀河である。 最も低メタルのレッドクランプは [Fe/H] = -1.8 のレオＰである。
　マゼラン雲に対しては Kato et al 2007 をはじめとする多くのサーベイが 実施された。中でも Vista survey of the Magellanic Clouds = VMC ( Cioni et al 2011 ) が深い。

　マゼラン雲のレッドクランプ構造　

　図１０にはそれらのサーベイの結果をシミュレイション計算と較べた。モデル から予想された細かい構造が観測に反映している。内部赤化が弱い領域では、 第２レッドクランプを伴う小さく固まったレッドクランプ主要部が現れる。その 巾は小さくて、年齢、メタル量の異なる種族の混合で説明される。そのような 個所は LMC の外辺部で見られ、そこでは第２レッドクランプに加えて、垂直 構造と水平枝も見える。 30 Dor 周辺のように濃い部分では、微分赤化の影響 で構造がぼやけて見える。 		　ＳＭＣの深度　

　Gardiner, Hawkins 1991 は銀河の深さに対応する分散 sigmageo2 を以下の式で定義した。

　　　　　sigmageo2 = sigmatotal2 - (sigmaint2 + sigmaerr2)

ここに、sigmaint　は種族構成に伴う分散、sigmaerrは 測光に伴う分散で、赤化と測光エラーがよく定義された箇所での参照値である。SMC では 2σ 深さが 12 kpc と主張された。現在、 SMC 西側ウイングでは、レッドクランプの巾、 それに分裂は種族効果で説明できる範囲を越えていると看做されている。

　M 31　

　図１０には M 31 の低減光領域での Panchromatic Andromeda Hubble Treasury (Dalcanton et al 2012) を示す。M31 にも LMC と同様な垂直構造が見える。しかし、 広いカラー幅は赤化方向と一致しないので、微分減光の結果と思えない。メタル量が 非常に広い範囲に亘っている可能性がある。



図１１．(a) SMC 星団 NGC 419 (Girardi et al 2009) の HST CMD. (Girardi et al 2009) 拡張ターンオフと二重レッドクランプの双方が見える。 (b) Girardi et al 2013 による最も簡単な説明。

　３．７．マゼラン雲星団中のレッドクランプ　

　光度極小の発見　

　星団距離一定の仮定は長い間、レッドクランプ光度の年齢効果を調べる際に 採用されてきた。 Corsi et al 1994 は、この仮定で、 t = tHeF 星団 NGC 2209 でレッドクランプ光度極小が起きることをＢＶバンドで発見した。 それより古い年齢で光度が平坦になる現象は、かれらの同じデータで示されて いた。ただし、サンプル数は少ない。彼らのサンプルの幾つかが Ferraro et al 2004 ) により近赤外で観測された。彼らは NRGB/NRC が tHeF 後に上昇することを見出した。残念ながら彼らは tHeF を決定することは出来なかった。

　星団距離による LMC, SMC の幾何学　

　 Grocholski et al 2007 はレッドクランプ等級から個々の星団までの距離を決定し、星団の分布が円盤 フィールド星と同様であることを確認した。SMC に関しては Crowl et al 2001 が星団レッドクランプ距離を用いて SMC がかなり深いことを示した。

　レッドクランプ構造　

　更に深い近赤外、 HST 測光によりこの分野の研究にはまだ余地がある。過去 １０年の HST 観測の集積からレッドクランプ構造に関し多くの発見があった。 第１に、若い星団ではレッドクランプが t ≥ 2 Gyr 星団に較べ引き伸ばされ ていることが判った。これは tHeF 以前と以後とでレッドクランプの 経路に大きな違いが生じる（図５d）ことと一致する。第２に、単一星団中に 固まったレッドクランプと引き伸ばされたレッドクランプの双方が共存する 例がある。著しい例は NGC 419 である。そのコアは 341 星から成るコンパクト な集団である。それに加え　47 星からなる第２レッドクランプがある。第２ レッドクランプの上部がコンパクトな主要部と混ざっているなら、この異なった 進化史を持つ中心核ヘリウム燃焼星の比は単純な星計数よりさらに大きい。 図１１にはこの星団の CMD と古典的な年齢混合モデルの予測とを比較した。 		　二面性の原因　

　Girardi et al 2009 が示唆し、 Goudfrooij et al 2014 が確認したが、 大きな中間年齢星団、NGC1751, NGC1783, NGC1806, NGC1846, NGC1852, NGC1917, でターンオフ年齢 tHeF 付近のものでは、この二面性が 期待されるし、実際に観測されている。その上、それら全ては拡大ターンオフ を示す。この二つの現象が同じ原因から生じる：主系列後を離れる際の質量の 広がりがまたレッドクランプの二相性を生み出す、と考えるのは自然である。 しかしその広がりの原因については意見が一致しない。星団内の年齢の広がりか、 回転のような効果が星毎に違うのか不明である。

　ターンオフ質量と MHeF の決定　

　原因が何であれ、二重レッドクランプを持つ星団は MHeF に強い 制限を掛ける。これらの星団のターンオフ質量が MHeF を含んでいる からである。ターンオフとレッドクランプのカラー差はターンオフ質量の良い 指標になっている。このように、これらの星団ではターンオフ質量と MHeF の両方を、カラー差とレッドクランプ形態とから決められる。Girardi et al 2009 はこのアイデアに基づいて NGC 419 の年齢を 1.35 Gyr と定めた。

　４．レッドクランプ法への注意　

　４．１．標準光源　

　モデルの不定性　

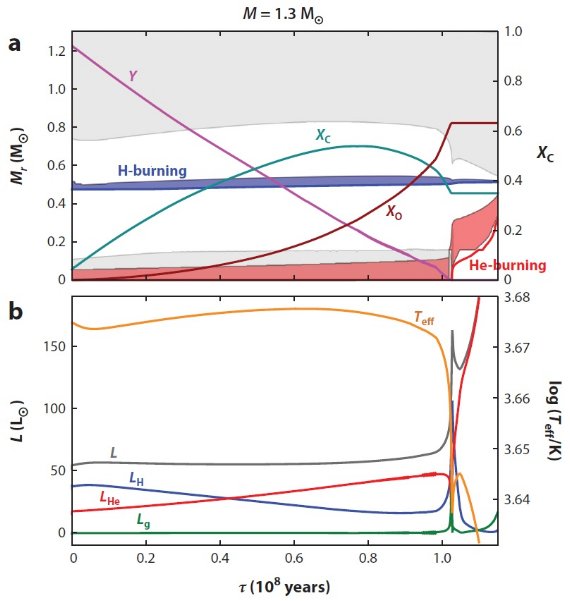
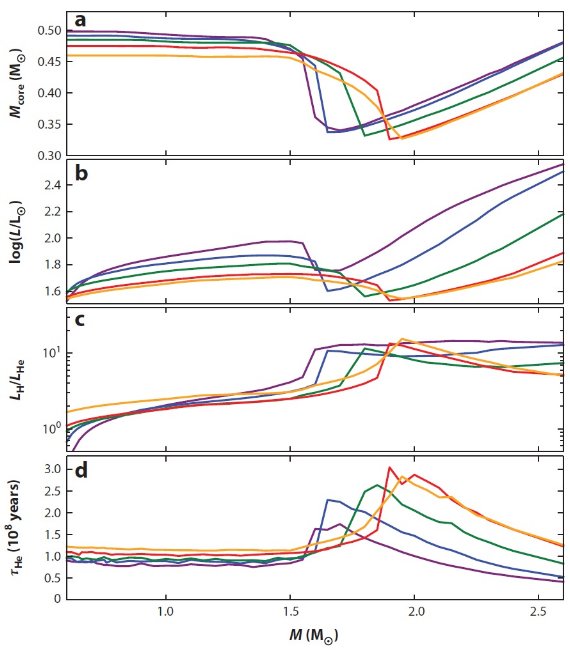
　 Cannon (1970) はレッドクランプの光度が一定で距離指標に用いられる可能性を指摘した。 問題は絶対等級の較正である。モデルとしてはプラズマニュートリノによる エネルギーロス、電子伝導、状態方程式、オパシティ―の不定性が問題で、 中心核ヘリウム燃焼発火時の中心核質量に 0.01 Mo 程度、等級にして 百分の数等の不確かさが残る。

　光度関数フィット　

　観測的な等級較正には正確な視差が必要で、 Paczynski, Stanek (1998) はヒッパルコスを利用してレッドクランプ星の絶対等級を決めた。 彼らは、σπ/π < 0.1 の星全ての光度関数 を次の式でフィットした。
N(λ) = a + b Mλ + c Mλ2 + d exp [ - (MλRC - Mλ)2 ]
2σλ2


ここに λ はバンドを表し、当初は I バンドが採用された。右辺の二次 式は赤色巨星による背景部を示し、最後の項が平均値 MλRC, 散布度 σλ　 のレッドクランプガウシアン分布を示す。系外銀河の距離指数 μ0 は次の式で決まる。

　　　　　μ0 = mλRC - MλRC - Aλ + Δ λ

ここに、Δλ は種族効果の補正である。

この方法に関し以下の３点に注意が必要である。



　４．１．１．二次式＋ガウシャンでレッドクランプ平均等級が決まるか？　

　追加構造成分　

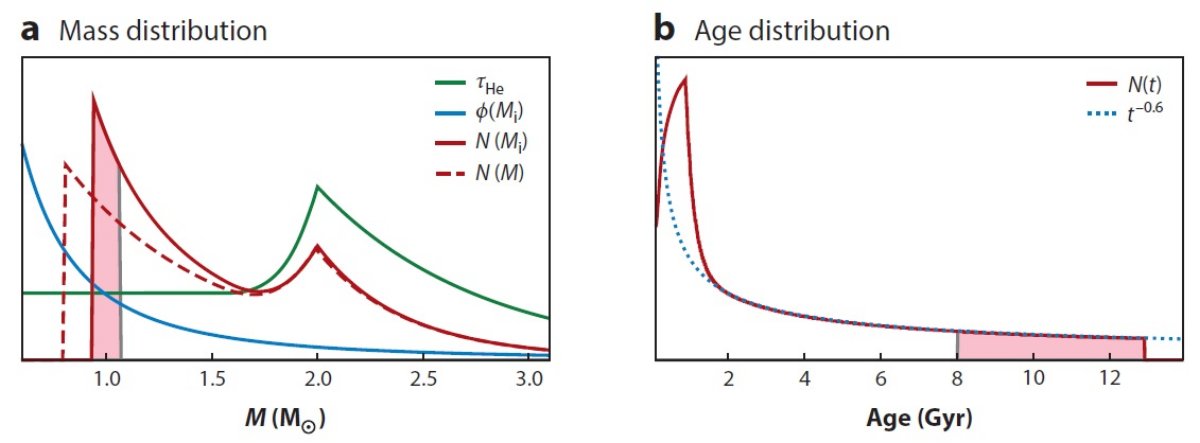
　多くの場合、レッドクランプ等級の散布度は測光エラーと同じくらいである。従って、 上に述べたガウシアンフィットは平均等級を定める近似式として十分である。 測光エラーに加えて、レッドクランプは進化経路に伴う等級、カラー巾を持つ。 大事なことはそれらが平均の両側で対称ではない点である。例えば、ヘリウム核 燃焼末期、光度大の時期には進化スピードが速くなるので、光度関数は平均値の 大きい側では詰まった形になる。種族構成の年齢幅が大きいと、第２レッドク ランプ、垂直構造、水平枝などの副構造が加わる。その上、赤色巨星枝バンプが レッドクランプと同じ等級レベルに割り込んでくる。

　種族合成モデルのフィット　

　原則としては、これら全ては種族合成モデルのフィットで避けることが可能で ある。そのような試みは既に始まっている。例えば、 Wegg, Gerhard (2013) は X-型バルジの研究において、スキューネスと赤色巨星バンプの効果を考慮し ている。

　４．１．２．観測された種族 Mλ,0RC は独立か？　

　Paczynski, Stanek (1998)　

　レッドクランプ研究で基本文献となった、 Paczynski, Stanek (1998) で驚くべき結果の一つは、ヒッパルコスとバーデの窓とでレッドクランプの 固有 V-I カラーの違いに拘わらず、 I 等級が誤差内で同じだったことである。 カラーの差はメタル量分布の差と解釈され、 MI,0RC が 種族に依らない証拠とされた。

　種族補正項 ΔMλRC 　

　しかし、この値を LMC に適用した結果 Udalski (1998), Staneck et al. 1998 は通常値より 15 % 短い距離を与えた。その結果、 Cole 1998, Girardi et al 1998, Girardi 1999, Girardi, Salaris 2001 は 種族補正項 ΔMλRC を導入した。これは 年齢、メタル量に依存する量で測光だけから決めるのは難しい。そこで恒星 種族の理論モデルに頼る必要がある。

　説明　

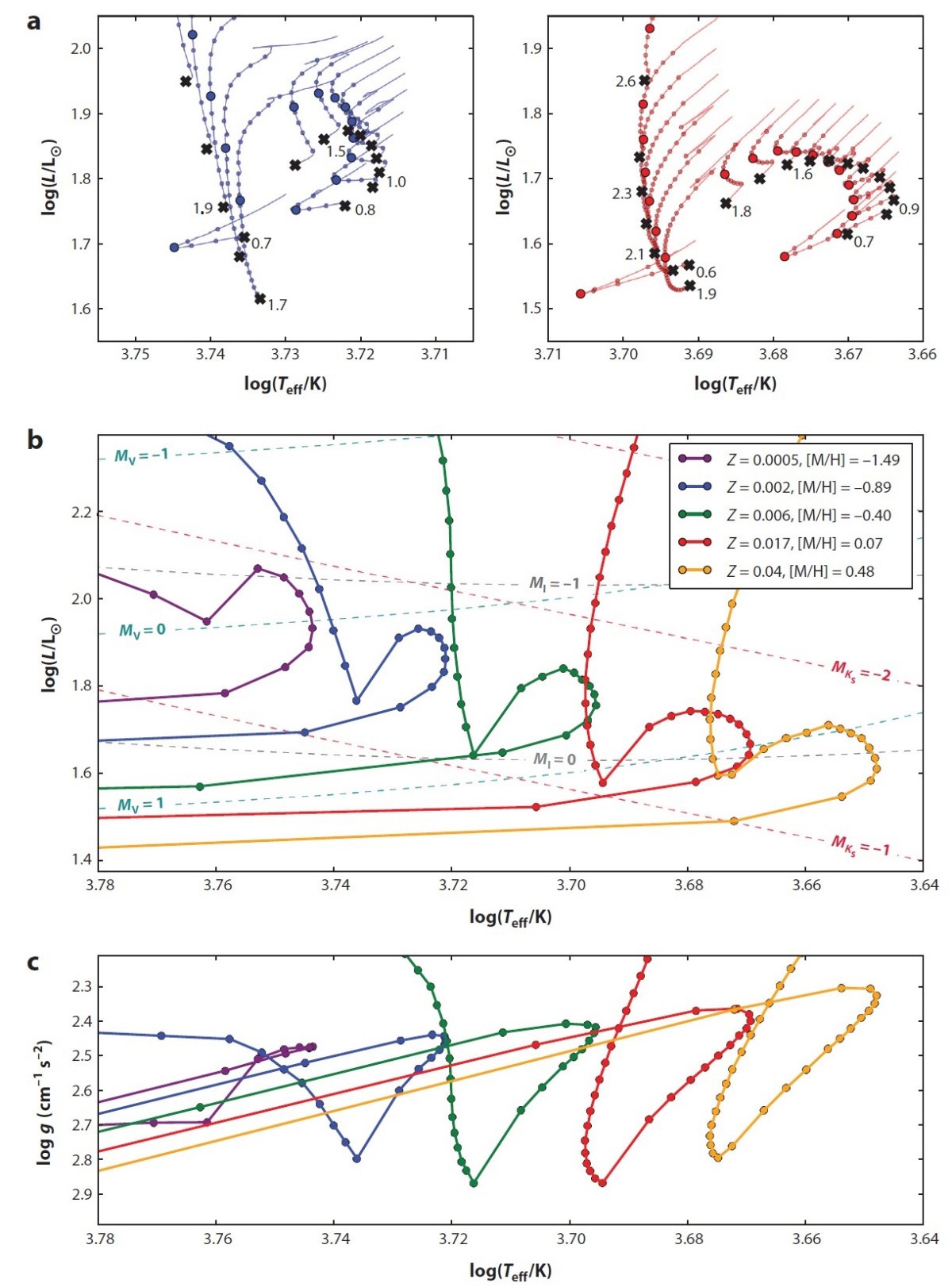
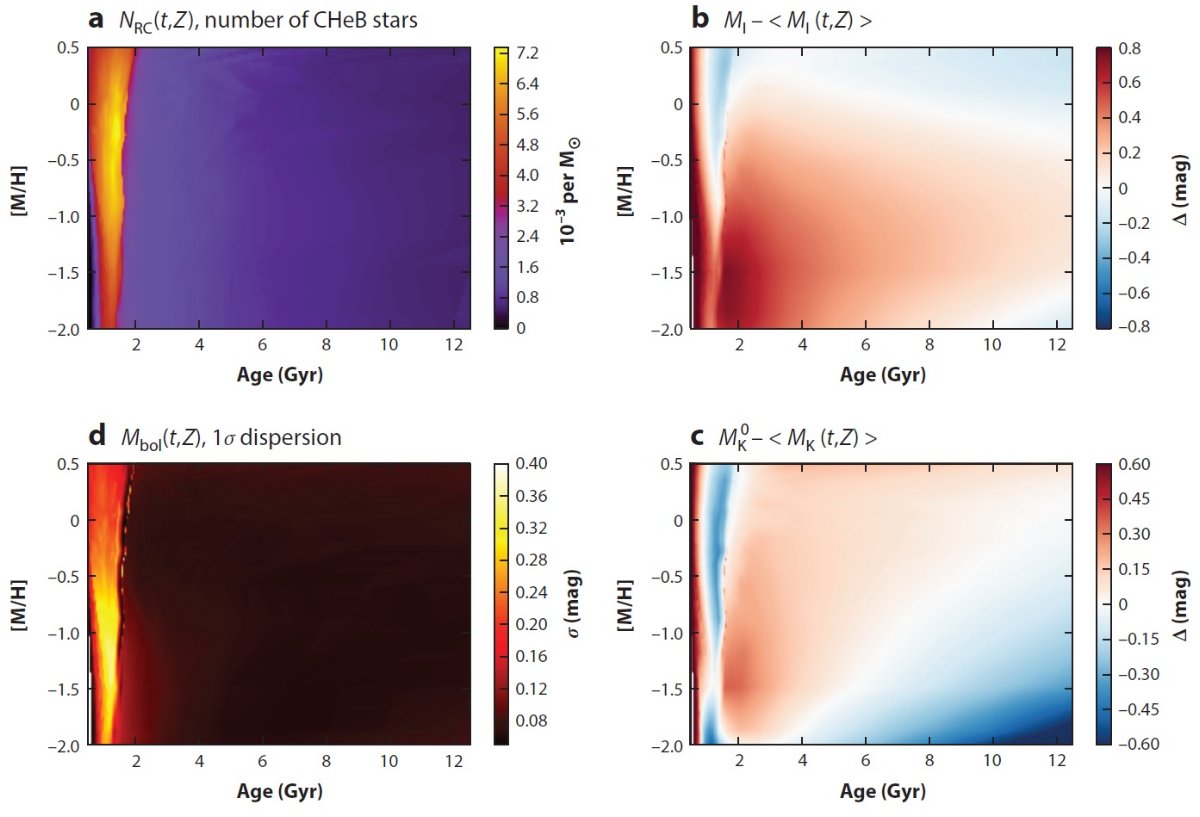
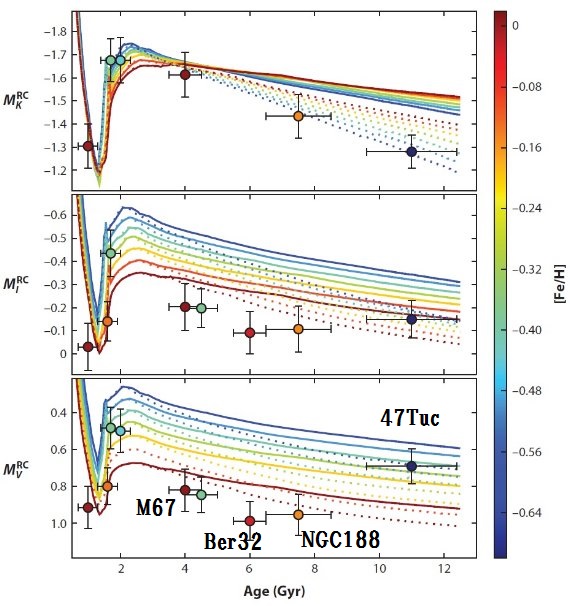
　詳細は、SFH, AMR, 採用モデルに関係し長くなるので省き、なぜヒッパルコス、 LMC どちらも (V-I, I) CMD 上レッドクランプが水平に見えるのに種族効果 が必要なのか、Girardi, Salaris 2001 を簡単に述べる。図３b で分かるように、 MI,0RC のメタル量と年齢への依存性はかなり違う。 太陽近傍では過去 10 Gyr 近くの間メタル量はほぼ一定で、図５ｂ上では 勾配の緩い線上に乗る。従って、MI,0RC は 2 - 8 Gyr でほぼ一定である。これが CMD 上でレッドクランプが水平に分布する理由である。 ＬＭＣでも似た状況が起きるが、メタル量で 0.4 dex 下を走る水平線となる。 その結果、CMD 上ではレッドクランプがが同様に水平に分布するのであるが、 その位置が 0.3 mag 低いのである。MI,0RC の種族効果 は Alves et al 2002, Percival, Salaris 2003 が調べ、Pietrzynski et al 2010 でも受け入れられている。

　４．１．３．種族効果が最小なバンドはどれか？　

　ＩからＫへ　

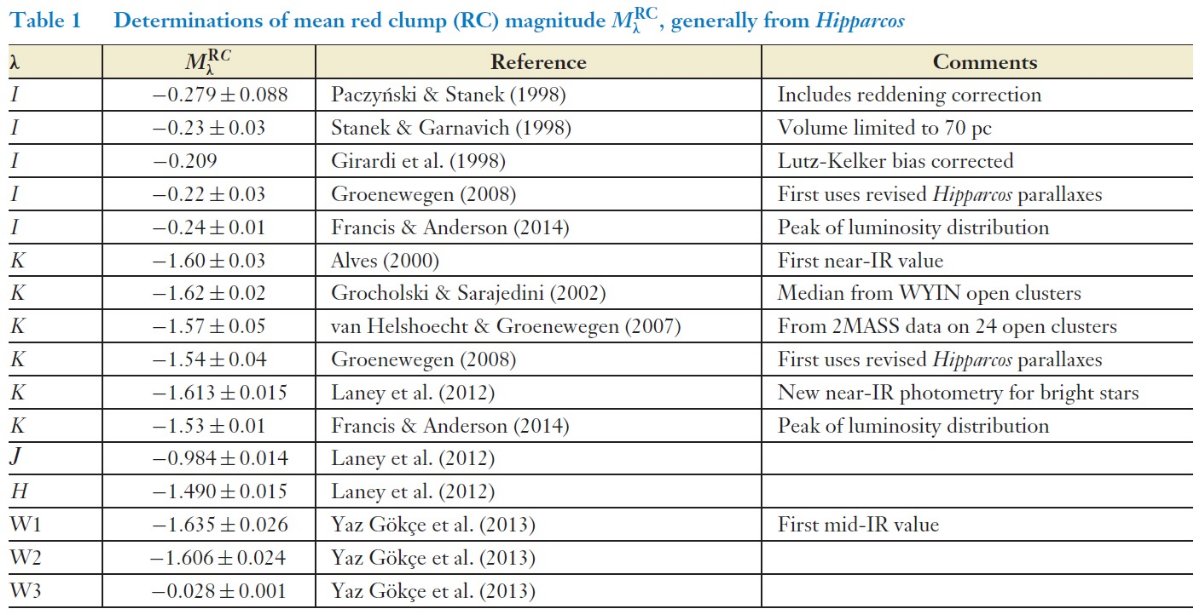
　 Alves (2000) は K バンドの種族効果が最小であると述べ、Salaris, Girardi 2002 はそれを ヒッパルコス・LMC・SMC 系で確認した。図３ｂを見ると分かるが、これは主に、 MKs 一定ラインがメタル系列と平行に走ることが原因である。その ようなことが原因で、RC 法は I バンドから近赤外へと移って行った。 Laney et al (2012) はヒッパルコスレッドクランプ星の近赤外測光をやり直した。これらの再較正の 結果は表１にまとめた。それらの多くは、細かい点、すなわち測光完全性、 ルツ・ケルカー、トランプラー・ウィーバーバイアス、などにまで配慮している。 更に、van Leeuwen 2007 のヒッパルコス視差の改訂版も Groebewegen 2008 では使われている。これらは皆百分の数等の補正である。Francis, Anderson 2014 は分布のピークと平均値の間に 0.1 等の差があることを指摘した。

　多波長観測　

　どのバンドでも種族効果が百分の数等は残ることを考えると、上記の努力 全てはレッドクランプを正確な標準光源とするには不十分である。それらは単 に既に小さな系統誤差を減らしたに過ぎない。それに対し、 Alves (2000) は、同じくらいの分光メタル量のヒッパルコス、バルジサブサンプルを選び、 それらの固有カラーは同じという仮定で、 VIK バンド測光から、バルジの距離 と減光を同時に決定した。この方法は実際上レッドクランプ距離の平均値を決め ることになる。同じ方法を LMC に適用して Alves et al. 2002 は I バンド 種族効果に整合する効果を見出した。



表１．レッドクランプ平均等級の決定例。主にヒッパルコスを利用。

　４．２．減光探索子　

　減光マップ　

　レッドクランプを減光探索子に用いる方法は、Wozniak, Stanek 1996、 Stanek 1996 に始まり、 バルジに適用された。銀河においても例えば図１０ に示すような LMC 30 Dor の減光の研究に応用されている。Tatton et al 2013 はこの領域の詳細な減光マップを VMC データの赤方広がりから作った。同様の マップは Subramaniam 2005 により OGLE-III データを用いて LMC/SMC で作ら れた。

　減光係数　

　レッドクランプはまた減光係数の決定にも用いられる。 Nataf et al. (2013) は　バルジ、De Marchi et al. 2014 は 30 Dor 領域でそれを行った。 		Nishiyama et al. (2009) は近赤外減光曲線の決定を行った。これ等の仕事は広い領域に渡り、固有性質 の系統変化がないことを前提にしている。 しかし、 M 31 や M 33 のような 大きな系では低減光領域を用いた較正が途中に必要である。LMC でさえも Balbinot et al 2015 が示すように中間年齢星と高齢星の分布に勾配がある ので種族効果を考える必要がある。

　バルジ減光マップ　

　バルジにおいては、レッドクランプの一様性はより信頼できる仮定である。 Gonzalez et al (2011), Wegg, Gerhard (2013) は VVV データに基づき、バルジの広域減光マップを作った。

　４．３．密度探索子　

　密度決定の基本式　

　 Lopez-Corredoira et al. (2002) は 2MASS データを用いて銀河系外側領域１２方向のレッドクランプ星の視線 に沿った分布を調べた。その方法は、(K-Ks, Ks) CMD 上に垂直に近い構造 を探し、その経路を距離と減光の効果と解釈する。経路上の点の実距離は、

　　　　　r = 10Ks-MKs+5-AKs(r)

で定まる。AKs = 0.675 E(J-Ks) が用いられた。視線に沿った密度 分布は、視線に沿った光度関数 A(m) から次の式で定められる。
D(r) = A(m)δm
ωr2δr


基本的にはこの方法で、 Lopez-Corredoira et al. (2007), Wegg, Gerhard (2013) はバルジ構造を探り、 Lopez-Corredoira et al. (2006), Cabrera-Lavers et al. (2008) は銀河系円盤のワープとフレアを調べた。

　このＲＣ方法には次の不安がある。

　心配(a) 赤色巨星からの混入　

　J-Ks=0.75 で赤色巨星からの混入があり、それらの距離は過大評価される。 その結果距離分布がぼやけるが、 Lopez-Corredoira et al. (2002) が行った数値実験ではその結果導かれる円盤スケール長はあまり大きなエラー は生じないとのことである。その上、 Wegg, Gerhard (2013) では逐次近似の途中に RGB バンプの位置と混入も組み込んでいる。

　心配(b) 近傍矮星の混入　

主系列 J-Ks = 0.85 付近の折れ曲がり Sarajedini et al 2009 は銀河系フィ ールド星の CMD にやはり垂直構造を生じさせる。そのカラーはレッドクラン プに心配なほど近く、高銀緯と Ks > 13 の暗い方の双方でレッドクランプ をしのぐ強さになる。 Lopez-Corredoira et al. (2002) と図８a を見よ。

これらの混入を考えると、レッドクランプ法の使用は巨星が優勢な領域、つまり 明るい等級で、銀河面に沿った付近またはバルジに限定すべきであろう。 		　極端なケース　

　密度評価のためにきれいなレッドクランプサンプルを得る困難さは外側銀河系 方向で著しい。場合によっては、ＣＭＤ上でどれがレッドクランプかを定める 事自体が前景星のために困難となる。例えば、Bellazzini et al 2006 は 大犬座銀河らしき天体をレッドクランプ星で辿った。ただし、Lopez-Corredoira et al 2007 はそれに反対している。この場合、レッドクランプはぼんやりした 塊りとして現れ、その性格はブザンソンモデルとの比較から決められた。
　別の例として、 Minniti et al. (2011) は銀河円盤の縁を決めるのに VVV 観測のレッドクランプを使った。この場合、 レッドクランプは CMD 上に見えもしない。検出されたのは星の数密度が落下 する光度レベルである。言うまでもないが、これらは極端なケースで将来 結果が大きく変わる可能性がある。

　心配(c) 種族効果によるバイアス　

　視線に沿って年齢勾配があると、レッドクランプと星全体の数比は一定とい う仮定が壊れる。t = 1 - 4 Gyr の星に重みが掛かってしまう。

　心配(d) 固有カラーの変化　

　年齢とメタル量はレッドクランプ固有カラーに影響する。したがって、等級 と共にカラーが変わるのは赤化のせいという仮定が壊れる場合がある。実際、 Laney et al (2012) が観測したヒッパルコスレッドクランプ星は年齢とメタル量に起因する固有 J-Ks カラーの巾 0.2 mag を有する。これは AKs と間違えると 0.13 mag に相当する。

　心配 (c) が最も深刻　

　最近有力になりつつある、円盤形成の「内側から外側へ」シナリオ、渦状銀河 の円盤全体に亙って平均年齢とメタル量の勾配があるという証拠 (MacArthur et al 2004, Gonzalez Delgado et al 2015) を考えると、 心配 (c) が最も深刻である。薄い円盤では 1 - 4 Gyr の若いレッドクランプ星 の割合が変化しているからである。厚い円盤、バルジではこの問題は重要では ない。

　４．４．運動と化学進化　

　レッドクランプが例えば G-型矮星 (Juric et al 2008, Ivezic et al 2012)) より優位に立つ点はこの星が明るく、遠方まで見通せる点にある。Pavel 2014 はこの星が磁場の探索子に使えるとさえ示唆している。RAVE (Williams et al 2013), APOGEE (Bovy et al. 2014, Nidever et al 2014, Lopez-Corredoira 2014, Lopez-Corredoira et al. 2014) のレッドクランプデータが調べられている。 それらの研究の主目的は前に述べた密度分布と同じである。分光データには レッドクランプ星と赤色巨星が混在しているし、また 1- 4 Gyr の若い星に 重みが掛かっている。したがって、レッドクランプ星のメタル量分布を調べても 星全体のメタル量分布と同一視することは出来ない。この問題を逃れる唯一の 途は恒星音響学である。これにより個々のレッドクランプ星の年齢を十分な 精度で決定する (Miglio et al 2013) ことが出来る。 　バルジでは年齢の広がりによる影響は大幅に低減されている。ヒッパルコス レッドクランプが同定された後に、Mao, Paczynski 2002, Sumi et al 2003 は バルジレッドクランプ星を使ってバルジの星流を検出しようとした。この試み は OGLE-II のエラーによりまだ十分な成果は生み出していない。

　４．５．年齢　

　RGB - RC カラー間隔法　

　Hatzidimitriou 1971 は銀河系とマゼラン雲の散開星団では RGB - RC カラ ー間隔が年齢と線形の関係にあることから、中年星団の大雑把な年齢を調べた。 この関係は Girardi 1999 の進化モデルからも分かる。惜しいことに、この 方法は殆ど用いられず、現代のＣＭＤ再現法に圧倒されてしまった。

　ＣＭＤ再現法　

　ＣＭＤ再現法は Harris, Zaritsky 2001, Dolphin 2002 が開始した。これは 近傍銀河の星形成史を導くのに使われた。しかし、 100 kpc を越えると、 HST でさえ主系列ターンオフの古い部分は観測できなくなってくる。そのような場合、 RGB と RC にしか古い種族は現れない。 		　レッドクランプモデルの寿命精度　　

　Dolphin 2002 はそのような場合でも古い星形成史を再現できることを示した。 これは RC/RGB 比が年齢に鋭敏だからである。これは幸運な状況ではあるが、 RGB と RC の寿命が信頼できる恒星進化モデルが必要である。これは RC に 対してはまだ達成されていない。レッドクランプモデルの寿命エラーはまだ 20 % 程度ある。

　５．問題点　

　５．１．標準光源としての精度　

　種族効果　

　レッドクランプ法による距離に対しては種族効果の影響が常に疑われてきた。 種族効果補正量が分かっていれば、局所群銀河までの距離誤差を百分の数等級 にまで低下できる。それらはヒッパルコス較正の誤差や星間減光の誤差である。

　レッドクランプ星は異質な集合である　

　レッドクランプ星の年齢は 1 - 10 Gyr に亘るので、銀河の化学進化と星 形成の時間変化のほぼ全てを記録している。ただ、 1 - 4 Gyr に強くバイアス が掛かっている。レッドクランプは広い年齢領域と初期質量に亘り、赤色巨星 枝の頂点に達し、ほぼ一定のヘリウム核でヘリウムフラッシュを起こすという 進化経路を共有している。ヘリウム燃焼はほぼ一定のヘリウム核質量で決まる が、水素燃焼殻の強度は外層部質量に左右される。LH/LHe は 質量やメタル量の異なるレッドクランプ星の間で0.35 - 4 に亘る。 その結果、総光度は核質量の単純な関数では表されない。

　でも標準光源として、　

(a)　多数のヒッパルコスサンプルで正確な全体等級較正ができた。

(b)　近傍銀河でも多数観測可能である。

このように、レッドクランプ星は決して理想的な標準光源とは言えない。古典 セファイドや RR Lyr がいくら統計的には劣る絶対等級較正であっても、 レッドクランプの方が距離決定で優れていることはない。 		　星形成史の情報の必要性　

　実際面で重要なのは、銀河の星形成史を知って、種族効果の補正 MλRC を得ることである。しかしこれは、深い 測光と CMD 全体の解析がないと無理である。距離決定には星形成史の不定性 が原因のエラーが必ず含まれる。

　赤色巨星の混入　

　もう一つの問題は混んだ領域では赤色巨星の混入が避けられないことである。 普通赤色巨星は光度関数で２次式で近似される背景として処理される。しかし、 これは不十分である。それは赤色巨星バンプがレッドクランプと同じ等級 区間で光度関数の折れ曲がりを引き起こすからである。すると、光度関数の フィットにもレッドクランプと赤色巨星の双方に対するモデル光度関数を 作って、χ2 フィットを行いたくなる。しかし、そのため にはまたもや完全な星形成史が必要となる。

　最終的には CMD フィットが良い　

　星形成史の情報がこうまでも必要であるなら、もう一歩踏み出して、レッド クランプ距離決定法は CMD フィット法で置き換えられないか問うても良いだ ろう。この方法は、すでに良く開発されており、Harris, Zaritsky 2001, Dolphin 2002, Rubele et al 2012 のソフトウェアが公開されている。 レッドクランプは CMD 上最も鋭い構造だから、こうして決まる距離は当然 レッドクランプの位置に大きく依存し、星形成史も自然に考量されることになる。 この方法は距離決定法として、一発で決める単純な方法の対極にある。しかし、 それは測光ζの全情報を利用することになるし、ボーナスとして距離以外に 銀河の星形成史や減光まで得られる。

　この方法もその基礎には近傍レッドクランプ星の等級較正が必要である。 そのため、ヒッパルコスの誤差の大きさは問題である。これが GAIA では 軽減されるだろう。

　５．２．ミクシング、質量放出、回転、連星　

　コアオーバーシューティング　

　対流層の広がりは未だに大きな問題である。主系列コアのオーバーシュー ティングは MHeF を小さくし、その結果、レッドクランプと 第２レッドクランプにある星の質量区分を変え、Mi と Mcore RC の関係も変わる。さらに、コアオーバーシューティングは 中心核ヘリウム燃焼期の長さを変化させる。

　混合過程　

　中心核ヘリウム燃焼期の長さを変化させるもう一つの要因は、その 最終期に起きる不確かな混合過程である。セミコンベクションと breathing pulses (Castellani et al 1971, 1985) は最終期、 12C(α, γ)16O 反応が中心部で活発に なる時期、に利用可能なヘリウム量を増加させる。この 12C(α, γ)16O の反応率も問題である。 しかし、もしコアオーバーシューティングが有効になるなら、 セミコンベクションと breathing pulses の効き目は二次的になる。 現在盛んに用いられている恒星モデルでは温和な対流オーバーシューティング が採用されている。（Girardi et al 2002, Pietrinferni et al 2004, Bressam et al 2012）それは、コア半径を古典的なシュワルツシルド境界の先 に　0.2 スケール高だけ伸ばすものである。その場合、中心核ヘリウム燃焼期 の長さは 20 % 以下の量だけ変化する。従って、τHe の不定性 を 20 % として良いだろう。 		　恒星音響学から混合過程を決める　

　このような混合過程を観測から制限する試みは二つある。一つは 星団内のレッドクランプ星の数を数え、光度を測定するという古典的な方法、 もう一つはフィールドレッドクランプ星の恒星音響学である。 驚くことに第２の方法の方が中心核ヘリウム燃焼星モデルを決めるには 有効なようである。Constantino et al 2015, Bossini et al 2015 は 幾つかの混合方式がアシンプトティック周期間隔 ΔΠ1 と EAGB バンプ光度に及ぼす影響を調べた。ケプラーのデータをそれと較べた 結果は、温和なオーバーシューティング領域が断熱的な温度層構造を成している モデルを支持した。

　赤色巨星期の質量放出　

　もう一つ、レッドクランプ進化に関してよく言われるのは赤色巨星期におけ る質量放出である。これはターンオフ年齢とレッドクランプ星質量との関係を 変える。その影響が大きいのは Z ≥ 0.5 Zo で（か？） Mi ≤ 0.9 Mo の星である (Girardi 1999). なぜなら、レイマーズ　1975 や Renzini, Fusi Pecci 1988 の古典的質量放出式が赤色巨星期に十分の数 Mo の質量を放出す るのは、これらに限るからである。それでもレッドクランプ星の絶対等級は かなり影響（図６）される。しかし、最近の Heyl et al 2015, Miglio et al 2012 の研究は RGB 放出がより低いことを示唆する。とはいえまだ状況は 完全解決ではない。

　回転、連星　

　さらに、回転、連星の問題がある。それにはマゼラン雲大星団の広がった ターンオフや二重レッドクランプの観測が重要であろう。しかし、これらは まだ未開である。

　６．結論　

　問題となる点　

　この記事は、初期の楽観的なレッドクランプが優れた距離指標であるという 意見から、混入星、種族効果、年齢・メタル量バイアスを考慮すべきという より悲観的な意見まで幅広い観点からレッドクランプの多くの問題を検討した。 問題となる点を列挙すると、

１．年齢・メタル量効果
　レッドクランプ星は年齢・メタル量が広い範囲に亘る。それが平均等級と 平均カラーに影響する。 ２．年齢分布バイアス
　レッドクランプ星の年齢分布は 4 Gyr 以下に重みがかかる。したがって、 銀河の化学進化、古い円盤種族の運動を探るには適していない。

３．
　レッドクランプ星モデルの寿命は 20 %, 光度は 0.2 等の誤差がある。 これは、星団の CMD フィットや近傍銀河の CMD フィットに際しては大きな 問題である。 		　最良の使用法は CMD フィット　

　したがって、レッドクランプ法の改善にはまだなさなければいけないことが 多数ある。我々は、レッドクランプ星の最良の利用法は CMD フィットを 通してであると考える。これは、レッドクランプ星を他の種類の星と同等に 扱うのであるが、混入や種族効果を自然に考量することになる。

　将来　

　１．ガイア　

　ガイアはレッドクランプ星の絶対等級を太陽近傍、星団で決め、レッドク ランプの詳細な構造を明らかにするのに大きく貢献する。しかし、それでも 銀河の種族効果とその星形成史への依存性は残る。

　２．ＬＳＳＴ　

２０２０年からは LSST がレッドクランプ星の測光と視差を大きく改善する だろう。 		　３．恒星音響学　

　レッドクランプ星研究に関する最大の進展が進行中である。それは、恒星 音響学観測である。 PLATO = PLAnetary Transits and Oscillations of stars (Rauer et al 2014), TESS = Transiting Exoplanet Survey Satellite (Ricker et al. 2014), K2 = Kepler 2nd phase (Stello et al 2015) は レッドクランプ星の質量、半径、距離、年齢を決めるデータを集積している。 ΔΠ1 が得られるのはその一部だが、他の恒星音響学 パラメター (Δν, νmax) だけからでも銀河考古学 を行うのに十分である。

　４．ＷＦＩＲＳＴ　

　WFIRST 2024 の近赤外撮像 (Spergel et al 2013)は銀河系全体での レッドクランプ星を検出し、バルジ、銀河面の地上観測で問題となる 測光完全性や混み合いの問題を克服する。