Old Stellar Galactic Disc in Near-Plane Regions according to 2MASS: Scales, Cut-Off, Flare, and Warp

　アブストラクト

　１．イントロダクション　

　２．ワープしない円盤のモデル　

　３．ＣＭＤを用いて円盤パラメタ―を決める　

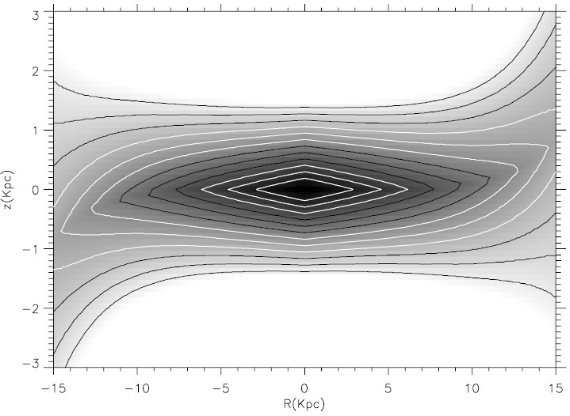
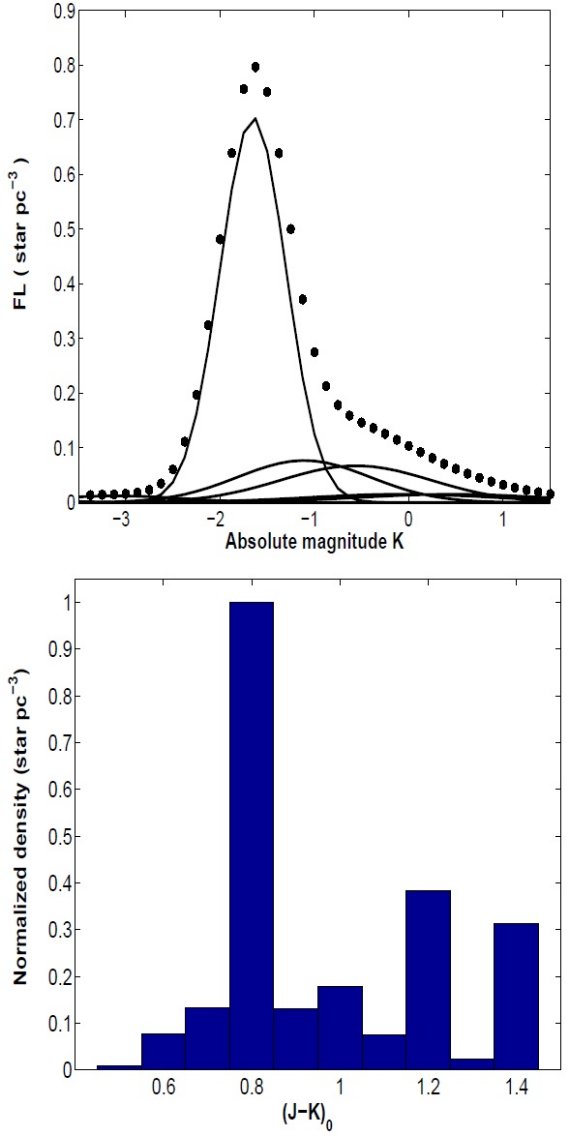
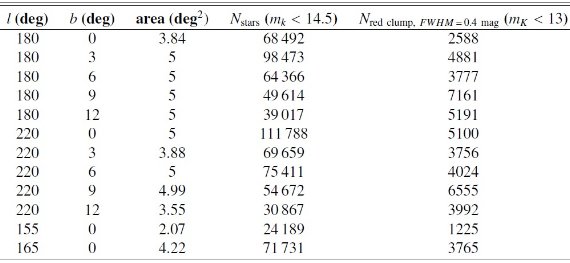
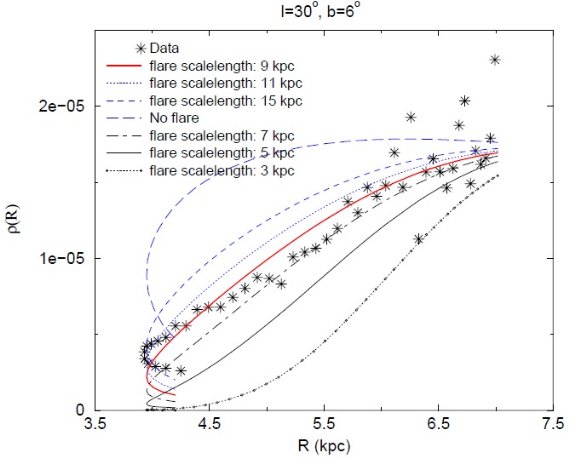
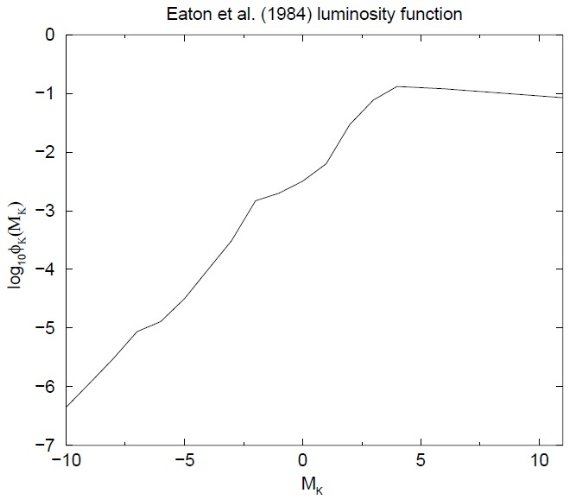
３．１．巨星の選択　 　CMD　 　図１に 2MASS (J-K,K) CMD を示す。K 区間ごとに J-K ヒストグラム を作り、ガウシャンフィットを行った。レッドクランプの左側にあるのは 矮星である。右側の K < 13 の明るい星は M-型巨星と AGB 星であろう。 MK = -1.65 を仮定する。軌跡を追えるのは K < 13 の 区間である。それより暗いと矮星が多くなりレッドクランプを分離 できない。 　レッドクランプ星の計数　 　図１にはレッドクランプのピークをつないだ線が描きこんである。 レッドクランプ星は、J-K でピークの 0.2 以内と決める。そしてそれらを 星計数する。 ３．２．星密度。円盤スケール長　　 星計数の基本式　 　A(m) = 立体角 ω 内で、１等級当たりの星の数。 　φ(M) = 光度関数。M で積分して 1 に規格化。？ 　D(d) = 星数密度、として計数基本式は、 　　　　　A(m) = ω ∫r2D(r)φ(M)dr この論文で用いる等級区間は K = [8.5, 13] を 0.1 mag 刻みにした。 レッドクランプの絶対等級、固有カラーは一定、MK = -1.65, (J0K)o = 0.75 と仮定する。 なので、光度関数はデルタ関数である。 減光は次の式で決まる。 　　　　　AK = [(J-K) - (J-K)o]/1.52 1.52 は Rieke, Lebofsky 1985 から採った。 　以上の式から視線方向に沿った、減光と、密度分布が決まる。

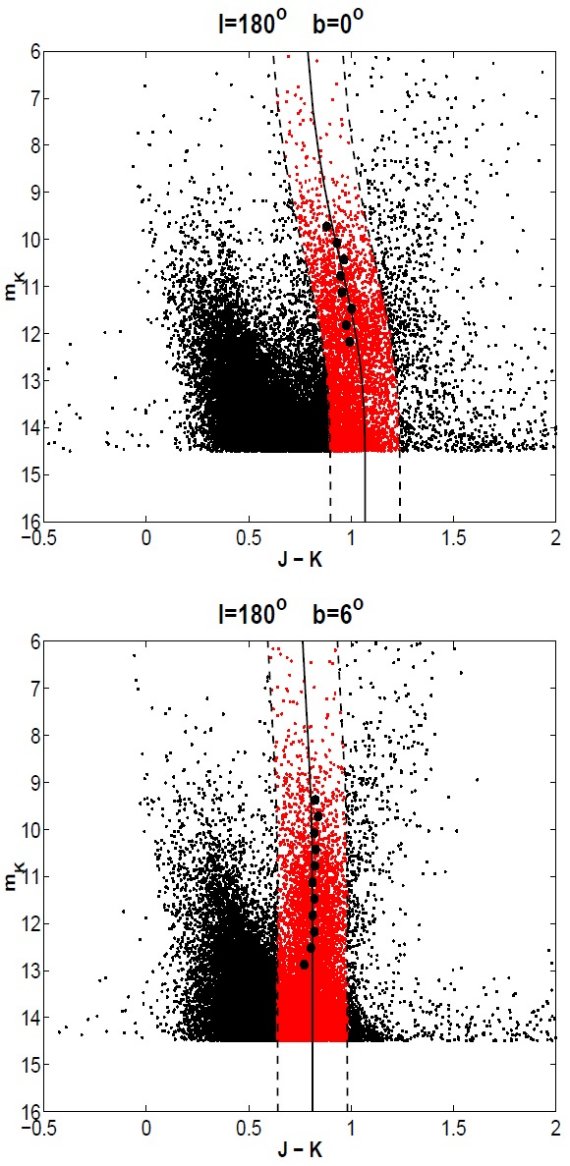
図１．二つの領域での CMD. 銀河面領域の強い減光は K-巨星の帯の巾を少し 広げる。尾根の極大はガウシャンフィットで決まる。実線はフィットの軌跡。 破線はレッドクランプ区間の境界。

　３．３．方法のテスト　

図２．mK = 11 における、反中心方向視線上での K 絶対等級と (J-K)o の分布、SKY モデルによる。変動は巨星タイプの違いによる。 プロットの極大がレッドクランプに対応する。 　３．３．１．レッドクランプ分布とディラックデルタ関数との差　 　レッドクランプの固有等級カラー分布を調べるために、図２には "SKY" モデルを使って求めた K 等級と (J-K)o の分布を示す。

図３．実際の密度 ρ = exp(-d/H) と方程式(12)と ディラックデルタ関数仮定した光度関数との折りたたみとの比較。 図４．赤破線： R=12.9 kpc でカットされた円盤密度分布。黒実線 星の半数は MK = -1.65 で半数は MK = [-1.4. +2] に分布しているとした時、それらをレッドクランプと看做して得た分布。 　３．３．２．カットオフはレッドクランプカラーの低光度巨星混入で隠されるか？　 　図３に見るように、クリアカットにはならないが、カットオフの存在は 確認される。 　３．３．３．矮星の混入　 　３．３．４．レッドクランプ星の赤化とメタル量効果のあいまいさ

　３．４．選択領域　

2MASS から表１にある 12 領域が選ばれた。領域は 2 - 5 deg2 の大きさで、十分な数が確保できている。その銀経は l = [150, 225]

表１．選択領域。

　５．結果　

図６．モデル（６）上でのレッドクランプ密度フィットの H と χ,sup>2 の関係 　フィットの手続きは以下の如く行った。 （１）b = 0 データを用いてスケール長 H を決める。 　　　K < 13, l = 155, 1165, 180, 220 データを用い。指数型円盤 をフィットした。データ点の数 N = 184 に対して H = 2.1 kpc で χ,sup>2 が最小値 143.2 を取った。図６を見よ。 （２）太陽近傍密度 その時のレッドクランプ星太陽近傍密度は ρo, red clump = 1.31 10-5 stars pc-5 である。 ( ヒッパルコスと較べどうか？ あれは完全でないか？)

図７．モデル（６）面上でのフィット。 図７に、この値を用いた円盤モデルを示す。３．２．節で述べた方法で 得たレッドクランプ星の密度も図に示した。視線方向毎に密度が少し 異なるのは、主に、減光のむらが原因である。全体としては、 フィット解はデータによく合っている。 （３）スケール高の決定 　　　l = 180, 220 での銀河面から離れた領域のデータを用い、先に決めた H と併用して、スケール高の入った密度分布とフィットすると、 スケール高 Hz(Ro) = 310 pc　 フレアスケール長 HR, flare が決まる。

図８．レッドクランプ星密度の銀河面高度による変化。モデルは H = 2.1 kpc, Hz(Ro) = 310 pc,　HR, flare = 3.4 kpc. R 大になると密度勾配が緩くなることに注意。 (12 領域でこんなに多数の R, z 組み合わせ のデータが取れるのだろうか？ ) 　フレアの証拠　 　図８と図９様々な銀河面高度での観測密度をモデルと較べた。どちらの 図からも、銀河中心距離と共にスケール高が増加することが判る。 これはフレアの明らかな証拠である。

図９． l = 220 b = 0, 3, 6, 9, 12 方向での密度変化。 モデルは前と同じ。 カットオフ？　 　もう一つ図７と図９から、密度は分布は R = 15 kpc まで指数関数型 を維持している。従って円盤のカットオフはあるとしてもその先である。

　３．６．内側銀河面にフレア？　

使用可能なデータは？　 　これまで調べた範囲は |l| > 90 で、得られたフレアスケール長も R > 10 kpc について得られた結果である。l = [45, 90] の範囲 では R = [8, 9] kpc の範囲についての情報しか得られない。 従って、|l| < 45 のデータが必要である。その上、|l| < 30 は 面内バー Hammersley et al. 1994, Lopez-Corredoira et al. 2001, の影響が大きいので除くべきである。現在、使用可能な 2MASS データは限られて いるので、 (l, b) = (30, 6) 領域を用いる。 内側銀河のスケール高　 　図１０はその方向での視線に沿った密度の変化である。 図には様々なモデルの予想も描きこまれた。これを見ると、 H = 2.1 kpc, hz(Ro) = 310 pc の 円盤を記述するにはフレアが人ようなことが判る。しかし、フレアの スケール長は 3.6 kpc という短さではあり得ず、　9 kpc 程度は必要である。 内側銀河のスケール高は確かに、太陽近傍より短いが、 　　　　　hz(5 kpc) = 0.73 hz(Ro) である。この結果は、 Kent et al. 1991 の hz(5 kpc) = 0.67 hz(Ro) とも合致する。

図１０．レッドクランプ密度分布。曲線は式（３）の H = 2.1 kpc, hz(Ro) = 310 pc で、異なるフレアスケール長 hR, flare に対応。図から内側銀河でフレアが必要と分かる。そのベスト スケール長は 9 kpc である。

　４．星計数を用いて円盤パラメタ―を得る：第２の方法　

図１１．K 光度関数。Eaton et al 1984 による。

　４．１．結果　

図１２．モデル（６）の面上での星計数フィット χ2

図１３．面上での星計数フィット。破線＝非ワープベストモデル(H=1.91 kpc). 実線＝ワープベストモデル（H = 1.97 kpc, εw = 5.25, φw = -5°, Aw = 2.1 10-19 pc)

　５．星ワープを求めて　

図１５．positive count / negative count 星. 実線＝ワープモデル。 破線＝傾いた円盤モデル

５．１．結果　 　 　 　 　５．２．傾いた円盤？

図１６ワープの模式図。リングは 1 kpc おき。ワープ最大の線も描いた。

５．３．レッドクランプでワープを確認する

図１７．正銀緯密度/負銀緯密度。(l, b) = (220, ±6) 実線＝ワープモデル。破線＝太陽高度の影響。

５．４．星ワープとガスワープ

図１８．実線＝星ワープの最大高度。破線、点線＝ガスワープ。 　５．５．ワープを含む円盤によるフィット

　６．フレアを決める二つの方法の比較　

　６．１．明るい星への円盤モデルの適用　

図１．

図１９．振幅 ρo の限界 K 等級による変化。Eaton et al 1984 LF を仮定し、我々のモデルで計算。

図２０．mK < 9.0 の星計数データとフィット。 破線＝ワープモデル。

６．２．高銀緯への応用

図２１．高銀緯での星計数。低銀緯をフィットしたデータが高銀緯も カバーしていることに注意。

　７．結論

図２２．銀河系ＸＺ面でのカット。

図２３．最終モデルの ρ = 0.005 star pc-3 等密度面。 縦方向縮尺５倍。