|
最近、レッドジャイアントクランプは局所群銀河の距離指標になるという
議論がある。この方法による距離決定の精度はヒッパルコスから決まる近傍
クランプの絶対等級と、遠方銀河中のクランプ星絶対等級との系統誤差
ΔMIRC による。
この論文では、モデルから得られる平均クランプ I 等級を年齢とメタル量
の関数として表す。種族合成モデルからの簡単な式により、任意の銀河に
対する平均クランプ I 等級を与えた。このモデルを用いて、銀河内クランプ
星の質量、年齢、メタル量分布を何が決めるかを説明した。このような考察は
これまで無視されてきた。我々は、最近または現在星形成が起こった銀河、例
えば渦状銀河円盤、ではクランプ星の年齢分布は 1 - 3 Gyr の若い星に強い
比重がかかり、したがって平均メタル量は高めになることが判った。楕円銀河
やバルジのような古い種族が支配的な系ではこの現象は起きない。 太陽近傍、バルジ、マゼラン雲、カリーナのクランプ種族の詳細なモデル化 を行った。星形成史、化学進化は文献から採った。ヒッパルコスモデルは メタル量、カラー、等級分布の点で分光データからの結果に合致した。 バルジ、マゼラン雲、カリーナモデルを用いて、それらの銀河に対する ΔMIRC を与えた。 |
Udalski の クランプ星 - RR Lyrae 関係がモデルから再現できることを示
した。しかし、モデルとデータの間の類似にも関わらず、Udalski, Popowski
が導いたような ΔMIRC - [Fe/H] 線形関係は
一般には成立しない。事実、クランプ星の分布は年齢 - メタル量関係や、
星形成史のように、線形関係では記述しきれない要素を含んでいる。 モデルの予測する振る舞いは Sarajedini, Twarog, et al. による散開星団 データからも支持される。 LMC, SMC 星団に対する Udalski データはクランプ 星等級のよい年齢依存性を与えない。我々は星団データの解析には 1 - 2 Gyr 年齢のクランプ星を含めるべきことを主張する。それらは最近星形成を 行った銀河の平均クランプ等級を決める際に重要だからである。 最後に、バルジ、マゼラン雲、カリーナの改訂クランプ距離を与えた。それら の信頼度も議論した。 ΔMIRC が最大になるのは マゼラン雲とカリーナで、それらは距離指数 0.2 - 0.3 等遠方になる。バルジ は逆に多分 0.1 等程度近くなる。 |
|
種族効果は無視できる? ΔMIRC = MIRC(Hipp) - MIRC(galaxy) = 種族効果 1998 年頃レッドクランプ I 等級の種族効果は無視された。その理由は、 種々の恒星系、例えばバルジ、M 31、LMC, SMC で IRC が V-I カラーに対して水平の広がりを示したからである。 種族効果は無視できない? レッドクランプ法をマゼラン雲に適用した最初の試み (Udalski et al. 1998) はマゼラン雲距離指数 = 18.1 - 18.2 という極端に小さな値を与えた。これ は種族効果を無視したための誤りではないかと強く疑われる。Cole 1998, Girardi et al 1998 は恒星進化モデルに基づいて、種族効果が無視できない ことを訴えた。 観測的な種族効果 Udalski 1998a,b はバルジ、LMC, SMC, カリーナのレッドクランプを RR Lyrae 星 V 等級のメタル依存性, MVRRLyr = (0.18±0.03)[Fe/H] + constant. 仮定で比較し、 MIRC = (0.09±0.03)[Fe/H] + constant. という非常に穏やかなメタル量、年齢依存性を導いた。 その上、LMC, SMC 星団のレッドクランプ等級を比較して、Udalski 1998b は MIRC の年齢による変化は t = 2 - 10 Gyr で無視できる とした。最近 Udalski 2000 は太陽近傍星の分光データを用い、関係式 MIRC = (0.13±0.07)[Fe/H] + constant. を導いた。これらは全体として、ΔMIRC の非常 に緩いメタル量依存性を示す。この場合 LMC に対して ΔMIRC < 0.1 mag で依然として LMC 短距離 説が支持される。 |
Udalski 解析の欠陥 Udalski 1998a, 1998b, 2000 の結果は Zaritsky 1999, Popowski 2000 に も使用された。しかし、彼の解析には欠陥がある。この論文は主にその点を 議論する。問題になる微妙な点は、 Udalski 1998a, 2000 では MIRC の年齢依存性が、また、Udalski 1998b では MIRC のメタル量依存性が無視されていることである。 このため、低メタルの星は明るい、若い星は明るい傾向があると、 観測データ中に存在する年齢 - メタル量関係が MIRC の年齢依存性とメタル量依存性を覆い隠して いる可能性がある。そして、正にこの傾向がモデルから予想されるものである。 星団選択にも問題 Udalski 1998b が選んだ星団は 2 - 10 Gyr であった。この年齢巾は レッドクランプ星の年齢巾全体は覆っていない。さらに彼が SMC 星団に与えた 距離補正は大き過ぎ、彼の年齢効果解析における系統誤差を生み出している。 注意しておくが、Udalski 1998b は高齢レッドクランプが 0.3 - 0.4 等暗い ことを見出しているのに、後の仕事では完全に無視され、等級一定と されている。同時期、Sarajedini 1999 と Twarog et al. 1999 は銀河系 散開星団の距離を主系列フィットで定め、 MIRC に大きな年齢、メタル量依存性を見出した。 線形表示は危険 もう一つ考慮すべきは、レッドクランプ星のように、年齢、メタル量の巾が 大きい天体ではその等級をメタル量、年齢の線形依存性を仮定するのは適当 とは思えないという点である。 |

|
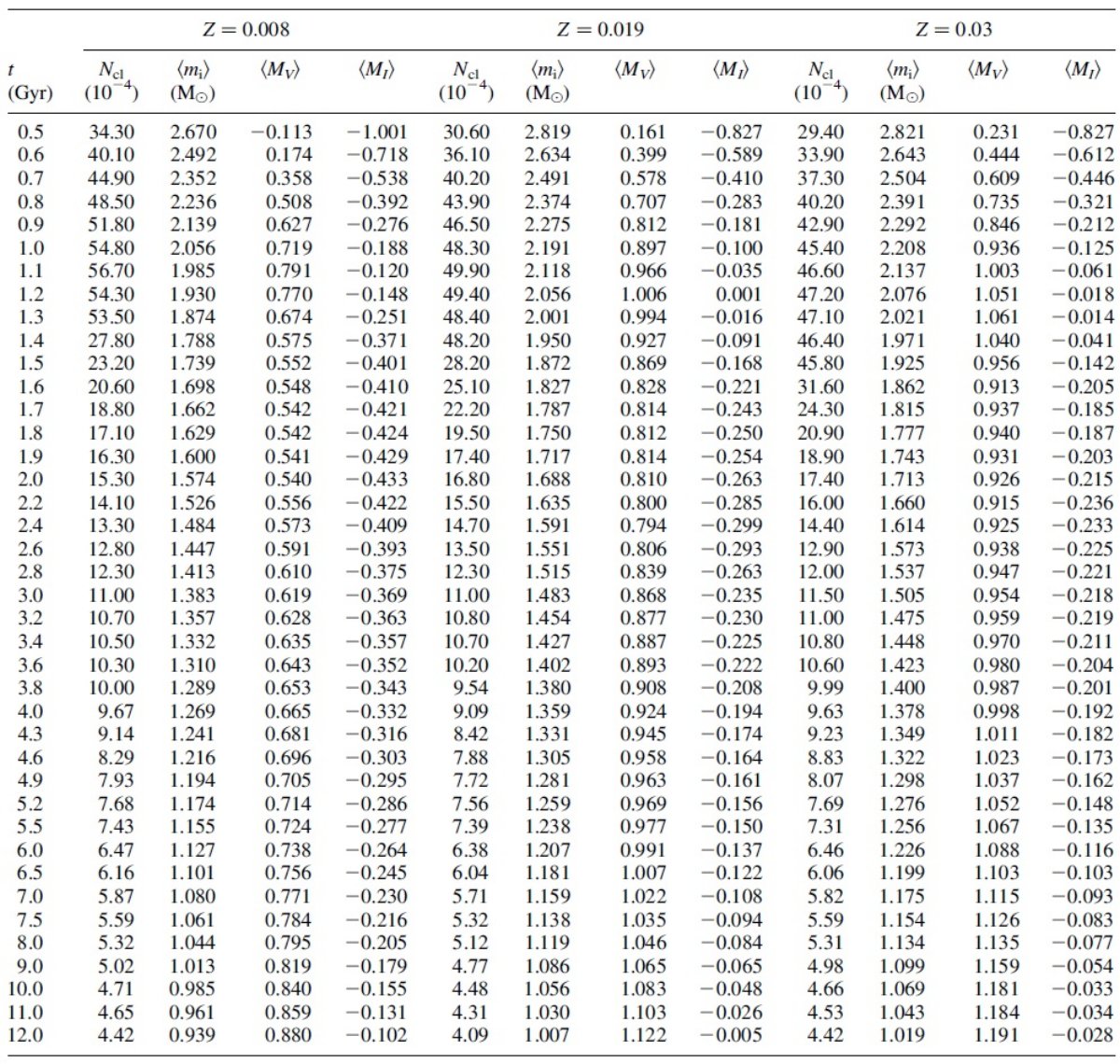
平均等級の計算 等時線上でのクランプ平均等級は、以下の積分を核ヘリウム燃焼期の星に対して 行うことにより得られる。
ここに、φ(mi)はサルピータ初期質量関数、初期質量 mi で ∫φ(mi)dmi = 1 Mo に規格 化されている。Ncl(t,Z) は初期に生まれた星 1Mo 当たりのクラ ンプ星の数である。
( φ(mi)が現存の 星に限られるのか、最初に生まれ既に寿命が尽きた星まで含むか、規格化の 問題であるが注意が必要。白色矮星の扱いも問題か?) 表1はこうして求めた平均クランプ等級を示した。内挿のためのより広範な情報が、 http://pleiadi.pd.astro.it から得られる。 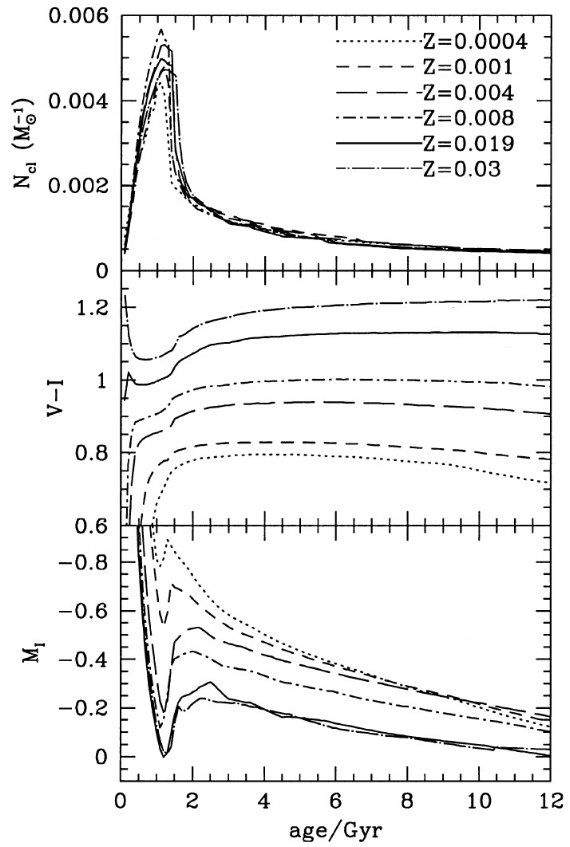 図1.等時線上のクランプ星数、カラー、平均等級の年齢とメタル量による 変化。 |
平均クランプ星初期質量 ⟨mi(t,Z)⟩ ⟨mi(t,Z)⟩ = クランプ星の平均初期質量は次の式で 与えられる。
図2=I バンド光度関数 図2は幾つかの等時線上における I バンド光度関数を示す。図から、 (i) 与えられた (t, Z) でのクランプ星等級の巾は狭いので、平均を等級で行 うか、光度で行うかは問題でない。 (ii) 等級の散らばり巾は低メタル、低年齢で大きい。高年齢、高メタルにな ると、光度関数は鋭い針状のピークを示す。明るい側に尾が伸びるので、平均 等級は常に光度関数極大等級より明るい。このズレは幾つかの (t,Z) 組に 対しては 0.1 等に達する。 銀河のクランプ平均等級 ここまでは、一本の等時線上のクランプ星の平均等級を考えてきた。銀河の 平均等級は星形成率を考慮して次の積分を実行する。
ここに Ncl(gal) は,
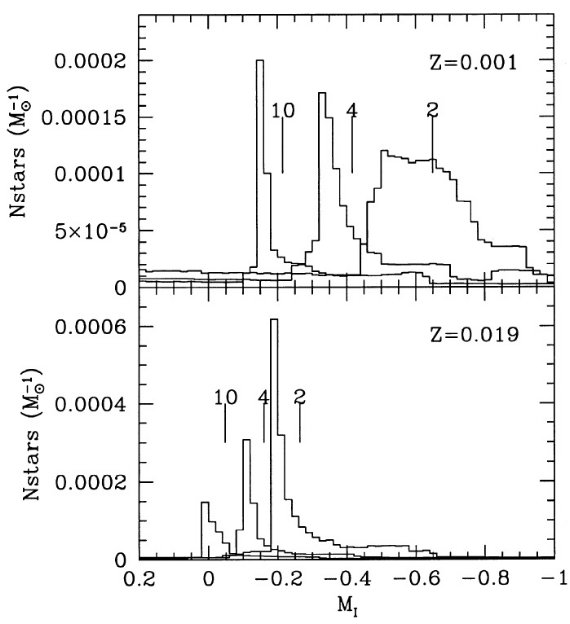 図2.クランプ領域の t = 2, 4, 10 Gyr における光度関数。上:Z = 0.001. 下: Z = 0.019. 縦線=平均レッドクランプ等級。 |
|
方法1と2 前章で述べた方法を "方法1" と呼ぼう。第2の方法では、まず与えられた 銀河モデルに対して合成 CMD を作る。次にその光度関数から、 MIRC を計算する。これを "方法2" と呼ぶ。 |
テスト結果 モデル銀河を使って検定テストを行い、両者を比較した。結果はどちらも 類似の結果を与えた。 |
|
ヒッパルコスサンプル ESA カタログには視差エラー 10 % 以下のレッドクランプ星が 1500 星載 っている。これは等級エラー 0.21 mag に相当する。ヒッパルコスサンプル は 125 pc まで完全で、それらに対し BA 測光がそれらの星に対しなされた。 I 等級は 1/3 に対して完了している。Lutz-Kelker バイアスはそれらの 平均等級に対しては 0.03 mag 以下の影響しかない。 クランプ星の誕生率 クランプ星の誕生率は次式で与えられる。 dNcl/dτH = ψ(t=τH) φ(mTO)|dmTO/dmTO| ここに mTO = ターンオフ質量、τH = 主系列寿命、 ψ(t=τH) = ターンオフ星が生まれた時点での星形成率。 クランプ星の寿命 τHe を掛けて、年齢分布が決まる。図4 には星形成率一定の銀河に対する年齢分布を示す。年齢分布は 1 Gyr に ピークを示し、その先ゆっくり低下して行く。星形成率一定というこの場合 では、クランプ星の半分以上は 2 Gyr より若い。この結果は一般に考えられ ている、クランプ星は中間種族と高齢種族の両方を同じくらいに示している という考えと鋭い対比をなす。 年齢分布について (i) 2 Gyr より高齢な星の数の漸減は、後主系列星の誕生率が低下するためで ある。M = 0.8 - 2 Mo では、主系列寿命は τH ∝ mTO-3.5 であり、一方核ヘリウム燃焼期間 τHe = 108 yr で一定である。これにサルピータ 初期質量関数 ∝ mTO-2.35 を合わせると、 t > 2 Gyr では、mTO-3.5 ∝ t-0.6 となる。 (ii) t = 1 Gyr (M = 2 Mo) 付近で、τHe は局所極大 2.5 ×108 yr に達する。これがピークを増幅する。 |
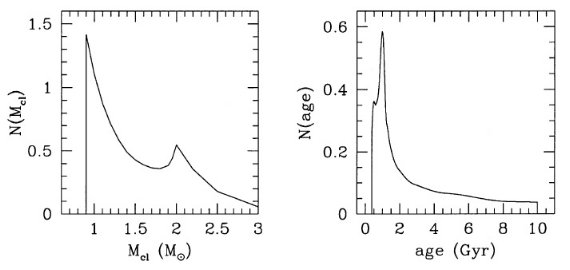 図4.星形成率一定の場合の、左:クランプ星の質量分布、右:クランプ星の 年齢分布。 (iii) それより若い方では、τHe の低下が、クランプ星形成 率の増加より僅かに急にである。このため、年齢分布の減少を招く。0.5 Gyr より若い核ヘリウム燃焼星の数は決して無視できるものではないのだが、それら はクランプ星よりずっと明るくなる。このため、クランプ星の年齢分布は 0.5 Gyr でカットされる。 一般的な星形成 Ncl ∝ φ(mi)τHe dNcl/dt である。星形成率一定の仮定はより一般的な連続星形成史 の特別な場合に過ぎない。 |
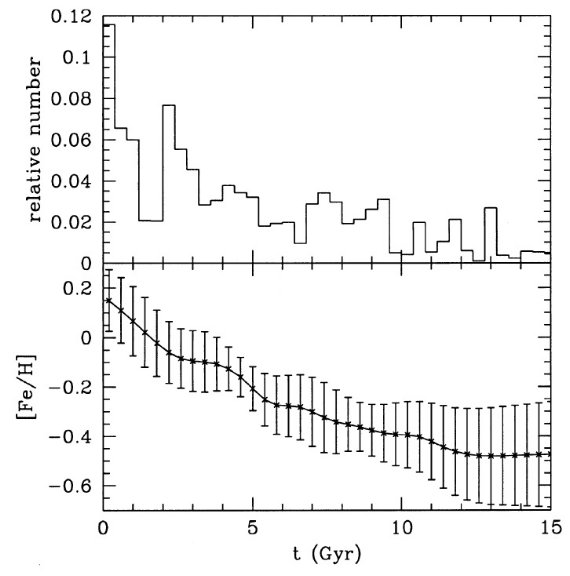 図5.太陽系近傍に適用した星形成率と年齢メタル量関係。 上:Rocha-Pinto et al 2000b が導いた体積限定の近傍矮星 の年齢分布。下:対応するメタル量分布とその標準偏差。 近傍の星形成 Carraro et al. 2000 によると、近傍の星形成は 9 Gyr 昔から最近まで連続 的であった。矮星の年齢は矮星年齢を彩層活動度から推定した。彼等は星形成 に幾つかのバーストがあることを認めた。また、図5から分かるように、若い 星の年齢分布が古い星より大きい。 シミュレイション 図6には図5の関係を使ってシミュレイションした結果の CMD である。 また、図7には同様に合成した光度関数を示す。このシミュレイションから 決めたクランプ平均光度は MIRC = -0.171 mag で観測値 -0.23±0.03 (Stanek et al 1998) に極めて近い。 |
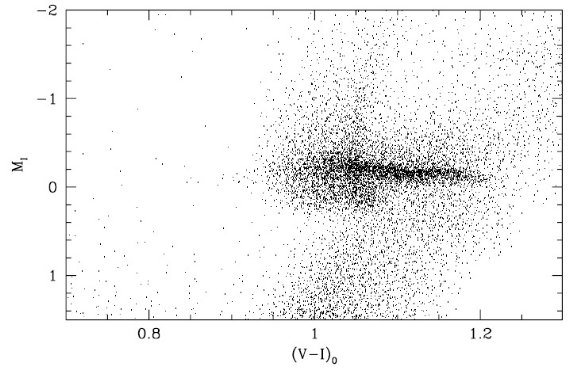 図6.図5データから導いた合成 CMD. クランプ星の総数 10,000 個を仮定した。 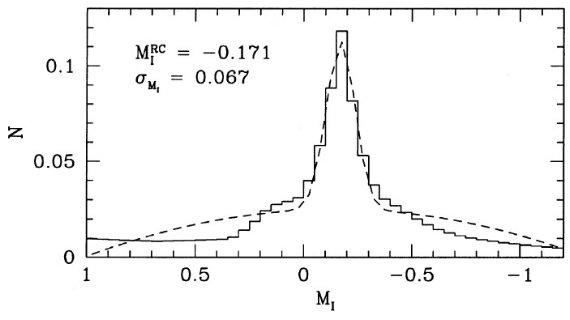 図7.図5のデータから合成した光度関数。破線=ガウス+2次式フィット。 |
|
DDO 測光からメタル量 近傍クランプ星のカラーの広がりは単にメタル量の広がりと解すべきでなく、 年齢の広がり (1 - 10 Gyr) も重要な役割を果たしている。Hog, Flynn 1998 は近傍 K 巨星(大部分はクランプ星)581 個のメタル量を DDO 測光から 求めた。彼らの結果は V-I カラーが [Fe/H] と相関しないことを示した。 図8=分光メタル量分布 我々は Cayrel et al 1997 カタログから, 分光的に決めた [Fe/H] を得た。選ばれた 334 星中 160 個がクランプ星であった。残りの大部分は 第1巨星枝星であった。その結果を図8に示す。この図でもやはり、 メタル量とカラーの相関はない。メタル量分布は平均 [Fe/H] = -0.12 dex, 散布度 0.18 dex ガウシャンで近似される。この小さな散布度は、 近傍クランプ星は比較的若く、最近数 Gyr に形成された円盤星のメタル量を 反映しているのである。 |
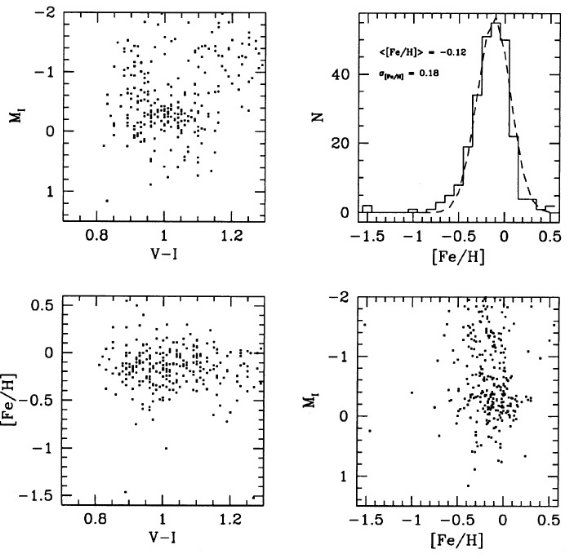 図8.ヒッパルコスカタログのクランプ星のメタル量分布。左上=CMD. 右上=メタル量分布。平均 -0.12 dex, 散布度 0.18 dex のガウス型で良く近 似される。左下=[Fe/H]-(V-I). 右下= MI-[Fe/H]。 |
|
モデルメタル量分布 我々のモデルからメタル量分布も導くことができ、図9に示す。モデルから 予期されるメタル量は [Fe/H] = [-0.7, 0.3] と広い。しかし、分布自体は 非常に狭い。平均メタル量 ⟨[Fe/H]⟩ = 0.03 dex, σ I = 0.17 dex. である。オフセット 0.15 dex はあるが、この 結果は観測結果とよく似ている。 モデル年齢分布の影響 [Fe/H] 分布の巾の狭さは図9の年齢分布を見ると納得できる。クランプ星の 平均年齢は 2.5 Gyr であるが、年齢分布のピークは 1 Gyr である。これらの 年齢までに円盤メタル量は既に [Fe/H] = 0.0 になっているので、クランプ星 の大部分は同じようなメタル量を示すのである。オフセット 0.15 dex の原因 は明らかでない。 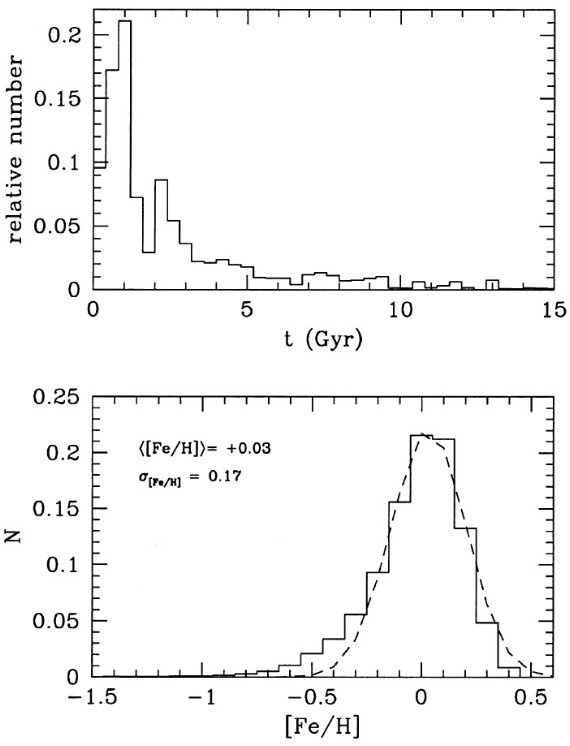 図9.我々のヒッパルコスモデルの、上:年齢分布、下:メタル量分布。 それらの平均年齢= 2.5 Gyr. [Fe/H] 分布は平均 0.03 dex, 散布度 0.17 dex ガウシャンで良く近似される。 |
図10=モデル計算の[Fe/H]-(V-I)、
MI-[Fe/H] 関係 図10には我々のヒッパルコスモデルから計算した [Fe/H]-(V-I) 関係と MI-[Fe/H] 関係を示す。オフセット -0.15 dex を除くと、図8 とよく似ている。 Udalski 2000 の誤り Udalski 2000 は [Fe/H] 別に分けたクランプ星に対して フィットを行い MIRC を求めた。彼は次に その結果を用いて、 MIRC のメタル量依存性を求めた。 しかし、その結果は実は太陽近傍でのメタル・年齢関係に依存しているので 一般性は主張できない。 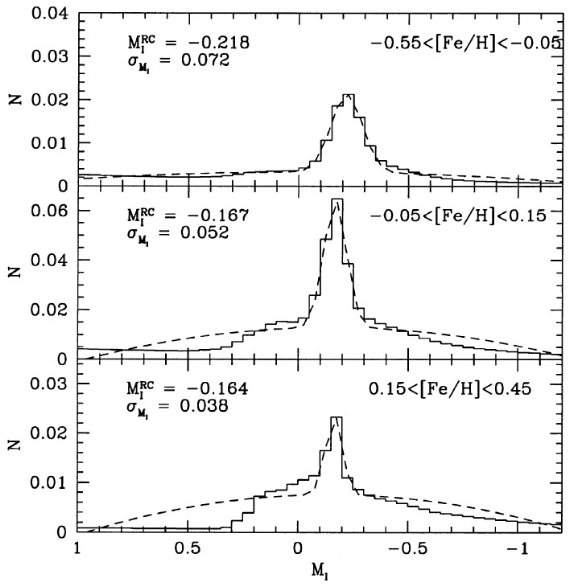 図11.我々のヒッパルコスモデル(図6)の光度関数をメタル量区分 毎に示す。 |
|
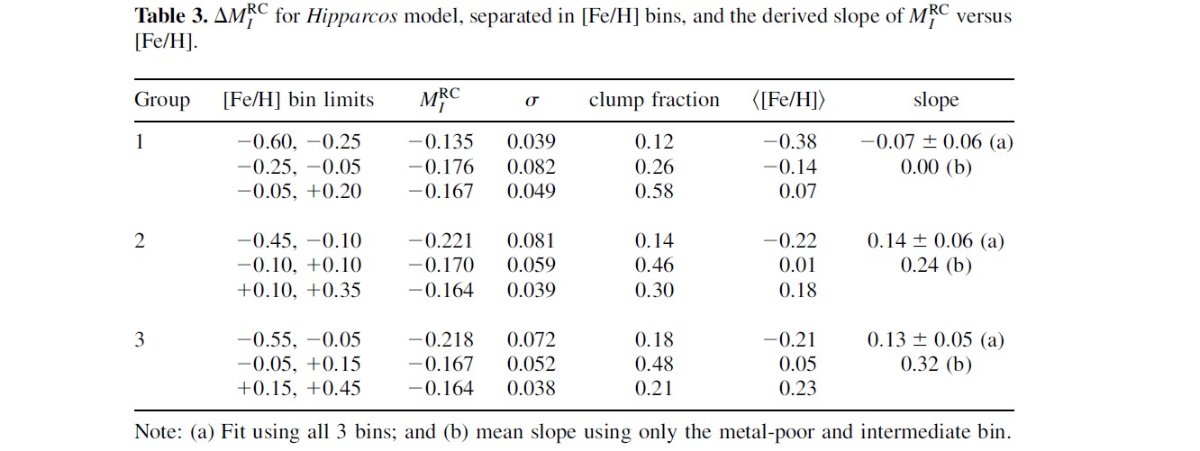
同時期に生まれた星から成る 前章ではモデル計算がヒッパルコス観測を再現することを見た。 モデル信頼性に関するもう一つのテストは星団クランプを用いて行われる。 星団は同時期に生まれた星から成るので、ΔMIRC の観測値をモデル予測と比較できる。 サンプル星団 Sarajedini 1999 は 8 星団の年齢、[Fe/H], ΔMIRC を与えた。また Twarog et al. 1999 は NGC 2506 の同様なデータを与えた。 これら星団の年齢は 1.9 - 9.5 Gyr に及び、メタル量は [Fe/H] = [-0.39, 0.15] である。 ピーク値再計算 Stanek, Garnavich 1998 による MIRC(Hipp) = -0.23±0.03 を用いた。ただし、Sarajedini 1999 は平均値でなく、 分布ピークを用いているので、我々は 2.1.節に述べたようにモデルピーク値を 再計算して較べた。 Udalski 1998b とは異なる 図12には ΔMIRC を観測とモデルとで較べた。 観測が ΔMIRC のはっきりした年齢、メタル量 依存性を示していることが明らかである。また、モデルが観測を再現している ことも明らか。注意しておくが、Udalski 1998b は LMC, SMC データから t = [2, 10] Gyr で MIRC が年齢、メタルに依存しないと している。ただ、LMC, SMC 星団の年齢、メタル量の精度は銀河星団にくらべ 誤差が大きい。さらに SMC では距離効果が ±0.2 mag に達することも 忘れてはいけない。Udalski 1998b は彼のサンプル中最高齢星団では平均値より 0.3 - 0.4 mag 暗いと述べている。これは我々の得た緩い光度低下の表われ であろう。 この後の重要な観測 最近星形成を行った銀河では、クランプ星の大部分が 1 - 2 Gyr の星で占め られる。ところが、 Udalski 1998b でも Sarajedini 1999 でも 2 Gyr より若い 星団が欠けている。したがって、将来の観測的研究においては若い星団のデータ 取得が極めて重要である。 |
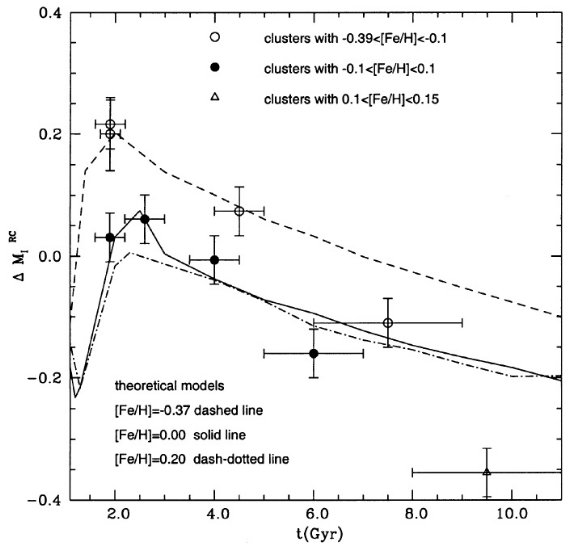 図12.ΔMIRC の観測とモデルとの比較。 |
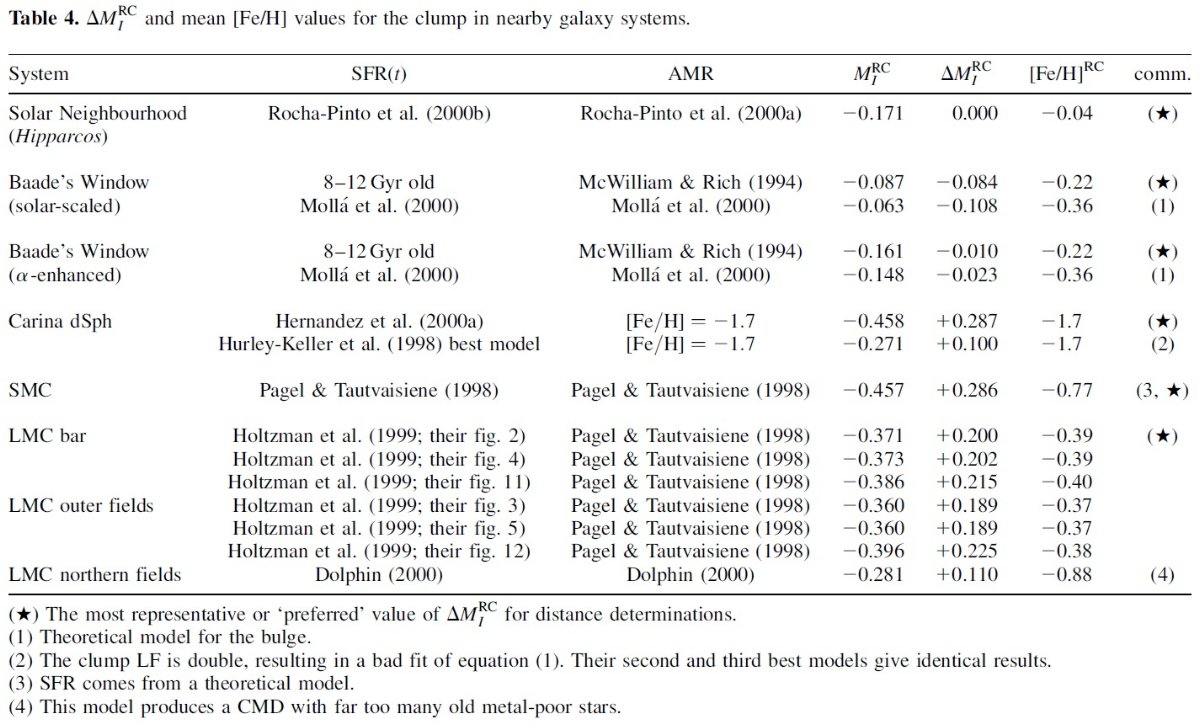
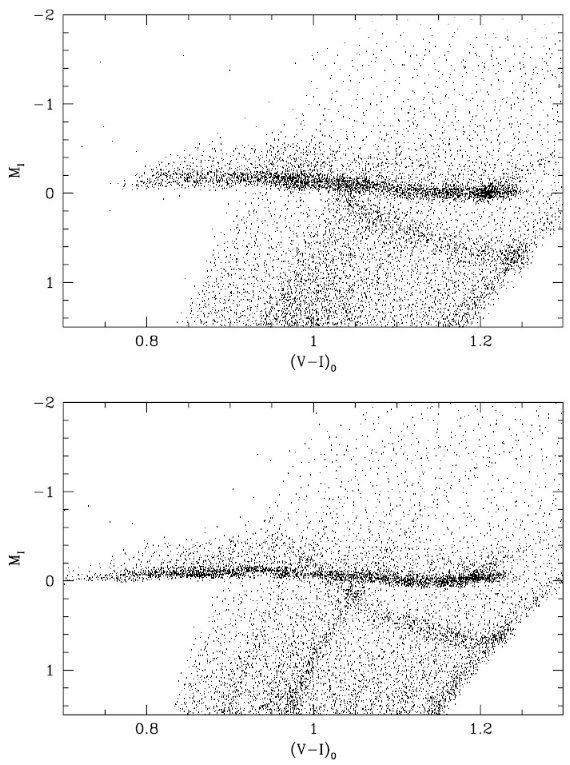 図13.図6と同様の合成 CMD, ただしここはバルジ用。上: t = [8, 12] Gyr で一定星形成。メタル分布はいつも McWilliam, Rich 1994 の [Fe/H] 分布を仮定。下:Molla et al. 2000 のバルジモデルによる星形成史 と年齢 - メタル量関係を仮定。 バルジ星は 5 Gyr より古いと仮定する。高齢レッドクランプ星の等級は 0.025 mag/Gyr という非常に緩く暗くなる。Ncl(t) はほぼ 平坦である。つまり、クランプ星の年齢分布は図1から分かるように、 単に星形成率に比例するだけとなる。このため、実際の星形成史がどうで あったかは MIRC の結果にあまり影響しない。 これは若い星種族が欠けているからである。 |
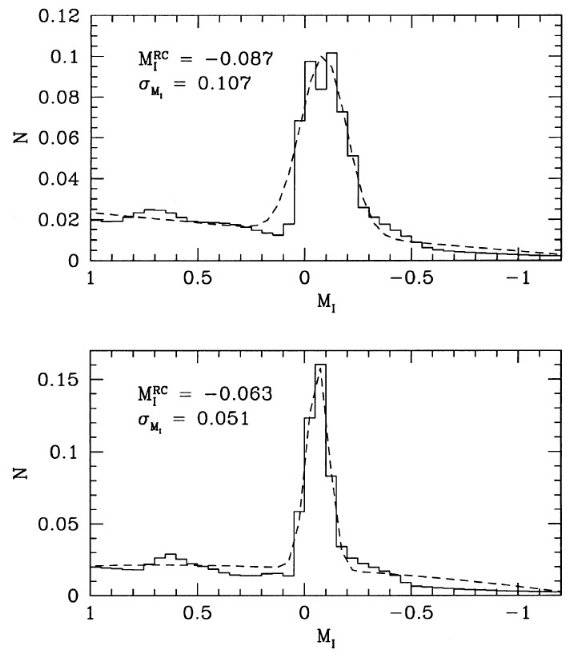 図14.図7と同じモデル光度関数だが、図13のバルジモデルを使用。 二つのモデル 図13には二つのモデルを示す。第2モデルは現在に至るまで減少しつつ 星形成を仮定している。どちらもクランプの分布は水平で、Paczynski, Stanek 1998 が示した観測と一致する。両モデルの MIRC は等しく、どちらもヒッパルコス等級より約 0.1 等大きい。 低光度は高年齢のため 表4にあるようにバルジの平均メタル量は太陽近傍値に近い。従って、 我々のバルジモデルの平均等級が暗いのは平均年齢が高いことが原因と考えられる。 |
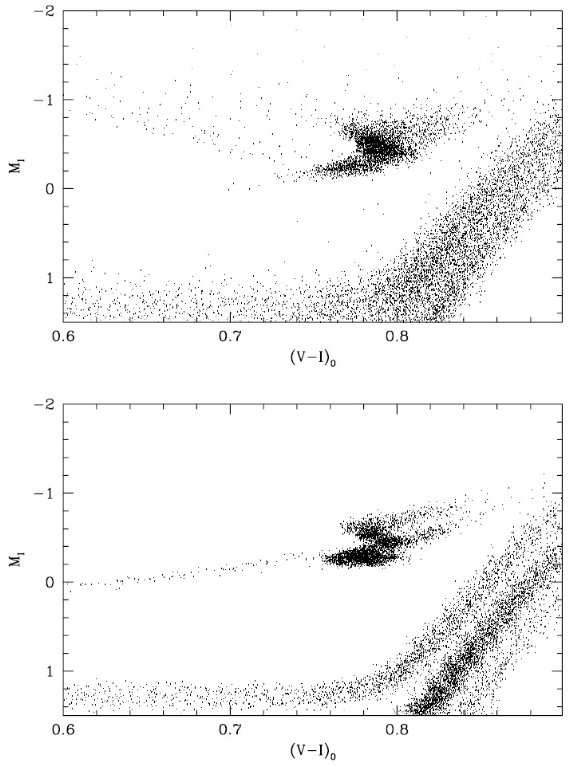 図15.図6と同じだが、カリーナに対するモデル。上: Hernandez et al 2000a の星形成史と年齢 - メタル量関係を仮定した。下:Hurley Keller et al. 1998 を使用。 |
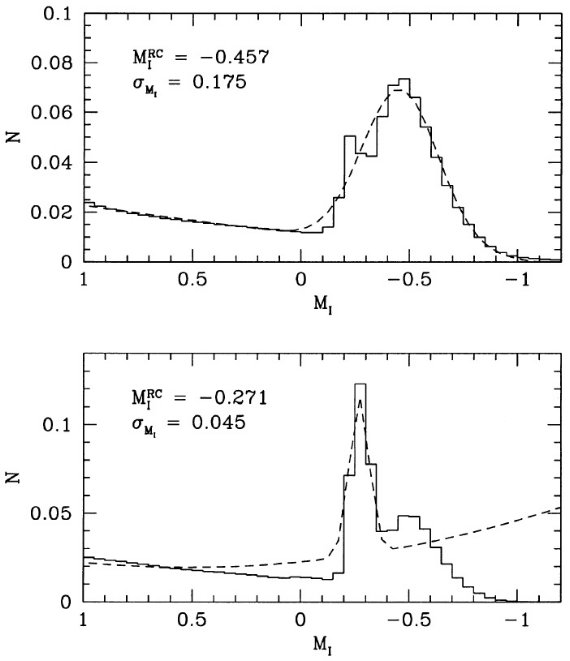 図16.図7と同じだが、カリーナモデルに対する光度関数。 低メタルサンプル カリーナ銀河は [Fe/H] = -1.9 という低メタル量から非常に面白いサンプル を提供する。その上、15, 7, 3 Gyr 昔に星形成爆発を起こした証拠がある。 星形成爆発の相対強度比によっては図に示すようにクランプ星の光度関数が ダブルピーク型となる。これは観測と合わない。Hernandez et al 2000a の モデルはデータと合う。 |
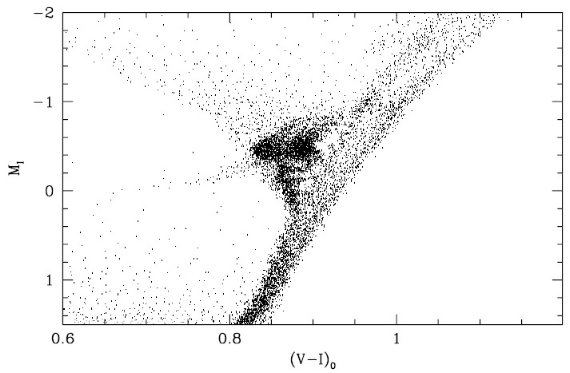 図17.図6と同じだが、小マゼラン雲用。Pagel, Tautvaisiene 1998 の 星形成史と年齢 - メタル量関係を使用。 |
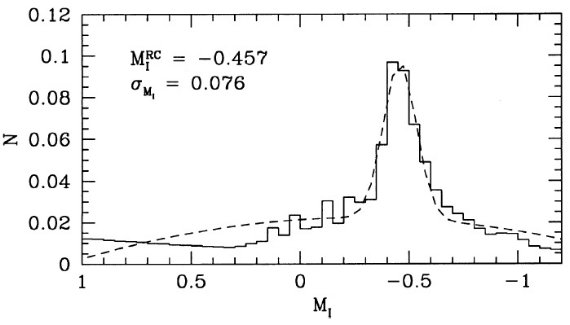 図18.図7と同じだが、図17のモデルを使用。 |
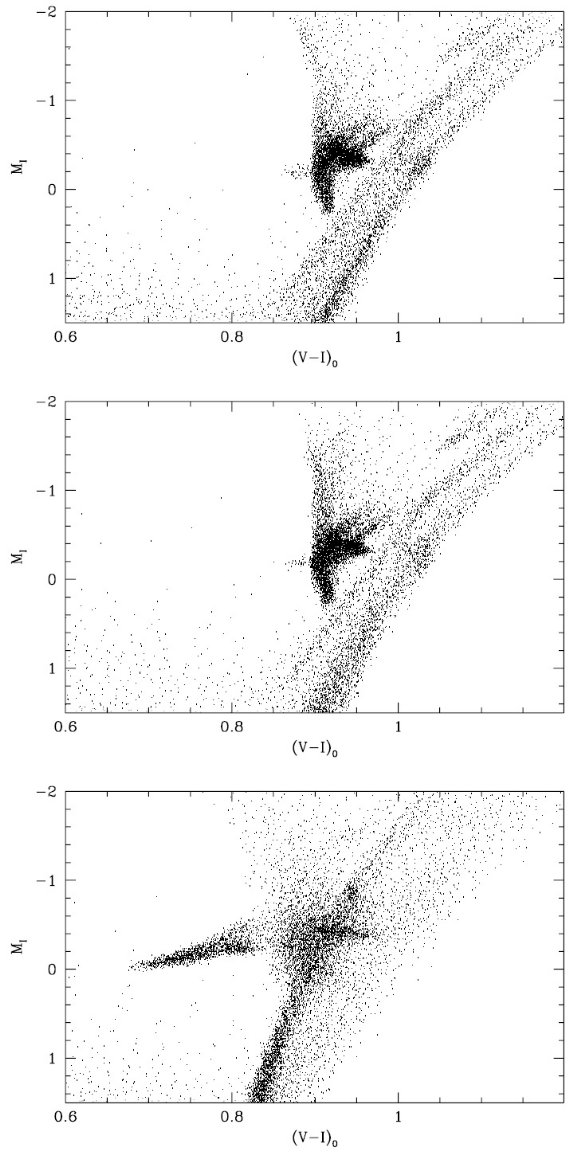 図19.図6と同じだが、大マゼラン雲用。 上:Holtzman et al. 1999 のバー領域星形成史と年齢 - メタル量関係を使用。 中:Holtzman et al. 1999 の周辺領域星形成史と年齢 - メタル量関係を使用。 下:Dolphin 2000 の周辺領域星形成史と年齢 - メタル量関係を使用。 |
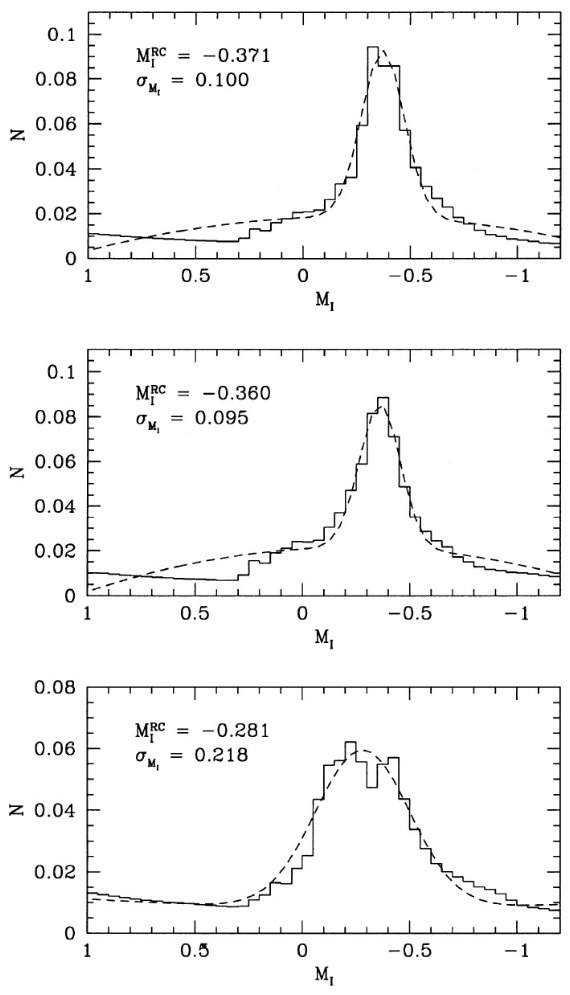 図20.図7と同じ。LMCモデル使用。 |
|
[α/Fe] ハローのような種族では α 元素 = O, Ne, Mg, Si, Ca, Ti が Fe に対して超過することが知られている。バルジでも [Mg/Fe], [Ti/Fe] = +0.4 が知られており、バルジの星形成が短期間に起きた証拠とされている。 バーデの窓 そこで、バーデの窓に対して [α/Fe] = 0 と 0.35 でフィットを試みた。 その結果、クランプ星が 0.08 mag 明るくなることが判った。 |
マゼラン雲、カリーナ マゼラン雲ではクランプ星の大部分は 3 Gyr より若く、そのような星では α 超過は強くないだろう。カリーナの状況は不明である。この銀河の クランプ星は若すぎもしないし、短期間で生まれたわけでもない。 十分な分光観測が必要である。 |
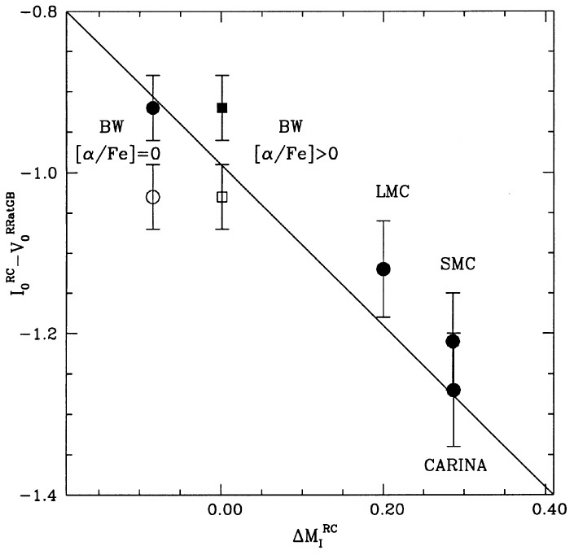 図21.観測 I0RC - V0RRatGB と ΔMIRC との関係。黒丸=表4データ。 I0RC - V0RRatGB は Udalski 1998a だが、バーデ窓だけは Popowski 1998a から。実線は勾配 -1 の直線。 白印=バーデ窓データだが、 OGLE I と OGLE II のゼロ点の差を補正した。 四角は α 金属元素の超過を考慮したモデル。 |
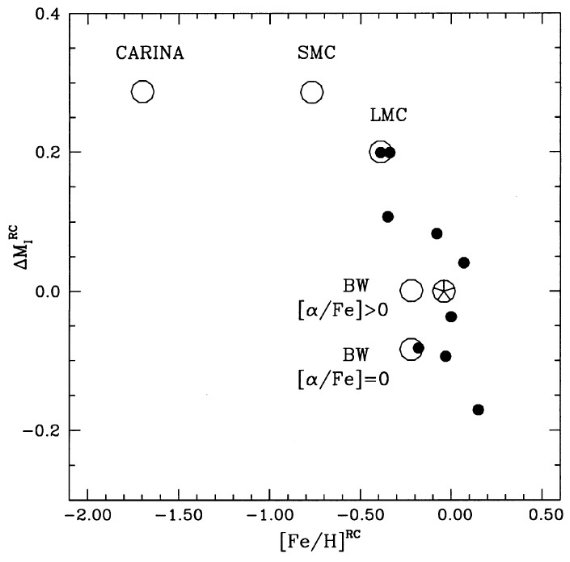 図22.ΔMIRC と レッドクランプ平均 [Fe/H] の関係。 大きな白丸=表4の天体。黒丸=図12の散開星団。星丸=ヒッパルコス。 バーデ窓はアルファ元素超過のありとなしのモデルを示した。 |
|
我々はモデル計算から多数の観測的特徴の再現に成功した。それらを順次述べると、 ヒッパルコス (a) MI - (V-I) 図 (b) [Fe/H] 分布を幅の狭いガウシャンでフィットできた。 (c) [Fe/H] と (V-I) の相関不在。 (d) 観測的に弱い MI - [Fe/H] 勾配の検出。 バーデの窓 MI - (V-I) 図上での幅広でほぼ水平なクランプ。 LMC 印象的な垂直構造=暗い第2クランプ+明るい尾がクランプ部の青い側に存在。 水平枝星の青いプリューム。 SMC とカリーナ 小さくまとまったクランプ 2 Gyr より高齢の銀河系散開星団 年齢とメタル量によるクランプ光度変化。 |
[Fe/H] 異存性 バルジ、マゼラン雲、カリーナに対し、観測的な MIRC - [Fe/H] 関係。 MIRC と年齢、メタル量の関係 モデルが予測する MIRC と年齢、メタル量の関係は 複雑で、MIRC - [Fe/H]、 MIRC - log t 関係を線形表示するのは無理がある。今回の研究で次の点が明らかになった。 (i) MIRC はメタル量、年齢の双方に依存する。 (ii) 与えられたメタル量に対し、MIRC - 年齢関係は 複雑で単調な変化を示さない。 (iii) 与えられた年齢に対し、MIRC は メタル量に伴って 増加する。しかし線形関係ではない。 (iv) 銀河においては、異なる年齢種族のレッドクランプへの寄与度がことなり、 数 Gyr より若い種族が存在すると、レッドクランプではそれらが支配的となる。 |
|
|
|
