Galactocentric DDistance with the OGLE and Hipparcos Red Clump Stars


Paczynski,B., Stanek
1998 ApJ 494, L219 - L222



　アブストラクト

　ヒッパルコス星

　ヒッパルコスから選んだ精度 10 % 以下で減光補正したレッドクランプ星を減光 補正したバーデの窓レッドクランプ星と比較した。それぞれには、約 600 と 10,000 個のそういう星が含まれる。カラー範囲 0.8 < (V-I)o < 1.4 ではレッドク ランプ星の平均 I 等級がカラーに依らないことが判った。光度関数をガウシアンで フィットして得たピークは、MIo,m = -0.28, 分散 σRC = 0.2 mag である。

　バルジ星　

　これから決めた銀河系中心距離は Ro = 8.4 ±0.4 kpc である。BW のレッド クランプ星の数が多いので統計誤差は 1 % である。近傍星は割りと青く、分散も 小さい、⟨(V-I)⟩ = 1.01, σ(V-I) = 0.08、であるが、 バルジ星では、⟨(V-I)o⟩ = 1.22, σ(V-I) = 0.14 である。バルジ星のメタルは近傍星より高く分布巾も大きいらしい。

　1.イントロ　

　ヒッパルコスと OGLE のレッドクランプ星観測結果の比較　

　銀河系中心距離は Ro = 8.0 ±0.5 kpc Reid 1993 である。ヒッパルコス カタログ Perryman et al 1997 はこの値を改良するだろう。この論文の目的は ヒッパルコスと OGLE のレッドクランプ星観測結果を比較して銀河系中心距離を 導くことである。

レッドクランプによるマップ　

　銀河系中心距離を星に基づいて求める方法には次の４つの困難がある：

１．精度が近傍星絶対等級に依存する。

２．星間減光を銀河系中心、太陽近傍で決める必要がある。

３．銀河系中心、太陽近傍間で星の質量、化学組成、年齢が違うかも知れない。

４．天体数が少ないと統計誤差が大きい。

レッドクランプ星には上の第４問題がない。しかし、これまで銀河系構造の問題には あまり使われてこなかった。しかし、最近 Stanek 1995, Stanek et al 1994, 1997 は レッドクランプをバーのマップ作成に使い、Wozniak, Stanek 1996, Stanek 1996 は ＢＷの減光マップに使用した。


　２．方法と予備的な結果　　



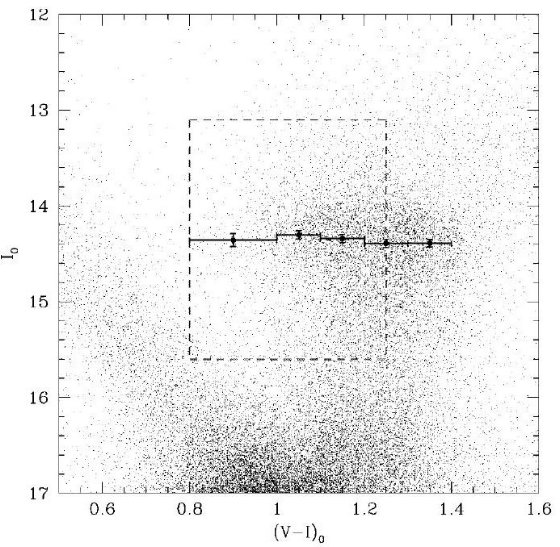
図１．バーデの窓で Av < 1.5 の低減光領域にある星の色等級図。破線四角は 近傍星との比較に用いた領域。カラーで５区間に分けてレッドクランプ最高密度 等級 Io,max が　0.8 < (V-I)o < 1.4 で示されている。Io,max がカラー に依らないことが明白に判る。

バーデ窓のレッドクランプ　

　Stanek 1996 の減光マップを使い、ゼロ点として Gould, Popowski, Terndrup 1997 と Alcock et al 1997 を利用して、バーデ窓の Av < 1.5 領域を選んだ。図１は その色等級図である。カラー５区間毎に下の式をフィットした。



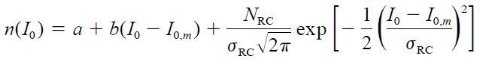
図１に 3 σ エラーバー付きでピーク値を示した。カラー依存性は認められない。

ヒッパルコスのレッドクランプ星　

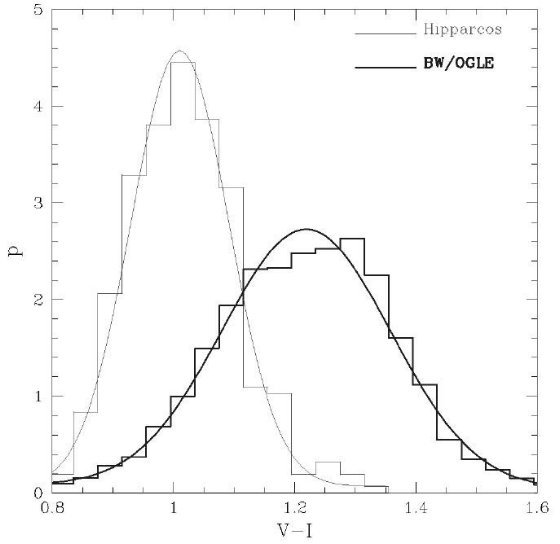
　ヒッパルコス視差精度が 10 % 以下の星を図２にプロットした。カタログのカズンズ (V-I) カラーは色々な文献から取られている。この研究では (V-I) のソースに A, C, E, F, G つまり、 I 測光が行われた星のみを使用した。 そのような星は 664 個あった。色区分を二つにして同様の処理をしたが、やはりカラー の影響は見られない。 		>


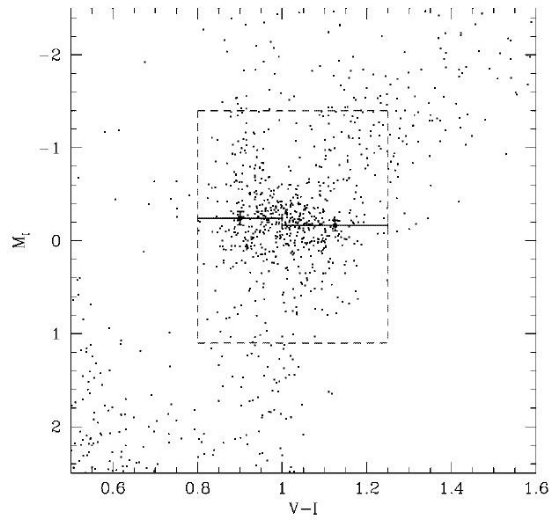
図２．視差精度が 10 % 以下のヒッパルコス星の色等級図。破線がレッドクランプ 領域。 0.8 < (V-I) < 1.25 カラー区間を２分して MI,max が 示されている。平均カラー ⟨(V-I)⟩ ≈ 1.0 で、バーデ窓の ⟨(V-I)o⟩ ≈ 1.2 がバルジの高メタル性を示していることに 注意。ヒッパルコスカラーは少数以下二桁しか与えられていないので、図に 人工的な筋が現れるのを防ぐためカラーの第三桁目に出鱈目な数字を入れた。

　銀河系中心距離

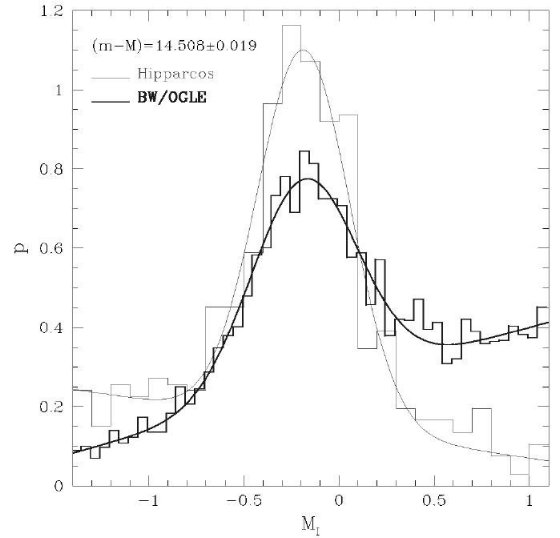
　このように、太陽近傍でもバルジでも、レッドクランプ星にカラー依存性が見られ ないことから、二つの比較から銀河系中心までの距離を求めても安全と考えられる。 第１近似として、ヒッパルコス星の減光は無視する。バーデ窓では 0.8 < (V-I)o < 1.25 の 7174 星、ヒッパルコスカタログでは 0.8 < (V-I) < 1.25 の 664 星 をカラー区間毎にフィットした

　銀河系中心までの距離　

　。その結果、バーデ窓で Io,max = 14.323 ±0.009、ヒッパルコスで MI, max = -0.185 ±0.016 を得た。距離指標は (m - M)BW = (Io,max - MI, max) = 14.508 ±0.019, dBW = 7.97 kpc となる。

　図３にはＩ−光度関数を示した。ガウスフィットの巾はＢＷで σ = 0.28 mag, ヒッパルコスで σ = 0.24 mag である。


図３．細線：太陽近傍レッドクランプ星の MI 光度関数。
　　　太線：バルジレッドクランプ星。 		　図４はカラー分布を示す。ＢＷ星が赤いことは明らかである。


図４．レッドクランプ星のカラー分布。どちらも規格化されている。サンプルは -0.485 < MI < 0.115 である。バルジ星は赤く、高メタルと 考えられる。


　４．エラーの補正　

　系統誤差　

　銀河系中心距離についた統計エラーは非常に小さい。これはレッドクランプ星の 数が多かったからである。しかし、系統誤差がある。

　視差のエラー　

　10 % エラーでよかったかを確認するため、5 % サンプルで再計算した。 星数は 240 にへり、MI, max = -0.173 ±0.027 となった。これは MI, max = -0.185 ±0.016 の範囲内である。

　距離バイアス　

　視差エラーでサンプルを限定すると、固有光度が明るい星は遠くまで精度よく 測れるので距離バイアスがかかる。この結果、図３に見えるようにヒッパルコス サンプルには明るい星の割合が高い。その結果、背景の赤色巨星光度関数の勾配 b が 変化する。b の変化はガウシアンピーク位置を移動させる。二つのサンプル間の差を 補正するため、ヒッパルコス星の各等級ビンの中の星数に以下の数字を掛けた。
f ∼ aBW + bBWMI
aH + bHMI

　この補正をヒッパルコスヒストグラムに施してから、改めてフィットするとＢＷと 同じ赤色巨星背景と共に新しいガウシアンピーク、MI,max = -0.125 ±0.019 を得た。これは 0.06 等の変化である。

サンプルを距離リミッテッドにすれば？

　星間減光　

　星間減光の効果を評価するため、ヒッパルコスサンプルの中から d < 70 pc の 228 星を選んだ。このサンプルに対し、先の距離バイアスの補正も施してピーク 値を求めると、MI,max = -0.192 ±0.023, σRC = 0.208 となった。このサブサンプルの平均距離は ⟨d<70⟩ = 50 pc であった。残りの 437 星 d > 70 pc に対しては MI,max = -0.094 ±0.027, σRC = 0.234, ⟨d>70 ⟩ = 106 pc となった。遠い星のサンプルは 0.098 mag 暗かった。平均距離の 差は 56 pc であった。この関係を d = 0 まで外挿すると、近距離サンプルより 0.088 mag 明るくなるので、MIo,max = -0.192-0.088 = -0.279 を得る。 ただ、注意しておくが、ここに使用した減光は AI ≈ 1.75 mag/kpc で通常使われる値（Mendez, van Altena 1998）よりかなり高い。

ＢＷ距離と銀河系中心との距離差　

　ＢＷ距離は銀河系中心と以下の２点で差がある。

（１）バーが傾いているので (l, b) = (1°, -4°) 方向の最高密度点の 距離は銀河系中心より幾分近い。

（２）一定の立体角内では遠方ほど大きい体積を占める。したがって、観測星 の分布は遠方の星に重みがかかる。

我々は Stanek 1997 の E2 バーモデルを適用して上の二つの効果を計算した。 その結果、銀河系中心は 0.02 mag 遠くなることがわかった。BW 平均等級を 求める際の系統誤差の最大の原因は減光のゼロ点エラーで Gould et al 1997, Alcock et al 1997 によると ±0.05 mag ある。

系統誤差を考慮した銀河系中心距離　

そうすると、 (m - M)GC = 14.323 - (-0.279) + 0.02 = 14.62 ±0.05 となる。 Ro = 8.4 ±0.4 kpc である。

　種族の差　

　年齢、組成、質量はまた別のタイプの系統誤差を生む。実際、カラーは明らかに 系統的に異なっている。進化モデルによると、2 - 12 Gyr では有効温度は主にメタル量 に支配されている。するとバルジ種族は太陽付近より高メタルであることになるが、 それはそれで、McWlliams, Rich 1994 の得たバルジと太陽近傍の巨星ではメタル量が 同じくらいという結論に反する。また、高メタルの上限も両方で似たくらいにスーパー メタルリッチである。Castro et al 1996

分光された星の測光値はないのか？　あれば、分光メタル量 とカラーの関係が調べられる。



何がカラーとメタル量の違いを生むのか？　

　現在のところ、何がバルジと近傍星のカラーの差を生むのか不明である。単に分光 サンプルの数が少ないための見かけの差かも知れない。それとも、分光で見る メタル量が吸収線に基づくのに対し、測光メタル量は主に対流層の連続吸収を 見るという差が効いているのかも知れない。


　４．議論　　

カラーに依らない I 等級　

　我々はカズンズの I 等級が (V-I) カラーに依存しないことを観測から 導いた。年齢とメタル量の広い範囲に対して I 等級を計算することが非常に 重要である。バルジと太陽近傍とでは種族が異なり、理論モデルから MI,max - (V-I) 関係を導くことは重要である。 		　レッドクランプ法　

　レッドクランプ法は優れているがヒッパルコス星の I 等級は 30 % 程度で しか求まっていない。１００万個の　Tycho カタログ星の I 測光は極めて 有益である。