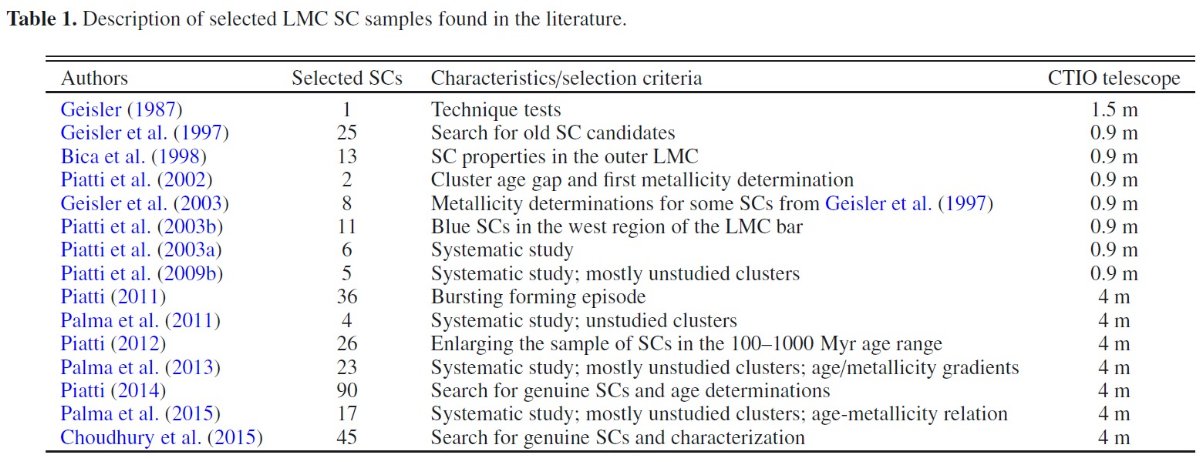
| ワシントンシステムで観測された 277 LMC 星団の基本的性質をカタログ化した。 82 個は最近我々が研究した。星団パラメタ―:投影補正距離、赤化、年齢、 メタル量は基本的に同じ方法で決めた。それを簡単に述べる。我々は観測累積 関数を用いて、年齢、メタル量、投影補正距離の分布を副サンプル毎に求めた。 | 我々の新しい 82 星団はワシントンシステムで測光された LMC 星団の数を 40 % 増加させた。その内 42 個は基本性質が初めて求まった。単独星団は複合 星団よりも一般に高齢であることが判った。そして、どちらも log(年齢) の 分布関数の形が非対称である。我々は年齢をパドヴァ等時線を用いたフィッティ ングで決めた年齢と較べた。 |
|
ワシントンシステム ワシントンシステムは当初 G-, K-型星の研究 Canterna (1976) のために考案された。Geisler et al 1991 の較正を経て、銀河系の若い星団 から古い星団 Claria et al 2007, Piatti et al 2009a にまで、また LMC/SMC の星団 Geisler et al 2003 に使われるようになった。このシステムは星団の 距離、赤化、年齢、メタル量という様々なパラメタ―を決められる素晴らしい 道具であることが判った。その良さは Geisler et al 1991, Geisler et al (1997), Geisler, Sarajedini (1999) で示された。特に C, T1 フィルター、または C, Rc フィルターはメタル量決定 に有効である。このフィルターを用いて Palmer et al (2015) は LMC の t = 2 - 3 Gyr における化学進化を明らかにした。 |
195 既知星団 + 82 新サンプル これまでに 195 LMC 星団の基本パラメタ―がワシントンシステムで決定され た。表1には、それらの出典をまとめた。我々は Palmer et al 2013, Palmer et al (2015) においてそれまで未研究の 40 星団のパラメタ―を決定した。この論文では その後決まった 42 星団も加えて新たに 82 星団のパラメタ―を報告する。 こうして約 40 % 増加したサンプルは全て同じ処理方法でパラメタ―が決定さ れている。サンプルの等質性は統計処理に有利である。 |

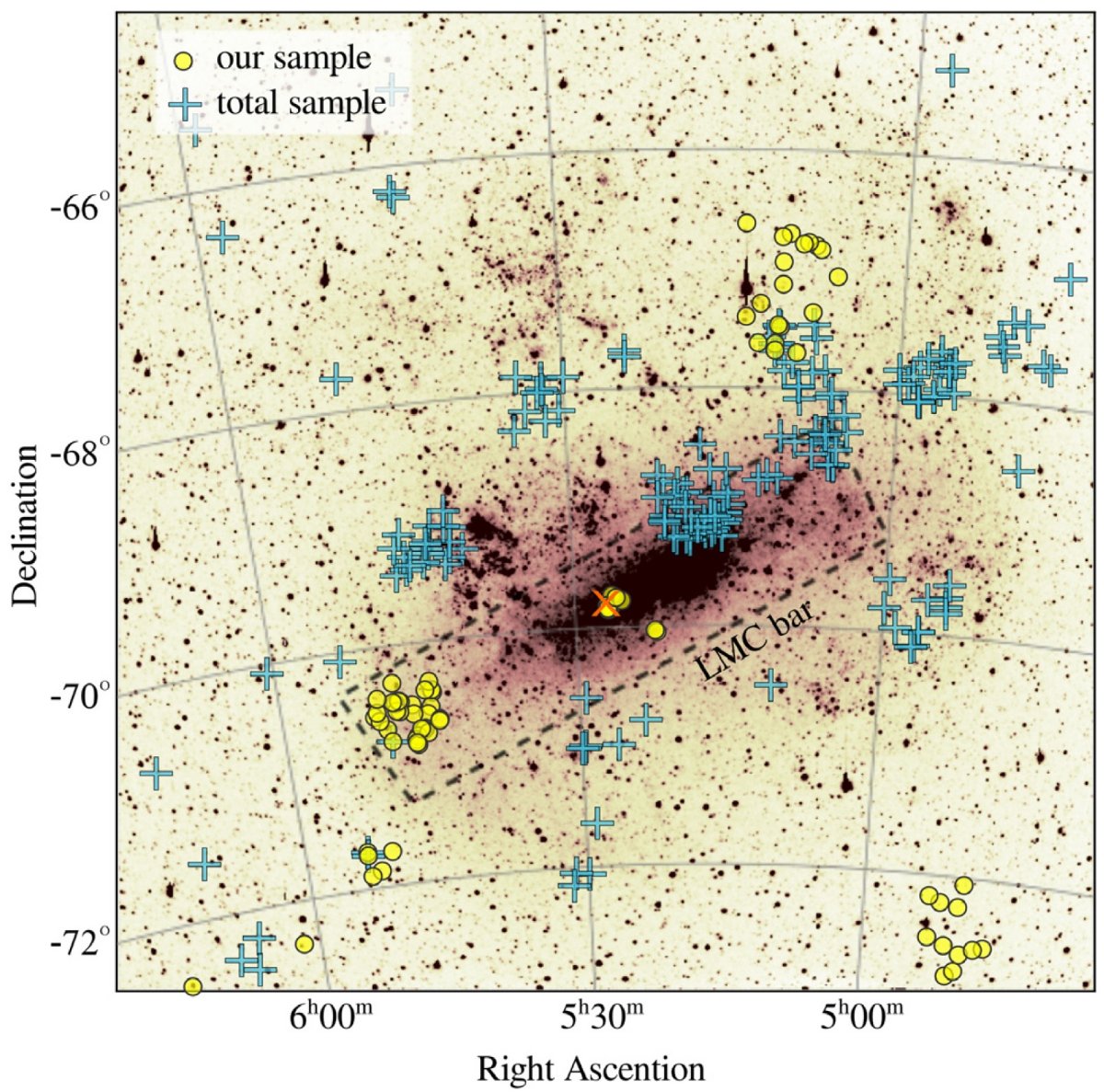
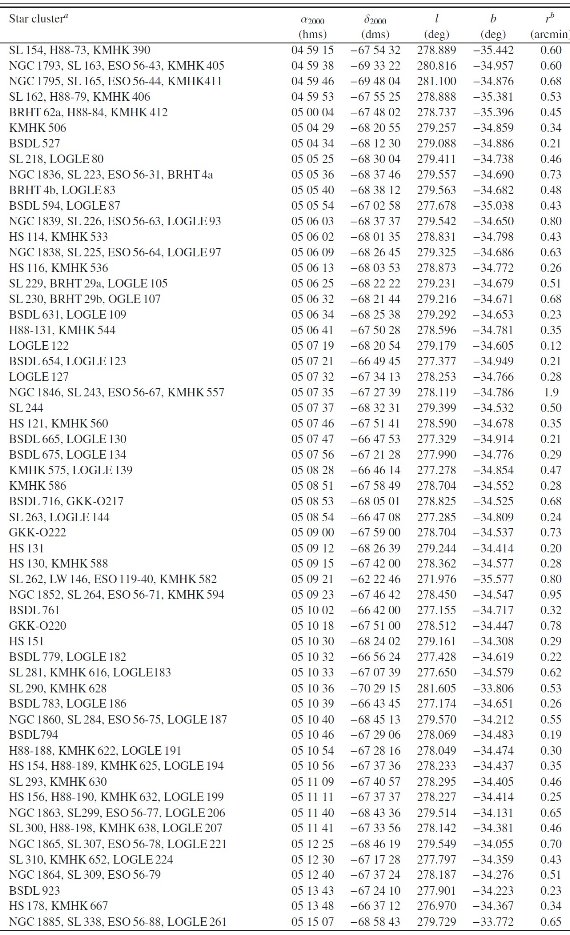
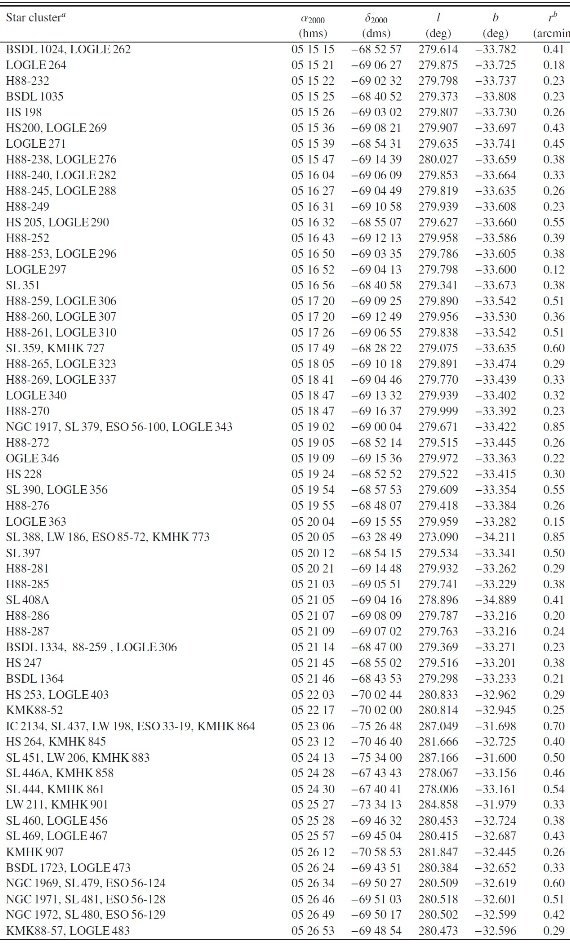
| 観測は全てセロトロロ CTIO で C, T1, Rc フィルターにより行われた。今回の 82 サンプルはビクターブランコ 4 m 望遠鏡により 2000 に行われた。 | 全サンプルのリストは表A1に与えた。図1はサンプルの分布を示す。 |
|
半径 星位置にガウス分布をフィットして、その中心で決める。誤差要因の最大は 星団星とフィールド星の数比が小さいことである。中心が決まったら、その周 りの密度分布を測定し、背景密度まで落ちた所で半径とする。具体例は Palma et al 2013 に示す。星団が淡過ぎる時は、Bica et al 2008 の値を 使用した。 投影効果補正距離 d = 投影効果補正距離 d(p) = 投影角距離 p = 星団位置の方位角。北向きから時計回りに。 P' = ノード線の方位角 = 145°±4° i = LMC 円盤面と天球面との傾き = 35.8°±2.4° とすると、次の式が成り立つ。 d = d(p){1 + [sin(p-p')2][tan(i)2]}1/2 NGC 1928 (J2000, α=5h20m47s, δ = -69°28'41") を LMC の 光学中心と仮定する。p' と i の値は Olsen, Salyk 2002 から採った。 赤化と距離 星団赤化は Burstein, Heiles (1982) マップを内挿して求めた。表A1の第4列から分かるように、E(B-V) は 0.00 - 0.23 の間である。 Schlegel et al. (1998) を使わなかった理由は LMC や他の明るい系外天体の周辺では 100 μm 放射からの赤化が怪しい Piatti, Claria, Parisi, Ahumada (2011) からである。 LMC 距離指数には Saha et al 2010 による (m-M)o = 18.50±0.10 を採用する。Subramanian, Subramanian 2009 によると、円盤の厚みは 3.44 ±0.16 kpc である。星団間の距離指数の差は Δ(V-Mv) = 0.3 mag まであり得る。等時線を星団 CMD に合わせる時に不定性は 0.2 - 0.3 mag なので、全星団に単一の距離指数を適用するためにエラーに大きく貢献するわけ でもない。 |
年齢とメタル 星団の年齢とメタル量は二つの独立の方法で決める。いずれにせよ、最初の 仕事はフィールド星の混入の除去である。今回の 82 星団の CMD は Piatti, Bica (2012) の方法を採用して統計的にフィールド星混入の掃除を施した。 等時線法 次に、掃除済み CMD を採用した E(B-V) と (m-M)o でずらした CMD を得る。それから、年齢とメタル量を変えて、それに最も合う等時線を 探す。このために、ワシントンシステムで表示した等時線を パドヴァグループの Girardi et al 2002 とジュネーブグループの Lejeune, Schaerer 2001 は Z = 0.019, 0.008, 0.004 ([Fe/H] = 0.0, -0.4, -0.7) 等時線を、Bressan et al. 2012 は [Fe/H] = [-0.84, -0.19] 間でほぼ 連続な等時線群を与える。我々のサンプル中、 Palma, Claria, Geisler, Piatti, Ahumada (2013) が調べた 23/82 星団は初め Girardi et al 2002 の等時線でフィットしたが、 今回の解析では Bressan et al. 2012 の等時線を使用した。こっちの方が、 Z の間隔が細かいからである。一般にはパドヴァとジュネーブのどちらを使っ ても殆ど同じ結果になる。図5にパドヴァ等時線の違う組合わせを使用した 場合の差が示されている。 δT1 法 星団年齢を決める第2の方法は δT1 = レッドクランプとターンオフの 等級差、を使う。 Geisler et al. (1997) に δT1 と年齢の較正が与えられている。ただし、この方法は 1 Gyr 以上の中年、高年星団に限られる。そんな星団でも、混み合いや星数不足で レッドクランプがはっきり定義できない場合が多く、そんな時にはこの方法が 適用できない。 SGB = 標準巨星枝法でメタル量決定 Geisler, Sarajedini (1999) は t > 2 Gyr の星団でこの CT1 法は、Da Costa, Armandroff 1990 の VI 法よりも3倍メタル量感度が高いと主張した。 |
5.1.観測的累積分布関数観測的累積分布関数のよいところは、只の分布関数と違い区分の巾に依らない ことである。 表2.比較に使用したサンプル 5.2.統計的な結果5.2.1.メタル量分布分布の差は有意か?図2上は S1 と S2 サンプルのメタル量ヒストグラムを示す。S2の巾の方 が狭いが、ピーク位置は S2 で [Fe/H] = -0.39, S1 で [Fe/H] = -0.42 と 近い。実際 t-テストの結果も両サンプルの平均値の差がゼロであることは 95 % の確立で有意であった。 図2下=メタル量の累積分布関数 図2下は Girardi et al.2002 等時線フィットと Bressan et al.2012 等時線フィットによる累積分布関数を較べた。 Girardi et al.2002 等時線はメタル量 [Fe/H] = -0.7, -0.4, 0.0 と 間隔が粗いので、分布ピークに当たる [Fe/H] = -0.4 で累積分布関数に大きな ジャンプが起きる。一方、Bressan et al.2012 はメタル量間隔が細かいので、 累積分布関数がより滑らかである。そのメタル量中間値は [Fe/H] = -0.36 で ある。 |
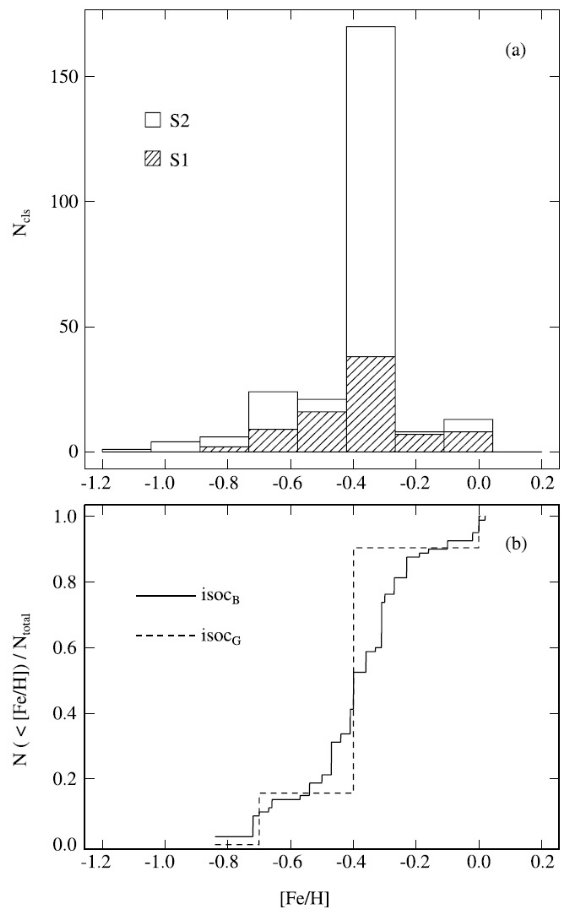 図2.上:LMC 星団のメタル量ヒストグラム。白棒=S2サンプル。斜棒=S1サン プル。下:S1サンプルメタル量の累積分布関数。破線= Girardi et al.2002 等時線フィット。実線= Bressan et al.2012 等時線フィット。 |
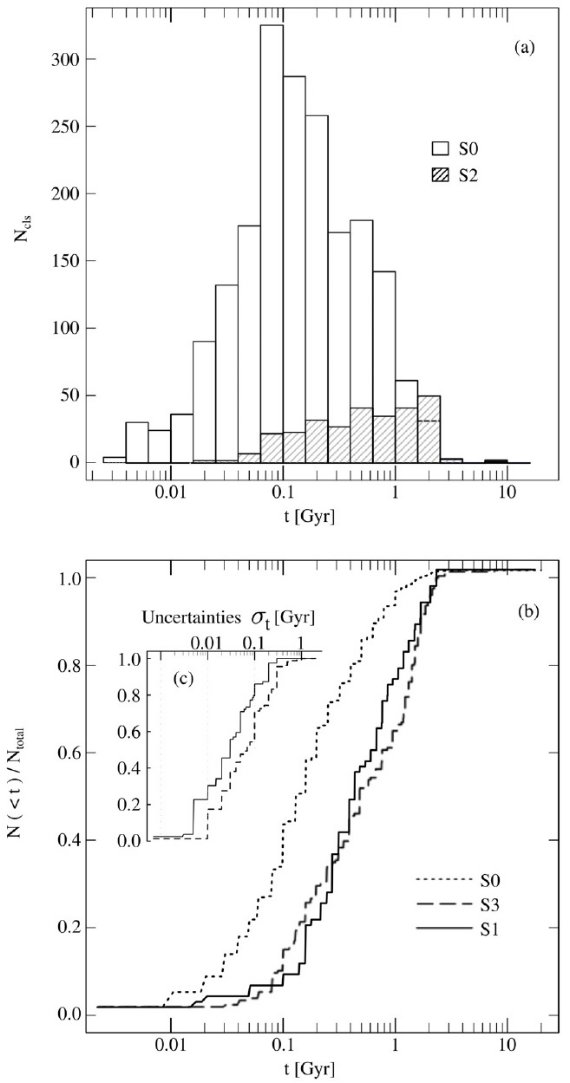
5.2.2.年齢分布図3は年齢分布を示す。図3上を見ると、 S0 と S2 とではピーク年齢 が異なる。S0 サンプルは主に 1 Gyr より若い星団から得られているので、 理解できる。図3.上:年齢ヒストグラム。白棒= S0 サンプル。斜棒= S2 サンプル。 下:年齢累積分布。実線= S1。破線= S3。短破線= S0。 |
 |
5.2.3.単独、複合星団の年齢と特性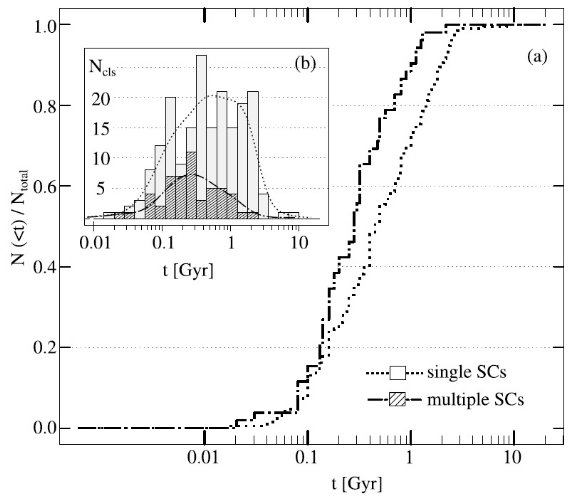 図4.単独星団と複合星団の年齢分布。一点鎖線=複合星団。点線=単独星団。 内枠は年齢ヒストグラム。白棒=単独星団。斜棒=複合星団。 図5.年齢決定。破線=Girardi et al. 2002. 実線=Bressan et al 2012. (a):二つの方法で決めた年齢の相関。線形フィットの勾配は 0.98. これは 高齢の時に少しバイアスがあることをいみする。 (b): 二つの方法の年齢比。(c): 累積年齢分布。(d): 不定性分布。 |
5.2.4.異なるモデルによる年齢決定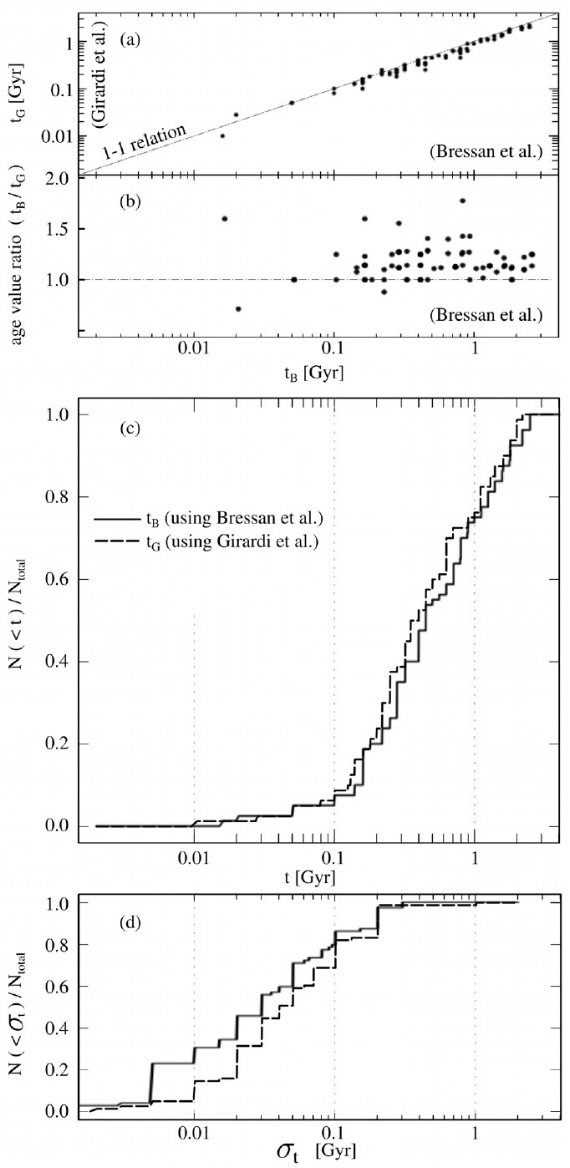 |
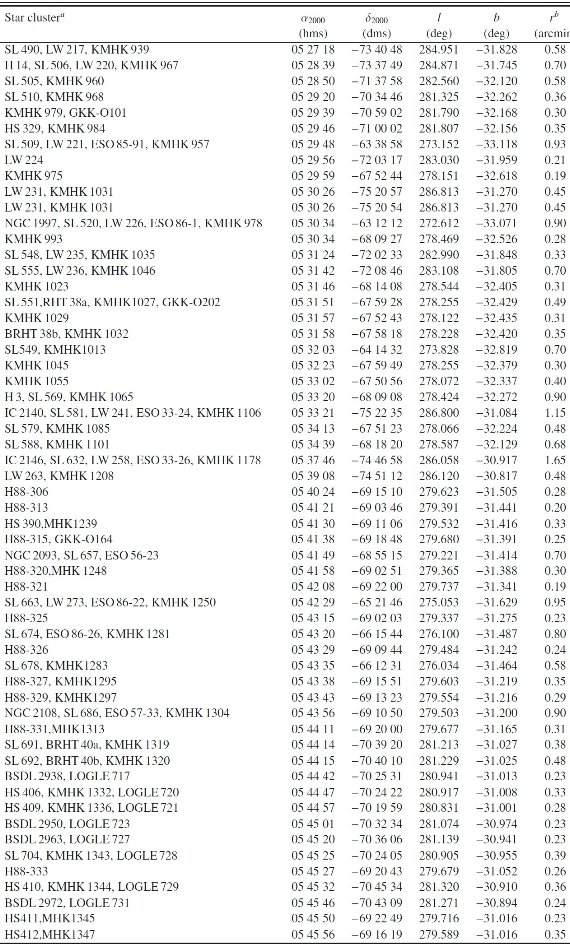
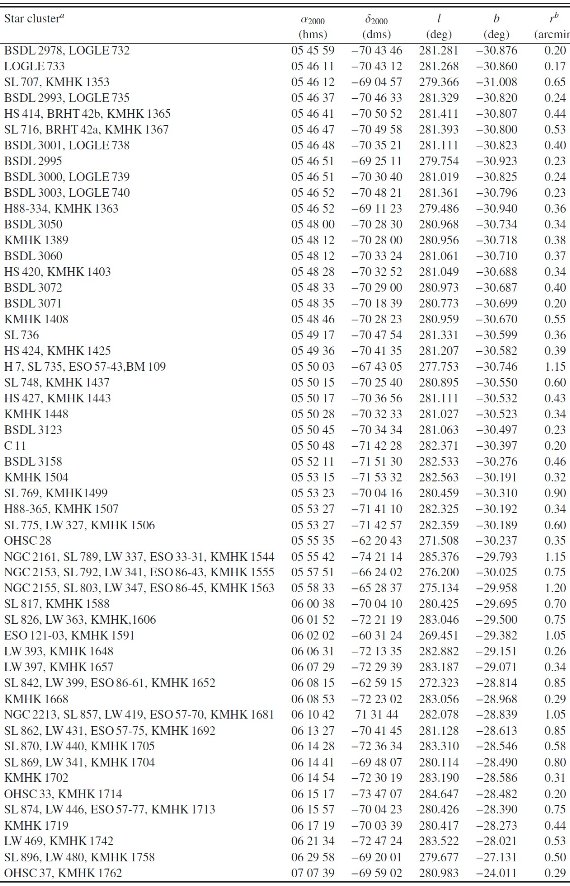
表A1:ワシントンシステムで観測された LMC 星団A2の列AgeI = 等時線フィット年齢, [Fe/H]I = 等時線フィットメタル量 AgeII = δT1 法年齢, [Fe/H]II = Geisler, Sarajedini 1999 法 Note a,b,c は以下の文献にも パラメタ―価がある。 a: Glatt et al (2010) b: Popescu et al (2012) c: Pietrzynski, Udalski (2000) |
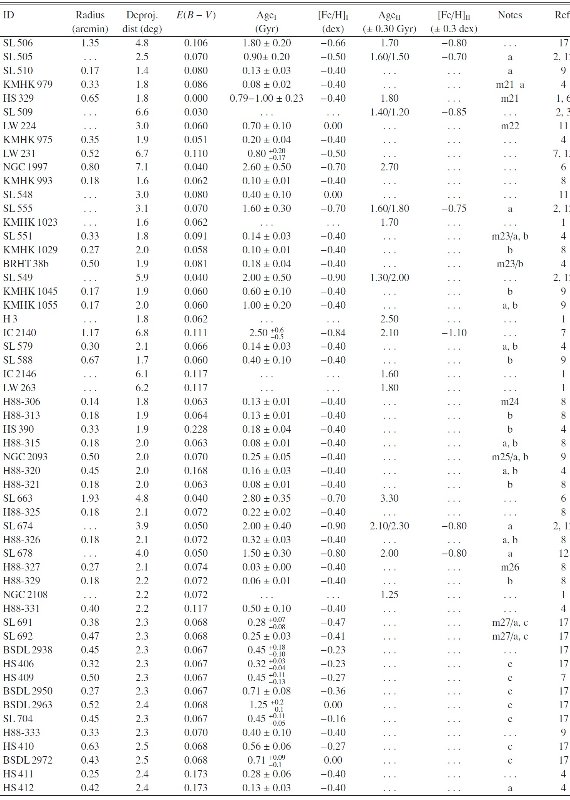
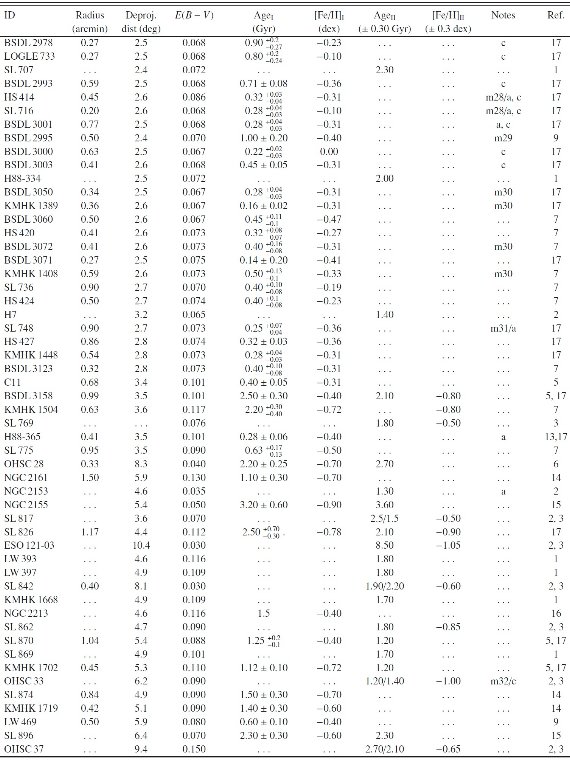
表A2: LMC 星団の基本パラメタ―ReferenceReference はワシントン測光を行った他の研究。 星団名 星団名は以下から採った。 SL = Shapley, Lindsay 1963 LW = Lynga, Westerlund 1963 HS = Hodge, Sexton 1966 C = Hodge 1975 H88 = Hodge 1988 OHSC = Olszewski et al 1988 KMK = Kontizas et al 1988 KMHK = Kontizas et al 1990 BRHT = Bhatia et al 1991 LOGLE = Pietrzynski et al 1998, 1999 BSDL = Bica et al 1999 |
表A1:ワシントンシステムで観測された LMC 星団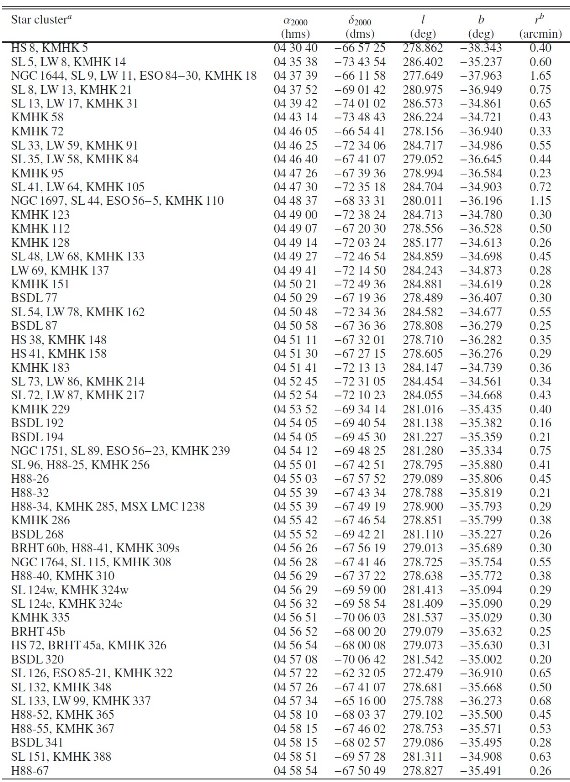 |
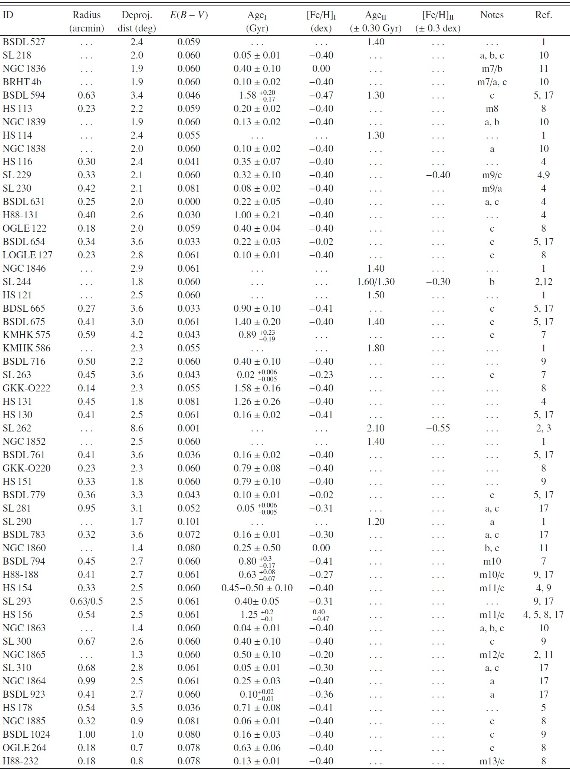
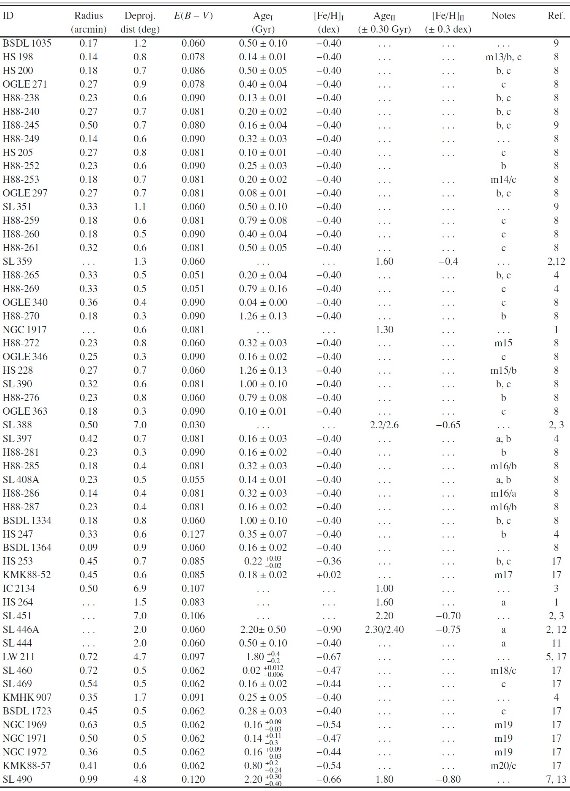
表A2: LMC 星団の基本パラメタ―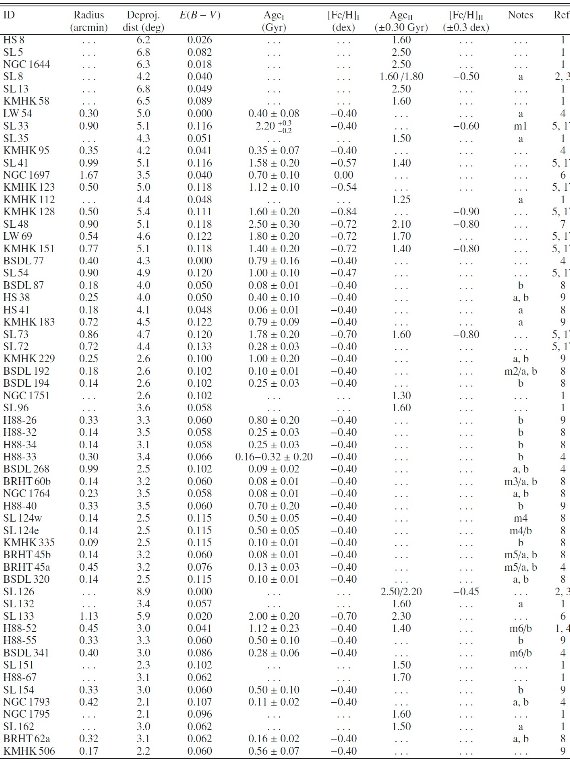 |
 |
 |
 |
 |
 |
 |
 |
 |