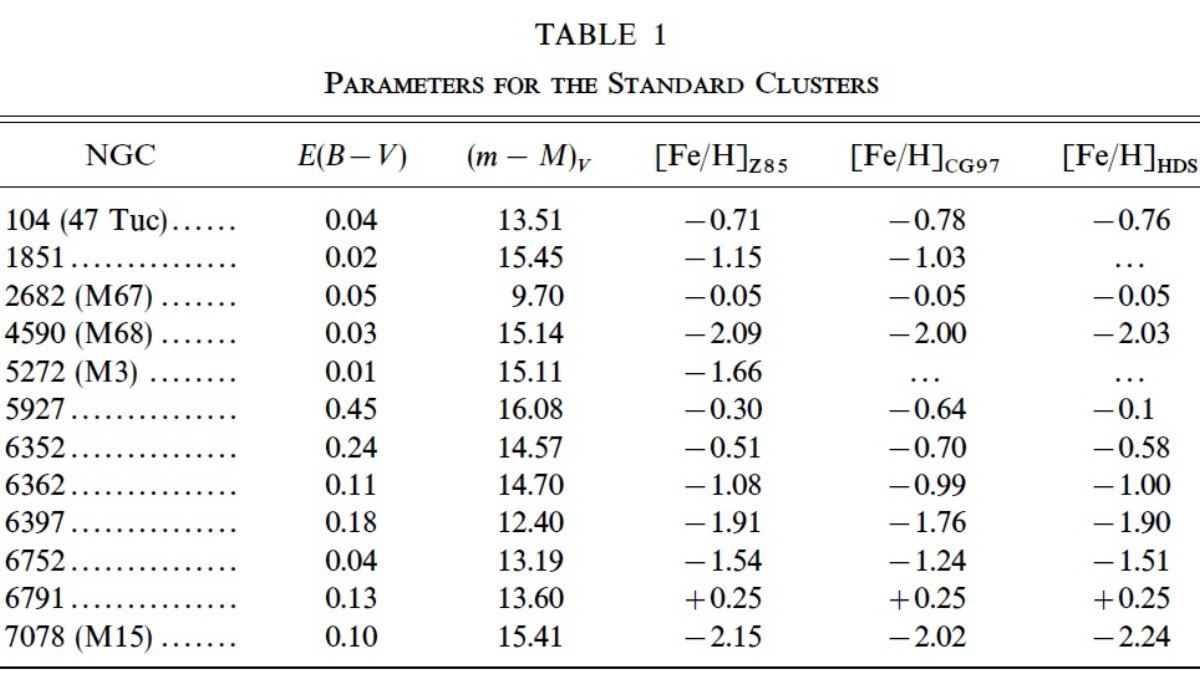
| 10個の銀河系球状星団と2個の高齢散開星団をワシントンシステム C, T1 フィルターで測光した。それらはメタル量が既知で、[Fe/H] = [-2.25, +0.25] を間隔 0.2 dex でカバーしている。各星団毎に二つの 独立な観測が行われ、内部チェックを行い、外部の既存測光と比較した結果、 測光精度は ≤ 0.03 mag であった。 Da Costa, Armandroff (1990) が V, I で行った手法を真似て、Lee et al 距離指数を適用して、[MT1, (C-T1)o] 巨星枝を作った。 各巨星枝には約 350 星が含まれる。 次に、与えられた MT1 における (C-T1)o カラー のメタル量に対する感度を決めた。ワシントンシステムは V, I システムの 3倍感度が良いことが判った。MT1 = -2 (巨星枝先端の少し下、 大体 MI = -3 相当)で、47 Tuc と M 15 は (C-T1)o では 1.16 mag 離れるが、(V-I)o ではわずか 0.38 mag しか離れない。 MT1 = -2 における (C-T1)o は Zinn スケールの メタル量と線形の関係がある。MT1 = -2.5, -1.5 においても 他の2メタル量スケールで較正した。ワシントン法は暗い等級でも同じ メタル量感度をしめし、巨星枝は水平枝の下でもよく定義される。 t ≥ 5 Gyr でこのメタル量恒星は有効であり、そこでの年齢効果は無視 出来るほどに小さい。 | 従来ワシントン測光で使用されていた2色図法に較べ、今回の方法は多くの 利点がある。(1)フィルターが2枚で済む。(2)赤化と測光エラーに対し 鈍い。(3)メタル量への感度が高い。(4)低メタル天体に向いている。 Geisler et al (????) が古い技法で以前決められた値よりずっと低メタル であったとした5つの低メタル球状星団は新しい技法では Zinn スケールと 良く合う結果を出した。以前に出た異常に低い値は古い方法が低メタル量 領域で感度が悪いための結果であった。しかし、古い技法も [Fe/H] ≥ -1 では有用である。 我々は Sarajedini が開発した、赤色巨星枝の形、水平枝の T1 等級、水平枝等級での RGB (C-T1) 見かけカラー、 を用いて、赤化とメタル量を同時に決める方法を拡張した。この方法は、 E(B-V) を 0.025 mag, メタル量を 0.15 dex まで決められる。 我々は赤色巨星枝バンプの T1 等級を各較正用星団で測った。 その結果、水平枝とバンプの等級差はメタル量と密接に関連することを 見出した。この特性はまたメタル量決定に使える。メタル量は RGB の傾き からも決まる。 RGB 先端の MT1 は MI 程には年齢やメタル量に 対して一定でない。それでも [Fe/H] ≤ -1.2 の星団に対しては有用な 距離指標である。この範囲にある6つの基準星団に関して、 ⟨MT1(TRGB)⟩ = -3.22±0.11(σ) で あり、メタル依存は小さい。この結果は Bertelli et al 1994 のモデル 等時線の予想と良く合う。 |
|
RGB の利用 Sandage, Smith 1966 以来古い星種族の RGB カラーがメタル量の指標になる ことは広く認められてきた。Hartwick 1968 は (B-V)0, g = 赤化補正後の水平枝レベル RGB カラー、をメタル量決定に用いた。Searl, Zinn 1978 は赤化フリーカラー指数対 Mv プロットからメタル量の大小を決めた。 Da Costa, Armandroff 1990 は V, Ic の波長間隔が大きいことに目をつけ、 RGB 上部全体を用いて、 [MI, (V-I)o] 面上に標準 RGB 系列を作った。この方法は大変評判がよく様々な研究に使われた。 Sarajedini 1994 は標準 RGB から赤化とメタル量の双方を同時に決定できる ことを示した。一方多くの研究、例えば Lee, Freedman, Madore 1993 は 年齢とメタル量の広い領域において MI が一定であり、従って 良い距離指標であることを示した。こうして V. Ic 測光の有用性が 確立した。 ワシントンシステム Geisler (1994), Geisler, Sarajedini 1996 は C, T1 測光 で同様の試みを行った。ワシントンシステム Canterna (1976) は広帯4バンドシステムで、Wallerstein, Helfer 1966 が G, K 巨星の メタル量と温度を効率的に定めるために提案した。 |
Geisler, Claria, Minniti
1991 はワシントンシステムの二色図は個々の晩期型星のメタル量を高精度
で予測することを示した。ただし、非常に低温の低メタル星では感度が下がる。
また、遠方の球状星団の積分カラーからメタル量を決定する力も立証された。
C フィルターは U と似て、3500 - 4500 A の多数のスペクトル帯を含んで
いるので、低温巨星ではメタル量に敏感である。しかも U より幅が広くかつ
赤い側に寄っているため測光精度が上がり、かつ大気減光がより小さい。
T1 は Rc と殆ど同じで、より幅が広い。このバンドは低温度星
のフラックス最大付近での連続光レベルを与える。ワシントンシステムは
この他に M と T2 の2フィルターがあるが、必要度は落ちる。
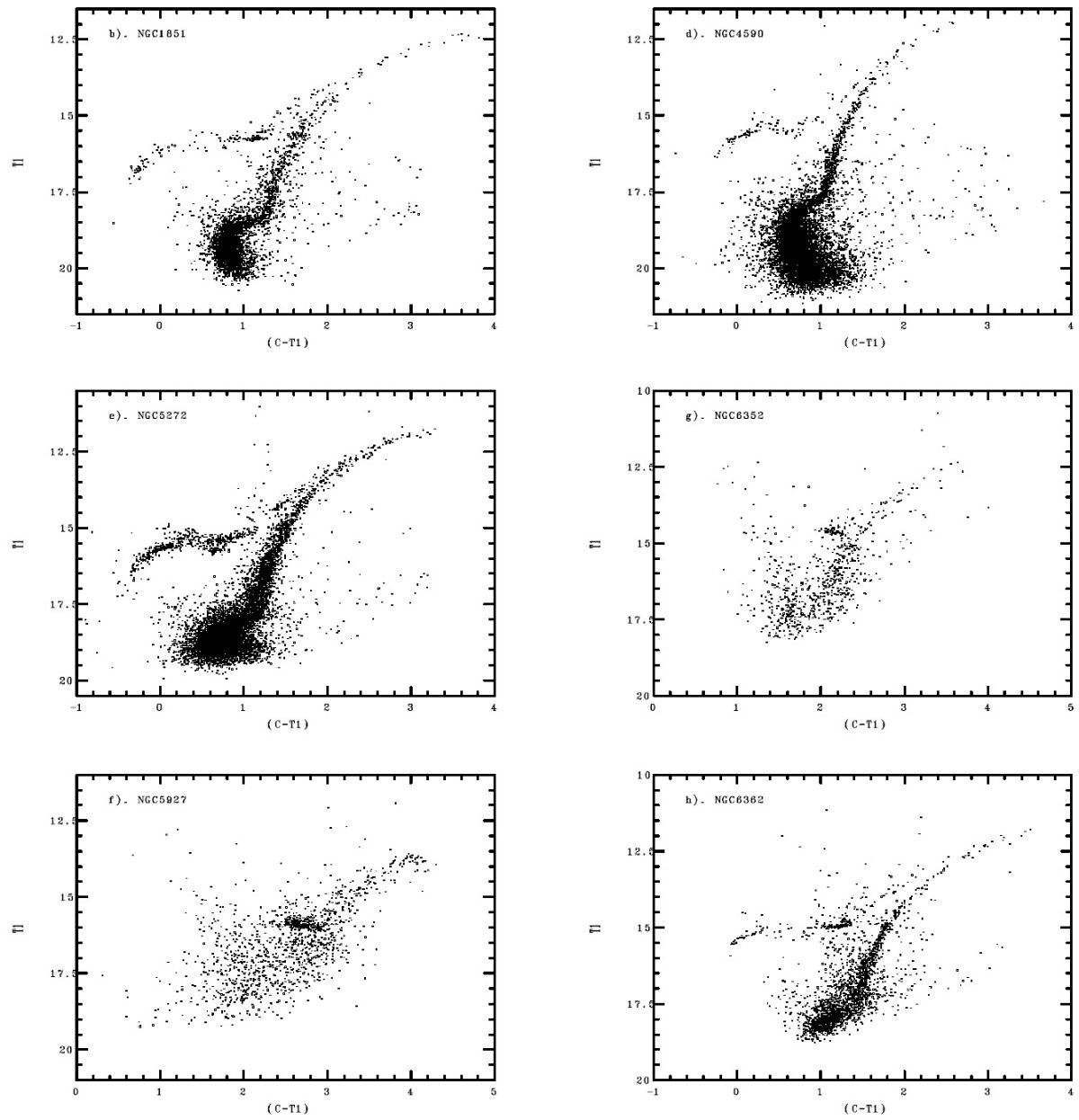
標準赤色巨星枝 このように、ワシントンシステムがメタル量に高感度である利点を 生かして、Da Costa, Armandroff 1990 に倣って、 ワシントンシステム (T1, C-T1) で標準 巨星枝を作る試みを開始した。初期の成果は Geisler 1994, Geisler, Sarajedini 1996 で発表したが、星団数が不足している。 今回は十分なサンプルを用意した。 |

2.1.サンプル選択球状星団表1に標準星団を載せた。10個の球状星団が 0.2 dex のメタル量間隔 で [Fe/H] = [-2.15, -0.3] までをカバーしている。 散開星団 それより高メタル量 側は高齢散開星団 NGC 2682 (M 67), NGC 6791 を採用した。ほぼ太陽組成の 星団も存在するが、それらは強い赤化を受けていて、距離、メタル量共に 確定していない。NGC 6791 は年齢 10 Gyr (Tripicco et al 1995) で、高 メタルかつ星数が多いという利点に恵まれている。 M 67 は年齢 4 Gyr (Dinescu et al 1995) で年齢効果が表れ始める点でやや問題がある。しかし、 太陽組成では最も古く、最も良く研究されている星団である。こうして、 Da Costa, Armandroff 1990 の倍の12サンプル星団を使う研究を行った。 |
2.2.観測フィルター観測は CTIO 0.9 m で14晩、KPNO 0.9 m で3晩、KPNO 4 m で3晩、 CFHT で1晩行った。典型は的な C フィルターの組み合わせは、 Geisler 1996 によると 3mm GB3 + 2 mm BG40 である。T1 は 既存の T1 または RKC を使用した。 標準星 各測光夜ごとに Geisler 1990, 1996 からの 24 - 40 標準星を観測した。 幾つかは1回以上観測した。カラーとエアマスの十分な巾がカバーされる よう気を付けた。 |
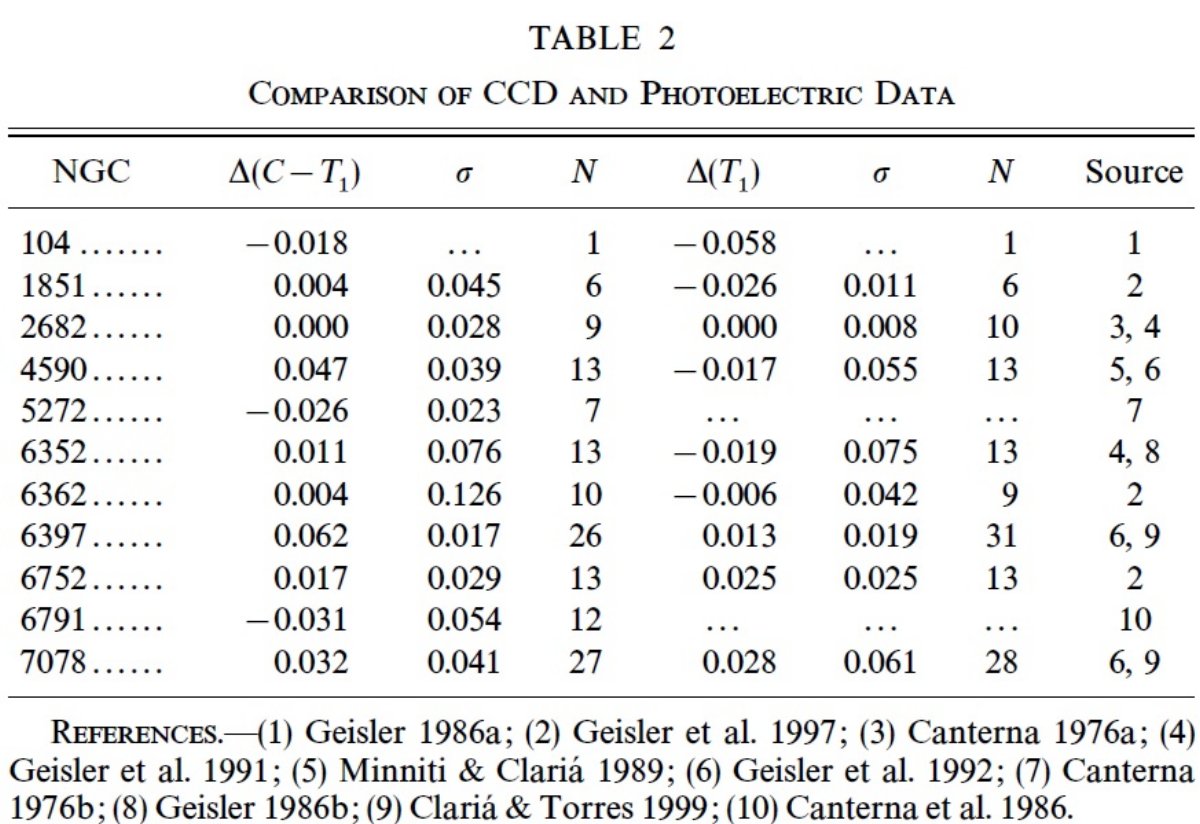
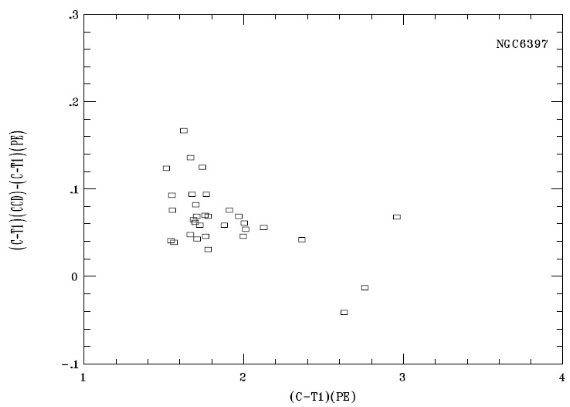 図1a.CCD測光と光電測光の差。(C-T1) カラーの差と光電 (C-t1) カラーとの関係。 |
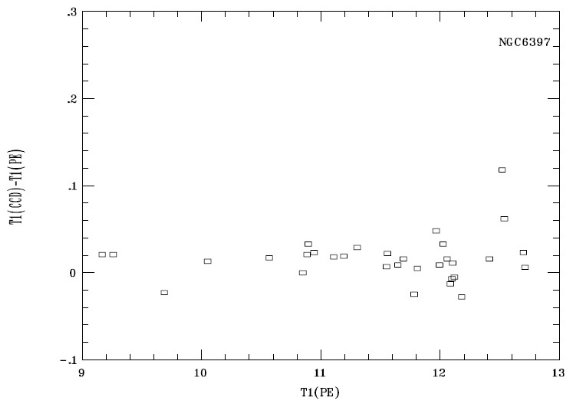 図1b.CCD測光と光電測光の差。T1 等級の差と光電 (C-t1) カラーとの関係。 |
|
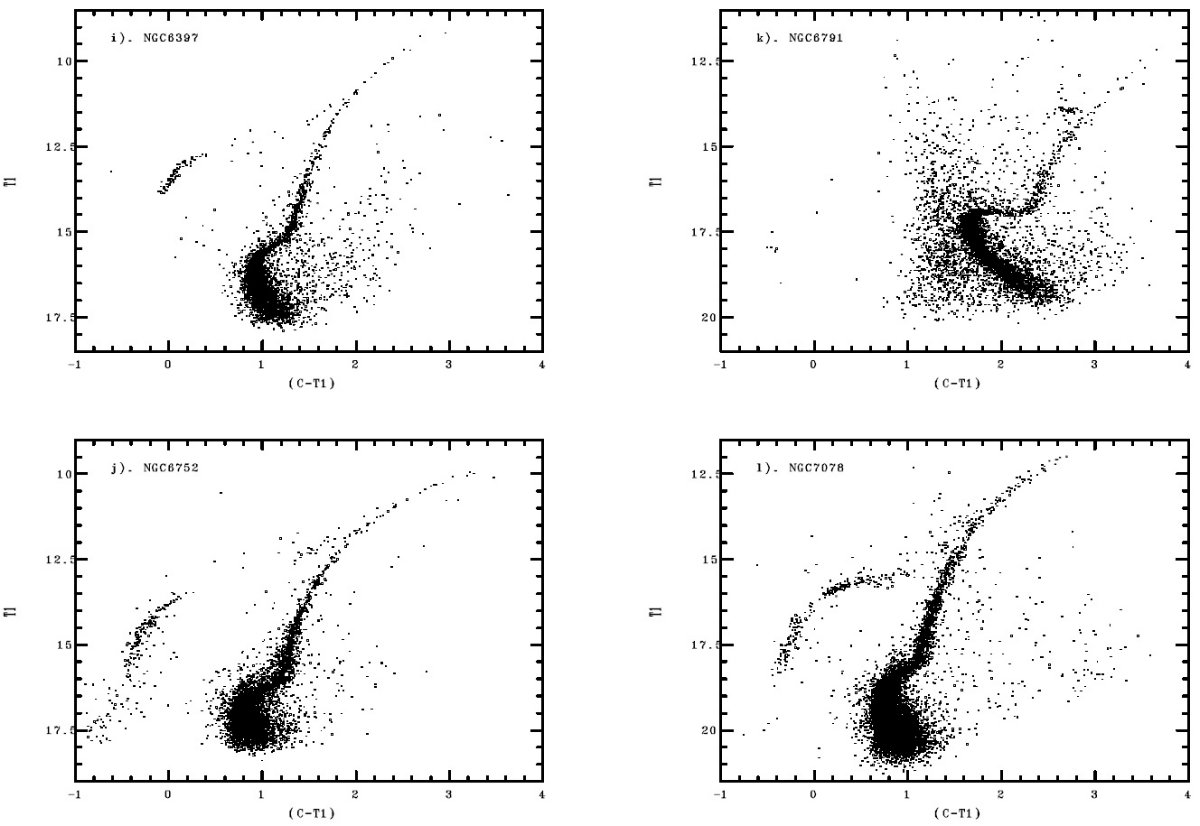
標準巨星枝 赤化と距離の不定性を考えると、観測等級で巨星枝を扱うのが安全である。 そこで、解析は観測された明るい方の5等級を対象とする。標準巨星枝を 得る最初の手順はそこから明らかな HB, AGB, フィールド星を除去する。 次に3次式フィットを行う。そして、3 σ 以上離れた点を捨てる。 こうしても 10 球状星団で平均 361 個の星が残った。散開星団は星数が 小さいので、 NGC 2682 ではわずか 14 個、 NGC 6791 で 56 個しか使 えなかった。 フィット式 フィットの独立変数は T1 として、次のように3次式とした。 (C-T1) = a + b (T1-O) + c (T1-O)2 + d (T1-O)3 3次式係数は表3に、フィットの結果は図3に示す。 赤い方で外れる星団 ほぼ全ての星団でフィットはよいが、 NGC 6572, NGC 104, NGC 5927 では TRGB 付近で曲率が極端になり、さらに極度に赤い星で等級が暗くなる場合もある。 それらは上手くフィットできなかった。それらの星団では手描きの曲線で補足した。 NGC 104 の場合、(C-T1) = 3.9 まで手描きで追ったが、その先には二つの星が 更に暗く赤い領域にある。 |
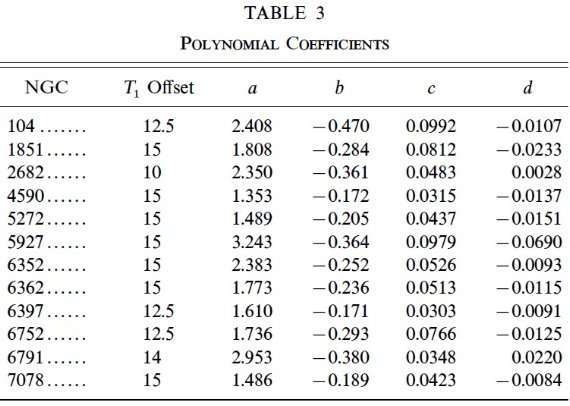 表3.フィット多項式の係数 |
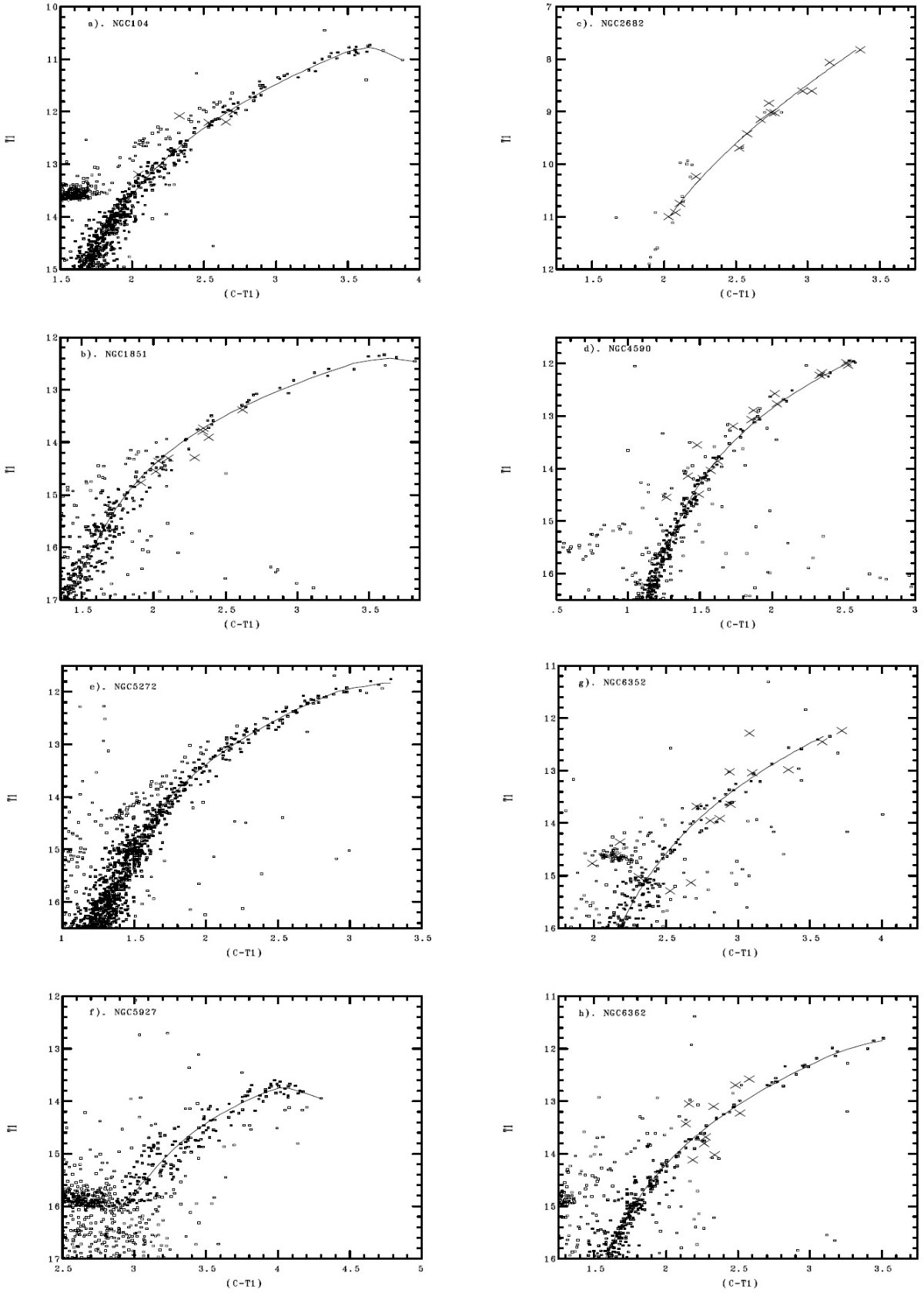
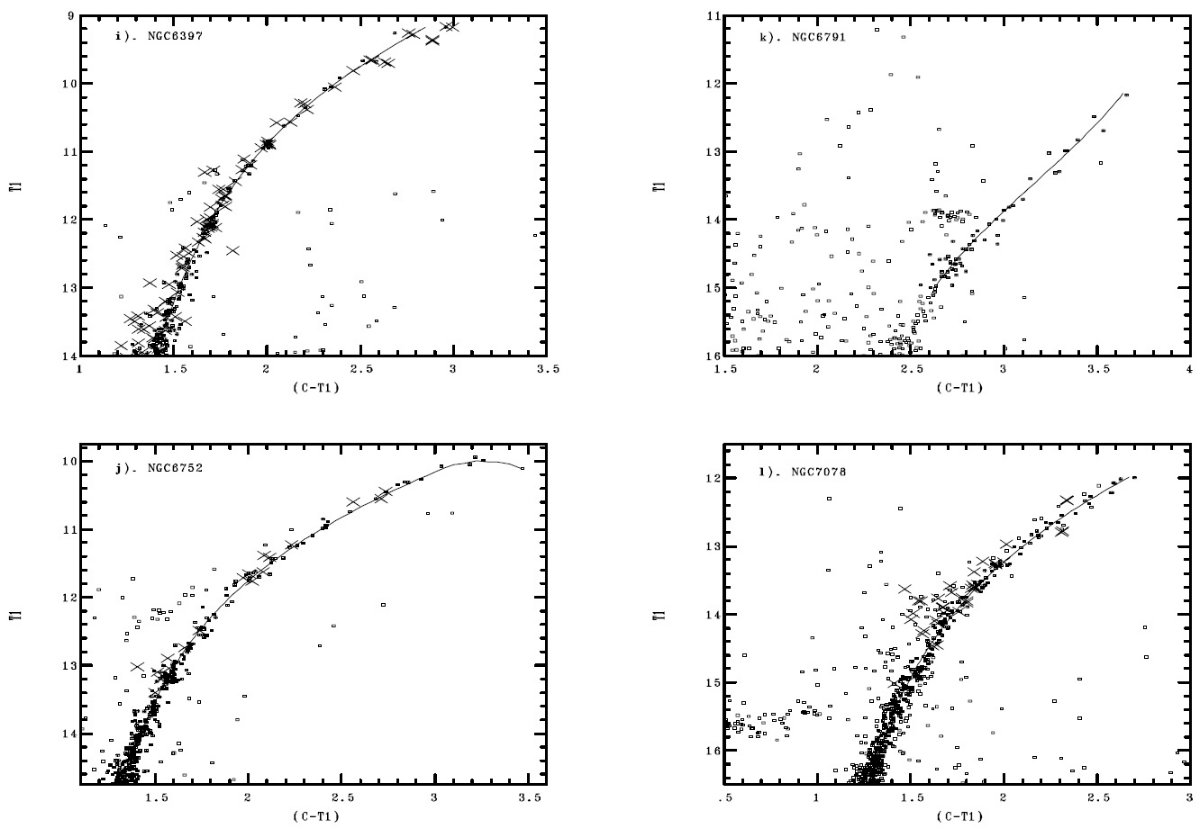
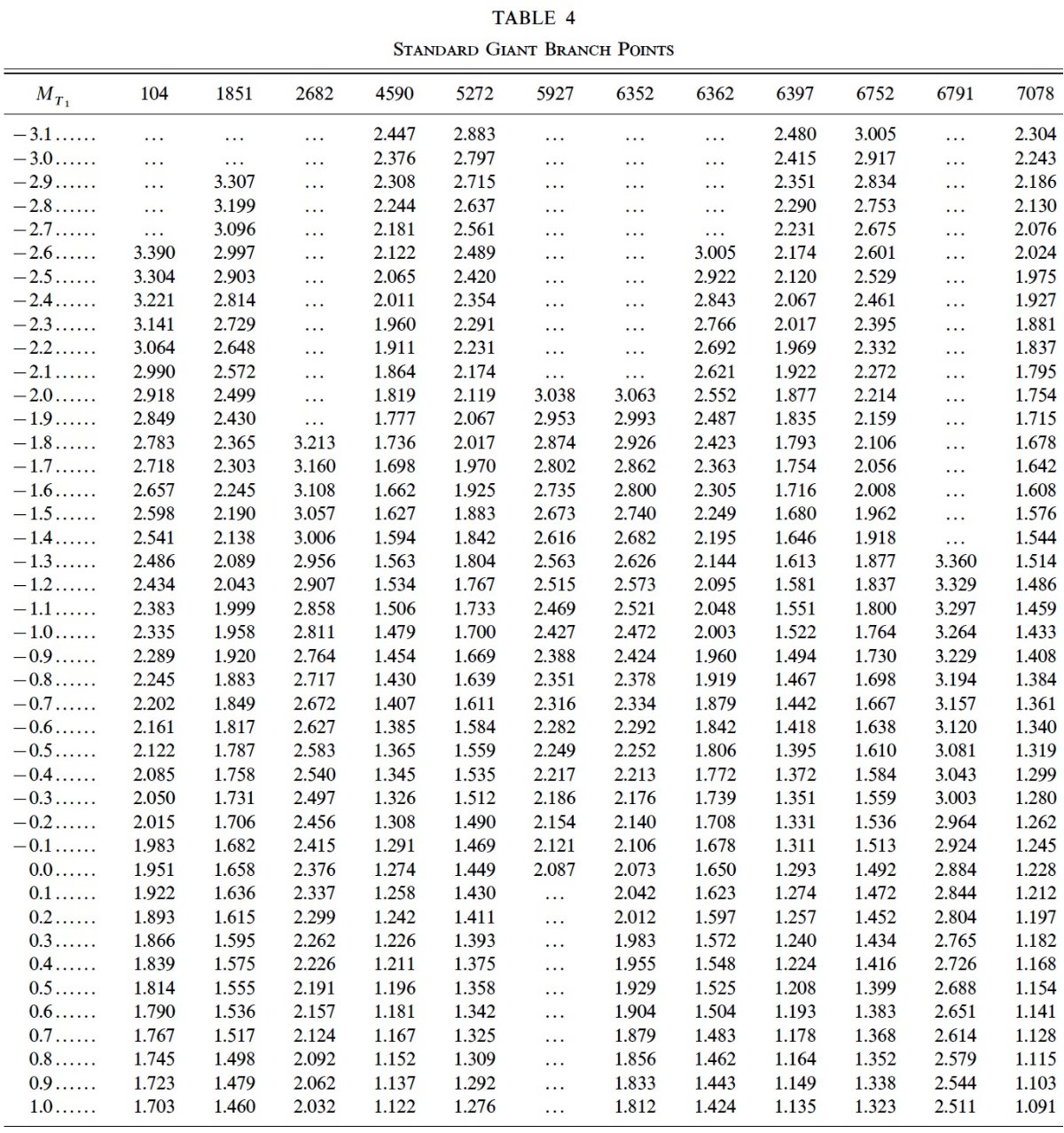
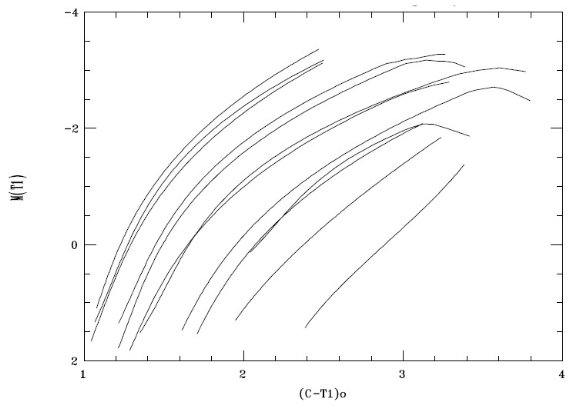 図4.ワシントンシステム [MT1, (C-T1)o] 標準巨星枝. MT1 = -1.5 で、左から右へ、 NGC 7078, NGC 4590, NGC 6397, NGC 5272, NGC 6752, NGC 1851, NGC 6362, NGC 104, NGC 5927, NGC 6352, NGC 2682, NGC 6791. 赤化補正 これまでの見かけ等級 CMD を絶対等級 CMD に直すため、まず赤化補正を 行う。球状星団には Zinn 1985 を用いた。 球状星団の距離 ヒッパルコスの結果を球状星団に応用した研究は互いに矛盾している。 そこで、我々は Lee, demarque, Zinn 1990 の球状星団 RR Lyr 等級 Mv(RR) = 0.82 + 0.17 [Fe/H] を用いることにした。[Fe/H] には Zinn 1985 を用いた。その他色々な補正が 個々の星団にあるらしいが略。 |
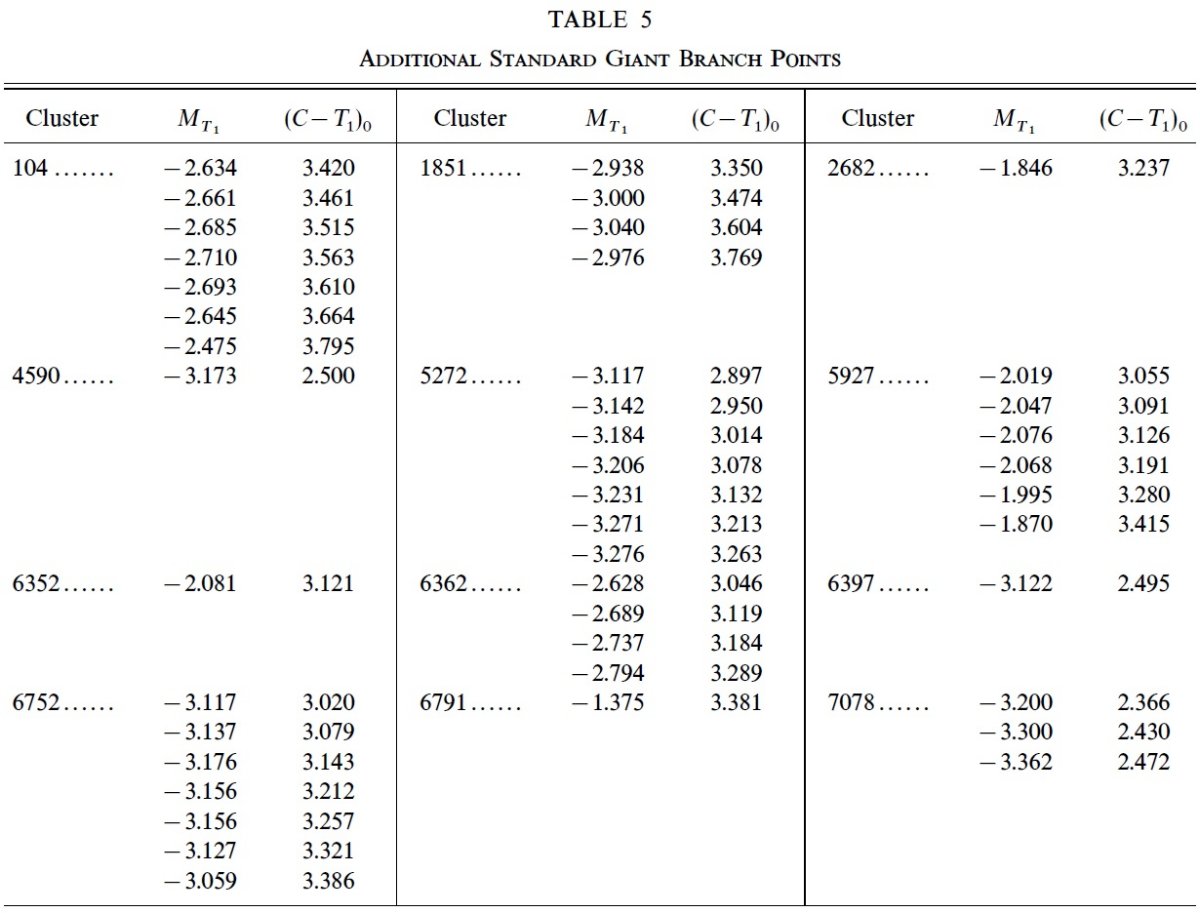
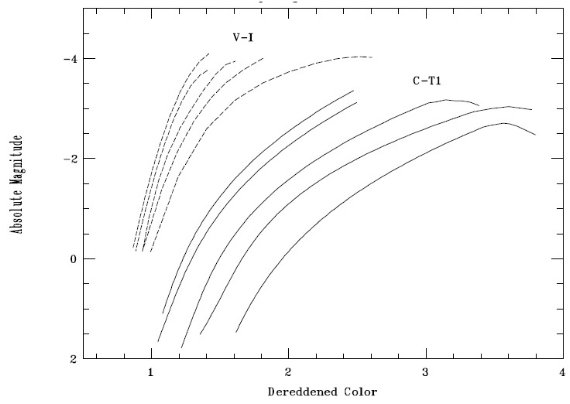 図5.標準巨星枝 CMD の比較。破線= [MI, (V-I)o]. 実線=[MT1, (C-T1)o]. 各群、左から右へ、NGC 7078, NGC 6397, NGC 6752, NGC 1851, NGC 104. ワシントン CMDの方が広がっていることに 注意。 散開星団の距離 散開星団の距離は単純に良い文献値の平均を取った。こうして得られた (m-M)o は表1に載せた。 表4、5 = 標準巨星枝の表示 表4には標準巨星枝を ΔMT1 = 0.1 mag でサンプル点を示す。 表5には TRGB 付近の追加点を載せた。E(C-T1) = 1.97 E(B-V), AT1 = 2.62 E(B-V), Av = 3.2 E(B-V) を採用したので、 MT1 = T1 + 0.58 E(B-V) - (m-M)v 図4に標準巨星枝を絶対等級表示した図を示す。図から TRGB の MT1 は ほぼ一定だが、高メタル星団で TRGB 等級が上がることが分かる。カラーの分離は ワシントンシステムで著しいことが図5から明らかである。 |
|
何等で較正すべきか? メタル量較正は、様々な値の既知メタル量を持つ標準巨星枝に対し、一定の MT1 レベルでの (C-T1) カラーを測って行う。図4から分かるように、 標準巨星枝は明るい方で間隔が開く。また、明るい星を使える方が観測には有利 である。しかし、高メタル星団の MT1 は低メタル星団の光度に 達しない。また、上部赤色巨星枝は星が少ない。従って適切な値の設定が大事に なる。 DaCosta, Armandroff 1990 は当初 MI = -3, TRGB の1等下、 を採用したが、後に MI = -3.5 に変更した。 3通りの MT1 でメタル量較正 我々は MT1 = -2.5, -2, -1.5 の3通りでメタル量較正を行う。 MT1 = -2 は低メタル星団の TRGB から約 1 等下で、DaCosta, Armandroff 1990 の MI = -3 に対応する。MT1 = -2.5 は遠方の低メタル星団に向いており、一方 MT1 = -1.5 は星の数 が多く、巨星枝の決定精度が上がる利点がある。 高メタルでは巨星枝を外挿 サンプル中最も高メタルの球状星団 NGC 6352 ([Fe/H]Z85 = -0.51) と NGC 5927 ([Fe/H]Z85 = -0.30) は MT1 = -2 に 達するかどうかであり、二つの散開星団 NGC 2682 = M 67 ([Fe/H]Z85 = -0.05) と NGC 6791 ([Fe/H]Z85 = +0.25) にはその明るさの星がない。我々はこれらの星団の巨星枝を外挿して MT1 = -2 における (C-T1)o を定めた。 NGC 6791 の場合には MT1 = -1.5 に対してさえも幾分かの外挿が必要であった。-1.5 mag ではかなりの数の AGB 星の混入が避けられない。しかし、MT1 = -2 では AGB が RGB に融合してしまうので (C-T1) カラーの決定にはあまり影響 しない。(C-T1) カラーの分離は (V-I) より優れていて、図5から分かるように HB の下でさえメタル量効果が残っている。 |
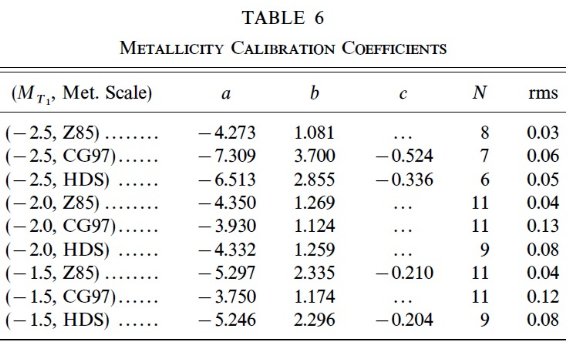 表6.メタル量較正式の係数 Zinn85 メタル量スケールに ? Zinn 1985 の球状星団メタル量スケールは Da Costa, Armandroff 1990 でも 採用されている標準である。しかし、Carretta, Gratton 1997 (CG97) は高分散分光 から、 Zinn85 スケールは本当の [Fe/H] スケールに対して非線形な関係にある と述べた。Rutledge, Hesser, Stetson 1997 は CaII 三重線強度の広範な研究 からこの結論を支持した。 |
|
3種のメタル量スケール 結局我々には3種のメタル量スケールがある。 (1)Z85 スケール (2)CG97 スケール:Rutledge et al 1997 が与えたもの。 (3)HDS スケール:Rutledge et al 1997 表3の高分散スペクトルの結果の平均値 表1にはこの3種の値を載せた。NGC 1851 の Z85 値は -1.33 だが、多くの 研究は -1.15 の方が適当としており、表1ではそちらを採用した。 元素間相対比の変化 CG97 と HDS は Fe 存在比を表している、つまり Fe 量を直接測っている。 一方、Z85 は多くの多くの方法の合成で、多くの元素比が噛んでいる。しかし 一般には Fe 量を示すと考えている。赤色巨星の温度は電子供給元素 Mg, Si, Fe の量で決まると考えられる。それらの相対比は大きな温度効果を示す。 これが Z85 と CG97 との差を生むのであろう。 Mg/Fe と Si/Fe は低メタル 球状星団で高い値を示す。それらは太陽組成では低い。しかし、 Pal 12 の ように正常星団と異なる組成パターンをもつ星団もあり、それらのメタル量の 決定には注意を要す。 9通りの較正 このような事情で、3通りのメタル量スケールと3通りの MT1 の組み合わせで計9通りの較正を行った。読者は己の好む組み合わせを選ばれたい。 |
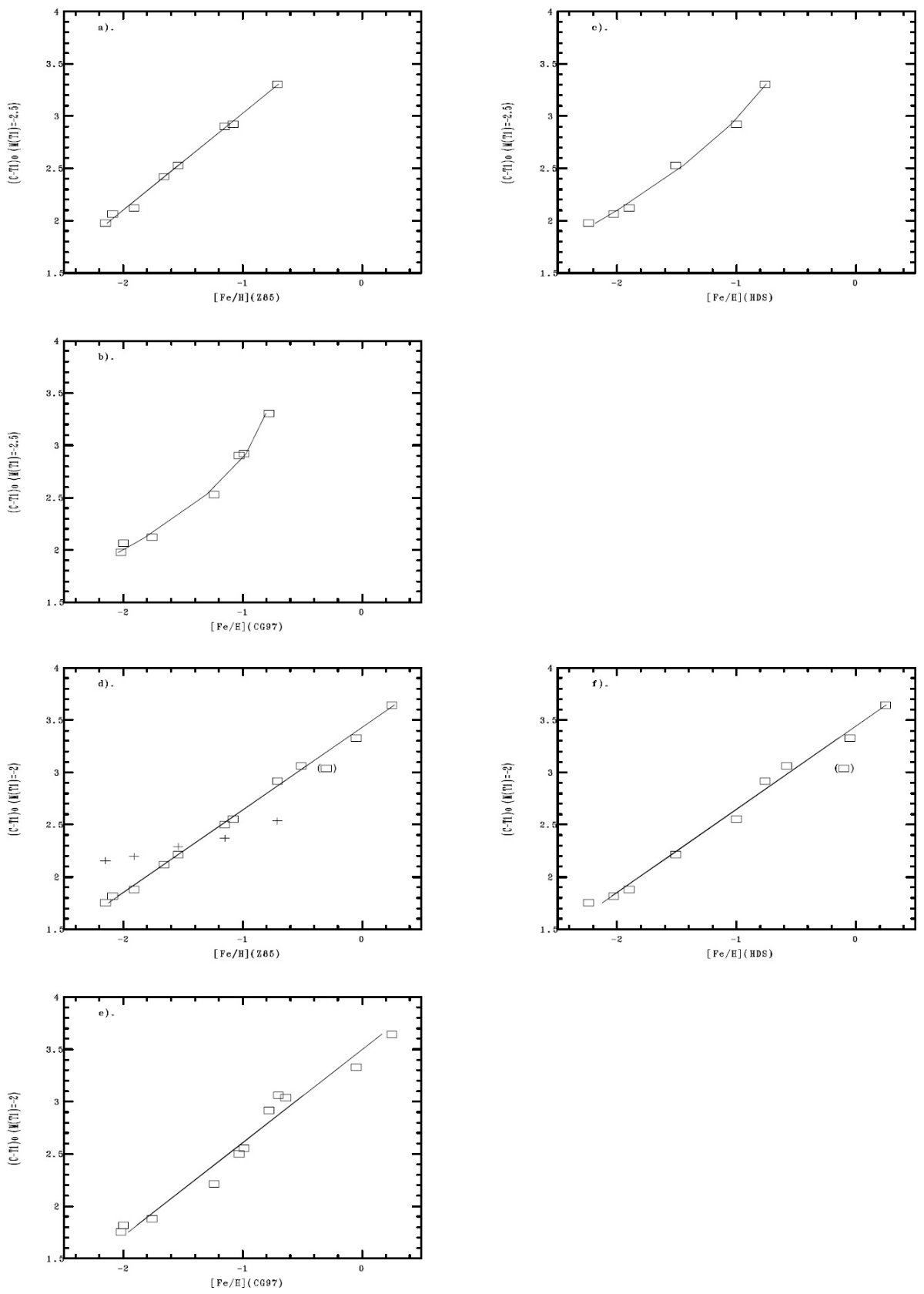
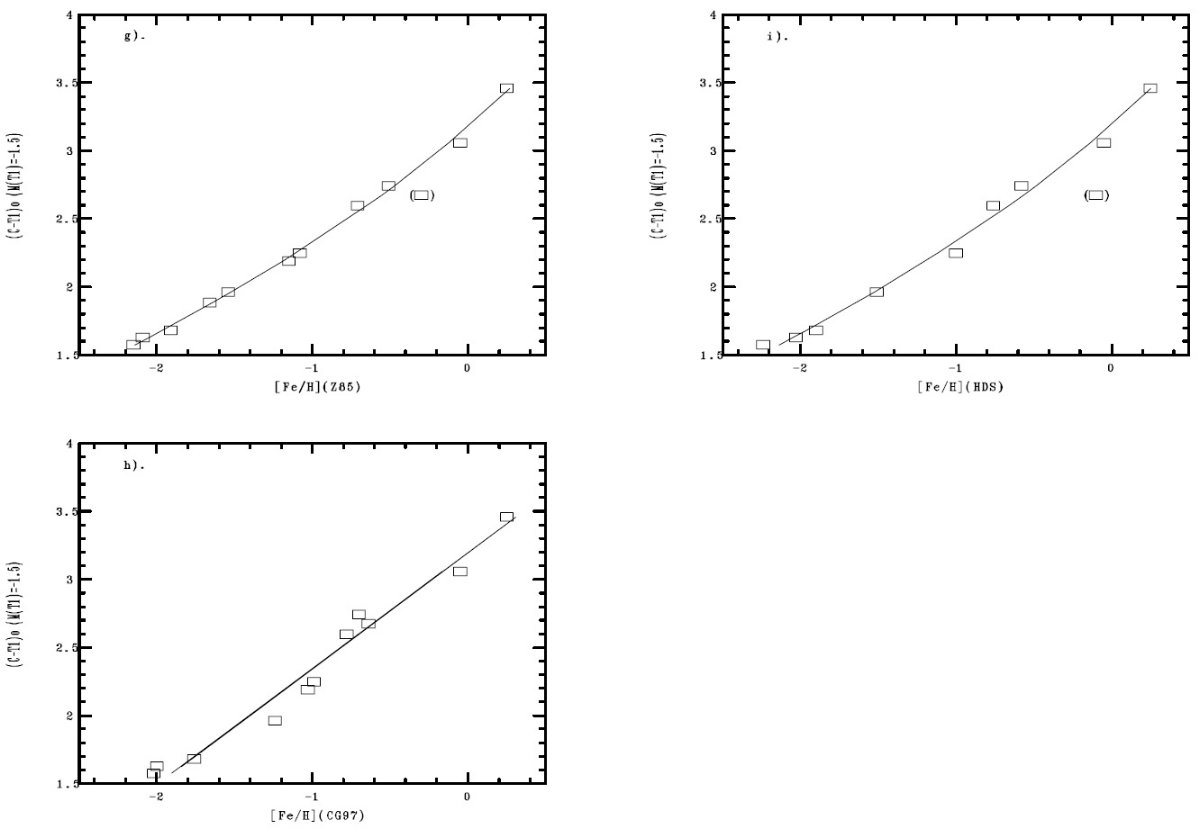
較正結果の近似式 較正の結果は1次式と2次式の二通りに表現した。 [Fe/H] = a + b (C-T1)o [Fe/H] = a + b (C-T1)o + c (C-T1)o2 表6に係数を示す。フィットには全星団を同じ重みで用いたが、(-2, Z85), (-1.5, Z85), (-2, HDS), (-1.5, HDS) セットだけは NGC 5927 データを除い た。それらではこの星団の位置のずれが大きすぎたからである。 (-2, Z85) 較正がよい 図6に較正フィットを示す。図を見ると、Z85 のセットの rms が小さいこ とが目立つ。特に (-2, Z85) 較正の良さは印象的である。 次が HDS 較正である。 CG97 -2mag, -1.5 mag は最低であった。 我々は NGC 5927 を外した (-2, Z85)セットを推奨する。そのセットの図 図6(d) には Da Costa, Armandroff 1990 サンプルで今回と共通する5星団 をプラスサインでプロットした。その際、 (V-I)o に 1 を足してワシントン システムと比較できるようにし、Z85 メタル量を使った。今回の図がメタル量 に対してより鋭敏であることがわかる。 メタル量決定の手順 このように、今回の方法では測光観測を行った後、 Lee et al 1990 スケール で距離を得て、赤化を同じ測光から決めて [MT1, (C-T1)o] を 作り、次に規準 MT1 値における(C-T1)o からメタル量を求める ことが可能である。実際の応用では、距離決定にメタル量が影響するから、 逐次近似法が用いられる。 |
|
ワシントンシステムは2色図でメタルを決める ワシントンシステムは G-, K-巨星のメタル量を決めるのに用いられてきた。 古典的な用例は Geisler, Claria, Minniti 1991 に述べられているが、C, M, T1, T2 フィルター測光から成り、2色図上の星の位置からメタル量が決め られる。通常は温度に敏感な (T1-T2) カラーとメタル量に敏感な (C-T1) カラーのセットが用いられる。 巨星枝法は2色図法より高感度 Tregzger 1981 はメタル量指数 X の鋭敏度 S = dX/d[Fe/H] として定義した。 ワシントンシステム2色図法では S = 0.04 (低温で低メタル星)から 0.48 (暖かで太陽メタルの星)まで変化する。本論文の1次式較正では S = 1/b で 与えられる。(-2, Z85) セットに対しては S = 0.79 となる。つまり、2色図 法の 1.6 - 20 倍のメタル量感度を持つと言える。その上、2色図法は 低温で明るい赤色巨星が較正領域外となるのも減点である。 |
エラーの比較 メタル決定法が測光エラーに対してどう反応するかも重要な点である。 Geisler, Claria, Minniti 1991 によると、測光エラー σ(C-T1) = 0.025, σ(T1) = 0.02 の場合に2色図法によるメタル量エラーは 暖かい高メタル 星で 0.09 dex, 低温低メタル星で 0.83 dex である。標準巨星枝法では我々は 同じ測光エラーに対し、メタル量エラー 0.034 dex と評価した。これは、 2色図法の 2.7 - 25 倍良い。 赤化の影響 最後に、赤化の影響を較べよう。Geisler, Claria, Minniti 1991 によると、 赤化が ΔE(B-V) = +0.03 変化すると導かれるメタル量の増加は 0.02 - 0.60 dex, 最大値は低温低メタル星の場合、である。一方、巨星枝法では メタル量が 0.12 dex 減少する。つまり、暖かい太陽メタルの星では2色図法 は巨星枝法より赤化に対する抵抗性が強い。しかし、低メタル巨星では 巨星枝法の方が赤化の効果が小さい。 総合比較 まとめると、2色図法が競争力を有するのは、巨星枝法が年齢効果を受ける 5 Gyr より若く、比較的高メタルの場合である。これは古い散開星団が 相当する。それ以外は巨星枝法が有利である。 |
|
メタル量感度 Da Costa, Armandroff 1990 の V - I 標準巨星枝法は広く使われ、恒星種族 研究用に WFPC2/HST で F555W, F814W セットが選ばれたほどである。 ワシントン法と比較するため、DCAサンプル中最も高メタルな NGC 104 と 最も低メタルの NGC 7078 で MI = -3 における (V-I)o の差を 測ると 0.381 であった。相当する MT1 = -2 での差は (C-T1)o で 1.164 であった。つまり、ワシントン法は V - I 法の3倍感度が高い。 測光エラーへの感度 この巾の違いはそのままエラーにはね返る。同じ測光エラーならば、 ワシントン法の方が3倍高精度でメタル量を決められる。 赤化抵抗性 赤化が ΔE(B-V) = +0.03 増加すると、V-I メタル量は 0.19 dex 減少 する。その時 C-T1 メタル量の現象は 0.12 dex である。従って、ワシントン法 は赤化の影響を V-I 法の半分強しか受けない。 |
観測時間 このように、ワシントン法は V-I 法に較べ多くの点で優れている。ただし、C フィルターは実際の観測において、精度を上げるには長時間の観測が必要と言う 欠点がある。一般的には低メタル星団に対してはワシントン法が有利であり、 高メタルになると V-I 法の観測精度が上がる。 B - V 法 (V, B-V) CMDにおいても標準巨星枝は可能である。Sarajedini, Layden 1997 によれば、 NHC 104 と NGC 7078 は Mv = -2 において (B-V)o で 0.743 の 差を示す。これは感度比で言うと、ワシントン法の 2/3 に当たる。 |
|
M 67 のエラー評価 年齢とメタル量の間の有名な縮退効果について触れないわけにはいかない。 我々の標準星団の年齢は NGC 2682 (M67) の 4 Gyr から他星団の 10 - 15 Gyr に及んでいる。二つの散開星団はメタル量較正に高メタルサンプルを 必要としたからである。これら二つの年齢効果は小さいと期待している。 NGC 6791 は 10 Gyr で球状星団との年齢差による年齢効果は無視できる。 NGC 2682 (M 67) は 4 Gyr で若いので慎重になる。図6を見ると M 67 は フィット線の青い側に位置している。しかしこのずれは小さく、それによる メタル量への影響は 0.1 dex 以下である。したがって、我々のメタル量較正 は 4 Gyr より古い星団全てに適用可能と言える。 等時線 Leijeune 1997 は UBVRIJHK 等時線にワシントンシステム CMT1T2 等時線 を加えて解析を行った。それによると 5 Gyr より若くなると、同じメタル量で も巨星枝が青い方へずれて行くことが判る。 |
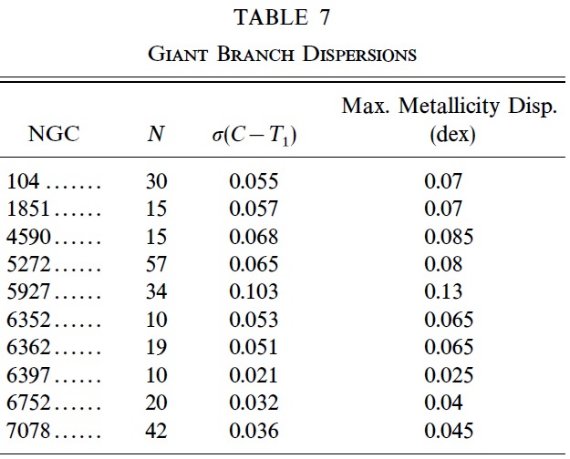 表7.巨星枝の分散 |
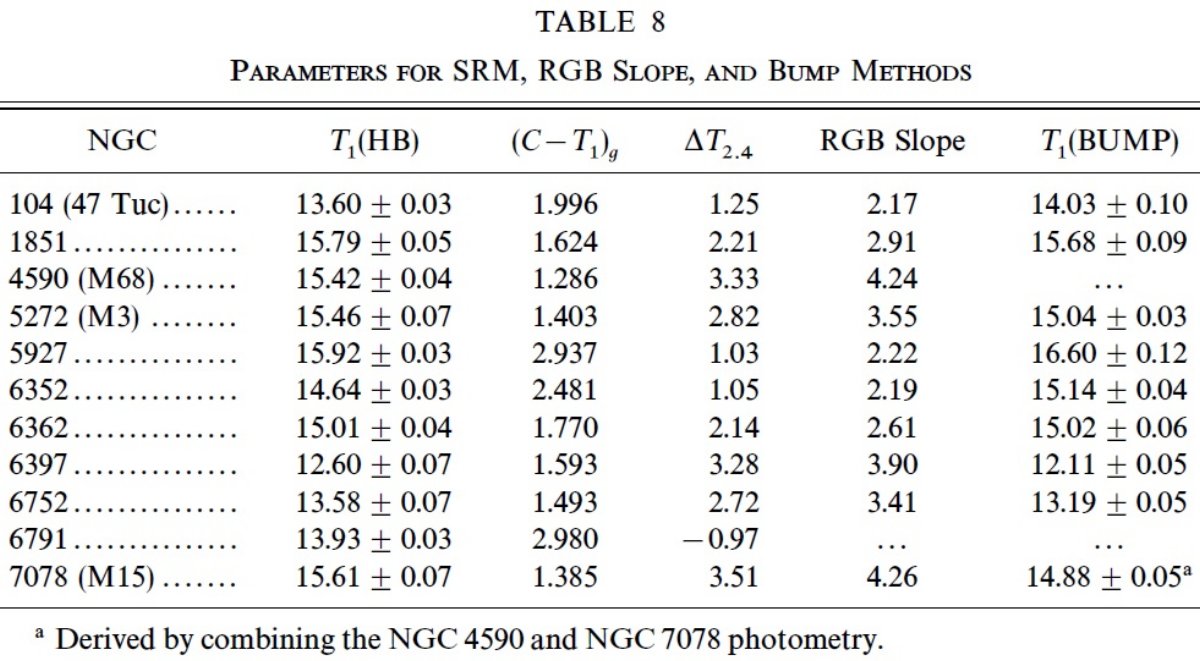
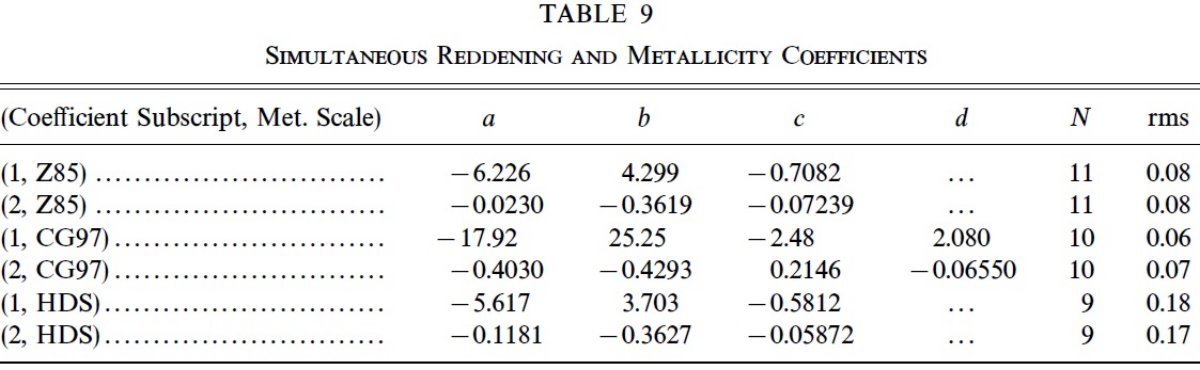
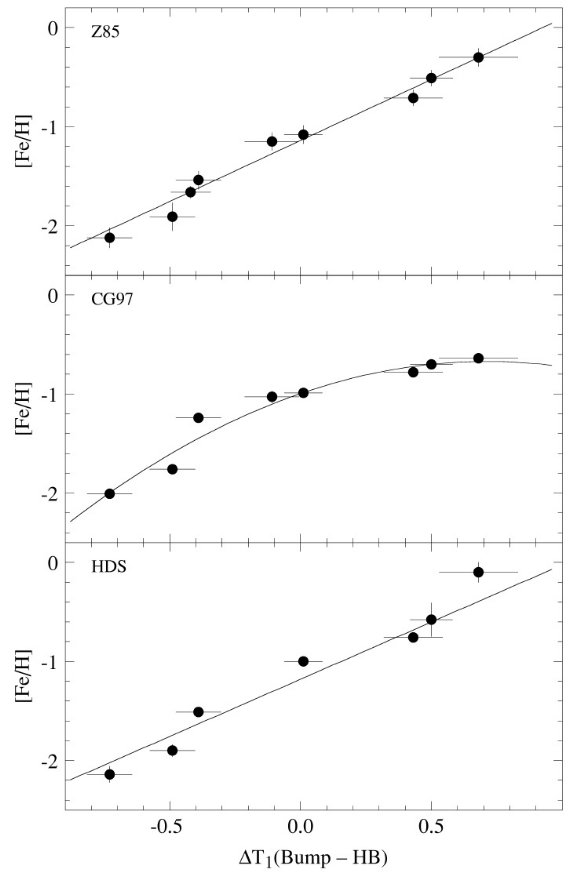
6.1.赤色巨星枝勾配からのメタル量決定Hartwick 1968 は赤色巨星枝の勾配がメタル量の指標になることを示した。 勾配を次の式で定義する。
ここに、(C-T1)-2 = HB より 2 等明るい赤色巨星枝カラーである。 メタル量を次の式で表す。 [Fe/H] = a + b S-2 + c S-22 表10に係数 a, b, c を示す。図8には3種の方法で決められたメタル量との 関係を示す。勾配法の利点は赤化も距離も知らなくてよいことである。 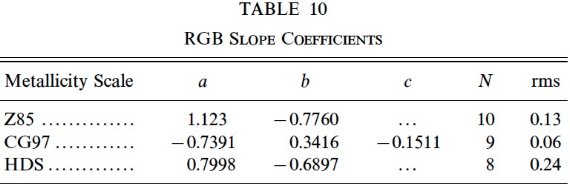 表10.赤色巨星枝勾配の係数 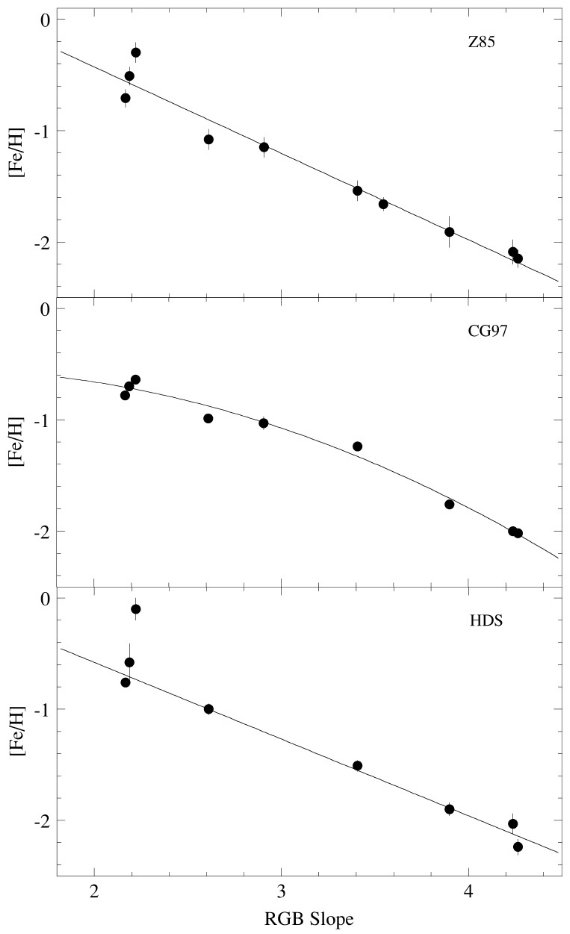 図8.3方法のメタル量と赤色巨星枝勾配との関係 |
6.2.赤色巨星枝バンプの等級によるメタル量決定星が第1赤色巨星枝を上る途中で、その進化が停留する時期がある。 この時期は年齢とメタル量に依存する。この等級を水平枝との差で ΔT1(Bump-HB) と表す。6 Gyr より古い星団ではこの量への 年齢の影響が小さい。(Thomas 1967, Iben 1968) メタル量を次の式で表す。[Fe/H] = a + b ΔT1 + c ΔT12 表11に係数 a, b, c を示す。図9には3種の方法で決められたメタル量との 関係を示す。 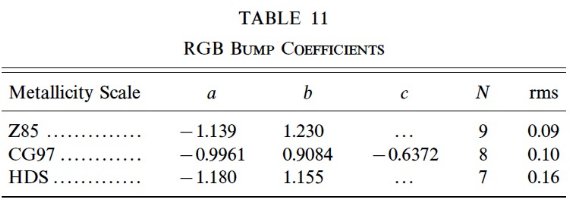 表11.赤色巨星枝勾バンプ等級の係数  図9.3方法のメタル量と赤色巨星枝バンプ等級との関係 |
|
RR Lyr 不安定帯の限界は理論的からも観測からもよく決まっている。
多数の RR Lyr 星とHB 星が存在する星団ではその境界の固有カラーと
観測カラーの差から赤化が導かれる。NGC 1851, 4590, 5272, 6362, 6752,
7078 ではそのようにして赤化が得られた。 NGC 6752 には RR Lyr が存在
しないのだが、不安定帯の端近くに青色水平枝星があるように見える。
一方、 NGC 6397 の最も赤い青色水平枝星は不安定帯よりかなり青側に位置
する。
(何を言っているのか? ) |
図2を眺めると、青色水平枝星はかなり緊密な系列を成しているが、 RR Lyr
星は暗く赤いのから明るく青い星までより散らばった分布を示している。この
二つの群れの境界はかなり良く決まっている。我々のサンプルからは、 ⟨(C-T1)o⟩ = 0.17 ±0.03 Sandage 1990 はこの境界を (B-V)o = 0.18 とした。これは Geisler 1996 の 変換を使うと、(C-T1)o = 0.22 に当たる。そこで、我々は (C-T1)o = 0.18 ±0.04 を採用した。 |
|
MT1(TRGB) を距離指標に I(TRGB) は最近よく使われる標準光源である。 Lee et al 1993 はこれが 距離指標として非常に有用であることを確立した。我々は T1 でもこれが 使えることを示す。図4を見ると、 [Fe/H] &le: -1.15 では MT1(TRGB) のメタル量依存性が非常に小さいことが判る。我々のサンプル中のこの範囲にある 星団6個の平均は、 MT1(TRGB) = -3.22 ±0.11 より高メタルでは MT1(TRGB) が急速に増加するので距離指標とし ては使えない。この振る舞いは MI(TRGB) でも [Fe/H] で見られる。 モデル等時線との比較 Geisler 1996 は T1 と Rc 等級はゼロ点で 0.003 等しか違わないので 同じに扱えることを示した。そこで、 Bertelli et al 1994 の等時線モデルの R を T1 と考えて比較したのが図10である。プラス印はモデルで、 [Fe/H] = +0.4 モデルで t = 10 Gyr, [Fe/H] = 0.0 モデルで t = 4 Gyr, それ以外は t = 12 Gyr である。四角は我々のサンプルである。一致は非常に良い。 MI(TRGB) は [Fe/H] ≥ -1.2 ではメタル量依存性が大きいが、 低メタル星では t = [3, 20] Gyr に対して一定値 MI(TRGB) = -3.22 を採用できる。 |
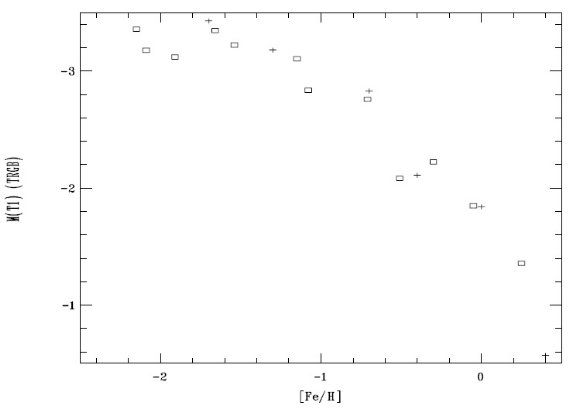 図10.TRGB MT1 とメタル量の関係。四角=標準巨星枝。 プラス=Bertelli et al 1994 のモデル等時線。[Fe/H] ≤ -1.2 では MT1 がほぼ一定値を取るので距離指標に使える。 |
| Da Costa, Armandroff 1990 が V, I バンドで行った解析を C, T1 バンドで 行った。サンプル球状星団の標準巨星枝の解析から TRGB の 2 等下での (C-T1)o カラーがメタル量推定に適していることが判った。 | ワシントン法は VI 法の3倍メタル量感度が良いことが判った。また、 ワシントン二色図法よりもほぼ全ての面で優れている。ワシントン法は 5 Gyr より古い星団のメタル量を決める際に年齢効果が無視できるほどに 小さい。 |