Maps of Dust Infrared Emission for Use in Estimation of Reddening and Cosmic Microwave Background Radiation Foreground


Schlegel, D.J., Finkbeiner, D.P., Marc Davis
1998 ApJ 500, 525 - 553



　アブストラクト

100, 240 μm から温度とコラム密度を出す。　

　COBE/DIRBE と IRAS/ISSA の全天 100 μm から 黄道光と点源を除いたもの を示す。ISSA マップではスキャンパターンを事前に除いた。DIRBE 100, 240 μm データからダスト温度を求めた。その結果、 100 μm マップをダストコラム密度に 直す事が可能となった。ダスト温度は 17 - 21 K である。この変動幅はコラム密度を 5 倍変化させる。その結果、DIRBE の精度と IRAS の分解能を兼ね備えたマップが 完成した。

HI との相関が強い　

　全銀緯に渡り、色々の大きさの糸状の模様が見えた。高銀緯ではダストマップは 21 cm マップと相関が良い。しかし、分子雲方向、HI 放射がサチっている箇所では ズレがはっきり見える。これに反し、高速度雲の方向ではダスト放射が弱いが、 それは予想されていた。

黄道光を除去と宇宙背景放射　

　DIRBE 100 μm と Leiden/Dwingeloo 21 cm との相関と DIRBE 25 μ から 黄道光を除去した。宇宙背景放射は 140 μm で 32±13 nW m-2 sr-1, 240 μm で 17±4 nW m-2 と驚くほど高い。 これはハッブルディープフィールドに検出される光学銀河からの総計の２倍である。

応用例　

　これらのマップの主な応用は銀河系の減光を新しく決めることである。その較正 には楕円銀河のカラーが用いられた。銀河団中の最も明るい 106 楕円銀河と 384 楕円銀河の B - V と Mg ライン強度を使って、ダストのコラム密度と 減光量との関係が較正された。このマップは Burnstein-Heiles 赤化マップに 比べ赤化が低いから中間の領域で２倍の精度を持つことが判った。赤化が大きい所 ではさらに高精度となる。また、宇宙背景輻射に混入するダストからのミリ波放射 や軟Ｘ線吸収の評価にも使える。

　1.イントロ　

Burstein-Heiles との比較　

Burstein-Heiles 1978, 1982 ではダスト/ガス比をモデル化（北半球）したり 一定（南半球）と仮定した。今回はその比に何の仮定も設けない。我々の 仮定はもっと弱く、減光カーヴを一定とすることである。100 μm マップの 較正には APM 銀河サーベイ (Maddox et al 1990) を用いて行った。100 μm マップと HI マップとの相関がよいことから、我々は Burstein-Heiles との結果 から大きくずれることは予想していない。しかし、多くの糸状模様では減光が 大きい。それらは BH マップでは見過ごされてきた。さらに、低銀緯のオリオン やへびつかい座領域では HI 放射がサチっているがダストは依然として光学的に 薄い。

　２．DIRBE マップから得たダストコラム密度　　

　２．１．DIRBE データセット　　

マップの再構成　

　DIRBE データは 393,216 0°.32 ×0°.32 ピクセルから成る。我々は その 41 週マップから年平均マップを "sky-cube" 投影で作製した。それを次に 通常の ランベルト投影、0.0250 deg2分解能、　に直した。

　２．２．黄道光の除去　　

DIRBE データの再制作　

　惑星間塵(IPD) は約 280 K の放射を放っている。黄道面上でその強さは 10 MJy sr-1 程度になり、その減光量は A(B) ≈ 10-6 mag である。25 μm マップを IPD 混入モデルの作成に用いた。 全波長で同じ時期のデータが使われるように DIRBE 年間平均データを再制作（？） された。黄道光混入のゼロ点は高銀緯での HI マップで制限した。

　２．２．１．時間と太陽離角　　

DIRBE マップの筋模様　

　COBE の観測戦略により、黄道付近ではデータの S/N 比が低い。ピクセル当たりの 観測数は 黄道面で 200、 黄極で 800 である。DIRBE マップには黄道に対して垂直な 筋模様が見える。天空上で隣り合ったスキャンは時間的に異なる走査に対応していて それらは太陽離角が変化しており、異なる IPD コラム密度を通して見ているからで ある。

太陽離角の影響が強い　

　各週の観測から「週別スカイマップ」を作った。これを足して年平均スカイマップ が作られた。「週別スカイマップ」は全天をカバーしない。しかし、それを眺めると 深刻な問題が浮かび上がってくる。黄道面付近では 25 μm フラックスは太陽離角 e の強い影響を受けている。41 週間の間に e = 64° - 124° 変化し、 フラックスはファクター２変化した。100 μm IPD フラックスとの比較も e に関し強い温度変化を示した。これは IPD 密度の動径変化を考えれば容易に 説明できる。視線が太陽近くを通過する時は太陽離角が大きい時より高温で大量の ダスト層を通過するからである。問題をさらに複雑にするのは１０個のパスバンド は全てが同時には観測されていない。年間平均マップは観測回数で平均されている だけで太陽離角の効果は考慮されていない。

重み付き年間平均スカイマップ　

　測定ノイズより観測時期による系統的変化の方が大きい場合には単純な回数 平均は不適当である。あるピクセルに付加される重みは 25 μm と 100μm マップとでは異なる。こうして重み付き年間平均スカイマップが作られる。それらは お互いに比較しあえない。そこで、異なるパスバンドの同じピクセルに対しては 同じ重みを付けて 41 週間マップを再結合した。IPD 温度勾配は e が小さい箇所で 大きいので e < 80° のデータは除去した。こうしてできたマップは ノイズと人工的模様が年間平均マップより少し悪い。しかし、人工模様は両波長 で同じである。このため、25 μm マップは他波長での IPD 混入を除去するのに 使用可能となった。

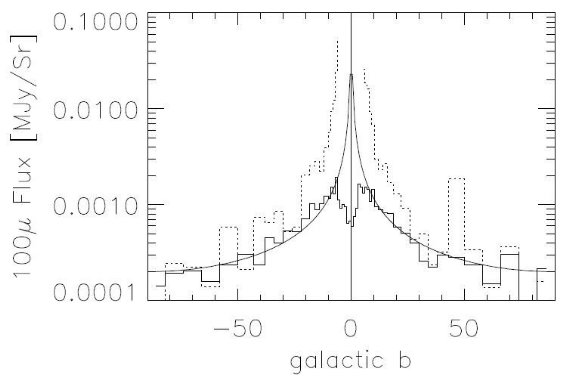
　２．２．２．黄道光のスケールとゼロ点　　

100 μm マップは H I は線形関係　

　黄道光の空間ー時間変化は複雑で解析的モデルを作るのは難しい。我々は 高銀緯で低フラックス領域では 100 μm マップは H I と線形の関係に あると仮定した。

25 μm マップは IPD 放射　

　25 μm マップは IPD 放射が支配的と考える。あるところではシラスが数％の 寄与をしている。そういう所は同じ黄緯の両側のピクセルから内挿して置き換えた。 一次近似として、25 μm マップを定数倍して 100, 240 μm マップから引いた。 これにより HI と黄道光補正の 100, 240 μm マップとの差の分散を最小化する 事を狙った。

25 μm マップによる黄道光補正　

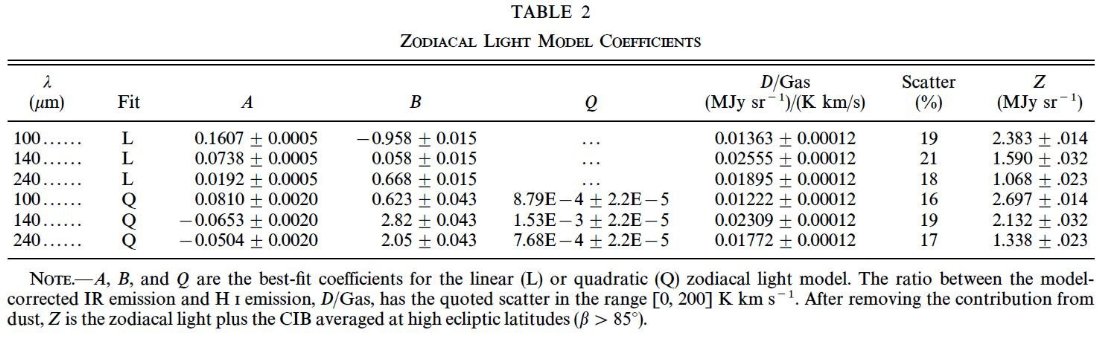
　12 μm と 60 μm とで黒体温度を仮定すると黄道と黄極とで 10 % 以下の 変化しかない。そこで第１近似として、IPD 温度を一定とする。DIRBE 25 μm マップを直接定数倍して長波長での黄道光成分と看做す。バンド b での 補正はしたがって、

　　　DbL = Db - AbD 25 - Bb 　　(1)

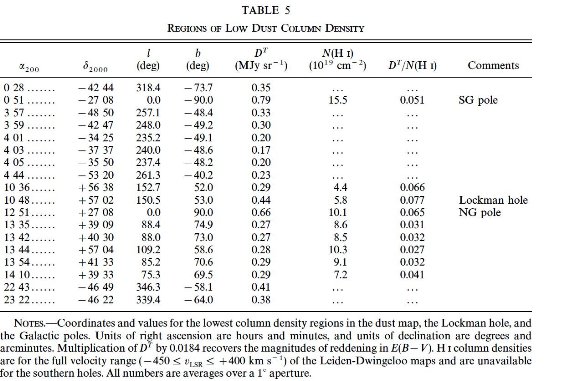
ここで、定数補正値 Bb は非黄道光補正、例えば銀河系や系外銀河 からの寄与、を表わす。25 μm マップは点源の寄与が小さいが、強い１０点源 は局所平均の計算の際にはマスクした。それらは表１に載せた。それらは 100, 240 μm マップではマスクされていない。


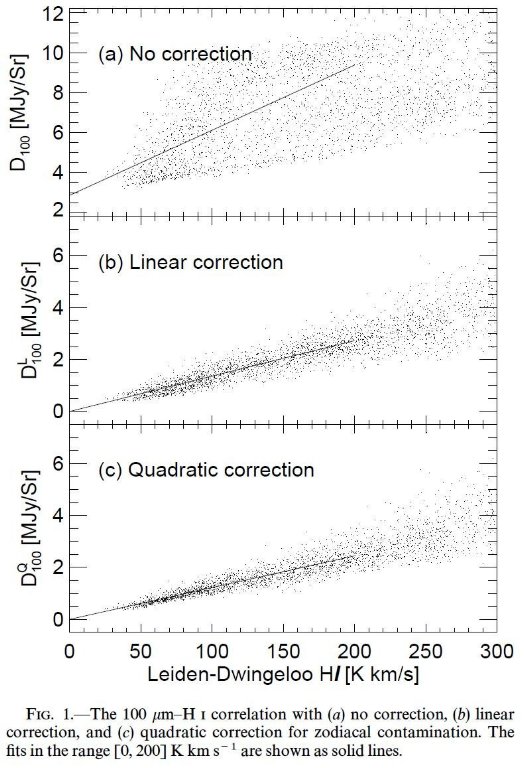
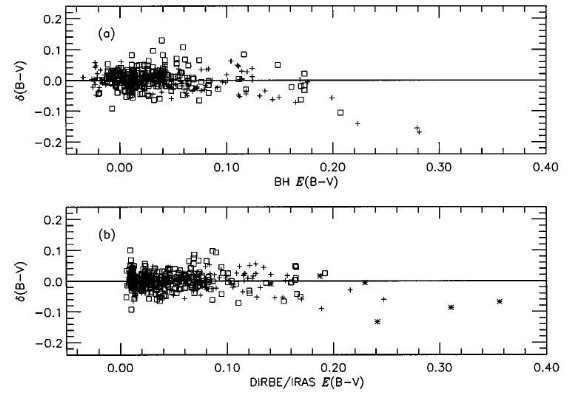
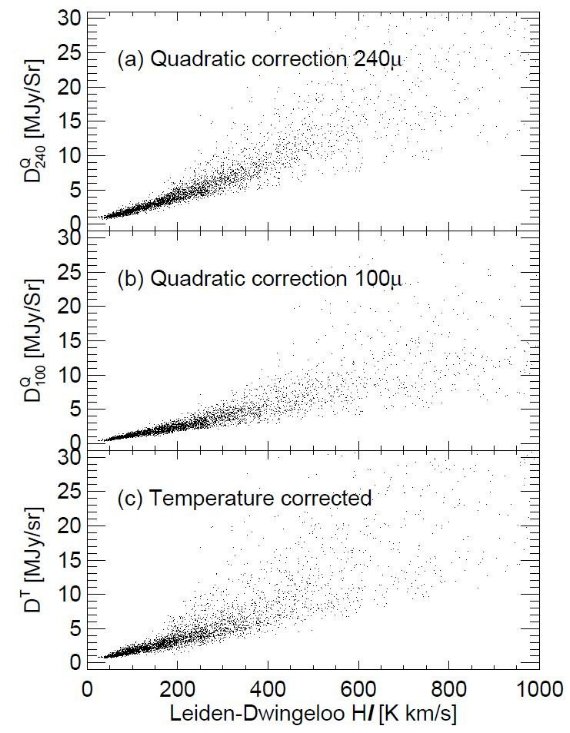
図１．100 μm - HI 相関図。(a) 補正なし。(b) 一次式補正後。(c)二次補正

 黄道光モデルの係数　

　HI 柱密度を DL と比べた。21 cm 放射は -72 < vLSR < +25 km/sec で積分された。この 21 cm 放射がDbL と 比例するとして、最小二乗法で (1) の係数 Ab と Bb を 決めた。

IPD 温度の変化によるエラー　

　12/25, 25/60 のカラー温度を決めると放射率の α = 1 で 5%, 2 で 10% の 温度変動がある。100 μm バンドはスペクトルのレイリージーンズ帯にあるので この結果は黄道光にそのまま 5 - 10 % の誤差となって跳ね返る。黄道では黄道光の 100 μm での寄与が 10 MJy sr-1 に達するので、これは 1 MJy sr-1 のエラーを意味する。

二次の黄道光補正　

　近似を上げるために次の式で二次の補正を行った。

　　　DbQ = Db - [ Ab + Qb D25] D25 - Bb 　　(3)

　結果は図１（ｃ）に示した。分散は線形近似で 19 %, 二次で 16 % である。240 μm ではその差はほとんどない。Leiden-Dwingeloo 観測の代わりにベル研 HI サーベイを使用した結果 100 μm マップのゼロ点の変化は 0.013 MJy sr -1 になった。


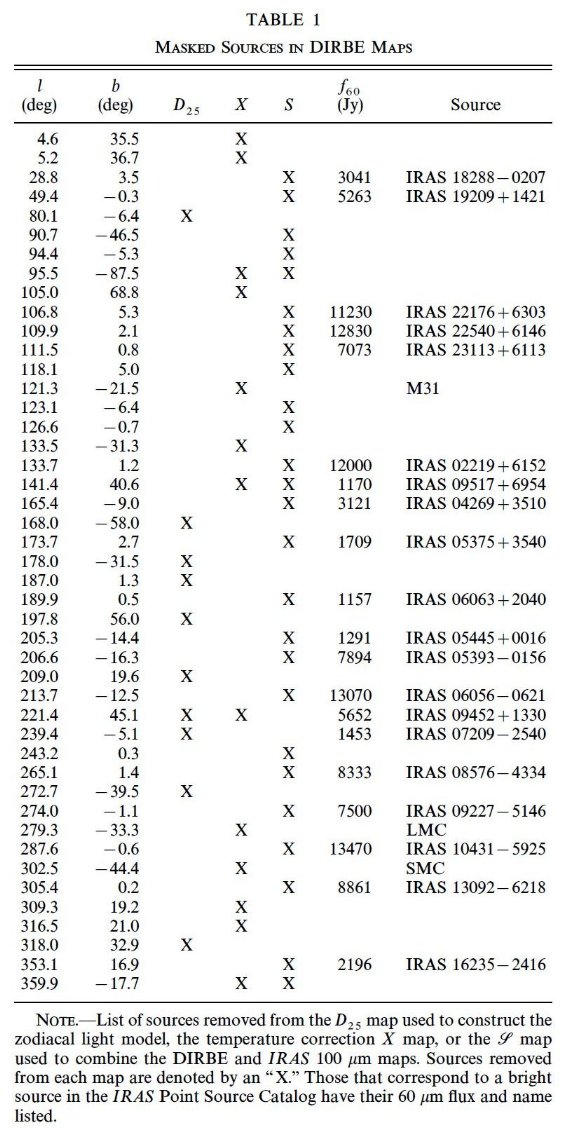
表１．マスクされた天体のリスト。

表２．黄道光モデルの係数。Ｑは二次式フィットの係数。Ｚは IR 放射強度と HI 強度の比。

フィットの係数　

　原則としてフィットは HI ガスとダストの総柱密度との間で行われるべきである。 ダストの総柱密度は 100 μm と 240 μm マップの複雑な関数であり、黄道光 係数は両マップに対して同時に決定する必要がある。二つの非線形フィットの係数 ６個は安定でない。それは、 DIRBE 240 μm 高緯度領域での S/N 比が低過ぎる からである。そのため、 100 μm と 240 μm のそれぞれで独立に係数を決め た。ダスト温度が黄緯によって大きく系統的に変化しない限り、我々の黄道光モデル に対するフィット係数は正しいと考えられる。２．３節で論じるが、ダスト温度の 銀緯による変化はノイズを越えるほどでない。

フィットの定数項　

　最小二乗近似は黄道光の除去にのみ用いられた。除去が上手く行ったかどうかは 遠赤外光と HI 放射との間の分散が最小かどうかで判る。 HI 放射に付随しない ダスト光、例えば HIIR 内ダストからの光のようなものもある。そのような場合、 フィット係数の解釈が変わる。傾き Ab は電離ガスが混ざった中性ガス を意味するが、下駄の Bb は装置オフセット、宇宙背景輻射、地球を 丸く囲むHIIR 内のダストが原因となる。

黄道光除去エラーの影響は小さい　

　この様な黄道光除去法は最終的とは言えない。 DIRBE チーム (Kelsall et al 1988) による３次元モデルが進行中である。しかし、現在の解析には、我々の モデルで十分である。最悪の場合、100 μm の黄道光削除後のマップで残差の 分散 HI < 100 K km/s が黄道光の差し引きミスが原因であったとしても、この エラーの rms は 0.05 MJy で A(B) = 0.004 にしかならない。

２．３．黄道光除去により宇宙背景輻射(CIB)検出　　

黄道塵温度一定の理由　

　DIRBE 観測の主目的の一つは CIB を測定することであった。これは大変困難な 課題で、現在まで上限しか得られていない。今回のフィット式の定数項は CIB 検出 か、装置の人工的な効果を意味する。黄道塵は薄い円盤状分布なので、黄緯が高い 方向では塵と太陽との距離は 1 AU で一定であり、したがって温度も共通であろう。 黄緯が高い方向では塵温度を同じと看做すのは合理的である。このように、線形モ デルは黄道光の除去には十分なのである。しかし、黄道と黄極とで 25 μm マップは 3.5 倍しか変わらない。適当なレバーアームが重要である。

表３．100, 140, 240 μm における宇宙背景輻射



100 μ では失敗。140, 240 μm は？　

　100, 140, 240 μm に |β|の関数として線形回帰解析を行った結果を 表３に示す。エラーは 95 % 形式的確実度の巾を示す。選ばれた黄道光モデルが 原因の系統誤差は含まない。定数項Ｂに対するエラーは主に係数Ａの共変関係 の結果である。 100 μm では CIB 検出は出来なかった。黄道光が強過ぎる ためである。140, 240 μm では 定数項 B はゼロではない。これはおそらく CIB 検出であろう。


　２．４．DIRBE 温度マップ　

100μm/240μm からカラー温度を決める　

　DIRBE＋λ-2放射率 で決めたダスト温度は 17 - 21 K の範囲に 分布している。この温度範囲に対し、100 μm 放射強度は 5 倍の変動を示す。
x=1.4388/λ(μ)T4だから、 0.4343x=0.6249/(λ(μ)T4)で、0.6249/(100*0.0017)=3.68, 0.6249/(100*0.0021)=2.98である。つまり、ウィーン域なので、10(3.68-2.98) =5 倍となる。
したがって、ダスト柱密度の導出には温度情報が重要である。DIRBE には 100, 140, 240 μm の 3 バンドがある。それぞれの S/N メディアン値は |b| = 10° で 164, 4.2, 4.9 である。100 μm での S/N が高いので、このマップに 100μm/ 240μm から決めたダスト温度を書き込んでいく。140μm は S/N が低く、100 μm に近いので使わない。

　２．４．1. ダストの遠赤外スペクトル　

吸収係数の波長依存性は α ≈ 2.0 　

　星間物質は遠赤外で光学的に薄いので、

Iν = ∫ds ρ κν Bν(T)


である。一般に吸収率は遠赤外ではべき乗則に従うので、

κν ∝ να


Draine, Lee 1984 モデルによると、遠赤外ではグラファイトが支配的で、 α ≈ 2.0 である。仮に非晶質炭素だと α ≈ 1.0, シリケートなら α ≈ 1.5 となる。我々は α ≈ 2.0 を選ぶ。この選択は 温度評価に直接響くが、最終的なダスト柱密度は α にそう依存しないことが 後で判る。その原因は DIRBE のバンドがウィーン領域にあることによる。 		複温度のダスト柱密度への影響は１割以下　

　半径 a > 0.05 μm の「古典的」グレインは星間輻射と熱平衡にある。 この先で各視線方向に単一温度を付与するが、もし視線が複数の温度領域を通る 場合、単一温度だと柱密度を系統的に低く見積もる結果となる。図２には、． 18° のダストに、温度 TB のダストを割合 fB で混ぜた時、単一温度でフィットした場合の柱密度の見積もりを示した。 15 K < TB < 21.5 K の範囲では見積もりは低く出るとしても 10 % 以下である。ファクター 2 の差が生じるのは、 TB < 12 K か、 TB > 33 K の時である。 ことに注意せよ。

非常に小さいダストの寄与は無視する　

　 a ≤ 0.005 μm の非常に小さいダストは無視した。それらは IRAS が発見した 12 - 60 μm のシラス放射に寄与するが λ > 100 μm への貢献は小さい。


図２．18° のダストに、温度 TB のダストを割合 fB で混ぜた時、単一温度でフィットした場合の柱密度の見積もり。見積もりが常に 低く出ることに注意せよ。


　２．４．２．温度マップの形成　

スムーズ化　

　100, 240 μ マップはノイズが高いので、低 S/N 領域ではフィルタリングが 必要である。一つのやり方はもっと大きいビームで均すことである。これは細かい スケールの情報を捨て去ることになる。Wiener filter 法では高 S/N 領域のビーム をそのままにしておく。しかし、高 S/N ピクセルの傍の低 S/N ピクセルに重みが 掛かり過ぎ、明るいソースの周りにハローを生じさせる。 　ハローが生じないようにする方法は、各ピクセル毎に局所的にフィルターを 掛けることである。ダストが殆どない領域の温度は一様と仮定する。

強度比マップ R 　

　まず M31, LMC, SMC など 13 天体を除去した。次に FWHM = 1°.1 のガウシアン フィルターを 100, 240 μm マップ全体にかける。このマップ上に強度比　

R = D100S/D240 S


ここに、

DbS = W DbQ + (1-W) ⟨ DbS ⟩


DbS はガウシアン平滑化した後の局所的 DIRBE フラックス と、背景平均フラックスとの重み付き平均である。背景平均フラックス ⟨ DbS ⟩ は南銀極と北銀極で定める。

この後のＷ決定法は省略する。

カラー補正ファクター Kb(α,T) 　

　強度比マップ R からカラー温度へ移るには、ダストの輻射率モデルと DIRBE 装置 の振動数反応率 W(ν) が必要である。これらは以下の式で結び付く。

Kb(α,T) = ∫ dν Bν (T)να W(ν)
なぜＫがカラー補正ファクターなのか、判らない。 		モデル強度比　R(α,T)の計算　

Db = Kb(α,T)Ib (T)


ここに、Ibは b における本当の輻射強度、D は観測出力である。 K に T が入っているのは、入力フラックス(変形 BB(T) を仮定)がソース温度 T で形 が変わり、観測バンド内で感度曲線と非線形な反応を起こすからである。

Ｋをこう使うんなら、
Kb(α,T) =[ ∫ dν Bν (T)να W(ν)]/[ ∫ dν Bν (T)να ]
じゃないのか？

R(α,T) を計算するには、

R(α,T) = D100 = K100(α,T)I100(T)
D240 K240(α,T)I240(T)


を多数のＴについて計算し、内挿式を作った。こうして決めた温度Ｔのマップを図３に 示す。白は高温、黒は低温部を表わす。空の大部分は中間灰色であるだが、高銀緯の 分子雲が暗い糸状模様を示している。幾つかのホットスポット（白）は LMC, SMC, Ophiuchus, Orion の O 型星である。

柱密度の計算　

　基準温度を To = 18.2 K とし、

DT = D100Q X

X(α,T) = B(To)K100(α,To)
B(T)K100(α,T)


ここに B(T) はプランク関数。X は観測 100 μm フラックスをダスト(温度 T ) が規準温度 To だったとした時のフラックスに変換するファクターである。 上の R(α,T) と　X(α,T) の式を連立させて T を消去する。すると、 Ｘ を R の関数として導くことができる。

log X = -0.28806 - 1.85050(logR) - 0.02155(logR)2


ダスト温度 T は R の式を逆に解いて、

log T = 1.30274 + 0.26266(logR) + 0.04935(logR)2


DT マップが我々の求めるダスト柱密度である。



図３．α=2 の場合の温度マップ。左は NGP 中心、右は SGP 中心のランバート 投影図。数字は銀経。銀緯は 30° 毎。低温分子雲と高温星形成域 に注意。


　３．ＩＲＡＳ分解能に折り込む　

ISSA データの再解析手順　

　COBE の長所はフラックス較正とゼロ点ドリフトの補正がよいことである。欠点は 分解能 0.7° FWHM で粗く、糸状構造や点光源を検出できないことである。 そこで、IRAS データのより良い分解能の利用を考えた。再解析に用いたのは IRAS Sky Survey Altas (ISSA) で、次の手順を施した。

１．ISSA プレートを destrip し、人工効果の振幅を 1/10 以下にする。
２．deglitching アルゴリズムにより、細かい模様を消す。
３．3 % の IRAS 欠落部分は COBE データで補う。
４． > 1° の IRAS ゼロ点ドリフトは DIRBE により補正。
５．各分解能は IRAS の 6'.1 にする。
６．銀河は除去。
７．星は |b| > 5° でf100 > 0.3 Jy まで除去。

これらの措置で、黄道光の混入は無くなった。

　３．１．縞模様を消す　

フーリエ空間での縞の除去法　

　IPAC が行った縞模様除去の後もまだ縞々が残っている。そこで、我々は ISSA を 構成する 430 枚のプレートの一つ一つのフーリエ変換を得た。その例を図４に示す。 中心から発している光線が縞を表わしている。通常、IRAS は異なる角度で 2 - 3 回 走査するので、フーリエ空間への混入は異なる波数で起こる。そこで、他の角度での 走査からの相当波数で起き換えられる。



図４．(a).IRAS HCON-0 画像。(b). フーリエ変換。中心が波数＝０． (c). 縞模様除去後の画像。(d).除去後のフーリエ変換。

　３．１．１．悪い波数の基準　

　まず、３枚の HCON 画像を重ねる。次に周りより 0.7 MJy sr-1 以上 高いピクセルを周囲円環の中間値で置き換えられる。次に、6' FWHM のガウシアン 平滑化を施した。縞模様は波数の極座標表示では放射状になるから、各θ 毎に メディアンを求め、それを背景パワーとする。それとの比 γθ が 1.2 より小さい場合は「良い」、1.6 より大きい場合は「悪い」とする。

　３．１．２．アルゴリズムの説明　

　各 HCON 毎に縞消去を行い、その後加え合わせて結合マップを作った。領域カバーが 不完全な画像もあるので、フーリエ空間での加算は不適当である。そこで実空間で縞 の除去を行った。

良いパワー　

　こうして、γθ < 1.2 の「良い」パワーだけから 「よい」パワー Fgood を得た。図５には一次元パワースペクトルの比 を示す。縞消去の結果、高振動数部分がファクター２程度抑えられることが判る。





図５．縞消去画像と生画像のパワーの比。データはプレート199, 216, 217 より。


　３．２．グリッチの消去　

　その他、小惑星のような一時的天体、検出器のグリッチなどがある。複数回の観測 があると、それらを同定、消去できる。

　３．３．ＩＳＳＡとＤＩＲＢＥの比較　

ISSA マップを DIRBE に合わせる　

　ISSA と DIRBE データの結合の目的は IRAS の高空間分解能と DIRBE の高範囲 較正を保持することである。ISSA HCON-4 マップは黄道光除去後の DIRBE 100μm マップに対し、1° 以上のスケールではゼロ点とカラー応対が合致するよう処理 された。IRAS データが存在しない領域では DIRBE 分解能マップで代用した。

WG(3'.2) ＝IRAS 画像の平滑化　

　Wheelock et al 1994 は 100 μm で　ISSA レベルは DIRBE より 38 % 高いこと を見出した。我々も IRAS シラスが同じ割合で高いが、点源は DIRBE と同じことを 見出した。 分解能を合わせるため、ISSA 画像を FWHM = 3.2' のガウシアンで均し WG(3'.2) を作った。

強度差マップによるゼロ点補正　

　1° より広いスケールでの IRAS ゼロ点を DIRBE に合うよう補正するため、 強度差マップ G を作製した。この G を縞消去 IRAS マップ Ides に 加えることで、最終マップが IRAS の細かい空間情報と DIRBE の大きいスケールでの 較正との双方を保持するようにした。

Icorr = C・Ides* WG(3'.2) + G
強度差マップの作成　

　強度差マップは同じ空間分解能のマップ同士で引き算を行わなければならない。 しかし、IRAS, DIRBE のどちらも PSF がガウシアンでないのでこれは困難な作業 である。 DIRBE PSF は 42' × 42' でべき乗型テールを有する。ただ、何度 も走査された結果、平均 DIRBE は半径 21' の丸い帽子型で近似される。この PSF を WSQ(21') と表わし、DIRBE の黄道光２次式除去後のマップを DQ として、

G = [DQ - C・Ides*WG (3'.2)* WSQ(21')]* WG(40')


明るい天体　

　IRAS と DIRBE とでカラー反応が異なるため、明るい天体の周りでは残差異常が 生じた。それらは、NGC 253, 銀河面、LMC, SMC である。これらの領域は周囲の メディアンで置き換えた。この操作は厳密には正しくなく、絶対エラーは大きくなる が、相対エラーとしては小さい。

IRAS 未走査領域　

　ISSA 空白域は 境目の扱いに注意してDIRBE データで埋めた。詳細は省略する。

ダストの柱密度　

　100-240 μm 放射に関与するダストの柱密度は次の式で求めた。

　DT = Icorr X

ここに DIRBE 100 μm フラックスを補正済み IRAS 100 μm フラックスで 置き換えた。温度補正マップＸは DIRBE 空間分解能の 1° である。ただ、 再処理された IRAS マップの分解能は 6'.1 である。

　４．点光源と銀河の除去　

　減光マップのためには銀河系の赤外シラスが大事である。我々のダストマップに はダストからの拡散光とボクグロビュールのような局所的塊りを表わす。 星、惑星状星雲などの点状光源はマップから除去されなければならない。系外天体 も一定のフラックス値にまで下げる必要がある。。

　４．１．戦略　

ピクセル値の置き換え　

　目標は汚染源を最もそれらしい値で置き換えることである。最も簡単な解はフラッ クスにその PSF を掛けて光源から差し引くことである。しかし、 PSF の形はガウ シアンでもなく、円対称でもない。その上、形が走査の方向に依存する。これらの 不定性、および系外天体の多くは点光源でないことのため、PSF 差し引き法は取ら ない。点光源に対しては、5'.25 以内(f100<10 Jy)又は 7'.5 以内 (f100≥10 Jy) を周辺のメディアン値で置き換える。拡がった天体 の場合、観測半径＋1'.5 以内のピクセルを内部と同じ面積の周囲の円環内メディ アンで置き換える。

置き換えの例外　

総計で |b| > 5° では 1.2 % のピクセルが置き換えら れた。LMC, SMC, M31 のピクセルは除去されない。|b|<5° では銀河や星の 除去は PSCZ 銀河探査と混同のおそれがない領域でのみ除去した。 IRAS 100μm マップではシラスとの混同があるので天体の同定は行わない。その 代わり、シラスとの混同の可能性が低い 60 μm 点源カタログを使って同定が 行われた。

　４．２．系外天体　

　IRAS が検出した銀河には広範な研究が行われた。多くの近傍銀河は ISSA 上で 角度分解されている。LMC, SMC, M31 M32 は例外として、大きな銀河 70 個が我々 のマップから除去された。銀河の半径 ＝ 25 mag arcsec-2 + 1'.5 として除去、置き換えを行った。NGC 253 の半径は　36' として IRAS ヒステリシス 効果を除いた。

　同定された 5320 銀河、98 系外HIIR, 210 星、136 PN が除去された。

　４．３．星の除去　

　Strauss et al 1990 によると、f602 < f12 f25 が星の領域である。|b| > 5° では f60 > 0.6 Jy の　4697 星がマップから除去された。


　５．マップを用いて赤化を決める　

BH マップ　

　過去１７年間 Burnstein, Heiles 1978, 1982 の減光マップが用いられてきた。 これは HI 21 cm に基づくものである。δ > -23° では、較正が 13 deg2 での Shane-Wirtanen 銀河カウントに基づく局所 HI - ダスト 比を使用している。一方、 DIRBE/IRAS ダストマップは直接にダストを測っている。 HI の電離、分子化、光学的厚みなどを配慮する必要はない。その上、 DIRBE/IRAS マップは質が一様である。これに対し、BH マップは |b| < 10° は省き、 その他にも 21 cm データのない SGP 付近の 1080 deg2 領域が除かれ ている。

赤化式　

　我々が用いた赤化式は、
E(B-V) = p DT = p Icorr X

ここに、DT は点源除去後の、IRAS 分解能、DIRBE 較正 100 μm マップ である。

ダストマップのテスト（Ｉ）　

　銀河の赤化はマップの較正を直接行う方法である。例えば、Postman, Lauer 1995 による銀河団中最大楕円銀河のサンプルを見てみよう。106 銀河の B-R が与えられ ている。これらの赤色偏移は z < 0.05 で、全天に均一に分布している。我々は 論文から k-補正後のカラーを採る。E(B-R) = 1.64 E(B-V), RV = 3.1 としよう。
　まず、銀河の固有 B-R と E(B-V) との間に相関がないと仮定する。BCG 銀河の固有 B-R 分布はガウシアンではないので、ノンパラメトリック統計で検定を行う。 Spearman rank 相関係数を減光補正 B-R と E(B-V) の間で決めた。p < 0.0118 と p > 0.0196 では認められる相関がランダムな分布から出現する確率は 5 % 以下で あった。したがって、マップの規格化に対して 95 % コンフィダンスで　p = 0.016 ±0.004 である。このやり方を確認するため、同じ統計を BH 赤化則、 E(B-V) = q EBH に対し適用した。ここに EBH は BH (B-V) 赤化である。0.66 < q < 1.05 に対し　BCG 銀河は B-R と赤化に何の相関も 示さず、 q = 1 が許容されることを示した。

ダストマップのテスト（ＩＩ）　

　Faber et al 1989 によると、Mg2 指数は楕円銀河の固有 B-V カラーと 強い相関がある。メタル量、星種族年齢が増すと、Mg2 指数は大きくなる。 この指数は赤化に影響されない。Faber et al 1989 に乗っている 472 楕円銀河は 全天に渡り、かつ赤化の強い領域内にも分布する。カタログ中の 389 銀河は ≤ 30" アパーチャでのカラー、Mg2 指数, 赤化が与えられている。 内 5 個は観測が怪しいので除いた。k-補正、赤化補正後の B-V カタログカラーは BH マップからの補正値と少し差がある。ある領域、 230° < l < 310°, -20° < b < +15° では、BH マップはデータを欠いている。
　我々自身の再解析のため、カタログ B-V カラーに表から赤化量を加えて、 k-補正 のみ施された B-V カラーに戻した。このサンプルに対して赤化補正を行い、 得られた(固有)B-V を　Mg2 指数 に対して１次回帰式で表わした。 この式の値と(B-V) との残差 δ(B-V) を計算した。 δ(B-V) と使用した E(B-V) との Spearman rank 相関係数を計算して、残差に相関があるかどうかを 調べた。BH 赤化を使用した場合には残差相関は見られなかった。DIRBE/IRAS マップ に p = 0.0184±0.0014 を用いた結果は, δ(B-V) の標準偏差が 0.028 に落ちた。しれぞれの結果を図６に示す。
BCG サンプルによる p の絞り込み　

　Faber et al 1989 サンプルは大きくて、固有カラーの分散が小さいので、 p に より強い制限を課すことができる。これは Rowan-Robinson et al 1991 が IRAS データのみで行ったことだが、IRAS のゼロ点が不安定な為にあまりよい結果は得ら れなかった。赤化エラーが赤化の大きさに比例するとして、
σD-I = F EB-V)

と仮定する。さらに、Mg-カラー関係の内部分散を σBV = 0.0257 とする。この分散は空の綺麗な領域での実測値である。各銀河の総エラーは σ D-I と σBV の二乗和になる。f を増加させていき、 フィットの &ki;2 が自由度になった所で止める。そこが赤化のエラー である。こうして、 BH モデルでは f = 0.29, 我々のモデルで f = 0.16 を得た。 つまり、 DIRBE/IRAS 赤化波精度 16 % である。

銀河系数法が赤化決定に不適当なわけ　

　当初は APM 銀河探査(Maddox et al 1990) を使うつもりであった。しかし、問題 があった。APM を用いて決めた p は上に挙げた値の倍くらいとなった。 銀河カウントの感度がダスト量に対してこのように過剰に鋭敏なのは、銀河カタログ が等級と同時に表面輝度リミッテッドであるためである。前景のダスト が増えると、銀河からの総フラックスだけでなく、等輝度半径を縮小させる。この 結果、銀河が星に分類されたり、全くカウントされなくなったりするのである。




図６．(B-V)残差 対 Mg2 関係。
　　(a) BH マップ。 (b）DIRBE/IRAS マップ。＋＝南天で BH のダスト/ガス比
　　　情報が欠けた。* =　ＢＨ値がない。


　６．解析のまとめ　

　遠赤外データから、 100 - 240 μm 放射ダストの均質な柱密度マップを作った。 解析の主な段階は次のようにまとめられる。

１．年平均 DIRBE マップは同じ黄道光ダストが再生されるよう処理された。太陽 角が 8° 以下のデータは用いなかった。

２．DIRBE 25 μm マップを用いて黄道光モデルが構築された。モデルパラメター は高銀緯でダストが HI 21 cm 観測結果と合致するように調整された。

３．IRAS/ISSA 100 μm マップ上の縞模様はフーリエ空間フィルタリングで 除いた。

４．小惑星や他の非ガウシアンノイズは非グリッチ化アルゴリズムで除いた。 		５．IRAS と DIRBE 100 μm マップを結合した。DIRBE ゼロ点と較正は保存した。

６．f60 > 0.6 Jy の星と銀河は、|b| > 5° では殆ど 除去された。銀緯がそれ以下では部分的な除去が実行された。

７．ダストのカラー温度は DIRBE 100 μm, 240 μm マップから決めた。温度 修正マップを適用して、 100 μm シラスマップをダスト柱密度マップに変換 した。

８．温度補正ダストマップは、楕円銀河の赤化で較正した。B-V 対 Mg2 相関の利用により、較正の定数を 10 % 精度で求めた。


　７．議論　

　７．１．赤外シラスの性質　

細かい糸状構造　

　新しいデータは我々の最小スケールにまでいたる沢山の糸状構造を示す。図７． にはその一例を示す。BH イメージ、ライデン・ドウィングロー HI 画像、 DIRBE 分解能でのダストマップ、DIRBE/IRAS 分解能でのダストマップである。 この図は左側に Polaris Flare, 右側に Draco 分子雲複合体を示す。図の最も 小さい構造は IRAS データの分解リミットに近い。もっと高分解能データが あればさらに細かい構造が明らかになるであろう。

全天マップの特徴　

　図８には全天マップが示された。高銀緯の薄い模様を強調するため、図は対数 スケールである。糸状のシラスアーチが両極の間をつなぎ、幾つかの穴が見える。 ロックマンホール, l=150°.5, b=53°, はそれらの一つで、0.39 MJy sr -1 である。 南半球にはさらに遠赤外強度の低い領域がある。それは、 l=346°.4, b=-58°.0, l=239°.7, b=-48°.6, で 0.18 MJy sr -1 である。 残念ながら、それらが HI でも最低の穴になるかを実証 できる HI データがない。

穴の性質　

　穴の位置と輝度は表５にまとめられた。銀河南天の大きな領域、b < -40°, 160° < l < 320°, は低輝度で、宇宙背景輻射やレッドシフトサーベイ の際には前景混入の最も少ない領域として向いている。


表５．ダストの穴　



図７．l = 100°, b=+35° を中心に 90°×30° のマップ。
(a) BH マップ。(b) HI マップ。(c) DIRBE マップ。(d) DIRBE/IRAS マップ


図８．全天ダストマップ。（ただ説明と違い、左が北、右が北？）


揺らぎのパワースペクトル　

　高銀緯での８領域で強度揺らぎのパワースペクトルを計算したものが 図９である。どれにも特有のスケールが見られない。全体としては、 P(k) ∝ k-2.5 で表わされる。パワーの振幅は各領域毎に 異なる。これはシラス構造が極端に位相可干渉性を有することを示す。 揺らぎがランダムなフェーズパワーで近似できると仮定することは、シラス の記述として間違っている。

　７．２．ダストマップと HI マップとの差　

強度比の散らばりの原因　

　図１０に見られるように、ダストと HI との相関は低フラックスでは極めて 緊密である。しかし、高フラックスでは大きな分散が目立つ。240 μm は ダスト放射のレイリー・ジーンズ領域にあるので、100 μm マップよりは HI マップの方と相関がよいと期待できる。ところが、実際には逆で、240 μm 対 HI 図の分散が大きい。これは一部は 240 μm マップのノイズが大きいせい である。しかし、分散の増加は明らかに冷たい分子雲で起きている。そこでは 水素の大部分が分子で、かつ 100 μm は温度に対し指数関数的に反応するが 240 μm は線形に応答する。低柱密度の領域でも HI - ダスト柱密度　分散 が大きい。これは、視線方向に沿っての電離領域の割合が揺らいでいるためか、 ダスト対ガス比が実際に変動するためかであろう。

図９．ダストのパワースペクトル。実線は北銀河半球の４半球、点線は南 銀河半球の４半球。

　

図１０．HI 強度との相関。(a) DIRBE 240 μm. (b) DIRBE 100 μm. (c) ダスト柱密度。高密度ではガス対ダスト関係が劣化する。


ダスト対 HI 比　

　図１１には、ダスト対 HI 比を示す。HI ガスは -450 ≤ vLSR ≤ +400 km s-1 を × 0.0122 Mjy sr-1/K km s-1 で変換したものを用いた。この比には揺らぎがあり、それが空間的に固まっている ことから、ノイズに起因するパターンではないと思われる。高銀緯は大部分中性の 灰色である。ダスト対ガス比が高い所は白色で示されている。

高銀緯でダスト対ガス比が高い所　

　HI が飽和しているためダスト対ガス比が高いのは オリオン (l ≈ 180°, b ≈ -20°), へびつかい座 (l ≈ 0°, b ≈ 15°) である。 Polaris Flare (l ≈ 150°, b ≈ 40°) も目立つ。図１１を 図３と比較すると、ダスト対ガス比が高い所はダスト温度が低い箇所である。これは その領域が UV 光にたいして厚くなっているためであろう。銀河円盤の上に CO ガス を探す試み(Hartmann, Magnani, Thaddeus 1997) は失敗したが、この領域では水素 分子が大量に存在する可能性は強い。 		ダスト対ガス比が低い所　

　ダスト対ガス比が低い所は図では黒である。これらの領域は主に遠方の高速 HI 雲で、ダストがあったとしても照らす UV 光が弱いために低温で 100 μm 放射 が出ないのであろう。マゼラン流は一部が銀河南半球に一部があるが、高速度雲の 殆どは銀河北半球で目立つ。

比が変動する原因　

　ダスト対ガス比は銀河北半球では銀河系中心から反中心にかけて勾配を持つように 見える。南半球にもあるのかもしれないが、オリオン雲のために乱されて良く分から ない。高銀緯領域でもこの比には ±15% 程度の揺らぎがあり、それが 10° に渡るスケールで続くことから、実際にダスト対ガス比に変動があるのか、装置に よる人工効果かも知れない。

図１１．ダスト対ガス比。左：ＮＧＰ，　右：ＳＧＰ


高銀緯では　BH と DIRBE/IRAS 赤化は合う 　

　図１２は DIRBE/IRAS 赤化 - BH 赤化　のマップ（|b| > 10°）である。 BH マップは基本的には HI マップをゼロ点調整と銀河計数に基づいて作成した ものである。したがって、 BH 赤化マップは今回の赤化とオフセット値を除いて は高銀緯で非常によく一致する。オフセット値を直すと、0.02 等を越える箇所は 殆どない。 		ズレの大きなところ　

　しかし、低銀緯とオリオン、へびつかい座のような分子雲方向になると大きな 系統的なズレが現れる。これらの変異は図１１のダスト対ガス比に反映されている。 これらのずれは全天銀河計数では重要な影響を持つ。この論争はいまだに決着して いない。

図１２．DIRBE/IRAS 赤化 - BH 赤化。左：ＮＧＰ，　右：ＳＧＰ　


　７．３．銀極方向の赤化　

ゼロ点の決定が困難な理由　

　ダスト柱密度の絶対ゼロ点の決定は困難である。21 cm マップのゼロ点が不確実 なのは電波望遠鏡のサイドローブがあるからである。さらに、 21 cm マップからは 電離領域内ダストが消えている。DIRBE 装置は冷却板とのチョッピングでゼロ点が 安定しているが、DIRBE/IRAS マップでは黄道光の汚染と背景輻射のため不確実に なっている。赤化の直接測定も同様に困難である。系外銀河では固有が不明であるし、 系内天体では近傍星とハロー星の間でのダスト柱密度の較正が必要となる。これらの 比較は選択効果の影響を被り、数百パーセクより遠いところでの天体は使えない。 ある研究では銀極方向は減光がゼロと主張され、他の研究は E(B-V) &asymp: 0.02 - 0.05, 即ち A(B) ≈ 0.1 - 0.2 とした。

銀極方向の赤化　

　ゼロ点の議論はこれまで銀極方向での赤化量に集中していた。表５に見られる ように赤化最小点は銀極ではないが、大部分の研究は NGP か SGP に対して行わ れた。幾つかの大規模な研究が北銀極方向の A, F 型星のカラー測定に向けられた。 Hilditch, Hill, Barnes 1983 は 銀河面から 200 pc 以上上で b > 75° の A, F 星 34 個の平均赤化 E(B-V) = 0.011 を得た。特に 90 > l > 180 ° の４半面では E(B-V) = 0.000 であった。Perry, Johnston 1982 は類似の 研究で NGP 方向 200 pc 以内の星の赤化が無視できるほどであると結論した。 SGP では Perry, Christodoulou 1996 が SGP から 15° 以内の 73 星に対し、 E(B-V) = -0.010±0.016 という結果を出した。 		データの再解析　

　Teerikorpi 1990 はこれらのデータを再解析し、以前の結論には統計バイアスが 掛かっていることを指摘した。彼によると平均赤化は銀河面から 400 pc で E(B-V) = 0.04 である。

我々の銀極減光　

　我々の得た値は NGP の 10° 以内平均で E(B-V) = 0.015, SGP で 0.018 で ある。これは減光量に直すと、NGP で 0.065, SGP で 0.080 となる。100 μm でも HI でも銀極の放射を受けているので、銀極方向に非ゼロの減光を想定するのは 当然である。もし、A, F 型星にバイアスが掛かっていないのなら、観測されたガス とダストは数百パーセクより遠方にあることとなる。

局所バブルの影響　

　理論的には高銀緯のダストが完全に蒸発していると考えるのは不合理である。銀極 方向のダストは局所バブルの衝撃波に焙られるが、それは分子雲内部で進むと考え られるダストの合体に対して逆方向の効果を持つ。グレインサイズ分布はさらに小さ い側で頭打ちになり、 Rv を下げるだろう。しかし、UV, 可視域減光に効く小さな グレインを消滅させはしない。

DIRBE/IRAS 減光マップと BH マップとのズレ　

　多くの解析にとって赤化ゼロ点の変化は大きな影響を及ぼさない。しかし、遠方 ＳＮの測光に対しては効果は大きい。この効果を見落とすと q0 の 決定に大きな系統誤差を導きいれる。何故なら、減光補正は 近くの SN に対する B-, V- 等級の方が遠方ＳＮの R-, I- 等級より大きいからである。
　DIRBE/IRAS 減光マップと BH マップとの間にはズレが認められる。両者のズレの |b| > 45° でのメディアン差は E(B-V) にして 0.020 である。BH マップが 系統的に低い。我々は今回の結果の方が信頼度が高いと考える。



　７．４．宇宙背景輻射の測定　

系外背景光と宇宙星形成史　

　系外背景光(Extragalactic Background Light, EBL) の予想値は、
νIν = 0.007 ρB c2(ΔZ)(c/4π)(1+zf)-1
ここに、 ρBは現在のバリオン密度、ΔZ は赤方変位 zf の時代に作られたメタル量である。ΩB h2=0.025, ΔZ=0.02 とすると、 νIν = 37/(1+zf) nW m-2 sr-1 となる。したがって 背景光のレベルが高いことは低赤方変位でのメタル形成が盛んであったことを 意味する。星形成がダスティな領域で行われたかどうかにより、フラックスが UV/Visble/NIR で現れるか 100 - 300 μm 域で現れるかが決まる。

背景光の推定　

　2.3.節で黄道光と定数項の除去を論じた。表3にはその際の定数項 Bb が限界黄緯|β| の関数として載せられている。フィットを低黄緯へと広げる につれ Bb が低下することが判る。これは黄道光の線形モデルが不十分 なための現象である。しかし、|β| > 20° では 140, 240 μm フィ ットは安定となり、ゼロから 		有意に離れる。このフィットに基づき、我々は |β| > 30° モデルから導いた値を採用する。表3の値を変換すると、 νIν = 15 nW m-2 sr-1 (100μm), 32 nW m-2 sr-1 (140μm), 17 nW m-2 sr-1 (240μm) となる。

銀河計数との比較　

　この値は銀河計数(Malkan, Stecker 1997)から期待される背景光に比べ4倍大きい。 それよりは大楕円銀河に起きた巨大星形成活動に合うようだ。Puget et al 1996 は COBE/FIRAS データから 400 - 1000 μm で等方的な背景光の検出を報告している。 我々の背景光は彼らの測定の外挿線の上端に載る。

可視背景光　

　HDF における可視域背景光の値は Madau et al 1997 によると 7.5 nW m-2 sr-1 で、ここに報告された値の約半分である。Vogeley 1997 によると、検知される銀河をマスクすると残った拡散光成分の強度は個々銀河の和 に較べ極めて小さい。したがって、早期星形成はダスティな環境で起こり、放射光は 遠赤外で占められていた可能性が高い。



　８．まとめ　

減光マップ　

　IRAS は高空間分解能で、DIRBE はフラックスの絶対較正に優れていてダスト 温度の決定に向いている。点光源と系外銀河を除去してダスト柱密度マップを 作った。このマップは E(B-V) で与えられている。空間分解能は 6'.1 で 赤化の精度は 16% である。このマップは Burstein-Heiles マップと天空の 大部分で一致する。特に減光の高いところでの信頼度が高い。 		銀極　

　BH マップは E(B-V) で 0.020 低いと思われる。銀極では我々の値は A(B) = 0.065(NGP), 0.080(SGP) である。それより低い A(B) = 0.02 のホールがある。



　Appendix　B　様々なバンドでの減光量　

RV 変化の影響　

　DIRBE/IRAS ダストマップは減光に貢献するダストを忠実に反映していることを 示した。我々は E(B-V) を他のバンドに拡張する必要がある。

RV = AV = AV
AV - AB E(B-V)


RV は Clayton, Cardelli 1988 の測定では 2.6 から 5.5 の間で変化し、 薄い星間空間での平均値は 3.1 である。高密度領域では合体によりダスト半径が 大きくなるため、吸収がグレイになりその結果 RV は増加すると考えら れる。この変化は特に青い波長側で Aλ に大きな影響を及ぼす と考えられる。その効果は可視域では O'Donnell 1994, 赤外、紫外では Cardelli, Clayton, Mathis 1989 による関数でよく表現される。ただ、λ > 8000 A では変動は無視できる。

減光曲線の妥当性　

　幸運にも薄い星間雲では単一の RV ≈ 3.1 減光曲線を適用して よい。濃い星間雲の星を入れても Clayton, Cardelli 1988 の 76 測定の分散は RV ≈ で 0.7 である。これは、AV/A∞ で 10 %, AV/A∞ で 6 % の分散になる。驚いたことに 濃い Taurus-Auriga 星間雲の中にある赤化の大きな星でも Kenyon,Dobrzycka,Hartmann 1994 は RV = 3.1 を見出した。Rieke, Lebofsky 1984 は減光曲線が 1 < λ < 13 μm で適切であることを示した。


図１３．IRAS PSC 星の二色図。斜線が効果的に銀河（線の上）と星（線の下）を 分離する。四角の箱は厳しい基準で星だけを 70 % 選んだ。図には天体の １/１０ だけプロットしている。 		あるバンド b での減光 Δmb　

　あるバンド b での減光 Δmb は V バンドでの減光 δmV から下の式で求められる。

Δmb = -2.5 log [ ∫dλ Wb(λ) S(λ)10-(AλΔmV/2.5) ]
∫dλ Wb(λ)S(λ)


ここに、Wb はシステムの量子効率、S(λ)は天体の光子光度で ある。我々は楕円銀河の赤化をダストマップの規格化に用いたので、ここでは天体 として楕円銀河を採用する。Kennicutt 1992 から通常楕円銀河の平均 SED を求め、 彼の波長範囲外では S(λ) ∝ λ を仮定する。上式の表現は 低い減光の極限 ( ΔmV → 0 ) で評価し、次に AV = 1 にスケールし直すのである。

実例　

　システムレスポンスは大気、望遠鏡、フィルター、検出器のレスポンスの コンボリューションである。可能な場合には我々はフィルター毎に良く使われる 標準星に対するシステムレスポンスを採用した。全てのパスバンドに対する結果 が表６に載っている。有効波長 λeff はバンド全体に対する 減光と減光曲線上で同じ値を与える波長である。表の最後の列は減光量を光電 測光観測で決まる E(B-V) に変えるものである。RV = 3.1 ダスト モデルを採用して、ダストマップにこの列の値で掛け算をして与えられたバンド での減光を得るのである。




図１４．100 μm における暗い星の混入フラックス。実線ヒストグラムはカットオフ リミット以下の暗い星のフラックス。点線は個別に除かれた星の合計フラックス。


　　　　　表６．幾つかのバンドにおける減光強度


　Ａｐｐｅｎｄｉｘ　Ｃ　データ　

　100 μm マップ　とダストマップはウェブから取ってこられる。
http://astro.berkeley.edu/davis/dust/index.html

1. |b| > 5° では系外天体の除去に努めた。0.6 Jy (60 μm)は除いていない。

2. IRAS 未観測ゾーンと土星の周りはDIRBE データで置き換えた。

3.　IRAS と DIRBE の 100 μm パスバンドは少し異なる。補正を行った。

4. LMC, SMC, M31 はマップから除去しなかった。これらの銀河を通しての赤化の正確な な測定は不可能である。というのはそれらの温度構造がDIRBE の分解能では得られない からである。これらの銀河への典型的な赤化量は周辺の円環のメディアンから得た。
E(B-V)= 0.075(LMC), 0.037(SMC), 0.062(M31) である。 		5. |b| < 5° では混入源の除去は行われていない。銀河系の温度構造は 分解されていない。その上、我々の赤化と観測された個々の赤化との比較も 行われていない。したがって、この領域での赤化は信頼できない。

6.　ダスト柱密度から赤化への変換のエラーは 10%

7. DIRBE/IRAS ゼロ点を BH マップに合わせたいならば E(B-V) を 0.020 引くと良い。