Line Derived Infrared Extinction toward the Galactic Center


Fritz + 9
2011 ApJ 737, 73 - 93


　アブストラクト

　観測　
　ISO-SWS と SINFONI によるミニスパイラルの水素輝線観測結果を用いて、 銀河中心方向 1 - 19 μm の減光曲線を導いた。減光フリーのフラックス 基準には VLA で観測した 2 cm 連続光を用いた。

　近赤外減光則　
　内側 14″ × 20″ 領域で A2.166μm = 2.62 ±0.11で、λ < 2.8 μm でのべき乗指数 α = -2.11 ±0.06 であった。この値は最近の近赤外減光勾配の結果と 一致する。 		長波長側で平坦になる　
　しかし、より長波長になると減光はより灰色になる。炭素質 およびシリケイトのグレイからなる星間ダストモデルでこの 減光曲線をフィットすることは不可能である。氷を含む他の成分が 必要である。

　銀河中心距離　
距離に依存する減光を我々の距離に依存しない減光と結びつけて 銀河中心距離 Ro = 7.94 ± 0.65 kpc を得た。 Sgr A* (r<0.5″)に対しては AH = 4.21 ±0.10, AKs = 2.42 ±0.10, AL′ = 1.09 ±0.13 である。

　１．イントロ　

　減光曲線からダストの性質を探れる　
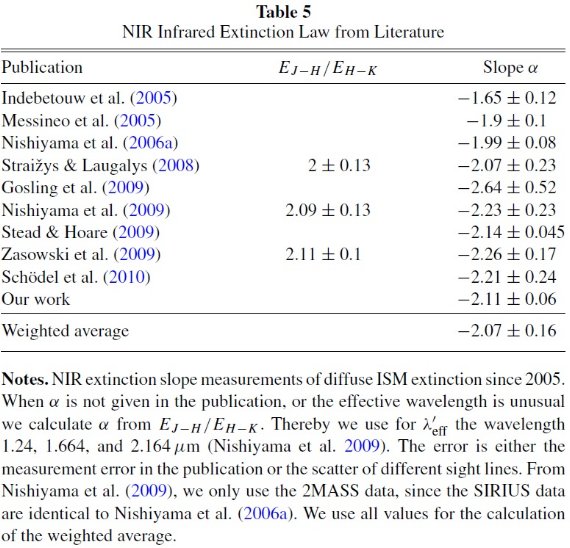
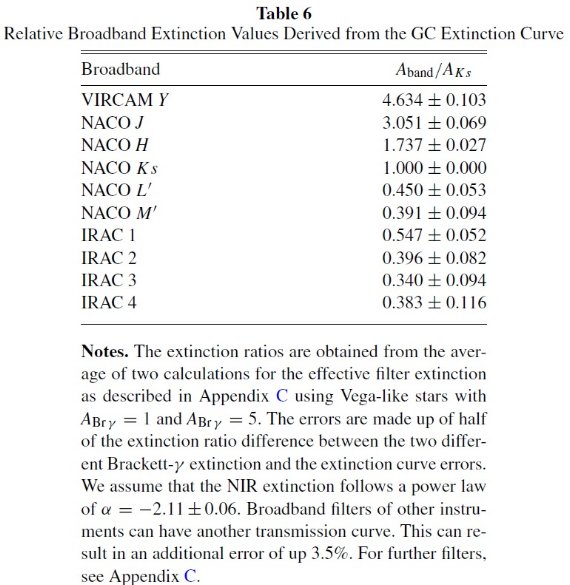
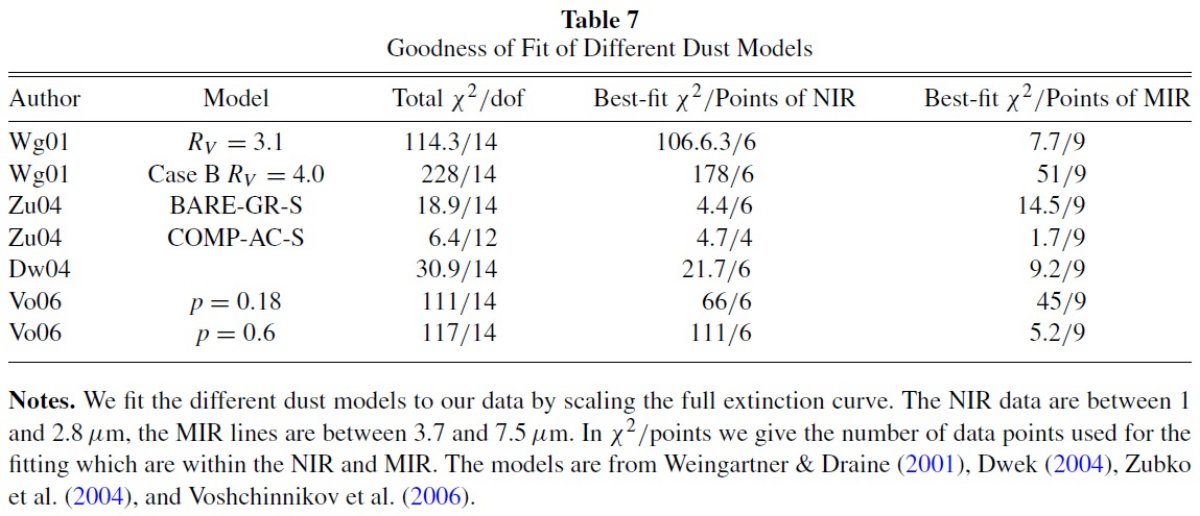
　赤外減光は大きな赤化を受けた天体の光度を復元するために重要であることは Schultz,Wiener 1975, Cardelli et al. 1989, Mathis 1990 の研究からも明らかである。加えて、赤外減光曲線からは星間ダストの 性質に対する重要な手掛かり (Compiegne et al. 2011) が得られる。減光曲線と放射を組み合わせるとダストのサイズと組成を導ける。 こうして、星間ダストはシリケイトと炭素質(Draine 2003)から成ることが判った。 しかし、さらに複合粒子、例えば氷や穴、も必要なのかについては未確定である。

　
　銀河中心は大きな減光のために赤外減光の研究に適している。 Rieke, Lebofsky 1985 は数個の赤色超巨星を用いて図１のような普遍減光則を導いた。

　レッドクランプの利用　
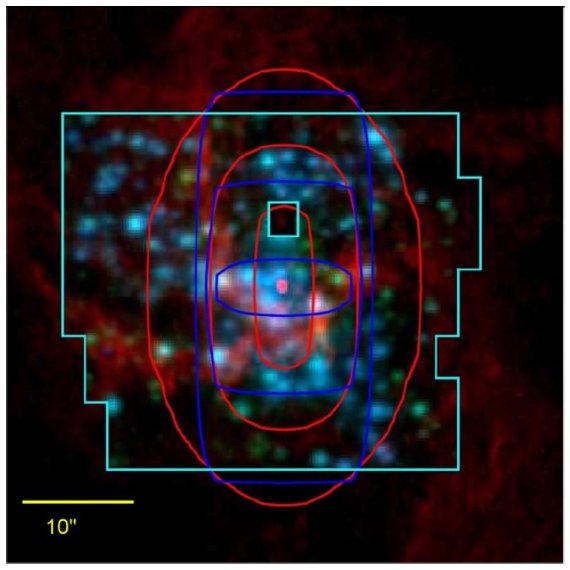
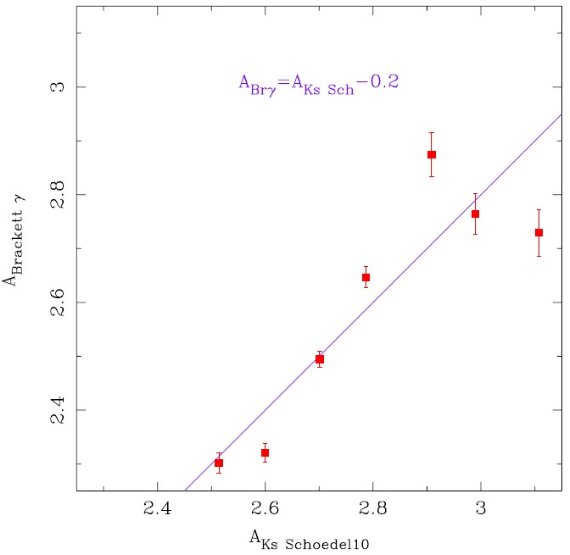
　 Nishiyama et al 2006 は多数のレッドクランプ星を用いて赤外減光を測定した。この方法では レッドクランプの絶対等級(Groenewegen 2008) と銀河中心距離(Reid 1993, Genzel et al 2010) が必要である。この方法を用いて、Schodel et al 2010 は Sgr A* 方向で AH = 4.35±0.18, AKs = 2.46±0.12, AL′ = 1.23±0.20 を定めた。

　水素輝線法　
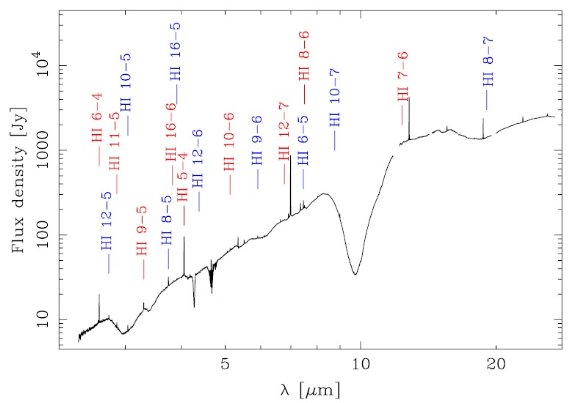
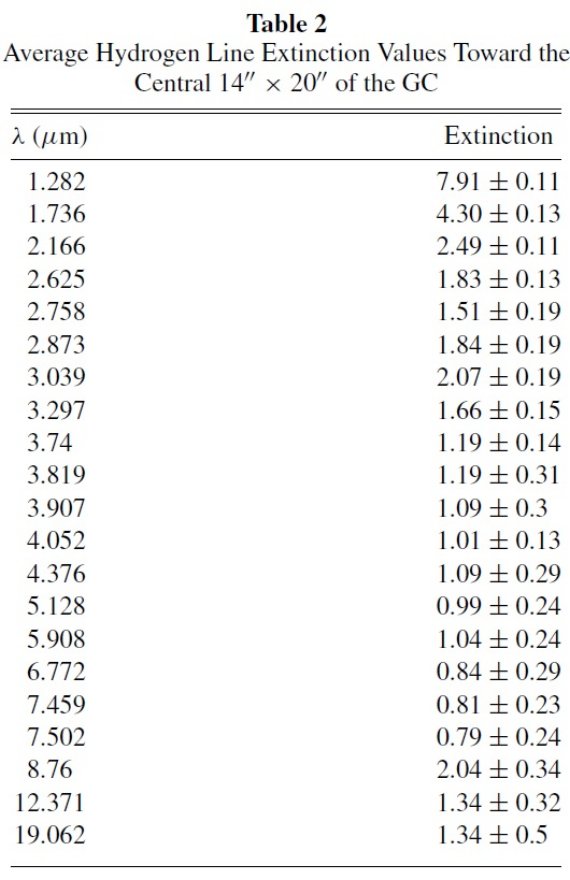
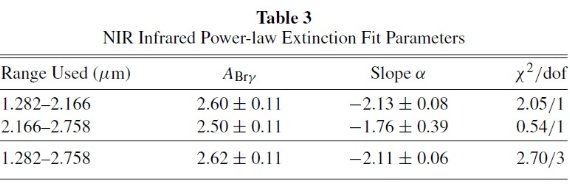
　もう一つの方法は水素輝線を使う。 Lutz et al 1996 と Lutz 1999 はミニスパイラルの ISO-SWS スペクトルを用いて 減光を定めた。輝線の固有強度比は星スペクトルより不確定性が小さいので (Hummer,Storey 1987) この方法の信頼性の方が高い。さらに輝線の波長は 広帯フィルターの有効波長よりよく決まるという利点もある。その上、 赤外では輝線の数が通常使用されるフィルターの数より多い。

輝線からは絶対減光量が出ない　
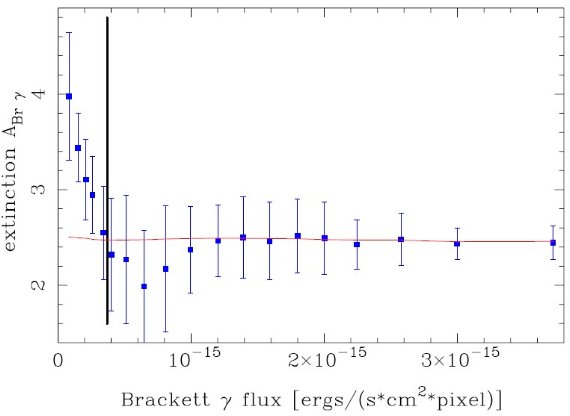
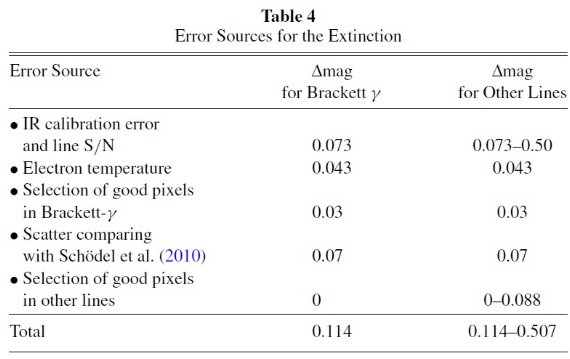
　星の測光法でもそうだが、得られるのは減光の相対比のみである。減光量の絶対較正 には減光の強さが無視できるほど弱い長波長での観測が必要である。Scoville et al 2003 は銀河中心での Paschen-α 1.87 μm の減光を定めるために 6 cm 連続光 を用いた。

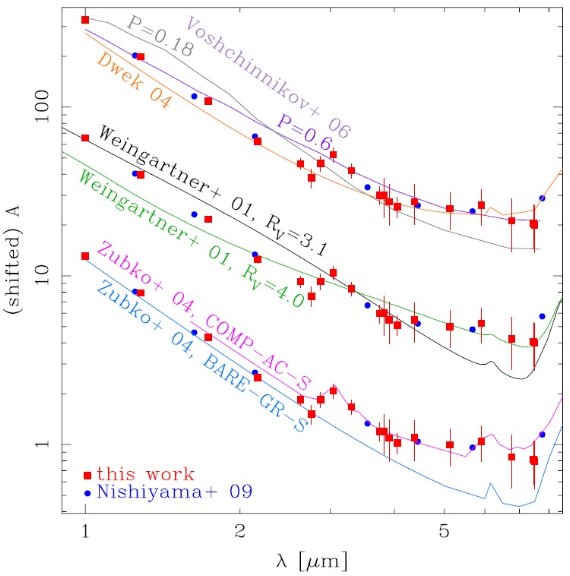
　様々な減光曲線　
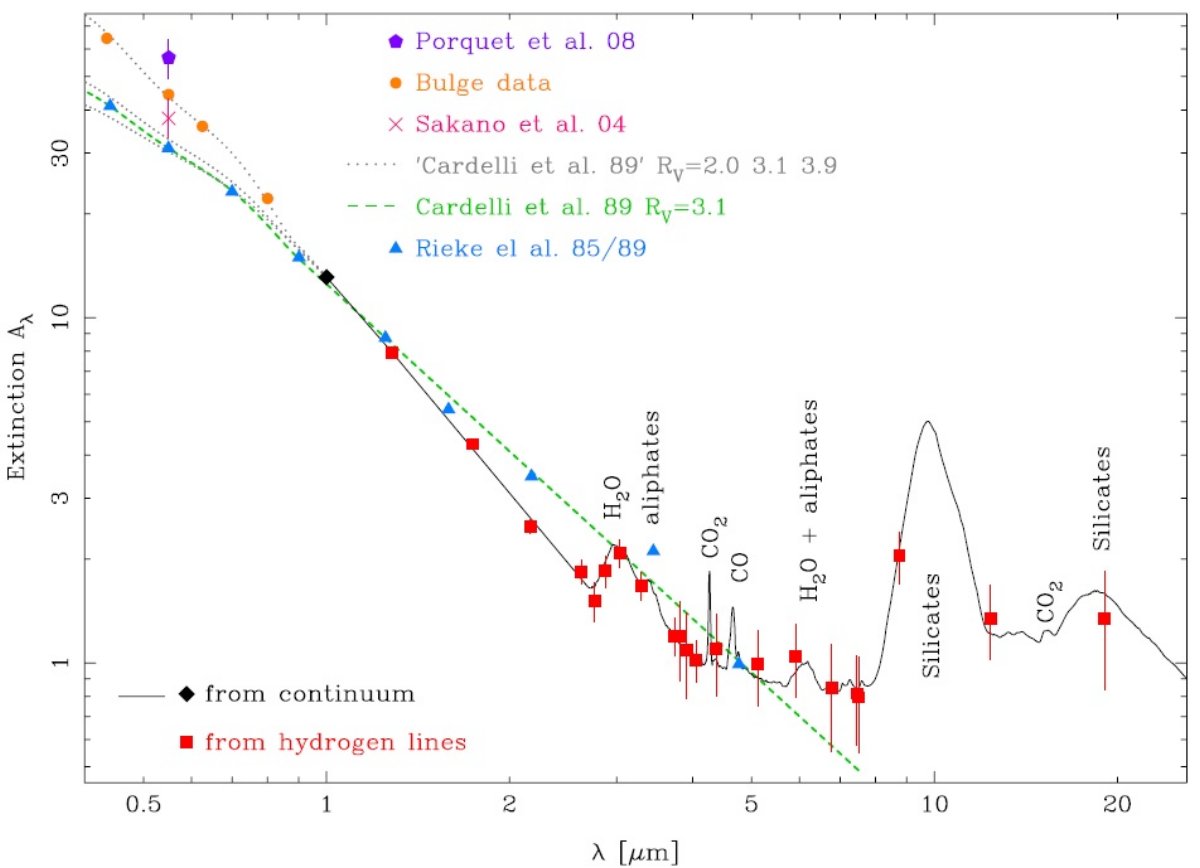
　こうして求められた様々な減光曲線を図１に示す。


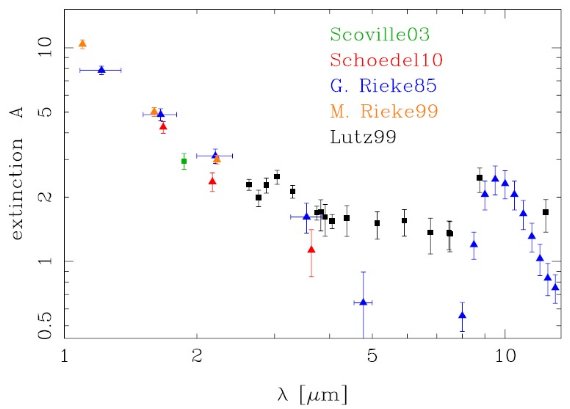
図１．これまで発表された Sgr A* 方向の減光。三角：星から導かれた減光。 四角：ガスラインから導かれた減光。
大部分の観測方向は Sgr A* から少しずれているので、Schodel et al 2010 の 減光マップを用いて Sgr A* 方向での値に修正した。Rieke,Lebofsky 1985 の場合は Rieke 1989 の絶対減光値で補正した。



　この論文は輝線法を用いる　
　この論文では、1.28 - 19 μm 水素輝線から相対減光曲線を求め、 2 cm 電波 連続波の観測で較正する。

　２．データセット　

　２．１．電波データ　

観測視野　
　図２には電波、近赤外画像を視野区画と一緒に示した。電波データは VLA の A, B, C, D 配置による 2 cm 連続波観測を結合したものである。

　非熱的成分の除去　
　ミニスパイラルと Sgr A* には非熱的電波が出ている。ミニスパイラルに 関してはその放射と減光強度の相関を 4.2.節で調べた。 Sgr A* は点源なので ガウシャンでフィットして引いた結果、図３に示すように見えなくなった。

　IRS 2, IRS 13 領域　
　これらは平均より高い電子温度を持っている。論文では単に飛ばした。

　VLA の最大構造　
　最短干渉計配列に対応するフリンジ長よりより大きな構造は測れない。その 結果フラックスが過小評価になる危険がある。今回は D 配列で 50″ までは 検出されるのでミニスパイラルに関しては心配いらない。



図２．異なる観測の視野。赤＝ 2 cm 電波連続波。青＝ SINFONI H 画像。 緑＝ SINFONI Ks 画像。薄緑＝SINFONI 区画。IRS 7 周囲は穴。青線＝ 2.6 μm 付近での ISO PSF 90, 50, 10 %. 赤線＝ 19 μm 付近での ISO PSF 90, 50, 10 %.


図３．上： 2 cm 電波連続波マップ。ガウシャンフィットで Sgr A* を除去した。
下：SIMFONI Bracket γ マップ。星のラインを示す領域は隣接ピクセルの値で 置き換えた。IRS 7 （穴）は周囲のメディアンで置き換えた。

　２．２．ＩＳＯ観測　

　2.4 - 45 μm スペクトル　
　我々は Lutz 1999 の ISO-SWS データを使う。これらは図４に 示すように波長 2.4 - 45 μm のスペクトルである。

　SWS の視野　
　図２に見るように、SWS の視野はほぼ四角で、λ < 12 μm では 14″ × 20″、λ = 12 - 28 μm では 14″ × 27″ である。視野中心は Sgr A* に置かれた。


　２．３．SINFONI　

　1.2 - 2.4 μm スペクトルは VLT 搭載の積分フィールド分光器 SINFONI で撮った。図３にはそこで得られた Br γ マップが 載っている。

図４．銀河中心の ISO-SWS スペクトル。赤で示した水素輝線が減光測定に使われた。





表１．減光を導出するのに使ったラインと連続光の組み合わせ

　３．ラインマップの作成　

　３．１．ラインマップ　

　SINFONI データを使って、 Br-γ, Br-η, Pa-β ラインマップを 作った。表１を見よ。　

　３．２．フラックス較正　

　フラックス較正には VLT アダプティブオプティックス NACO を使用して 2006 Apr 29 に撮った銀河中心の Ks 画像を用いた。同じ日には標準星も ゼロ点の不定性 0.06 mag の精度で観測された。この較正を SINFONI データに 翻訳するために、SINFONI キューブから疑似 Ks 画像 FSIN, Ks を取り出す。

その後の処理法は略す。


図５．J バンド SINFONI データからのラインマップ。青＝ 1.18 μm 画像。 緑＝ 1.3 μm 画像。赤＝ Paschen-β 画像。

　４．水素輝線から減光を導く　

　ライン a, b の間の相対減光　
　二つのライン a, b の間の相対減光は、 観測されたライン比 F(a)obs/F(b)obs と理論的ライン比 F(a)exp/F(b)exp とから 次の式で導かれる：
Aa-b = -2.5 log ( F(a)obs/F(b)obs ) 　　　　　(3)
F(a)exp/F(b)exp


　絶対減光値を出すには？　
　上の式だけでは、絶対減光値が出ない。出すには独立な方法で減光量が 求まっているか、減光が無視できるほど小さい波長 b での観測が必要である。 そうすれば、F(b)obs から既知のフラックス比 (Baker, Menzel 1938) を用いて、 F(a)exp が計算できる。

　ケースＢ　
　我々は彼らのケース B を用いる。これは星雲がライマン放射に対しては不透明であるが、 他の放射全てに透明であるという状況である。（ケースＡは全ての放射に透明。）

　　　　　F(a)exp = c × F(b)obs 　　　　(4)

c はケースＢのモデル計算から決まる。詳しくは 4.1 節を見よ。

　絶対減光値の計算式　
　本論文では、b として電波波長を、 a に赤外波長をとる。絶対減光の式は、
AIR = -2.5 log ( F(IR)obs ) 　　　　(5)
c × F(radio)obs


　ケースＢ仮説の妥当性　
　ケースＢのライン比は Hummer,Storey 1987 から採った。 仮説の検証として、 ISO-SWS スペクトルの 7.50 μm ラインに注目した。 これは 6 - 8 と 8 - 11 の二本のラインがブレンドしている。
(1/36 - 1/64 ≠ 1/64 - 1/121 だが？ )
7.5 μm 減光は 7.46 μm の 6 - 5 ラインの減光と 0.05 mag しか変わらない。これは ケースＢが銀河中心に妥当であることを意味する。
(全くついていけない。)

　４．１．電子温度 Te　

ミニスパイラルの電子温度　
　電子温度 Te はラインフラックス比に影響する。ミニスパイラルの電子温度は、 H92α(8.3GHz) を使って Roberts,Goss 1993 が、 H41α(8.3GHz) を使って Shukla et al 2004 が共に約 7000 K という値を得た。

Y+ の影響　
　電子温度 Te は Y+ = He+/H+ にも以下のように 依存する。
Te = ( Teraw 1 ) 0.87
1 + Y+


ここに Teraw は Y+ = 0 と仮定して決めた Te である。 Y+ = 3 % を使うと Te = 6800±500 K となるので、これを使う。

　誤差？　
　Te のエラーは絶対減光に 0.043 mag. のエラーを生む。

　電子密度　
　電子密度には 104 cm-3 を使う。ただし結果は これにあんまりよらない。

　４．２．減光計算　

Br-γ 減光　
　初めに、Br-γ マップと電波データ(図３参照)との直接比較から、式 (5) を用い Br-γ 減光を得た。
　次に式(3) を用い、他の全ての輝線について、 Br-γ との相対減光を求めた。そこに Br-γ 減光を足して絶対減光を得た。

　理論的フラックス比　
　Hummer,Storey 1987 の理論的フラックス比は、
( FBr-γ ) = (1.327±0.052) 10-11 erg s-1 cm-2 mJy-1
Sff exp


これと観測されたライン／電波比を式（５）に代入すると、Br-γ 減光マップ が得られる。

　非熱的放射の効果　
　非熱的放射の効果を知るため、図６に Br γ フラックスビンに対する 減光量を図示した。ほとんどの線フラックスに対し減光量は一定である。しかし、 3.7 × 10-16 erg-1 s-1 cm-2 pixel-1 以下では減光量と Br γ フラックスは逆相関になる。



図６．中央 14″ × 20″ の減光と Br-γ フラックス の関係。四角は各フラックスビン内でのメディアン減光量。フラックスが小さい時は 減光量はフラックスと逆相関する。しかし、図中の縦線 3.7 × 10-16 erg-1 s-1 cm-2 pixel-1 より大きな フラックスでは相関がない。赤線＝そのフラックス以上のフラックスを持つピクセル 全ての積分減光。変動は見られない。
(「積分減光」って何だ？ )
これは、ミニスパイラル の輝度が低い部分では Sgr A* East からの非熱的放射の影響と考えられる。 しかし、我々は全 ISO ビームの積分フラックスのみを用い、それは明るい部分からの フラックスで大部分が占められている。さらに、 IRS 2, IRS 13, IRS 16NE, IRS 16C は マスクした。このような制限を加えた後の領域で決めた減光は Schodel et al 2010 の減光 マップとよく似ている。

　Schodel et al 2010 と比較　
　Schodel et al 2010 と比較するために、Br-γ と電波のフラックスを 0.1 mag 巾のビンに集めた。次に、ビン毎の減光量をそのビン内の全フラックスを用いて計算した。 結果は図７に示した。二つの差は 0.1 等の分散を示す。

　フラックスバイアス　
　低減光領域からのフラックスは大きいので、積分フラックスは低減光領域からの光 が主となり、減光曲線が平坦になる。この効果をテストしてみたが、小さいことが判った。

　H バンド　
　H バンドでは水素線は固有強度が弱く、さらに減光も強いので観測強度は一層弱くなる。 地球大気の OH 線も H 帯では強い。これらの理由で、 Br-η 1.736 μm のみが 検出可能である。



図７．この論文と Schodel et al 2010 Ks 減光マップとの比較。



表２．銀河系中心方向 14″ × 20″ 水素輝線の平均減光

　４．３．減光の導出　

　減光則の特徴　
　導かれた減光は表２と図８に示した。1.2 - 2.8 μm では対数表示で直線 で波長と共に減少する。より長波長では減光曲線はでこぼこになる。以降では 1.2 - 2.8 μm を近赤外、2.8 - 26 μm を中間赤外と呼ぶ。

近赤外べき乗指数　
　近赤外減光則は次の形にフィットできる。

　　　　　Ab = Aa × (λa /λb)α

　五本の近赤外輝線に対して、α = -2.11±0.06, ABr-γ = 2.62±0.11 である。

　べき乗指数は一定か？　
　上のフィットの χ2 = 2.70 (DoF=3) であり、べき乗の表現が適切である ことを示している。表３に示すように、波長域を赤と青に分けてフィットした結果、 赤波長域では　α = -1.76±0.39 を得た。ただしこの値は青領域の値の 0.9σ 内であり、有意とみなせない。

　3.7 - 8 μm の減光則　
　3.7 - 8 μm の減光則は次の形でフィットできた。

　　　　　A(λ) = (1.01±0.08)×(λ/4.9μm) -0.47±0.29
つまり、中間赤外減光は近赤外減光より灰色である。







表３．近赤外減光則のべき乗指数




図８．銀河系中心方向 14″ × 20″ の平均減光。 1.28 - 18 μm では水素輝線（赤四角）を用い、1 μm に対しては星の カラーを用いた。黒線＝連続放射光を用いての内挿線。
(「連続放射光を用いて」意味不明 )
Lutz et al 1996, 茶色丸＝ Chiar et al 2000 のより大きな減光をマークした。中心バルジデータ、Sumi et al 2004, Nishiyama et al 2008, Levnivtsev et al 2010, を使い可視域まで伸ばした。 紫五角形＝ Sgr A* の X 線観測から出した Av（Porquet et al 2008）. 桃色十字＝Sgr A East 前面のガスの X 線観測から出した Av (Sakano et al 2004) 青三角＝ Rieke, Lebofsky 1985 Rieke 1989 の減光曲線は得られた減光曲線と異なる。 今回のデータは, 緑破線＝ Cardelli et al 1989 Rv = 3.1 減光則とも異なる。銀河中心方向の可視減光は不明である。 その範囲を示すために灰色点線（上から Rv = 2.3, 3.1, 3.9）で Cardelli et al 1989 減光曲線を描いた。

　５．議論　

　５．１．これまでの研究との比較　　

　Rieke, Lebofsky 1985　
　彼らのデータは主に銀河中心付近の星から得られたが、彼らの得た結論の一つ、 J から M までは傾き -1.54 の単一のべき乗則は我々の結果と反する。その 理由はおそらく、
（１）赤外減光則が普遍的で、Rv も間接的に定めた。
（２）使用した星の変光
であろう。（１）に関しては彼らは ο Sco を E(V-K)/E(B-V) = 2.744 Schultz,Wiemer 1975, と Sneden et al 1978 を仮定して較正に用いた。しかし、この関係は銀河中心の外 で得られたもので、適用可能性は低い。次に、彼らは銀河中心の E(V-M)/E(B-V) と IRS 7 の絶対等級を使って、 Rv = 3.09 を推定した。この仮定で彼らは ３つの星の M 等級を使用して Rv の下限値を決めた。 Rieke, Lebofsky 1985 の使った星の全てが超巨星というわけではなかっただけでなく、変光が特に IRS 7 で 報告されている。こうして、彼らの間接的に決めた Rv は系統的な誤差を生んだ。 試みに、 Rv = 2.98 と下げて解析すると、我々は彼らのデータから J から K の間で α = -2.04 を得た。この値は我々の結果にほぼ一致する。

　Rieke 1999 の NICMOS データ　
　Rieke 1999 は NICMOS データを用いて Rieke, Lebofsky 1985 の更訂を試みた。彼は IRS 16 のスペクトルから減光の絶対値を出した。今度は HK 間で α = -1.58, JH 間で α = -1.95 となった。他の研究では 勾配は一定(Draine 1989) である。我々は Maillard et al 2004 の NICMOS 等級 を用い、分光的に早期型星と認められた (Paumard et al 2006, Bartko et al 2009) では近赤外でカラーがゼロであることを利用して減光則を調べた。その結果は α = -2.11±0.05 であり、NICMOS データは我々の結果と矛盾しないことが わかった。
( Rieke 1999 の結果のチェックではない。)
Viehmann et al 2005 の L-, M-測光　
　Viehmann et al 2005 は ISAAC L-, M-測光を行い、AM/AL = 0.966 ±0.05 を得た。我々の NACO 広帯域測光によると、AM/AL = 0.88±0.23 で一見一致しているようだが、彼らの M-フィルター(4.66 μm)は FWHM=0.10 μm でそこには CO 吸収帯がある。

Scoville et al 2003
　Scoville et al 2003 は P-α 線を用いて銀河中心の減光を測った。 彼らは P-α (1.87 μm) と連続光 1.90 μm 狭帯域画像を NICMOS で撮り、ラインマップを作成した。さらに、VLA ６cm 連続波マップを無減光 フラックスの基準とした。彼らの減光マップを用い、我々は ISO ビーム内の 平均減光を AP-α = 3.54 と求めた。この値は我々の AP-α = 3.56±0.11 と一致する。

　Schodel et al 2010　
　Schodel et al 2010　はレッドクランプの減光値から EH-Ks = (AH - AKs)/AKs を求めた。次に彼らは EH-Ks から星のカラーを使って Ks 減光マップを作った。驚いたことに、 マップの平均値は AKs = 2.70 で、レッドクランプから求めた減光より 大きい。Schodel et al 2010 の表 A-2 を見ると分かるが、個々の星の H-Ks が レッドクランプのより大きい。その理由はよく分からない。

　Schodel et al 2010 減光の平均値　
　上の二つのどちらが正しいかよく分からないので、平均を考える。Schodel et al 2010 全領域に対して、AKs = 2.62±0.16 である。彼らの減光マップ全体に 関しては平均 AKs = 2.70であるが、ISO 視野での平均は 2.68 であった。 従って、我々は平均値（2.62?）に 2.68/2.70 を掛けて補正し、我々の減光と比較する 最終値として AKs = 2.60±0.16 を得る。

　２種の減光値　
　Ks で起きた減光値が二つでる現象は他の波長でも起きた。そして、最終的に我々の 減光値と比較すべき値として、 AH = 4.58±0.24, AL′ = 1.30±0.19 を得た。

　我々の広帯測光減光値との比較　
　我々の広帯測光減光値を Schodel et al 2010 と比較すると、

　　　　　AH,lines - AH,Sch = 0.07±0.25

　　　　　AKs,lines - AKs,Sch = 0.07±0.17

　　　　　AL′,lines - AL′,Sch = -0.10±0.23

以上の結果は我々の減光値が Schodel et al 2010 と合致していることを示す。

　減光エラーの源　
　表４には減光エラーの源を挙げた。我々の結果は近赤外ではべき乗則によく フィットし(χ/dof = 0.71)、それは既に確立 Cardelli et al. 1989 している。


表４．減光エラーの源

　５．２．銀河中心距離 Ro　

　
　Schodel et al 2010 はレッドクランプ星の "total luminosity modulus" = 減光＋距離指標 を求めた。かれらは Ro = 8.03±:0.15 kpc を仮定して 減光を定めた。ここでは減光の差を Ro に押し付けて、Ro(Ks) = 7.78±0.63 kpc, Ro(H) = 7.78±0.95 kpc, Ro(L′) = 8.41±0.94 kpc, を得た。 これらの加重平均は　Ro = 7.94±0.65 kpc である。

　西山の Ro　
　 Nishiyama et al 2006 は内側バルジのレッドクランプ星を使って、 Ro = 7.52±0.36 kpc を得た。 我々の値はそれより 0.6σ だけ大きい。両者はレッドクランプ星の絶対等級に 同じ値を使っているので、二つが大体一致しているのは減光等の他のエラーが考えて いるほど大きくないことを示す。 		レビュー値と比べると　
　我々の値は Reid 1993 のレビューで与えられた Ro = 8.0±0.5 kpc, 最近の Genzel et al のレビューで与えられた直接と間接測定からの Ro = 8.15±0.14±0.35 kpc, 直接測定だけからの Ro = 8.23±0.2±0.19 kpc とも合致する。

　レッドクランプ光度　
　逆に、Genzel et al 2010 の与えた Ro の直接測定値を認め、レッドクランプ等級 を修正することが出来る。その場合、銀河中心周辺のレッドクランプは

　　　　　MKs = -1.59±0.13

となる。一方我々および Schodel et al 2010 が用いた値は MKs = -1.47 であった。この差は小さく、われわれは Salaris,Girardi 2002 が述べているように、レッドクランプの等級は 星形成史、メタル量に対し比較的安定であることを認めた。
( これは、それに Ro の導出も ちょっと議論がいい加減。)

　５．３．減光の空間分布と Sgr A* の減光　

　Schodel et al 2010 マップに調整　
　我々のデータは減光マップを作るに十分な S/N に達していない。しかし、 減光の絶対値に関しては Schodel et al 2010 より精度が高い。従って、 彼らのマップの ABr-γ 減光値を 0.976 掛けて補正して用いる のが合理的である。こうして得た調整減光マップ上で Sgr A* 位置での値を求めると、 AH = 4.21±0.10, AKs = 2.42±0.10, AKs = 1.09±0.13 であった。

　ミニスパイラルの減光　
　ミニスパイラル自体の減光はどのくらいだろうか？それが有意に大きければ、 ミニスパイラルの Br-γ フラックスと減光強度の間に相関が出るはずだが、 出なかった。

中心核での減光が 1/4　
　視線に沿って減光が起こる個所にさらに制限を加えたい。そこで、Schodel et al 2010 の表 A.2 に載っている星の H-Ks カラーを調べた。それらの星のほぼ全ては 固有カラー　|H-Ks|o < 0.2 である。したがって、H-Ks 値は大体赤化による 値と考えてよい。そこで、表のいくつくらいが減光ゼロと看做せるかを調べた。 まず、Ks で暗くてかつ青く、銀河中心の減光を受けたら検出できないだろうと思わ れる星を除いた。これは近傍の前景星にバイアスを掛けないための措置である。 		すると 5/6324 星が減光ゼロと看做せることが判った。Philipp et al 1999 によると、 円盤(r > 3 kpc) とバルジ(300 pc < r < 3 kpc) からの輻射強度への 寄与は、銀河中心から r = 10″ の点では全輻射強度の 2.3 % である。ゼロ減光 星の数の割合 5/6324 = 0.1 % は フラックス比 2.3 % よりずっと小さい。従って、 円盤とバルジの星のかなりは減光を受けているに違いない。では次に、2.3 % の寄与を する星が減光量のどこまでを担っているかを考えよう。その結果、 AKs = 2.0 までは銀河円盤とバルジ(r>300pc) 星が担うと看做すべきであることが判った。 これは銀河中心までの全減光の 3/4 にあたる。
(AKs = 2.0 を出した過程が書いていないのは残念。r < 300 pc で全体の 1/4 の減光が発生 するなら、AKs(l, b = 0°) が l = 2° 付近で 1/4 落ちるはず。 )


　銀河中心方向の減光曲線は円盤減光　
　そういうわけで、減光の主要部は Mezger et al 1996 の述べた銀河中心核付近の巨大 分子雲で起きるわけではない。バルジにはダストが少ないので、減光の大部分は円盤で 生じるのであろう。したがって、銀河中心方向で測定された減光曲線は銀河円盤ダスト による減光の典型例と考えられる。

　銀河中心方向の減光曲線はバルジ平均と一致するか？　
　Marshall et al 2006 は銀河面の背後にあるバルジ星の減光を調べた。その結果の 平均は銀河中心方向の減光より小さい。しかし、中には銀河中心より大きな減光を示す 例(Ramirez et al 2008)もある。したがって、銀河中心方向がバルジ減光の中で 例外的とは言えない。

　５．４．近赤外減光　

　我々の勾配は過去の値より急　
　我々の近赤外データは α = -2.11±0.06(χ2/dof=2.70/3) のべき乗則に良く合う。この結果は Cardelli et al. 1989 が述べた近赤外減光則がべき乗型であるという説を支持するものである。ただし、 我々の得た傾きは多くのレビュー (Savage,Mathis 1979, Mathis 1990, Draine 2003) が与えた α = -1.75 より急である。しかし、それらの値は 可視でも赤外でも見える少数の星の観測に基づいていて、 Av ≤ 5 mag である。 これは大部分が太陽から 3 kpc 以内にあることを意味する。

　近赤外サーベイに基づく傾きは急　
　2005 年以降大規模近赤外サーベイデータが公開されると、沢山の減光測定が 減光の深い領域で行われた。それらは大体 α = -2.1 を出している。

　勾配の違いの原因　
　Stead,Hoare 2009 は effective wavelength(2005 以降) と isophotal wavelength(2005 以前) の差が勾配の差の原因ではないかと述べた。この点 については付録Ｄで詳しく述べるが、その差による α の変果は 0.07 程度で小さい。また、Fitzpatrick 2004 は太陽近傍の星のみを 2MASS から 選んで α = -1.84 を出している。

銀河面の場所により変わる？　
　 α = -1.75 と α = -2.1 を出したサンプル星が異なっている ことから、それらの減光則が異なる可能性が高い。その強い証拠として Fitzpatrick, Massa 2009 は Rv と α との間の相関を示した。ちなみに Rv = 3.1 に対しては α = -1.77 であった。彼らの仕事は 14 星の 120 nm - Ks に渡る観測に基づいている。どうやら、太陽近傍では平坦な減光曲線が 銀河系のほぼ全体に渡ってはより急になるらしい。当然この問題をさらに究明することは 非常に重要である。

　分子雲での減光則　
　大部分の分子雲では α = -1.8 (Roman-Zuniga et al 2007, Naoi et al 2006, Kenyon et al 1998, Flaherty et al 2007, Lombardi et al 2006) で平坦で ある。しかし、 α = -1 から -2.4 に渡る偏差(Froebrich, del Burgo 2006, Whittet 1988, Racca et al 2002, Naoi et al 2007) があることもここに記す。

　分子雲の寄与　
　ISO-SWS スペクトルには分子雲に特有な特徴が現れる。Whitett et al 1997 は 銀河中心方向の減光の 1/3 が分子雲によるもので、残りは希薄星間媒質によると 結論した。分子雲の寄与が比較的小さいことは Schodel et al 2010 の減光マップ から分かるように、銀河中心から数　pc の減光の変動が最大減光の 1/3 以下である ことからも支持される。これは分子雲減光は「石炭袋」のように星計数として見る 事は出来ないことを意味する。したがって、銀河中心方向の減光曲線を比較する際に は分子雲は使わない。


表５．過去の研究で得られた近赤外減光則

　最近得られた減光則との比較　
　表５には、最近得られた銀河系円盤とバルジの減光則を示した。それらの 重み付き平均は、α = -2.07±0.16 である。ここに使用した 9 つの 研究中 Indebetouw et al. 2005 のみが他と大きく異なる。したがって、減光則は内側銀河円盤とバルジでは一定 なのであろう。内側銀河円盤では太陽近傍よりも大きな減光寄与がある。したがって、 近赤外での急な勾配は銀河系全体ではより重要である。他の銀河でもおそらくそれは 同様であろう。

　５．５．可視減光　

　z-バンド減光　
　銀河中心が観測できる最短波長は z-バンドである。IRS 16 の星を Henry et al 1984, Rosa et al 1992, Liu et al 1993 から採った。 Schodel et al 2010 から IRS 16 星たちの赤化補正 Ks 等級を求めた。 星の固有カラーを (z-Ks)o=-0.25 とすると、IRS 16 星たちの赤化補正 z 等級を zo = (Ks)o - 0.25 で決められる。こうして、Az = zobs-zo が決まる。

　真の有効波長 λtrue 　
　この Az を P-α と銀河中心減光のための真の有効波長 λtrue （付録Ｄ参照）の間に突っ込まなければならない。Henry et al 1984 と Liu et al 1993 の場合、波長はおそらく λtrue である。 Rosa et al 1992 は 減光を受けた星と受けない星の中心波長を載せているが間違っているので再計算した。

　A1μm = 13.11±0.30 　
　こうして Henry et al 1984 α = -1.99±0.09、 Liu et al 1993 から α = -2.165±0.13、Rosa et al 1992 から α = -1.91±0.14 を得た。平均は α = -2.02±0.06 で、４．３節で得た α = -2.11± 0.06 と一致している。この平均勾配を用いて A1μm = 13.11±0.30 を得た。

　分子雲を考慮して Rv = 3.9 で可視域へ外挿　
　z-バンド減光を可視減光にどうつなげようか？前に見たように銀河中心方向減光の 1/3 は分子雲に依る。分子雲の寄与が平均を上回っていることは銀河中心方向への減光量が バルジ減光の平均を上回る原因となっていると思われる。そこで、減光の 1/3 に分子雲 の Rv = 5.5 を、残りの 2/3 に Rv = 3.1 を適用すると、平均値は 3.9 となる。 この Rv で Cardelli et al. 1989 減光曲線を描くと、ただし勾配のジャンプを抑えるため 0.91 - 1 μm では α = -1.85 として、可視域まで減光曲線を伸ばした。すると、 A0.55μm = 30.3 を得た。

Rv = 3.1 もあり得る。
　しかし、分子雲の大部分では Rv = 5.5 ほど大きくはない。したがって、 平均 Rv は 3.1 に近いであろう。その上、脂肪族(alophate) の 3.4 μm, ケイ酸塩(silicate) の 9.7 μm 吸収の強度は分子雲では希薄星間より も強い。さらに、 α = -2.11 という近赤外の急な勾配は分子雲では 典型的な値ではない。以上を考慮すると、標準の Rv = 3.1 の下で、0.91 - 1 μm では α = -1.95 として、 A0.55μm = 33 を得た。 		　バルジの他の領域　
　バルジの他の領域では銀河系中心よりずっと大きな Rv が得られている。 Udalski 2003, Sumi 2004, Revnivtsev et al 2010, Nishiyama et al 2008. 特に、 Nishiyama et al. 2008 は、 AV/AJ = 5.32±0.14 という値を導いている。 ちなみに、 Rieke,Lebofsky 1985 では、 AV/AJ = 3.55±0.16 である。 我々はバルジデータに Rv = 2.0, 0.91 - 1 μm で α = -2.02 を 採用、して Cardelli et al 1989 モデルをフィットした。z-バンド減光を外挿して A0.55μm = 44 を得た。

α と Rv の逆相関を使うと、　
　Fitzpatrick. Massa 2009 の図４には α と Rv の逆相関が示されている。 彼らの 13 点を２次式でフィットし、銀河中心方向の α = -2.11±0.06 を適用すると、 Rv = 2.48±0.06 となる。小さな Rv は大きな Av を意味する。 従って、これからもやはり、銀河中心方向の Rv は大きいと予測される。

　Ｘ線　
　Ｘ線（3-8 keV）では散乱より吸収が効く。化学結合は問題にならず、核子のコラム 密度が直接測られる。Sgr A* 方向では NH = 10.5±1.4 × 1022 cm-2 である。Predehl,Schmidt 1995 の NH/Av 値を使うと Av = 56.7±7.4 となる。一方、UV から 得られた NH/Av 値（Bohlin et al 1978, Draine 1989, Zubko et al 2004） を使うと Av = 53 - 59 となる。５．８．節で述べるベストフィットモデルを使うと Av = 48 となる。
　コラム密度のある割合は Sgr A East 超新星残骸のハロー電離ガスでダストの量に 変化があるかも知れない。Sakano et al 2004 によると、 Sgr A* East の熱いプラズマ のコラム密度は NH = 15 × 1022 cm-2、 冷たいプラズマのコラム密度は NH = 7 × 1022 cm-2、 である。Sgr A* 方向の視線に沿ってもそうであるなら Predehl,Schmidt 1995 の関係を使う と、 Av = 37.8 となる。

　まとめると　
　全体としては Rv < 3.1 の証拠の方が Rv > 3.1 より少し強いようだ。これは A0.55μm > 33 を意味する。しかし、可視域での直接観測のみが Rv の問題を解決することは明らかである。銀河中心にある最も明るい高温度星 16NW は減光が無ければ mV = 5.5 だが、減光を受けると mV = 34 - 43 になる。

　５．６．中間赤外減光　

　3.1 μm の H2O 吸収と 4.3 μm の CO2 吸収　
　> 2.8 μm には、 3.1 μm の H2O 吸収、 4.3 μm の CO2 吸収がある。これ等の吸収帯の 強度が視線方向により変化することは、Whittet et al 1988, Rosenthal et al 2000, Knez et al 2005 が指摘した。Rawlings et al 2003, Whittet et al 1997 は Av = 10 の希薄星間空間の方向で H2O 氷の吸収を検出できなかった。氷は分子雲にのみ付随するようである。Chiar et al 2000. これは銀河中心方向に見える銀河腕中の CO 雲によっても支持される。Sutton et al 1990. この CO は ISO-SWS にも見える。銀河中心から 12′ 離れた Quintuplet 星団の方向にも氷の吸収が見える。

　3.4 μm 脂肪族吸収　
　3.4 μm 脂肪族吸収は希薄星間空間ダストにより生み出される。Chiar et al 2000, Rawlings et al 2003. 銀河中心方向ではこの吸収が希薄領域の方向に 較べ２倍くらいに強い。 Gao et al 2010. この吸収は分子雲では検出されない。

　9.7 μm シリケイト吸収　
　9.7 μm シリケイト吸収の光学的深さとして我々が得た値は、 Δ&tau9.7 = 3.84±0.52 である。これは 7 μm 連続光 をから減光曲線を内挿した値に対する相対的強化分である。この深さは Chiar et al 2000 の 3.46, Roche,Aitken 1985 の 3.6 と一致した値である。 van Breemen et al 2010 によると、吸収の形は希薄星間空間での吸収帯と似て、 分子雲のとは少し違う。 		我々の値は Δ&tau9.7/E(J-K) = 0.70 ±0.10 である。この値は希薄星間空間に対する 0.34 より大きい。 分子雲方向も 0,34 か少し小さい値を示す。銀河中心方向がなぜ大きいのか、 内側銀河で、(シリケイトダスト/カーボンダスト) が大きいからかも知れない。 Gao et al. 2010 は多孔質なダストは強い 3.4, 9.7 μm 吸収を生み出す ことを指摘した。多孔性は Zubko et al 2004 のダストモデルでも要素の一つに 組み入れられ、我々の連続減光によくフィットする。

CO2 15 μm とシリケイト 18 μm　
　CO2 の吸収が 15 μm, Gerakines et al 1999) で見つかるが、 これは分子雲 (Knez et al 2005) ではずっと弱くなる。シリケイト 18 μm は CO2 よりずっと強い。

　4 μm での平坦化　
　 Rieke,Lebofsky 1985, Rosenthal et al 2000 は 7.5 μm までの減光を単一べき乗則でフィットした。 しかしこれは我々のデータの 4 μm から始まる平坦化とは相いれない。 3.7 - 8 μm には吸収帯はない。 　 Zasowski et al 2009, Jiang et al 2003, 2006, Gao et al 2009, Flaherty et al 2007, Roman-Zuniga et al 2007, 　 Nishiyama et al 2009, 　 Indebetouw et al 2005, は中間赤外域での平坦化を示唆している。 　 Nishiyama et al 2009, 　 Zasowski et al 2009, は希薄星間空間の減光を調べており、この平坦化は分子雲による 効果ではない。

　他の銀河の中間赤外減光　
　銀河では一様なスクリーンが想定できないので、解釈が難しい。しかし、 中間赤外の平坦減光曲線は一般的なものらしい。

　５．７．広帯域減光曲線　

　表６に本論文の銀河中心方向減光曲線から導いた広帯域相対減光値を 載せた。同じ名前でも透過曲線が異なるためのエラー、減光を導く際の 天体の固有スペクトルの違いの影響などは数 % のエラーを生む。


表６．本論文の銀河中心方向減光曲線から導いた広帯域相対減光値

　５．８．ダストモデル　

　Wg-モデル　
　Mathis et al 1977 のモデルはシリケイトとグラファイトグレインから成り、 それぞれのサイズ分布はカットオフ付きのべき乗則で与えられた。Li,Draine 2001 はサイズ分布に PAH 放射を説明するための極小サイズを加えた。ここでの比較には これを少し改善した Weingartner,Draine 2001 モデル (Wg-model) を使う。この モデルは、シリケイトは単一べき乗サイズ分布だが、炭素質グレインは３モードの サイズ分布を示す。小さいグレインが減り、最大グレインサイズが増加すると、 Rv が大きくなる。

比較用ラインの選択　
　H2O の 3-, 6-μm 吸収帯はモデルに含まれないので、観測の 方では関係する 4 本のラインを比較から外した。同様に、今回のモデルでは シリケイト吸収を扱わないので 8 μm より先の減光も外した。

　Wg-モデルで MIR 平坦部は現れない　
　Wg-モデルは全て近赤外の勾配が α ≥ -1.7 であり、λ < 2.8 μm では観測と不一致である。中間赤外では Rv が大きいとより平坦になる。しかし、 一方では、Rv ≥ 4.0 の Wg-モデルは Rv = 3.1 モデルより χ,sup>2 が 悪い。Nishiyama et al 2009 の減光は Rv = 3.1 モデルと不一致で、 Rv ≥ 4.0 モデルの方がましであった。

　空孔モデル　
　Voshchinnikov et al 2006 は空孔を含むダストモデルを考えた。これは、２種類のサイズ分布 を持つ空孔性のシリケイトダストと、一つのグラファイトダストから成る。それでも 7 μm 以下の波長の減光の特徴は説明できない。このモデルの利点は空孔度によって J - K 間の勾配を調節できることである。ただし、彼らの３つのモデルとその混合のどれも 観測を説明できない。

　Zubko et al 2004 モデル, Dwek モデル　
　Zubko et al 2004 は Rv = 3.1 減光曲線に合うようにグレインサイズをフィットした。 色々な成分を含むモデルらしいが面倒なので割愛。Dwek（針グレイン） も同様。

Zubko 合体粒子モデル　
　一番成績がよいのは、シリケイト＋炭素質＋(シリケイト/有機物/氷/穴) の３成分 モデル。特に炭素質グレインが非晶質炭素だとよい。


図９．観測減光強度とモデルの比較。赤四角＝水素輝線から決めた本論文の値。 青丸=西山らの内側バルジの値。モデルは、Weingartner,Draine 2001, Zubko et al 2004, Dwek 2004, Voshchinnikov et al 2006.




表７．ダストモデルのフィット適合度(Goodness of Fit)

　６．まとめ　

　１．A2.166μm = 2.62±0.11　
　Sgr A* 周りの 14″ × 20″ の平均 A2.166μm = 2.62±0.11

２．AH, AKs, AL′ , 　
　Schodel et al 2010 の減光マップを利用して、 AH = 4.21±0.10, AKs = 2.42±0.10, AL′ = 1.09±0.13. を得た。

　３．銀河中心距離　
　Shodel et 2010 のレッドクランプに本論文の減光を適用して、銀河中心距離 Ro = 7.94±0.65 kpc 		４．近赤外勾配　
　α = -2.11±0.06 で、2004 以前に言われていた α = -1.75 より急である。最近の色々な結果の重み付き平均は、α = -2.07±0.16

　５．モデル　
　一番良いフィットは Zubko et al 2004 の合体粒子を含むモデルであった。