Interstellar Extinction Law in the J, H, and K Bands toward the Galactic Center


西山，長田、日下部、松永、直井、加藤、長嶋、杉谷、田村、田辺、佐藤
2006 ApJ 638, 83 - 846



　アブストラクト

　銀河中心方向での減光対赤化比(the ratio of total to selective ectinction ) を J, H, K で求めた。IRSF/SIRIUS 観測領域は |l| ≤ 2.0 度、0.5 度 ≤ |b| ≤ 1.5 度である。減光と赤化の追跡には色等級図上でのレッドクランプの 位置を用いた。結果は、AKs/EH-Ks = 1.44±0.01, AKs/EJ-Ks = 0.494 ±0.006, AH/EJ-H = 1.42 ±0.02 で、以前に決められた 値より著しく小さい。 　これらの値からから、AJ: AH: AKs: = 1 : 0.573±0.009 : 0.331±0.004、 と EJ-H/EH-Ks = 1.72 ±0.04 と求めた。指数型減光則 Aλ ∝ λ -1.99±0.02 は良い近似式である。さらに、AKs/ EH-Ks が観測領域に渡って小さな変化を示すことが分かった。これは、減光曲線 の普遍性が近赤外に関しては当てはまらないことを意味する。

　1.イントロ　

　減光則決定の方法　
　減光則決定でよく用いられるカラー差法(CD Method)ではカラー差を利用し、 E(λ - λ1)E(λ2 - λ1) を λ-1 の関数として求める。通常は E(B-V) が分母に使われる。 減光量の絶対値 Aλ が求まるのは、 減光対赤化比(the ratio of total to selective ectinction ) Rv = Aλ/E(B-V) が決められた場合のみである。

　外挿法による Rv の決定　
　色超過は観測から求まるが、Rv は観測から直接には求められない。Rv は 減光曲線を λ-1 = 0 へ外挿することで決められる。 E(λ - λ1)E(λ2 - λ1) 対 λ-1 図の交点から、 -Rv が決まる。なぜなら、

limλ-1-->0 E(λ - V) = -Av =-Rv　　　　　（１）
E(B - V) E(B - V)

この図上で、 E(B-V) で規格化された波長 λ での減光量は、-Rv レベルから測った Aλ/E(B-V) の高さで表される。その関係は、

Aλ = E(λ - V) -(-Rv)　　　　　　　　（２）
E(B - V) E(B - V)

　外挿には次の不定性が伴う：
（１）ダスト放射の混入
（２）大きなダストによるグレイな減光の存在
赤外波長帯では Aλ の値は小さい。したがって、式（２）の右辺を見ると 分かるように、Rv の小さな変化も赤外域では Aλ に大きな影響を 及ぼす。 		　RC 法　
　Wozniak, Stanek 1996 はレッドクランプ(RC) を用いてバルジ方向の減光を定めた。その結果、 Udalski 2003, Sumi 2004 は Rλ を精密に決定することに成功した。 バルジまでの距離を一定と仮定すると、異なる減光を受けた RC 星は色等級図上で勾配 Rλ = Aλ/E(λ' - λ) の直線上に 並ぶ。この方法を RC 法と呼ぶことにする。この方法は Krelowski, Papaj 1993 の 減光変動法(Variable Extinction Method) や Mihalas, Binney 1981 の星団法(Cluster Method) に基づいている。

　星団法　
　星団法では、メンバーの見かけ等級と絶対等級の差は減光がないなら一定と考え、 一定値からのずれは視線方法毎の減光の差に起因すると考える。 Rλ を 求めるには個々星のスペクトル型と測光値が必要である。

　RC 法の利点　
　RC 法でも星団法と同様に、減光則は共通と仮定される。しかし、分光観測は必要とせず、 測光観測から直接に Rλ を求めることができる。そのため、 Rλ の決定は、CD 法での減光曲線の外挿に比べより信頼性が高くなる。 Rλ の決定は Aλ に直結する。可視光では RC 星の観測は 低減光領域に限られるが、赤外では大きな減光の領域でも観測が可能である。

　目的　
　この論文では、銀河系中心方向の RC 星観測データから、 、AKs/EH-Ks = 1.44±0.01, AKs/EJ-Ks を求める。

　２．観測　

　観測は 2002 March - July と、 2003 Apr -Aug に IRSF/SIRIUS を使って 行われた。


図１．観測領域。各四角は９フレームから成る。白四角は減光が強いため測光 精度が低い。

　３．データ整約　

　基準星　
　標準星 9172 (Persson et al 1998) を2002 年観測では 1 時間おきに、 2003 年観測では 30 分おきに観測した。この星の等級を SIRIUSU システム で J=12.48, H=12.12, Ks=12.03 とした。

　RC ピークの決定　
　4' × 4' の四角領域の色等級図を作り、その中の RC 選択領域で 光度関数とカラー分布を作った。それをガウシアンでフィットしてピーク値を 決めた。ピーク値は 13.4 ≤ Ks ≤ 14.6, 0.4 ≤ H - Ks ≤ 1.2 の範囲で変化した。このため、 RC 選択域は四角毎に動かした。減光の強い 領域では等級精度が落ちるので、ピーク等級が 10 σ 限界等級 J=17.1, H=16.6, Ks=15.6 より 1等以上明るい四角のみを採用した。


図２a．(17h46m10.0s, -27deg13'48".1) 方向の色等級図。四角の中を用いて RC ピークの色と等級を決めた。







図２b．RC 選択域の星の光度関数。





図２c．選択領域における H - Ks カラーの分布。平均カラーと平均等級は ガウシアンフィットから定めた。

4' 角の四角内でも減光量が激しく変わる可能性はないか？ その場合にピーク値に対応する減光、赤化はどんな平均値を意味するのか？



　４．結果　

　色等級図上のレッドクランプピーク　
　図３にはレッドクランプピークの (Ks, H-Ks), (Ks, J-Ks), (H, J-H) 図上での分布を示す。 直線はデータ点への最少二乗近似である。三つの図の直線勾配はそれぞれ、 AKs/E(H-Ks) = 1.44 ±0.01, AKs/E(J-Ks) = 0.494 ±0.006, AH/E(J-H) = 1.42 ±0.02 を与える。ここから、AJ: AH: AKs = 1 : 0.573±0.009 : 0.331±0.004 を得る。


図３a．レッドクランプピークの (Ks, H-Ks)図上での分布。直線＝ 最少二乗近似。


図３c．レッドクランプピークの (H, J-H) 図上での分布。直線＝ 最少二乗近似。 		　二色図上のレッドクランプピーク　
　図４にはレッドクランプピークの (J-H, H-Ks) 図上の分布を示す。直線フィットから 求めた傾きは E(J-H)/E(H-Ks) = 1.72±0.04 を与える。





図３b．レッドクランプピークの (Ks, J-Ks) 図上での分布。直線＝、 最少二乗近似。


図４．レッドクランプピークの (J-H, H-Ks) 図上の分布。直線＝最少二乗フィット。

　減光則の場所による変化　
　観測領域を次の４つに分割する：
N+ : +2 > l > 0 , +1 > b > 0
S+ : +2 > l > 0 , 0 > b > -1
N- : 0 > l > -2 , +1 > b > 0
S- : 0 > l > -2 , 0 > b > -1
　図５にはこれら分割領域の色等級図を示す。小さいが明らかな差が図の間には 存在する。N+, S+, N-, S- で、AKs/E(H-Ks) = 1.46 ±0.02, 1.45 ±0.02, 1.34 ±0.02, 1.51 ±0.03 であった。減光則を Aλ ∝ λ-α で近似した際には、N+, S+, N-, S- で α = 1.96, 1.97, 2.09, 1.91 となる。データ点が不足しているため、AKs/E(J-Ks), AH/E(J-H) の変化は調べられなかった。
( 一点でパワー則？。)

図５．AKs/E(H-Ks) の分割４領域における変化を示す。
( 右上図ではっきり認められるが、Ks > 14 で勾配が緩い。 大きな減光、多分分子雲中心部、での減光則に変異がある効果？)

　５．議論　

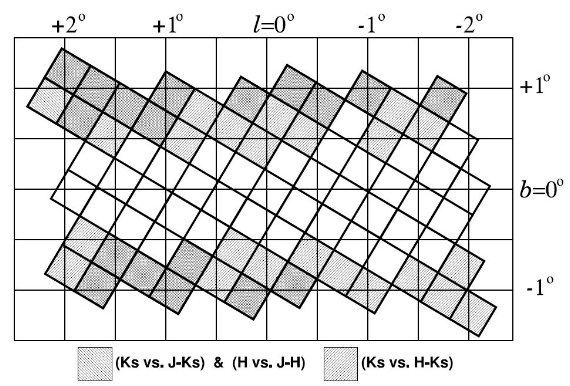
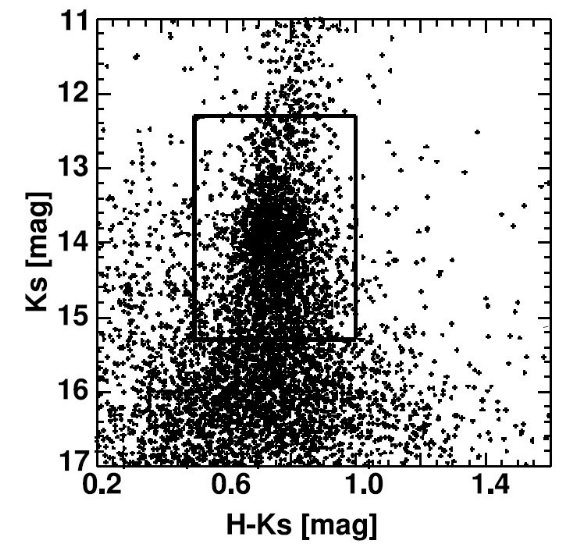
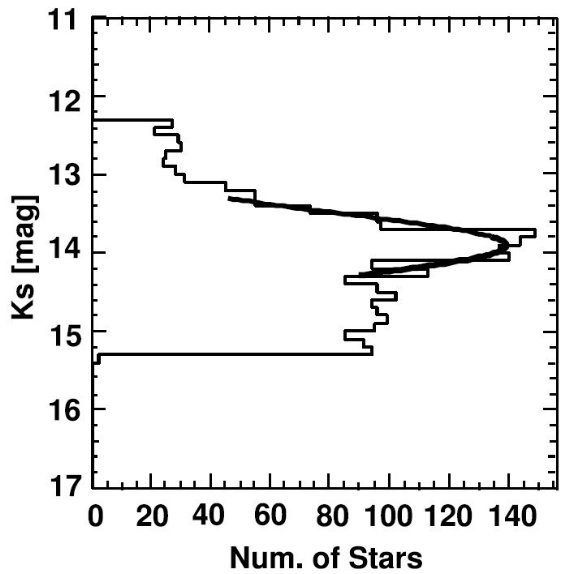
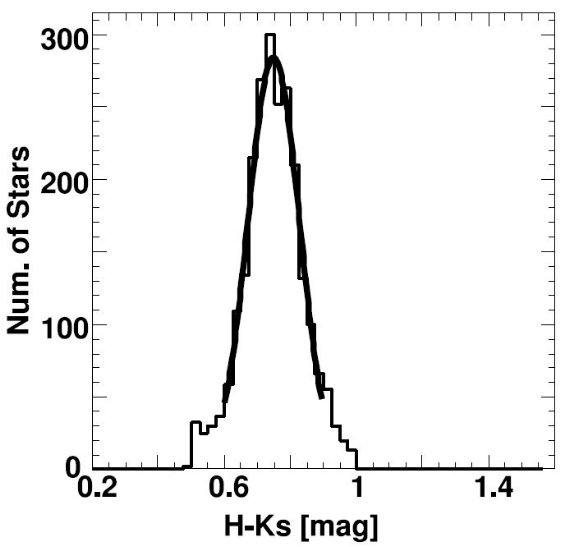
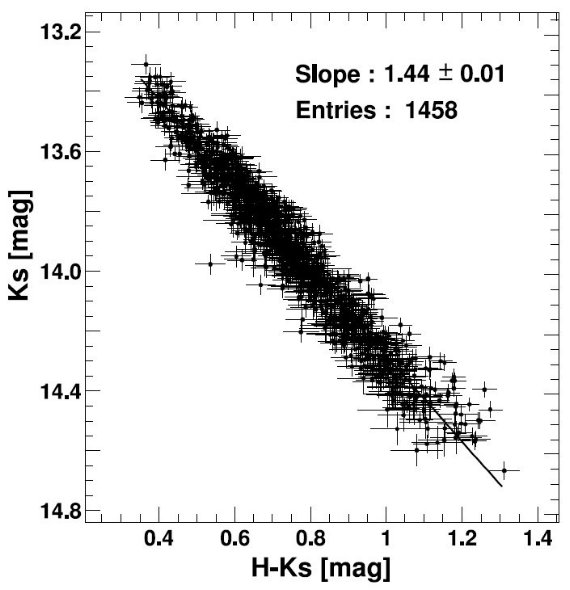
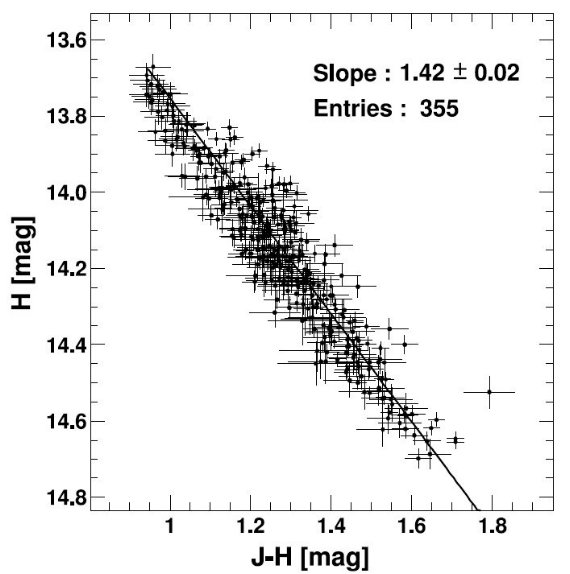
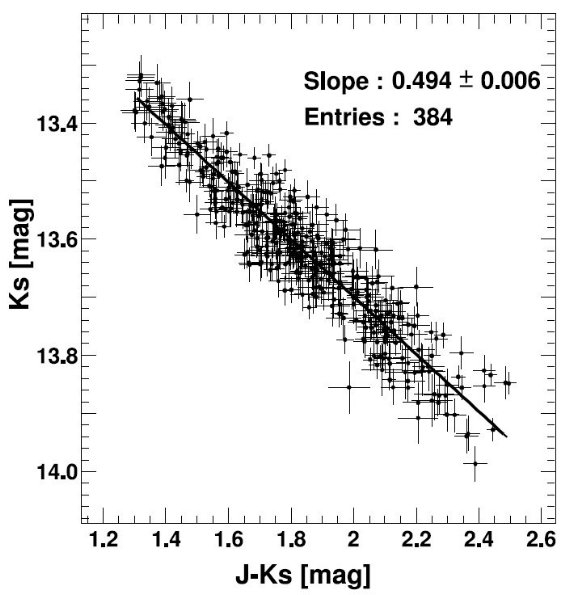
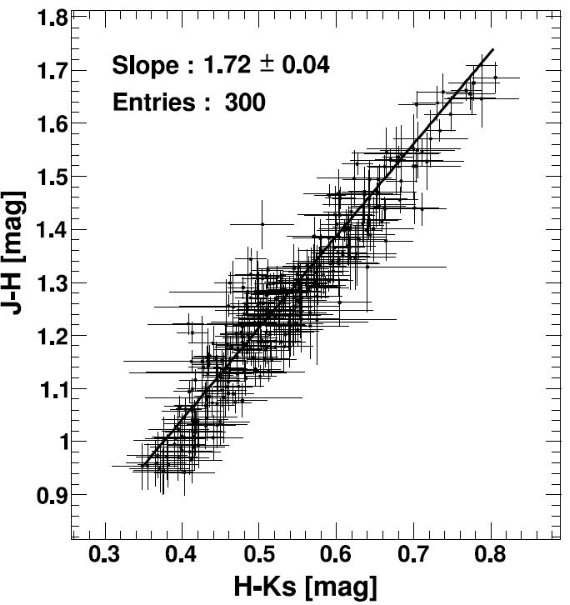
　５．１．Ｒの誤差　

　メタル効果　
　Alves 2000 は 238 ヒッパルコス星を用いて太陽近傍のレッドクランプ星の 絶対等級を MK = -1.61 ±0.01 と決定した。 Salaris, Girardi 2002 によると、メタル依存度は ≤ 0.05 mag/[M/H] で非常に小さい。我々が見つけた 傾き変化をバルジ内のメタル量変化で説明するにはメタル量が減光量と強い相関を持つ 必要がある。さらに、Frogel et al 1999, Ramirez et al 2000 によると、|l| ≤ 4 deg ではメタル勾配は存在しない。

　距離効果　
　他の原因として RC 星の距離が l により変化する Nishiyama et al 2005 ことがある。 観測した銀緯範囲で等級は 0.05 変化する可能性がある。その時、AKs/E(H-Ks) = 1.37/0.95 - 1.42/0.95 = 1.44 - 1.49 の変化の可能性がある。しかし、そのためには 前と同様距離と減光に相関が求められ、ありそうにない。

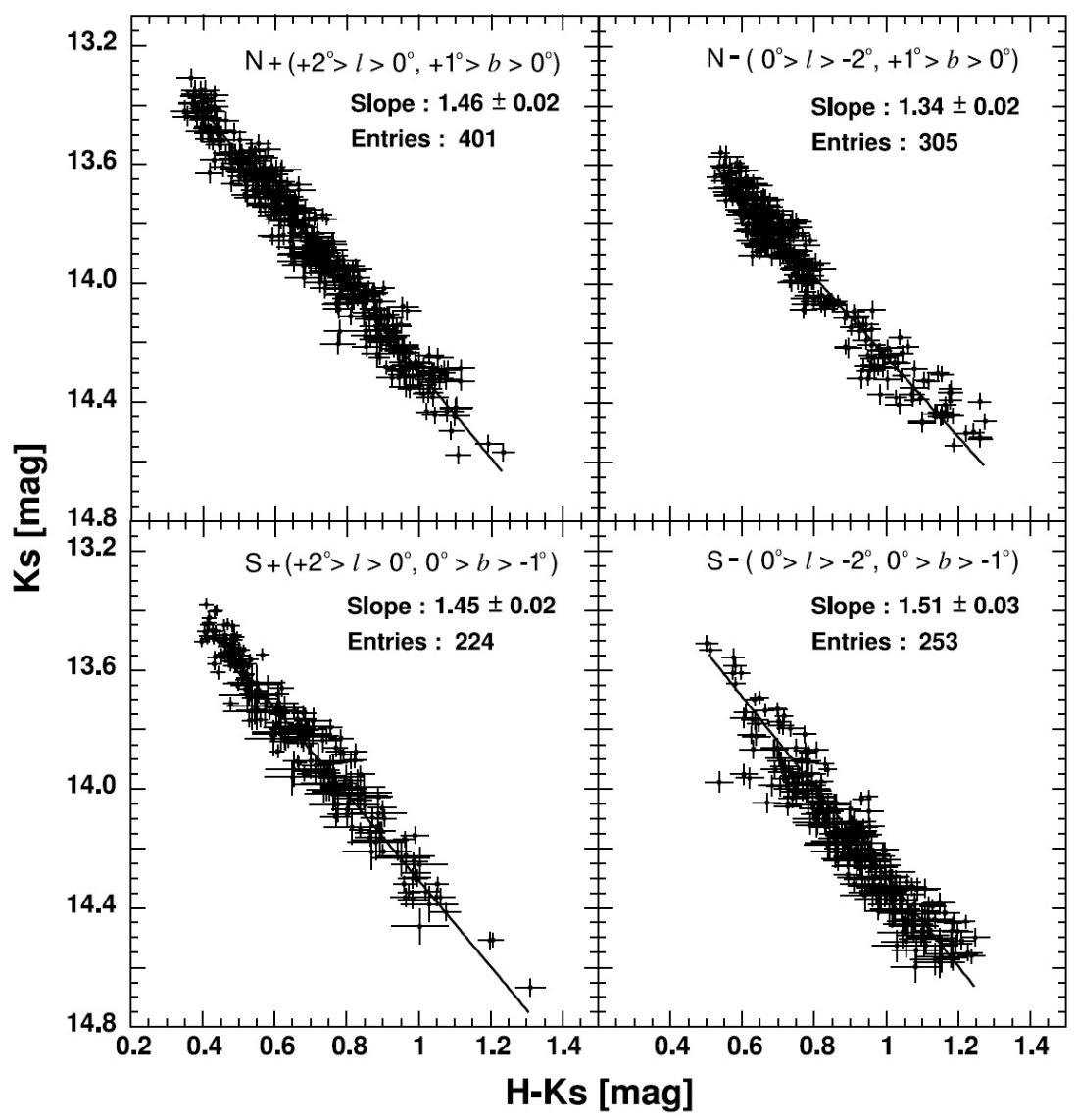
　選択バイアス　
　(Ks, H-Ks) 上の天体を、強い吸収を受け(Ks, J-Ks) 図上にない赤い星 0.5 ≤ H-Ks ≤ 1.2 と、ある青い星 0.4 < H-Ks ≤ 0.7 に分けて、勾配を求めた。すると、赤い星は AKs/E(H-Ks)=1.43, 青い星は 1.46 であった。これは減光量による選択バイアスが数パーセントの変化をもたらすことを 意味する。

　有効波長　
　IRSF/SIRIUS システムは MKO システム Tokunaga et al 2002 と似ている。その有効波長 は Tokunaga, Vacca 2005 の A3 式にしたがって計算された。典型的なバルジ RC 星　が AKs = 0.4 - 1.6 の減光を受けた時、Kurucz 1993 モデルで Teff = 4750 K, [M/H] = -0.1 dex, log g = 2.0 を計算した結果、吸収による波長変化は　0.01 μm 程度長い方に伸びることが分かった。すると、J=1.25, H=1.64, Ks=2.14 μm となる。 変化は小さく、SED にあまり依存しない。したがってこの論文では有効波長の減光量による 変化は一定値とする。

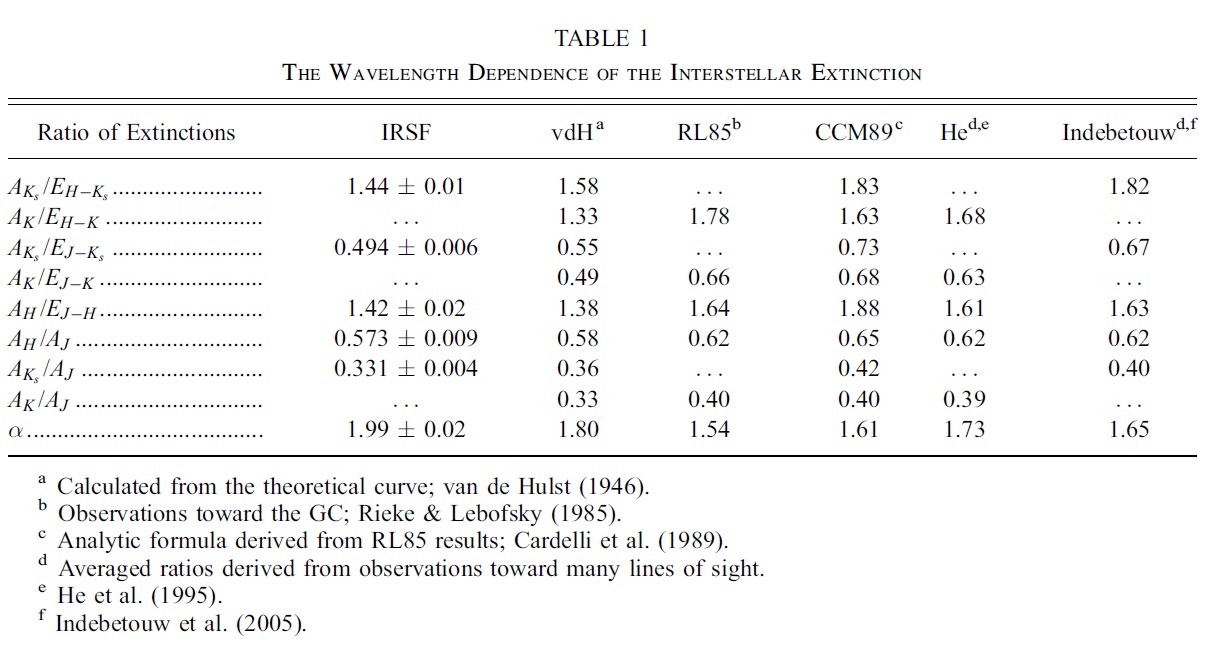
　５．２．以前の研究との比較　

　van de Hulst No.15 曲線　
　表１に以前の結果を載せた。我々の今回の結果はそれらと大きく異なる。我々の減光対赤化比は 小さめで、これは波長が長くなったときに Aλ が急速に低下していることを 示す。したがって、パワー則の指数 α は大きい。　van de Hulst No.15 曲線は現在も Glass 1999, Jiang et al 2003 などにより使用されているが、我々の結果は No.15 に最も 近い。

　Rieke, Lebofsky 1985 　
　Rieke, Lebofsky 1985 (RL85)は 銀河中心方向の 5 つの超巨星と ο Sco に CD 法を適用して近赤外減光則を導いた。彼らの結果はしばしば標準減光則として引用 されている。彼らの観測は K バンドで行われた。我々は Cardelli et al 1989 の近似式 を用いて Ks での値を計算した。RL85 では銀河中心天体に対して Rv = 3.09, E(V-K)/E(B-V) = 2.744 とした。仮に Rv = 3.0 とすると AJ/AV : AH/AV : AK/AV = 0.260 : 0.142 : 0.081 となる。勿論 Rv の下限値は RL85 においては L, M, 8 μm, 13 μm での減光量から定められている。しかし、それらの波長での観測はかなり大きな誤差を 伴う。特に注意したいのは彼らの L, M, 8 μm 観測の結果は ISO による λ 2.4 μm での観測結果と不一致である。したがって、RL85 と我々の結果との不一致は観測方向 による減光則の変動の結果かも知れないが、Rv の不定性が原因の可能性もある。

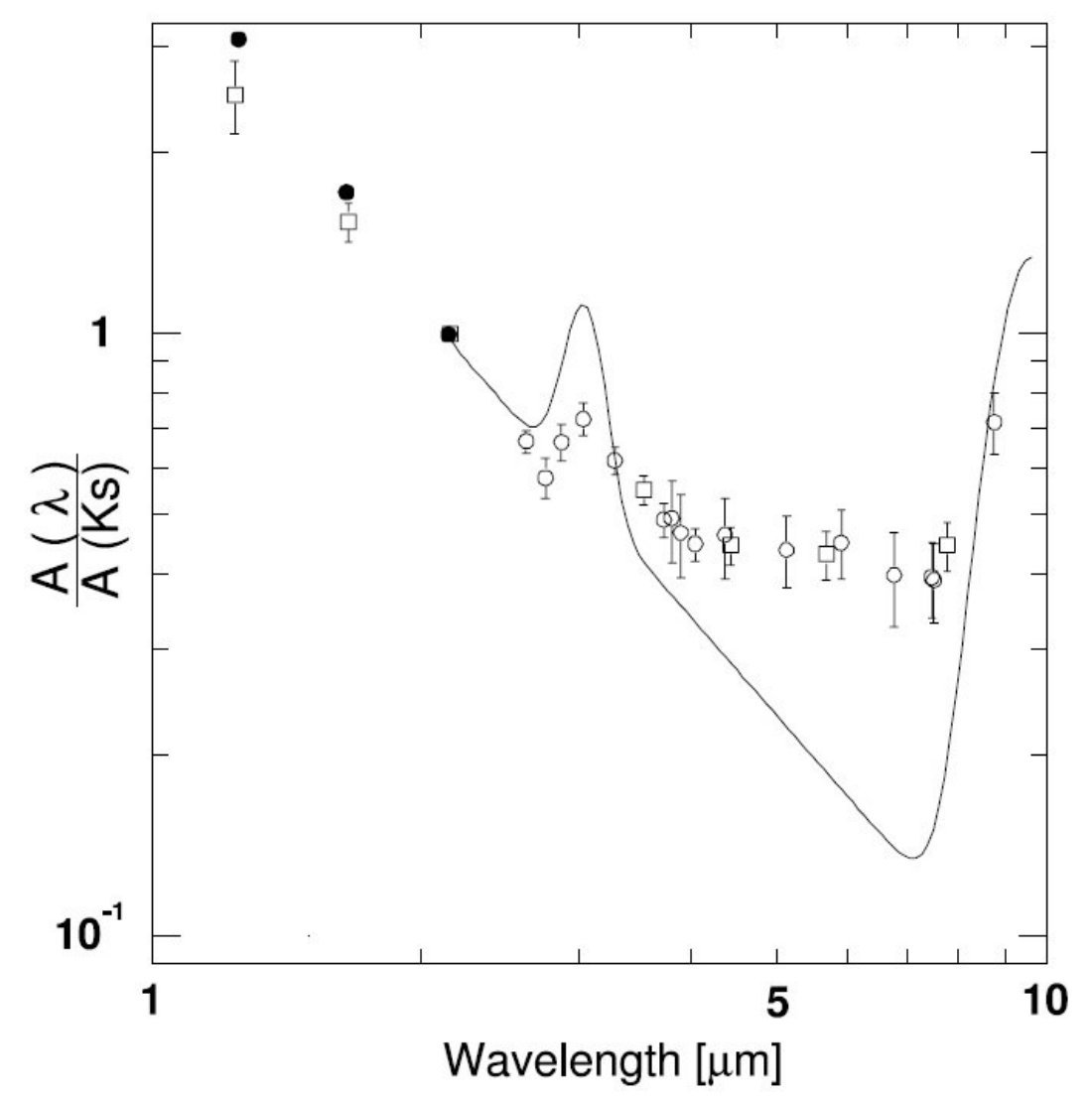
　Indebetouw et al 2005　
　Indebetouw et al 2005 は Spitzer と 2MASS データに CD 法を適用して、l = 42 deg と l = 284 deg の２方向で Aλ/AK を求めた。彼らは E(λ - Ks)/E(J - Ks) から まず AJ/AK を求めたのだが、 その際に単位距離当たりの減光量は一定として RC 星の二色図上の軌跡を定めた。彼らの 結果は我々のと異なる。ただし、彼らの図５において、 E(λ - Ks)/E(J - Ks) が λ-1 で切り取る値は、彼らの色等級図上 RC 星の軌跡をフィットして 求まる -AK/E(J-K) = -0.67 より大きく（よりマイナスでない）、 我々の値 -0.494 に近いことを注意しておく。Spitzer データは 3.55 ≤ λ ≤ 8.0 での減光則を定める能力を有しているが、注意深さが必要である。



表１．星間減光の波長依存性。

　５．３．赤外でのべき乗型減光曲線　

He et al 1995　
　He et al 1995 は　南天で 154 個の OB 星を観測した。彼らはべき乗型減光則を 仮定して減光を求めた。データの分散は大きいが、彼らの結果は我々と明らかに 異なっている。

Moore et al 2005
　Moore et al 2005 も指数型を仮定して 9 個の UCHIIR と 2 つの PN に対し CD 法を適用した。彼らは 1 < &lambda < 2.2 μm で H 再結合線 を観測し、減光指数 α が　1.1 から 2.0 の間に散らばることを見出した。 減光が大きい天体では α が小さくなることから、彼らは高減光領域では グレインが大きく成長しているのではないかと論じた。我々が銀河中心方向で求めた 勾配の急な減光則は視線に沿っての星間空間では物質密度が希薄なのかも知れない。 		　長波長域　
　より長波長では二つの仕事がある。Lutz et al 1996 と Lutz 1999 は ISO SWS に よる銀河系中心方向の観測、Rosenthal et al 2000 はオリオンでの SWS 観測を 行った。どちらもある波長での減光を仮定しているのでオフセットエラーの可能性が ある。しかし、銀河中心はオリオンと異なる。 Lutz 1999 は銀河中心方向では λ ≥ 2.5 μm で減光が平坦となり、標準グレインモデルから期待される 7 μm 付近での減光極小を示さない。
　我々の 1.2 μm < λ < 2.2 μm で急な指数を持つ減光則が 他の結果と異なることは近赤外でさえも視線方向毎に減光則が変化することを意味する。

図６．銀河中心方向の減光比 Aλ/AK。 黒丸＝今回。白丸＝Lutz et al 1996. 白四角＝Indebetouw et al 2005。 実線=　オリオン OMC-1 H2 輝線の相対強度比から 求めた減光曲線。Rosenthal et al 2000.

　６．結論　

　我々は銀河中心方向のレッドクランプ星を用いて、J, H, Ks での 減光曲線を導いた。我々の結果は明らかに以前求められた結果と異なる。 　差の原因は CD 法での小さなオフセットかも知れないし、視線方向により 減光則が変わるためかも知れない。