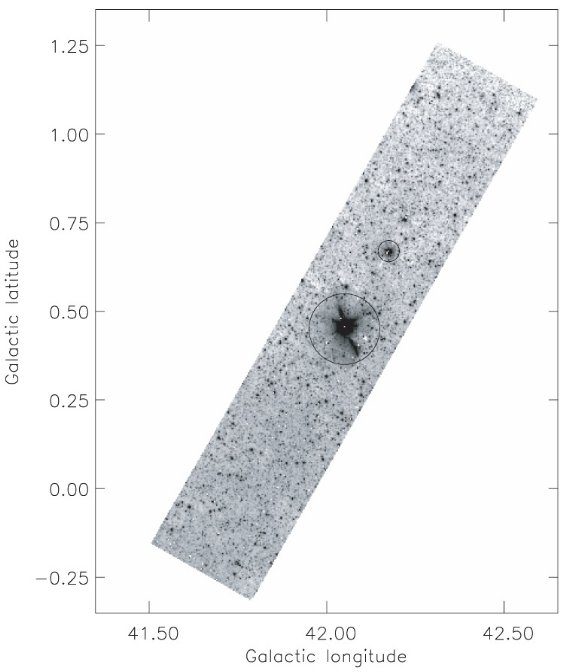
図1.l = 42° 方向の GLIMPSE 3.6 μm 画像. 中央の明るい点は サチッた星。その周辺は測光から除いた。
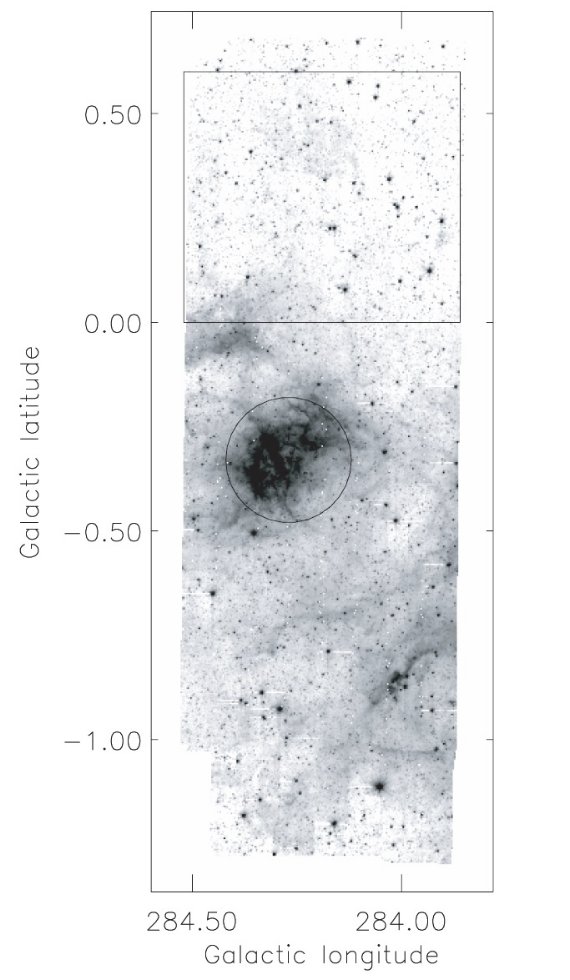
図2.l = 284° 方向の GLIMPSE 3.6 μm 画像. 巨大 HIIR RCW49 は丸で示されている。星形成、星雲、強い CO 放射から離れた フィールド領域が四角で囲われている。
|
l = 42° と l = 284° 方向で 1.25 μm ≤ λ ≤ 8.0
μm の範囲で Aλ/AK を定めた。l = 42° 方向は
静謐であり、l = 284° 方向は巨大 HIIR RCW 49 を含む活発な領域である。 どちらも 2MASS と GLIMPSE の画像がある。 A |
カラー・カラー図から (Aλ - AK)/
(AJ - AK) を測った。これから Aλ/AK
を出すには AJ/AK が必要である。そのため、巨星の見かけ JHKs 等級
を二つの視線方向で測り、赤化量を等級(距離)の関数として定めた。こうして、
AJ/kpc, AK/kpc を求め、そこから AJ/AK を
導いた。 得られた Aλ/AK は 3 - 8 μm で平坦であった。 これは Lutz et al 1996 の結果と大体一致する。 |
|
E(J-K)/E(H-K) は方向により変わるか? 多くの研究が λ = 1 - 4 μm 領域では Aλ ∝ λ-β の形をしていることを示唆している。Martin, Whittet 1990 は希薄星間空間と ρ Oph と Tr 14/16 雲の外側層で β = 1.8 とした。 β = 1.8 を用いると、E(J-H)/E(H-K) = 1.8 &plumn;0.1 となる。値自体は 使用フィルターで多少変動する。しかし、この値は分子雲では異なり、 luminous southern stars に対して E(J-H)/E(H-K) = 1.47 &plumn;0.06 (He et al 1995), 石炭袋で E(J-H)/E(H-K) = 2.08 &plumn;0.03 (Racca et al 2002 and references therein) となる。 NIR と 10 μm バンドの中間は? 1 - 2 μm のべき乗則と 10 μm 帯との中間領域に関しては不確定さが残っている。 Bertoldi et al 1999, Rosenthal et al 2000 はオリオンの H2 ラインの観測から ≤ 4 μm まではべき乗則が続いているとした。しかし、エラーバーが大きいので 強い拘束はかけられない。 |
4 - 8 μm での減光の平坦化 Lutz et al 1996 は銀河系中心方向の Aλ が λ = 3 - 9 μm で平坦になることを見出した。彼は 1999 年のより多くの再結合線の観測からその結論を 再確認した。 2MASS + GLIMPSE での A(λ) 決定 2MASS + GLIMPSE での A(λ) 決定は J 1.240 μm, H 1.664 μm, Ks 2.164 μm, 3.545 μm, 4.442 μm, 5.675 μm, 7.760 μm (K2 III 星のスペクトルと IRAC フィルター で決めた isophotal wavelengths)で行う。 フィルターの影響は小さく、例えばフラットスペクトルでは 2MASS で 1.235, 1.662, 2.159, SSC provided isophotal wavelengths は 3.535, 4.502, 5.650, 7.735 μm である。 |
 図1.l = 42° 方向の GLIMPSE 3.6 μm 画像. 中央の明るい点は サチッた星。その周辺は測光から除いた。 |
 図2.l = 284° 方向の GLIMPSE 3.6 μm 画像. 巨大 HIIR RCW49 は丸で示されている。星形成、星雲、強い CO 放射から離れた フィールド領域が四角で囲われている。 |
|
Aλ/>AK の式 Aλ/AK を求めるには下式を使う。
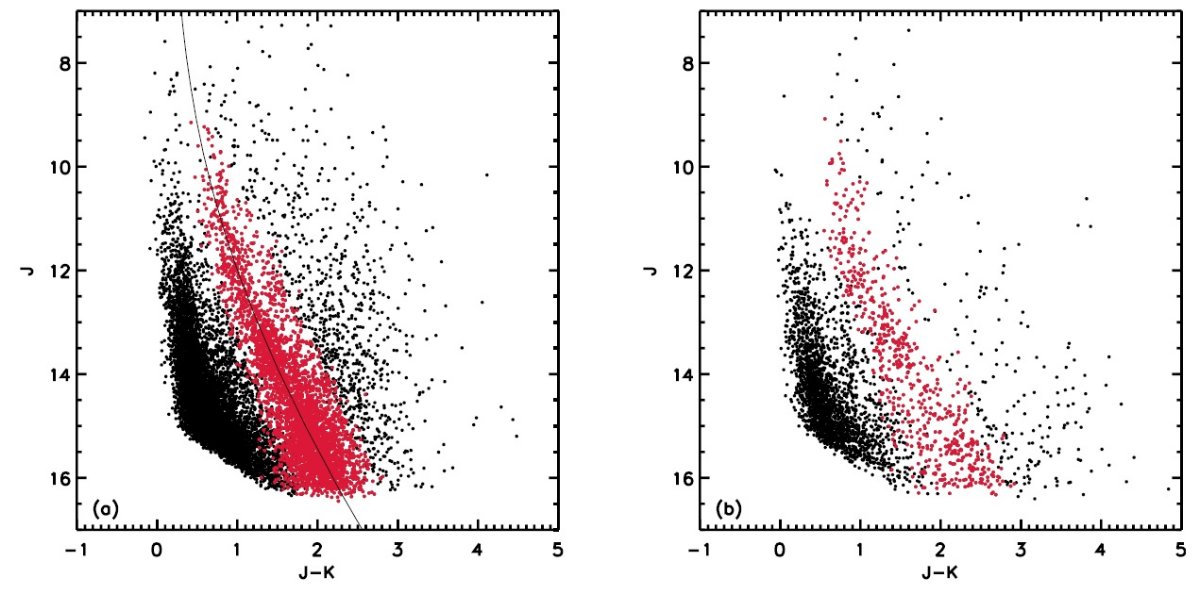
まず AJ/>AK の決定から AJ/>AK は 2.25 から 2.75 まで広がっている。 (Cardelli et al. 1989, Fitzpatrick 1999, Draine 2003 )。本論文では自分たちの データから, 色等級図上のレッドクランプ軌跡を使って独自に AJ/>AK を決める。 3.1. AJ/>AKJ - (J-K) 色等級図に主系列と巨星の二つが見える図3には、l = 284° 付近、RCW 49 を外した領域の星の J - (J-K) 色等級図 を示した。この図は円盤成分がバルジ成分に卓越する銀経での典型的な色等級図である。 J - K = 0.5 付近に垂直に伸びるのは様々な距離の矮星で、この図内には 8365 星ある。 (J-K) = 1 - 3 は主に巨星である。距離効果が分布を縦に引き伸ばし、赤化は右下に 引っ張る効果を持つ。主系列星と巨星は平行なずれを示していない。これは、矮星の分布 が赤化のみでなく、固有光度が低い冷たい矮星の参入にも影響されることを考えると、 理解できる。 レッドクランプ星 それに対し、巨星は絶対等級とカラーの巾が小さいレッドクランプ星が卓越している。 レッドクランプ星を使った銀河系構造の研究は、Lopez-Corredoira et al 2002, Drimmel et al 2003 が行い、視線に沿った減光が計算された。図3上、巨星のさらに 赤い側にある 859 星はおそらく固有カラーが赤い AGB 星だろう。 |
フィッティング 減光が一様と仮定すると、 J = Jo + 5 log(d/10pc) + cJ(d/10pc) J-K = (Jo-Ko) + (cJ-cK)(d/10pc) フィットに際して、 Lopez-Corredoira et al 2002 の決めた MK = -1.65, H-K = 0.75 を固定値として採用するか、これらも変数とするか、どちらも可能である。 我々は、図3のようにレッドクランプ星を選び、IDL の amaeba プログラムでフィットした。 減光パラメタ―の値 求まった cJ, cH, cK から、AJ/AK = 2.5 ±0.2, AH/AK = 1.55 ±0.1, AJ/AH = 1.65 ±0.1 を得た。また、 cJ = 0.35 ±0.15 mag/kpc, cH = 0.25 ±0.1 mag/kpc, cK = 0.15 ±0.1 mag/kpc であった。 これらは通常採用されている値、cV = 0.7 mag/kpc, (?) cJ = 0.2 mag/kpc に比べ 1 σ 大きい。 視線方向の高減光域 色等級図を調べると、視線に沿って、高減光領域が見つかった。それは、 l = 284°, J = 12.7, J-K = 1.3 と J = 14.3, J-K = 1.7 である。 RCW 49 HII 領域方向での遠方側雲の減光は強いので図3ではその先には星が見えない。この 雲が RCW 49 に付随する雲とみなすと RCW 49 までの距離は 5 ±1 kpc となる。 一方 l = 42° 方向のフィットは困難である。これが AGB 星の混入がより激しいからで さらに、バルジの J = 14 の暗い星が入るからである。しかし、得られた値は上の値と 矛盾しない。 |
|
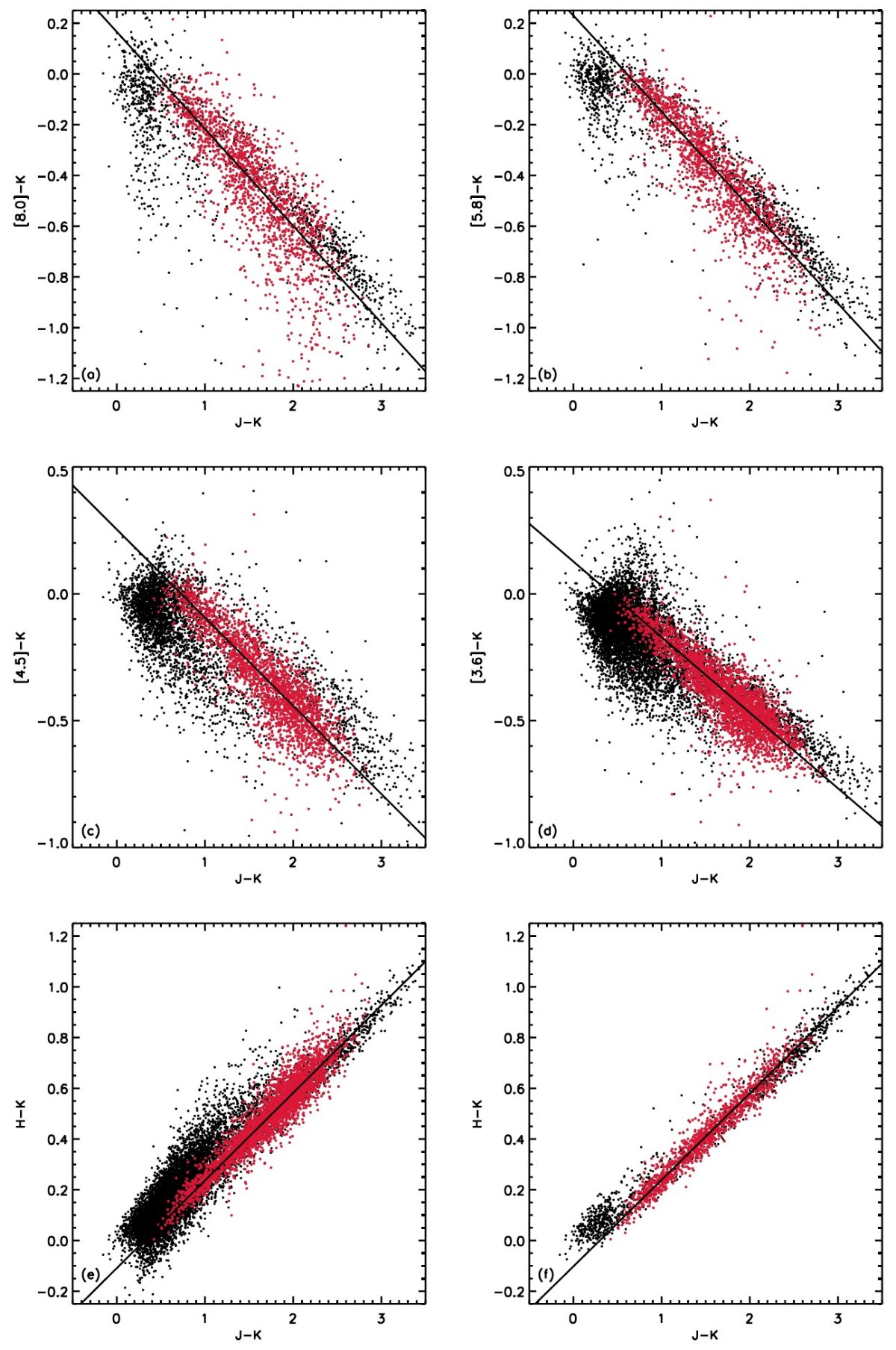
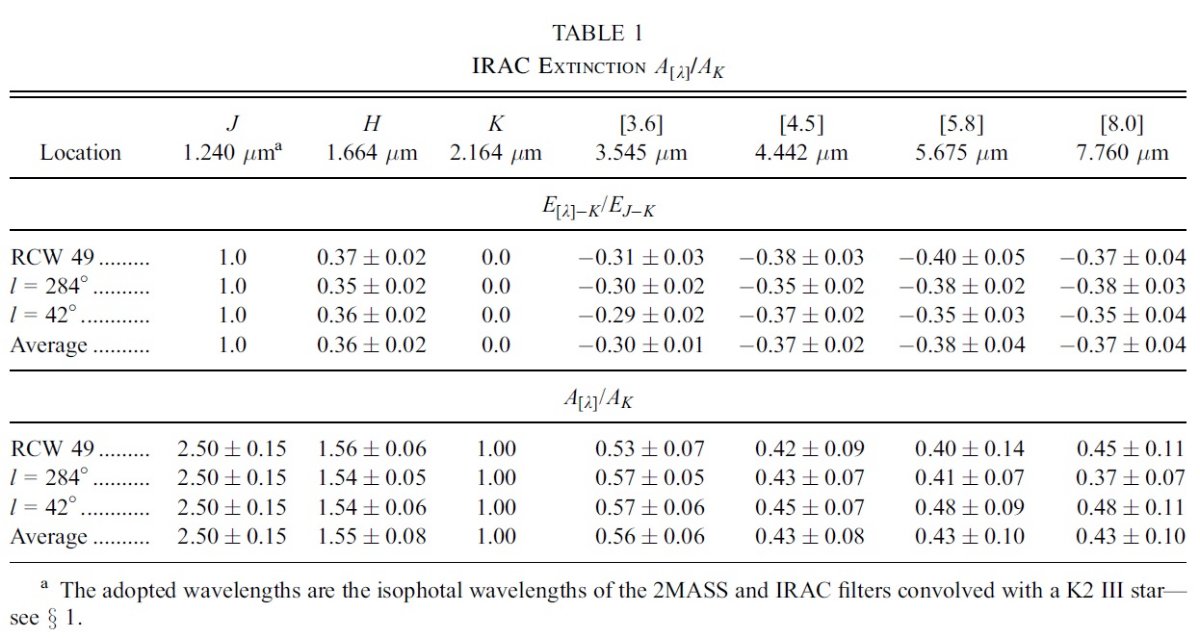
2色図の勾配 = E(λ-K)/E(J-K) 図4には2色図を示した。フィット直線の勾配 = E(λ-K)/E(J-K) である。 図5には得られた E(λ-K)/E(J-K) を 1/λ に対してプロットした。 Kenyon et al 1998 の方法 Kenyon et al 1998 は雲の裏の星と離れたフィールド星のあらゆる組の等級差を プロットすることで、 E(λ-K)/E(J-K) が得られることを示した。表1には この方法で得た勾配を示す。 |
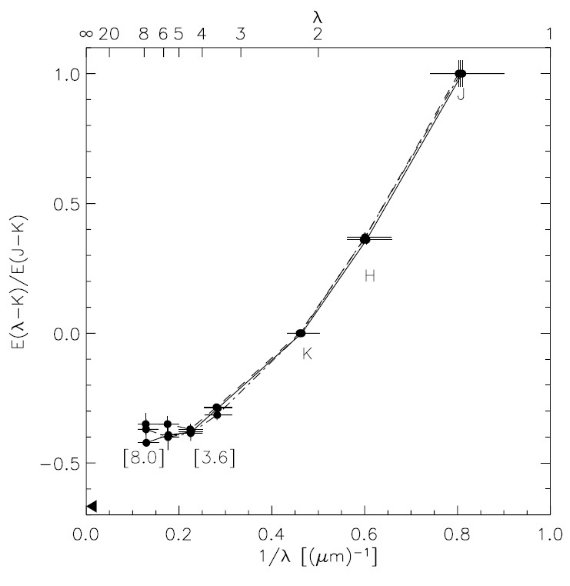 図5.色超過の比 E(λ-K)/E(J-K) 対 1/λ . 直線= 284° 付近フィールド星. 破線=42° 付近の星. |

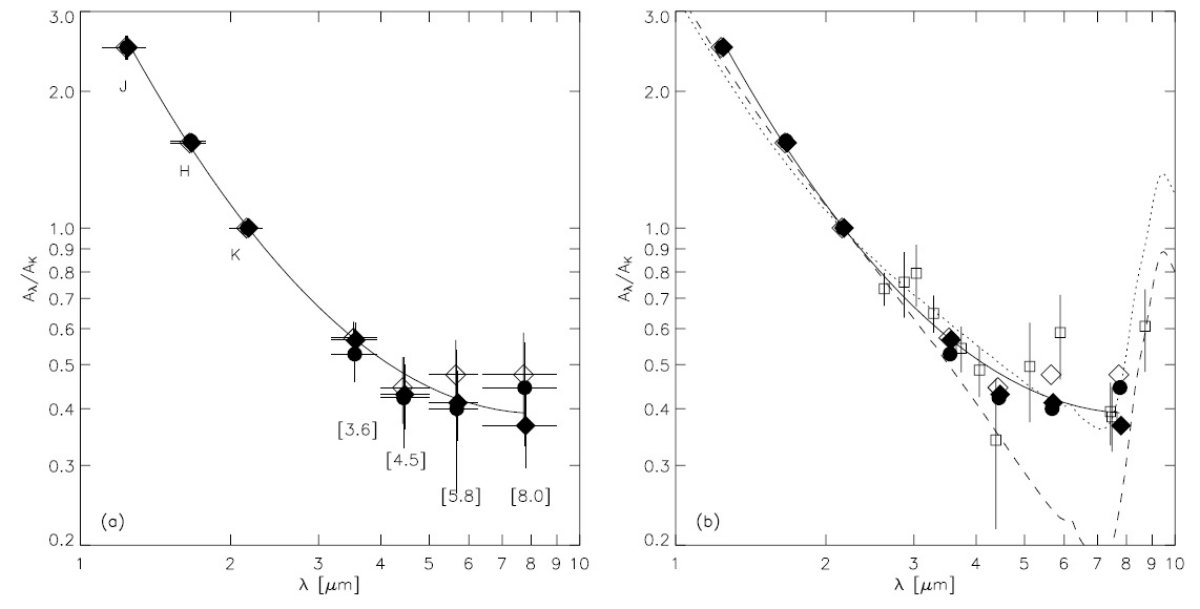
4.1.A(λ)/A(K)A(λ)/A(K) は3領域でほぼ同一図6には、A(λ)/A(K) を l = 284°, 42° のフィールド、および RCW 49 方向の3つについて示した。一致はよい。フィットは近似的に以下の式で 表される。 log[A(λ)/A(K)]=0.61(&plumn;0.04)-2.22((&plumn;0.17)log(λ) +1.21(&plumn;0.23)[log(λ)]2 この式は λ = 1.25 - 7.75 μm で有効である。ちなみに、β = 1.8 のべき乗則 だと、上の係数が 0.60, -1.8, 0.0 になる。 |
A(K)/A(V) は一定か? A(λ)/A(K) に比べると光学域の減光則は方向によりかなり変動することが知られている。 変動は Rv = Av/E(B-V) の変化で表現される。 Cardeli et al. 1989 によると、Rv = 3.1 に対し、 A(V)/A(K) = 8.8 であり、 Av = 5 に対しては A(V)/A(K) = 7.5 である。一般的にはだから、A(V)/A(K) を近赤外減光から 推定することは難しい。 |
|
べき乗則からの逸脱があった 我々の減光は近赤外で得られたべき乗則からの逸脱を示している。 Lutz et al 1996 Lutz 1999 は銀河系中心方向の ISO SWS スペクトル 2.4 - 45 μm 中の 水素星結合線の強度比をモデルから得た固有強度比と比較して、 A(λ)/A(K) を求めた。彼らはそれを Draine 1989 のモデル減光曲線 から得た A(K)/A(V) を用いて A(λ)/A(V) に変換した。図6を 見ると彼らの A(λ)/A(K) は我々と大体合うが、ばらつきが大きいことが 分かる。 ( ほとんど全部 分子雲かと思ってたよ。) 分子雲と希薄星間空間の減光の差 Whittet et al 1997 は 銀河中心方向 Av = 25 mag のうち、分子雲減光が 5 - 10 mag あるとした。われわれの方向の分子雲寄与を Dame et al 2001 の CO データから評価した。ただ、分解能は低い。これによると、我々の方向での減光への 分子雲寄与は数等しかない。 |
一様性 二本の大きく異なる方向、1本の HIIR 方向、銀河系中心方向で似た減光則が 得られたことから、 4 - 8 μm 減光則は一定と考えてよい。 9.7 μm 帯の影響 フィルターから計算すると F(8) にはシリケート吸収の影響は2%以下である。 偏光と吸収 GL2591 では p(4μm)/p(8μm) = 2.5, BN では p(4μm)/p(8μm) = 2.0 , GL2591 では p(10μm)/p(8μm) = 3.7, BN では p(10μm)/p(8μm) = 4.3 と同じ変化を示す。しかし、われわれの測定は A(4)/A(8) = 1.32 で上の値よりずっと小さい。だから、 10 μm 減光を引き起こす グレインは 4, 8 μm 減光の原因となるグレインと異なるのであろう。 |