Rieke85

The Interstellar Extinction Law from 1 to 13 Microns

Rieke, Lebofsky

1985 ApJ 288, 618 - 621

　アブストラクト
　ο Sco と銀河中心方向のいくつかの星で 1 - 13 μm 測光を行った。それらの星と VI Cyg No.12 減光則は 1 - 13 μm で同じであった。3 μm の先の減光則および減光対色超過比 R ≈ 3.09±0.03、Av/τ_Si = 16.6 ±2.1 を得た。

　1.イントロ　
　3.5 μm より短波長側ではほぼ全ての観測は単一の減光則と矛盾しない（Mathis 1979）。シリケイト吸収が測られたのは VI Cyg No12 (Rieke 1974, Gillett et al 1975) と銀河系中心天体 7 (Becklin et al 1978) である。しかし、その減光則は短波長側と異なり一致しないとされた (Becklin et al 1978) 。ここでは幾つかの観測から偏差が見つからなかったことを報告する。

表１．観測結果

　２．新しい観測　

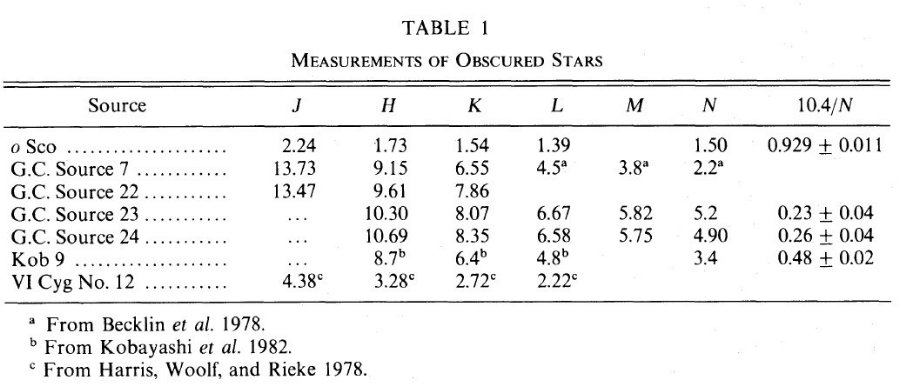
　観測概要　
　表１に我々の観測結果をまとめた。完全のため他観測も追加してある。銀河中心天体の番号は Lebofsky et al 1982 に従った。λ < 10 μm 測光は UAO 1.54m (ビーム径 5".6) と 2.3 m (7".8)、参照フィールドは 10" 東西、で行った。銀河中心天体の 10 μm 観測は IRTF で行われた。 ο Sco の観測は UAO, IRTF で行った。データ整約は Johnson 1966, Low,Rieke 1972 に従い、標準星として 58 Oph, 22 Sco, Ψ Oph, γ Sgr を用いた。

　10.4 μm の狭帯観測　
　10.4 μm の狭帯観測も実施した。有効波長がほぼ等しい広帯 N 測光と合わせ、個の観測からシリケイト吸収の深さを決めた。

　混入の問題　
　銀河中心 22 は近くの低温天体からの光の混入が 5, 10 μm で起きた。天体 23 も 10 μm で同様の問題が起きた。それらは解析では用いなかった。

　　　　　表２．色超過

色超過の導出手続。論文内の数字を拾ってきて再構成すると、

星名 タイプ (J-K)o (H-K)o (K-L)o (K-M)o (J-K) (H-K) (K-L) (K-M) E(J-K) E(H-K) E(K-L) E(K-M)

οSco A5II 0.70 0.19 0.15 ---

VICyg12 F 1.66 0.56 0.50 ---

GC7 1.13 0.30 0.15 -0.21 7.18 2.60 2.05 2.75 6.05 2.30 1.90 2.96

GC22 1.25 0.35 0.21 -0.19 5.61 1.75 ... ... 4.36 1.40 --- ---

GC23 1.25 0.35 0.21 -0.19 ... 2.23 1.40 2.25 --- 1.88 1.19 2.44

GC24 1.25 0.35 0.21 -0.19 ... 2.34 1.77 2.60 --- 1.99 1.56 2.79

Kob9 1.13 0.30 0.15 -0.21 ... 2.3 1.6 ... --- 2.0 1.45 ---

Ave

E(V-L) = [ 1 - E(K-L) ] E(V-K) + E(K-L) ・ E(V-M)
E(B-V) E(K-M) E(B-V) E(K-M) E(B-V)

E(V-M)/E(B-V) = [E(V-K)+E(K-M)]/E(B-V) = E(V-K)/E(B-V)[1 + E(K-M)/E(V-K)]
E(V-M)/E(B-V) < Av/E(B-V) = R なので、E(V-K)/E(B-V) = 2.744 を仮定しただけでは不十分である。 E(V - λ)/E(B-V) 曲線が V バンドと λ^-1 = 0 で、それぞれ 0, -R への接続が不自然にならなければ E(K-M)/E(V-K) は E(K-M)/E(V-K) < R/[E(V-K)/E(B-V)]-1 という制限しかかからない。仮に R = 3.09, E(V-K)/E(B-V) = 2.774 という数値を代入すると、E(K-M)/E(V-K) < 0.114 A(V) = A(V-K) + A(K-M) + A(M)
λ(K)^-1=1/2.2, λ(M)^-1=1/4.8 間を直線で外挿すると、A(M)/E(K-M) = (1/4.8)/(2.6/2.2*4.8)=2.2/2.6=0.85 なので、
A(V) = E(V-K) + E(K-M) + A(M) = E(V-K) + 1.85 E(K-M) として大きく違わない。
R = 3.09 を仮定すると、．．．うーん。先へ行かない。
赤外しか等級が分からない星の個々の減光曲線と R はどう決めてるんだろう？

　

　３．討論　

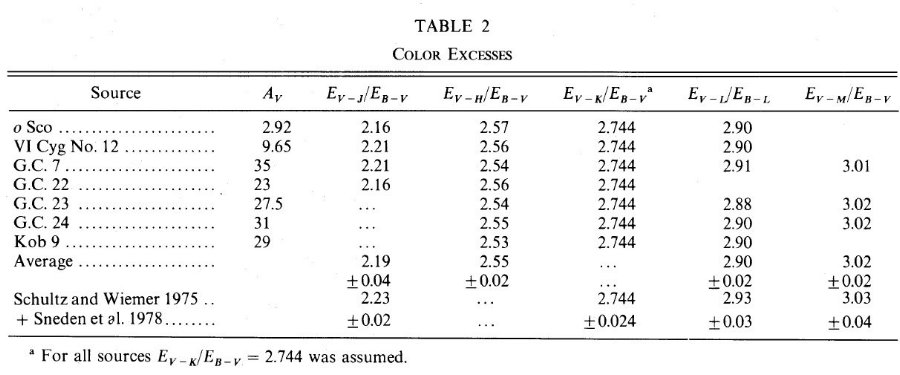
　３．a. 近赤外測光　
　ο Sco　
　ο Sco の　λ > 0.55 μm でのカラーは通常星が Av = 2.92 の平均減光則による赤化を受けていると看做せる。　λ < 0.55 μm でのカラーは予想よりずっと青く、 R = Av/E(B-V = 4.0 となる。この大きな R が例外的な現象なのか、この星が正常な A5II タイプの星からずれているためなのかはっきりしない。 R の値は赤外での赤化の決定には大きな影響を持たないことを注意しておく。　この R の不定性を考慮して、我々は減光則を求めるために E(V-K)/E(B-V) = 2.744 という値から出発する。この値は Schultz, Wiemer 1975 と Sneden et al 1978 の重み付き平均である。

　VI Cyg No.12
　VI Cyg No.12 も表２に追加の比較性として載せてある。観測は Harris, Woolf, Rieke 1978 で E(V-K)/E(B-V) = 2.744 を仮定した。

　銀河中心星　
　銀河中心星は λ < 1 μm では観測できないので Av を測ることは不可能である。そこで、ここでも E(V-K)/E(B-V) = 2.744 を仮定して赤外色超過を計算することにした。計算に際しては、銀河中心星がそのスペクトル型の通常星と同じカラーを持つことを仮定する。つまり、Kob 9 と IRS 7 は (J-K)o=1.13, (H-K)o=0.30, (K-L)o=0.15, IRS 22, 23, 24 は (J-K)o=1.25, (H-K)o=0.35, (K-L)o=0.21, (K-M)o = -0.19 と仮定する。測光誤差は 10 % 以下だが、あり得るカラー異常、強い減光による非常に急なスペクトル勾配を考慮して、カラーには 0.4 の誤差を見込む。減光が大きいのでこの程度の誤差は許容できる。

　共通減光則　
　表２には R = 3.09 を仮定して求めた銀河中心星の色超過を示した。全ての星で、本論文の測光から求めた Av は 2.0 - 2.4 μm 分光測光による連続光勾配から決めた Av と一致した。表２を見ると、銀河系中心方向の減光則は ο Sco や VI Cyg No.12 減光則とあまり変わっていないことが分かる。そこで、それらの重み付き平均をとり、Schultz, Wiemer 1975 や Sneden et al 1978 の "普遍減光則" と比較した。一致が良かったのでこの３つを合わせて一つの減光則としてまとめ、表３に示した。

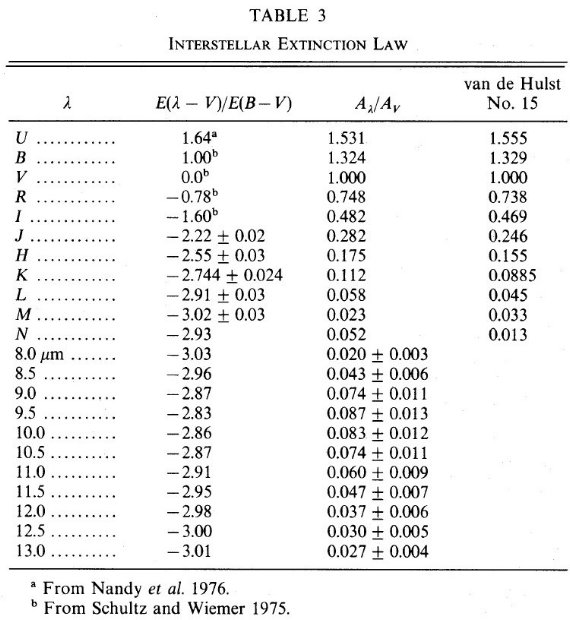　　　　　表３．減光則

　３．b．R の値　
　G.C. 7　
　銀河系星は R = Av/E(B-V) の値に制限を加える。R が大きくなることは中立の灰色吸収を加えることに相当する。この灰色吸収の上限は G.C. 7 の光度から得られる。もう少し弱い制限が Kob 9 から得られる。

M 型超巨星の上限光度　
　Humphrey は M 型超巨星に上限光度が存在することを示した。表４には局所群銀河内の最も明るい M 型超巨星を示す。M31 には十分なデータがない。 Kob 7 はスペクトル型と光度の点でこれらの星と類似の天体であろう。

　G.C. 7 の光度　
　Kob 7 の光度は銀河中心距離 D と R によって決まる。 D は 7 - 9 kpc の間と考えられている。下限として 6.5 kpc をとると G.C.7 の下限光度を R の関数として決められる。表４にその下限値を示した。表を見ると、R > 3.15 では G.C. 7 の光度が大きくなり過ぎることが分かる。R の下限値は M, 8, 13 μm での減光が負にならないという条件から R > 2.99 と決まる。もし減光が L から M　にかけてレーリー散乱より急に減少するというやや強い条件を付けると R > 3.03 となる。これらの上限と下限から R = 3.09 ±0.03 とする。

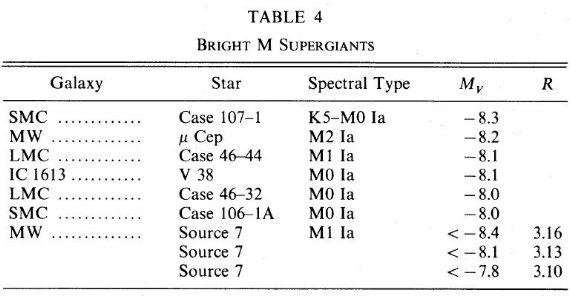表４．明るい M 型超巨星　

　３．c．10 μm 減光　
　シリケイト吸収の深さ τ_Si
　シリケイト吸収は 8 μm と 13 μm の吸収の間をべき乗則でつないで連続吸収と考え、それと吸収量との差として定義される。我々は Lebofsky, Rieke 1979 の 2 フィルター法を採用した。この方法は吸収帯の形は決められないが、吸収の深さ τ_Si を定める。表５にその値を示す。

　シリケイト吸収の誤差　
　まず、シリケイト放射は高温ガスに伴うので関係ない。ただ、星自体に初めからシリケイト吸収があると困る。そこで、スペクトル型が判明している星のみを使うことにした。それぞれの星には異なる強さのシリケイト放射が想定された。その補正を加えて計算した星間シリケイト吸収を表５に示した。

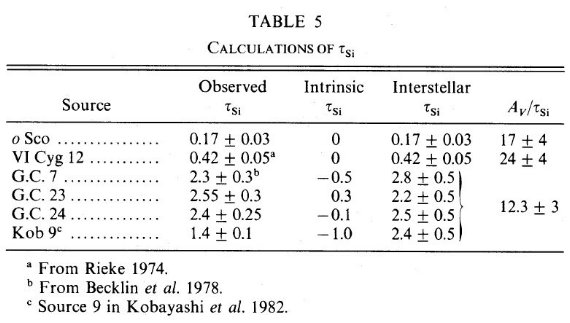表５．τ_Si の計算

　３．d. 星間減光則　
　星間減光則は表３にまとめられた。λ < 1 μm の結果は Schulttz, Wiemer 1975, Nandy et al 1976, Sneden et al 1978 に依っている。λ > 1 μm は本論文とここに引用した結果との平均である。 1 - 5 μm にかけては色超過を直接測り、R = 3.09 を仮定して減光量を導いた。1 - 5 μm にかけては、ダストの吸収率は μ Cep と Trapezium の放射スペクトルに比例すると仮定して、さらに Av/τ_Si = 16.6 として直接導いた。

　４．結論　
（１）分子雲の外では減光則は一定らしい。

（２）R = 3.09±0.03

（３） Av/τ_Si = 16.6

（４）減光則は表３の通り。