|
GC 方向の古典セファイド 55 個から NIR - MIR 減光則を3つの方法で導い
た。
(MIR 変光の処理は? ) 得られた相対減光則は AJ/AKs = 3.005, AH/AKs = 1.717, A[3.6]/AKs = 0.478, A[4.5]/AKs = 0.341, A[5.8]/AKs = 0.234, A[8.0]/AKs = 0.321, AW1/AKs = 0.506, AW2/AKs = 0.340 である。 |
対応する系統エラーも調べた。以前の研究と比べると、我々の MIR 減光則は
極めて低く、急勾配である。7バンド最適距離の方法を用い、我々の 55
セファイドサンプル星の平均距離精度を 4 % に改善した。銀河中心セファイド
4つを用いて、銀河中心距離 Ro = 8.10±0.19±0.22 kpc とした。
(筋が怪しい気がする。最後の方で 論理を整理した。) |
|
銀河中心方向セファイド Matsunaga et al (2011) は銀河中心核円盤にセファイドを3つ発見した。 その後の探索で GC 方向には 52 個のセファイドが見出された。 銀河系中心までの距離は NIR 減光則の違いにより, 約 10 % の系統誤差が 含まれる。Matsunaga et al (2016) は銀河中心距離に対し、大きい方の値を 支持し、また中心核円盤以外にはバルジ内にセファイドが存在しないとした。 |
星色超過図と色超過・減光図 従って、無バイアスな減光則の導出が望まれる。減光則には二つの方法がある。 一つは、赤色巨星とレッドクランプ星色超過図の解析である。もう一つは色超過・ 減光図である。 |


|
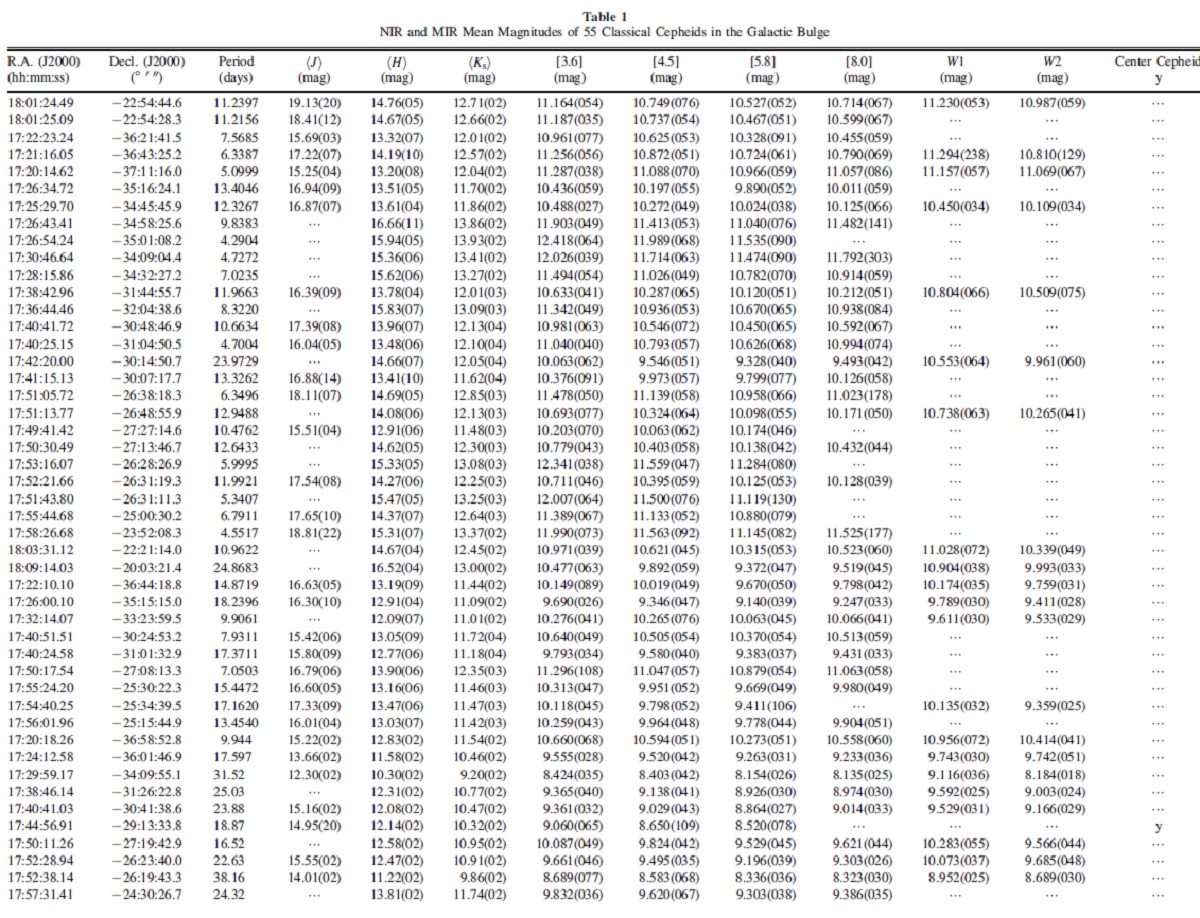
サンプル Matsunaga et al 2011 GC の3セファイド Dekany et al 2015a 2つのセファイド Dekany et al 2015b 35セファイド, l = [-10.5, +10] Matsunaga et al 2016 GC 方向の 29 セファイド 全体では 55 星。 NIR データ NIR データは Matsunaga et al 2011, 2016 の SIRIUS/IRSF データ、Dekany et al 2015a, 2015b の VVV データから採った。数の多さからこの論文では VVV システムに統一する。 VVV システムの有効波長は、 J = 1.254, H = 1.646, Ks = 2.149 μm である。 CLIMPSE II GLIMPSE II のサチュレイションと限界等級は、 [3.6]: 7.0 - 15.5 mag. [4.5]: 6.5 - 15.0 mag. [5.8]: 4.0 - 13.0 mag. [8.0]: 4.0 - 13.0 mag. |
WISE WISE の 5σ 限界等級は、 W1: 16.5 mag. W2: 15.5 mag. W3: 11.2 mag. W4: 7.9 mag. サンプル星の W4 は限界等級外であった。W3 の精度も信頼できない。 WISE の空間分解能 GLIMPSE の空間分解能は 1.2" だが、WISE の空間分解能は 6" でわるい。 この混み合い効果のため、GC セファイドの半数は WISE カタログに載ってい ない。GLIMPSE II でもその影響はあるが、サンプルセファイドはほとんどが [3.6] ≤ 11 mag, 中心セファイドでは [3.6] < 9 mag と明るいので 混み合いの影響は暗い星ほどでない。表1に等級を示す。 |
|
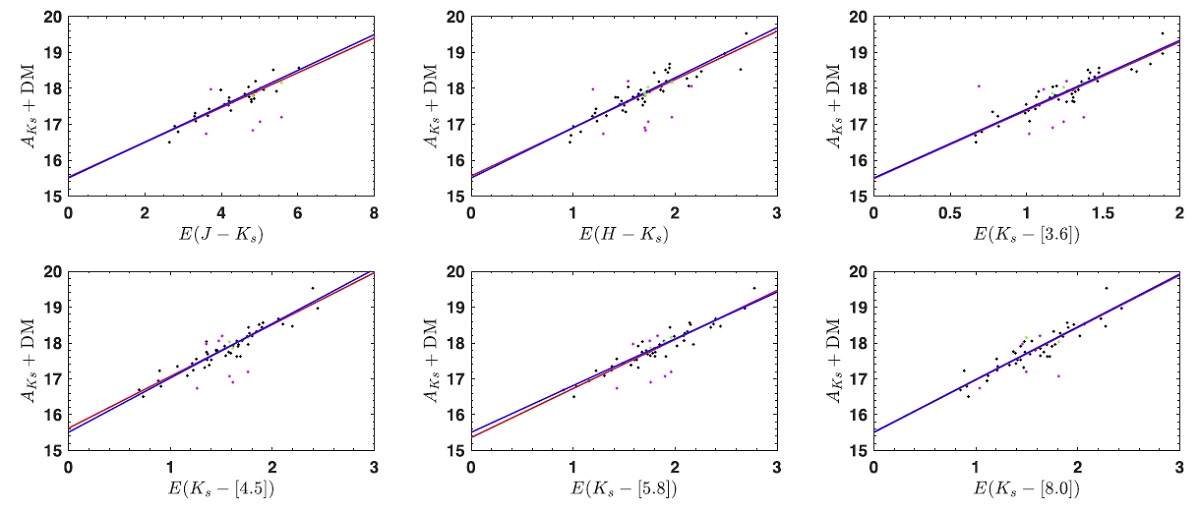
NIR と MIR PLR Chen et al. 2017 は、主系列フィットで決めた星団距離に基づいて、古典 セファイドの NIR を導いた。Wang et al 2018 は NIR PLR から決めたセファ イドの最適距離を用いて MIR 8バンドでの PLR を決めた。 固有カラー こうして、J, H.Ks, [3.6],[4.5], [5.8], [8.0], W1, W2 の平均絶対等級を 決めることができたので、差を取って、固有カラーを計算した。 3.1.色超過・減光法3.1.1.距離と相対減光図1=色超過・減光図図1に,例えば E(J-Ks) のような色超過, 縦軸に A(Ks)+DM = ⟨Ks⟩- ⟨MKs⟩ を採る。この図の勾配が減光ベクトルを表す。 この図のゼロ切片=DM である。この方法を適用するには、距離が等しい必要が ある。そこで、図からは 2σ 不確定レベルの外にある 9 星を除いた。 (GC でないのに図4を見ると、偶々 距離一定になったのは単なる幸運か? 事前には使えない仮定だった。) 図1の黒点は b = [-0.1, +0.1], l = [-10.5, +10.0] の 46 セファイドである。 ただし、中心 l = [-1, +1] はそうでない。 |
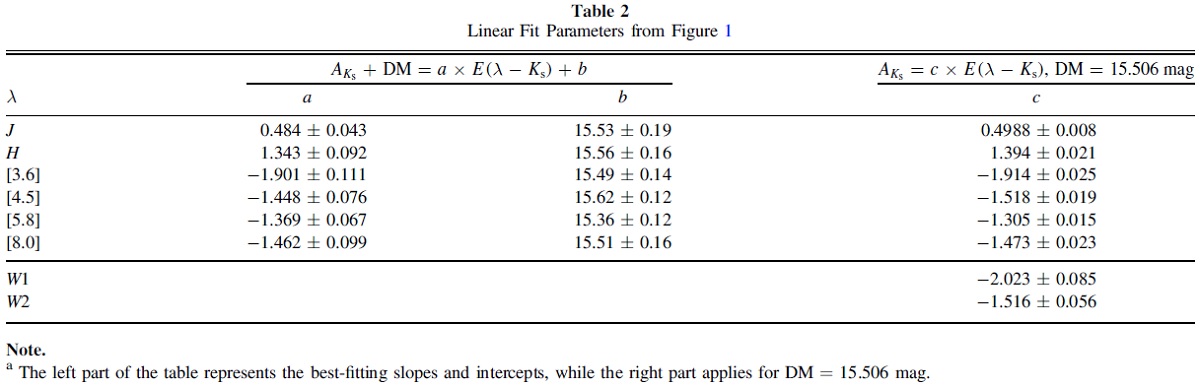
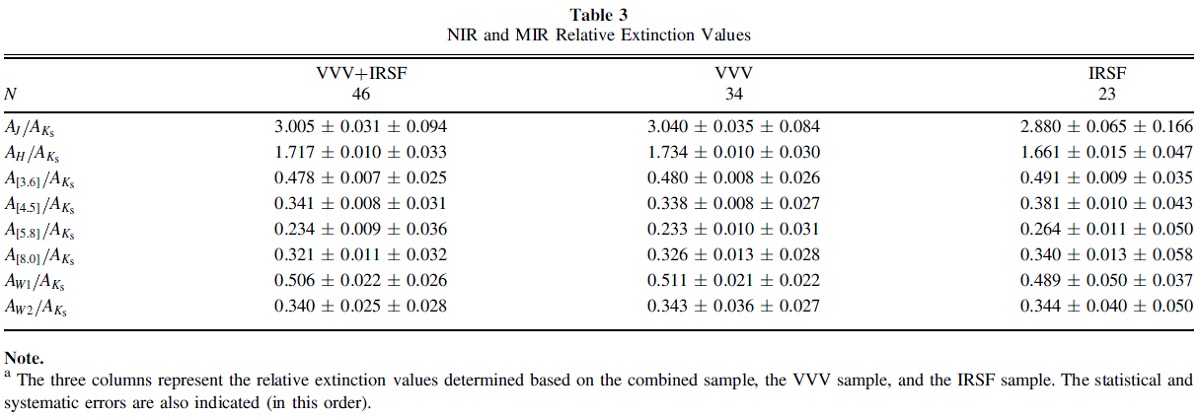
DM 図1の赤線はそれぞれのサンプルに対するベストフィットである。 6つの切片の平均値 DM = 15.506±0.108 mag を固定して、勾配のみを パラメターとしたベストフィットが青線である。 表3=相対減光則 こうして決めた図1の勾配から相対減光則が求まる。それを表3に示す。 VVV と IRSF が同じ天体を扱っていることを確認するために、それぞれのみ で求めた値を比べた。一般に VVV の散らばりの方が小さい。 べき乗則指数 α NIR 減光則をべき乗則指数 α で表した結果、α = 2.05± 0.05±0.05 を得た。有効波長には VVV を使用した。ここに第1エラーは フィットエラー、第2エラーは系統エラーである。 3.1.2.相対減光の不定性系統誤差は2つある。一つは共通の DM を個々の色超過・減光フィットに 適用したため、二つ目は PLR を絶対等級と固有カラーの導出に用いたので、 PLR ゼロ点のエラーが減光のエラーになる。 PLR ゼロ点は HST 視差が 求まった 10 天体から決めた。 |
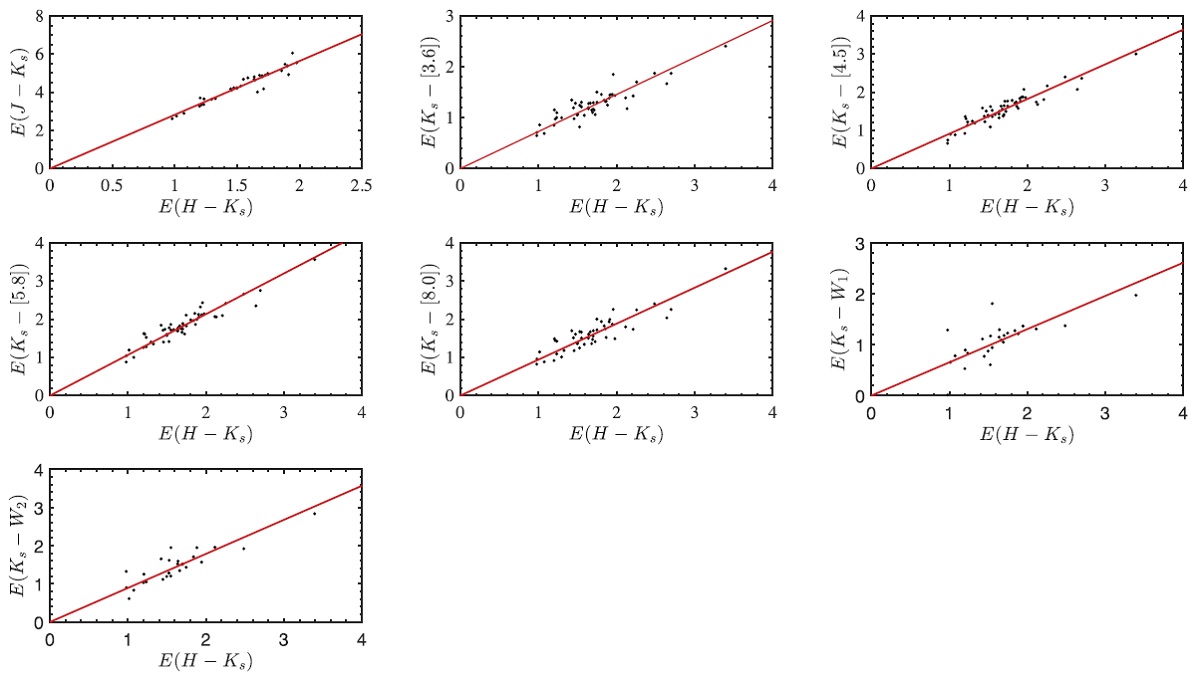
| 色超過比 (color excess ratio = CER) E(λ-Ks)/E(H-Ks) も良く使わ れる。図2はその結果である。A(H)/A(Ks) の値を仮定すると、相対減光曲線 が決まる。ここでは A(H)/A(Ks) = 1,717 (表3)を使う。 | こうして決まった相対減光則は 3.1 と良く合う。 |
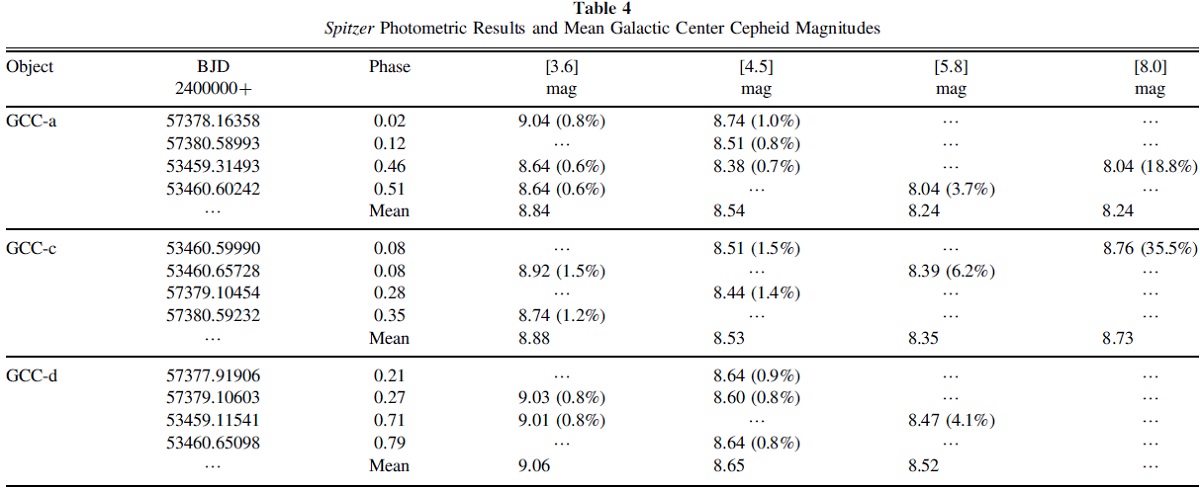
|
GLIMPSE II 測光 3.1. と 3.2. で減光則を出したが、ここでは GC 中心核円盤中の4 セファイド l = [-0.1, 0.1], b = [-0.1, 0.1] の減光則を出す。 4つのセファイド GCC-a,-b,-c,-d の平均 JHKs 等級は Matsunaga et al 2016, その位置は Matsunaga et al 2015 にある。 GLIMPSE II イメージデータを解析し、4 セファイドの point response function フィッティングとアパーチャ測光 の両方を行った。両者は 2 % 精度で一致したが、 GCC-b のみは、アパチャフラックスが 20 - 50 % 大きかった。画像を調べると 1" 以内に二つの星が付随していた。そこで、この星は外した。 表4には残りの3つ GCC-a, -c, -d の測光結果を示す。 GC への減光 GC 距離=8.3±0.2±0.4 kpc を用いて、絶対等級と見かけ等級 から減光量を計算した。この距離は様々な文献値の検討 de Grijs, Bono 2016 から採った。 減光則 表5から導いた相対減光則は他の銀河中心方向セファイドと似ている。 |
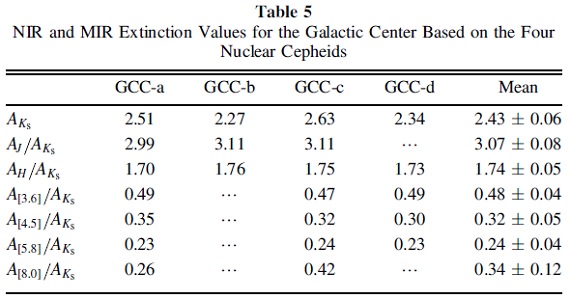 表5.スピッツアー測光結果とGCセファイドの平均絶対等級 |
|
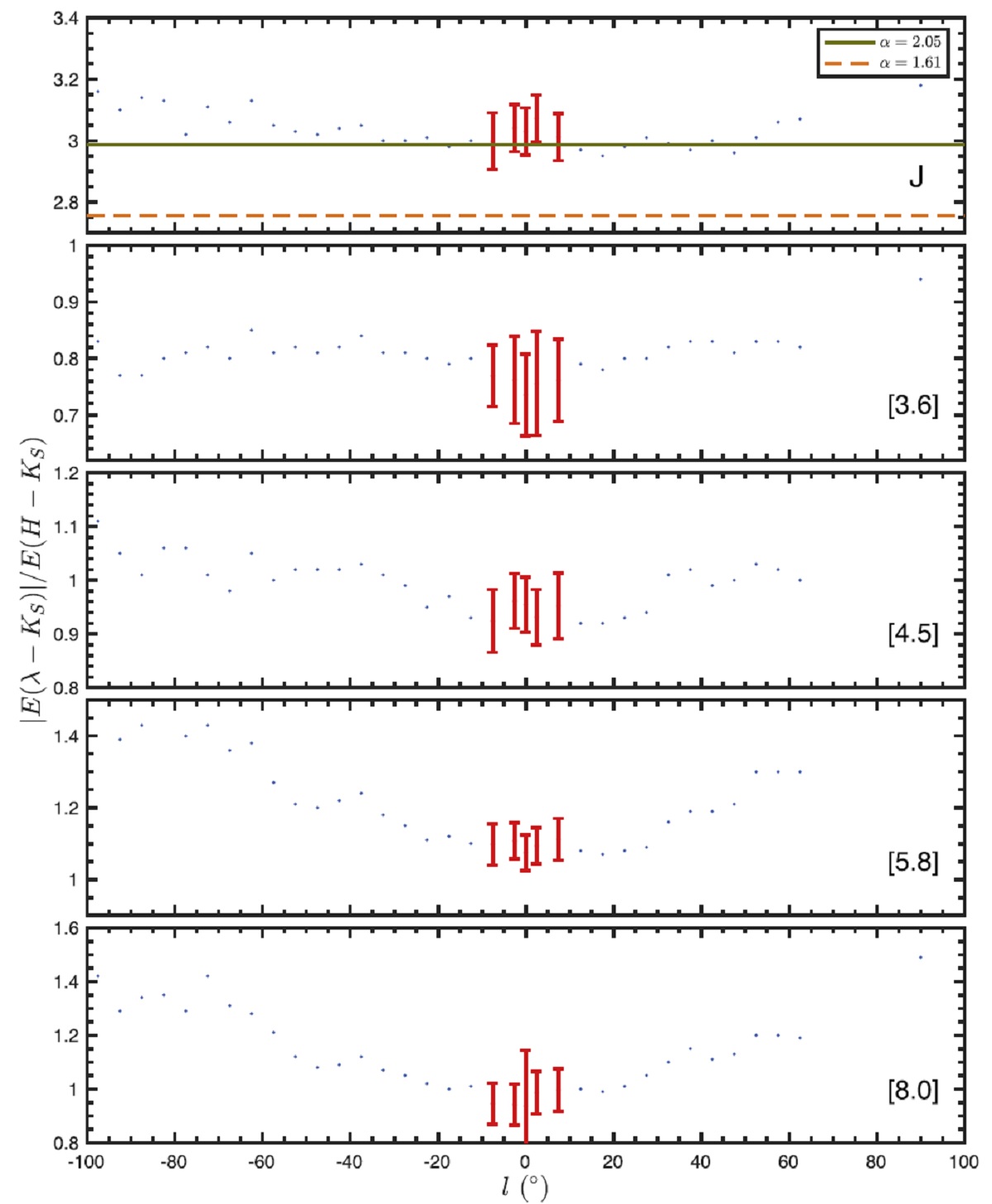
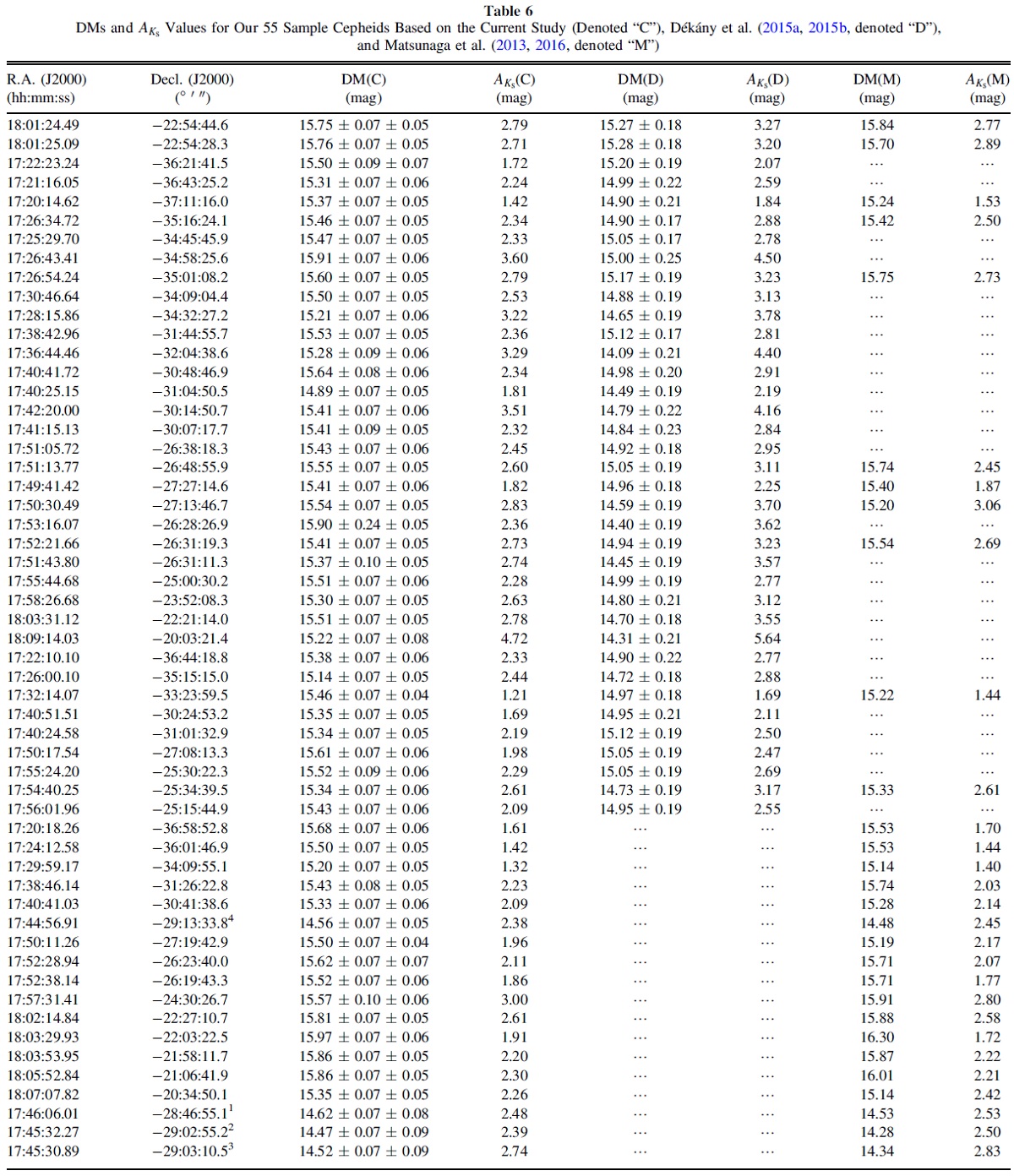
CER のある方向 Zasowski et al (2009). は RC を用いて、 CER = E(λ-Ks)/E(H-Ks) の銀経 l による変化を調 べた。彼らは l = [10, 65], [65,350] l = 90 の方向を調べたので、 GC は 抜けていた。我々の CER は l = [-10.5, +10] をカバーしている。 2MASS 有効波長への変換 我々の CER を 2MASS isophotal wavelength に直すため、J,[3.6], [4.5], [5.8], [8.0] に 1.077, 1.033, 1.026, 1.023, 1.026 を掛けた。 これらのファクターは NIR 減光則に α=2.05 のべき乗則を仮定し、 CER2MASS/CER の評価から得た。 (ここで使っている NIR 波長は 2MASS で なく VVV 波長。J 1.254, H 1.646, Ks 2.149 μm) |
図3: CER-l図 図3は CER と l の関係を l = [-100, 90] で示した。l = [-20, 20] の範囲 では CER に大きな変化はないことが分かる。これは Zasowski et al (2009) が |l| = [10, 20] で得た結果とも合う。 内側銀河系の減光則 NIR では l = [-100, 90] の E(J-Ks)/E(H-Ks) の変化量は、α = 1.61 と 2.05 での値同士の差よりずっと小さい。 (この辺りの議論の筋が不明瞭なの だが...) GC 方向での値 A(H)/A(Ks) = 1.71 を仮定して決めた相対減光則はべき乗則よりも 正確で、内側銀河系全体に適している。 |
|
複数バンド 以前のセファイドは主に H, Ks での減光量と Ks からの距離で扱われてきた。 しかし、エラーが大きい。エラーを小さくするには、減光と距離を複数バンド で扱い、最適値を使う必要がある。 最適 DM この論文では J,H, Ks, [3.6], [4.5], [6.8], [8.0] の測光を組み合わせた。 W1, W2 で検出された星は殆どなかったので使用しなかった。 個々のバンドで DM は、 DMλ = ⟨mλ⟩ - Mλ - Aλ である。 (この Aλ は A(Ks) と平均減光則から出した値か?もし仮定した DM から出した Aλ を使えば、上の式からは単に最初に仮定した DM がまた出るだけだから。 A(Ks) は測定値とすると、DM(Ks) は最初の仮定値か?) それらから、平均重み付き平均 DM は、 ⟨DM⟩ = (ΣDMλ/σ λ2)/(Σ1/σλ 2) ここに、σλ は λ バンドの等級エラーである。 次に、平均 DM ⟨DM⟩ の重み付き標準偏差が導かれる。 (うーん、分からん。) その値は A(Ks) に依存する。最適化 DM と A(Ks) は標準偏差が最小になる という条件で決まる。我々の結果は表6の第3、4列に示す。 |
エラー 我々の DM エラーは次の二つからなる。 (1)統計エラー=標準偏差と PLR との大きい方 標準偏差は前に述べた。PLR エラーは σ1 = SQRT{(ΣerrPLR2) /(n-1)Σ1/σλ2)} ここに、σλは平均等級のエラーである。 (2)PLR のゼロ点と減光則に伴う系統誤差 3.1.2.節に述べたように、 NIR, MIR PLR ゼロ点のバイアスは 0.033 mag で ある。減光則に伴うエラーは上の σ1 と同じで、ただし errPLR を errext に置き換えたものである。 errext は表3から得られる。6バンドの減光にはいくらかの相関 が存在し、NIR 減光と MIR 減光は反相関である。完全独立と完全相関とで 不確実性は 0.045 mag と 0,040 mag である。我々は大きい方を採用した。 エラーのまとめ 表3第3列にあるように、DM の第1エラーは 0.07 mag, 第2エラーは 0.06 mag である。バルジ中の 55 セファイドに対しては距離精度は 4 % にまで改善 された。以前の報告の精度が 7 % なので、大幅な改善である。比較すると、 Matssunaga et al 2013, 2016 との差には系統誤差がなく、平均 8 % の散らばり である。一方 Dekany et al 2015a, 2015b との間には主に使用した減光則の 違いによる 27 % もの系統誤差がある。 |
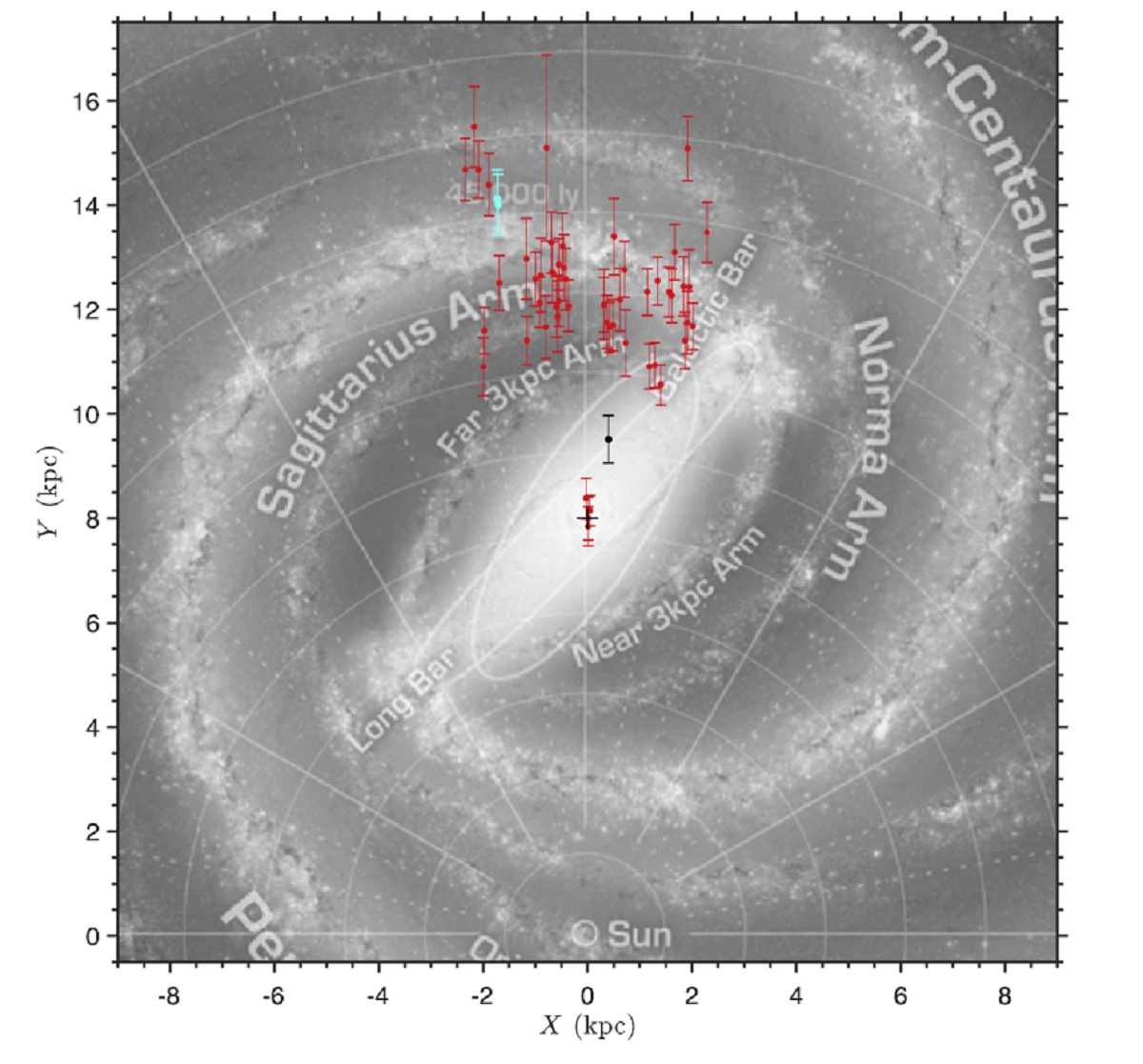
4.2.セファイド分布セファイドの分布図4はセファイドの分布図である。多くは 12.5 kpc でDekany et al 2015b の求めた平均値 9.5 kpc より遠い。我々のサンプルは銀河中心の反対側にある 第1、第2腕の上に位置する。内側バルジでは、4つのセファイドだけが中心 核円盤上にある。内側バルジにはこの4星以外にはなく、減光を正しく扱った Matsunaga et al 2016 の結果を支持する。 中心核円盤の近くにあるセファイド 図4の黒点で示した中心核円盤の近くにあるセファイドに注意したい。 Ro = 9.5 kpc を仮定して、この星は GC から 1.5±0.4 kpc にある。 (どれだ? 17:40:25.15 の星?) この星は l = -2.4, P = 4.7 d で A(Ks) = 1.89±0.09 mag である。 減光が大きいので、前景にあるタイプII セファイドではないだろう。その場合 には D = 3.9 kpc となる。 (GC 手前でも A(Ks) = 2 もあり得る?) Marci et al 2015 によると、第1倍音セファイドは P = [0.27, 5.91] d で 基本振動セファイド P = [1.14, 52.9] d と重なる。したがってこの星は 第1倍音 かも知れない。その場合、第1倍音の PLR を用いると、DM = 15.46± 0.09 mag となる。他の 46 セファイドと同じく腕に載る。J光度曲線か視線速度 情報が欲しい。 |
4.3.銀河中心距離Ro4つのセファイドは銀河中心近くにある。その平均から GC 距離として、 DM = 14.541&plumn;0.050(統計誤差)±0.056(系統) mag, Ro = 8.10±0.19(統計誤差)±0.21(系統) kpc を得る。 Matsunaga 値との比較 Matsunaga et al 2011 の3セファイドからの値 Ro = 7.9±0.2(統計誤差)±0.3(系統) kpc, Matsunaga et al 2016 の4セファイドからの値 Ro = 7.6±0.4(統計誤差) kpc と比べると、我々の値は著しく誤差が 小さい。我々の距離は de Grijs, Bono 2016 が推奨する値 Ro = 8.3±0.2(統計誤差)±0.4(系統) kpc に合う。 |
|
Dekany et al 2015a,b の減光値 Nishiyama et al. (2006) の A(H)/A(Ks) = 1.62±0.04 から導いた、 Nishiyama et al. (2009) A(Ks)/E(H-Ks) = 1.63±0.04 を採用した。 Matsunaga et al 2013, 2016 の減光値 Matsunaga et al 2013, 2016 は Nishiyama et al. (2006) の A(H)/A(Ks) = 1.73±0.03 に基づき、 A(Ks)/E(H-Ks) = 1.44±0.01 を採用した。 我々の値 我々のセファイドからの評価では A(Ks)/E(H-Ks) = 1.39±0.07 であった。この値は Matsunaga et al 2013, 2016 の採用した値 1.44 に近い。 |
減光のエラーが距離誤差の最大の要因 系外銀河などのセファイド距離の決定では減光効果は無視する。それらに 対してはメタル量効果が大きい。しかし、銀河中心方向のセファイドに対しては 減光のエラーが距離誤差の最大の要因である。従って減光則に含まれる 系統誤差を注意深く解析しなくてはいけない。 赤色巨星やレッドクランプ星に対する色超過法だけでなく、特定のレッド クランプ星に関する色超過・減光法も多くの仮定に基づいている。それが 系統誤差に結び付く。 |
|
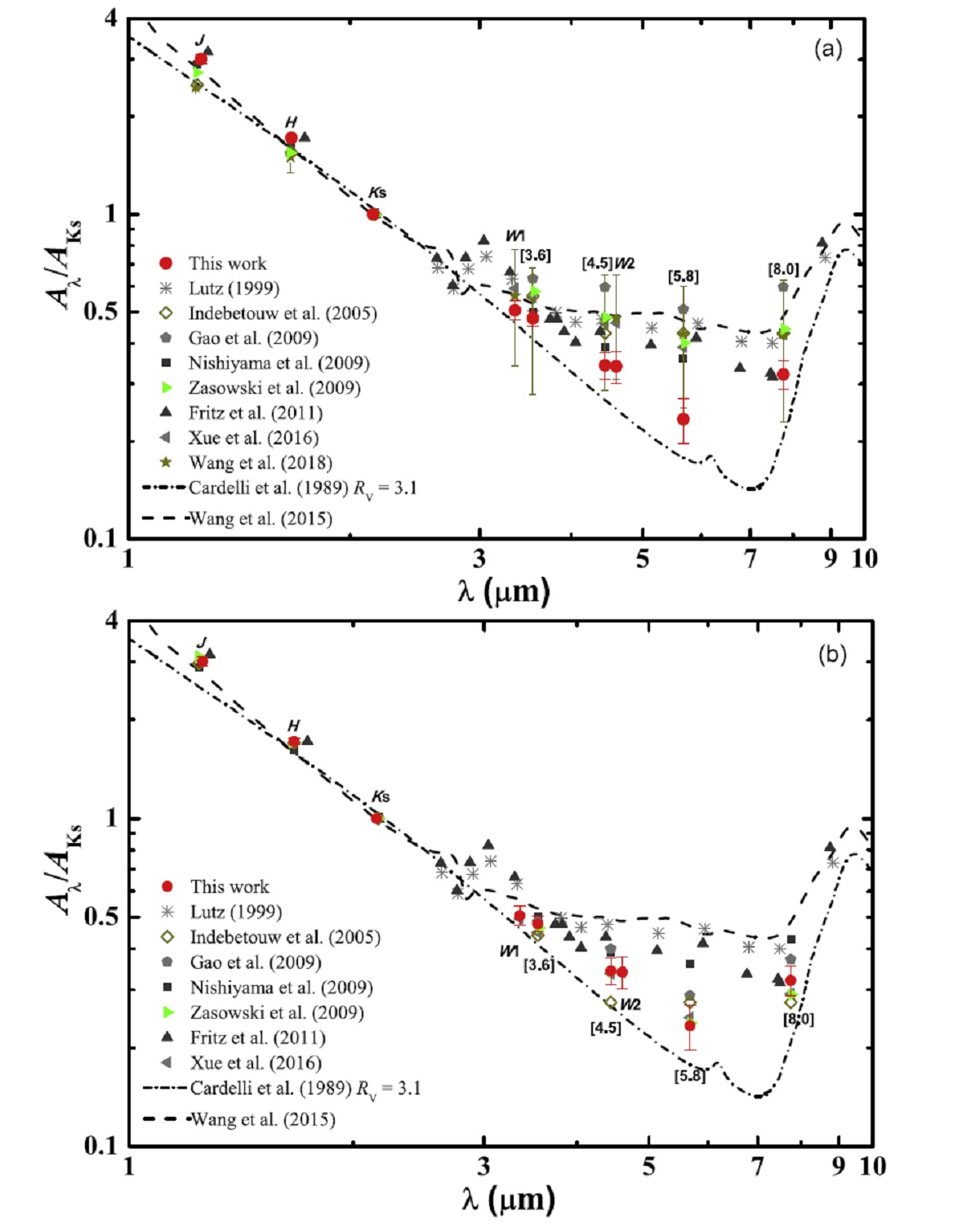
α = 1.6 - 1.7 則 Rieke, Lebofsky (1985) は 7 μm まで A(λ) ∝ λ-1.61 とした。 これはオリオン星雲の H2 ラインから Bertldi et al 1999, Rosenthal et al 2000 により α = 1.7 と確認された。 また Draine 1989 は シリケイトーグラファイトモデルが 9 μm まで、 α = 1.7 が持続すると述べた。しかし、 Lutz et al. (1996) は Sgr A* 方向の減光曲線は 3 - 8 μm で平坦であることを発見した。 この結果は Lutz et al 1999, Nishiyama et al (2009) Nishiyama et al (2009), Fritz et al (2011) により確認された。 NIR べき乗則からの乖離 今世紀になってからは、 Indebetouw et al (2005), Flaherty et al 2007, Gao et al 2009, Wang et al 2013, Xue et al 2016 らが NIR べき乗則からの乖離を次々と報告した。 我々の MIR 相対減光値が最も低い 図5(a) で分かるように、以前の異なる方向での減光則と比べると、我々の MIR 相対減光の結果は減光値が最も低い。特に [5.8] バンドで著しい。 他から外れる主な原因 我々の MIR 減光が他の減光則から外れる主な原因は、仮定される AJ/AKs, AH/AKs の値にある。 CER 法ではそれらの値を仮定する必要がある。 前に挙げた著者たちが使用したのは、 Indebetouw et al (2005) が AJ/AKs = 2.50, Gao et al 2009 が AJ/AKs = 2.52, Zakowski et al (2009) が AH/AKs = 1.55, Xue et al 2016 は AJ/AKs = 2.72 を仮定している。 もしそれらの値の代わりに我々が GC 方向セファイドについて得た、2MASS システムで AJ/AKs = 3.119, AH/AKs = 1.703 という値、VVV システムでは 3.003, 1.717 を使うと、それら4研究の結果も 我々と同じ急で低い MIR 減光則となる。図5(b) を見よ。 |
RC と RG の固有カラー補正を注意深く扱った二つの研究、
Zakowski et al (2009)
と
Xue et al (2016)
は我々の結果と完全に一致する。
(直前の文章では異なると言ってい ないか?) Indebetouw et al (2005) の結果も近赤外の相対減光値を我々の値に補正し、誤差を考慮すると、我々の 結果に合致する。 Gai et al 2009 は我々の値より高いが、これは固有カラー 補正の不足による可能性がある。 ("intrinsic color correction" は測光系の変換の話ではなく、星の固有カラーをどう扱うかなの話らしい が、具体的な数字は書いていないので不明。) AH/AKs は一定 3.4.節の話と合わせ、我々は AH/AKs は我々が 扱った内側銀河系全体で一様な値と結論する。GC 中心の星を使って求める AH/AKs はべき乗則 α = 1.6 を使うより良い。 これは Gaia により多くの RC 星の距離が決まれば明らかになるだろう。 Wang et al (2018) が決めた減光値は AKs = 0.10 - 0.63 mag の 近傍セファイドに基づいている。低い減光値は我々が導いたような MIR 減光値 に対しては、測光エラーや距離不定性からの影響を大きく受ける。 GC 方向での以前の研究 GC 方向での以前の研究と比べると、我々の結果は は Lutz et al 1999, Nishiyama et al (2009) Nishiyama et al (2009), Fritz et al (2011) の値より低い。ただ、それらは他の領域での結果より平坦度が低いが。 Nishiyama et al (2009), の結果はバルジ RC に基づいている。彼らの RC 星には前景星が混入している。 前景 RC 星の減光は "integrated relative extinction " の MIR 平坦減光へ 導く。それに対し、我々の 55 セファイドサンプルは距離が確定しているので MIR 減光の評価ができている。 |
|
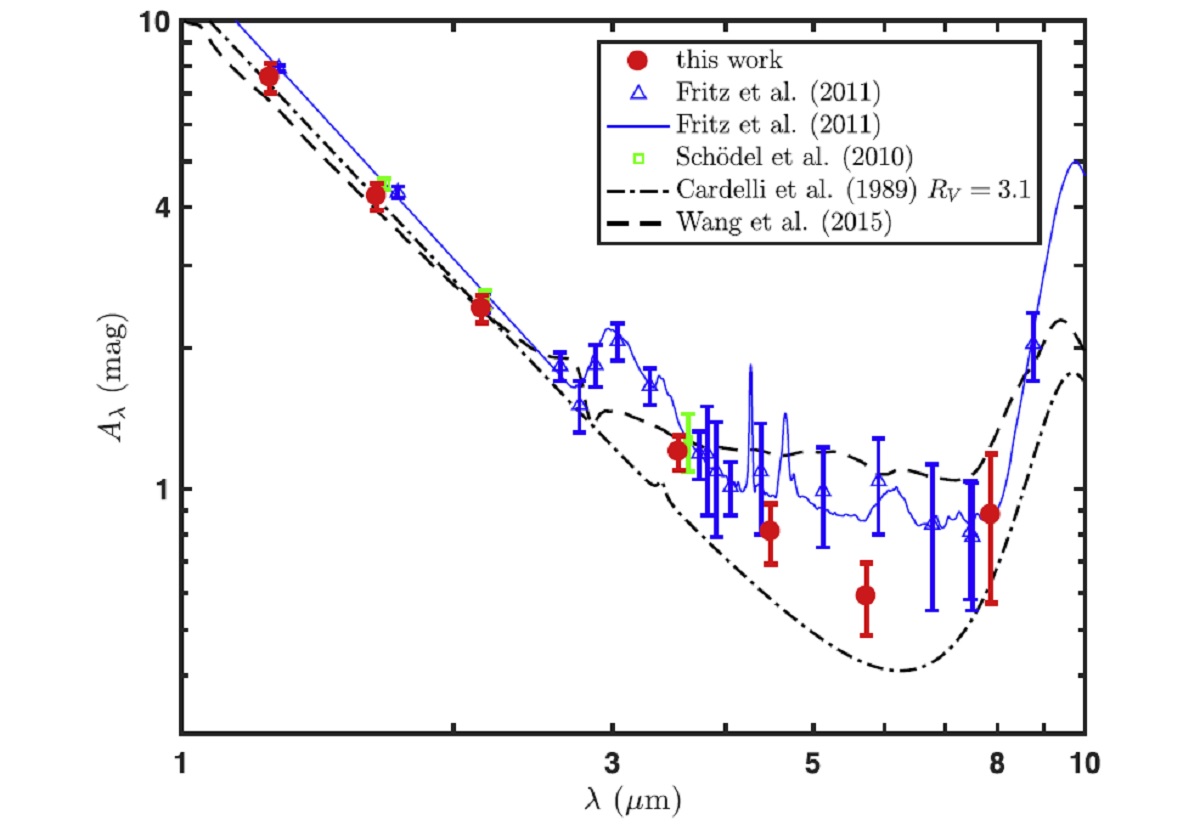
セファイド減光と RC 減光 3.3.節表5に、GC 4セファイドの平均減光を示した。これは Schodel et al. (2010) が VLT のアダプティブオプティクス撮像で得た RC から導いた 減光と比較されるべきものである。 彼らが導いた Ro = 8.03 kpc を我々の Ro = 8.1 kpc で補正すると減光 の一致はさらに良くなる。 Fritz et al 2011 との比較 彼らの HI 線の分光から導いた NIR 減光は我々の値と合う。MIR では |
急勾配な MIR 減光は われわれの急勾配な MIR 減光は正しい。なぜなら、GC セファイドに平坦な MIR 減光を適用すると、 Ro = 6.5 kpc という小さすぎる値になって しまうから。 |
|
議論のスジがよく分からない。自分の理解では、 (1)星団(距離=主系列フィット)セファイドから周期光度関係 (2)差をとって、周期固有カラー関係。 (3)55 セファイドの個々星に対し、周期から出した絶対等級と固有カラーを 使い、色超過とm−M を計算してプロット。 (4)それらのセファイドが等距離にあると仮定して、直線フィットの切片を その想定共通距離とし、フィット直線の勾配から55セファイドの相対減光則 を決める。 (5)GC 4セファイドは 55 セファイドには含まれない。Ro = 8.3 kpc を 仮定して、PLR から出した M と m から銀河中心減光則を出す。 |
(6)各セファイド距離の決め直しを行う。55 セファイドと 4 GC セファイド のそれぞれに各グループ毎の相対減光則と色超過を適用して、バンド毎の距離 を求め、その重み付き平均距離を各星の距離とする。各バンドの減光はしたが ってKs バンドの減光量に依存する。それは標準偏差が最小になるという要請 で決める。 (7)55 セファイド、GC セファイドの減光量は共通距離から決めたのである が、こうして、今度はそうして求めた減光量から距離が決め直される。この時 の減光量は共通距離から各星の各バンド毎に決めた減光ではなく、共通減光則 と、A(Ks) から決める減光である。 (8)GC に関して言えば、こうして得た GC 4セファイドの平均距離として 8,1 kpc を得る。 一番問題に思えるのは、(4)の等距離仮定と思う。その仮定の下でフィット 線を E(J-K) = 0まで伸ばして、仮定した等距離が幾つかを決め、それに基づ いて、A(Ks)/E(J-Ks) が決まる。こうして相対減光則 A(λ)/E(λ-Ks) が決ま っていく。 |
|
(1)前に挙げた距離一定の仮定 (2)各バンドでの周期光度関係の明示 |
(3)GC で Ro=8.3 koc (DM = 14.6)を仮定して3つの星の A(λ) を出し、 次に個々星のバンド平均 DM を算出して3つの星の DM から平均 Ro = 8.1 kpc を出している。しかし、もともと 8.3 kpcを仮定して A を決めたのに、どの 星の距離も 8.3 kpc より小さい(表6)ということがあり得るのか? 個々の星の A(λ)とDM(λ)が明示されていない。 |