VLT の AO (NACO)に IRS 7 (Ks = 6.5 - 7)をガイド星として、 撮像した。H, Ks 観測 には NACO S27 カメラ、視野 28″×28″, 0.02705″/pixel, が用いられた。ディザリングで視野 40″×40″ を得た。
L′ 観測
L′ 観測には NACO L27 カメラが用いられた。
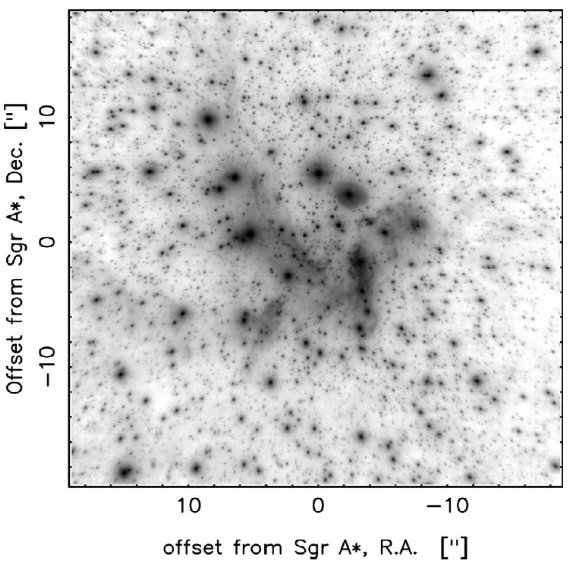
図2.L′ バンドのモザイク画像。
| 銀河中心 1 pc の近赤外減光則のべき乗指数を正しく求めるため、正確な 測光データを得た。アダプティブオプティックス+カメラの組み合わせ、 VLT の NAOS/CONICA、 を用いて観測した。測光には anisoplanatic 効果を 考慮して、系統エラーを 2 % に抑えた。レッドクランプ星を用い、H, Ks, L′ バンドの減光とべき乗指数を測定した。さらに、 H-Ks - Ks、 L′ カラーに基づいて減光マップを作成した。 | 7700 星の Ks 等級を求めた。さらに、 H and/or L′ 測光も行った。 最近の公開観測データから Ro = 8.03±0.15 kpc を求めた。エラーは 2 % である。この Ro と RC 法により、銀河系中心 1 pc 領域の平均減光を AH = 4.48±0.13, AKs = 2.54±0.12, AL′ = 1.27±0.18 と決めた。べき乗指数は αH-Ks = 2.218±0.24, αKs-L′ = 1.34±0.29, であった。この減光則と星の H-Ks カラーを用いて、 Ks 減光マップを作成した。エラーは 10 % 以下である。このマップの減光は 星のカラーエクセスから導かれたが、arcsec スケールで変動する。 平均は AKs = 2.74±0.30 である。Sgr A* の 0.5″ 半径 内での平均減光は、 AH,SgrA* = 4.35±0.12, AKs,SgrA* = 2.46±0.03, AL′,SgrA* = 1.23±0.08 である。 |
|
銀河系中心核星団(NSC) NSCの回転速度の測定から少なくとも部分的には NSC の成因は物質降着で あることが判った。NSCの分光観測から多数の若い大質量星が Sgr A* から 0.5″ 以内に多数存在することが判った。それらは 400 万年前に起きた 星形成バーストの証拠である。若い星の配置は非等方的で、少なくとも 50 % は回転円盤状にある。 中心核星団観測は(1)混み合いと(2)高減光を伴う 銀河系中心核星団の観測は(1)混み合いと(2)高減光の二つの困難がある。この ため NACO/VLT を用いても Sgr A* から 0.5 pc 以内では 2 Mo 以上の星しか検出でき ない。これは中心核星団の 10 % しか見えないということである。 Sgr A* 周囲の雲 Sgr A* 周囲 2 - 3 pc には近赤外でも透過不能な多数の雲が存在している。 (どんな雲?論文は何? Schodel et al 2007 の図1は投影で Sgr A* 近くに黒い斑点が見えるが、物理的に近いのか?ミニスパイラル のようなプラズマと分子雲の関係は?) 中心 1 pc の平均減光は AK = 3 に達する。 AV/AK の値は、9 Rieke,Lebofsky 1985, 16 Nishiyama et al 2008, 29 Gosling et al 2009, などがある。J バンドでさえも観測可能なのは最も明るい星に限られ、可視での観測は 不可能である。 分類。分光ー測光? アダプティブオプティックスに補助された積分フィールド分光の結果、Sgr A* 0.5 pc 内の数百の星の分類ができた。しかし、この方法は観測にも解析にも極端に時間がかかる。 分光的手法でせめて早期型星と晩期型星を分けられないだろうか?Buchholz et al 2009 は CO バンドヘッドを使った分類法が可能であることを示した。 |
近赤外減光則 10年前までは 1 - 8 μm 減光則は ∝ λ-α の形で、 α = 1.75 (Draine 1989) と信じられていた。これに対する疑問は Lutz et al 1996 による ISO/SWS の結果が λ > 3 μm でずれていくことから始まった。 現在、近赤外では単純なべき乗則は十分によい記述と認められているが、ただしべき指数 はもっと大きい、 λ > 3 μm の状況は未確定である。 Nishiyama et al 2009, の結果は > 3 μm での減光則の低下は以前考えられていたよりずっと緩やかで、 殆ど一定値に近いことを示唆している。 Gosling et al 2009, は近赤外べき乗指数が 5″ のスケールで変動するとさえ主張している。 最近の減光マップ Schodel et al 2007 と Buchholz et al 2009 は銀河系中心 0.5 - 1 pc の減光マップを 作った。しかし、それらの仕事では減光は他の目的の副産物であった。例えば、どちらも λ-1.75 減光則をそのまま用いている。また、測光精度も十分でない。 論文の目的 この論文では、GC NSC の研究を上に上げた2点に注意して行った。すなわち、AO を用いて 測光精度を上げ、減光補正を正確にした。この論文では H, Ks, L′ バンドの撮像を 銀河中心に対し行い、 Sgr A* 周囲 1 pc 内にある数千の星の測光を行った。我々は絶対減光強度 と減光則を定め、分解能 1″ - 2″ の詳細な減光マップを作成した。 |
|
H, Ks 観測装置 VLT の AO (NACO)に IRS 7 (Ks = 6.5 - 7)をガイド星として、 撮像した。H, Ks 観測 には NACO S27 カメラ、視野 28″×28″, 0.02705″/pixel, が用いられた。ディザリングで視野 40″×40″ を得た。 L′ 観測 L′ 観測には NACO L27 カメラが用いられた。 |
 図2.L′ バンドのモザイク画像。 |
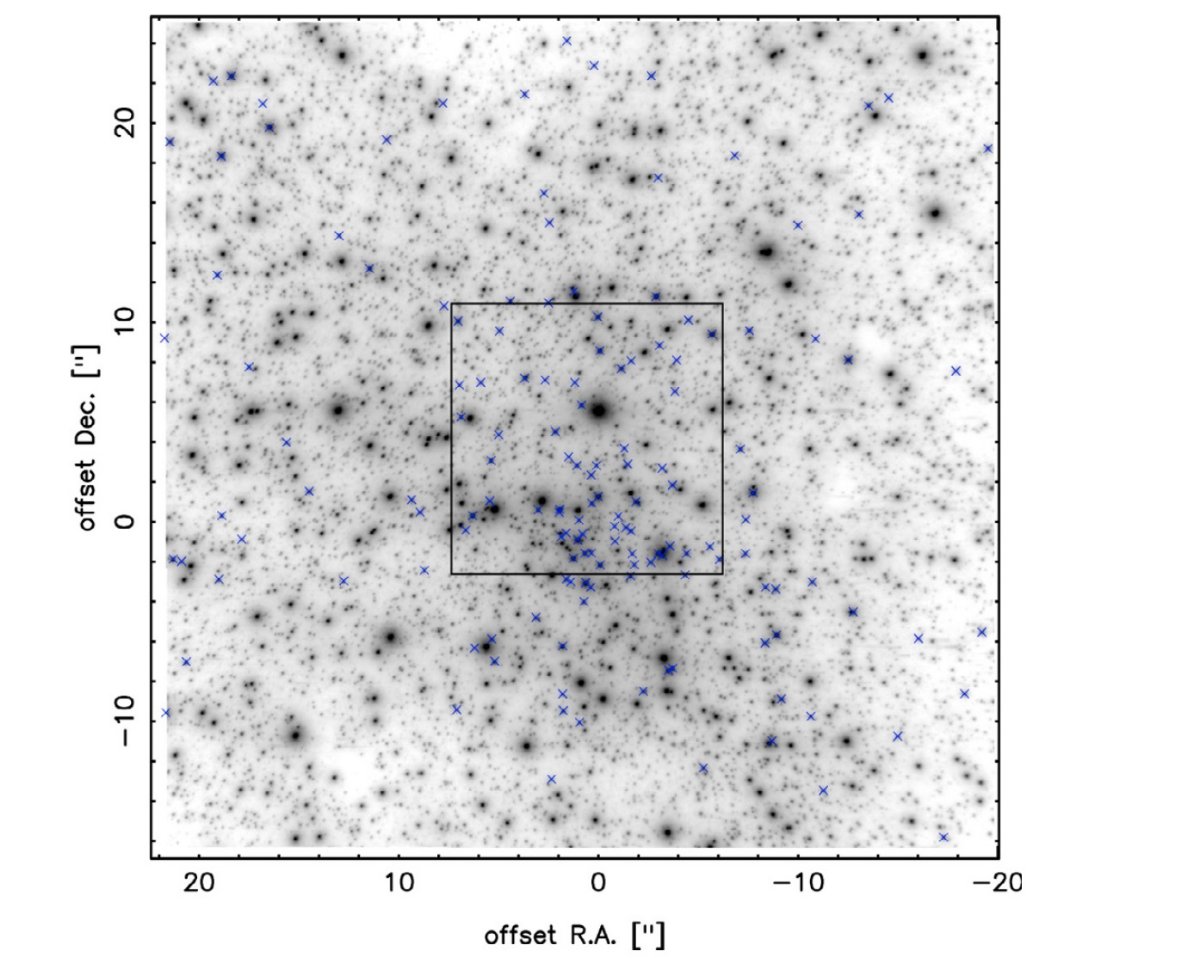
|
色等級図上のレッドクランプ 図4の上、中に見える濃い帯はレッドクランプである。レッドクランプのカラーと 等級は年齢とメタルの依存性が特に t > 1.6 Gyr では小さい。 光度関数上のレッドクランプ 図4下には光度関数が示してある。ここでもレッドクランプははっきりしたコブとして 現れる。指数関数+ガウシャンでフィットして求めたガウシャンピーク位置は、 HRC = 17.60±0.04(17.58±0.016) KsRC = 15.59±0.04(15.57±0.009) L′RC = 14.25±0.03(14.22±0.008) である。カッコ内は混み合いによる完全度の補正を行わなかった場合の値である。 レッドクランプ星の絶対等級 レッドクランプ星の絶対等級は MK = -1.54±0.04 (2MASS システム Groenewegen 2008), MK = -1.61±0.03 (Alves 2000) と された。両方ともヒッパルコスカタログに基づいている。ここではより新しい値を 使おう。K 等級と Ks 等級の差は約 0.01 mag である。(Nishiyama et al 2006) Nishiyama et al 2006 は銀河中心への距離指標を (m-M)o = KsRC,intr - MKs + ΔMK KsRC,intr は赤化補正後の Ks 等級、MKs は Ks 絶対等級、 ΔMK は種族効果補正である。我々は Nishiyama et al 2006 と同じ -1.54, ΔMK = -0.07 を採用した。銀河中心距離を 仮定すると、上の式は赤化 MKs = 補正等級を与える。その値を観測等級と比べれば K バンド減光 強度が求まる。 銀河中心距離 銀河中心距離には多数の値が提案されてきた。これらは、(たぶん)独立な方法で求められており、 それらの重み付き平均 Ro = 8.03±0.15 pc は妥当な値であろう。これは (m-M)o = 14.52±0.04 に対応する。この値を用いると、 KsRC,intr = 13.05 ±0.09 を得る。 光度関数ピークと Ks 減光量 光度関数ピークから KsRC = 15.59±0.07 である。これから AKs = 2.54±0.12 を得る。H-Ks = 0.07±0.03, Ks-L′ = 0.07±0.03 を仮定して、同様の方法で、AH = 4.48±0.13, AL′ = 1.27±0.18 を得た。 べき乗指数 α べき乗減光則を仮定すると、 H - Ks, および Ks - L′ 間の減光べき乗指数を 求めることが可能で、αH-Ks = 2.21±0.24, αKs-L′ = 1.34±0.2 となる。ここで採用した有効波長は λeff,H = 1.677±0.018, λeff,Ks = 2.168±0.012, λeff,L′ = 3.636±0.012 である。有効波長に関する詳細は 付録Aに述べた。 領域内の微分減光 図4を見ると分かるが、Ks ピークには H-Ks 依存性がある。レッドクランプ星の 固有カラーと等級の巾が狭いことを考えると、図4に見える帯は領域内の微分減光 が原因と思われる。そこで、我々は H-Ks の狭い区分ごとに Ks 光度関数を作り、 そのピークを求めた。この手法は、 Nishiyama et al 2006 の方法とよく似ている。ただ、彼らは空間の区分ごとにピークを定めた点が違う。 微分赤化の勾配 図5には H-Ks 区分ごとのレッドクランプのピーク Ks 対 H-Ks の関係を示す。 勾配は αH-Ks = 2.54±0.15 である。この値はエラーの範囲内で 前に求めた 2.21±0.24 と合う。 不完全度 図4を見ると赤化が大きくなるにつれ測光完全度が低下することが判る。それは 我々は完全性の補完は行わなかった。しかし、赤い方や青い方の星を除いてフィットしても 目立った違いは出ないので、不完全度が勾配に影響するとは考えない。 Ks - L′ 図4の中段を見ると、L′ 対 Ks - L′ に明確な傾向は見られない。それで αKs-L′ の決定は行わなかった。 |
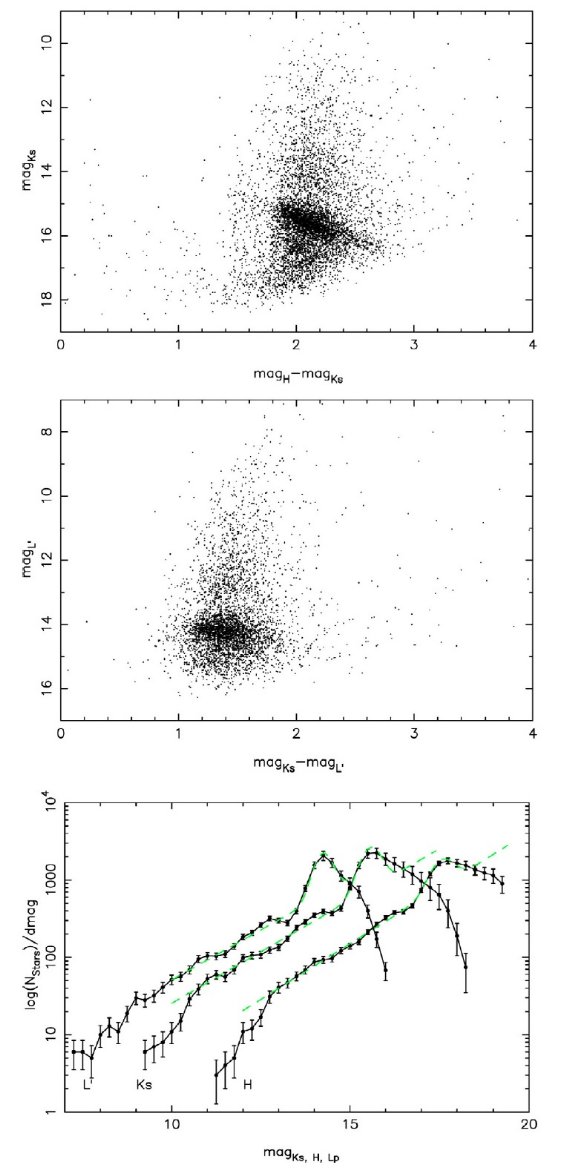 図4.上:Ks - (H-Ks)、中;L′ - (Ks-L′)、下:(混雑による)完全度 補正後の L′, Ks, H 光度関数。緑破線=指数関数+ガウシャンのフィット。 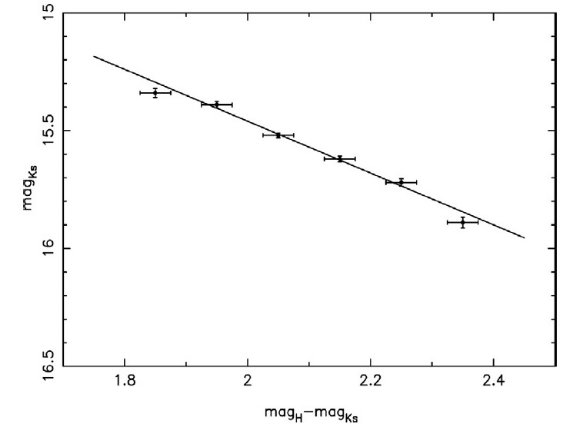 図5.H-Ks 区分ごとのレッドクランプのピーク Ks 対 H-Ks の関係。 |

|
前景星と後景星 前景星は H-Ks < 1.8、 後景星は H-Ks > 2.8 として排除した。そして、 各点から最近星 20 個を選んでその H-Ks 中間値を計算した。 色超過 固有カラーとして、(H-Ks)o = 0.07 を採用した。0-次補正として、Ks < 14.5 の星は (H-Ks)o = 0.2 としてみたが、それらの星は全体の 16 % で補正効果はほとんどなかった。また、 Buchholz et al 2009 により早期型星とされた星のカラーは (H-Ks)=-0.03 とした。 こうして決めた E(H-Ks) は べき乗減光則 αH-Ks = 2.21±0.24 を 仮定して AKs に変換した。 AKs 分布 図7に AKs 分布を示した。平均 AKs = 2.74、標準偏差 0.30 の ガウス分布でよくフィットする。 赤化補正色等級図 減光マップを用いて、微分減光補正色等級図が作られた。結果が図8に示されている。 図4と比べると以下に分散が減少したかが分かる。レッドクランプは非常によく定義され、 赤色巨星枝がその右に伸びている。 早期型星の選別 図8破線の左側は前景星か早期型星と考えられる。既知早期型星 Buchholz et al 2009 は青丸で示した。これにより、赤化補正 H-Ks で早期型星を分別する方法の 信頼度がチェックできる。 Ks < 14 では約 65 % の既知早期型星が正しく 早期型と認識された。では、晩期型星が早期型星と誤認される確率はどのくらい だろうか?今回の視野を他の研究に合わせ、Sgr A* から 12″ 以内で Ks < 14 の星を調べよう。この制限内ではほぼ 100 % の星がスペクトル型 を分類されている。その内、約 30 % は赤化補正カラーによる分類が誤っていた。 このエラーの原因としては、 (1)測光エラー (2)減光マップ分解能より小さなスケールで減光が変動している (3)星周減光 などが考えられる。しかし、ここでの方法の粗さを考えると成功率 2/3 は かなりのもので、大規模で早期型星を拾い出すにはかなり有用であろう。ただし、 Ks > 14 では赤化補正 H-Ks は我々のサンプルを早期型と晩期型に分離 するには粗すぎて使えない。 早期型星 II 図1では、H-Ks 中間値より青い星を、前景星は除いて、十字マークしてある。 Paumard et al 2006, Buchholz et al 2009, Do et al 2009 の報告にある多数の 早期型星が正しく選別されている。前節に述べた 30 % エラーを考えると、同じ くらいの数の星が網から逃れているかも知れない。しかし、これは広帯域画像で 早期型星を分別した最初の試みであり、Buchholz et al 2009 の Sgr A* からの 距離 0.5 pc を越えて早期型星の集団があるという発見を確認する。 |
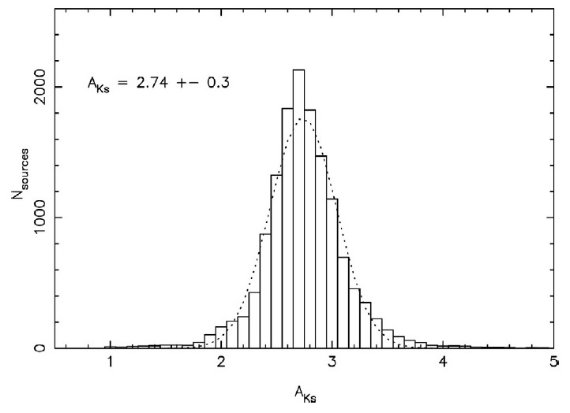 図7.AKs 分布。 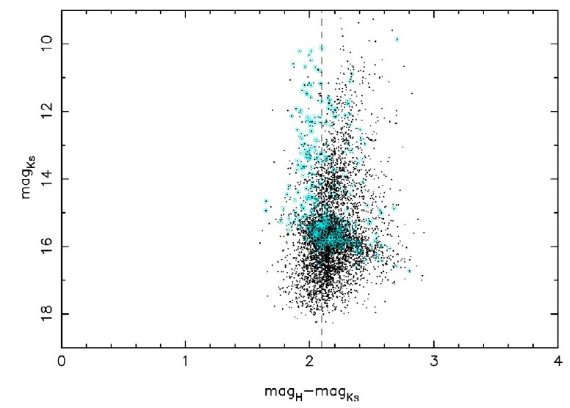 図8.微分減光を補正した色等級図。平均 AKs = 2.74. 破線=平均 H-Ks カラー。 青丸=既知の早期型星。 |
|
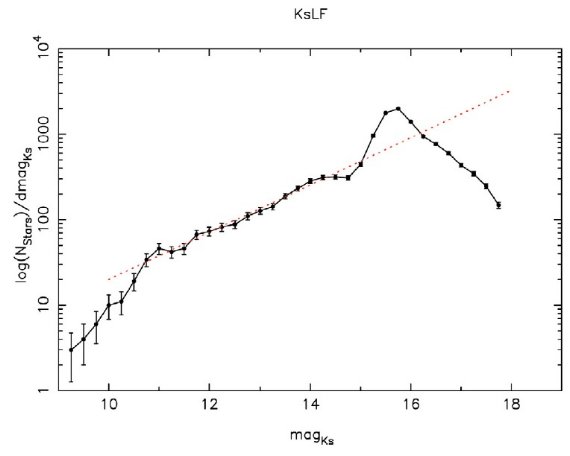
図9には、前景、後景星を除いた、銀河中心の微分赤化補正 Ks 光度関数
を示す。フィット直線とデータを比べると、完全度は Ks = 17 で 50 % に
落ちていることが推定される。 図9.前景、後景星を除いた、銀河中心の微分赤化補正 Ks 光度関数。 平均減光は AKs = 2.74 である。この光度関数は測光 完全度の補正はしていない。赤破線= 11 < Ks < 14 の直線フィット。 勾配は 0.27±0.02 |
 |
|
有効波長 Nishiyama et al 2006, Gosling et al 2009, Stead, Hoarse 2009 によるとべき乗指数の決定は有効波長に強く依存する。 そして、有効波長は天体SEDやフィルター透過曲線に依存する。本論文の 有効波長に関しては Tokunaga,Vacca 2005 に従った。付録A3を見よ。 べき乗指数 我々の見出したべき乗指数は以前の値よりかなり大きい。しかし、最近の値は かなり我々の値に近い。 Gosling et al 2009 は αJ-Ks = 2.64±0.52 を出したが、同時に 5″ という 小さなスケールで値が変動するとした。我々は指数の空間変動は調べなかった。 Nishiyama et al 2009 は銀河系バルジ中心核で αH-Ks = 2.0, αKs-3.6 = 1.37 を導いた。Stead, Hoarse 2009 は UKIDSS で 8 領域を調べ、 αNIR = 2.14±0.05 を出した。これら の値は我々の結果と 1 σ の範囲で一致する。 ( 「一致」は強引?) 例外は我々が Ks - (H-Ks) 図から導いた αH-Ks = 2.54±0.15 であるが、それは Ks, H それぞれに対する減光量の差から導いた αH-Ks = 2.21±0.24 と重なる。しかし、導出法の直接性から 後者の方がより信頼度が高いと判断する。 減光マップ H-Ks カラーから導いた減光マップは Buchholz et al 2009 のとよく似ている。しかし、 全体の減光量は我々が AKs = 2.74±0.30 に対し、彼らは AKs = 3.14±0.43 で大きい。この差は彼らが Draine 1989 の平坦な 減光曲線を採用していることが主原因である。Scoville et al 2003 のも似ているが 輝線を使っているので範囲が限られている。彼らはまた、最近の値と大きく異なる α = 1.6 を使用している。 強い減光域 強い減光の個所が Sgr A* の 12″ E, -13″ S にある。そこでは 暗黒雲の背後の星が見えない。そのため、減光の推定値は低く出過ぎている可能性 がある。 Sgr A* の減光量 Sgr A* の近傍には "S-cluster" と呼ばれる星団がある。図6に示した減光マップは Sgr A* 方向の減光の決定に使える。Sgr A* から 0.5″ 以内の円内では、 AH,SgrA* = 4.35±0.12, AKs,SgrA* = 2.46±0.03, AL′,SgrA* = 1.23±0.08 を得た。これらの減光値は過去に使用 された値と異なる。正確な減光値は Sgr A* モデルに重要である。 中心領域エネルギー源 中心パーセク領域において、大質量星からの電離フラックスと電離ガスとの 関係は長い間問題となってきた。 Najarro et al 1997, Lutz 1999 は He I 星の 数が異常に多いと述べた。Martins et al 2007 はラインブランケッティングを 考えれば総光度と UV 光度が低下するので問題は解決すると主張した。 しかし、Najarro et al 1997 と Martins et al 2007 の間の問題は、使用した 減光量の違いに起因すると思う。それらはべき乗指数を以前は小さく見積もり過ぎて いたからである。"S-stars" の性質にも減光の評価は影響する。例えば S2は AK = 2.25(Martins et al 2008) なら矮星であるが 2.8 となると巨星である。 |
減光と天体の見かけ形態 図10には、青=検出した星、赤=中間赤外 PAH 放射、緑=減光の関係を図示 した。図を見ると低減光の領域が SW から NE に向かって走っているのが分かる。 この結果、銀河中心核星団は見かけ上銀河面に沿って伸びているかのように見える こととなった。同様に Sgr A* NW の低減光域はそのあたりの恒星密度を見かけ上 高める結果となった。減光がいかに見かけの様子を変えるかは Scoville et al 2003 の図1にも明らかである。  図10.青=検出した星。赤=中間赤外 PAH 放射。緑=減光。の関係を図示。 |
|
銀河中心パーセクの測光 銀河中心パーセクにある 7700 星の Ks 測光を行った。その多くは H, L′ 等級も与えられ、オンラインで公開されている。この領域の AO 測光はこれまでに いくつか公表されてきたが、今回は次の理由で優れている。 (1)前の観測は狭かった。 (2)isoplanatic effect が正確に扱われていなかった。 (3)例えば、Lucy-richardsom 法ではバイアスがかかる。 (4)測光較正が透明に述べられていない。 銀河中心パーセクの減光強度とべき乗指数 レッドクランプ星の絶対等級と銀河中心距離とから減光を決めた。 次にバンド間の減光比からべき乗指数を決めた。得られた指数は初期の値より急な 勾配を示すが、最近の結果とはよい一致を示す。3 &my;m より長波長での減光の平坦化 も確認された。 減光マップ 小区間の平均 H-Ks カラーに基づいて 40″×40″ (1.5pc×1.5pc)の減光マップ を作った。マップの空間分解能は 1″ である。マップはオンラインで入手可能である。 マップの平均は AKs = 2.74 でレッドクランプから決めた値と良く合う。 Ks-L′ カラーからのマップは、星密度が不足、ミニスパイラル光の混入などのため 精度は劣る。それでも H-Ks マップに見られる大局的特徴は確認された。 |
赤化補正した色等級図 減光マップを用いて赤化補正した等級を用いて色等級図を作った。図上の 分散が著しく小さくなった。その結果、赤色巨星枝星と若く青い星の分離が 可能となった。Sgr A* から投影距離 > 0.5 pc に多数の若い大質量星が 存在することを確認した。 副産物としての Ro 過去の銀河中心距離を集めてみたら、最近の値は Ro = 8.03±0.15 kpc と集中が良い。 Sgr A* から 0.5″ Sgr A* から 0.5″ では、AH,SgrA* = 4.35±0.12, AKs,SgrA* = 2.46±0.03, AL′,SgrA* = 1.23±0.08 である。これは Sgr A* の近赤外光度が以前考えられていた より 1.2 - 2.2 倍小さいことを意味する。 有効波長 有効波長は大気透過率、フィルター、光学系、減光、星のタイプなどの複雑な 関数である。本論文で採用した有効波長は上のパラメタの推定、観測時の条件 などから決まった。 |