Extinction Maps towards the Milky Way Bulge: 2D and 3D Tests with APOGEE


Schultheis + 15
2014 AJ 148, 24 - 33



　アブストラクト

　銀河系マップは重要であるのでその精度をテストする必要がある。 バルジ方向の大規模分光サンプルによる減光測定を用い、測光法で求められた 2D, 3D の様々な減光マップを調べた。高分解能 H-バンド APOGEE スペクトル から星の大気パラメタ―を決めた。 　恒星の等時線モデルと組み合わせて、バルジ方向 2400 巨星の距離と減光を 定めた。それらを近赤外、中間赤外測光観測から求まったバルジの 2D, 3D マップと較べた。波長間隔の長い NIR + MIR カラーは平均すると APOGEE の減光と良く合う。

　１．イントロダクション　

　バルジ２Ｄ減光マップ　

可視(OGLE, MACHO) RC
　 Stanek 1996, Sumi 2004, Nataf et al 2013

NIR RGB
Schultheis et al. 1999, Dutra et al 2003

NIR colors
Gosling et al 2006

VVV RC
Gonzalez et al 2012

RJCE (H - 4.5)
Majewski et al 2011 		　バルジ３Ｄ減光マップ

COBE を説明するダスト分布
Drimmel et al 2003

　 2MASS+ブザンソンモデル
Marshall et al 2006

　 その改訂版
Chen et al 2013

　 さらにそのバルジ版
Schultheis et al 2014a
　
この論文　

　高分散近赤外スペクトルで内側銀河の星間減光 3D 分布を求める。 その結果を既存減光マップと比較する。

　２．サンプル　

　２．１．ＡＰＯＧＥＥ　

スペック　

　APOGEE = Apache Point Observatory Galactic Evolution Experiment (Majewski et al 2010) = R 22,500 で 300 - fiber H(1.5 - 11.6 μm) 分光。 望遠鏡は SLOAN 2.5 m 鏡。2MASS から選んだ H = 12 - 14 の 10,000 星が対象。 S/N = 100.

　データ　

　視線速度は 0.5 km/s で決まる。組成も決まる。SDSS-III データ公開では 55,000 星のスペクトルが公開された。

　２．２．星のパラメタ―　

　方法　

　星パラメタ―は APOGEE Stellar Parameters and Chemical Abundances Pipeline (ASPCAP, Garcia Perez et al 2014) により決まる。これらは FERRE code (Allende Prieto et al 2006) によるモデルスペクトルと 観測スペクトルを χ2 フィットして決める。 グリッド上のスペクトルの 内挿には ASSεT code (Kesterke et al 2008, Koesterke 2009) が用いられた。新しい ATLAS9 モデルが将来導入予定。

　精度　

　Meszaros et al 2013 は DR10 ASPCAP Teff, log g, [M/H] の精度を評価 した。σ(Teff) = 161 K, offset(log g) = 0.2 - 0.3 dex, σ ([M/H]) はメタルによるが　0.2 - 0.3 程度。

　２．３．本論文で使うサンプル　

　最初は, APOGEE 最初の２年サンプルから、 l = [-10, 10], b = [-10, 5] を選んだ。そこから、パラメタ―がモデルグリッドの縁になったもの などを除いた。最後に 2433 星が残った。


図１．APOGEE サンプル 2433 星の分布。二つの赤バツ印は GC とバーデの窓。

　３．減光と距離の導出　

　等時線グリッド　

　[Fe/H] = [-2.5, 0.5] を 0.2dex 刻み, Δlog t を 0.05 刻みで、パドヴァ等時線を計算した。ただし、この等時線は Teff = [3500, 4000], 2.0 < log g の範囲で恒星モデルが 疎らになる。
　ASCAP では複数の元素のラインを使用するため、 [Fe/H] でなく、[M/H] を与える。しかし、Meszzaros et al 2013 に よると、両者は一般には近く、さらに彼らの較正を行うとその差は 0.1 dex 以下になる。そこで、我々は等時線で使われる [Fe/H] を [M/H] と同じ と仮定した。α 増強型の星ではこの仮定は正しくなく、付加エラーを 呼び込む可能性がある。

　等時線サンプル点との同定　

　星毎に我々はメタル量が最も近い等時線を選び、その上で さらに最も近い Teff と log g を持つサンプル点を選択する。 内挿は用いない。|ΔTeff| > 500 K または |Δlog g| > 0.5 となった星は棄てる。図２にはこうして決めた Teff と log g の 差をプロットした。Teff が左側に伸びている尾は Teff = [3500, 4000], log g > 2.0 の星から成り、等時線がカバーしていない領域である。

　色超過と減光の決定　

　APOGEE サンプル星は 2MASS J, H, Ks を持っている。同定した等時線上の 点は MJ, MH, MKs を持つ。両方を 使うと色超過 E(J-Ks) が求まる。西山他 2009 の減光則を用い、 A(Ks)ASPCAP = 0.528 E(J-Ks) とする。

図２．観測から ASPCAP で得た (Teff, log g) と等時線上で 対応するモデル点の (Teff, log g) との差。等時線上の点の配置が 不均一なため、Teff の差は尾を引いている。

　パラメタ―決定誤差　

　等時線上の最近傍サンプル点のパラメタ―と ASPCAP パラメタ― との差、及びASPCAP 決定誤差の二つからの合成エラーは、

で与えられる。個々の星の ASPCAP パラメタ―に対してこのエラーを 付与して、もう一度等時線フィットを行った。こうして、 A(Ks)ASPCAP 評価のエラーを決めた。しかし、このエラーには星の 大気モデルと等時線の選択から生まれる系統誤差は含まれていない。

　距離の決定　

　減光が得られると、距離 d(pc) は次式で決まる。
　　　　　log d = 0.2(Ks-MKs) + 5 - A(Ks)ASPCAP
上に述べたエラーの大きさは 30 -40 % 程度である。我々の結果を Anders et al 2013 のベイジアン統計に基づくより洗練された方法で 求めた距離と較べた。rms 散らばりで 30 % くらいであった。 表１には、我々が求めた減光と付随する距離を　他の 2D マップから 決めた減光と較べた。

図３．距離とそのエラーの関係。エラーには等時線フィットのエラー と ASPCAP による星パラメタ―決定エラーが含まれる。赤点＝中間値。 エラーバー＝６つの距離区分内での標準偏差。

　４．個々の星の減光と、 2D 減光マップへの比較　

　４．１．星の減光の評価と 2D 減光マップ　

比較する対象は
RJCE
Majewski et al. 2011 の 手法。WISE W2(4.6μm) は Spitzer IRAC 4.5 μm に比べると ピクセルサイズが大きく、バルジでは極めて不利である。そこで、 IRAC を使った減光と較べた。

EHK
Lada et al. 1994 は 全ての星が (E - Ks)o = 0.13 であると仮定して E(H-Ks) を 導いた。これは後の NICE 法 (Lombardi, Alves 2001, Gosling et al. 2009 は への第１歩である。しかし、統計的に洗浄されたバルジの NICE マップはまだ作られていない。

G12
Gonzalez et al. 2012 は VVV 公開データを用い、レッドクランプ星を使った減光マップ を 2′×2′ の分解能で 求めた。我々は BEAM calculator webpage http://mill.astro.puc.cl/BEAM/calculator.php を用いて個々の星に最も近い 2′ ピクセルの 減光を回収した。

N12
Nidever et al. 2012 は RJCE 法を使い、「全ての星、中間減光値」で減光マップを 作った。論文が提供する query script を用いて我々は個々の 星に対し、最も近い 2′ ピクセルの 減光を回収した。


(RJCE, EHK は個々の星に対する 減光だが、G12, N12 はピクセル値なので不適当ではないか？ )



図４．我々の A(Ks)ASPCAP を他の４つの方法で求めた A(Ks) と比較した結果。赤点＝中間値。

　４．２．結果と議論　


図５．我々の A(Ks)SPCAP と G12, N12, RJCE, EHK との 差の Teff による変化。

　図４　

　図４には我々の A(Ks)ASPCAP を他の４つの方法で求めた A(Ks) と比較した結果を示す。全体として、 G12, N12, RJCE とは |A(Ks)| < 0.2 の範囲で合っている。しかし、 EHK とはずれが 大きい。特に A(Ks) が大きい星に対して EHK は過大な A(Ks) を与える。 差が一番小さいのは RJCE で A(Ks) が大きい箇所でも 0.1 mag の範囲に収まっている。G12 との差の平均はゼロに近いが散布度は 特に A(Ks) 大で大きい。

　図５、６、７

　図５は Teff, 図６は log g、 図７は [M/H] に対する A(Ks) の 差をプロットした。EHK が Teff = 4200 K より低温の星に対して A(Ks) を過大に評価する傾向が明らかである。log g に関しても log g > 2.5 では EHK の過大評価が見て取れる。

　差が生じる原因　

　G12 と N12 は主系列矮星や低減光のレッドクランプ星、 RGB 星に対し 減光を過大に評価している。これはそれらの減光マップがマップを作る のに使われた星に対し平均総減光に重みがかかっている結果である。
(ASOCAP が近傍の星を選んでも それに対する G12, N12 減光値は最近のピクセル平均を使うらしいから そもそも比較が成立しないのではないか？ )
　EHK 法の場合、採用した (H-Ks)o 値は星が RGB を上がって行くに連れ 不適当になっていくことが問題である。RJCE 法の場合非常に赤い星を 除いて星のタイプによる影響は殆どない。0.03 mag の系統誤差は仮定した 固有カラーの誤りを反映している。したがって、この値を修正しさえ すれば、差は殆ど誤差内に収まる。RJCE 法は非常にロバストなよい手法 であると言える。

図６．我々の A(Ks)SPCAP と G12, N12, RJCE, EHK との 差の log g による変化。


図７．我々の A(Ks)SPCAP と G12, N12, RJCE, EHK との 差の [M/H] による変化。


図８．丸の位置での、黒点＝我々の A(Ks)SPCAP、青線＝ Drimmel et al 2003、赤破線＝Marshall et al 2006、緑一点鎖線＝ Schultheis et al 2014 の視線方向距離による変化。。

　５．３Ｄマップとの比較　

　５．１．３Ｄマップ　

Marshall et al 2006
Marshall et al. 2006 は Robin et al. 2003 のブザンソン銀河系モデルに 2MASS データを合わせ、l = [90, -90], b = [-10, 10] の 3D マップを作った。距離 - カラー関係を仮定し、 観測カラーと合成モデルカラーと比較し、赤化量をモデルからの距離に付与 する。この方法は 2MASS の分解能 3″ のため、バルジの 混み合い領域で、限界等級のため減光大領域では適用不能である。マップの 分解能は 15′ である。

Chen et al. 2013
Chen et al. 2013 は　GLIMPSE + VVV データに改訂版ブザンソンモデルを合わせ、 l = [10, -10], |b| ≥ 2 の 3D 減光マップを作った。この マップは Schultheis et al 2014 が　l = [10, -10], b = [-10, 5] の全 VVV バルジ領域へ拡張した。分解能は 15′ である。

Drimmel et al 2003
Drimmel et al. 2003 は Drimmel, Spergle 2001 のダスト３Ｄ分布モデルに基づく３Ｄ減光マップを作った。 分解能は 21′ である。

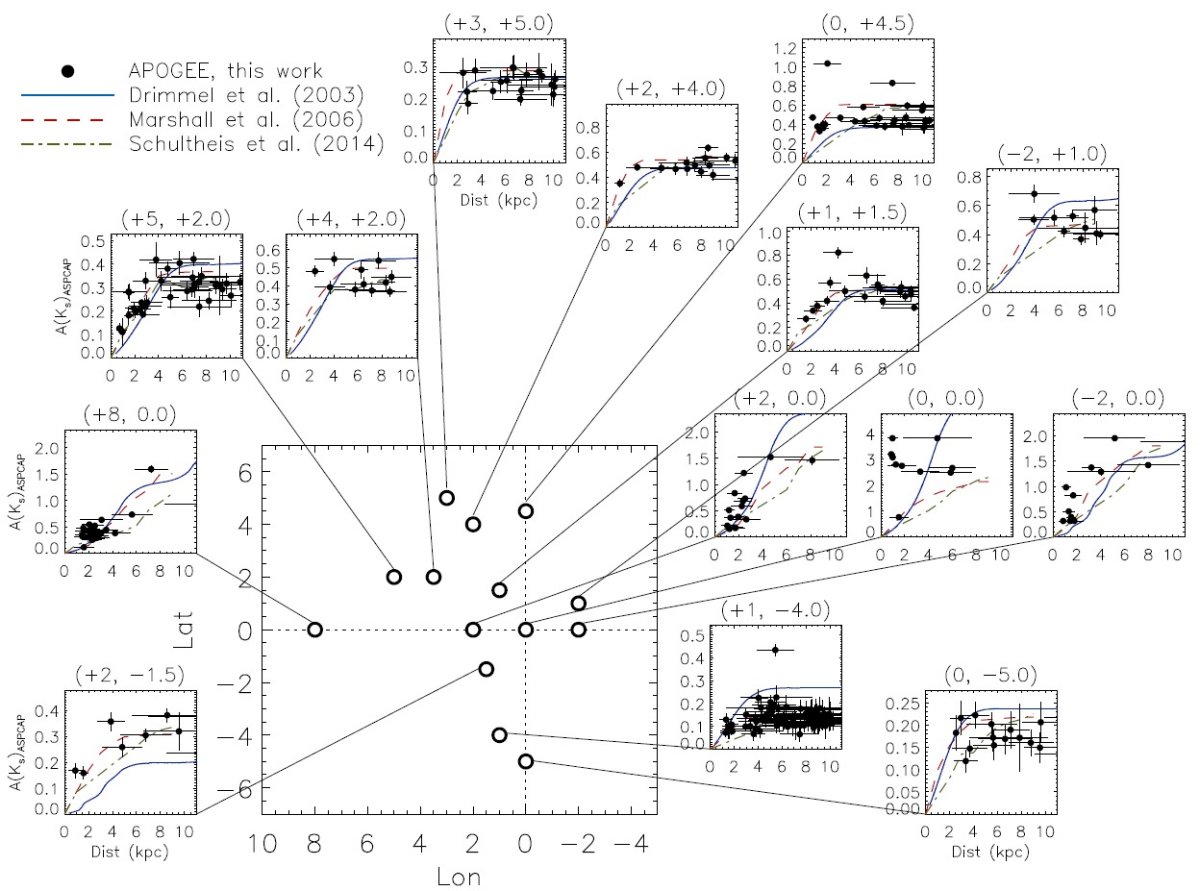
　図８＝３Ｄマップの比較　

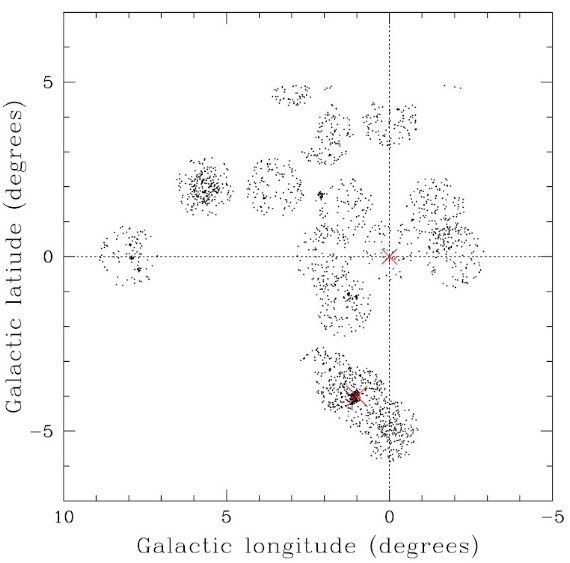
　上のマップから、APOGEE バルジ星の 0.25 deg2 領域内の 距離 1 kpc 間隔での減光を得た。図８にはそれぞれの視線方向において、 減光値を比較した。Marshall et al 2006 と Schultheis et al 2014 の 3D マップは 10 kpc 以内に限定される。

　５．２．結果と議論　

　全体として我々と合うものはなかった　

　図８を見ると、全体として我々と合うものはない。 Drimmel et al. 2003 の結果はズレが最も大きい。彼らは内側銀河の円盤に沿っては 2MASS CMD に対して減光で 20 % の誤差があり得ると認めている。 視線方向の大部分で APOGEE 星は d < 4 kpc の星を欠いている。 それでも以下のようなコメントが可能である。 		　 4 - 6 kpc の減光平坦部　

　我々はは急な減光増加とその先 4 - 6 kpc における平坦化を全ての 視線方向で示す。しかし、高減光方向 (l, b) = (8, 0), (2, 0), (-2, 0), (0, 0) で、比較マップのどれにもそのような平坦部は存在しない。残念 ながら、この平坦部の存在を確認するにはデータが不足している。

得意距離　

　 Marshall et al. 2006 は d < 4 kpc の減光を良く再現している。彼らは 2MASS データ の混み合い制限を受ける、d = 8 kpc 付近で A(Ks) が急落するという おかしな結果を招いている。一方、 　 Schultheis et al. 2014 は d > 4 kpc では信頼度が高い。

　Drimmel et al. 2003　の特徴　

　 Drimmel et al. 2003 は、(l, b) = (4, 2), (-2, 1), (1, -4), (0, -5) では超過、 (2, -1.5), (1, 1.5), (0, 4.5), (2, 4) では不足する。

　最内側バルジ方向では太陽近距離で強い減光　

　　最内側バルジ方向、l = [-2,2], b = [-1,1]、では太陽距離 d < 3 kpc で 強い減光が検出された。この特徴をとらえたのは我々以外では 　 Drimmel et al. 2003 のみである。

　窓　

　(l, b) = (0, -5), (1, -4) 領域の APOGEE 星は d = [2, 10] kpc に 広がっている。これら低減光領域は Marshall et al. 2006, Schultheis et al. 2014 では良く再現されているが、 Drimmel et al. 2003 は過大評価になっている。特に d ≥ 5 kpc でそうである。　 低減光域の小さな空間変動はとらえにくいので可視観測が重要である。

　APOGEE-II

　APOGEE-II がでるとバルジ全域の３Ｄ減光マップが得られるであろう。

　６．追加の議論　

　６．１．２Ｄ　対 ３Ｄマップ　

　図９に、我々の A(Ks) と他の３Ｄマップ A(Ks) との差の距離による変化 を示した。二つの 2D マップ G12, N12 は d > 3 - 4 kpc では ASPCAP の 結果と合うが、短いところでは過大評価になった。
(短距離というのは、ピクセル内の 短距離にある APOGEE 天体の A(Ks) をピクセルに対し N12, G12 の A(Ks) と較べたということか？それは過大になるのは当たり前だが、そんな馬鹿な 比較をするはずはないから、私になにか勘違いがある。 )

　６．２．減光則の依存性　


図９．我々の A(Ks) と他の３Ｄマップ A(Ks) との差の距離による変化。


　６．３．進化経路ライブラリーへの依存性　


図１０．パドヴァとバーゼルモデルでの A(Ks) の差

図１１．パドヴァで求めた距離とバーゼルモデルでの距離の比の 距離による変化


図１２．パドヴァとバーゼルモデルでの距離の差の (a)Teff, (b) log g, (c) [M/H] 依存性。

　７．結論　

　概略　

　APOGEE サーベイのデータは個々の星のスペクトルと共に星パラメタ― Teff, log g, [M/H] を与える。このデータベースを使い、銀河系内の減光 の最も強い箇所、バルジと内側銀河の減光量を定めた。この論文では バルジ巨星 2433 個の恒星パラメタ―を等時線モデルにフィットして、 それらの減光と距離を定めた。

　比較　

　それを使い、 これまでの 3D マップの結果と較べた。RJCE 法は信頼度 が高いことが判った。しかし、 APOGEE の結果と全距離範囲で一致した結果 はなかった。 		将来　

　したがって、減光 3D 分布にはまだ改善すべき点が多い。

　エラー　

　エラーの原因となりうる進化モデル、減光則、大気モデルなどの影響も調べた。