A Three-Dimensional Galactic Extinction Model

　アブストラクト

　１．イントロダクション　

　２．銀河系減光モデル　

減光の計算　 　ダスト分布 ρd(x) が与えられたら、ある点までの減光 Av(x) は 次の式で計算される。 　　　Av(x) = 1.086 τv=1.086κv ∫0xρdds　　　(1) 我々のダスト分布は、ワープは入るがその他の点では軸対称で温度勾配の ある円盤、既知 HIIR から導かれる腕、オリオンーシグナス局所腕を含む。 　ダスト分布モデルの修正　 　 Drimmel, Spergel 2001, における渦状腕は、 Geogelin, Geogelin 1976, Taylor, Cordes 1993 の HIIR マップに基づいていた。ただデータは 銀河系反対側で欠けているので、腕もそこで欠けていた。円盤全体での現実 的な腕の配置を得るために、Bland-Hawthorn, Maloney 2002 の拡大モデルを 採用した。銀河系モデルの他のパラメタ―は変えていない。 図１は新しい腕によるダスト表面密度分布を示す。新しい腕の拡張により、 COBE/DIRBE マップとのフィットに変更はなかった。これは DIRBE の空間 分解能が粗く、向こう側の腕を分解できないからである。 ( 輝度は変わるはずではないか？) ただ、このモデルは再検討が必要である。というのは、モデルでは |l| < 20 に腕の接点を予想しているが、そのような証拠は FIR マップには見られないから である。 　リスケーリング　 　DIRBE 240 μm データとモデル輝度との違いを方向毎に補正するために、 滑らかなモデルに小スケールの構造を加えた。ある DIRBE ピクセルに対しては、 ３つの成分の内の一つを選んでリスケールした。どれを選ぶかは、 柱密度の変化が相対比で最小の成分という基準を採用した。一般には、 銀河面付近では腕が選ばれることが多い。視線にそった選択成分はリスケール ファクター倍される。 (視線方向内で最も寄与の大きい 成分が選ばれる。円盤近くでは自動的に腕となる。それが良い理由は何か？ ) 　SFD マップによるリスケーリング　 　リスケールされたダスト密度は次の式で表される。 　　　　　ρd=Σfiρi 　　　　　（２） ここに i = 円盤、腕、局所腕を表す。fi は方向の関数で fi=fi(l, b) である。リスケールされる成分は １つだけで、残りの fi = 1 である。SFD マップへの リスケーリングは fdisk = ASFD - Σi≠diskAi(∞) Adisk(∞) で与えられる。

図１．渦状腕を伴うダスト分布モデルからのダスト表面密度マップ。 太陽の位置は中心左の点で示される。 円盤成分のみがリスケールの必要がある。高銀緯では ダスト柱密度に寄与するのは円盤のみだからである。 ( 低銀緯でも全て円盤が 選ばれるのか？前節では腕が選ばれると書いてあったが、どうなっているんだ？ ここでは高銀緯でのリスケールを論じているのかも知れない。) 　リスケーリングの効果　 　図２にはリスケーリングなし（上）とあり（下）の場合について 減光マップを示す。図３，４では低銀緯でおけるリスケーリングの重要性 を示すため、COBE/DIRBE J バンド観測（十字）とリスケールモデルとを 比較した。 ( どこにリスケールの利点が 現れているのか不明。J バンドは星の光にダストの減光が加わった図 だな。遠いところの寄与は少ない？)

　３．応用　

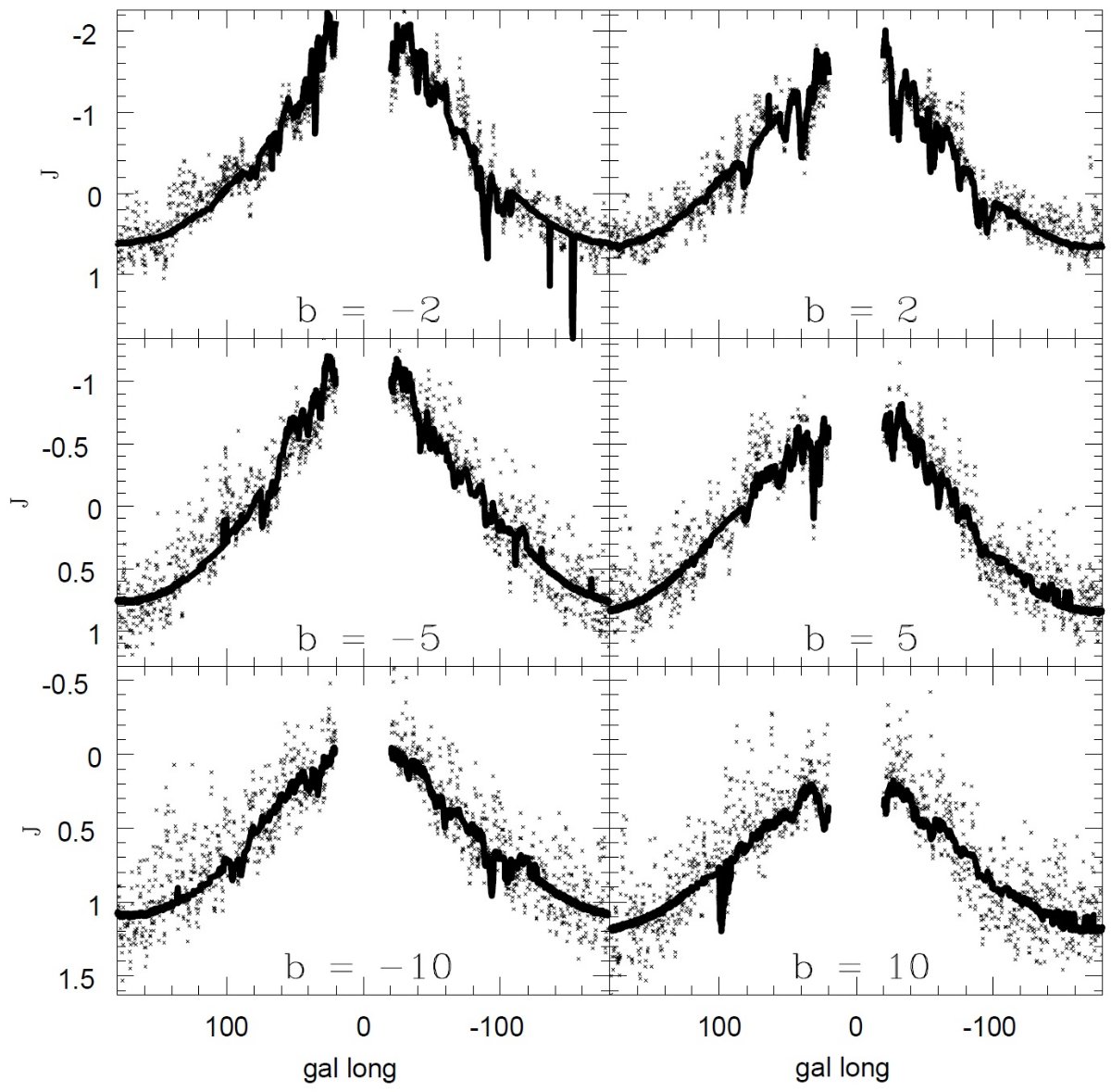
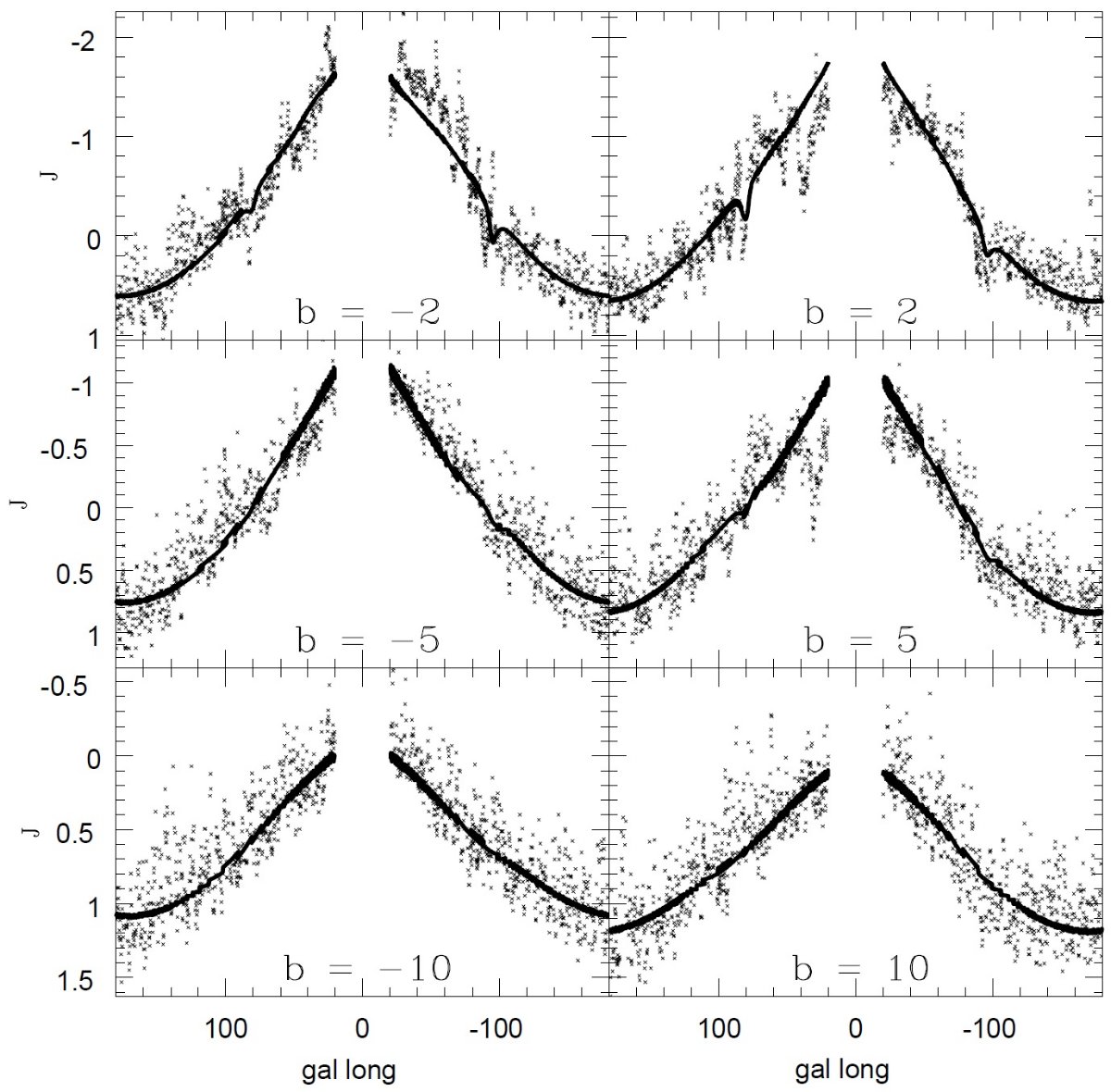
図５．銀河中心から 15 kpc までの、ダスト渦状腕成分による銀河面上減光 分布。銀河中心は中央。太陽は中心の左側。渦状腕接線方向がはっきり見える。 最高減光量は Av = 5.7 mag である。 グリッド計算　 　先に x, y 方向に 200 pc, z 方向に 20 pc の 30×30×1 kpc グリッド上で減光を計算した。任意の点までの減光はその内挿で与える。 誤差は 0.2 % である。また、局所腕、太陽近傍のためにもっと細かい小体積の グリッドも作った。 　DIRBE ピクセル　 　リスケーリングは DIRBE データと平滑モデルとのズレを調整するために 導入されたので、リスケーリングファクターは DIRBE の各ピクセル毎に 決められている。このため、リスケーリングファクターを引き出す操作は やや複雑である。それは COBE のデータ構造が独特なためである。 以下にその方法が記されているが略する。

図６．ダストの全成分＝円盤、渦状腕、局所腕（オリオンーシグナス腕） による減光。最高減光は Av = 37 mag. 腕成分による減光　 　図５には銀河面上での腕成分だけの減光分布を示す。接線方向 の強い減光が明瞭に示されている。 　全成分による減光分布　 　図６には全成分による減光分布を銀河面上で示す。

　４．データとの比較　

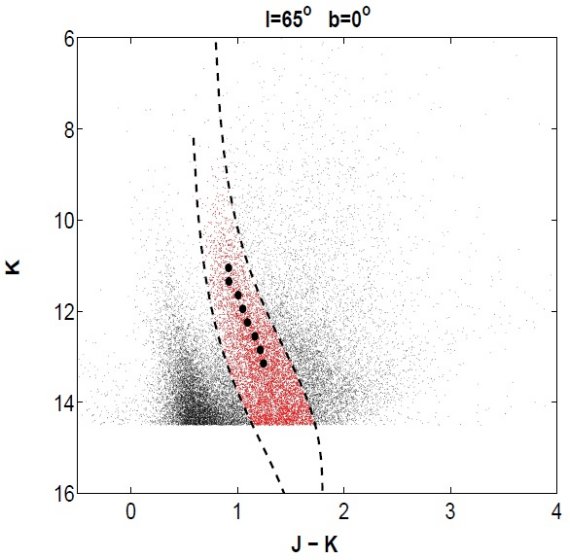図７．低銀緯の代表例 (l, b) = (65, 0) における 2MASS 色等級図。 破線＝レッドクランプの選択区域。黒円＝等級ごとのレッドクランプピーク。 　ASFD と A&inf; の比較　 　 　ASFD と リスケール前の A∞ とは両方とも COBE FIR データを用いているが、 手法は全く異なる。そこで、|b| = [5, 40] で両者を比較した結果、 0.096 mag の誤差で合っていることが判った。 レッドクランプ法との比較　 　 Lopez-Corredoira et al. 2002 は 2MASS から 1°×1° 領域の (J-K, K) 色等級図を作った。 彼らはそこから抜き出したレッドクランプ星の与えられた見かけ Ks 等級ごとに ピークカラー (J-K)K を決め、以下の式で色超過を得た。 　　　　　AK(K) = [(J-K)K-(J-K)0] /1.52　　　　　(8) レッドクランプの絶対等級を MK = -1.65、固有カラー (J-K)0 = 0.75 として、減光と距離が決まる。 　レッドクランプ法の誤差　 　減光の誤差は平均カラーの誤差から決まる。 　　　　　σA(K) = σ/(1.52√N) ここに、σ = カラー分布の標準偏差。ここで与えたエラーは統計的な エラーのみで、固有カラー等の系統誤差は入っていない。 矮星の混入　 　矮星の混入は K = 13 では有効でない。一方 2MASS は K = 14 まで完全 である。この二つの理由で色超過の決定は K = 13 までで行った。 　対象領域　 　彼らはこの方法を銀河面に近い、内側銀河系と外側銀河系の領域で実施し、 満足のいく結果を得た。

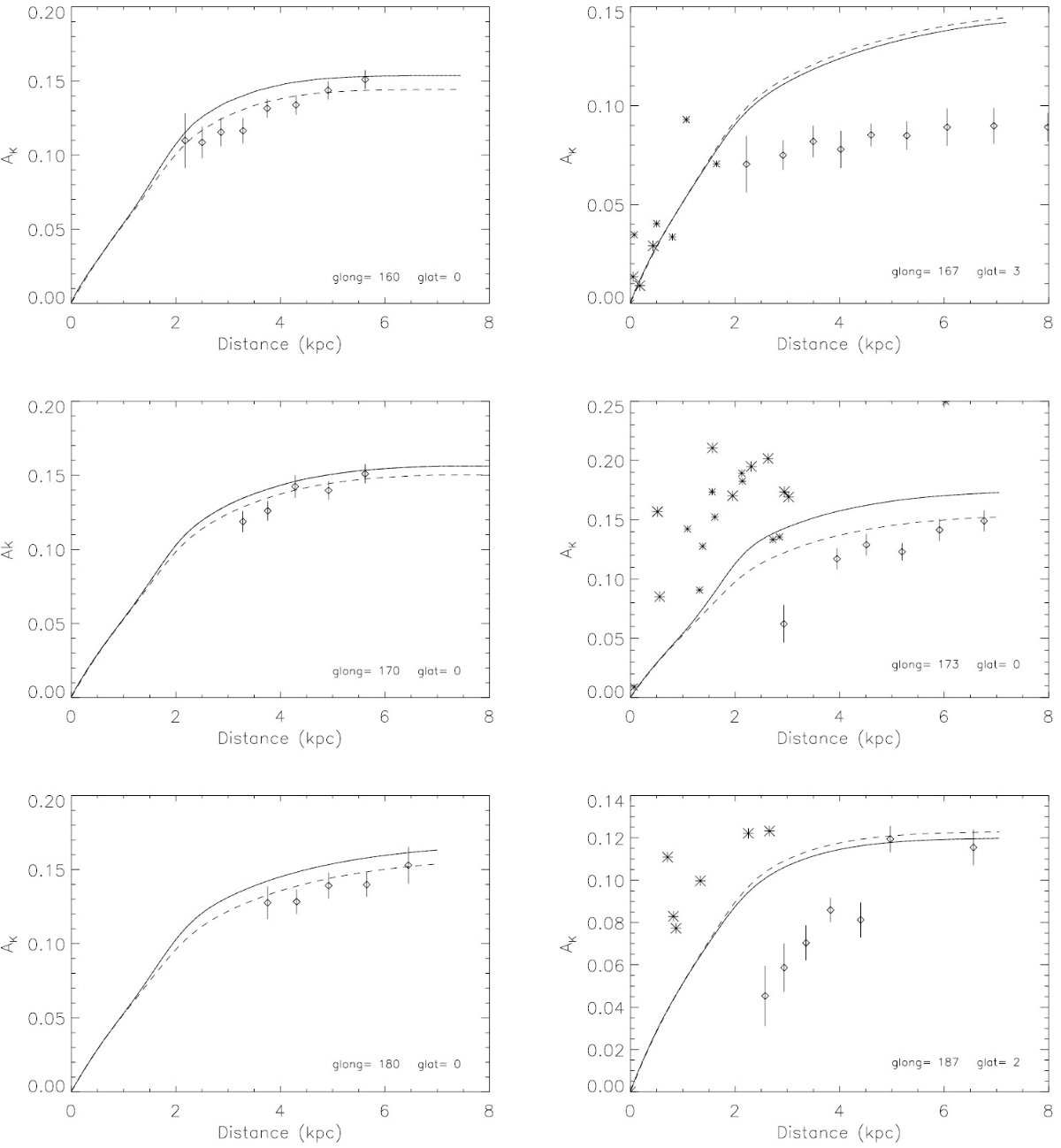
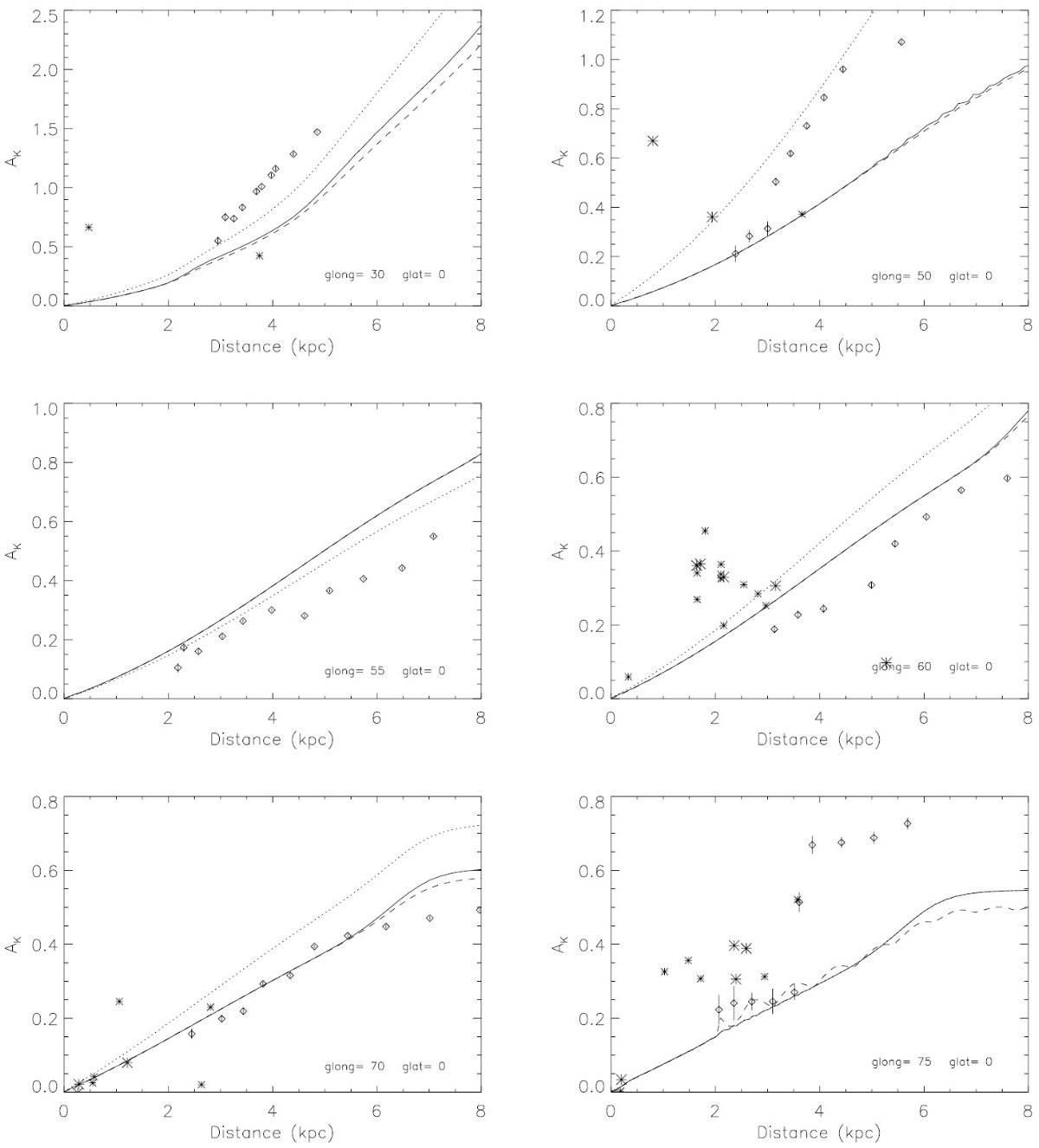
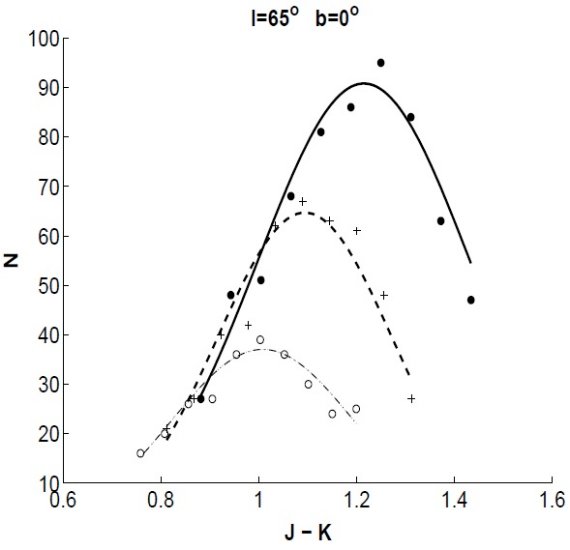図８．(l, b) = (65, 0) でのレッドクランプの等級別の色分布。 白丸: mK = [11.5, 11.8]。十字：mK = [12.1, 12.4]。 黒丸: mK = [12.7, 13]。曲線＝フィット。 レッドクランプ法との比較　 　図９、１０は幾つかの視線方向で、我々のモデルとレッドクランプ法とを 比較したものである。データある場合には OB 星の観測から決まった 減光 Neckel et al. 1980, 1995, も載せた。我々の減光が 2 kpc までであるのに対し、 レッドクランプ 法は 8 kpc に達している。 　図９：OB 星の効果　　 　図９左側は OB 星を含まないりょういきであり、我々の結果とレッドクランプ 法との一致はよい。右側は OB 星を含み、一致が悪い。これは部分的には OB 星でダストが加熱されて　FIR 放射が強くなった結果と思われる。 それらが l = 173, 187 で見られる。 　図１０：　 　図１０には内側銀河系での比較を載せた。典型的な差は 20 % 程度であるが、 腕の接線方向、 l = 30, 50、ではずれが大きくなる。あと色々な接線方向に ついてごちゃごちゃ。

　５．まとめ