3D Structure of the Milky Way Disk: The Distribution of Stars and Dust beyond 0.35 Ro

　アブストラクト

　１．イントロダクション　

　２．データ　

図１．J バンド各ピクセルのローカルエラーの銀経による変化。 　ZSMA マップ　 　ここでは Kelsall et al 1998 による、黄道光除去マップ (ZSMA) を使用 する。このデータセットは各バンド 393,216 ピクセルから成る。全スカイマップ が Arendt et al 1998 に載っている。 　近赤外点源の除去と局所エラー　 　NIR データに 5x5 ピクセルのメディアンフィルターを掛けて、点源を除去した。 許容範囲は局所メディアンの 0.5 - 1.5 倍である。局所エラー σλ は各ピクセルを中心とする 7x7 区域の除去データを除いた標準偏差である。 図１には σJ の銀経による変化を示した。

図２．上：平滑化：非平滑化データの比。下：ローカルエラー σ240. 　遠赤外放射　 　遠赤外放射にはあらゆる角度スケールで構造が見られる。それらは尾根やピークとして 現れる。このため局所エラーの計算には近赤外と別の工夫が要る。また、 S/N も低く、 黄道光を引いた後が負になるピクセルもあった。ある種の平滑化が必要である。 平滑化　 　各ピクセル点を中心に 7 x 7 ピクセル区間で２次式フィットを行い、 ピクセル点でのその式の値を平滑値とする。図２にはローカルエラー σ240 のマップを示す。 　排除領域　 　|b| > 30 データは除かれた。これは円盤の星とダストに関心があるためである。 同様に、|l| ≤ 20, オリオン星雲、アンドロメダ、 M33, マゼラン雲の近傍も除いた。 その結果、 240 μm で 173,569 ピクセル、NIR は点源を除去した後に 152,371 ピクセル残った。合計 478,311 ピクセルがフィットの対象となる。

　３．モデル　

　３．１．前準備　

　３．２．ダスト放射モデル　

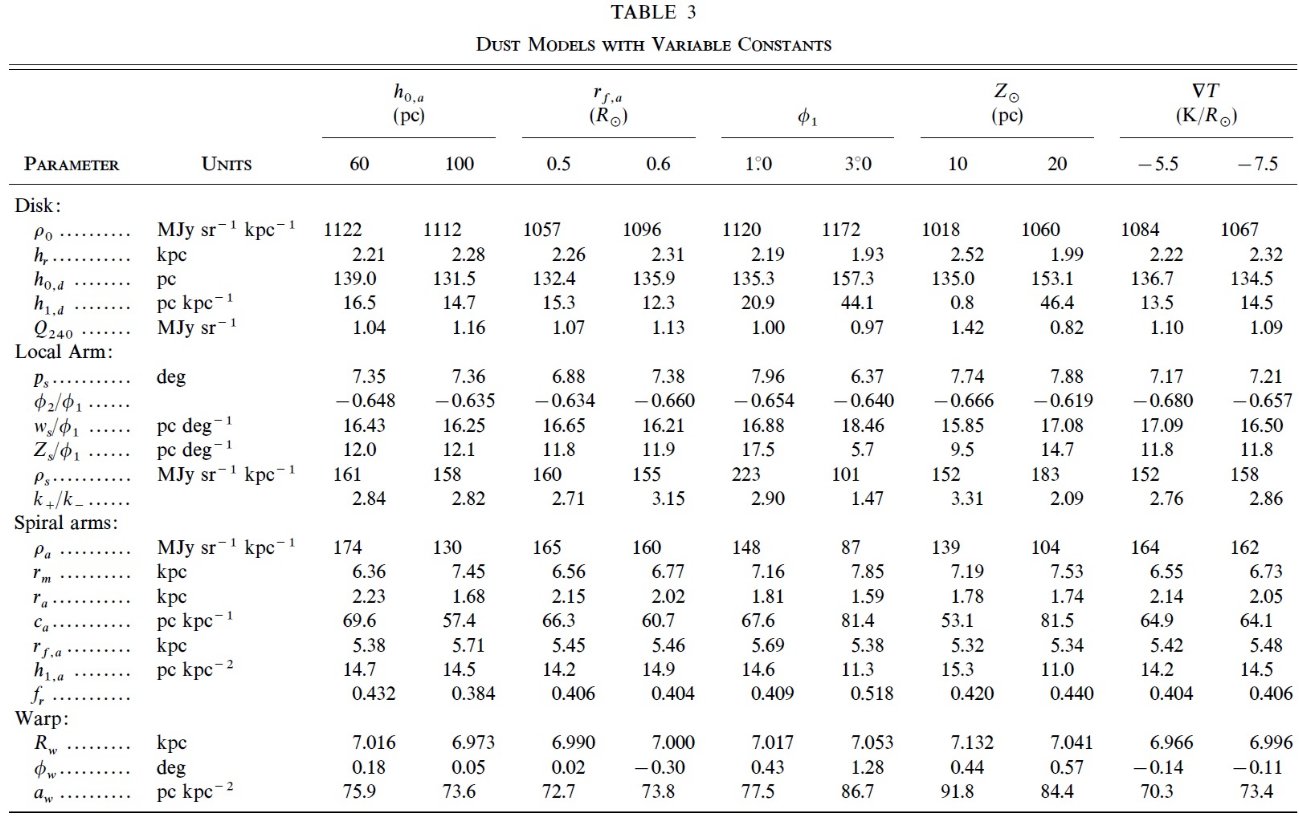
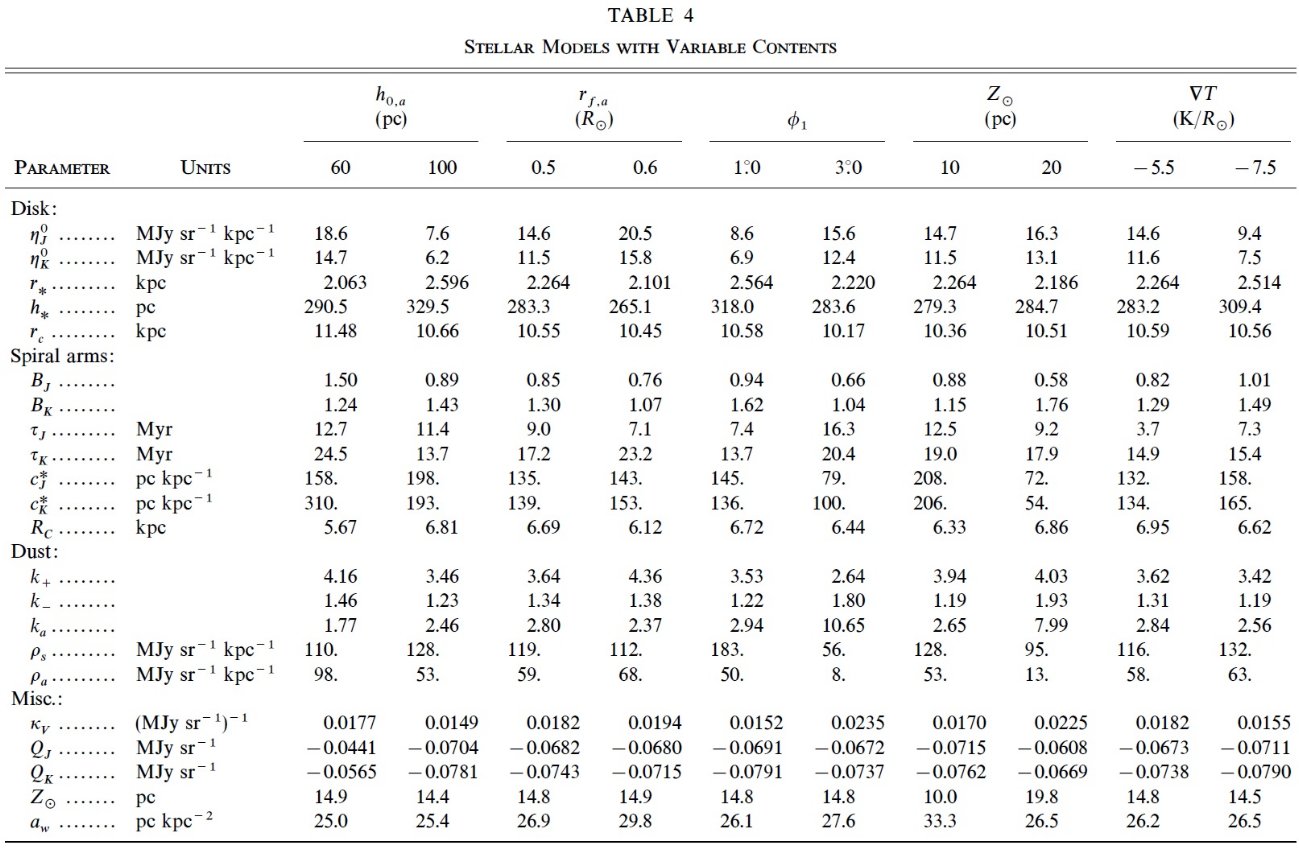
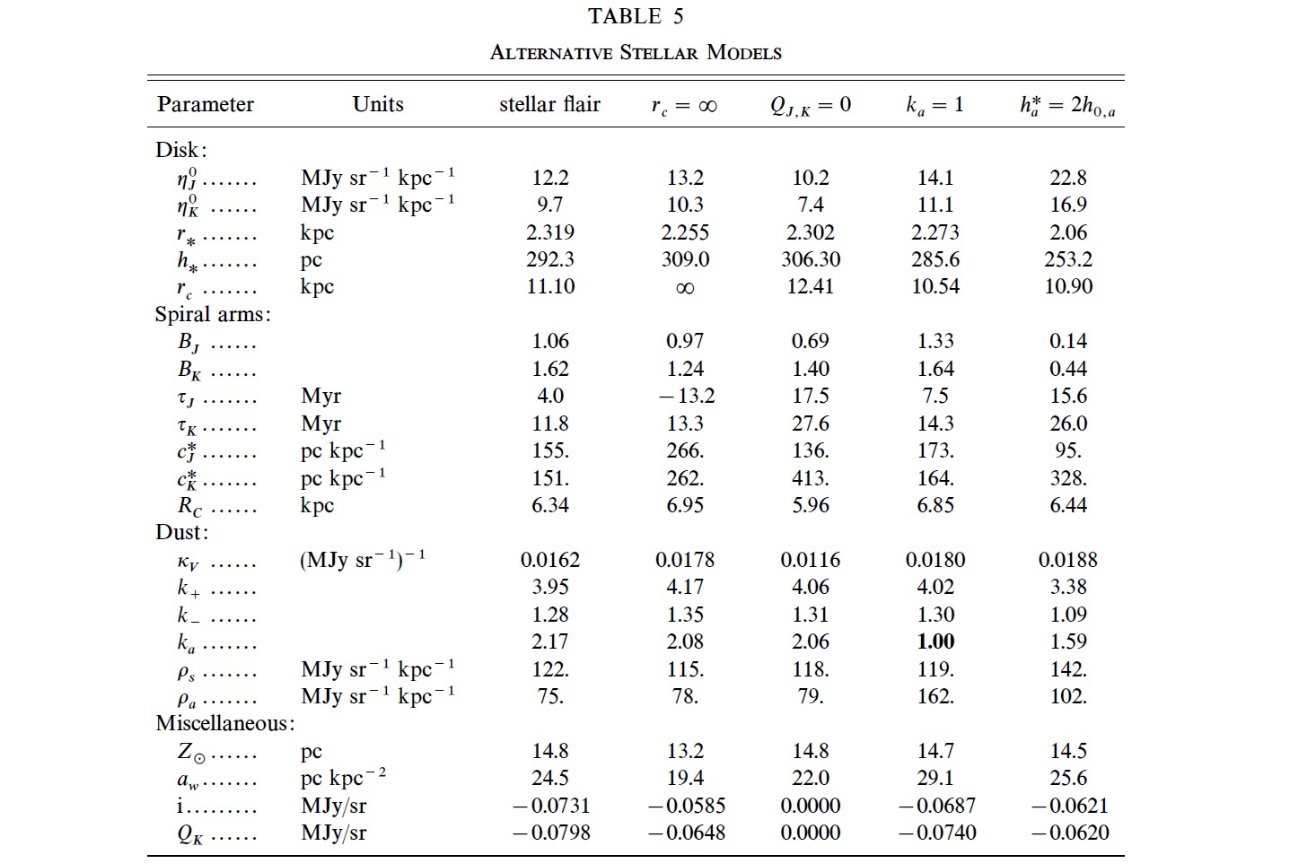
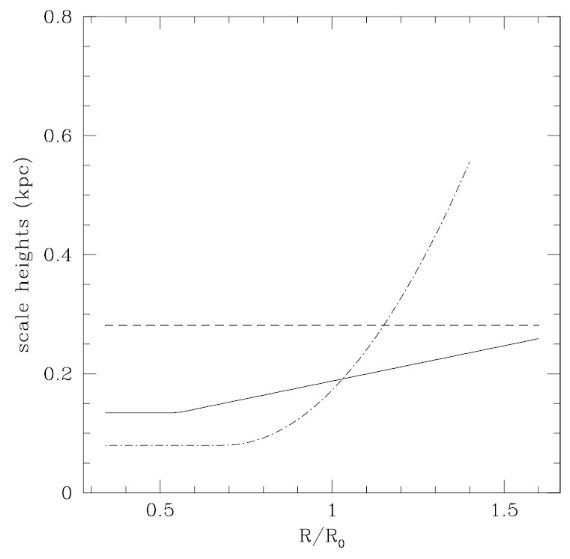
240 μm 放射の基本式　 　D(l, b) = ∫(kdρaxi + kaρ arm + k+, -ρloc) ds + Q240 ここに、Q240 は宇宙背景放射である。 　kdρaxi = 円盤　 　指数型円盤は次の式で与えた。 　　　　　ρaxi = ρ0 exp(-r/hr) sech2(z/hd) 円盤のフレアは線形表式で与えた。 　　　　　hd = h0, d + h0, d(r - rf) 　　　　　(r > rf) 　　　　　　　　 = h0, d　　　　　　　　(r ≤ rf) 円盤の穴　 　円盤の穴は以下の式で取り込められる。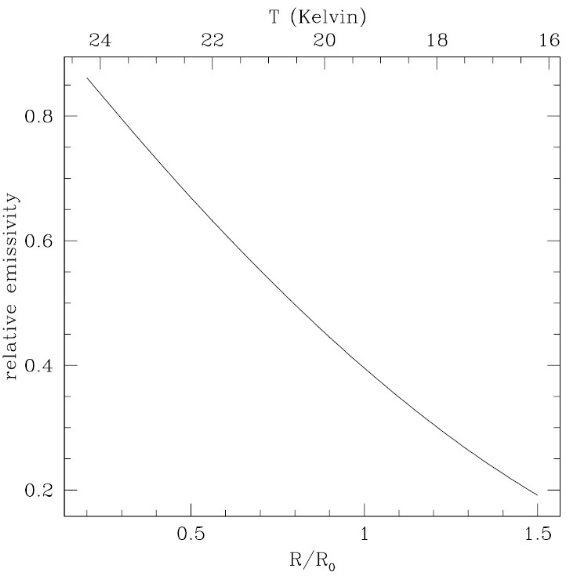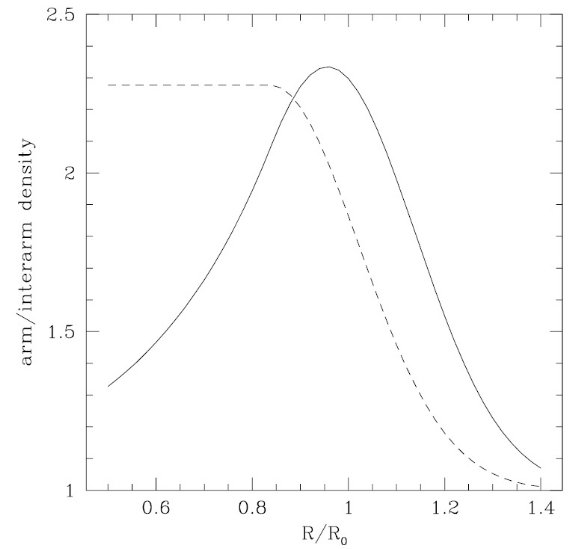 　　　　　ρaxi = ρ(Ro) exp[ -(r-0.5)2 /0.252]　　 　円盤のダスト温度　 　ダスト温度は、 Sodroski et al 1997 が見出した HI 温度を近似して、 　　　　　T = 26 - 6.8(R/Ro) 図３に示されるように、ダスト放射率は R = 1.5 Ro までは温度に比例する。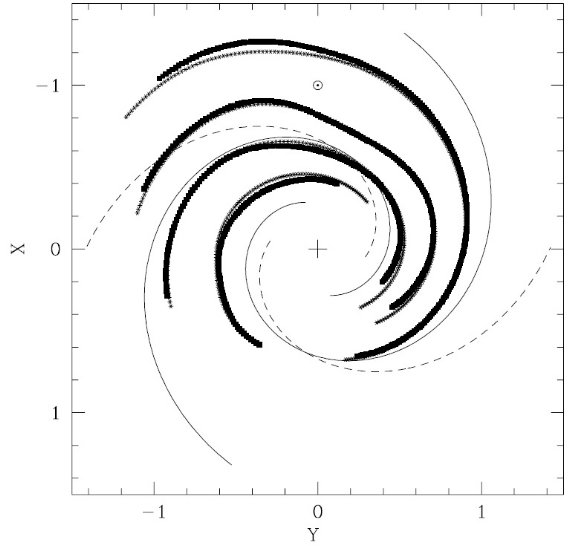 　腕の密度分布　 　腕の配置は、HIIR 位置に基づく Georgelin, Georgelin 1976, Taylor, Cordes 1993 を採用した。腕を横切る密度プロファイルは銀河面上で半巾 wa ∝ r、 フレアリングスケール高 ha のガウシャン とする。銀河系の任意の位置に対し、i-番腕までの最短距離 di (i = 1,...,4) が決まる。その中で exp[-(di/wa)2] が最大 である腕からの寄与を考える。すると、 　　　　　ρarm = ρa ga exp[- (di/wa)2]exp[-(z/ha)2] ここに、ρa は腕の規格化密度、ga は腕に沿った密度の 動径（？）方向カットオフで、 　　　　　ga(Ra) = exp[-(Ra - rm) 2/ra2]　　　　　(Ra > rm) 　　　　　　　　　= 1　　　　　　　　　　　　　　　　　(Ra ≤ rm) ここに Ra = 腕の最近接点の銀河中心距離。 (rm は腕の終端半径？) 半巾 wa とスケール高 ha は Ra の関数である。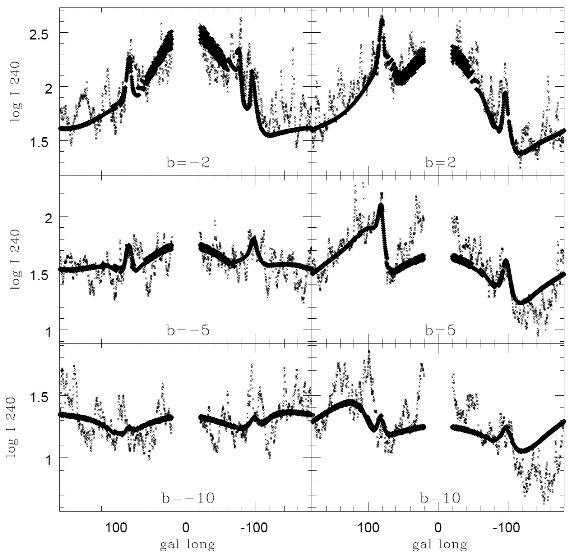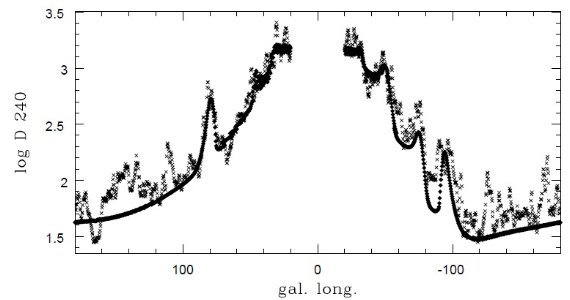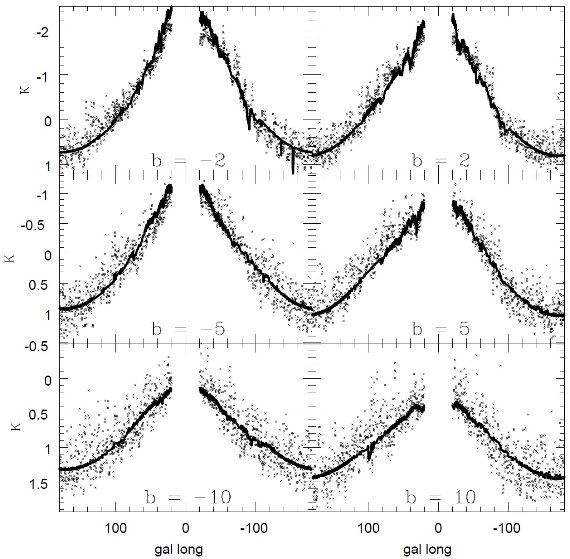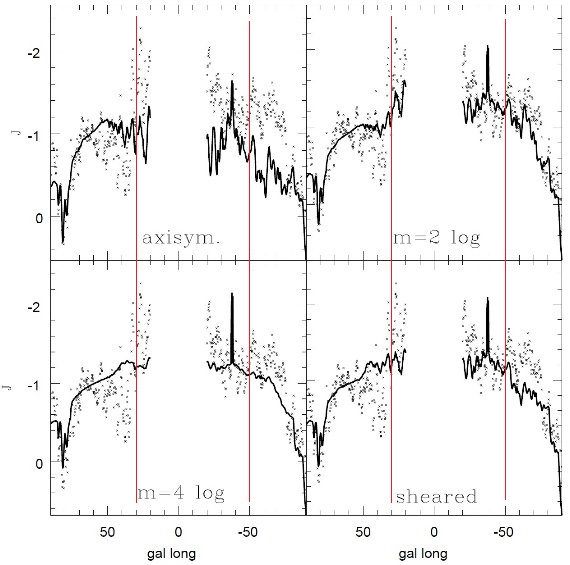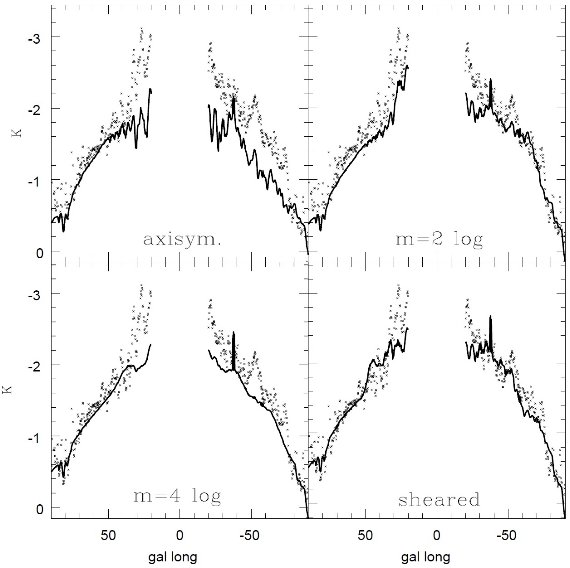 　　　　　wa = ca Ra 　　　　　ha = h0,a + h1,a (Ra - rf,a)2　　　　　(Ra > rf,a) 　　　　　　　 = h0,a　　　　　　　　　　　　(Ra ≤ rf,a) サジタリウス - カリーナ腕について　 　サジタリウス - カリーナ腕 (i = 3) には ca と ha に 縮小係数 fr を掛ける。l = ±50 の放射ピークを見ると、接点距離は同じくらい なのに、高さが随分違う。この差は i = 2 と 3 の腕が同等ではないことを示す。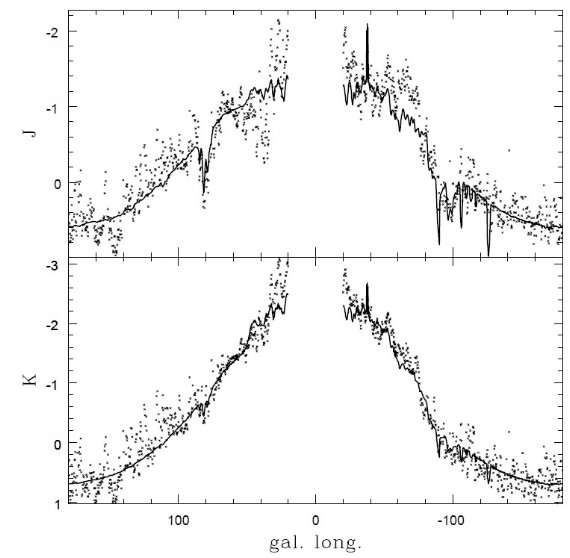 　腕の目印　 腕の接線 l = [80, -80] 範囲に見える　240 μm ピーク。 　 ペルセウス腕 l = [180, 90] に幅広の放射構造を示す。 　 オリオン局所腕の接線 低銀緯で見える l = 90 と l = -100 のピーク。NIR で吸収なので近距離。

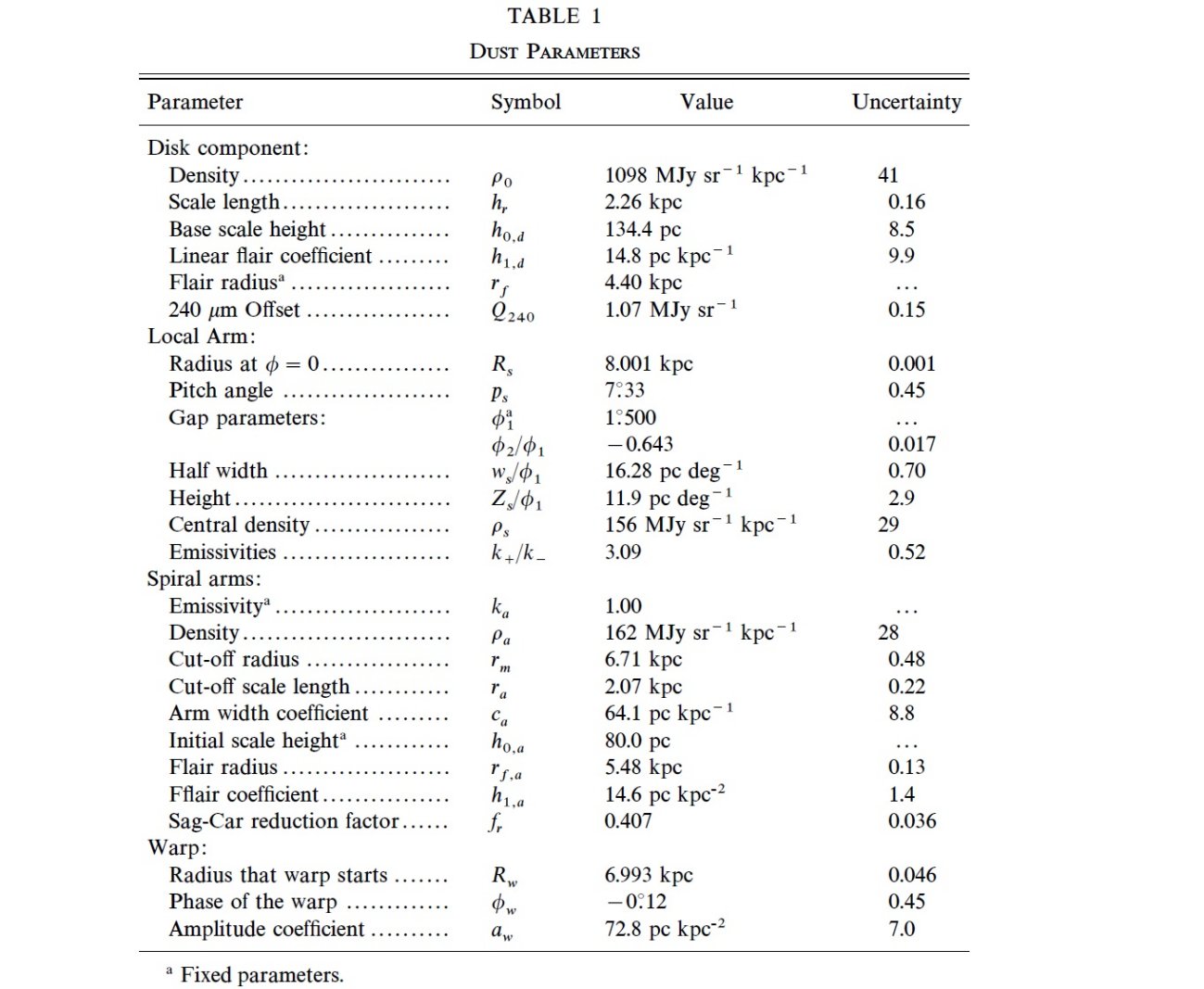
図３．銀河系半径(下)またはダスト温度(上)の関数としての相対的放射率 　オリオン局所腕の表示　 　(r, φ, z) = 銀河円筒座標で、太陽位置は (Ro, 0, Zo) である。 ps = 局所腕のピッチ角。as = tan ps。 腕の中心線は、rs = Rs exp( -asφ). (右手系で考えて φ を反時計回りにとると、 方位角が増すと rs が減る。φ は時計回りに測るのか？ ) 表１では Rs = 8.001 kpc, Ro = 8 kpc だから、ほんの僅か(1 pc !) 太陽の外側を通る事になる。 (どうやってその差が確定したのか分からない。 ) 局所腕の密度プロファイルは 　　　　　ρloc = ρs exp( -ds2/ ws2) ここに、ds2 = (r - rs)2 + (z - Zs)2、 Zs は局所腕のワープ銀河面からの 高さ、である。 (銀河面上の点(r, φ, z) に対しては局所腕の 軸上の点 (rs, φ, Zs) が対応し、ds はその間の 距離。) 　太陽は局所腕のギャップの中に　 　太陽を局所腕のギャップの中に位置させる必要のあることが判った。ギャップの端は φ1 と φ2 で指定される。太陽が希薄領域内に存在している ことは、 Paresce 1984, Frisch 1996 の研究からも分かっている。 計算上の都合で局所腕はピクセルサイズより小さくなった距離で打ち切る。 　局所腕輻射率の違い　 　局所腕の輻射率は正銀経側と負銀経側で異なる。これは両側で温度が異なる証拠である。 遠赤外放射率としては正銀経側の方がずっと明るい。一方、近赤外の吸収の特徴は 双方似通っている。

　３．３．恒星放射モデル　

　４．パラメタ―の調整　

ベストフィットを探すために χ2 を最小化した。 χ2 = Σ (Dmod - Dmod)2 σ2 上の和はバンドとピクセルに渡る。しかし、計算上の制限により全波長を同時に フィットすることはできなかった。そこで、まず FIR をフィットし、次に NIR を フィットする。 　４．ＦＩＲパラメタ―の調整　 　不定パラメタ―は事前にフィックス　 　FIR マップだけからダストモデルを出す際にいくつかのあいまいさが残る。それらは、 長さの基準 Ro = 1 として表すことにした。 図４．（上） DIRBE 240 μm 平滑化マップ。(中)モデル。(下）モデルと観測の差の相対値 図６．指定銀緯から 0.17° 以内の 240 μm プロファイル。

k ρ を k と ρ に分離困難。 FIR フィットでは k- = ka = 1 は円盤成分との相対比である。 Zo Zo = 15 pc 採用 腕のスケール高 h0,a h0,a = 0.01 Ro とする。 残った 22 パラメタ―がフィットに使われた。結果を表１に示す。 図４＝ 240 μm マップ　 　図４は 240 μm マップを観測（上）とモデル(中）で示す。さらに相対的なズレ、 (Dobs - Dmod)/Dobs を示す。この図から全体的な 様子を見てとることができる。しかし、この図では銀河面での変化がよく分からない。 そこに興味深い天体が集中しているのに。そこで、図５と図６では等銀緯プロファイル を示す。これから、モデルのずれが高銀緯で大きくなるように見える。しかしそれは 用いた対数スケールの効果である。図７は残差が高銀緯で小さいことを示す。 　ＦＩＲマップの特徴　 　放射プロファイルはモデルが銀河面での主要な特徴を再現していることを示す。 腕の接線 l = ±30, ±50, -80 と局所腕によるピーク l = 80, -100 は正しく位置している。天空図では局所腕は銀緯方向に大きく広がる二つの明るい 点として現れている。ワープは銀緯の正負での放射の対比から明らかである。 (何処が非対称？) ペルセウス腕は l = 80 から -140 (l=220) にかけての b > 5 での広い放射構造 として図６に明らかである。この腕は主に正銀緯側で見えるがそれはワープの効果である。 ( 外側円盤とどう分離するのか？) そしてそれが銀緯方向に大きく広がっていることが渦状腕のスケール高にフレアリング を要求する根拠である。ワープはまた l = -80 で銀緯方向にわずかに負方向にずれている ことも説明する。 図５．b = [-0.17, +0.17] の 240 μm プロファイル。バツ＝データ。菱形＝モデル。 図７．遠赤外データとモデルの差の対数。

　４．２．近赤外のパラメタ―調整　

図８．(上) J バンド観測天空図。(中）モデル J マップ。(下)モデルと観測の差。 （上）と(中)は対数表示。（下）は線形表示。 　図の説明　 　NIR のパラメタ―は表２に載せた。図８と図９には観測とモデルの天空マップ を比較した。相対差 (Dobs - Dmod)/Dobs も図示した。それを見ると、大きな差は銀河系中心から 30° 以内の銀河面 であることがわかる。図１０，１１，１２にはより詳細な銀緯一定線上での プロファイルを示す。 　銀経プロファイルの特徴　 　観測された NIR プロファイルは FIR に較べずっと滑らかである。また、軸 対称成分が卓越している。非軸対称性が現れるのは銀河面近くである。これは 主に減光の効果で　K より J で著しい。渦状腕は FIR ほどはっきりせず、K バンドで部分的に認められる程度である。局所腕による吸収構造が l = 80 と l = -100 にはっきりと見える。 　FIR リスケーリングの効果　 　FIR リスケーリングの効果が NIR の放射プロファイルに現れている。リス ケーリングにより人工的な特徴が出る場合もあるが、それよりしばしば、これ により NIR プロファイルの細かい構造が再現されるようになった。特に低銀緯 では、吸収がプロファイルを規定する効果がはっきり示された。 　ワープ　　 　NIR ワープは FIR ワープほどはっきりしないが、図１２の b = 5 と -5 図 を比較するとはっきり分かる。プロファイルは b = -5 では正銀経側に強く、 b = +5 では負銀経側に強い。 　K バンドのズレ　 　Ｋバンドのズレマップを見ると、モデルでは表現しきれていない構造が残って いることが判る。前に述べた銀河中心周り銀河面上のズレをおいても、 K マップには巾の広い大きな黒い斑点がみえる。l = 90 付近に広がる黒い染みは 局所腕によるものであろう。銀経負側の白い斑点は l = -90 以内に分布するが あまりはっきりしない。これらのシミは J でも同じ場所に見える。 図１１．各銀緯から 0.2° 以内のＪバンド放射分布。Ｋバンド。 バツ＝観測。実線＝「切り離し」腕モデル

図９．(上) K バンド観測天空図。(中）モデル K マップ。(下)モデルと観測の差。 （上）と(中)は対数表示。（下）は線形表示。 図１０．銀河面から 0.2° 以内の放射分布。(上)Ｊバンド。(下)Ｋバンド。 バツ＝観測。実線＝「切り離し」腕モデル 図１２．各銀緯から 0.2° 以内のＫバンド放射分布。 バツ＝観測。実線＝「切り離し」腕モデル

　４．３．モデルの一般的特徴　

図１３．ダストのモデル表面密度分布。太陽は中央上の小さな黒点。太陽が オリオン腕近くに位置することが判る。銀河中心の向こう側の腕は HII データ（HIIR）不足のため不完全である。 　ダストと星の面密度分布　 　図１３にはダスト、図１４には K バンドのモデル表面輝度分布を示す。 r ≤ 0.34 Ro 部分は不完全である。特にバルジに関連した構造は現れて いない。また、銀河中心の向こう側の腕も不完全である。これは腕の軸線 を HIIR の配置によって決めているからである。 　腕の強度　 　ダストと星における相対的な腕の強さは、腕対腕間域の銀河面におけるフラックス 比として図１５に示す。しかし、円盤と腕とのスケール高のちがいがこの差を 表面輝度では和らげる。図１６には様々な成分のスケール高を示す。 図１５．腕と腕間との密度比。破線＝星。実線＝ダスト

図１４．K バンドのモデル表面輝度分布。明るい輝点が太陽。 　局所腕　 　図１３には局所腕も表されている。しかし、銀河系全体として見る時には 局所腕は腕というより、腕間の橋、又は腕のはけ毛のようなもので円盤の あちこちに存在するものの一つに過ぎない。 図１６．スケール高の変化。破線＝星円盤。実線＝ダスト円盤。一点破線＝腕。

　５．不確定性と他のモデル　

　５．２．別のモデル　

図１７．軸対称モデル、３本腕モデル、ｍ=２、４本の対数螺旋腕モデル。「切り離し」腕モデル。 |l| < 90 の J - プロファイル。 　恒星フレアは確かでない　 　表５に別の恒星モデルを載せた。星円盤にフレアを付けたモデルは、フレアを ダストモデルと同じ距離から開始した。その結果は極めて穏やかで 6.6 pc /kpc であった。これはダスト円盤の半分以下である。しかし、 χ2 の 顕著な改善はなかったので積極的な証拠とはできない。 　４つの異なる仮定のモデル　 　NIR 放射の中に非軸対称の証拠を見つけるため、４つの異なるモデル、 ３つの渦状腕モデルと一つの完全に軸対称なモデル、を計算した。図１７と１８に その４本のプロファイルを示す。表６にはそれらのパラメタ―を載せた。 二つの対数螺旋モデルは単一の振幅パラメタ―Ｂを持っている。これは腕と円盤が 同じ星種族から成ると仮定したからである。一方、「切り離し」腕モデルは若い星がダスト から離れる期間をＪとＫで異なる値を取っている。図を見ると、 m = 2 対数螺旋と 剪定腕モデルは同じくらい良い。軸対称と、m = 4 モデルは特に l = 30 と l = -50 の盾座腕接線の方向で失敗している。 ( それほどの違いには、特に l = 30 では、 見えないが。) 　サジタリウス・カリーナ腕 　正銀経側にサジタリウス腕の存在は見えない。軸対称と m = 2 モデルは 他の腕モデルと同様 l > 40 の放射プロファイルを再現しているが、 前２者はサジタリウス・カリーナ腕を欠いている。しかし、m = 2 log モデルと 「切り離し」モデルを良く調べると、少なくとも負銀経では、サジタリウス腕が実在す ることが判る。m = 2 対数螺旋と「切り離し」腕のパラメタ―は良く似ているが、図 １９から分かるように、m=2 対数の大きなピッチ角はその見かけを大きく 変えている。これは、 l ≤ -50 の放射を節飯用としたためである。 この放射は　J で強く、実際、Ｋだけでフィットした結果(Drimmel, Spergel 2001) は 15.6° という小さな角度を与えている。

図１８．軸対称モデル、３本腕モデル、ｍ=２、４本の対数螺旋腕モデル。「切り離し」腕モデル。 |l| < 90 の K - プロファイル。 図１９．腕模式図。太線＝ 4 本スパイラル(HIIR に準拠)。星＝「切り離し」腕。破線 ＝ ２本対数螺旋（Ｊ）。細実線＝２本対数螺旋（Ｋ）。

　６．議論　

　７．議論