3D Self-Consistent N-Body Barred Models of the Milky Way

　アブストラクト

　１．イントロダクション　

　２．観測結果　

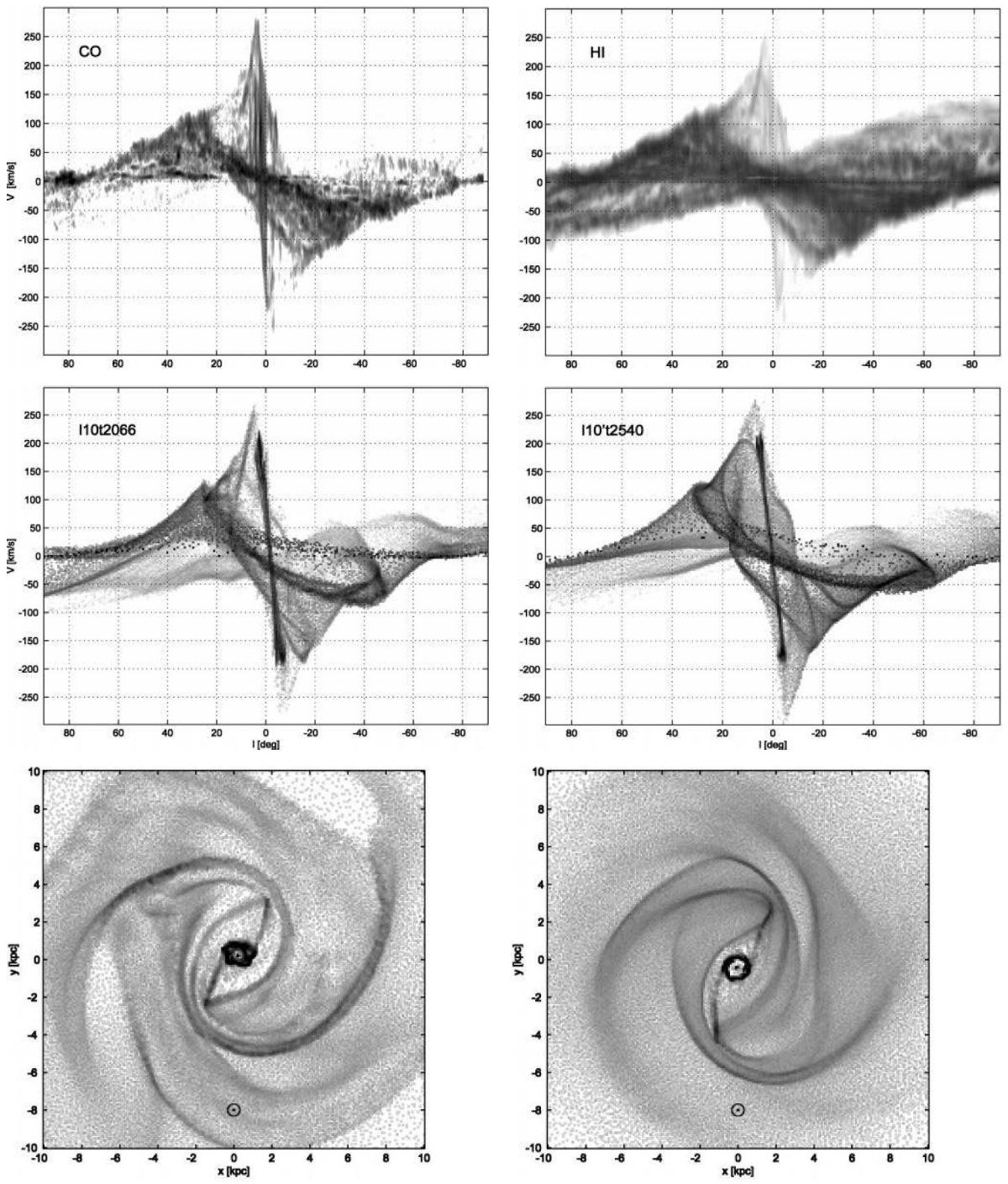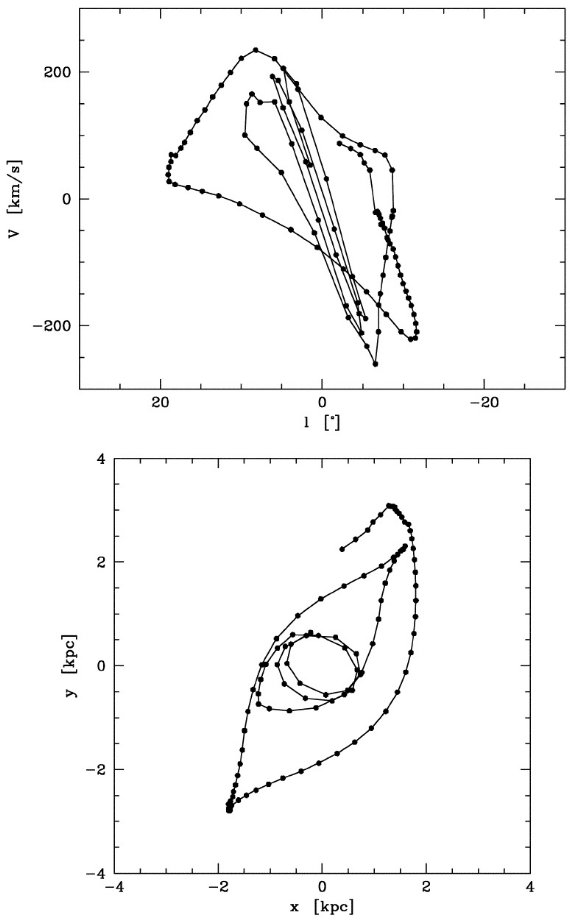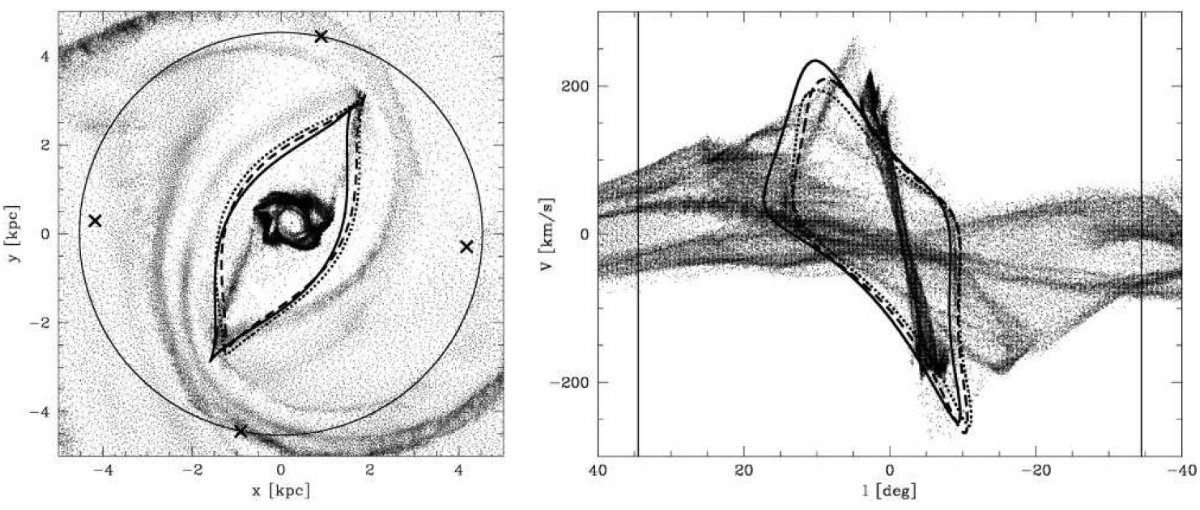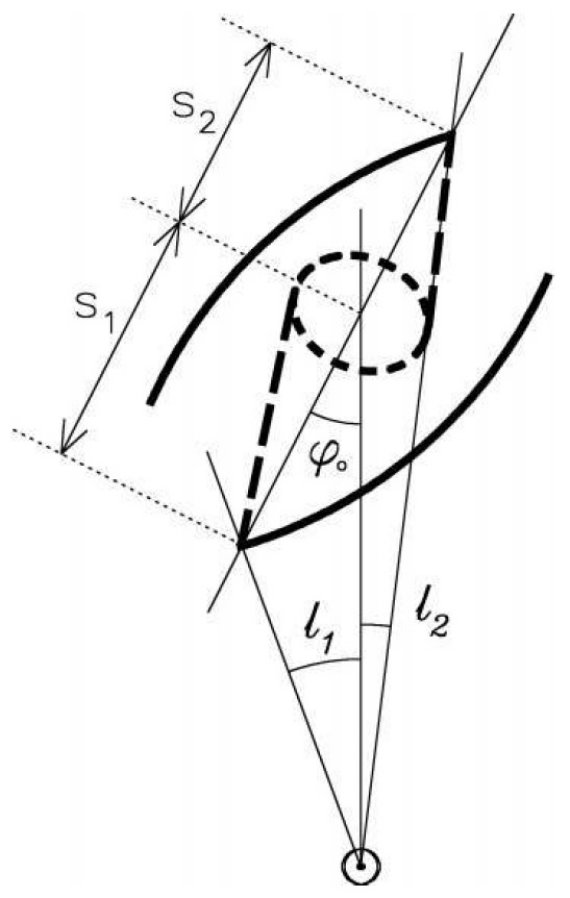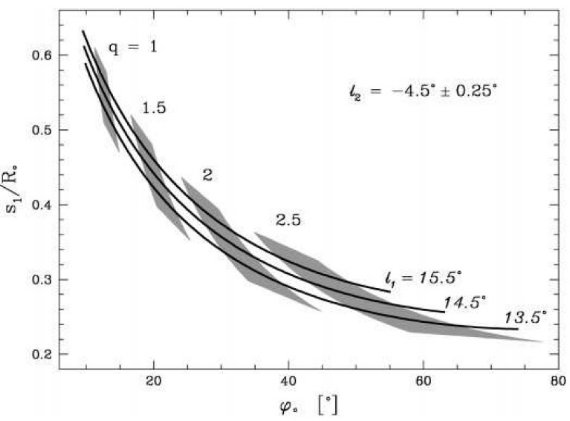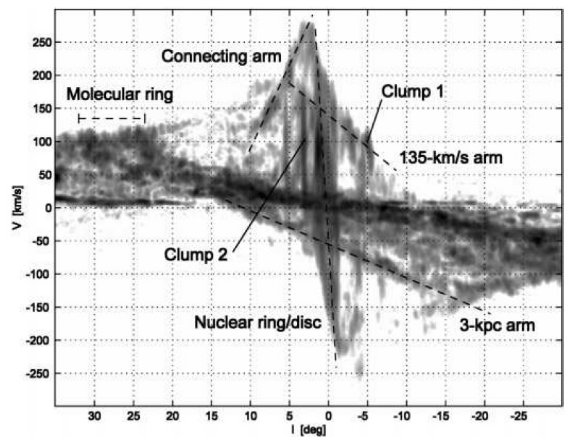
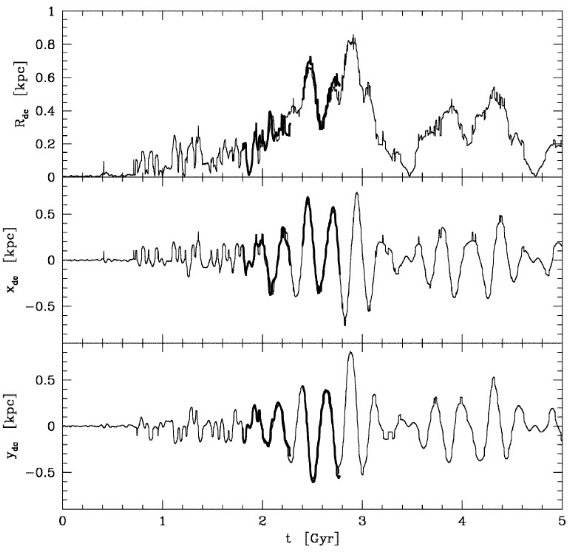
図１．12CO J=1-0 の b = [-2,2] 積分した l = [-35, 35] l-v 図 Dame, Hartman, Thaddeus (2001) 。 Bania 1977 のクランプと 破線 = 3 kpc 腕と逆側の対応腕, を示す。 　3 kpc 腕　 　この腕は Woerden et al 1957 が発見し、V(l=0) = -53 km/s である。その 接線角 l = -22 と当時 の Ro = 8.2 kpc から 3 kpc が出された。この腕を 膨張＋回転のリングでフィットする試み(Burke, Tuve 1964)は失敗した。 Mulder, Liem 1986 は回転バーポテンシャル中の密度波としてこの腕を説明した。 　 135 km/s 腕　 　Oort 1977 はこれが 3 kpc 腕の対応天体ではないかと疑ったが、V(l=0) = 135 km/s は 3 kpc 腕の対応とするには違い過ぎる。 　The connecting arm 　Rougoor, Oort 1960 に述べられ、多分中心核リング/円盤と外側の円盤を つないでいるように見えるところから付いた名前らしい。(l, v) = (10, 110) 付近で見分けられる。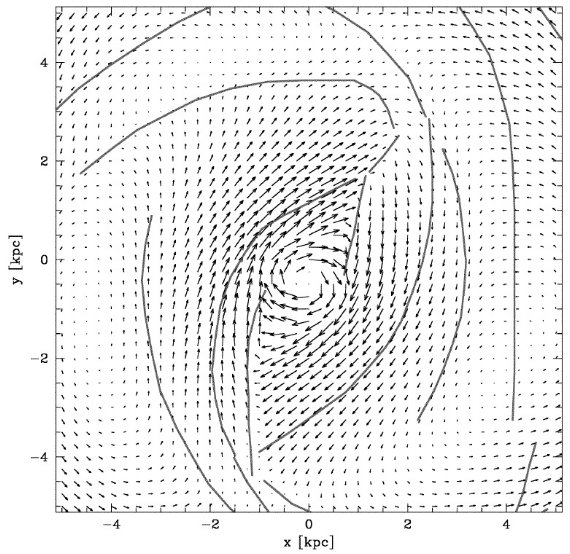 　中心核リング/円盤または中心分子域　 　l = [-1, 1.5] の中心がずれた濃い分子ガス。Scoville 1972, 海部ら 1972 は平行四辺形型の (l, v) 図から膨張分子リングと呼んだ。そのサイズから　 180 pc リングとも呼ばれる。このリングに囲まれた分子雲複合体は円盤上に分布し 回転速度は 100 km/s に達する。祖父江 1995 はそれらが二本のミニ渦状腕を 成すとした。 Binney et al. 1991 はこの四辺形を尖がり x1 と x2 軌道のガスと解釈した。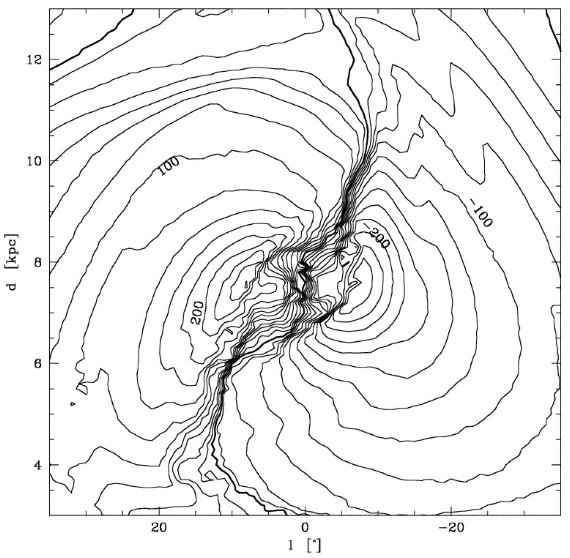 　分子リング　 　半径約 4 kpc のリング状に分布するガスであるが、空間分布はあまり良く 決まっていない。渦状腕がずれつつ重なり合っている可能性もある。正の 終端速度曲線近くで、二つの分枝を出し、夫々は　l = 25 と 30 に接点を持つ。 銀河に見られる内側リングに対応する構造 (Buta 1996）なのであろう。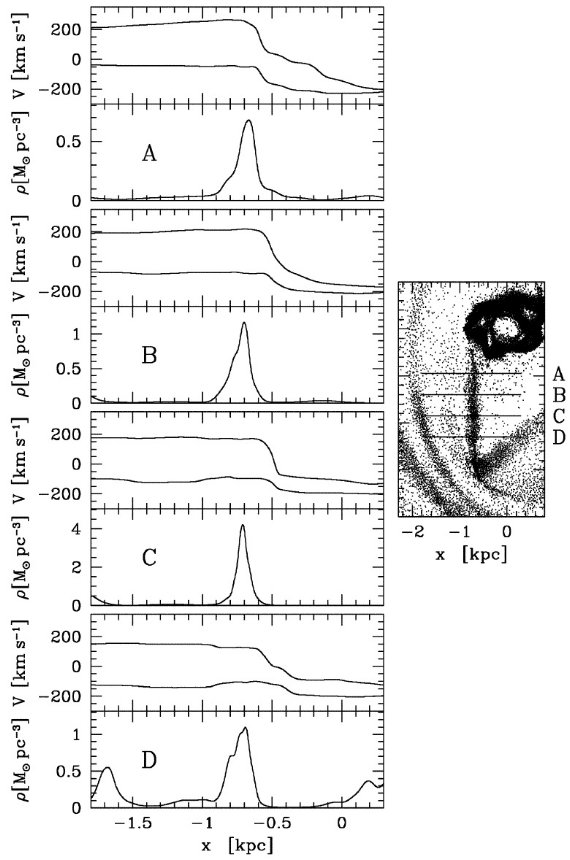 　クランプ１　 　135 km/s 腕の端 (l, b) = (-5, 0.4) に位置する。銀河系内の濃いガスの 集団としては最も著しい非円周運動を示す。夫々が 2.5 105 Mo の３つの副ユニットにから成る。 Bania 1986 を見よ。 　クランプ２　 　(l, b) = (3, 0.2) に位置し、速度巾が 150 km/s に及ぶ。 Stark, Bania 1986 によると 16 個の 5 105 Mo コアからなる。彼らはそれを バーポテンシャル中のダストレーンまたは内側渦状腕に沿った分子雲の 列を縦に見ていると解釈した。

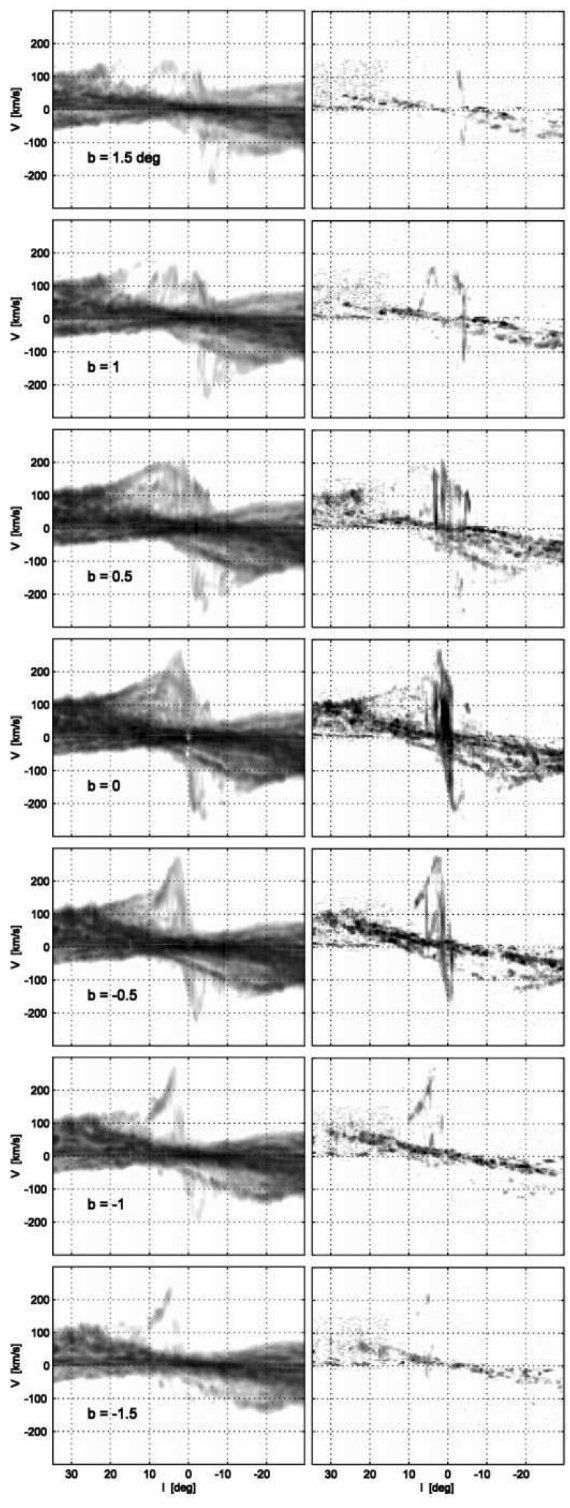
図２．b = [-1.5, 1.5] での ｂ毎の (l, v) 図。左： HI. 右： CO.

　３．計算方法　

　４．初期状態　

　５．時間進化　

　５．１．恒星　

図９．質量中心からの星重心の動き。上：距離。中：X 座標。下：Y 座標。

図１０．細線＝ガス固定、lxx シミュレーションでのバーパターン速度の時間変化。 太線＝live gas でのシミュレーション。 図１１．モデル lxxt1950 で減光補正した COBE K-バンド画像にフィットした結果。 実線＝ COBE. 破線＝モデル。

　５．２．ガス　

図１３．シミュレーション l10’におけるガス流の正面図。各枠は 20 kpc. 点線は星密度。

　６．l-v 図の解釈　

６．１．結合腕　 結合腕＝ダストレーン　 　図１６と図１７から分かるように結合腕は太陽に近い側のバーの軸衝撃波 である。この腕は、様々な銀河中心距離で衝撃波面を通過し、次に 衝撃波面とほぼ平行に集団となって中心核リング/円盤へと落ちていくガス雲 から形成されている。別の言い方をすると、結合腕は二つあるダストレーンの こちら側の分枝である。他のモデル、例えば l10t2066, では l-v 面での軸 衝撃波が l10't2540 より観測とさらに良く似ている。 　中心核リングによる吸収　 　観測 l-v 図に現れた結合腕はバーの存在の更なる証明である。結合腕は実際 にガスが集結した構造であり、 Mulder, Liem 1986 が言うような、視線上に 同じ速度のガスが重なって見える現象ではない。シミュレーションではガスが 常にショックの全長を表現するわけではなく、したがって、結合腕からの放射が l ≥ 10 で切れていても不思議はない。 図１６．モデル l10't2540 における x-y 面上の渦状腕と l-v 面上の構造と の関係。上図では、観測者に近い方の構造を遠い方の上に描いた。

l-v 動画では時々ガスの塊りが枝腕 から供給されて結合腕に沿って流れて行く。枝腕の終点から衝撃波に沿って 中心核リングまでの時間は 15 - 20 Myr である。もしもこのガスが中心核リング に吸収されなかった場合、向こう側の衝撃波にぶつかるまでのはさらに　10 Myr かかる。定常モデルでの計算結果によると、リングでの吸収率は 20 % 程度で ある。各衝撃波に含まれるガスは 4 107 Mo である。 　向こう側の軸衝撃波　 　図１６を見ると、向こう側の軸衝撃波は l-v 面ではほぼ垂直に立つ。図１ には l = -4 に正にそのような尾根が見える。この現象は衝撃波線の向きが視線 方向とほぼ平行しているからである。速度の変化は衝撃波に沿って流れるガス の速度が中心核リングに接近するにつれ急激に高速化するためである。 　６．２． 3 kpc と 135 km/s 腕　 135 km/s 腕　 　3 kpc と 135 km/s 腕は分枝腕である。二つの腕の間で観測される速度の非 対称性は、 135 km/s 腕が 3 kpc 腕よりも銀河中心近くを通過するためである。 図１７を見ると、135 km/s 腕のガスはガスに沿って運動し、ポテンシャル井戸 により深く落ち、ダストレーン衝撃波に打ち当たる前により大きな禁制速度に 達している。 　3 kpc 腕　 　3 kpc 腕のガスは 135 km/s 腕より遠方でダストレーン衝撃波をくぐった後、 中心核リング/円盤へとより高いポテンシャルエネルギー地点から落下を始める。 その結果、リング/円盤に近づく速度はより大きい。これが速度ピークが強めら れる理由である。しかし、モデル l10't2540 にはそのような速度非対称が 見えない。この非対称性は中心核/円盤と LSR との動径方向運動からも 生じる可能性がある。 　分子リングとの関連　 　 l = 25 に接点を有する分子リングの内側分枝は 135 km/s の外側への外延である。 図１７．バーの回転系でのモデル l10't2540 の速度場。灰色の曲線は渦状腕の 位置。 ( 3 kpc 腕のガスは腕を横切るのでは なく、腕に沿って流れている。その速度場はその両側と特に際立った差はない。 しかし、図１５右下の密度図を見ると、濃い密度で周りと同じ速度のガスが 3 kpc 腕の中を流れていることが判る。結合枝のガスを供給しているのは 3kpc のガス。だから 3 kpc 腕の終端はすごいことになる筈。うーん！ )

　６．３．バニアの雲塊　

衝撃波での速度変化　 　図１９にはモデル l10t2066 で において、結合腕に垂直な４本のすき間に 沿っての X-速度(下)、Y-速度(上)および密度分布を示す。衝撃波は x = -0.55 kpc 付近に発生し、その下流側に巨大なガスの集積を生み出す。衝撃波を越える 際に特に衝撃波に沿った速度成分 (Y-成分）は大きな変化を受ける。これは軸 衝撃波のズレ応力的性質を示している。 　速度構造の解釈　 　 Bania 1977 の雲塊２と l = 5.5 付近に見える垂直構造（図１）は 3 kpc 腕と中心核リング /円盤との間のどこかで今まさにダストレーン/衝撃波を横切ろうとするガスの 塊りを示している可能性がある。その上流側は前衝撃波軌道に沿って、準遠点 速度で動いているが、下流側は後衝撃波の内向き高速度へと加速されつつある。 その結果、図１８に見られるような大きな速度勾配が生まれ、観測としては 100 km/s を越す大きな速度巾が現れる。 図１８．モデル l10't2540 の b = [-2, 2] 等視線速度図。このモデルの密度 分布と l-v 図は図１５右側にある。線間隔は 20 km/s　で太線は 0 km/s を表す。 ( 図１７の垂直速度成分を等高線にしたと 考えてもいいし、もし、ＬＭＣのように、斜め上から見た時に観測される視線速度 分布と考えても良い。) 図１９．モデル l10t2066 において、結合腕に垂直な４本のすき間に沿っての X-速度(下)、Y-速度(上)および密度分布。衝撃波の右側では左下方向の運動が 衝撃波を過ぎると左方向に変わる。衝撃波面の 10 pc 以内に高密度帯が形成 される。

l = 5.5 の雲塊　 この解釈を支持する観測事実とし ては l 5.5 塊りの放射がほぼ同一銀緯に制限されていることがある。これはガスが 空間的に制限された領域内に存在していることを示す。また、この塊と同じ 銀経 l にある結合腕成分は、図２を見ると塊りと大体同じ銀緯 b を示す。 ( 図２ b = -0.5 の特に右側 HI 図 を見ると b = 5.5 垂直構造が 3 kpc 腕と結合腕を結んでいる。 ) 　クランプ２　 　クランプ２は同じ l で較べると結合腕に対し b で　0.5 の差がある。また 質量も 107 Mo ある。しかし、もしこのクランプが実際にその軌道 遠点付近にあるなら、衝撃波には非常にゆっくりと入って行き、 200 km/s を 越す高速ガスに当たるであろう。すると長時間の間には大きな運動量をえること になるであろう。その上、クランプはループを成す準 x1 軌道に 沿って動いていて、クランプ複合体の大きさがループ自体と同程度だと、エネ ルギーを自己散逸する可能性がある。 　クランプ２はダストレーンか？　 　もし、結合腕が実際にダストレーンをなぞって いるなら、 Stark, Bania 1986 が提案する、クランプ２はダストレーンであるという説は崩れる。銀河系に二 重バーがあれば別だが。注意しておくが、モデル l110't2540 の軸衝撃波は、もし バーの傾斜角が 15° であるなら、クランプ２の方により似ている様子を 示す。 クランプ１　 　クランプ１は Bania et al 1986 によれば、重力的には非拘束の幾つかの雲から なる。その位置は 135 km/s 腕の南端部分に当たる。モデル l110't2540 によると、 その運動はやや不鮮明である。このガスの一部はダストレーンに吸収され、 v = 100 km/s から v = 0 km/s へと大きな速度変化を受ける。もう一方、クラ ンプ１の l < -5 部分は外側へとずり出て行くが、遠点に達するまでは衝撃 波を越さない。図１６のマゼンタ色の線片を見よ。この雲が衝撃波に与える 運動量は衝撃波の外側部を曲げてしまう。遠方側ダストレーンは視線に沿って 並んでいるので、　l = -4 の垂直構造は実際にはダストレーンに沿って、 衝撃波に誘発された速度勾配を持って並んでいる雲の重なりである。図２０を 見よ。 クランプ１の星形成条件　 クランプ１は非常に乱されて、圧縮を受けている領域である。従って、 星形成の潜在的な発生地である。長谷川の私信によるとそこでの12 CO の J=2-1 対 J=1-0 ライン比は特に高く、濃い分子雲の存在を示している。 しかし、つよいズレ応力が星形成の進行を妨げている。 クランプの大部分はその大きな質量と衝突速度のおかげで、衝撃波を大した 影響も被らずに通過する。 図２０．シミュレーション l10 における SPH 粒子の(上) X-Y 面及び(下）l-v 面での軌跡。t = 1994 から 2200 Myr まで間隔 2 Myr でプロットした。 X-Y プロットはバーの回転系で表示した。バーの傾斜角は 25° である。l-v 図は (X, Y) = (0, -8) から見た図となっている。選ばれた粒子は t = 2066 に 分枝腕と衝撃波面の境界を図１５の左下枠で (X, Y) = (-1.4, -2.4) を 通り過ぎる。粒子が遠方衝撃波を通過する際の大きな速度変化に注意せよ。

　６．４．ガス円盤の傾き　

　６．５．中心分子帯　

　７．バーパラメタ―への幾何学的制約　

視点位置による l-v 図の変化　 　図２２では、視点の方向により、モデル l10't2540 の l-v 図が変化する 様子を示す。傾斜角 φ0 を小さくすると、構造の銀経巾を縮小 し、同時に視線速度を増加させる。135 km/s 腕の l = -5 にある膝はよりよく 再現されるが、3 kpc 腕から結合腕への遷移が負速度過ぎ、結合腕の傾きが急 になり過ぎる。逆に φ0 を大きくすると、禁制速度を小さくし、 終端速度ピークの位置を遠くへ離し、結合腕を分子リングの接点近くに移す。 距離を大きくすると銀経巾を狭くするが速度はあまり変えない。 　幾何学的関係　　 　バーの性質に制限を加える作業はモデルを誤ると間違えた結論を導くので 注意が必要である。しかし、バーの傾き角と大きさはモデルにあまり依存 せずに決めることが可能である。その原理を示した図２３では、l1 = 3 kpc 腕が軸衝撃波と交差する角度、l2 = 135 km/s 腕が軸衝 撃波と交差する角度、q = s1/s2 である。 図２３．実線＝分枝腕、破線＝軸衝撃波の幾何学表示。短破線＝中心核リングは 拡大表示されている。下は太陽。

すると、 si = sin |li| 　　　　　i = 1, 2 Ro sin (φ0+ji) tan φ0 = - 1 + q cot l2 + q cot l1 s1 = [ (1 + q) sin2l1 + q sin2l2 - q ] 1/2 sin2(l1 - l2) 完全に左右対称なら q = 1 であるが、実際には q > 1 である。また、上の式は 分枝枝と軸衝撃波の交差点と銀河中心が直線上に並んでいることが前提である。 　第２の分枝腕？　 　l-v 図上で、結合腕を　3 kpc 腕方向に外挿して l1 = 14.5° を得る。そこでは 3 kpc 腕の膝がギリギリ見える。一方、 135 km/s 腕は反対 側の衝撃波と l2 = -4.5 で出会う。図１を見よ。図２４にはそれから 得られる拘束条件を示した。明らかに φ0 が小さくなると、 長さ s1 は長くなる。しかしこれまでの所、 φ0 の 値は不明である。ただし、図１には向こう側分枝腕の第２の枝が l2 = -7±0.5 まで伸びていることを示している。それは　135 km/s より 低い禁制速度を持ち、さらにほぼ同じ銀経で垂直な速度構造を示す。こちらは 同じ腕から中心核リング/円盤に落ち込むガス成分なのであろう。その落下軌道 は衝撃波と平行なのではないか。もしそれが正しいなら、この腕は 3 kpc 腕とより対称性が高い。その場合は q = 1 となり、φ0 = 25± 4, s1 = 3.15 kpc である。ついでだが 135 km/s 腕に対しては q = 1.76, s2 = 1.8 kpc である。 共回転半径　 　早期型棒銀河では a = バーの半長径、 RL = 共回転半径とすると、 a/RL = 0.85 である。a に s1 を使うと RL = 4.0 kpc となる。 　動的シミュレーション　 　しかし、我々の非対称で時間変動するシミュレーションでは図２５に示す ように事情はもっと複雑である。 ( この先は議論が面倒で付いていくのが 困難になったので中断。) 図２４．バーのパラメタ―への制約のグラフ表示。実線＝式(２６)から異なる l1 毎に描かれている。灰色領域＝異なる q に対する式 (24) . s2 = s1/q と置き、 l2 = [-4.75, -4.25] と仮定して、l2 の不定性が q にどう伝播するかを示した。

　８．結論