| 銀河系 |l| < 10, |b| < 0.5 の HI, CO, CS 放射に筋の通った説明を 与えるモデルを示す。銀河中心のガス流は r = 2.4±0.5 kpc で共回転 するバーのポテンシャルに支配されている。このバーを我々は主軸角度 θ incl = 16±2° で見ている。最初の(?) CO 放射は ガスが x1 軌道から x2 軌道へと切り替わる所から 生じている。軌道名は Contopoulos に従った。この切り替わりはショックを 発生させ、(l, v) 図上に明白な特徴を残す。Sgr B のような銀河系中心部の 巨大分子雲は x1 軌道にある。 | HI 終端速度の外郭の構造から、中心部密度はバーの主軸沿いに 1.2 kpc まで、ρ ∝ r-1.75 であることを導いた。このため、 単純な接線速度解析では回転速度が低下する半径領域で、回転円運動曲線が 上昇するという結果になった。r = 3.5 kpc の分子リングは多分、 バーの外側リンドブラッドレゾナンスと関係する。その共回転内側では ガス密度が低下する。 |

|
母軌道 Contopoulos 1979, 1983 や Schwarzschild 1979 が強調したように、どんな ポテンシャルであれ、そこでの軌道構造を知るための鍵は閉軌道である。閉じて いない軌道は大抵の場合、背後にある安定な閉軌道からのエピサイクリックな 遠足と看做せる。 閉軌道 ガスの塊りをポテンシャル内に投げ込むと、雲同士のずれ摩擦が働き、閉軌道に 落ち着く。閉軌道にあるガスは散逸過程によりゆっくりとより低いエネルギー の閉軌道へと順に移って行く。(l, v) 図を閉軌道の集合として理解できるのでは ないか? 自己交差型軌道 ポテンシャルが非球対称の場合、次の可能性がある。 (i).安定閉軌道があるエネルギーで自己交差軌道に変わる。 (ii).あるエネルギーで1次系列から多次元系列へ変わる。 実際、ガスがバーポテンシャルの中心に接近する際の前行性(prograde)軌道の族、 Contopoulos, Mertzanides 1977 の x1、は中心近くでは自己交差型 となる。 x1 軌道から x2 軌道へ 数値計算(Athanassoula 1988, Mulder, Liem 1986)によると、自己交差型での 最高エネルギー x1 軌道にガスが接近していくと、衝撃波に遭遇し、 力学時間スケールの内に x2 軌道族へと沈み込んでいく。この軌道 族はポテンシャルの非常に深いところに位置する。このようなわけで、期待される (l, v) 図はエネルギーが比較的高い非自己交差型の x1 軌道と それより大分下の x2 軌道の組み合わさったものであろう。 |
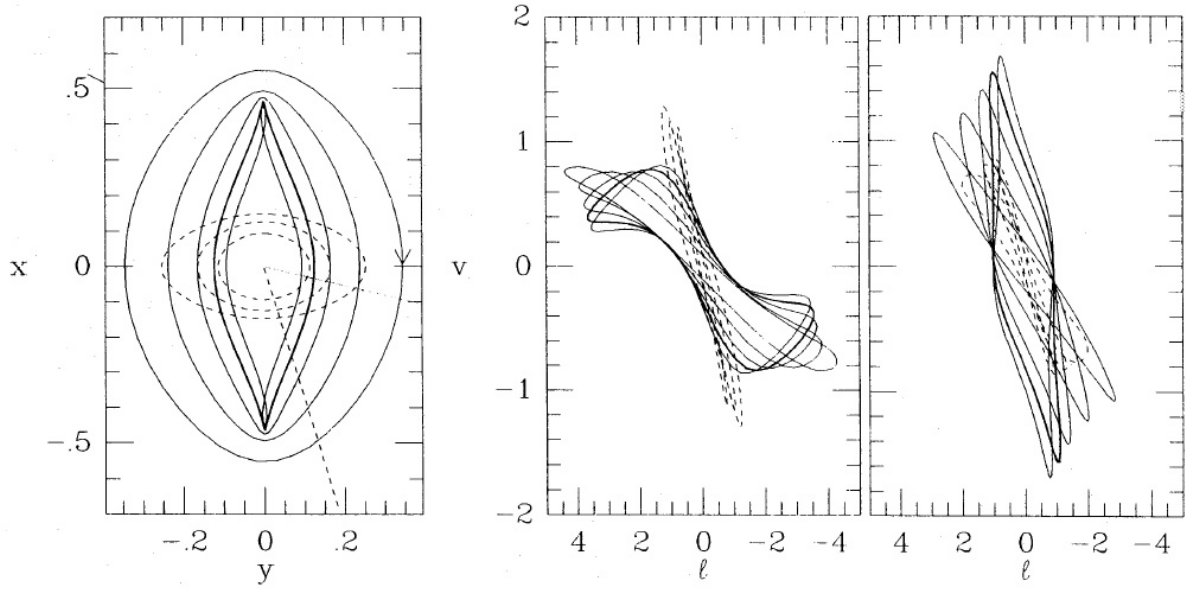
(l, v) 図 図1は入れ子となった軌道の系列(左図)と、それを主軸角 75°(中図) と 15° (右図)で見た (l, v) 図を示す。ポテンシャルは Ψ = (1/2)v02 ln(x2 + y2/q2) である。ここに、v0, q は定数。q = 1 は、一定回転速度 v0 を持つ軸対称ポテンシャルに対応する。内側に落ち込んでいくガス は x1 軌道を順に内側へ辿って行き、尖がり形 x1 軌道 に辿りつく。その次はぐんと沈み込んで最も外側の x2 に落ち着き、 そこから定常的な沈下を再開する。右図を見ると、視線方向が主軸に沿うに連れ、 (l, v) プロットが速度方向に引き伸ばされ、銀経方向には押しつぶされることが 分かる。 x1 軌道は、大体平行四辺形で軌道エネルギーが下がるにつれ 時計回りに向きを変えていく。バーの主軸に近い方向から見ると、 x2 軌道は (l, v) 面上でより薄い形をしており、 x1 軌道ほどの高速には 達しない。その理由は、x2 軌道は遠点が短軸、近点が長軸上にあるの 対し、x1 軌道は遠点が長軸、近点が短軸上にあるからである。 視線方向による (l, v) 曲線の変化 楕円形軌道をバーの長軸、または短軸方向から見ると、 軌道の対称性から 同じ視線上に重なる2点の視線速度は等しくなる。このため、 l - v 曲線は原点を通る曲線 となる。しかし、主軸と傾いた方向から見た時には、同じ視線上の二つの軌道点は異なる 視線速度を有し、l - v 曲線は原点を取り囲む膨らんだ曲線となる。結果として、 エネルギーの高い側から x1 軌道を降りてくると、 l - v 曲線は ほぼ直線状だったのが、次第に広がった長方形型になり、その長い方の対角線は v-軸に 平行となっていく。 |
|
中心付近分子雲の分類 銀河中心 1 kpc 領域 12CO, 13CO, CS は Bally et al 1987, Bally, Stark, Wilson, Henkel 1988, 1988 が 1′ 分解能で、もっと低分解能では Liszt, Burton 1978, Dame et al. 1987, HI では Burton, Liszt 1978, Sinha 1979 が観測した。これらのデータキューブ は大変込み入っている。 Bally, Stark, Wilson, Henkel 1988 は多数のつながった構造を見出した。 それらは次の 4 つに分けられる: (i)銀河系中心円盤 z 方向の速度分散 25 km/s に対応するスケール高の薄い円盤である。Sgr A と Sgr B はこの円盤中にある。 (ii)細長い構造 l で長く伸び、銀河面からそれている。(l, b, v) で孤立している。 典型例は Bally, Stark, Wilson, Henkel 1988 が述べた "the Polar Arc" である。 (iii)内部速度分散が大きい局所的な構造体。 (l, b) = (3, 0.2) のクラン プ2 (Stark, Bania 1986) が典型例。それらは銀河面からはずれて存在する ことが多いが、(l, v)図上では空間的にはコンパクトで、速度分散が大きな 構造を示す。(ii) の細長い構造体と似ているが、端の方向から見ているのでは ないか。 (iv)前景と後景の物質。 銀河円盤 R = 3 - 8.5 kpc のガスは銀河中心ガスと重なって見える。3 kpc 腕 を初めとする幾つかの雲は数十 km/s の速度を持つ。外側円盤のガスは特に内側 銀河の画像を乱しており、考察から除く必要がある。銀河中心物質と異なり、そ れらは CS ライン放射を伴わず、銀経に関して長く伸びている。 |
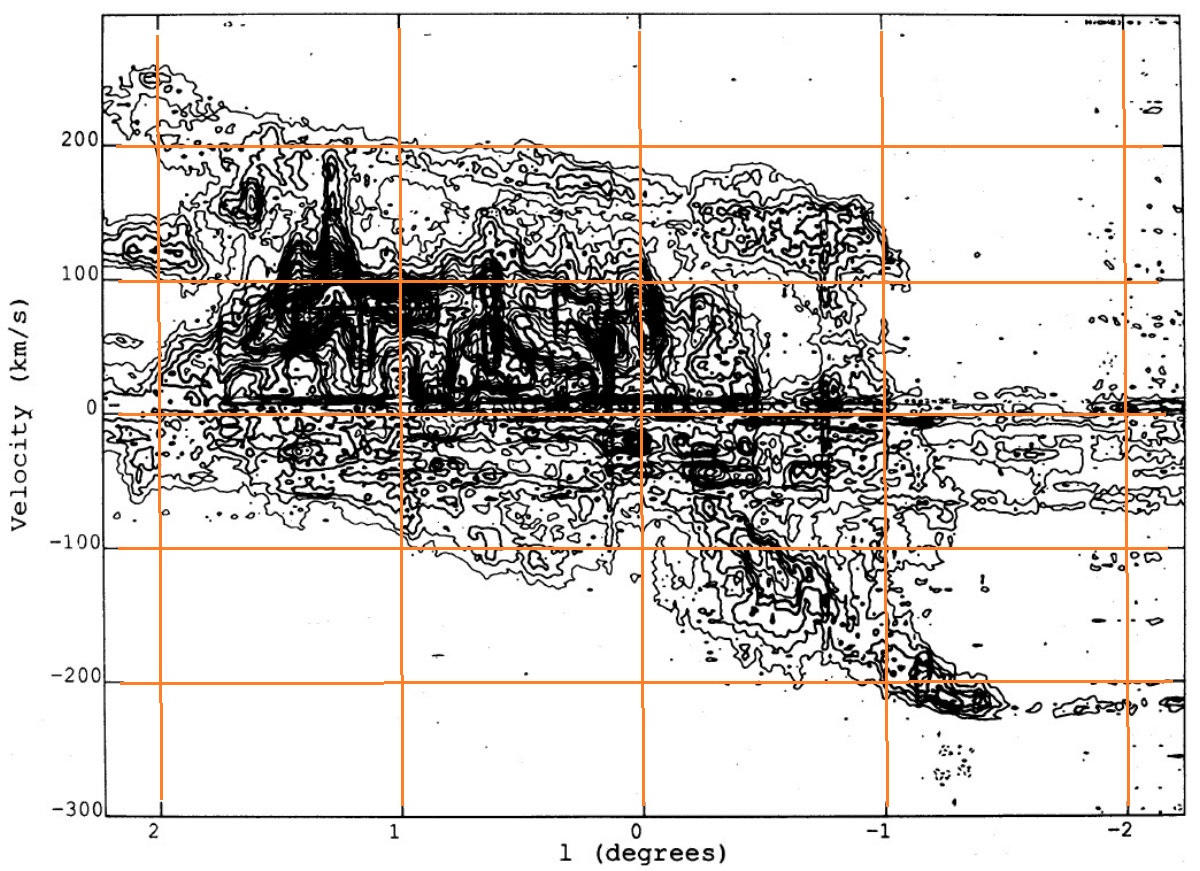
「銀河系中心円盤」をモデル化したい 銀河系中心部の (l, v) 図が複雑なことは、例えばハッブルアトラス 28 頁の M 83 画像にバー、ダストレーン、渦状腕、羽毛状構造があることからも予測さ れた。だから、全てを説明できるなどと考えず、 Bally, Stark, Wilson, Henkel 1988 の「銀河系中心円盤」をモデル化することを目指そう。図2には 12CO の b = [-0.1, +0.1] 積分 (l, v) 図を示す。ここで選んだ b は構造(i) を強調 し、構造(ii)-(iv) を排除している。勿論放射光の完全な分離は不可能である。 スケール高は雲内乱流が決定 図2に示したガスが閉軌道を巡っていることは十分にありそうである。特に、 そのスケール高は標準銀河モデルで CS ラインの巾に対応する予想値に一致する。 スケール高は銀河中心からの距離にほぼ比例して増加する。これは、閉軌道の 周りの速度分散が雲中の乱流によるものという仮定と合致する。 ( スケール高変化を比べた「距離」は 投影距離か?雲内の乱流が原因と言うことは雲が膨れ上がることがスケール高の 増加として観察されるということか?) 軌道面の傾き? さらに、以前のやや不完全な観測、Burton, Liszt 1978, Sanders, Solomon, Scoville 1984 で CO, CS の分布が銀河面に対し 7° 以上の傾きを持つと されていたが、今回の (l, b) 図にそのような特徴は現れなかった。ただし、 4° 以下の傾き角は否定できない。実際図2(b=[-0.1,+0.1]の(l,v)図)と Bally, Stark, Wilson, Henkel 1988 の図4(13CO b=[-0.6,+0.6]の(l,v)図)を比較すると、図2の特徴 である (l, v) = (1.8, 200), (1.8, -40), (-1.1, -200), (-0.8, 140) を 結ぶ平行四辺形の右下辺が b=[-0.1,0.1] への制限により刈り取られている ことが判る。 ( 理解できない。) これは、平行四辺形を形成するガスが正の (l, b)側に少し 傾いていることを示唆するものである。 |
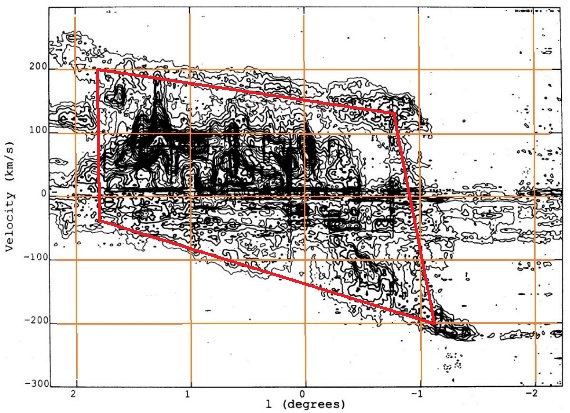 図2 の縮小版.12/sup>CO b=[-0.1,+0.1]の(l,v)図 | 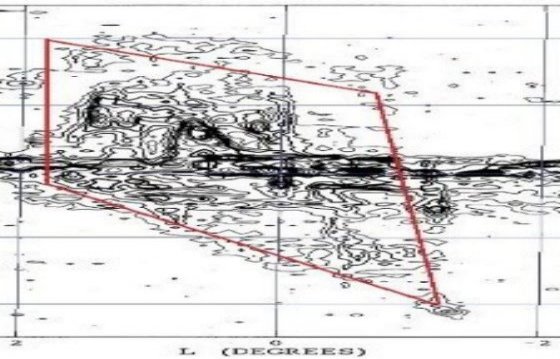 Bally et al 1988図4の縮小版.13CO b=[-0.6,+0.6]の(l,v)図 |
4.1.分子ガス尖がり軌道が平行四辺形 (l, v) 図を作った図2の平行四辺形が x1 軌道で作られたと言うのは魅力的な考え である。図2の右下部に見られる四辺形の縁の鋭さに注意せよ。これは平行 四辺形状を構成するガスが単一の軌道に効果的に埋め込まれていることを示唆 している。図1を見ると、複数の x1 軌道を重ね合わせると、鋭さ が失われることが判る。その上、もしも Bally, Stark, Wilson, Henkel 1988 の図4(13CO b=[-0.6,+0.6]の(l,v)図)のように平行四辺形の 右下部が付け加えられると、観測四辺形は驚くほどに垂直な右下辺を構成する こととなる。これは、この軌道が視線方向に沿って運動しながら加速を受けている 区分を有していることを示唆する。軌道には直線部分があるということだ。この ような軌道は、 x1 軌道のうちでも最後の少し手前の尖がり軌道 しかない。それより深い軌道 (x2 ?それともx1 最後の 尖がりにねじれが入った軌道?) になると、(l, v) = (-0.8, 100) 付近に広がった放射を生み出すはずだが、それは見られない。 ( 図1の右端の図を見ても、どうして。 x2 軌道が (l, v) = (-0.8, 100) ) を通るか分からない。 尖がり軌道の形は軸比にあまり依らない そこで、様々な軸比を持つポテンシャル中の尖がり軌道の形態を考えよう。 図3には軸比 q = 0.85, 0.90, 0.95 (軸比が b/a = 0.85 - 0.6 のバー)に 対する尖がり軌道が示されている。これらの直線部分は互いに 2.5° 範囲内 で平行である。(l, v) 図上の平行四辺形の垂直辺を観測するためには我々は 尖がり軌道をその直線軌道部分と同じ方向から見ている必要がある。こうして、 もし図2の平行四辺形に関するこの解釈を受け入れるなら、バーの主軸方向と 我々の視線方向とが成す角度を、バーの軸比に関係なく、数度の精度で決定 可能である。 x1 から x2 軌道へ x1 尖がり軌道から転がり落ちると、ガスは間もなく x2 軌道に落ち着く。図3の点線で3つのポテンシャルに対するこの軌道を示した。 Sgr A, B, C は (l, v) 図上でこれら x2 軌道の引き伸ばされた部分の 上に乗っている。その上、 Sgr B, C は (l, v) 線の上端と下端近くに位置する。 その付近はガスの滞在時間が長い。その理由はその付近が遠心点付近であり、かつ 天体が視線方向に運動していて重なるからである。図4は CS を図2の 12CO と同じスケールで示した。このラインは濃いガスを追跡するが、それが x2 軌道が作る対角線状の帯の中に納まっていることに注意せよ。 |
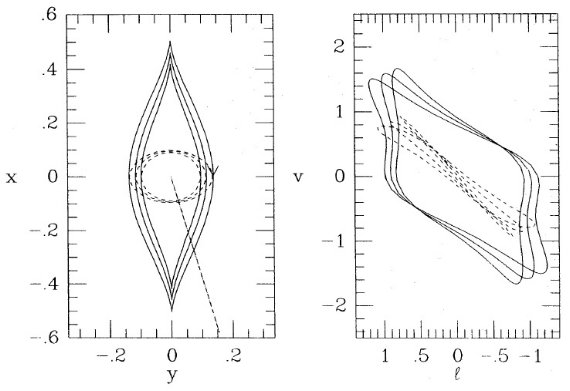 図3.実線=尖がり(cusped)軌道。点線=inscribe された軌道。ポテンシャルは 図1と同じだが、 軸比 q = 0.85(最外側)、0.9, 0.95 とした。q を変えると、 軌道の大きさが変わるが、その形はあまり変化しないことに注意。(l, v) 空間では 全ての尖がり(cusped)軌道は観測されるような平行四辺形を生み出す。右側の枠を 図2と較べよ。 細長さは軌道の形に影響小さい バーがより細長くなると、図3の x2 軌道はわずかに より楕円形的になる。しかしこの効果は目立たない程度である。このため、 x1 軌道から x2 軌道への切り替え付近の ガスからバーの細長さを求めることは難しい。 |
 図2縮小. 12CO マップ。 |
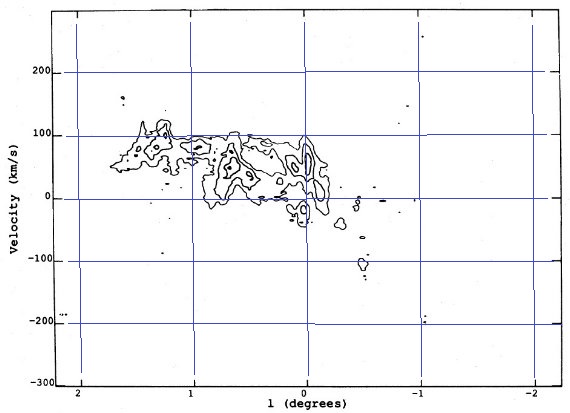 図4.CS b = [-0.1, +0.1]積分 (l, v) 図。 |
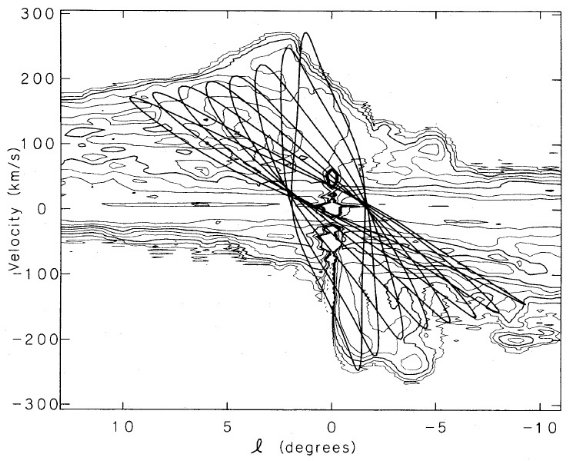 図5.HI b = [-0.5, +0.5] 積分 (l, v) 図(Burton, Liszt 178)。破線 = 0.4 K, 実線= 0.4, 0.8, 1.6, 3.2, 6.4, 12.8, 25.6, 50, 100 K. 内側1度は吸収が効いている。重ねて描いたのは、式 (2) 密度分布 で a = 1.2 kpc, α = 1.75, β = 3.5 の場合の軌道の l-v 軌跡である。共回転半径は rCR = 2.4 kpc とし、視線方向は バーの主軸に対し 16° 傾いている。銀河系中心に対する太陽の距離と 視線速度は Ro = 8.5 kpc, Vo = 14 km/s とした。速度スケールは、 ωrCR = 195 km/s, vC(Ro) = 214 km/s である。 CS と違い、HI は x1 軌道に存在 図2と Bally et al 1986 図4に現れる平行四辺形右下頂点の鋭さ は尖がり軌道のすぐ外側の x1 軌道には CS ガスがほとんどない ことを示す。図5には HI の (l, v) 図を示すが、図には平行四辺形らしき ものが見えない。l = 2° のピークから先は銀経の増加に伴い HI の上辺 輪郭は滑らかに低下していく。これは尖がり軌道外側の x1 軌道 に HI が詰まっていることを示す。分布外郭のピークは明らかに、尖がり軌道 付近での x1 軌道の伸長化の表れである。(図1と比較せよ) この上向きの反り返りは r ≤ 1 kpc での銀河系ポテンシャルに関するキー 情報を伝達している。 式(1)が合わない これまで我々は議論を式 (1) のような簡単な形に制限してきた。残念ながら 図5からこのような形は否定される。というのは、この形では閉軌道群の (l, v) 軌跡外郭が図5のようにはゆっくりとかつ着実に低下するようにでき ないからである。 根底にある問題は、平坦回転曲線では共回転半径 RCR と内側リンドブラッド 共鳴(ほぼ尖がり軌道の平均主軸半径)RILR の比 RCR /RILR が小さくなり過ぎることにある。この値が小さいと、 尖がり軌道が l ∼ 2° 付近の時、共回転による共鳴領域は l < 10 に達してしまい、図5に見られるような l = 10 で安定に HI を 載せて置けるような閉軌道を見出せなくなるのである。 回転曲線に合うポテンシャル RCR/RILR は外側に行くにつれ回転速度が大きくなる ようなポテンシャルに対して大きな値を取る。そこで、我々は次のような 密度分布を考えた: ρ(a) = ρ0(a/a0)-α a≤a0 (2) = ρ0(a/a0)-β a≥a0 ここに、a = sqrt[x2+(y2+z2)/q2) a0 と β は結果にあまり影響しないので取りあえず、 a0 = 1.2 kpc, β = 3.5 としておく。パターン速度 ω は RCR = 2.4 kpc となるように設定する。前の式(1)に出てきた 対数ポテンシャルは α = 2 に対応する。 q と ω を固定したまま で α を 2 以下に減少させると、ILR が内側に移ってくるので、 (l, v) 図の外郭はピークから緩やかに低下するようになる。q = 0.75、 α = 1.75 の時のよい合致例を図5に示す。太陽は銀河中心に対し 14 km/s で後退していると仮定した。他の q でも良く似た結果が得られる。 ただし、q を下げると (l, v) 面での曲率を小さくする効果がある。 図5の (l, v) 図では尖がり軌道の軌跡は角度 16°±2° の方向 から見た時のみ、図2の平行四辺形と同じ形と向きを持つ。 |
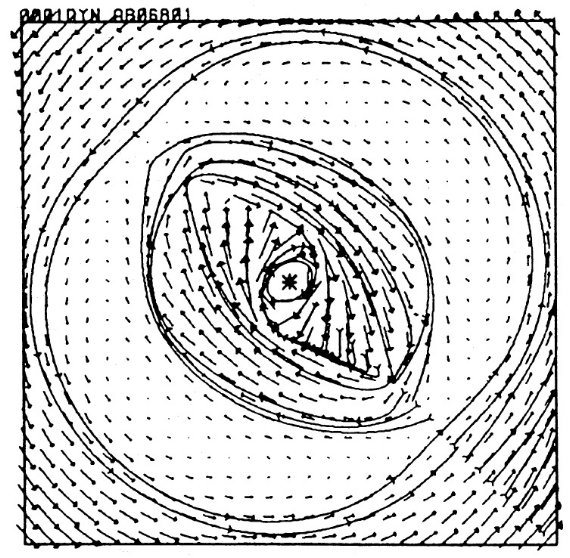 図6.回転バー中の準定常ガス流(Athanassoula 1988) の速度ベクトル。 中心付近で、尖がり軌道の付近で x1 から x2 軌道への 転換が見える。尖がり軌道の近心点ガスは x2 軌道遠心点ガスと 衝突し、 spray を生じる。これが尖がり軌道の内側を横断して尖がり軌道に 参加する。この結果、尖がり軌道にあったガスの速度が低下する。 平行四辺形の位置のずれ 我々が選んだパラメタ―では、図5の尖がり軌道は l = [-1.7, +2] に広 がっている。1.7 と 2 の差は視角効果である。図2の平行四辺形にも 同様の角度差が見られる。また、赤外測光による恒星密度のピークは l = 0 ° から数分角以内にある。したがって観測される平行四辺形の位置の ずれは実際に視角効果によるものらしい。 図の間の不一致 鋭い読者は、図の間の不一致に気付くだろう。図5の HI プロット上辺 は v = 270 km/s でピークに達している。一方、図2の平行四辺形は |v| = 220 km/s の外には出ない。平行四辺形は x1 の高速端にある 尖がり軌道の (l, v) 軌跡で、そこに HI がある、という我々の主張と 単純に合わない。 しぶきと速度低下 Athanassoula 1988 から採った図6がこの矛盾を解決し、同時になぜ尖がり 軌道の外には CO が存在しないかの説明も与える。この図は回転バー中の 準定常ガス流計算で得られた速度ベクトルを示す。ガスは x1 軌道 を出発し、ある個所で突然かなり低いエネルギーレベルの x2 軌道 へ移る。細かく言うと、尖がり軌道の近心点に近づいたガスは x2 軌道遠心点のガスと衝突するのである。この軌道遭遇により尖がり軌道に沿った ガス流は破壊されて、軌道内部の空間に飛び散る。このしぶきが反対側の軌道 まで到達すると、遠心点側から落ち込んできたガスとぶつかって混ざり合う。 大事なのは、遠心点から太陽の方向に近づいて来る軌道に沿った流れがこの しぶきによって減速されることである。というのは、混じり合うしぶきには 軌道と平行な運動量成分がほとんどないからである。こうして、ガス流は常に その軌道運動量をしぶきと分け合わなければならないので、定常軌道に は不足した速度で近心点に辿りつくこととなる。 ( 最初の衝突では残った軌道ガスの 運動には影響がなく、衝突により低エネルギー、低角運動量となった しぶきを介して、二次衝突・混入でエネルギーの低下が生じるという ことか?そこからは分子雲の軌道運動になるので x2 へ の移行は考えなくてよいのか?そこがはっきりしない。) (l, v) 図への影響 (l, v) 図上ではこの速度低下は平行四辺形軌跡の右下と左上の垂直辺を途 中で途切れさせるある。 効果を持つ。平行四辺形の斜辺は依然として真直ぐであるが傾きは少し 緩くなる。この傾いた部分は軌道ガスとしぶきの双方を含んでいる。 図2の平行四辺形を図3の x1 軌道と比べると、速度方向に squash されているが、これは最外側部の CO が純粋な閉軌道ではなく 以上のような力学的構造にあるからであろう。 CO 雲の形成 尖がっていない x1 軌道には CO ガスが存在しない。それは CO は上に述べた、速度低下に関与している衝撃波によって形成されるから である。一旦できた CO 雲は x2 軌道に移って、銀河系中心に 迎えるほど長く生き延びるようである。 |
|
重要なパラメタ―は、 (1)θincl = 視線方向 (2)α = 式2に出てくる密度勾配 (3)RCR = 共回転半径 である。θincl は 16° から数度以上はずれない。 | 図2の平行四辺形を尖がり軌道の軌跡と解釈するなら、α と RCR は互いに関連する。尖がり軌道の大きさを一定に保ったまま α を低下させると、RCR が大きくなる。CR の 下限値と RCR の上限値は Burton, Liszt 1978 の HI 観測 から決まる。彼らの観測によれば、 少なくとも R = 3.5 kpc には安定した ほぼ円軌道の周回運動が存在する。バー形状が強まる、すなわち q が小さく なると RCR = 2.4 kpc の周りの許容範囲が狭まる。残念なことに q がよく決まっていないのがモデルの不定性の原因となっている。 |
5.2.1.ガスの寄与薄いバーが四重極項の原因?銀河系中心円盤物質のこの力学モデルに使用されたのは円盤面上でのポテン シャルだけである。したがって、ポテンシャルの四重極項を与える物質の 面に垂直方向での分布には制約がない。ここで考えたパターンの高速回転から は厚みはあるにしろ、円盤状のバーが示唆され、回転楕円体的な3軸楕円体 は考えにくい。特に、太陽半径外側での HI 観測から Blitz, Spergel 1991a が導いた3軸楕円体成分は回転四重極の原因ではあり得ない。 ガスからの四重極成分への寄与 銀河系ポテンシャルの非軸対称に対する恒星からの貢献がどうであれ、四重 極成分に対するガスの寄与はかなり大きい。 Bally et al. 1988 によると、銀河中心半径 500 pc 以内のガスは 2 × 108 Mo である。この半径内のバルジ質量は 4 × 109 Mo であり、 その外側にはほぼ半径に比例して増加する。尖がり軌道の外側では HI ガスが 円盤の主要成分であり、Burton, Liszt 1978 によるとその総質量は 1 × 107 Mo である。これは力学的には無視できる量である。 このように内側 500 pc ではガスの質量比は 5 % である。その大部分は 銀河面近くの細長い軌道に沿って(図1)運動している。軌道の平均軸比は 0.4 である。ポテンシャルの四重極成分は単極成分と違い、「局所的な」物質 ( 分からない。) に影響される。したがってガスの四重極成分への寄与は質料比よりは大きい。 数値例 そこで、銀河面上 R = 500 pc と R = 1 kpc における重力の非動軸成分を 計算してみた。質量分布が式(2)に従い、軸比が 10 : 4 : 1 の場合と 同じ質量で同じ密度勾配を持ち軸比が 10 : 8.5 : 6 (これは Matsumoto et al 1982 の K 測光から得られた軸比である)の場合を比べた。 第2から第1へ形状を変化させると、動軸方向の力を 1.7 - 2 倍に増加させた。 しかし、接線方向力は平均して 17 倍になった。このように、ガス成分は 重力の接線成分の大きさを増加させるのである。 5.2.2.バルジの近赤外測光Matsumoto et al 1982 と DIRBE 画像最近 NASA が発表した DIRBE 観測結果によると、銀河系バルジは平たい ピーナッツ型に見える。画像はまた左側が大きく膨らんで見える。単純な 解釈は3軸バルジが銀経正の側が近い向きで斜めに横たわっているという ものである。Blitz, Spergel 1991b は Matsumoto et al 1982 の結果を 再解析してバルジの第4象限が第1象限より明るくて大きいと結論した。 近赤外と電波のバルジモデルは一致する 近赤外観測から得られたピーナッツバルジの配置は我々のモデルと合う。 バーを形成する円盤の n-体計算でもピーナッツが出来る。一般的にそれらは RC/1.2 まで広がる(Combes et al 1990). これは近赤外ピーナッツ は実際に高速回転していることを示す。 |
5.2.3.星の視線速度仮定ゆっくり回るポテンシャルでさえ、反対向きに廻る流れで平衡モデルを作る のは難しい。したがって、内部ストリームとパターン回転は同じ向きであり、 かつ剛体回転するバーの視線速度成分は観測される平均視線速度より小さいと 仮定しても安全である。 OH/IR 星 内側銀河の OH/IR 星 (Habing et al 1983, Winnberg et al 1985)は、 K-バンド測光と一致する平坦分布と密度勾配を持つに拘わらず 1 km/s/pc と いう極端に大きい回転速度を示す。上で得たパターン回転速度 ω = 81 km/s/kpc と比べると OH/IR 星のこの回転の大部分は内部ストリームである。 ( 傾いたバーに沿うストリームなら 手前が接近しても裏側は後退するだろう。OH/IR では両方が見えているか? チェックの必要がある。) したがって、OH/IR 星はパターン速度に拘束をかけない。 PN PNは銀河系中心に集中しており、その分散速度はバルジの典型値に等しい。 観測される平均視線速度は l にほぼ比例して増加する。それは、 l = -5 = 750 pc で -80 km/s, l = 5 で +50 km/s であり(Kinman, Feast, Lasker 1988) 回転速度 ω = 70 - 100 km/s/kpc は我々のモデルパターン速度と同じ くらいである。したがって、PN はバーの回転座標系の中ではかなりゆっくりした ストリームを持っている。b 6sim; 7° でのミラデータは l = 15 まで 存在(Menzies 1990) しやはり 80 km/s/kpc で回転している。これは観測された ミラと PN が熱い種族でその運動が回転に支配されていないなら自然である。 l ≤ 10 の星を地上から観測するためには星が銀河面から離れている必要が あり、観測されるこれらの星が「熱い」事は予想される事態である。 (観測されているのはバルジ種族なのか、 円盤種族なのか? ) 5.2.4.系外銀河小さいバーは見過ごされる?ここで議論しているバーは良く知られている棒銀河のバーに比べると著しく 小さい。例えば、NGC 4565 は銀河系の兄弟とも言われるが、 Gerhard, Vietri 1986 は NGC4565 と NGC 7814 の共回転半径を最小でも 15 kpc とした。我々の 中心核バーのように小さなバーは系外銀河においては分解能の問題で見過ごさ れているか(我々のバーは 20 Mpc では 40 arcsec)サチっているかであろう。 3軸不等バルジはしばしばバーと共存 系外銀河では3軸不等バルジはしばしばバーと共存している(Kormendy 1982) 3軸不等バルジと楕円、円盤との関係は不明である。 N-体計算では垂直運動 の共鳴励起の結果高速で回転するピーナッツバルジが形成される。これが 観測されたピーナツ形状のメカニズムかも知れない。 |
|
回転速度の減少は人工的な現象 HI 円盤と分子線平行四辺形の双方に対するモデルの基礎にあるのは、 少なくとも主軸先端距離の 1.2 kpc (=1.2/8.5*60=8°) までは、平均回転 速度が増加していくということである。以前、終端速度データから導かれていた 500 pc の先で起きる回転速度の劇的な減少は、円軌道回転という仮定から 生まれた人工的な現象である。回転三軸不等ポテンシャルでは軌道の形、そして それに伴う見かけの回転速度は共鳴点付近で急速に変化する。 新しい K バンド光度密度分布 改訂された回転速度は質量光度比の改定値に導く。これには、密度分布(2) 式を Matsumoto et al 1982 の近赤外観測にフィットする。図2、図5を合わせて ρ0 = ρ(a0) = 0.68 Mo pc-3 を 得る。 Matsumoto et al 1982 は表面輝度分布 jIR(a) ∝ a -1.8, ただし、 a = sqrt[x2+(y2+z2)2 /q2]楕円半径、を得た。 この勾配は z = 600 pc すなわち r = 800 pc で折れ曲がる。 ( どういう幾何学か? ) 我々はバルジの主軸は力学的に推測されているバーと同じ向きであり、かつここでは 簡単化のために軸の方向が視線と 16° でなく、完全に揃っている、つまり 0° であると考える。バルジは全体ポテンシャルの4重極に寄与するだけなので バルジの軸比は決めにくい。 ( よく分からない。平行四辺形を 生み出す4重極はバルジでなく、ガスだからか?バルジの4重極は何の 働きをするのか?その大きさはこの論文に出ている? ) |
しかし、ここでは a0 = 1.2 kpc と仮定する。すると、
Sandage,Becklin,Neugebauer 1982 の M 31 バルジ中心の較正値を用いて、
Matsumoto et al 1982 の放射率を K バンド光度密度分布に変えられる: jK(a) = 2.4 × 1034 (a/a0)-1.8 W kpc-3 /&mu:m = 1.3(a/a0)-1.8LoK pc-3 (3) このように、バルジの質量光度比は ΓK = 0.50 Mo /LoK である。もし M 31 と同じカラーであるとするなら、 ΓB = 4.1 Mo/LoB である。 ΓK ΓK は Rieke, Rieke 1988 が視線速度観測に、 速度等方性と内側中心方向まで R-1.8 が連続しているとの 仮定を組み合わせ、中心 10 pc に対して導いた値 2 よりかなり小さい。 バーポテンシャルでは、長軸方向、ここでは視線方向、に運動エネルギー が超過している。この非等方性は矛盾の一部を説明するが、真の中心部での L/M はここで扱った領域での値より本当に大きいかも知れない。 |
|
回転バーポテンシャル |l| ≤ 12° における HI, CO の (l, v) 図の特徴は、面上での r ≤ 1.2 kpc 銀河系ポテンシャルが軸比 0.75、密度変化 ρ ∝ R-1.75 のプロレート楕円体のものと仮定すると綺麗に説明できる。 その主軸は視線方向に対し 16° 傾いている。ポテンシャルは回転角速度 ω = 63 km/s/kpc = (1.6 &time; 107 yr)-1 で回っている。これは共回転距離 RCR = 2.4 kpc を与える。 このバーポテンシャルの特徴は以下の通りである: (1) CO (l, v) 図に現れる平行四辺形は尖がり軌道(Contopoulos の x1 軌道系列の最小のもの。)の軌跡が流体力学効果で少し変形を受けたもので 説明可能である。その外側の軌道では CO が不在であるのは、銀河系中心 CO は 強い衝撃波によって形成されるからと解釈される。この衝撃波が ILR 付近で x1 軌道からずっと低エネルギーの x2 へとガスを落とす のである。 (転位が ILR で起きるのは偶然? ) (2)l = 2 から L = 12 にかけて円運動速度 が増加する。 HI 終端速度が l = 2 から L = 12 にかけて、急激に低下する。この l 範囲 が意味するのは、共回転と ILR が十分にはなれていて、次に背後の円運動速度 は l = 2 から 12 へと増加していくということである。この円運動速度増加は 以前に円軌道の仮定から導かれた l = 2 から 12 に掛けての低下とは完全に 逆である。 平行四辺形が銀経 l 正方向にずれる CO (l, v) 図上の平行四辺形は銀経 l 正方向に 0.3 ずれる。これは視角効果 と解釈する。この結果はバーの近い側は正銀経側にあることを再確認する。 この他にいくつかの特徴がある: (1)共回転付近での HI の不在 R = [1.5, 3.5] kpc における HI の不在と CO 放射はバーによって自然に 説明される。というのは共回転の付近では、ガスが落ち着ける安定な準円軌道が 存在しないからである。我々が採用したパラメタ―と一定回転速度では、 RCR = 2.4 kpc であった。 |
(2)共回転から吹き飛ぶガス このパラメターで得られる外側リンドブラッド共鳴半径は、ROLR = (1+1/√2)RCR = 4.1 kpc である。バーが R < ROLR に収まっているため、OLR はそう強くないだろう。バーポテンシャル中のガス流 の研究によれば、 RCR 内側からほぼ ROLR までの領域 からガスが吹き飛んで ROLR 付近に溜まる。R = 3.5 kpc 分子リング をこの ROLR 付近のガスの集積で説明する。 (3)雲の位置 Sgr B, Sgr C は平行四辺形内部の x2 軌道の (l, v) 軌跡 上限と下限の近くで観測されている。そこは遠心点で速度が遅いのと、視線 方向に沿って動くのとで、集積して見える。雲がどの軌道族に属するかの情報 と近赤外減光データ(Glass, Catchpole, Whitelock 1987) から雲が銀下系中 心の手前側か後ろ側かが分かるなら、それらの真の銀河系中心距離がわかる。 (4)尖がり軌道の衝撃波 分子線の平行四辺形は殆ど単一の軌道に限られている。この尖がり軌道の 外ではガスのほとんどが HI である。これは分子ガスが尖がり軌道に伴う 衝撃波領域で形成され、 x2 軌道に転位し、そこで内部に観測 される分子雲を形成していることを示唆する。 (5)内部速度分散の大きな局所構造 Stark, Bania 1986 が調べた クランプ2のように内部分散速度が大きな局所構造は、 物質が x1 軌道の軌道直線部に分布しており、その向きが視線方向 と一致すると考えることで容易に理解できる。もし銀河系上方から眺めたら、 それらの物質はバーの長軸に沿ったダストレーンとして見えるだろう。その ような構造は棒銀河ではしばしば見られる。そのレーンに沿って大きな重力が 働くから、速度変化も大きくなるのは自然である。 (6)3 kpc 腕 予備的な計算だが、軌道共鳴の結果による構造がありそうで、それが 3 kpc 腕と関連する可能性がある。 |