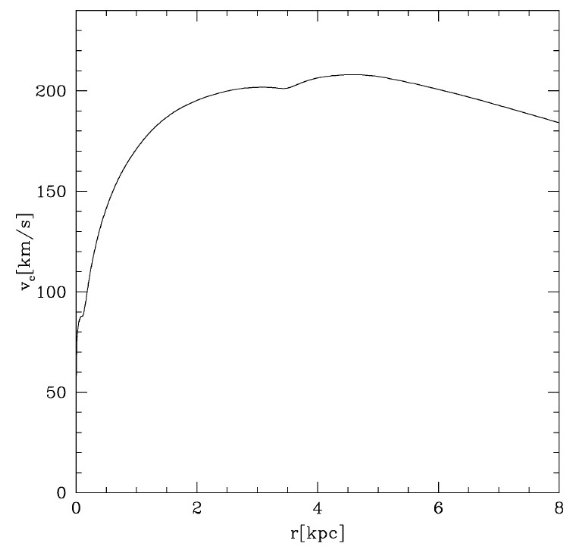
図1.軸角 20 の場合の標準モデル回転曲線。速度は第3章で述べるファクター ξ 倍されている。
2.3.計算
2.4.観測との比較
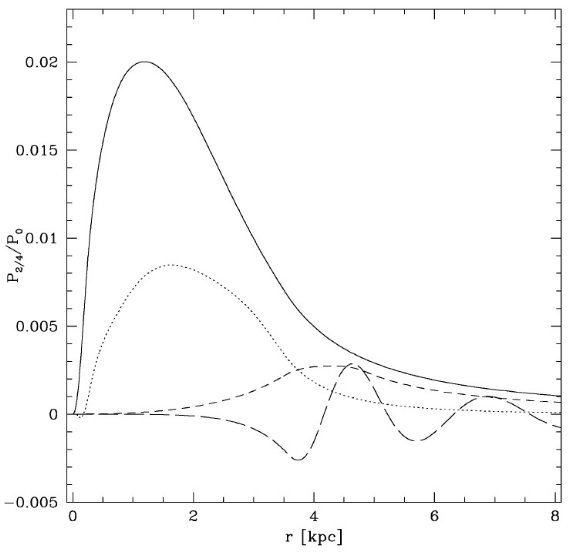
図2.標準ポテンシャルの4重極と8重極項。バー/バルジによる寄与(実線) と渦状腕による部分(点線)に分けた。多重項は単極項で規格化した。
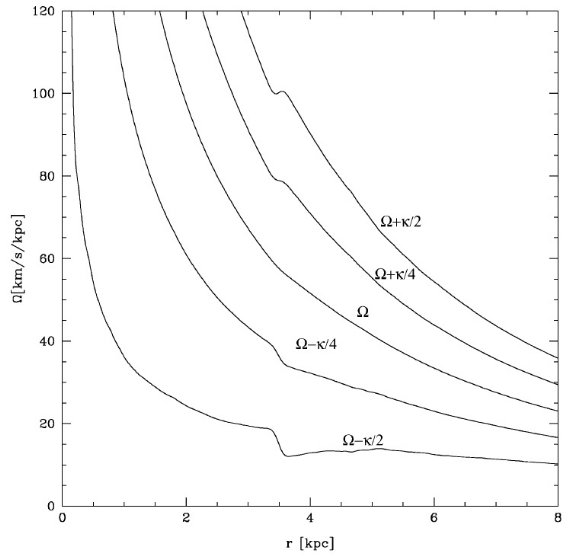
図3.標準質量モデルの共鳴ダイアグラム。
|
SPH計算による太陽円内ガス流の新しいモデルを提示する。重力ポテンシ
ャルはバルジと円盤の近赤外輝度分布から M/L 一定を仮定して決めた。
高密度の渦状腕を付けた重力場中のガス流は、渦状ポテンシャル無しの場合より
CO (l, v) 図に良く合う。さらに、4本腕重力ポテンシャルモデルの方が2本
腕より(l, v) 図は良く合う。 バーと渦状腕が別々の回転速度を持つモデルも考えた。最も大きい違いは、 後者ではガス渦状腕がバーの共回転領域を通過することである。そこでもガスは 腕に沿ったままであった。(l, v) 図ではこれはガスが排除された領域として現 れる。単一回転モデルではこの領域はガスで満たされる。なぜなら渦状腕は バー共回転領域では消滅するからである。 | 12CO データと比較した結果、我々は分離速度パターンの証拠を 見出した。最もデータに合うのは、バーのパターン速度 Ωp = 60±5 /Gyr, 共回転半径では 3.4±0.3 kpc である。腕のパターン 回転速度はそれほど良くは決まらないが、 大体 Ωsp = 20 /Gyr である。様々なパラメタ―で計算した結果、最もよいのは、 φbar = 20 - 25 であった。φbar = 20, Ωp = 60/Gyr, Ωsp = 20 Gyr は観測 (l, v) 図と極めて良い一致を示した。 |
|
シミュレーション Fux (1999) 星とガス SPH. ガス流は変動。ある時期には銀河系 CO 観測と合う。 Weiner, Sellwood 1999 解析的質量分布に対し流体計算。パターン速度と軸角に制限。 Englmaier, Gerhard (1999) Binney, Gerhard, Spergel(1997) の放射分布から M/L 一定の仮定で質量分布に直し、その重力ポテンシャル中の SPH ガス流を計算した。腕の接点方向を再現した。 パターン速度 これらガス流モデルで重要な量は非軸対称成分のパターン速度である。 Englmaier, Gerhard (1999) はバーのパターン速度 Ωp = 60 km/s/kpc を見出した。 Weiner, Sellwood 1999 は 42 km/s/kpc、 Fux (1999) は 50 km/s/kpc である。 Dehnen (2000) はヒッパルコスの速度分布を用いて太陽が OLR のすぐ外側に位置し、Ro = 8 kpc, Vo = 220 km/s の仮定で Ωp = 51 km/s/kpc を出した。 Debattista, Gerhard, Sevebster (2002) は Tremaine-Weinberg 法を内側円盤の年齢 8 Gyr OH/IR 星とセファイドの サンプルに適用してパターン速度 59±5±10(systematic)km/s/kpc を導いた。 |
様々なパターン速度 こうして、バーと渦状腕は異なる回転速度を有しているかも知れない。高速 回転バーの場合、共通のパターン速度は渦状腕が完全に共回転半径の外部にある ことを意味する。銀河の観測からはダストレーンが腕の内側にあることが判って いる。後退渦パターンではこれは腕が共回転半径の内側にあることを意味する。 この矛盾は腕の回転速度をバーより遅くすることで解決する。N体シミュレ イションの結果はバーと腕の回転速度が様々であることを示す。したがって、 多成分パターン速度モデルでガス流を解析することが自然である。 腕の数 4本腕か2本腕かで様々。 Drimmel (2000) は COBE/DIRBE K データは2本腕モデルが合い、しかし、 240 μm データは ダスト分布が4本モデルであることを支持するとした。 Drimmel, Spergel (2001) は 240 μm データから導いた彼らの放射モデルを K バンドデータと較べた。 彼らのベストモデルは星の分布は4本腕だが、内2本が強力と言うものであった。 その比は約 2.5 である。 この論文では ここでは、バーと腕がガスの運動にどう影響するかを調べる。質量分布は Bissantz, Gerhard 2002 の NIR 放射モデルに基づく。 |
| Bissantz, Gerhard 2002 は Spergel, Malhotra, Blitz 1995 の COBE/DIRBE データからダスト減光補正した近赤外放射モデルを使い、ノンパラメトリック なモデルフィットで中心 5 kpc のモデルを得た。その外側はパラメトリック モデルでフィットした。 | 銀河中心距離は Ro = 8 kpc を採用した。太陽は銀河面 14 pc 上方にある。 モデルに腕を加えるとCOBE データとのフィットが向上する。バルジ/バーは 長くなり、銀河面輝度分布の非対称性を再現する。モデルの軸角は 15 - 30 である。 |
 図1.軸角 20 の場合の標準モデル回転曲線。速度は第3章で述べるファクター ξ 倍されている。 2.3.計算2.4.観測との比較 |
 図2.標準ポテンシャルの4重極と8重極項。バー/バルジによる寄与(実線) と渦状腕による部分(点線)に分けた。多重項は単極項で規格化した。  図3.標準質量モデルの共鳴ダイアグラム。 |
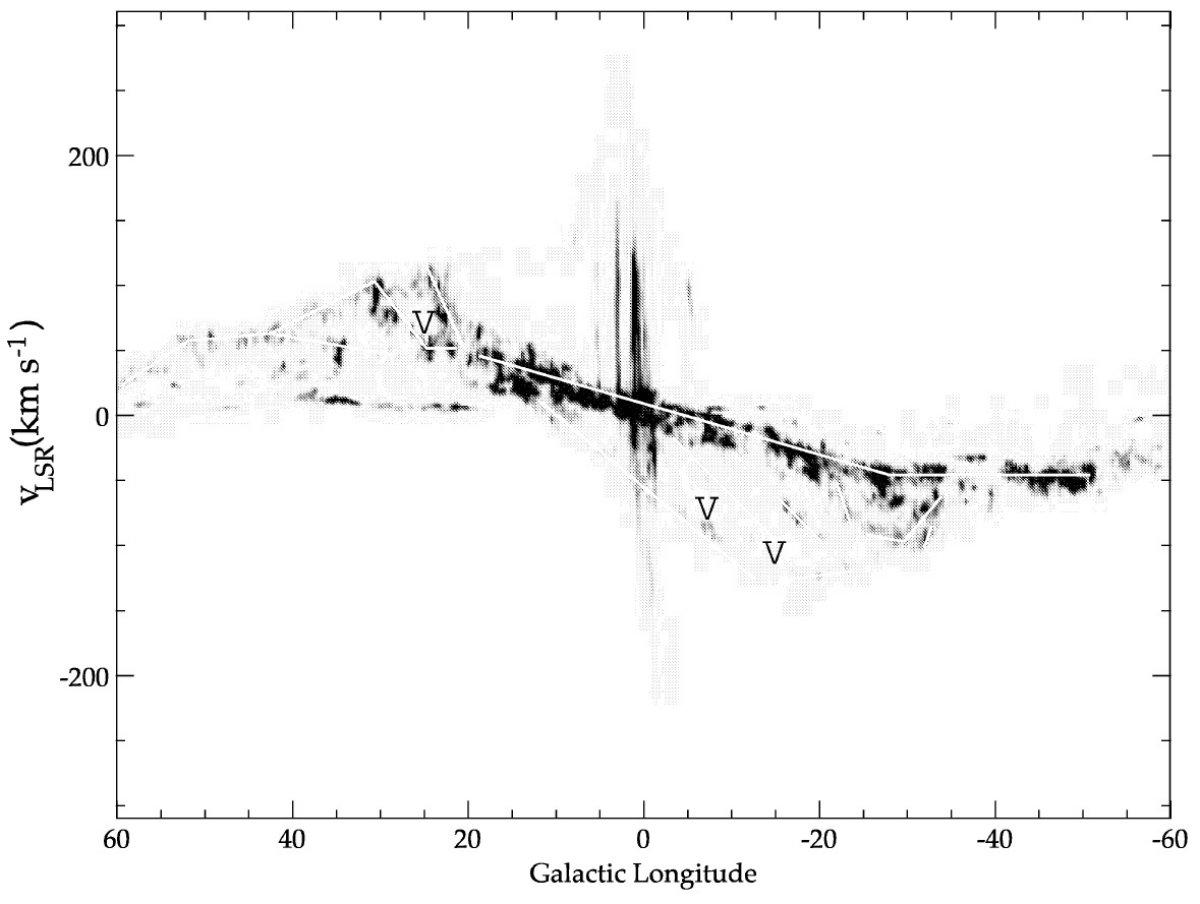
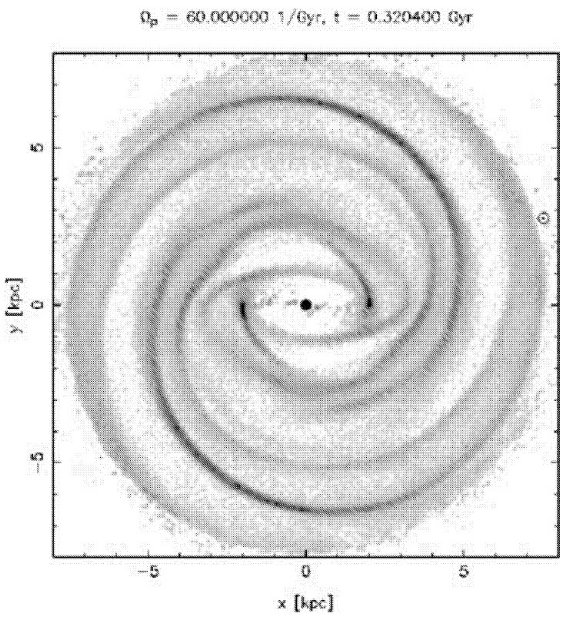 図5.t=0.32 Gyr での標準モデルガス分布。 |
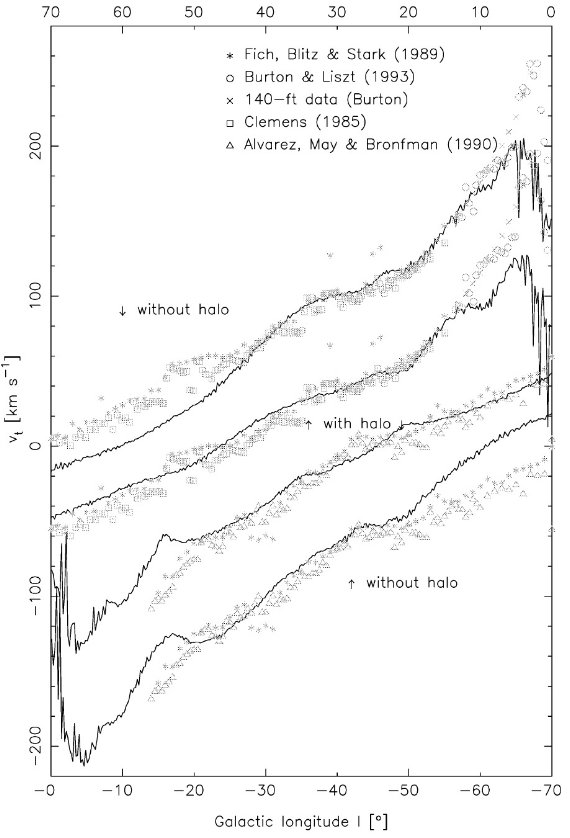 図6.標準モデルの終端速度曲線。進化時 0.32 Gyr.意味不明瞭 |
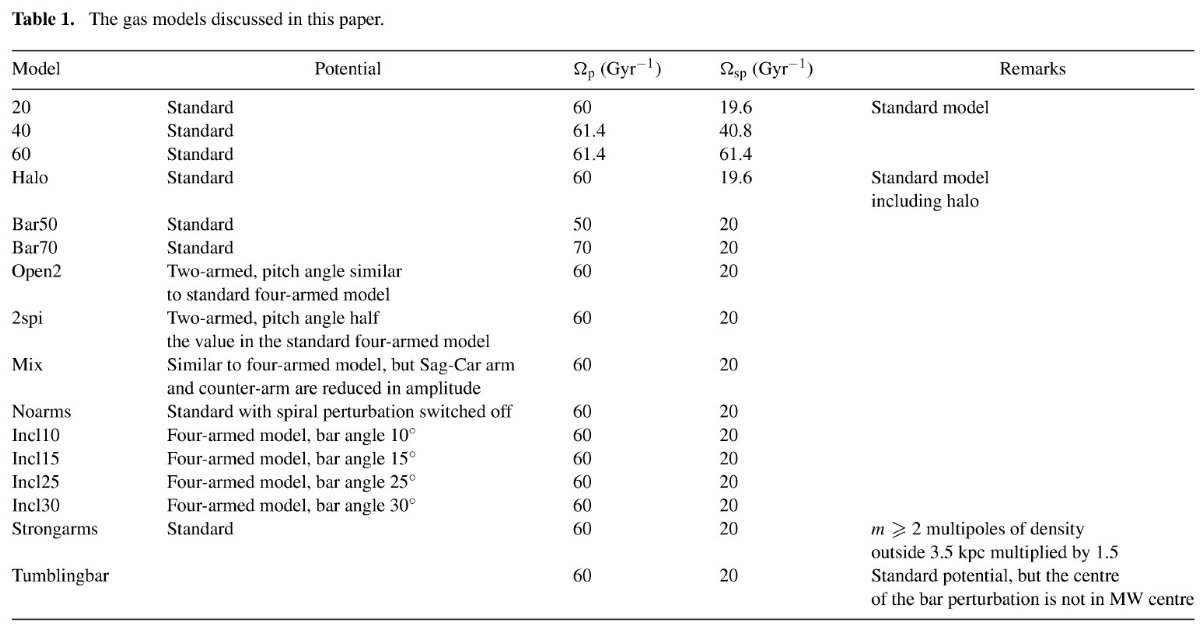
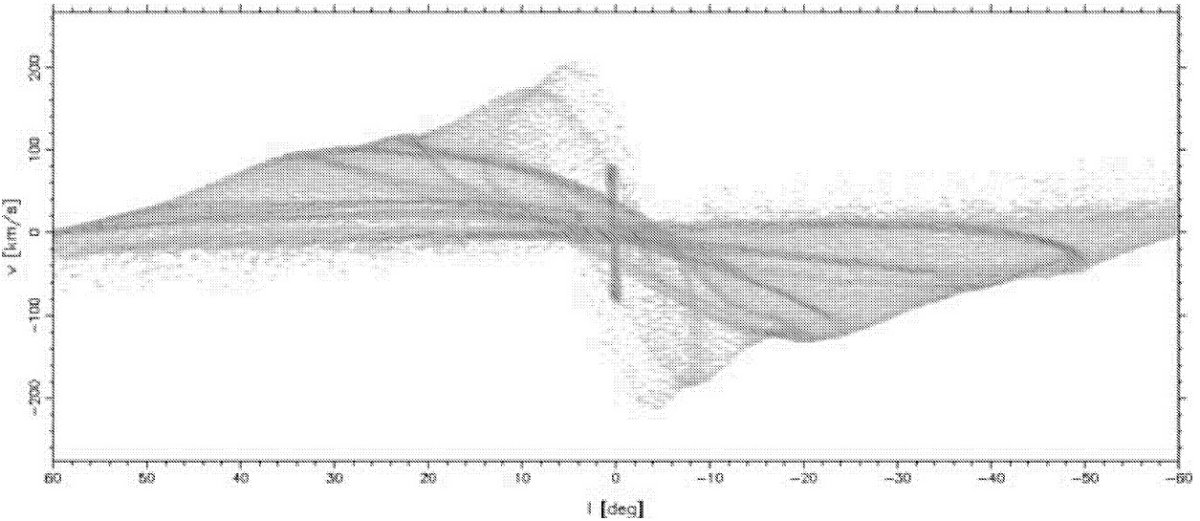
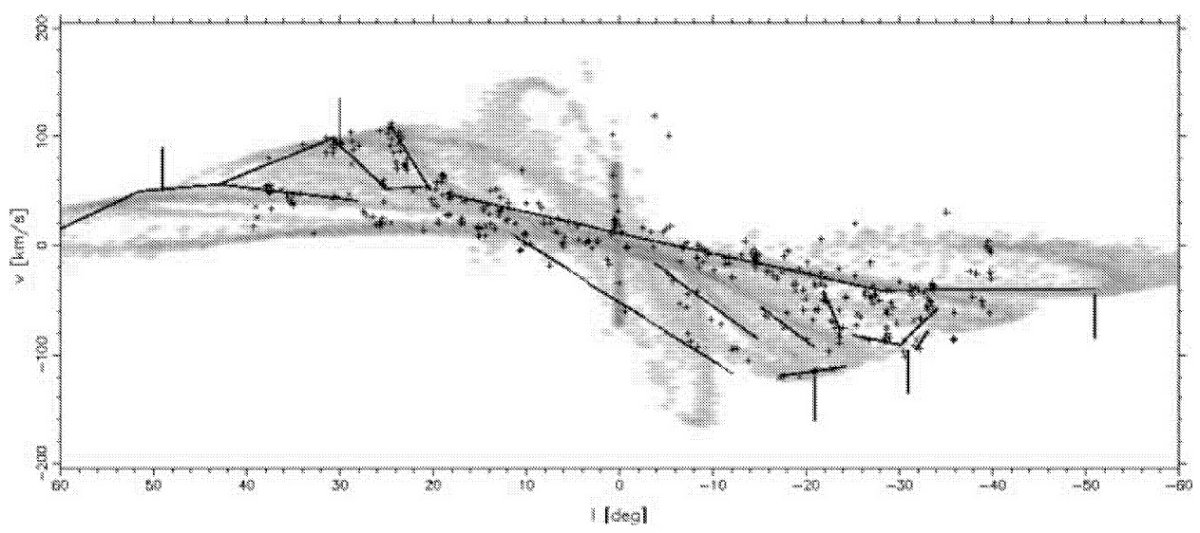
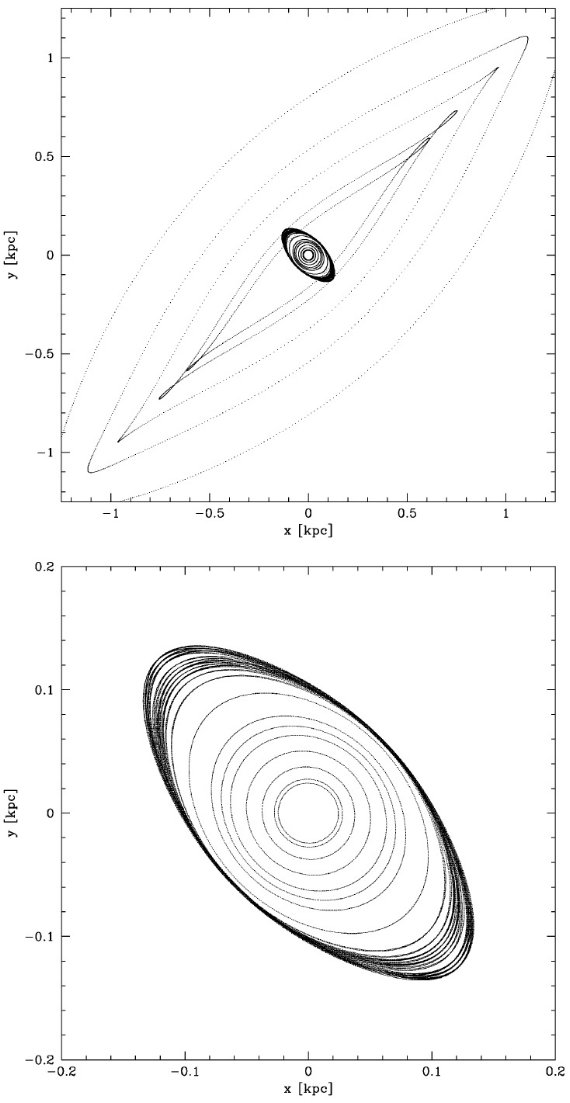 図10.バー領域内での x1 と x2 軌道の例。 軸角 φ = 20, 腕パターン速度 Ωsp = 20/Gyr, バルジパターン速度 Ωp = 60/Gyr を仮定。 外側 x2 軌道がバー主軸上で収束することに注意。 |
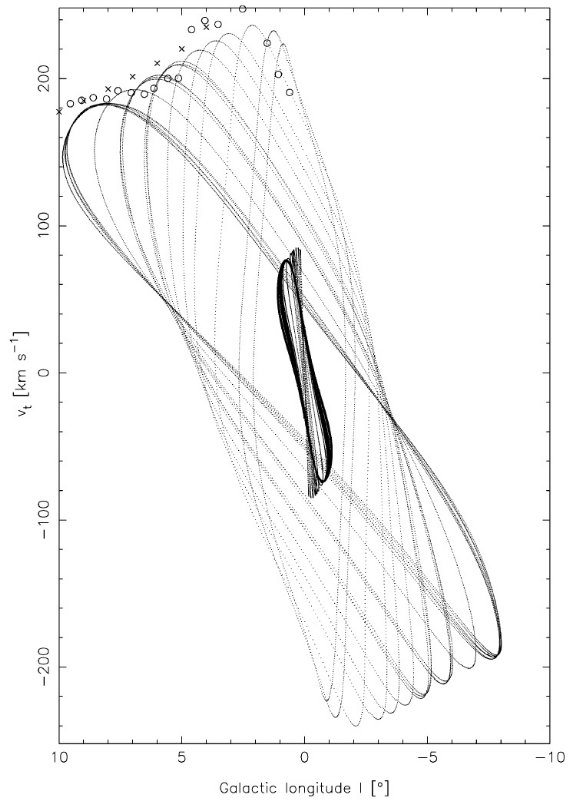 図11.図10の軌道を (l, v) 表示。 l = 2 のピーク速度は尖がり x1 軌道である。その内側に二つの自己交差軌道を示す。 外側 x1 軌道を観測終端速度と較べた。 x2 軌道は 85 km/s でピークに達する。 |
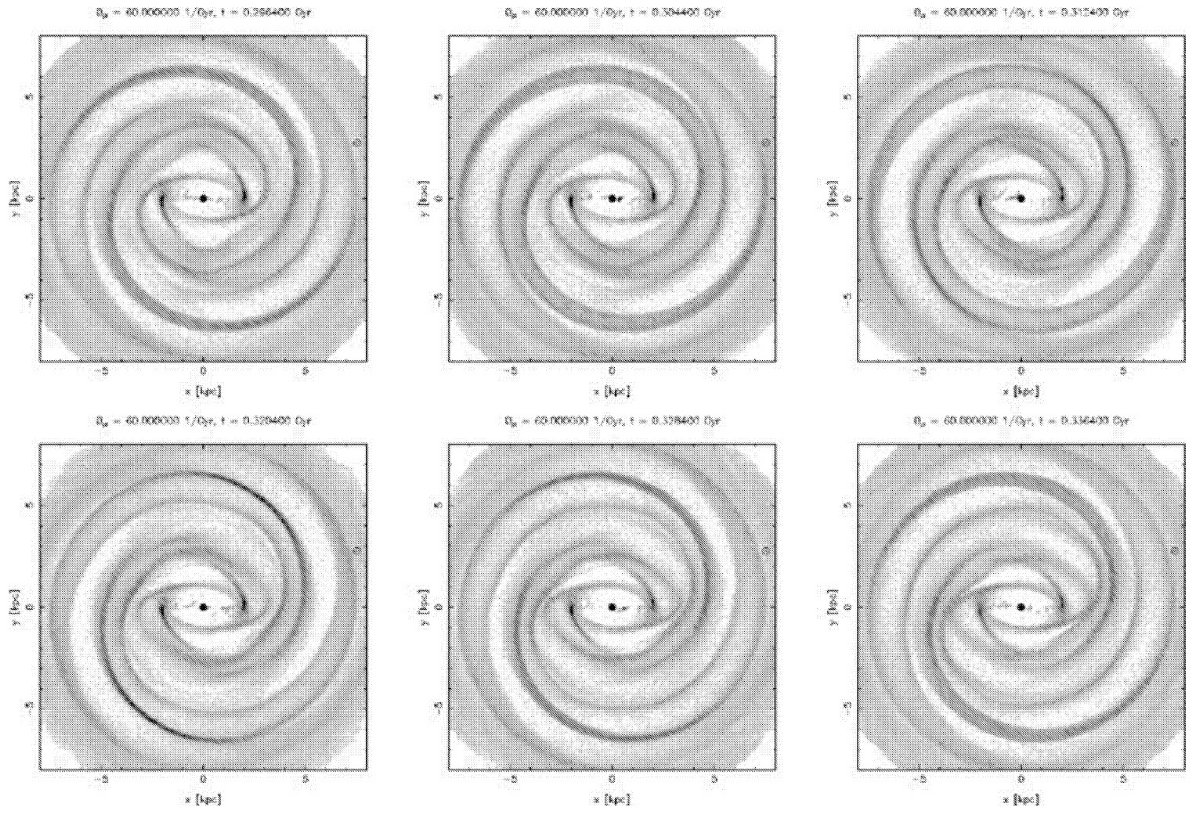
|
図12=速度分離モデルのガス密度 図12にはバーのパターン速度 Ωp = 60/Gyr, 腕のパターン速度 Ωsp = 20/Gyr の時のガス分布を示す。 バーの端から出る内側腕はバーと共に回転する。この内側腕は明らかにバーに より振り回されている。この内側腕はそれより遅い外側腕とバーの共回転半径 付近にある時間依存の遷移領域付近でつながっている。 内側腕の変動 図12(4), (5) ではバー端から直角に発生した腕がもう一方のバー端からの 腕と合流する。しかし、(1), (2) ではしない。 |
外側腕の振動 外側腕はバーとの異なる回転速度から予想されるような巻き込みを示さず、 バーに対して行ったり来たりの複雑な運動を示す。これは腕ポテンシャルとバーが ガス分布に対して同時に働くためである。 ( 何だか怪しげな気がする) |

|
|
|
