Gas Dynamics and Large-Scale Morphology of the Milky Way Galaxy

　アブストラクト

　１．イントロダクション　

　２．観測からの制限　

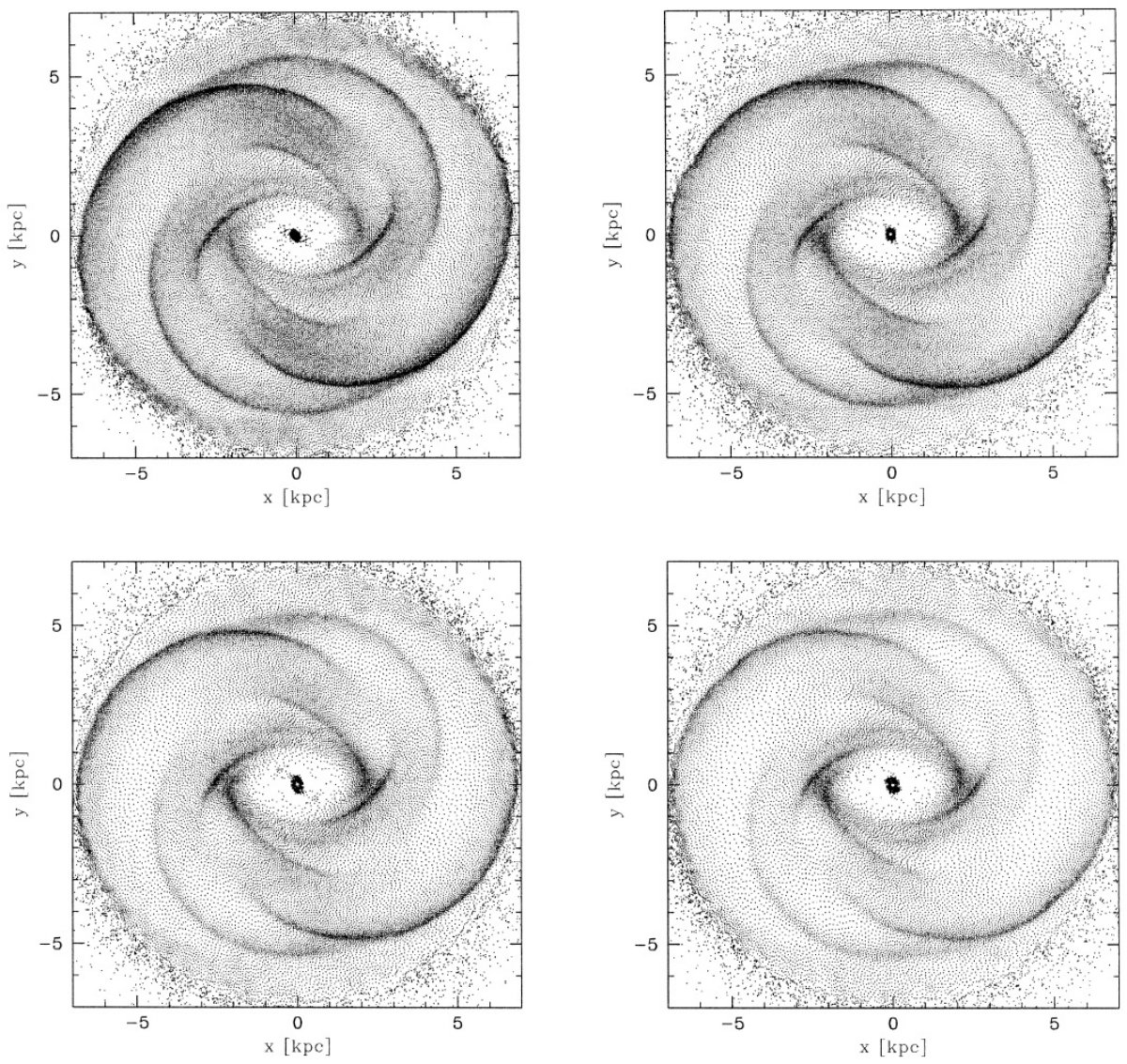
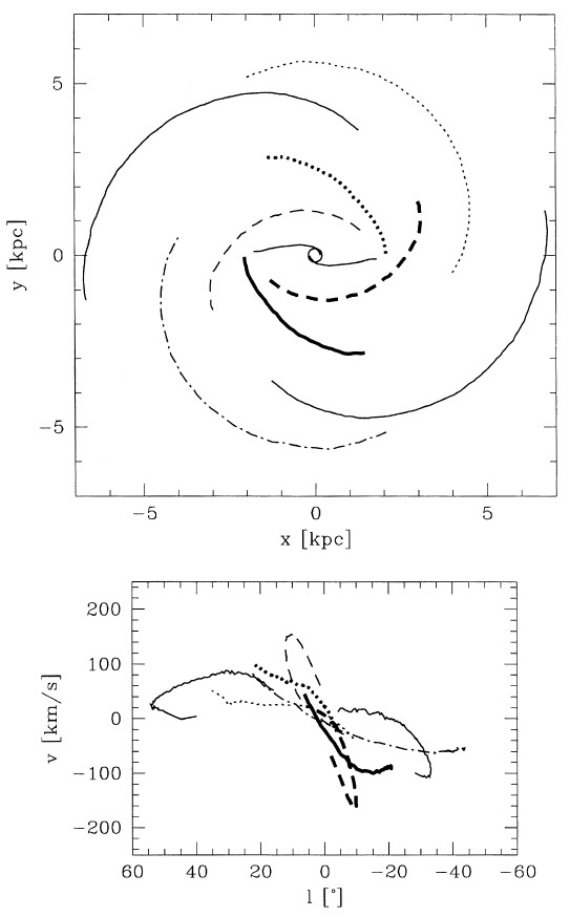
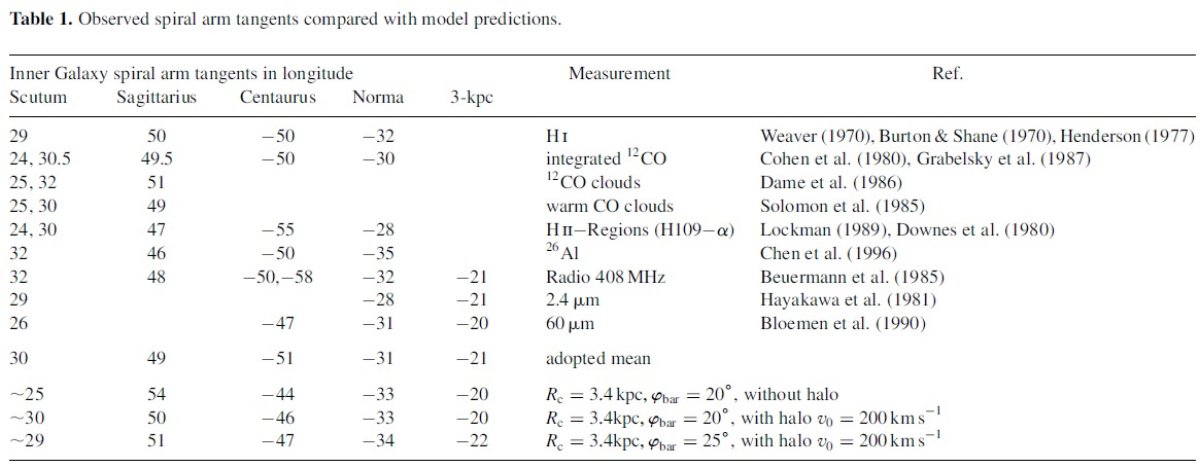
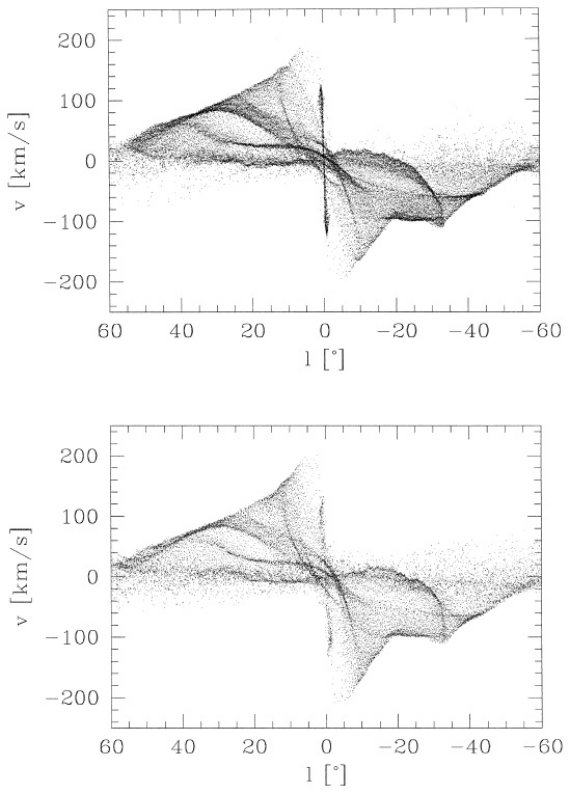
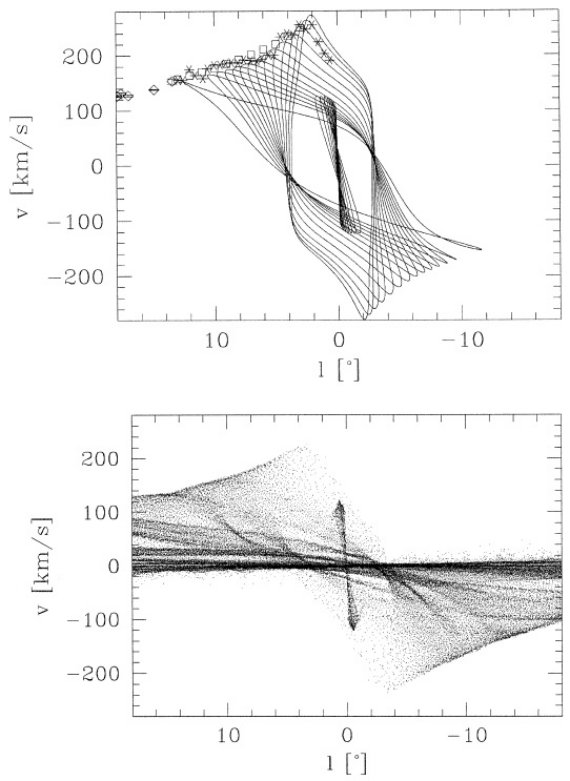
２．１．(l, v) 図　 　HI, CO　 　HI, CO の観測からのよいレビューは Burton 1992 を見よ。 　図１　 　図１には Dame et al による CO 観測の結果を (l, v) 図で示した。 vLSR への変換には |vsun| = 20 km/s, 方向 (l, b) = 56.2, 22.8) を仮定した。つまり太陽は銀河中心側で前方方向 に動いていて、usun=-10.3 km/s, vsun=15.3 km/s に相当する。 　２．２．(l, v) 図の解釈　 　円運動の特徴　 　ガスが円運動している時には以下の特徴がある： (i)　同じ円軌道上のガスの視線速度はゼロ。 (ii) vr = (ω-ωo)Ro sin l (iii) l = [-90, 90] では、終端速度 vr = [v(Ro sin l) - Vo]sin l (iv) (ii) 式の結果、l = [-45, 45] では円軌道は (l,v) 図で直線になる。 (v)　銀河系の縁は (l, v) 図の外縁を形作る。 　　　それは l = [0, 180] では v < 0, l = {-180, 0] では v > 0 である。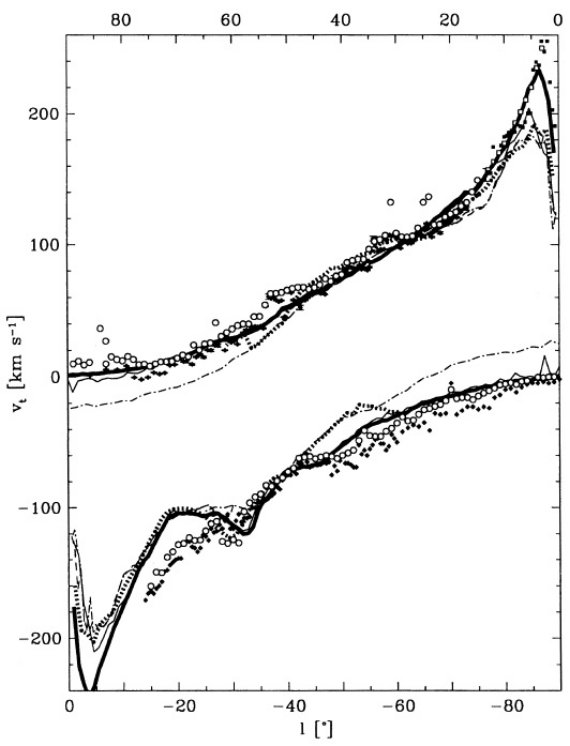 (vi)　終端速度から銀河系回転曲線を得ることが出来る。 　　　それには Ro と Vo, 及び太陽運動が必要。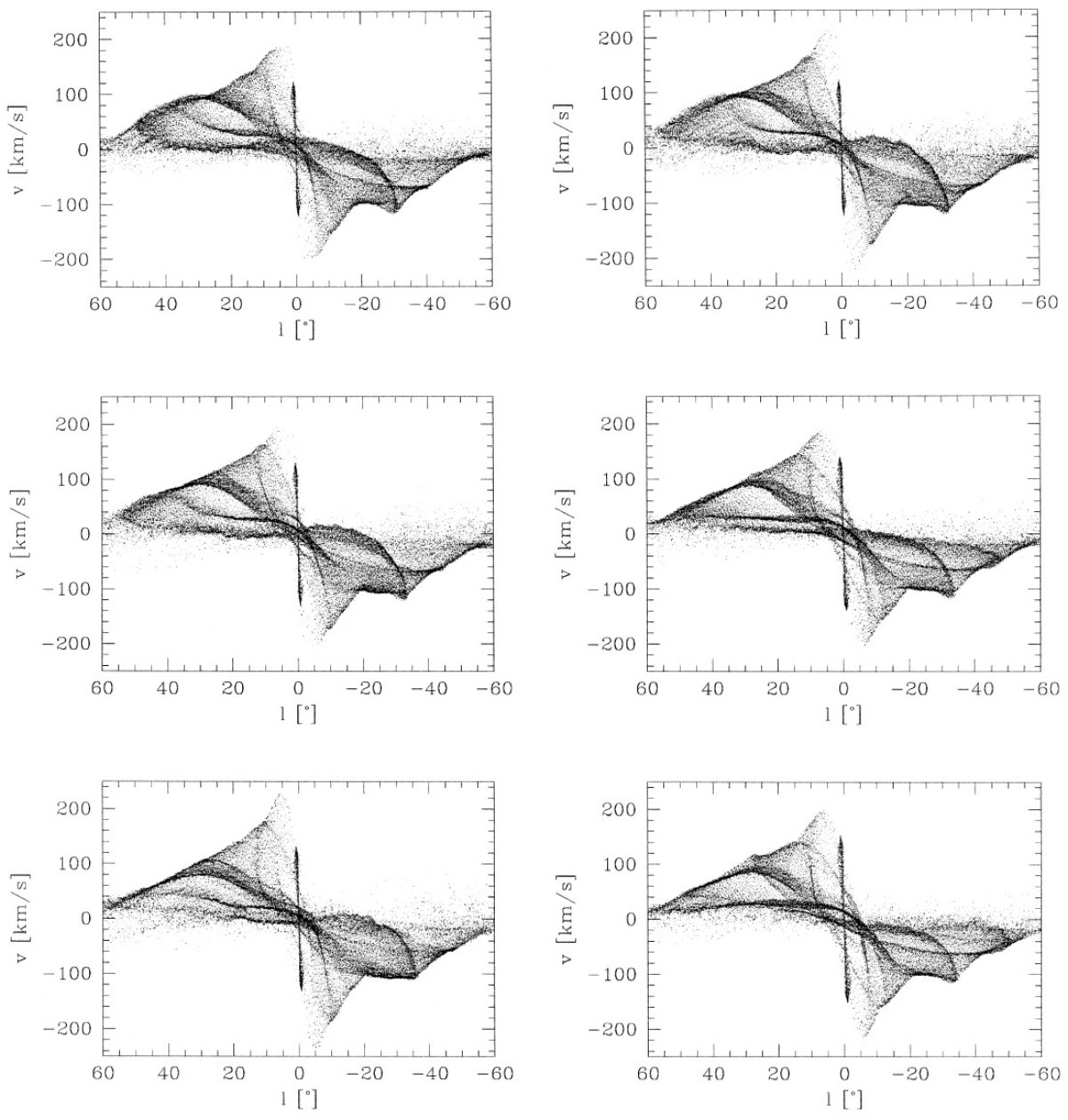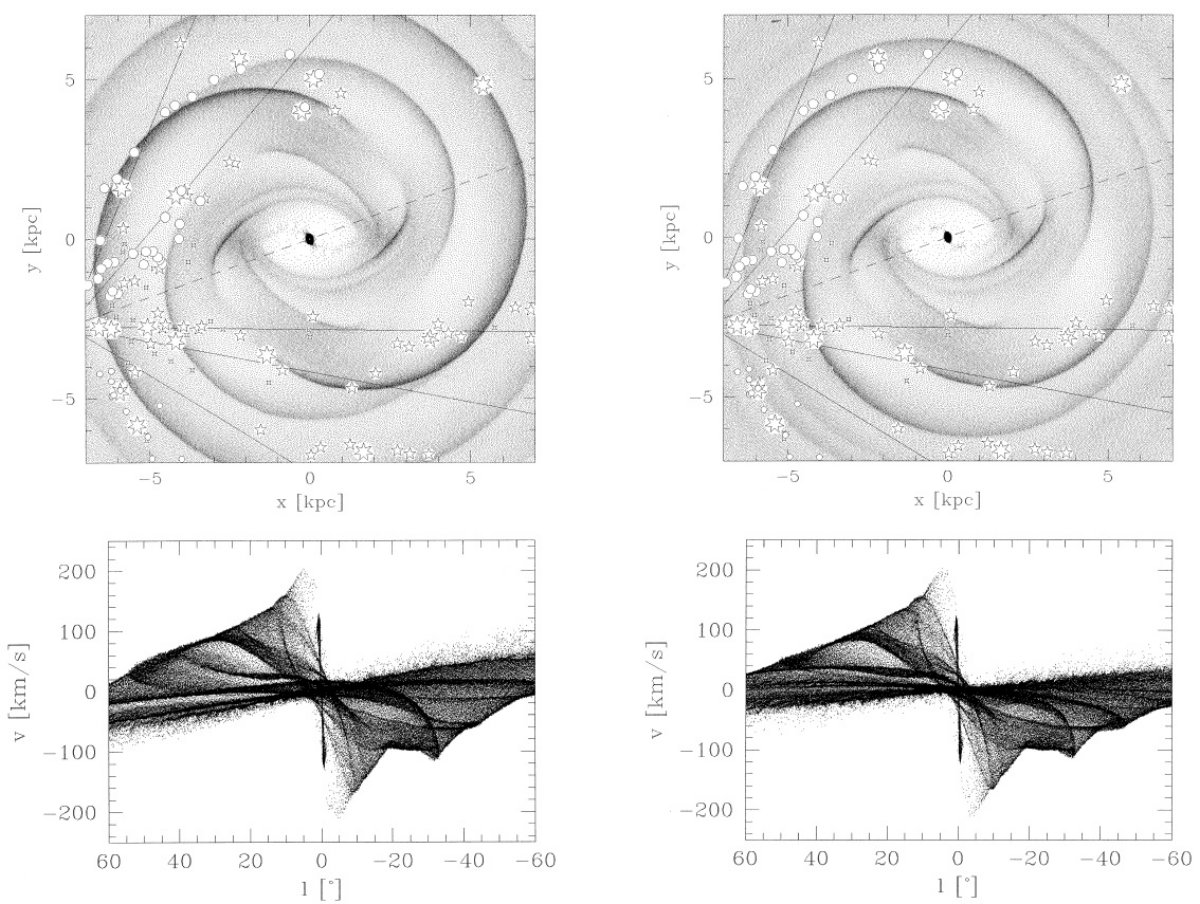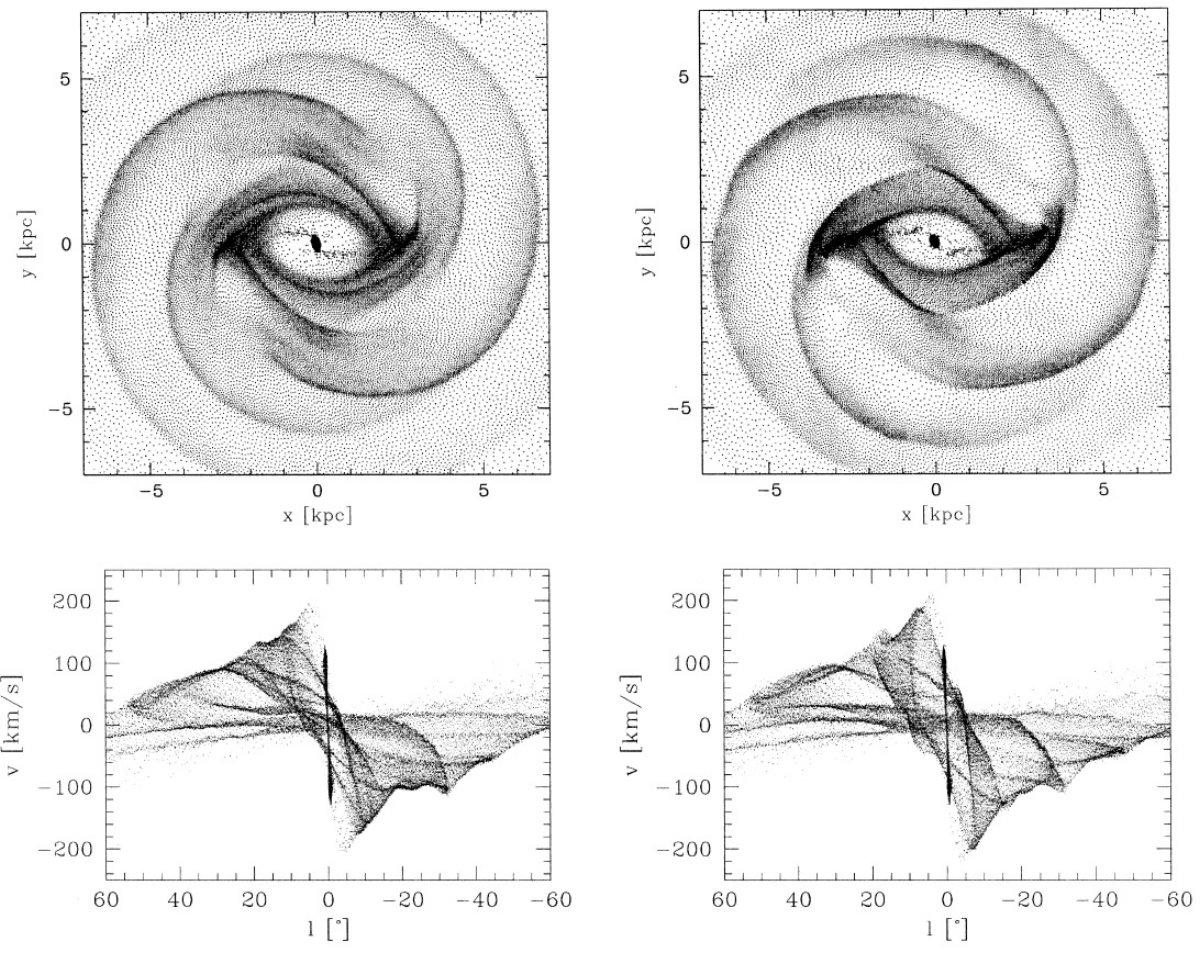 　禁止速度(forbidden velocity)　 　図１は l = [-90, 90] の (l, v) 図である。図には明らかに内側銀河に属していて （なぜ”明らか”なのかは不明）外側銀河のガスではないに拘わらず、視線速度のサイン が逆の構造が存在する。 これら禁止速度は大きいものでは vr ∼ 100 km/s にまで達し、内側銀河での非円周運動の直接の証拠を示している。この非 円周運動はまた、以前の研究では回転バーポテンシャルと結びつけて解釈された。 (Peters 1975, Mulder,Liem 1986, Binney et al 1991)

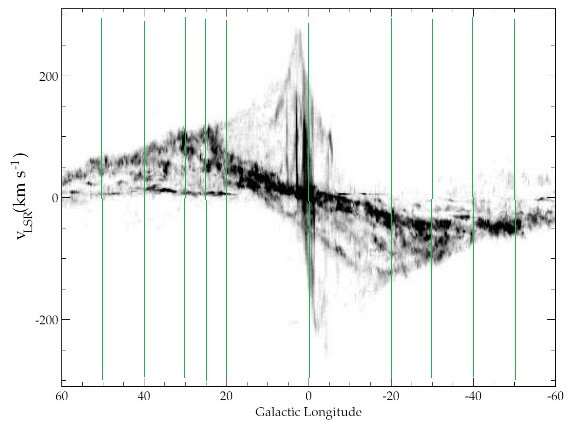
3 kpc 腕　 　それらの内で最も著しい構造は 3 kpc 腕である。図１では (l, v) = (10, 0) から (0, -50) を通過して (-22, -120) に達している。　 　|l| > 25 では円周運動　 　|l| > 25 では円周運動で観測 (l, v) 図を説明できる。12CO の 大部分は R = [4, 7] kpc の分子リングと呼ばれる領域(Dame 1993)から出ている。 これは実際にはおそらく二本のきつく巻いた渦状腕であろう。 図１．b = [-2, 2] 積分の CO (l, v) 図。(Dame et al in preparation)

２．４．渦状腕　 二つの渦状腕終端点　 　図２には HIIR, 分子雲の (l, v) がプロットされている。l ∼ ±50, l ∼ ±30 に二つの渦状腕終端点が見える。+30° 成分は 30 と 25 とに分かれる。 　渦状腕を追跡する天体　 　表１には渦状腕を追跡する天体を載せた。内側盾座終端点 l = 25 は時には 北の 3 kpc 腕とされる。 ( 意味不明 ) 　４本腕　 　主渦状腕の終端点はこのようにかなりはっきりと決められるが、両側の終端点を どうつなぐかはあまりはっきりしない。HIIR の分布から 　 (Georgelin,Georgelin 1976) は R = 4 kpc から太陽円を越すあたりまでの 4 本腕構造のスケッチを示した。 その後の研究で細部の修正はあるが、現在も基本的にはこの描像は支持されている。 　４本腕モデル　 　図２には我々の第４章で述べるモデルの (l, v) プロットを加えた。このモデル は COBE バーの端から発する２対の腕を持つ。モデルは観測から得られた腕の終端点 にかなり良く合っており、終端点同士がどうつながるかを教えてくれる。

図２．白丸＝ Georgelin,Georgelin 1976, Downes et al 1980, Caswell, Haynes 1987 による HIIR. 黒丸＝ Dame et al 1986, Bronfman et al 1989 の CO 分子雲。矢印＝分子雲の集積点。M < 10 5.5 Mo 以下の雲は落としてある。実線＝我々が標準とする φbar = 20 COBE バルジ/円盤モデルにおける渦状腕の 位置。

　３．モデル　

　３．１．質量分布モデル　

　３．２．重力ポテンシャル　

重力ポテンシャルを多重極展開　 　重力ポテンシャルを多重極展開して、 　　　Φ(r,φ) = Φ0(r) + Φ2(r,φ) cos(2φ) + Φ4(r,φ)cos(4φ) + ... ここに、Φ0は単極、Φ2 は４重極、 Φ4 は８重極項を表す。図３を見ると分かるように、より高次 の項は効かない。 　中心尖頭分布の扱い　 　R = 350 pc でポテンシャルを多重極分解からべき乗則に切り替える。もし 尖頭型ポテンシャルにしないと x2 軌道が含まれなくなることを 注意しておく。そうなると得られるガス流パターンは異なってしまう。 　回転曲線　 　図４にはこのポテンシャルから得られる回転曲線を示す。 (非軸対称ポテンシャルでの回転曲線？ ) 図３．標準 φ = 20° バーモデルにおける色々な多重極成分の寄与。

ダークハロー　 　もしバルジと円盤とが maximal, つまり M/L 比が終端速度に対応する最大の M/L 比を有しているなら、我々はダークハロー成分をバー領域に仮定する必要は ない。これは多分かなり本当であろう。と言うのは、この最大 M/L を仮定しても 円盤とバルジの質量は観測されたマイクロレンズ光学的深さを説明するには ファクター> 2 不足だからである。それで、ダークハローは考えない。 　一定回転速度　 　しかし、バーの共回転点より外側の渦状腕に対してはダークハローは幾分かの 影響を持つだろう。ただし、銀河面上のガス流のみを扱っているので、ダーク ハローの詳しい密度分布は不必要で、Φ0 成分をいじって遠方で 一定速度に接近するようにすれば良い。平坦回転曲線モデルは図４に示した。 このモデルで太陽円におけるダークハローの求心力への寄与は 23 % である。 図４．実線＝標準 φ = 20° バーモデルにおける回転曲線。 破線＝リングを抜いたモデル。点線＝外側回転速度一定モデル。スケール定数 ξ = 1.075 を仮定。

　３．３．有効重力ポテンシャル、軌道、共鳴図　

　３．４．流体モデル　

　３．５．モデルパラメタ―　

　４．結果　

　４．１．ガス流の形状　

図７．φbar = 20、共回転半径 Rc = 3.1 kpc の COBE バー におけるガス流。この図及びこの先の図では、バーの長軸は x-軸に沿っている。 太陽位置は x = -7.5, y = -2.7 kpc である。シミュレイションは N = 20,000 の SPH 粒子で行われた。初期円盤は R = 7 kpc まで広がっていた。ポテン シャルの多重極展開は l = 6, m = 4 まで行った。 ( l って何だ？) 　初期状態　 　最初のシミュレイションでは Ωp = 60 km/s/kpc、共回転 半径 Rc = 3.1 kpc のバーを仮定した。ガスモデルの初期状態は円軌道上で密度一定 として有効等温音速 cs = 10 km/s を仮定し、 N = 20,000 個 の SPH 計算を行った。 　４本腕構造の出現　 　図７にこの計算結果を示す。共回転の内側 R < Rc では二つの腕がバーの両端 付近に現れた。共回転の外側に４本の腕が見える。この４本腕構造は COBE バーポテンシャルで計算した全てに現れた。多くの研究者が４本腕は観測結果 に最も合う構造であると考えている。Vallee 1995 のレビュー参照。 　腕の出発点　 　４本腕の内２本は主軸の端、２本は短軸の端付近から発生する。他に ８重極項に対応して付加的な腕の対が起きる。この項を除去したモデルでは 二本の腕しか現れない。

図８．図７と同じだが、R > 3 kpc では m ≠ 0 の多重項をゼロにして ある。l = 0 項は変わらないので、遠回転曲線は変わらない。ガスモデルは 10 kpc まで広がり、 N = 20,000 個である。 バーのみによる構造形成　 　図８は、 3 kpc の先で m ne; 0 の密度多重項をゼロとした場合のシミュレ イションである。この変更は円回転曲線を変えない。ガス流の構造は全て 共回転の内側にあるバーにより導かれるが、それによる４重極モメントは小さい。 その結果、図には２本の弱い渦状腕が現れただけである。(l, v) 図には l = ±50° に接点が出来るが、このモデルでは l = ±30° 接点 は形成されない。精々僅かに密度超過が見られるだけである。こうして、 3 kpc 外側の構造を全て バーに負わせようとする図８のモデルは正しくない。 　短軸沿い 3 kpc のピークが重要　 　 3 kpc 外側でのポテンシャルの４重極、８重極の双方は短軸沿い 3 kpc にある 放射/密度ピークの効果が支配的である。図７と図８を比べ、我々は R = 3 - 8 kpc で観測に合う渦状腕を生み出すにはこのピークがかなり強くなければならないと 結論する。 　 　短軸上のこのピークは図７で二つの強い腕の頭付近に存在するガス粒子の 少しぼんやりした集積箇所に対応する。ガスの腕は通常星の腕に付随するの で、これは短軸上のピークは誤って脱投影された腕と解釈するのが妥当であろう。

　４．２．時間進化　（略）　

　４．３．(l, v) 図　

図１０．上：図９の t = 0.3 Gyr, 下：図９の t = 3 Gyr の (l, v) 図。 Ro = 8 kpc, Vo = 200 km/s 仮定。x2 軌道にある内側円盤、 終端速度曲線、渦状腕が明らかである。 　中心核円盤の (l, v) 図　 　図１０には図９の t = 0.3 Gyr と 3 Gyr の時の (l, v) 図を示す。 中心から鋭く立ち上がる明るい筋は x2 軌道にある濃いガス の円盤のものである。 　(l, v) 図上の腕　 　図１１の上図にはシミュレイション t = 0.3 Gyr での腕の位置、 尖頭軌道ショック（ダストレーン） ( 具体的にどれ？) 、 x2 軌道円盤が図示されている。この図で太陽は x = -7.5 kpc, y = -2.7 kpc にある。図１１下図は対応する（ｌ、ｖ）図である。 渦状腕が視線を２回横切るとそれは (l, v) 図上では弧の一部として見える。 図１１の細い実線の２本の外側渦状腕、内側銀河のバーに引き起こされた太いのと細い破線 でそれが起きている。 3 kpc 腕とその銀河中心向こう側の対応腕はバーで引き起こさ れている。

図１１．上：図９左上(t= 0.3 Gyr)から採った渦状腕のパターン。 下：(l, v) 図上での同じ腕の位置。 図から分かること　 (i)　l = [-60, 60] での腕の数と位置は近似的に正しい。 (ii)　モデルには　l = 0 で v ∼ -30 km/s を通過し、南の終端速度付近 で溶け込む腕が含まれている。定性的にこの腕は 3 kpc 腕と似ている。 ただ観測では v = -50 km/s を通過している。 (iii)　 x2 軌道円盤中ガス粒子の位置と速度は l > 0 の銀河 中心分子雲のそれに近い。 (iv)　終端速度曲線は l = 0 付近で大きな速度へ上がる。ただ、観測程大きく はならなかった。

　４．４．終端速度曲線　

図１２．銀河系終端速度曲線のモデル計算との比較。黒四角＝ HI (l = [0, 10]). Burton,Listz 1993. 白四角＝ HI (l = [0, 20]).Burton unpublished. 白丸＝ HI 終端速度 (Fich, Blitz, Stark 1989). 菱形（エラー付き）＝12CO 終端速度。Clemens 1985. 菱形（エラーなし）＝13CO Alvarez, May, Bronfman 1990. モデル終端速度は、一点鎖線＝低分解モデル。ハローなしで下降回転曲線、 点線＝高分解で範囲は狭い。細い実線＝低分解、一定回転速度。 太い実線＝高分解、一定回転速度（お薦め）全てのモデルで φbar = 20°, Rc = 3.4 kpc. 　スケール定数 ξ 　 　視線方向での最高速度を探して、モデル終端速度曲線を描いた。 Ro = 8 kpc, vLSR = 200 km/s を仮定した。これ等のモデル終端曲線を 観測終端曲線に眼視フィットして、スケール定数 ξ を決定した。質量 M とポテンシャルは ξ2 で変換される。 　ダークハロー　 　図１２にはいくつかのモデル終端速度曲線を観測と比較した。モデルの 空間分解能や計算範囲は互いに異なる。一点鎖線は R = 9 kpc まで広がった モデルで,　l ≥ 40 - 50 で観測と合わせるにはダークハローが必要で あることを示している。 　観測とモデルとのずれ　 　モデルと観測の間に大きな差が存在するのは次の２点である。 （１）l = 2 ピークとその先でモデルの v は小さい。モデル分解能？ （２）l = -20 付近での差が大きい。短軸 3 kpc の密度超過の不正確さ？ l = -20 の視線は、短軸 3 kpc 密度超過、3 kpc 腕の端、共回転外側腕の頭 の３つを同時に通過する。図１１を見よ。８重対称性による制限はこの領域に 対しては不正確な描像を与えるのかも知れない。

図１３．上： x1 軌道の上側外郭が内側終端速度曲線を 形成している。図には図１２と同じモデルポテンシャル中での x1 軌道を示す。各軌道は (l, v) 図上では平行四辺形状の形を描く。いちばん 内側の x1 軌道は尖頭軌道で l = 2 でピークに達する。その内側 ではガスは x2 軌道に切り替わる。その最高速度は 120 km/s で ある。比較のため、観測された北側終端速度を図に示す。 下：図１２の太い実線（高分解計算）に対応する(l, v) 図上での粒子分布。 この分解能でも尖頭軌道や内側の数個の x1 軌道は落ちている。 このプロットに現れる平行四辺形構造は内側上側で l = 3°, v = 220 km/s までしか達しない。一方、軌道では l = 2°, v = 270 km/s, 観測では l = 2°, v = 260 km/s である。 スケール定数　 　両側の終端速度曲線をフィットしてスケール定数として ξ = 1.12 を得る。 これは北側だけで以前に決めた 1.075 より少し大きい。 ( 改めて疑問だが、よく分からない量) 　 　図１２を見ると分かるが、 l = 2° のピーク終端速度は我々の低分解能 モデルでは再現されない。しかし、図１３からは、もし全ての軌道族が同じ スケール定数 ξ で拡大されれば観測は x1 軌道族の外郭 でうまく近似されることが分かる。 　テクニカルな話　 　計算上の色々な問題があるらしいが略。

　４．５．パターンスピードとバーの方向　

　４．６．渦状腕の接点　

　４．７．渦状腕重力ポテンシャル　

　５．結論