|
バルジと楕円円盤の形 内側銀河系の放射分布を、ダスト減光補正した COBE/DIRBE 表面輝度マップ からノンパラメトリックに、求めた。ベストフィットは太陽を銀河面の上方 14±4 pc に置いた時に得られた。得られた密度分布は細長い3次元 バルジが高度に非軸対称な円盤内に埋め込まれていることを示した。バルジの 軸比は 1 : 0.6 : 0.4 で長軸半径 2 kpc であった。長軸の近い側頂点は第1 象限にある。バルジを囲む楕円円盤は短軸 2 kpc, 長軸 3.5 kpc である。 |
パターン速度 どのモデルにも短軸方向 2.2 kpc の所に密度極小がある。それに続く、極大 は 3 kpc の所にあり、l = -22°, +17° の方向にある。この点は L4 に対応するのかもしれない。そう考えて、バルジバーの長さを 使うと、バーのパターンスピードとして Ωb = 60 - 70 km/s/kpc を得る。 数値実験 渦状腕を持つ銀河モデルを使った数値実験によると、COBE データから回復された 高度に非対称な円盤は、もし密度コントラスト > 3 ならば渦状構造を反映する はずである。これらの実験はバルジの方向角が 20° 付近であることを示唆している。 |
|
2次元の投影輝度分布からの復元 銀河中心部の構造が軸対称でない観測的証拠が集まている。 そのような場合でも、3面対称性を 仮定すれば、観測で得られる2次元の投影輝度分布から放射密度の3次元分布 の復元が可能であることを Binney, Gerhard 1996 が示した。 COBE/DIRBE は NIR, FIR の全天輝度分布を求めた。しかし、 NIR データには 減光補正が必要である。 減光観測 Arendt et al. 1994 はバルジの固有 J-K カラーが一定で、それが前面のダスト膜で赤化を 受けたと仮定して減光マップを求めた。Spergel, Malhotra, Blitz 199? は 240 μm 観測を使えばもっと信頼度の高い減光が得られることを示した。 この放射はダストの熱輻射であり、さらに幾ばくかの仮定を設けると、ダスト の空間分布を求められる。彼らが決めたダスト分布はその上、非軸対称で ダスト温度の勾配まで含んでいる。 ( 腕のような非対称性構造の影響が 強いと思われるが本当に大丈夫か? Spergel, Malhotra, Blitz 199? は論文になっていない。) その信頼性は、遠赤外データから出した、バルジ J-K 赤化マップが近赤外データ から固有カラー一定の仮定の下で出したものと一致することで実証された。 このように、我々の減光モデルは Arendt et al. 1994 のより優秀である。 |
放射と減光の混在 減光ダストが前面に膜状分布と仮定したので、 Arendt et al. 1994 は変光補正をしたバルジの輝度分布を得ることが出来た。しかし、 Spergel, Malhotra, Blitz 199? のモデルでは、放射と減光の場所が分離して いない。このため放射モデルによって減光の効きが違う。しかし軸対称の仮定 を置けば、かなり尤もらしい減光値が得られる。 (バルジ方向では放射と減光の分離は かなりよい近似ではないのか? ) 今回の独自な点 Dwek et al 1995 は Arendt et al 1994 の減光補正輝度分布を用いて バルジの放射密度のパラメタ―化モデルを作った。我々の解析は彼らと以下の点で 異なる: (i) Spergel, Malhotra, Blitz 199? の3次元減光分布を使用。 (ii) バルジの放射密度を Binney, Gerhard 1996 の方法で求めた。 3.5(L バンド), 4.9 μm(M バンド) 本論文では、減光の小さな 3.5(L バンド), 4.9 μm(M バンド)データ に対する解析を示す。 Ro = 8 kpc を仮定した。 |
|
デコボコな結果 Binney, Gerhard 1996 はリチャードソン・ルーシーアルゴリズムにより表面測光データを脱投影する 方法を述べた。論文中で行った数値実験では細かい波打ちは星数密度のポアソン 揺らぎが原因と仮定した。我々のデータは 1.5° 分解能で中心付近ではかなり 滑らかと期待された。しかし、Spergel, Malhotra, Blitz 199? のモデルで減光補正 した結果にわれわれの R-L 法を適用した結果は、中心領域データは予想より デコボコしていた。Kent, Dame, Fazio 1991 が述べたように減光の細かい上下が 近赤外測光に影響しているようだ。その結果、 R-L 法を直接適用すると不適切 なほどにノイジーな3次元放射密度分布が出てくる。 不満な状況の手当てに二つの処方箋を考えた。 第1の処方箋:ルーシーの改善案 ルーシー(1994) は R-L 法を次のように修正した。それは "prior" = 「特等」 放射密度というものを考える。逐次近似の各段階で、得られた近似モデルの 「特等」に対するエントロピーを計算する。ルーシーは最終モデルにおいて 尤度とエントロピーの一次結合が最大になるようにした。エントロピーの重み を α とする。 α が非常に大きいと回復された分布は「特等」に なる。α = 0 だと元々の R - L 法に戻る。色々な α で試したが、 残念ながら有望な結果は得られなかった。 |
第2の処方箋:Duhen の処方 そこで Duhen 1995 に従った平滑化を考えた。 (1)グリッドの定義 バルジの軸に平行な 30 × 30 × 20 × の直交グリッドを作る。 これは 0 ≤ x, y ≤ 5 kpc, 0 ≤ z ≤ 1.4 kpc に相当する。銀河系に 3組の面対称性を仮定するので、実際には |x|, |y| ≤ 5 kpc, |z| ≤ 1.4 kpc である。 ( この先の手続きが全然分からない。) |

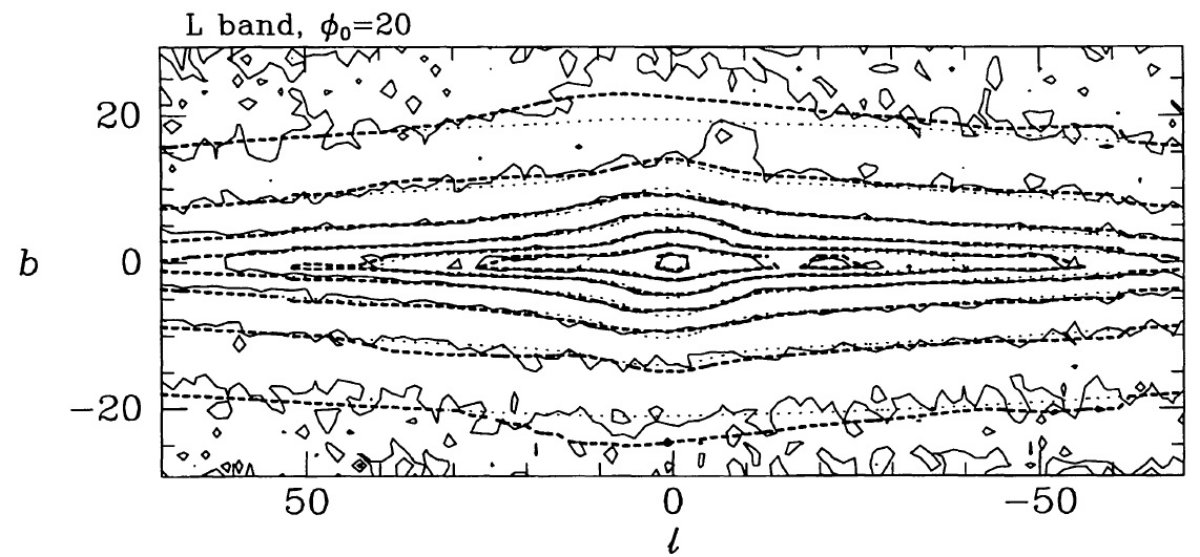
3.1.表面輝度分布スタートモデル図1は φ = 20° を仮定して L バンドデータを脱投影した結果である。 実線=観測輝度に減光補正を施したもの。点線=スタート解析解は二つの 指数関数円盤を重ねたものである: 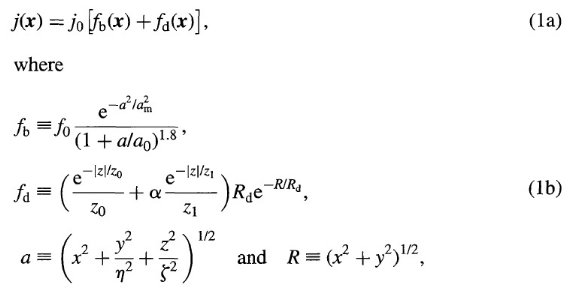 解析解とデータのズレ 解析解は既にデータをよく表現しているが、系統的な差異が明らかに存在する。 例えば、 l = 10° では点線の解析解は実線の内側に入り込んでいる。 (何を指しているか、不明 ) また、面近くで点線は実線より細長くない。 リチャードソン・ルーシー解はよい 図1の破線はリチャードソン・ルーシー逐次近似を5回繰り返したモデルである。 解はほぼ完全にフィットしていると言える。 |l| ≥ 45°, |b| ≥ 20° で系統的なずれが見えるが、これは「ボックス」の外側なのでやむを得ない。この 先では |l| ≥ 30°, |b| ≥ 15° に話を集中する。 |
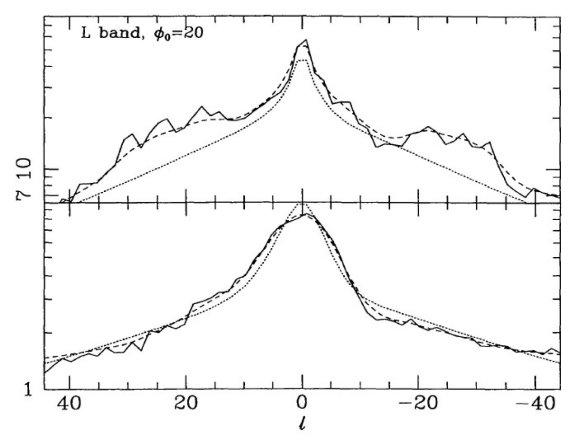 図2.表面輝度 I (l). 上: |b| ≤ 1.5° の平均 I. 下:3° ≤ |b| ≤ 4.5°. 実線=データ。破線=モデル。点線=初期値。 再現度は良い 図2には逐次近似で残差がどう改善されていったかを示す。上図を見ると、 逐次近似により、Kent et al 1991 が提唱したような、強い非指数 関数的円盤の導入で、低銀緯円盤部分の誤差が改善されたことが判る。 高銀緯部では、修正は小さいが |l| ≤ 10° の非対称性をモデル化 することに成功している。実際この図は平滑モデルが可能な限り上手くデータを 再現していることを示している。 |
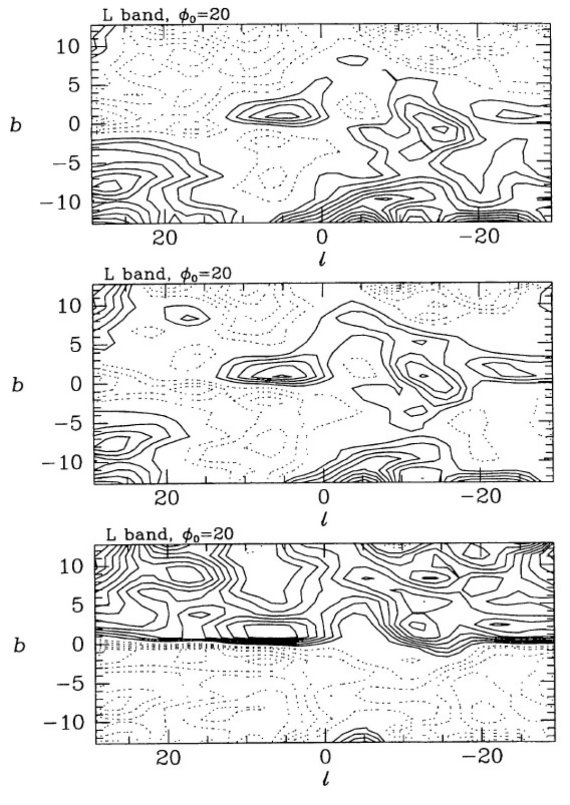 図3.仮定した3か所の太陽位置に対するフィットの残差=モデルーデータ。 上: 面の上 28 pc. 中: 面の上 14 pc。下:面上。φ0 = 20° を仮定。等高線間隔= 0.03 等。 Press et al. の SMOOFT ルーチン を用いて l で 7.5°, b で 3° の平滑化を施した。中央パネルは図1と 図2に対するものとなっている。実線=モデルの方が明るいことを意味する。 太陽高度 = 14 pc 図1と図2は太陽・中心線が主平面の 0.1° 上にあることを仮定して得た。 図3には、仮定した3か所の太陽位置、面の上 28 pc、 面の上 14 pc、面上、 に対するフィットの残差=モデルーデータを示す。面上モデル(下図)では b > 0 で正の残差が生じているのに対し、 29 pc モデル(上図)では再残差が b < 0 で起きている。14pc モデル(中)のバランスが最も良いことからこれが太陽位置を 反映していると考える。 |
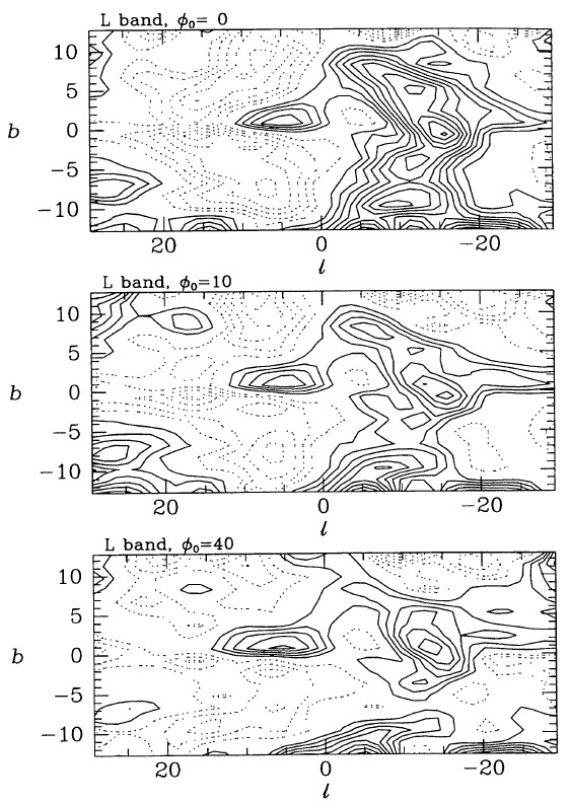 図4.太陽が面上 14 pc にある場合にバーの向き φ0 の変化 による残差=モデルーデータの違い。上: φ0 = 0°. 中: φ0 = 10°. 下: φ0 = 40°. φ0 の推定 図4では太陽が面上 14 pc にある場合に、バーの向き φ0 の変化 による残差=モデルーデータの違いを示す。上図は φ0 = 0°、 中図は φ0 = 10°、 下図は φ0 = 40°。 φ0 = 0° の場合、モデル輝度分布は l = 0 に関して対称で、 図4上図左側で負残差が強いのは観測輝度が l > 0 で強いことを意味する。 Blitz, Spergel 1991 が最初に指摘したようにこの現象は3次元放射密度がバー 状で、 l > 0 側が近いことを示唆する。この特徴は φ0 = 10° (中)では弱まるが依然として存在する。 φ0 = 40° 図(下) は図3の φ0 = 20° 図(中)と極めて似ている。ここでは正と 負の残差が l の正負両方で平等に混ざり合って存在する。どの φ0 にも (l, b) = (7, 0) と (-12, 0) に著しい残差正の島が見える。 φ0 = 20° と 40° 図を詳しく見ると、 φ0 = 20° の方が綺麗である。特に、 φ0 = 20° では対角線状に 伸びる残差が弱くなっている。従って、暫定的に 15 ≤ φ0 ≤ 35 とする。 |
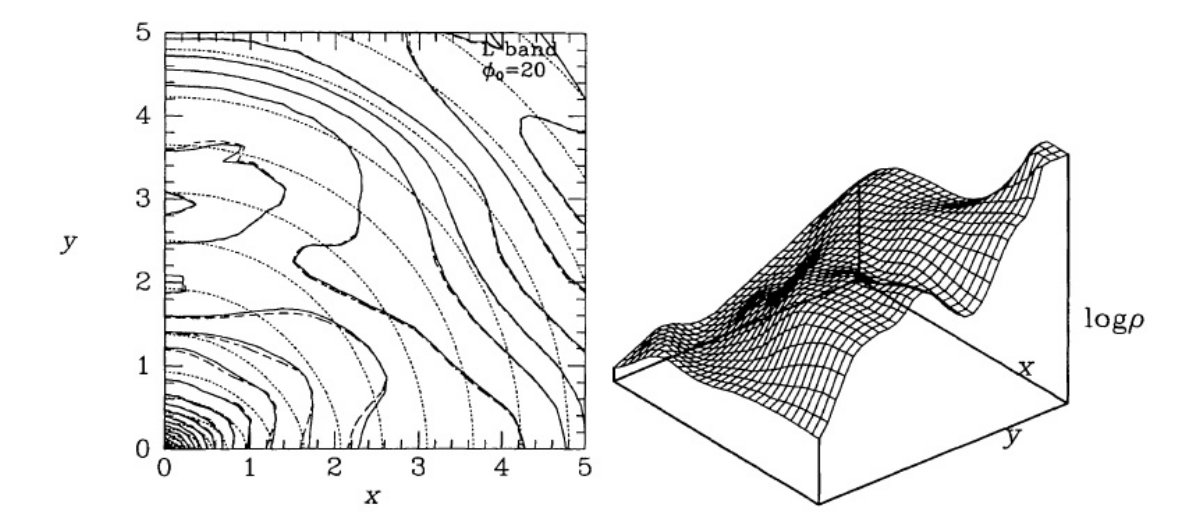
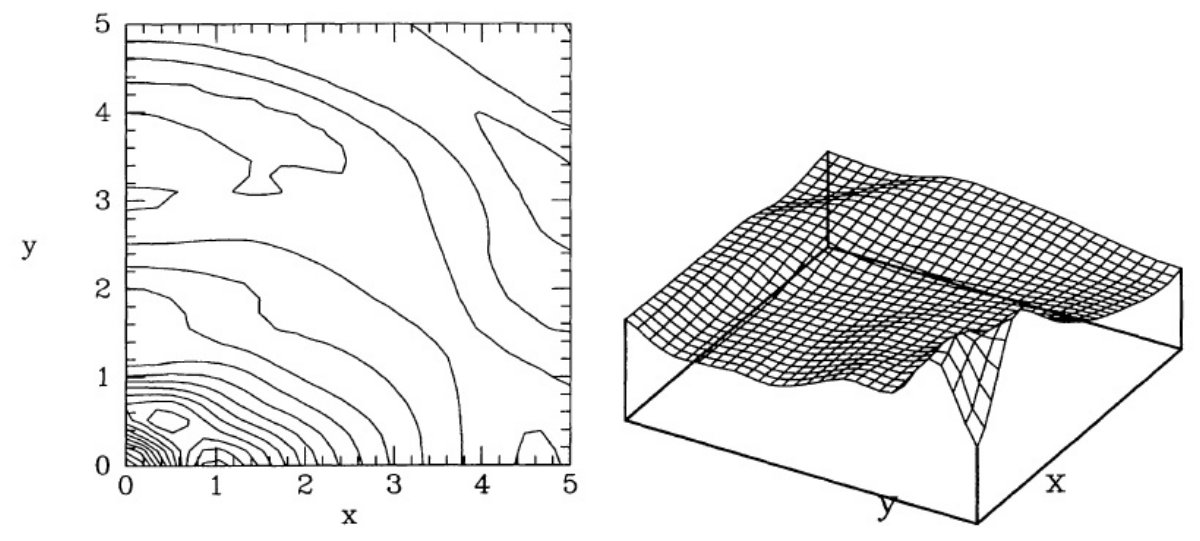
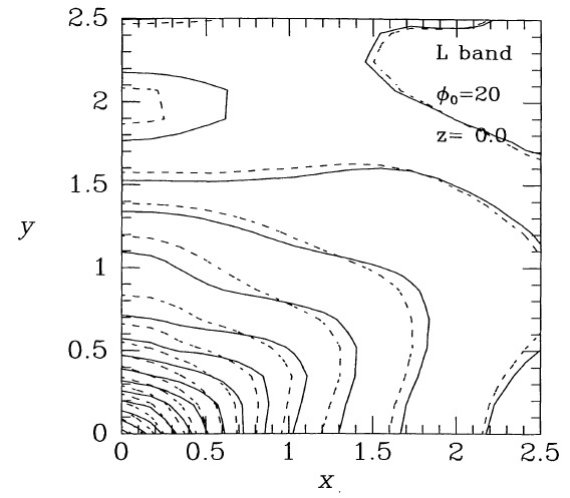 図6.実線=中心尖がりを表すべき乗則の指数を -1.8 から -1 に変化させた 時の等密度線。破線=比較用に図5。図5と違い内側 2.5 kpc なのに注意。 図5の解説 図5は図1で示したモデルの面内密度 j 分布を示す。、 φ,sub>0 = 20° である。右の立体図は左と同じ最終モデルの log j である。計算は リチャードソン・ルーシー法で、初期値は左図点線。作図のグリッドは x, y で 172 pc, z で 74 pc である。 省略部 この後、初期値の影響が論じられている。図6にはカスプの勾配が論じられている。 バーの存在 図5には半長軸径 3.5 kpc のバーが認められる。中心付近で対数等間隔の 等高線が密集するのはバーの中心が大まかにはべき乗的な密度分布を持つこと を意味する。バーの外側輪郭線は楕円から大幅にずれている。 z 方向分布 図7には同じモデルの xz, xy 面上での放射密度分布が示されている。下図の y = 1 kpc 付近で勾配が急なあたりはバルジから円盤成分への移行を示している。上図では移行は はっきり見えない。それでも x = 1.8 kpc 付近にそれらしい兆候が見える。図7の下から 3番目の等高線を使い、バーの軸比を 1 : 0.6 : 0.4 と定めた。z = 0.4 kpx の上では 等高線は z でほぼ等間隔の平行線となる。これはバーの垂直方向分布が銀河面から離れると 指数関数的であることを示す。中心付近の密度分布は Bailey 1980 のべき乗 分布と合致する。 図8の解説 図8は z 軸に沿って投影した柱密度分布である。外側輪郭線は依然として 楕円からずれているが図5ほどではない。 |
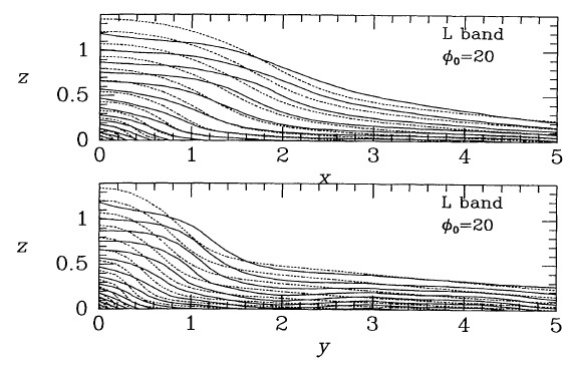 図7.図5と同じだが zx 面と zy 面。線間隔が 0.2 dex で図5の倍。 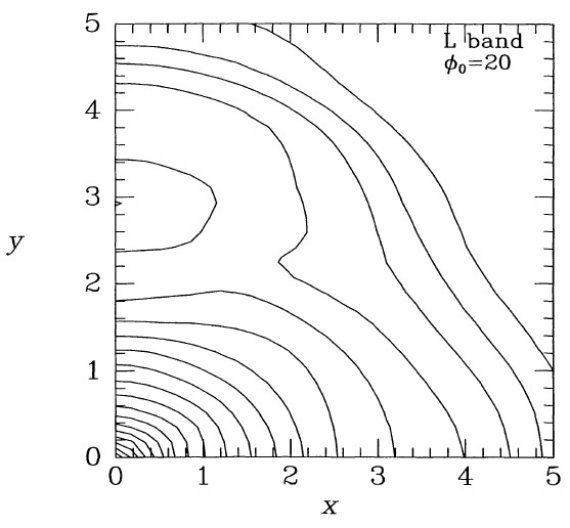 図8.図5モデルの z 軸に沿った投影。間隔は 0.1 dex. |
|
スケール高 銀河の厚みを表現するのにスケール高 z0 が重要である。 この値を決めるには、|z| ≤ 295 pc で、 ln j = ln j0 - z/ z0 でフィットする。図9は図5,6,7のモデルに対する、 z0(x, y) を示している。中心付近では 97 pc から、外側の 約 220 pc へと増加する。この増加が意味するのは、内側バルジの密度輪郭は R と z の分割不能の関数であることである。y 軸に沿っては z0 の極大は y = 600 pc であるが、x 軸に沿っては x = 1 kpc であり、これは 軸比 1 : 0.6 に合致する。バルジの外では、 z0 は銀河中心距離 R と共に低下していき、 y 軸に沿っては、R = 5 kpc で z0 = 120 pc に下がり、x 軸沿いでは R = 5 kpc で z0 = 150 pc となる。 これ等の値は Gilmore, Reid 1983 が星計数から得た太陽付近での値、 z0 = 300 pc と較べると著しく小さいが、 Kent, Dame, Fazio (1991) による Infrared Telescope (IRT) からの値とは一致する。赤外データからの値が小さい 理由は、円盤のスケール高が銀河中心距離と共に増加するためか、スケール高の 小さい超巨星が近赤外放射密度に効いているためかであろう。 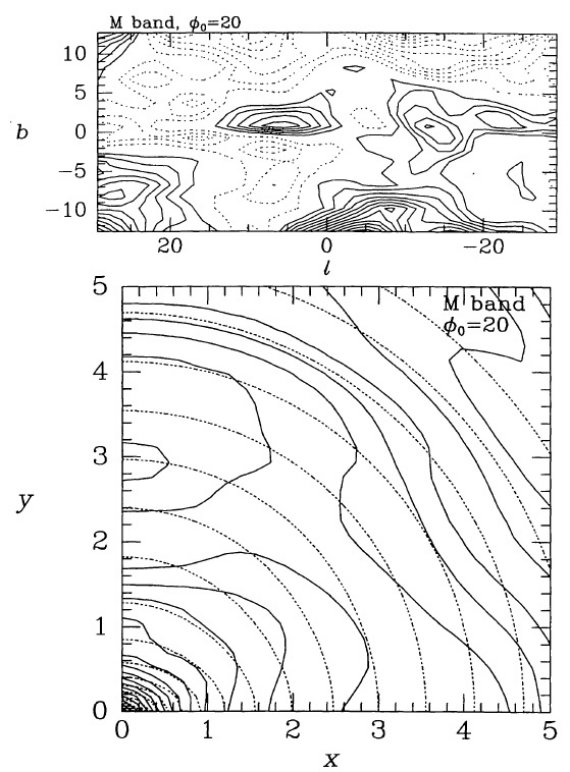 図10 M = バンドデータに対する φ0 = 20° モデル。 上:図3と同じパラメタ―。下:図5と同じ。 |
y軸上の盛り上がり 図5 - 8からバーは、 x ≤ 2 kpc までのべき乗則密度分布のコアが、 x = 3.5 kpc までの指数関数型の楕円形外環部に埋もれている描像が得られる。 R = 4 kpc を超えると、バーのすぐ外側に対して予想されるように、密度が大きく 低下する。y軸沿いに 3 kpc の所に局所的な光度極大がある。この極大は銀河面 に強く拘束されていて、|z| > 0.3 kpc では見当たらない。φ = 20 モデルでは、 (x, y) = (0, ±3 kpc) は l = -22 と l = ;17.3 の方向 に相当する。 ( 手前側 l < 0 の方が見込み角は大きくなり そうだが?) 図1を見ると、副次的な盛り上がりが l = -22 に、l = 17 には極大めいた構造が ある。この付近はバーの終端が支配的である。 M マップ 図10は M バンドデータに基づいたマップを示す。大体 L マップと似ている。 図10の上パネルは残差マップであるが、これも L バンドの図3と似ている。 φ = 40 マップ 図11は φ = 40 の仮定で得たモデルを示す。 r < 1 kpc で、このモデルは xy-面上でほんの僅かに細長いだけで、四角ぽい輪郭を示す。このずんぐりした四角な バーは x = 4 kpc, y = 2 kpc まで伸びる細長い密度超過の中に埋もれている。 y 軸に沿った谷=トラフは図5の φ = 20 モデルにも見られる特徴であるが、 こちらの方が強調されている。 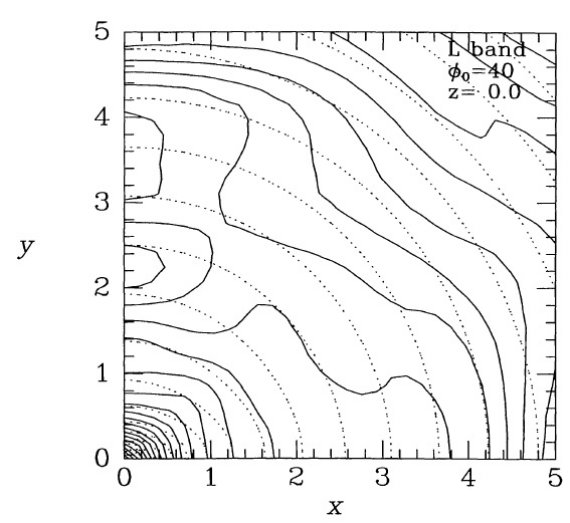 図11.L - バンドデータから φ = 40° の仮定で導いた主平面上の 等密度線。図5は φ = 20° での類似グラフである。 |
|
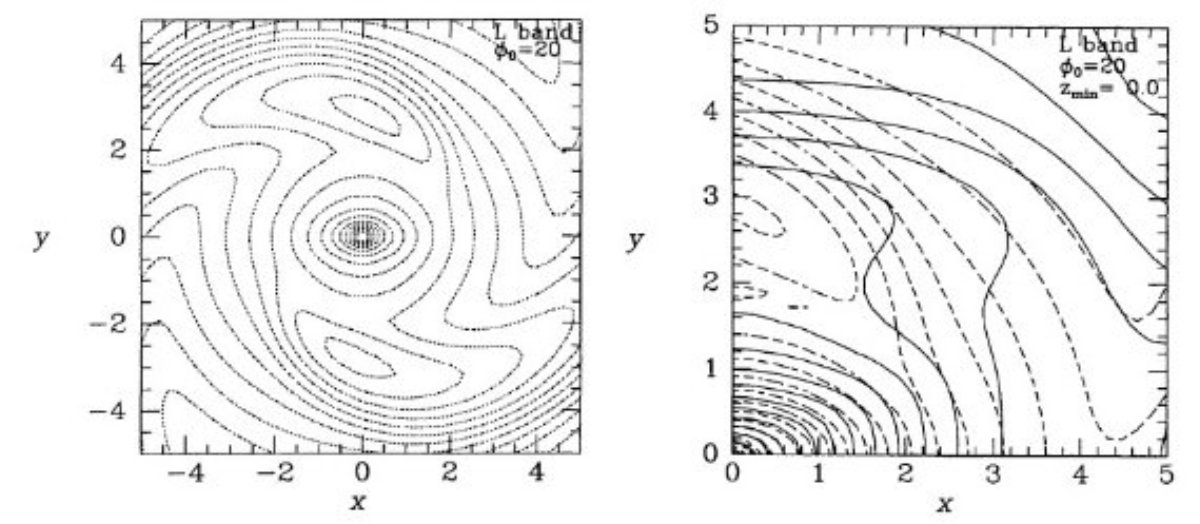
腕の主軸? Buta 1995 の銀河研究によると、実は銀河円盤は二本のきつく巻きこんだ 渦状腕が支配的で、近似的にのみ4重回転対称性の光度分布を成している。 その上、観測も数値シミュレーションもそれらの腕から導かれる主軸は バルジ主軸から少し遅れる。 ( 腕の主軸って何だ?) バルジと円盤の主軸同士のどんなズレも我々の逆変換法では押さえ込まれるだろう。 ( ここも分からない。) これまで述べてきたモデルは腕の存在によりどう影響を受けるか調べよう。 腕の影響を試す数値実験(八重対称性仮定) Binney, Gerhard 1996 では3回面対称=8重対称の仮定に基づき、ノイズの大きなデータから密度分布を 復元する能力を確かめた。しかし、我々は渦状腕が存在する際の性能は調べていな かった。図12にそのテスト結果を示す。元分布は(1)式に下の(2)式を掛けて 作った: 1 + ε cos6[φ - kR(r - rmax) - π/3] (2) ここに、ε = 2 tanh(r - rmax)、kR = 0.5 kpc である。 ( kRで割らなくていいのか? 腕は相対強度で見ると、 z 上方まで立ち上がっていることになる?) 式(2)は偶数乗のみなので2本腕を表している。2乗でなくて6乗を選んだのは 腕を鋭くするためである。式(1)と(2)のモデルを投影して擬データを作り、次に それをリチャードソン・ルーシー法で解いた。スタートは式(1)とした。図12の 実線= z 軸に沿って銀河面に投影した八重モデル解、破線=四重対称性を持つ擬データ である。中心付近では復元された等高線は元データに良く合っている。 その外側では、擬データの等高線は鏡面対称性から大きくずれていて、復元等高線は 擬データと大きく外れる。興味深いのはy軸に沿ってトラフ=谷の始まりが現れてきた ことである。 四重対称性仮定での数値実験 我々の逆変換法は八重対称性の仮定に大きく依存している。渦状腕はそれを 精々四重対称性に落とす。これに合う形の手法、すなわち銀河面に関して鏡面 対称で、銀河面上で点対称という対称性に合う近似法を定式化するのは単純 な作業である。この方法で良いところは、銀河面内でのバルジ主軸の方向に 関して事前の仮定を設ける必要が無くなることである。この手法の実験では スタートモデルは式(1)の η = 0.8, f0 = 390 モデルと した。残念なことに、この方法での回復性能は良くなかった。図13に結果 を示す。点線は式(1)に式(3)を掛けて作った4本腕の円盤の等密度線である。 1 + ε cos6[2φ - kR(r - rmax)] (3) ここに、kR = 1 kpc である。 ( kRで割らなくていいのか? ) 4本の内2本だけが回復されているが、それもかなり不完全である。回復された腕は 太陽からは端から見通す配置であり、その結果表面輝度が高くなっている。逆に回復 されなかった腕は真横から見られていた。このように、COBE データを4重対称性の 仮定で回復しようとする際には、銀河の腕が太陽ー中心線に対しどのくらい傾いている かが重要な要素となるであろう。 |
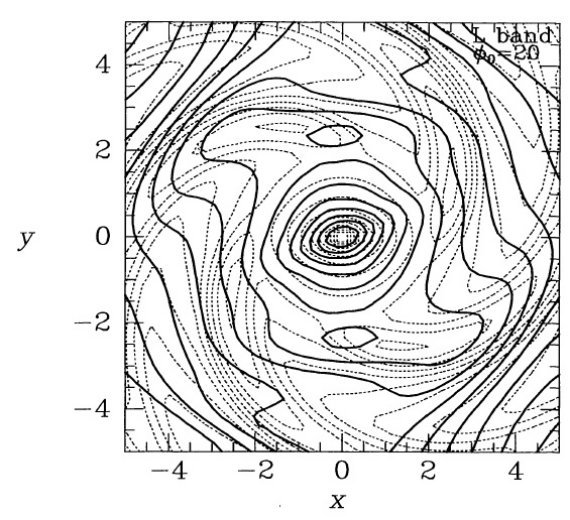 図13.点線=4本腕を含むモデルの主平面上の等密度線。実線=4重対称 リチャードソン・ルーシー法による脱投影解。太陽ー中心線は x 軸と 20 ° の角度を成すが、主軸の面内の傾きには何の仮定も設けない。 (当初モデルを復元解にしたら、 投影像との残差はゼロになり、明らかに最良解のはず。では R-L 法でそこに 達しないのは何故だろう? ) COBE データを4重対称性で回復 図14には COBE データを4重対称性の仮定で復元した結果を示す。左パネル はモデルの |z| > 300 pc の放射を銀河面に投影したマップである。この 図に関し2点述べる: (i) 左図は主にバルジ放射を表しているが、この図は最初の8重対称性を 仮定して求めた結果と似ている。回復された分布の長軸はほぼ長軸に沿っている。 4重対称性での回復には座標系の向きには特別な意味はない。したがって、この 図はバーの主軸が 20° に近いことを強く主張しているのである。 (ii)右図ではバーの周辺は軸対称から大きく離れている。特に y 軸上 3 kpc 付近に局所極大が見える。これは、8重対称性の仮定で回復された図に現れた 局所極大とよく似ている。y軸に沿った放射の高まりは |z| = 0 - 440 pc で 見られる。データに何かそこに高まりを必要とするものがあったのであろう。 内側の等密度線は太陽ー中心線の方向に 15° 傾いた。この効果は z が 高くなると消える。これは、渦状構造の影響なのかも知れない。 |
|
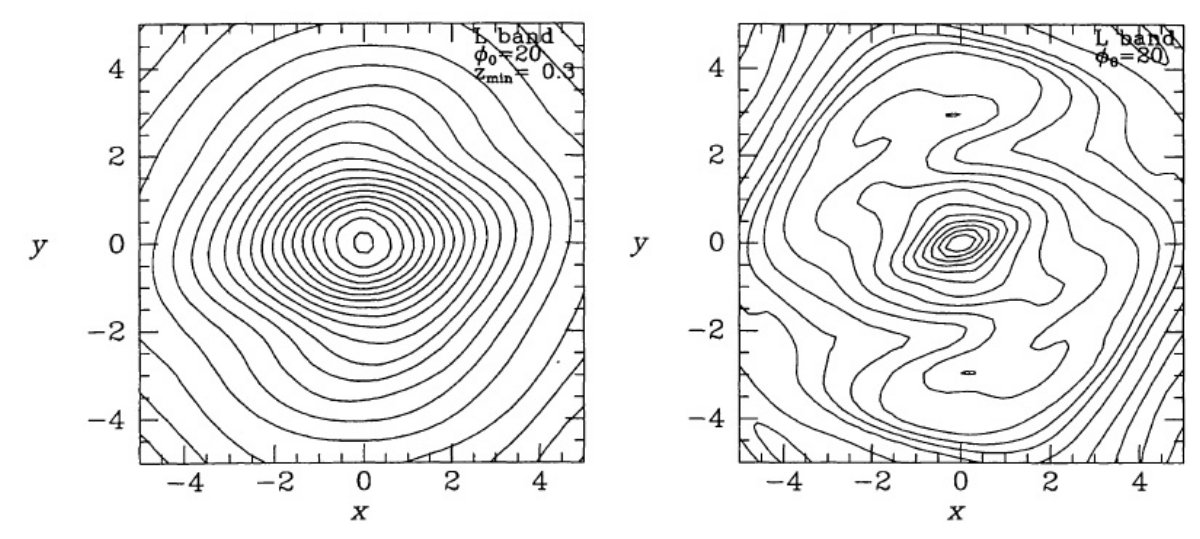
内側に先行(leading)渦状腕? 図14右図で奇妙な特徴は、短軸(=y軸)上の極大が先行(leading)渦状腕の 一部であるかのように見えることである。(図で銀河は時計回りに回転している) しかし、図をy軸に関して反転 (x → -x) させたモデルを投影した場合の残差 は著しく増大するので、この先行型形態はデータから絶対的に要請される性質なので ある。図13では復元された腕は元データと同じ向きに向いていた。このように、 図14からは内側銀河に先行型渦状腕が存在することが推定される。 4重対称性での復元実験 そこで、追随型渦状二本腕が存在する図12左の実験用放射分布からの画像 を、4重対称性の仮説の下で、復元する実験を行った。図15がそれで、図 12左に示される分布からの画像を復元したものである。図12左を復元した モデル図15は COBE データを復元したモデル図14と以下の点で似ている。 (i) 短軸上に局所極大が存在する。 (ii)先行腕と解釈可能な構造がある。 しかし、元分布の図12左よりずっと弱いが、図15は追随構造を示している。 そしてそれは、COBE 復元分布図14のどんな追随構造よりずっと強い。 図15に関しての注意 図15に関してはもう少し指摘すべき点がある。 (1)強い腕のみが復元分布に影響できる。図12左に見える腕はピークで 300 % に達している。 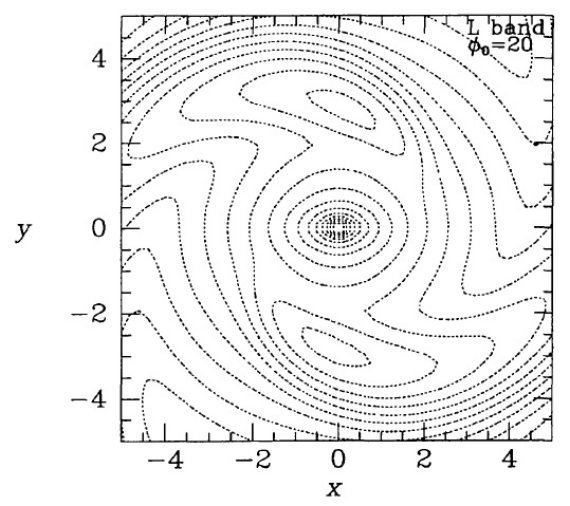 図12L.渦状腕モデルのz軸方向投影密度マップ。 |
(2)図15に見える短軸上の局所極大は人工的な原因で生まれた構造ではない。 それは、図12左にある渦状腕状の強い極大部を弱弱しく反映したものなのである。 (3)回復されたバーの向きが太陽ー中心線の向きに 15° よじられている。 図14右では COBE 回復等高線のいちばん内側部がほとんど同じくらいの 大きさで同じ方向によじれている。これは COBE 回復像のよじれは銀河面上の 腕の存在に影響された人工的な現象ではないかという疑いを支持する。 回復実験のまとめ 以上の実験の結果は以下の通りである。 (i) バルジの長軸は太陽ー銀河中心線に対して約 20° 傾いている。 (ii)振幅の大きな渦状腕は、見る角度が適当であれば、8重対称性または 4重対称性を仮定したモデルで復元可能である。 (iii)モデルを使用した実験の結果、腕構造は、復元分布に出現する y-軸 上の局所極大となり得ることが判った。 (iv)リチャードソン・ルーシー法により、渦状腕を回復する信頼度は低い。 それにも拘わらず、4重対称性テストでは内側渦状腕の巻き込み方向は 正しく示された。従って、銀河系データからの再現像である図14に先行型 渦状腕が現れたのは気になる。まったく人工的な効果の可能性も残る。 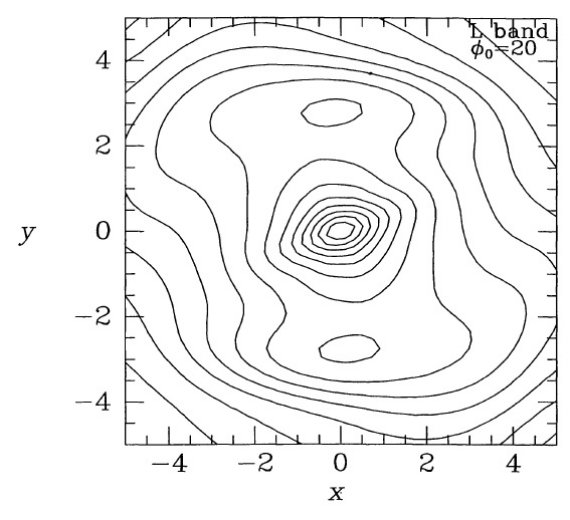 図15.左の渦状腕モデルを4重対称性の仮定の下で復元した結果。 |
|
COBE データから3次元バーを回復した COBE/DIRBE 近赤外データにダスト減光補正を行い、回復アルゴリズムを適用 して、銀河系半径 5 kpc 以内の放射密度3次元分布を求めた。2種類の異なる 対称性を仮定して求めたモデルは共に、強い非軸対称性と非指数関数型の円盤内 におかれた3次元バーを示した。 8重対称性モデル 8重対称性モデルによる復元では銀河系の3つの主軸の方向を予め設定しておく 必要がある。残差の大きさを調べた結果、 (i) 15 < φ0 < 35 (ii)太陽が銀河面の 14 ±4 pc 上にある。 ことが判った。L-, M- バンドの結果は良く一致していた。 4重対称性モデル このモデルには渦状腕を組み入れることが出来る。アルゴリズムはバーの方向を あらかじめ決める必要はない。回復モデルのバーの方向はほぼ φ0 = 20 であった。 スタートモデルの効果 回復モデルはスタートモデルの選択にはあまり影響されない。ただし、中心部の 尖がり強度は影響が大きい。データの分解能を 1.5° に平滑化したので、 尖がり度を区別するのが難しい。スタート時に強く尖がったモデルからはあまり 細長くない密度分布が得られる。中心部の密度勾配が与えられた場合、等密度線の 形はスタートモデルの形にほとんど依存せずに決まる。 バー もっとも良いモデルでは、3次元バーは短軸沿いに 1 kpc, 長軸では 1.8 kpc まで 伸びて、軸比は 10 : 6 : 4 である。中心付近の密度勾配は j ∝ a -α で近似される。しかし、スタートモデルの勾配に少し影響される。 銀河面に垂直方向の分布は 400 pc より離れるとほぼ指数関数的となる。 バーの周りには薄い、短軸で 2 kpc, 長軸で 3.5 kpc まで広がる楕円環が取り 囲んでいる。 Dwek et al 1995 のバルジ Dwek et al 1995 も COBE データを用いて、パラメタ―型モデルによるフィットを 行った。彼らはバーの軸比 a/b ≥ 3 であると結論した。我々のバーはそれほど 細長くない。ただし、モデル間の差のどれほどがこのバーの細長さbの差に起因 しているかどうか不明である。使用した減光モデルの違いも影響するだろうが、 大きな要因は、 (i) 我々のバルジモデルは Dwek et al 1995 より尖がっている。 (ii)我々は細長いバルジと、その周りの楕円円盤を区別したが、 Dwek et al 1995 はバルジのみが細長い。 我々のモデルは非パラメタ―型でフィットもより良い。 |
局所極大の実在性 我々のモデルは全て y = 2.2 kpc で密度の谷(trough)とその向こうの局所 極大を示した。さらに外側では非常に非軸対称な密度等高線を示した。これらの 構造は |z| < 300 pc に限られた。4重対称性モデルを使った数値実験から、 この谷とその先の副次的極大は実際に存在し、我々の復元法が生んだ人工的構造 ではないことが確かめられた。しかし、等密度線の形自体は画像を逆変換する 際に生じた人工的な効果かもしれない。腕と腕間空間との強度比は 300 % 必要 であった。この大きさの対比は M100 において報告されている。 φ0 = 20 φ0 = 20 は上のモデルフィットだけでなく、 Binney et al. 1991, Binney 1994, Gerhard 1996 による銀河中心付近でのガスの運動、 バーデの窓でのマイクロレンズィング、レッドクランプ星の分布(Stanek et al 1997) は全て小さな値の φ0 を支持している。 局所極大 y軸上にある局所極大は L4, L5 ラグランジュ点に溜まった 星からできているのかも知れない。それらは若く多分超巨星であろう(Rhoads 1996)。 したがって、質量で見るとその局所極大部の密度超過は光度超過ほどではないだろう。 いずれにせよ、もしラグランジュ点だとすると共回転は 3 kpc くらいの距離になる。 N-体モデル(Sellwood, Sparke 1988) によると、バーは共回転半径の 0.8 倍まで伸びる。だから、もしバーが 2 kpc まで伸びているなら、共回転半径は 2.5 kpc となる。もし銀河系の 基底にある回転速度が vc ∝ R0.1 Binney et al. 1991, で、vc(Ro) = 200 km/s であるなら、短軸上の極大位置からバーの パターン速度として、Ωb = 60 km/s/kpc を得る。一方、 垂直方向に厚いバーの長さ = 2 kpc からは Ωb = 71 km/s/kpc が得られる。参考のために、Binney et al は |l| < 10 での CO, HI 観測から Ωb = 63 km/s/kpc を、Kalnajs 1996 はバーデの窓での星の 運動から Ωb = 39 km/s/kpc を得た。 減光補正 我々のモデルの非軸対称構造は、≤ 0.4 mag の大きさの表面輝度の系統的な 銀経非対称性に依存する。従って、我々のモデルの信頼度は論文IIで示したダスト 減光補正の正確さが 0.4 mag より良いことに依存する。この補正は低銀緯で最大 であり、我々のモデルの最大の不確定性は円盤構造に与えられる。それに比べると、 バルジ構造はより安全である。 減光分布 論文IIの減光評価技法を Kent, Dame, Fazio (1991) の減光分布法と合体させると、より優れたダスト減光分布が得られるだろう。 伝統的な運動学モデルはガスの円運動を仮定しているという弱点がある。これは バーの存在と相いれない。ここで求めた質量分布モデルを使い、 適切なガス運動モデルを作れる。それを電波輝線観測と較べてより改善された ガスとダストの分布を決められるだろう。 |