The Mass-Loss Evolution of Oxygen-Rich AGB Stars and Its Cosequences for Stellar Evolution


ven der Veen
1989 AA 210, 127 - 146



　アブストラクト　

　O-リッチ AGB 星の半経験的マスロス式を与えた。基礎となるのは、ミラ型星 と OH/IR 星の OH-, CO-観測である。AGB 星はミラ型星から OH/IR 星へと進化 すると仮定する。これは IRAS 観測で支持される (van der Veen, Habing 1988) 見方である。IRAS 12-25-60 ２色図上で星は系列を成し、それは個々の AGB 星 のマスロス率が次第に増加していくためと解釈された。 　観測量＝光度、膨張速度、F25/F12 の関数としてマスロス式が導かれる。 その結果を以前の式と較べた。ガス/ダスト比を光度 L* と膨張速度 v の 関数として表せることが分かった。IRAS-PSC からマスロス率の時間変化＝進化 を導いた。F25/F12 区間内のサンプル数は F25/F12 と AGB 上での相対滞在 時間との関係を与える。マスロス式を試すために AGB 上で失われる総質量を 求めた。初期質量と到達最高光度との間に簡単な関係が導かれた。マスロス式 の時間変化をミラ型星と OH/IR 星のサンプルで調べた。周期、光度、外層質量 関係が得られた。それは球状星団、LMC の観測と良く合う。

　１．イントロダクション　

　１．１．ミラと OH/IR 星　

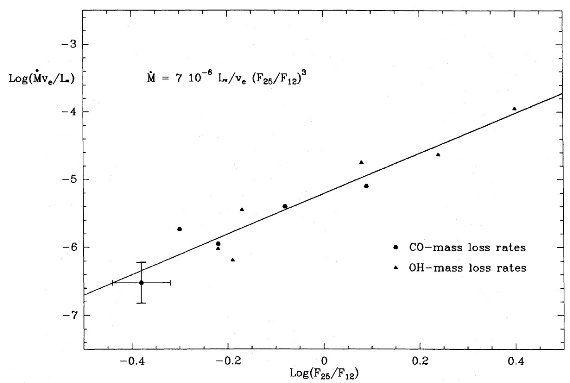
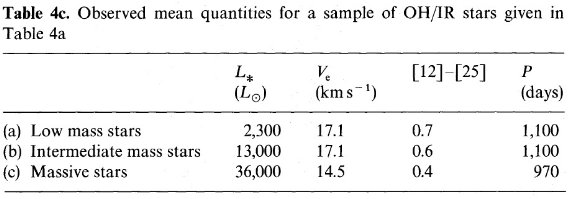
　ミラ型星と既知 OH/IR 星　

　図１に van der Veen, Habing (1988) からの、ミラ型星と既知 OH/IR 星に対する [12-25] - [25-60] 図を示す。 これ等の星が狭い系列内に位置することが判る。また、系列から外れて非変光 の OH/IR 星が見られる。
(IRAS 天体全般ではずっと広い巾を 示す。サンプルに働いた選択は何であるか？ )
この系列を指針として、広範な OH サーベイが te Lintel Hekkert 1987, Eder, Lewis, Terzian (1988) により行われ、約 1000 の新しい OH/IR 星が発見された。 そして 1 - 13 μm 赤外観測が Herman, Isaacman, Sargent, Habing (1984), Willems, de Jong 1988 により行われた。幾つかの OH/IR 星では位相遅れ法で 距離が求まり L > 2000 Lo であることが判った。これらから、ミラ型星と OH/IR 星が AGB 先端に位置することが明らかになった。
　この先、「ミラと変光 OH/IR 星」とダスト星(DGE星）を区別する。
(意味不明 )


　AGB 進化の式　

　　　L* = 5.925(Mc-0.495)　　　　　　　　　　　　　　　　(1a)

　　　dMc/dt = (Mc-0.495)/τN　　　　　　　　　　　(1b)

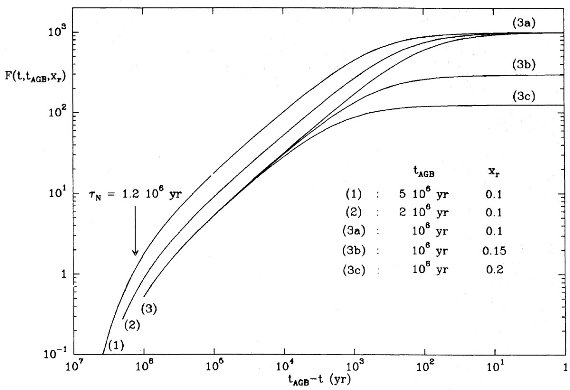
ここに τN = 1.2 Myr.

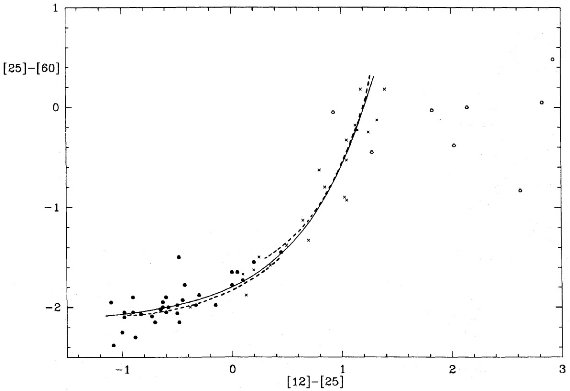
図１．既知ミラ型星と OH/IR 星の IRAS 二色図 破線＝ Bedijn (1987) のモデル進化経路。実線＝ van der Veen, Habing (1988) によるフィット線。

　２．ＡＧＢマスロス　

　２．１．大規模マスロスを想定させる根拠は？　

　１．チャンドラセカールマス限界　

　マスロスが起きないと、 Mc がこの限界を越えてしまう。そんなに SN は起きていない。

　２．Mwd の値　

　WD マスは -.5 - 0.6 Mo である。

　３．ＰＮ形成　

　マスロスなしの進化では、 AGB から PN に移るのに 5 105 掛かる。 PN 形成には 2000 年以内に 0.2 Mo のマスロス = 10-4 Mo/yr が、 PN 形成直前に必要である。

　超星風　

　このような必要性から、 Renzini 1981 は超星風を提案した。

　２．２．AGB マスロスの観測　

　１．CO　

　

　２．ＯＨ　

　

　３．赤外　

　

　３．O-リッチ星マスロス式　

　３．１．ガスのマスロス式　

　　　v(dM/dt) = τd(L*/c)　　　　　　　　　　　(2a)

図１のミラから OH/IR 星のマスロスが何桁も違う系列が一つの星の系列である とするなら、 v, L* はあまり変わらないから、τd が大きく 変わると考えなければいけない。R21 = F25/F12 として

　　　τd　∼ R21α1　　　　　(2b)　

(2a) と (2b) から、

　　　dM/dt (Mo/yr) = A1(v/15km/s)-1(L*/104Lo) R21α1　　　(3)

図２から、A1 = 7 10-6, α1 = 3 である。
(C-リッチの場合はどうなる？シェルモデルとの比較は？ )

図２．v(dM/dt)/L* と R21=F25/F12 の関係。dM/dt は Mo/yr 単位、 L* は 104 Lo 単位、v は 15 km/s 単位である。黒点＝ Knapp, Morris 1985 の CO 観測、三角＝ Baud, Habing の OH 観測. 　

　３．２．ダストマスロス　

　ダストマスロスの式　

　Herman et al 1986 は光学的に薄いシェルに対し、以下の式を得た。
(dM/dt)d =6.6 10-10 v F60 ( D ) 2 ( L* ) -0.5
Mo/yr 15 km/s Jy kpc 104 Lo


この式を変形するため、単位を省いて、 Fo = 7.8 10-4 BC (F12/Jy) (104Lo kpc-2)、(dM/dt)d は　(Mo/yr), v は 15 km/s, F60 は Jy, D は kpc, L* は 104Lo で表示する。

D2F60 = D2(F60/F12)(Ftot/BC)=L*F60/(BCF12)

更に、図１の (F60/F25) - (F25/F12) 関係 (ven der Veen,Breukers 1988) を使い、 (F60/F12)/BC = (F60/F25)(F25/F12)/BC = 42 (F25/F12)3 なので、

　　　(dM/dt)d = 2.7 10-8 v L0.5 (F25/f12)3　(6)

こうして、ガスマスロスとダストマスロスの双方が (F25/f12)3 を 含む形にまとめられた。（３）、（６）式から、（ガス/ダスト）比 μ は

　　　μ = 260 L*0.5v-2　　　　　　　　(7)



　補正項　

　上の式はシリケイト密度 3.3 g cm-3, グレインサイズ a の分布 n(a) ∼ a-3 を仮定している。その補正項 g を図３に示す。

図３．補正ファクター g 　

　４．O-リッチ DGE 星マスロスの時間変化　

　４．１．タイムパラメタ―としての F25/F12　


図４．選択した赤外源の累積数 Naj と F25/F12 の関係。

　F25/F12 = 1.2 - 3.5 は多分サンプル体積一定　

　マスロスの進化は F25/F12 として現れる。したがって、 F25/F12 区分内の IRAS 星の数はマスロス進化と関係する。しかし、F25/F12 により到達距離 が異なるので、それに伴い星の数が影響される。この問題を避けるために、 我々は F25/F12 = 1.2 - 3.5 の範囲を選んだ。そこは領域 IIIb と IV に 当たり、輻射補正 BC = Ftot/(νF,sub>ν,/sub>) ∼ 3 で安定して いるからである。

　累積星数＝カラー関数　

　星数の勘定 Nj は Δ(F25/F12) = 0.05 の区間で行う。ここで、 N1 は (F25/F12) が一番大きい区分である。累積数 Naj = Σ1 jNi は Nj より赤い星の総数である。結果を図４に示す。 F25/F12 = 1.5 - 4 でのフィットの結果は、

　　　Na = 3.7 10-3 (F25/F12)-4 　　　　　　　　　　(11)

である。しかしこの先では van der Veen, Habing (1988) に倣い、 F25/F12 = 0.35 - 3.5 で式 11 を使用する。

　Na と進化　

　tAGB = AGB マスロスの期間とすると、

　　　Na ∝ (tAGB - t) ∝ R21-4

t = 0 の時 F25/F12 = R21,0, t = tAGB の時 R21 = R21,F とする。

表１．残り時間 (tAGB - t) と R21 の関係。 tAGB = 1 Myr, [12-25] = 2.5 log R21.

上の比例式を正確ではないが１次式と考えると、

tAGB - t = R21-4 - R21,F-4
tAGB R21,0-4 - R21,F-4


この式は (t, R21-4) を (0, R21,F-4) と (tAGB, R21,0-4) で結んでいる。 R21,0-4 << R21,F-4 の 時には、この式は以下のようになる。

tAGB - t = R21,04 (R21-4 - R21,F-4)　　　　　(16c)
tAGB


R21,0 = 0.35, R21,F = 3.5 として上式に代入、

tAGB - t = 1.5 10-2 (R21-4 - 6.7 10-3)　　　　　　(16d)
tAGB


tAGB は 1 Myr を大きくは超えないだろう。それ以上ではコアマスが 大きくなり過ぎる。 　

　表１＝ R21 と残存時間の関係　

　表１には R21 と残存時間の関係を示す。 Habing (1988) は R21 > 1.0 の AGB 星の数を 35 kpc-3 とした。一方、 Wood, Cahn (1977) はミラ型星の近傍数密度は 250 kpc-3 とした。これらの数の比を 寿命の比と考えると、その比は約７倍である。図１から典型的なミラ型星 の R21 = 0.6 を取ると、 比は８であり、一致は良い。

　４．２．O-リッチ星のマスロス方程式　

　ストレイトな式　

　式３＝CO, OH 観測から決めた dM/dt と R21 の関係、
　　　dM/dt = 7 10-6 v L R213

　式16c = IRAS 星の R21 分布から決めたカラー変化の速度、
tAGB - t = R21,04 (R21-4 - R21,F-4)　　
tAGB

を組み合わせる。
(R21/R21,0)-4 = xr4 + (tAGB-t)/tAGB
R21 = R21,0[(tAGB-t)/tAGB+ xr4]-1/4
を式３に代入して

dM/dt = 7 10-6 (L/v) R21,03 [(tAGB-t)/tAGB+ xr4]-3/4　　　(17a)
ここに、xr=R21,0/R21,F＝0.1, dM/dt は Mo/yr, v は 15 km/s, L は 10,sup>4 Lo 単位である。

tAGB＝１Myr を仮定した時、tAGB-t > 100 yr なら、

　　　dM/dt ∼ [(tAGB-t)/tAGB]-3/4

　光度、星風速度が変わる式　

　コアマスの成長、ガス/ダスト比一定から導いた星風速度変化は次のように表 される。ここに τN = 1.2 Myr, t' = (tAGB-t)/ τN として、

　　　L(t') = Lfexp(-t')　　　　　　　　　　　　　(18a)

　　　v(t') = vfexp(-0.25t')　　　　　　　　　　　(18b)

ここに、Lf, vf は AGB 最末期での光度と星風速度である。 式 18a,b を式 17b に代入して、

　　　dM/dt = (dM/dt)o F(t,tAGB,τN, xr) 　　　　　　　　　　　　　(19a)

　　　(dM/dt)o = 7 10-6 (Lf/vf) R21,03 　Mo/yr　　　(19b)

　　　F(t,tAGB,τN,xr) = {exp[(tAGB-t)/tAGB][(tAGB-t)/tAGB + xr4]}-0.75　　(19c)

注意すべきは (dM/dt)o は t = 0 での dM/dt ではないということである。なぜなら、 F(t,tAGB,τN,xr) ∼ exp(-0.75 tAGB/τN) ≠ 1 だからである。

図５．関数 F(t,tAGB,τN,xr) 図は τN = 1.2 Myr 仮定。

　F(t,tAGB,τN,xr) 　

　図５には、 F(t,tAGB,τN,xr) を tAGB-t の関数として、様々な tAGB と τN　 に対して示す。この図には特徴的な３つの領域がある。

(i) 図の左側は τN が tAGB と同程度か小さい。(dM/dt) が 上昇すると共に F も大きくなる。

(ii) 中央部と右側では tAGB が τN より小さい、(dM/dt) が 上昇すると共に F も大きくなる。

(iii)右側では F は xr で決まる一定値に収束する。


(図５は L, v 一定のケースと比較しにくい。 両者の比、exp[(tAGB-t)/tAGB]（？）を描くとよい。 )

　５．総マスロス量、初期主系列質量、とマスロス期間　

　F の積分　

　総マスロス量は式 (19) を t = 0 - tAGB で積分する。 τN = 1.2 Myr, xr = 0.1 についての結果は

　　　∫F dt = 3.2 106(tAGB/1Myr)0.8

　　　Mlost = 0.95 (Lf/vf) tAGB0.8 Mo 　　　(21b)



　マスロス量表式の一般化　

式３を
　　　dM/dt = A(Lf/v)R21α1

式１６a を
　　　(tAGB - t) ∼ R21α2

とする。すると、

　　　dM/dt = (Lf/v)(tAGB - t)α1/ α2

となる。

表２．B と β の α1/α2 依存性。

この式を積分して総放出量を出した結果を、

　　　Mlost = B (Lf/vf)tAGBβ

とする。表２に、 B, β の値を α1/α に対して示す。
(β = α1/α + 1 かと思ったら違った！)
第３章では、A = 7 10-6, α1 = 3, α2 = -4 だった。

　５．２．初期質量と最大光度の関係　

　Lf と Mi の関係　

Mi = 初期質量
Mlost = AGB 期間中の総放出量
Mf = AGB 最末時のコアマス
fM = AGB 以前のマスロス補正項
Lf = AGB 最末時の最高光度

とおくと、

L*=5.9(Mc-0,5)から、Mc = 0.17L*+0.5、(L* は 10,000 Lo, Mc は Mo 単位)
Mlost = 0.95 (Lf/vf) tAGB0.8 なので、

　　　fMMi = Mlost + Mf
　　　　　　　 = [0.95(tAGB0.8/vf)+0.17] Lf　+ 0.5 		　ε = マスロス効率　

　こうして、Lf と Mi の関係がついた。この関係は我々が マスロス効率と呼ぶ以下の量に依存する。

　　　ε = Mlost/Lf = 0.95(tAGB0.8/vf)

この効率は、tAGB0.8 と vf に依存する。 tAGB の決定は困難である。恐らく、vf と Lf の双方に依るのではないか。

　ε ＝マスロス効率　

　ε が知れると、他の量は以下のように決まる。

　　　Mlost = εLf　　　　　　　　　　(25a)
　　　tAGB = (εvf)1.2　　　　　　　　　　(25b)
　　　fMMi = (ε + 0.17)Lf + 0.5 　　　　　　　(25c)


　５．３．マスロス期間の長さ　

　５．３．１．初期質量ー最終質量関係　


図６．初期質量ー最終質量関係。データ点は Weidemann, Koester (1983) から。白四角＝log g から決定。黒点＝ Te から決めた。点線＝ ε = Mlost/L* 一定の仮定で引いた。 初期質量の 20 % が AGB マスロス以前に失われたと仮定。

　図６＝初期質量ー最終質量関係　

　図６は Weidemann, Koester (1983) の図１を移してきたものである。この図の最終質量は散開星団中の白色矮星の 温度（黒点）や重力（白四角）から導かれた。初期質量は、星団年齢から 白色矮星冷却年齢を引いた年齢を、初期質量の関数として決まる前ＷＤ年齢 と較べて定めた。

　初期質量に対して複数の最終質量　

　図６から分かるように、一つの初期質量に対して複数の最終質量が対応する。 その説明は二つ考えられる。

(i) 白色矮星質量決定の誤差

(ii)マスロス効率 ε が星毎に、おそらくメタル量効果で、異なる。

表３． Weidemann, Koester (1983) の図で使われたマスロス効率 ε の平均値とメタル量。

　式１と２５を使い、次の式が出る。
Mf = fMMi + 2.9ε 　　　　　　　　　　　　(26)
1 + 5.9ε


　 ε は幾つか？　

図６に fM = 0.8 のラインを様々な ε を仮定して描いた。 図を見るとデータ点の多くが ε = 1.0 - 2.0 の間に位置する。実際、 Mf > 0.7 Mo つまり Lf > 12,000 Lo では Mi = 14 Mo を除く全ての点が ε < 2 にある。Mi < 3 Mo, Mf < 0.7 Mo の低質量になると、異なる ε のラインが 収束し、どれが正しい ε を決めにくくなる。 　ε = 1.5 と仮定し、式 25, 26 を用いると、

　　　Mlost = 1.5 Lf Mo　　　　　　　　　　(27a)

　　　Mi = 2.1Lf + 0.62　　　　　　　　　　(27b)

　　　tAGB = 1.8 vf1.2　　　　　　　　　　(27c)

　　　Mf = 0.081 Mi + 0.44　　　　　　　　　　(27d)

ただし、この式の使用には注意が必要である。式 27c は tAGB が vf のみで決まるとしているが、これは ε 一定の仮定に 基づいていておそらく誤りである。 tAGB は多分、 Mi とメタル量 に依存するであろう。式 27c は AGB マスロス期の長さの概算に使う道具と考 えられる。例えば、もし膨張速度を 8, 15, 24 km/s とすると、マス路期の長 さは 8 105, 1.8 106, 3.2 106 年となる。

　５．３．２．AGB マスロス開始時のコアマス　

　Mc(0) - Mi 関係　

　図７には前節で導いた AGB マスロス開始時の Mc(0) と Mi との関係を示す。 実線は、式 26 で ε 1.5, fM 0.8 の時の Mc - Mi 関係である。(3a),(3b),(3c) のラベルが付いた点線は、式 27a,b,c で vf = 8, 15, 24 km/s に対する。 Iben, Truran 1978 による、 Mc(0) = 0.50 + 0.075(Mi - 1) を用いた理論的な関係を破線（２） で示す。我々が導いた実線 (3a), (3b), (3c) を破線（２）と較べると、 実線は破線の 25, 40, 50 % 小さい。この差は我々が導いた AGB マスロス期間 が長い 8 105 - 3 106 yr 事による。

　Latanzio 1986 のモデル計算　

　　Latanzio 1986 のモデル計算も同じような結果をしめす。それも図７に示す。 その結果はわれわれの v - 15 km/s, tAGB = 1.8 106 yr に合う。Z = 0.001 のモデルはもっと大きな Mc を予想する。

　B と β の影響　

　５．１．節によると、 ε = B tAGBβ で ある。表２にはその結果を示す。

　５．３．３．主系列星、 AGB 星、PNe の近傍密度　

　tAGB を評価するもう一つの方法は、主系列星、 AGB 星、PNe の近傍密度を較べることである。 Habing (1988) は R21 > 1 の AGB 星密度を 35 kpc-3 とした。 表１からこの区間の長さは 1.5 10-2 tAGB である。 ONe 寿命を 25 kpc-3, 寿命 2 104 yr (Pottasch 1984) とし、 R21 > 1 の AGB 星が全て PNe になると仮定すると、 tAGB = 3.2 106 yr である。Gilmore, Reid 1983 は M > 1.3 Mo の近傍密度を 3.2 106 kpc-3 とした。 これらが全て、AGB 星になると考えると tAGB = 2 106 yr である。

図７．Mc - Mi 関係。実線＝式 26 で ε 1.5, fM 0.8 の時の Mc - Mi 関係。破線＝Iben, Truran 1978 モデルの TP-AGB 開始時の Mc - Mi 関係。点線＝この論文で導いた AGB マスロス開始時の Mc - Mi 関係。

　５．３．４．AGB マスロス期間のまとめ　

　Mi - Mf 関係 （ Weidemann, Koester (1983) ） を説明するためには AGB マスロス期間が 数 Myr 必要である。この結果を 得る際、 ε = Mlost/L* が Mi と Z に依存しないと仮定 した。こうして得た tAGB は近傍密度から導いたマスロス期間と よく一致した。 　唯一の矛盾は Mi > 3 Mo の高質量星での mi - Mc(0) 関係である。 (dM/dt) ∼ (tAGB - t)-0.75 の代わりに、 (dM/dt) ∼ (tAGB - t)-1 を使うと、この矛盾は 解消する。しかし、理論の不定性が原因かも知れない。

　６．いくつかの応用　

　６．１．(ve, L*) から (vf, L*) への変換　


図８a．膨張速度とカラーとの関係 　

図８b．光度とカラーの関係 　

　６．２．ミラと OH/IR 星への応用　

　６．３．M*(t) と Me(t)　


表４a．ミラ型星、OH/IR 星の観測物理量

表４b．表４a の ミラ型星、OH/IR 星の計算物理量


表４c．表４a の OH/IR 星の平均物理量




表５．ガス/ダスト=260, [12-25] = 0.5 の場合の異なる L に対する計算。

　６．４．O-リッチ星の質量変化　


図９．マスロス率、星質量、コアマス、外層マスの残存時間 tleft = tAGB - t との関係


図１０．観測光度、観測周期と計算残存外層質量の関係

　６．５．周期光度関係　


図１１．周期、光度、外層質量から求めた周期光度関係。異なる Mi に対する曲線 を示す。短破線と点線＝ AGB 時間の効果。長破線＝球状星団と LMC の PL関係。 　

　６．まとめと結論　

　IRAS = 新しい流れ　

　数年前まで PNe 直前の星進化を研究する際の最大の問題は観測の欠如だった。 IRAS が提供する約２０万の赤外データ、そのかなりが星、が状況を大きく変え た。 van der Veen, Habing (1988) では、IRAS に含まれる数千のダスト/ガス星の統計的性質を調べた。

　マスロス方程式　

　この論文では、CO, OH 観測データから求めたマスロス率を用い、マスロス方 程式を求めた。この方程式の利点は、それが観測量のみ、L*, ve, R21 で構成されていることである。単位光度当たりの転移ガス運動量

　　　 (dM/dt)ve/L* ∝ R213

が見出された。この方程式を Herman, Burger, Phenninx (1986) によるダストマスロス方程式から求まる単位光度当たりの転移ガス運動量 と較べると、

　　　 (dM/dt)dve/L* ∝ ve2 /L0.5R213

となる。ダストへの運動量転移が質量全体への運動量転移に等しいと仮定する と、ガス/ダスト比 μ ∼ L*1/2ve2 が導かれる。これは Jura 1984 による L* ∝ ve4 という結果と整合する。

　マスロスの進化　

　R21 分布密度をマスロスによるカラー進化スピードの逆数と考え、 マスロス率が AGB 進化最後の 104 年で強い増加を示すことを見出 した。これは Baud, Habing (1981) が OH メーザーの解析から見出した結果である。一つだけ異なるのは彼らは (dM/dt) ∼ (tAGB-t)-1 としたが、この論文では (dM/dt) ∼ (tAGB-t)-0.75 となったことである。 		　tAGB の推定　

　tAGB の推定には次の３つがある。　

(i)　Mi-f 関係。

(ii)　AGB 星の近傍密度と主系列星の近傍密度の比較。

(iii)　TP-AGB 開始時のモデル Mc と白色矮星の観測質量の比較。

(i), (ii) が 8 105 - 3.2 106 で一致するのに対し、 (iii) は 数 105 と短い期間を与える。この差は前の指数 -0.75 でなく -1 の場合にはずっと小さくなる。

　マスロス率の時間依存性　

　マスロス率の時間依存性は Herman, Burger, Phenninx (1986) が与えたミラと OH/IR 星サンプルを使って調べられた。その結果、
(i) ミラのマスロス率は OH/IR 星の 10 - 50 倍小さい。
(ii) ミラの質量は主系列星質量に近く、 OH/IR 星は白色矮星質量に近い。
(iii) ミラの光度は進化期間中に少し上昇する。


　周期光度関係　

　計算された現在質量 M* を使って L*. M+, P の関係を調べたが相関がない。 しかし、L*, Me, P の間に良い相関が見出された。この関係を用いて、周期 光度関係を導いた。 P 500 d 以下では P に伴い L の上昇が見られた。 これは LMC, 球状星団で見出されているものと合う。ただし LMC では M = 2 Mo、 球状星団で M = 1.7 Mo となった。距離を 20 % 下げると合う。

　多波長データの統合　

　この論文は全ての説明を意図したものではなく、 IR, CO, OH 観測を比較する ための道具を提供する目的で書かれた。