The upper mass limit for white dwarf progenitors and the initial-final mass relation for low and intermediate mass stars


Weidemann,V., Koester,D.
1983 AAp 121, 77-84



アブストラクト

　散開星団中の白色矮星から、母星質量の上限として 8 M๏ が得られた。 新しい Mf - Mi 関係は以前より平らで、白色矮星と惑星状星雲の中心星質量が 0.6 M๏ に集中している事実を説明する。

　０．イントロ　

　惑星状星雲中心星と白色矮星の質量分布の巾が驚くほど狭いことが判ってきた。 したがって、新しいデータを基に Mi - Mf 関係を求め直す。 　

　１．白色矮星になる星の上限　

散開星団のあまりパッとしない仕事　

　質量放出を正確に計算できないので、白色矮星の上限 MWD を理論で 予言できない。星風モデルからは、 MWD = 3(η=1/3), 5(η=1), 8(η=3) M๏ が予想されている。SW を入れると、さらに巾が 拡がる。理論がそのようなので、散開星団中で WD を探すことが重要になる。

　古典的な例としてヒアデスでは MWD = 2 (Tinsley 1974), 4(van den Heuvel 1975) がある。しかし、上限を確定するにはサンプル数が小さすぎる。同様に プレアデスのメンバーと思われる LB1497 は MWD > 6 を与えるが、 同様に確実な結論と言えない。

Romanishin, Angel 1980 は　NGC 2168, 2287, 2422, 6633 中に青い星を探した。 予想される WD 数と観測数との対比から、彼らは MWD として 5, 多分 7 とした。Koester, Reimers 1981 は NGC 2287, 2422 中の青い４つの星を分光により WD と確定したが、メンバーシップは少なくとも一つの星に関して怪しい。このため MWD をより良く確定することは出来なかった。Anthony-Twarog 1981, 1982 は M34 と プレセペ の測光観測にのみ基づいて小さすぎる Mto を得た。 		散開星団のよい仕事　

　Reimers, Koester 1982 は、非常に多数の星を含み、かつ遠方の散開星団 NGC 2516 のシュミット UV, red 乾板から青い９天体中に、6 個の WD を分光に依り検出した。 そして、その高度、温度 (> 30,000 K), 短い冷却年齢から、３天体は星団メンバー と考えられるとした。得られた表面重力は WD 質量として $gt; 0.9 M๏ を示す。この値はモデルー MWD の関数として光度関数中の進化の進ん だ星を与え、観測された数と比較する ー から MWD = 8+3 -2 M๏ を得た。 　この値は以前の結果と較べ統計的に有意であるばかりか、Mi - Mf 関係にとっても 大事である。というのは、それが母星質量と共に WD 質量も上がることを強調した からである。どうやら、 MWD は縮退 C/O 核を持つ星の上限 8 - 9 M๏ と一致するらしい。これは、Mengel 1976 の意見、すなわち C/O 核を発達させるのと同じ高い光度が大きなマスロスにより、爆発的な C/O 核燃焼 を妨げるであろう、に従い、 Weidemann 1979 が述べた、明るく、大きな C/O 縮退核 を持つ WD の提案が最初である。

　２．Mi - Mf 関係　

散開星団 WD の Mi 決定法　

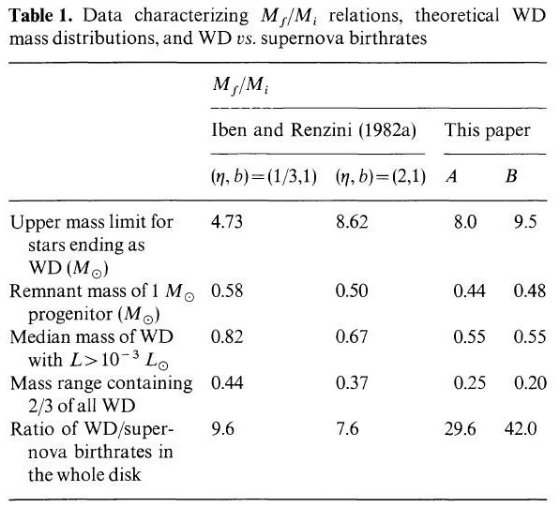
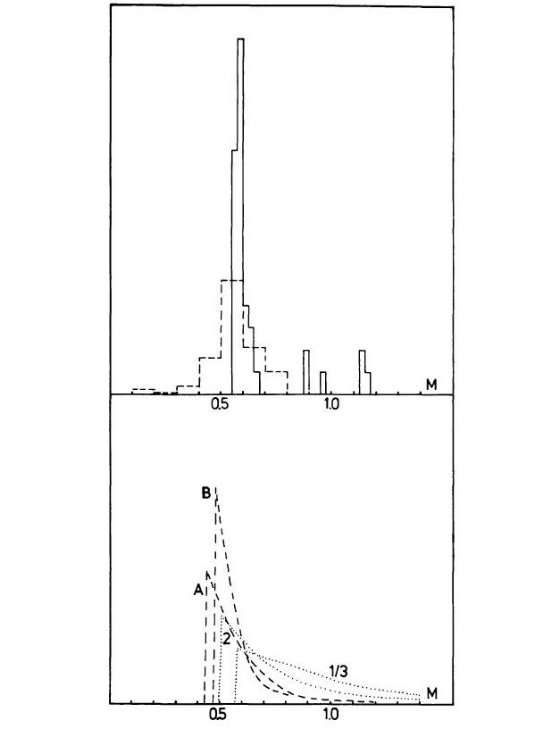
　星団メンバー WD は、温度、重力、質量(半径ー質量関係から)が決まるので、 星団 年齢から WD 冷却年齢を引いて WD 誕生年齢を出し、そこから Mi を出すことができる。 Mf の決定に表面重力を用いる方法 M(g)と、有効温度と距離から半径を決めて質量に至る 方法 M(R) の２種類あるが、どちらも 1977 年以来行われてきた。 　Koester, Schulz, Weidemann 1979, Schulz, Wegner 1981 は ヒアデス、プレアデス、 40 Eri B を調べた。　それらの結果は図１にまとめて示されている。

NGC 2518 の Mi 決定　

　Reimers, Koester 1982 は NGC 2516 の WD を調べた。 Koester 1982 の tcool を用いた３つの高温 WD の結果は、以下の通り。
星 2516-M(g)(M๏) Teff(K)tcool(107 (yr) Mi(M๏)
10.9530,0004.87.2
21.1436,0005.37.6
51.1733,5007.59.8
上の結果は、重い母星ほど重い WD を産むという予想と完全に合致する。

　星団年齢は Maeder, Mermilliod 1981 の等時線から決めた。ただし、ECHB = End of the Core Hydrogen Burning から AGB 開始までの進化時間は Becker, Iben 1979 と　Becker 1981 の計算(Y=0.28, Z=0.03)を内挿して得た。他の進化時間は短いので 無視した。

こうして、母星質量の関数としての進化時間は、tECHB(Maeder,Mermilliod) + tAGB-ECHB - tECHB(Becker) で与えられる。 　（第３項は要らないんじゃないか？）　 この値を t(Cluster) - tCOOL と比較して母星質量 Mi が決まる。

40 Eri B の 場合　

　40 Eri B には直接視差が与えられていて、M = 0.43 ± 0.04 (Heintz 1974) とされていた。しかし、 Wegner 1980 によればこの制限は少しきつすぎ、0.37 - 0.55 M๏ がもっともらしい。母星質量は接線速度 97 km/s から 考えて小さいだろう。

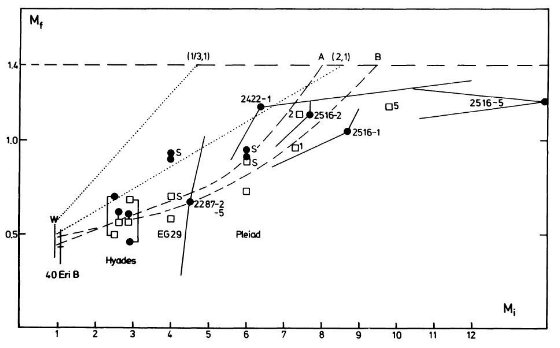
図１　点線＝Iben,Renzini 1982 (η, b) = (1/3,1), (2,1) 鎖線＝関係Ａ，Ｂ
　　　四角＝log g からの結果。黒丸＝半径からの結果。
　　　Ｓ＝Schulz,Wegner 1981,　Ｗ＝Wegner 1980

ケースＡ　と　ケースＢ　

　誤差の大きさを考慮して次の二つの関係を提案する。

Ａ： MWD = 8 M๏ で　ヒアデス、プレアデスを通る。

Ｂ： NGC 2516 を重視し、 MWD = 9.5 M๏ で チャンドラセカール質量に達する。

どちらも Mi = 5 M๏ 以下で平らになる点は共通である。しかし、この 観測的 Mi/Mf 関係と Iben,Renzini 1982 の直線関係との差は明瞭である。この 観測的関係に合わせるためには、マスロスが　3 - 6 M๏ で強い 必要があり、η > 1 の必要がある。

　提案された Mi - Mf 関係は平坦で WD 質量の巾が狭いことを自然に説明する。

　３．白色矮星の質量分布　

　Koester,Schulz,Weidemann 1979 は　M(R) を用いて、つまり距離が判っている WD の 有効温度と半径から質量を出す方法で、DA 型（全体の 80 - 90 %）の 2/3 が M = 0.57 - 0.59 M๏ に含まれると主張した。しかし、もっと 大きな分散があったとする論文も多く、この意見は直ぐには認められなかった。

　ごく最近、Greenstein が１０年以上に渡り収集してきた多色データを Weidemann が 解析した結果、上の見解が改めて確認された。Schulz 1977 が最初に使った広帯域測光 カラーは単波長測光カラーよりも優れていることが判った。

　理論的には RGB 端でのヘリウムコアマスが 0.45 M๏ なので、 WD 質量の下限はこの値で、高い方にはテールを引くと考えるのが妥当であろう。

４ 惑星状星雲中心星（nuclei of planetary nebulae :
　　　NPN）の質量分布　

Schonberner 法による NPN 質量の決定　

　Schonberner 法、星雲膨張から決まる NPN 年齢を AGB から WD への理論進化 経路と較べる、から導かれる NPN 質量巾は極めて小さい、0.58 M๏ をピークとし、 0.55 M๏ 以下にはなく、0.64 M๏ を越える天体は極めて稀、であることが判った。このピークの鋭さは主に、 AGB 光度 はコアマスで大きく変化し、 NPN　光度の大部分が 104 L๏ 以下であることが原因である。

NPN 質量分布は WD より狭い　

　観測の選択バイアスは若く明るい PNP に傾くが、距離で切ると 0.64 M ๏ を越えると急に減少することが判る。この局所サンプルには Schonberner

(Mv-Tevol)図でも、普通のＨＲ図でも 0.8 M๏ を越す大質量 PNP があるように見える。しかし、Schonberner 1981, 1982 は M(NPN) の関数としての理論的光度関数を重ね合わせて、観測と合うのは NPN 質量が 0.55 - 0.65 M๏ の間にある時であることを示した。

　この Schonberner 法は Pottasch 1982, Heap 1982 に使われて、 NPN 質量が 低質量側に集中していることが確定した。特に、Kohoutek, Martin 1982 は ＨＲ図からは高温で大質量に見える NPN の大部分が実は 0.55 - 0.85 M๏ にあることを明らかにした。

　Kaler 1982 による大きく広がった惑星状星雲の研究では、Zanstra 法を適用して NPN 質量が広い範囲に渡っていることが結論されていた。しかし、Schonberner 法ではこの質量巾は狭まる。Cahn, Kaler 1971 の距離を使うと、73 NPN 中 10 天体 が 0.64 M๏ を越す。もし、よく言われるように(Weidemann 1977, Jacoby 1980, 1981, Schneider et al 1982)、距離を 1.2 倍伸ばすべきとすると、 その数は５個に減る。そして、 0.64 - 0.60 に 8, 0.60 - 0.565 に 46, < 0.565 - 0.552 M๏ に 14 となる。それより下にはない。

NPN 質量の下限 = 0.55 M๏ の意味　

　したがって、NPN の 82 % が 0.58 ±0.03 という狭い領域に集中する のである。分布は 0.55 M๏ で鋭く切れている。明らかに、 0.45 - 0.55 M๏ の白色矮星は PN 段階を経ていない。それらの 星では、 AGB から電離光を放射するまでの進化がゆっくりしすぎていたか、そもそも AGB に辿りつかなかったか（ RGB 段階でマスロスが強く、直接 WD へ向かったか） (Sweigert 1974, Weidemann 1975) だろう。後者の場合、log g - log Te 図上で sdO として現れるはずである。(Hunger et al 1981, Mendez 1981)

　結論として、 NPN 質量分布は、 WD より鋭く、0.55 - 0.60 M๏ に Schonberner サンプルでは 85 %, Kaler サンプルでは 82 % が入る。

　５．銀河進化のためのモデル計算　

Mi - Mf 関係から WD, NPN 質量分布を再現できるか？　

　Koester, Weidemann 1980 は Mi - Mf 関係を使って、第３，４章で示されたような 観測 WD, NPN 質量分布再現を試みた。本論文ではそれを少し改良した。改良点は （１）ＩＭＦと、（２）高度スケールの扱い、である。

ＩＭＦ　

一方、IMF に関し、Miller, Scalo 1979 は、 太陽近傍の観測 LF から導かれる IMF はその際に仮定する銀河系星形成史に殆ど よらないことを示した。中間質量領域では、彼らの結果は Tarrab 1982 の散開星団 での IMF の研究で支持された。

　Tarrab は IMF が単一ではないと主張しているが、この論文では Miller,Scalo IMF と 12 Gyr の間、一定の星形成率を仮定する。Miller, Scalo はこの期間で 星形成率はファクター２の範囲で一定であると主張している。一定星形成率の仮定 は Twarog 1980, Twarog, Wheeler 1982 によっても支持されている。

高度スケール　

　計算では、銀河面に立てた 1pc2 の柱を考える。太陽近傍密度 ( 1pc3 ) への変換に、Koester, weidemann 1980 では、単純に主系列 星質量に応じたスケール高度で割るだけであった。今回は Wielen, Fuchs 1982 に 習い、各世代の星は薄い円盤上で形成され、

　　　　　　　　　スケール高度 ∼ σW(t)

と増加していくと仮定する。ここに、 t は星形成以来の時間、 ∼ σW は銀河面垂直方向の速度分散である。

σW2 = 1 ( 100 + 6 × 10-7 t ) 　(km/s)2
5.9

計算結果　

　計算の際の拘束条件は、

(i)　中央値質量＝ 0.58 ± 0.06 M๏
(ii)　ΔM = 0.3 M๏ 内に、全 WD の (2/3) が収まる。
(iii)　誕生率(WD) 対　誕生率(SN) = 10 - 40

　表１にその結果が示されている。ケースＡのみが上の条件を満たしていることが判る。 しかし、ケースＢも条件(iii)がぎりぎりでアウトになるだけでかなり良い。Iben, Renziniのモデルは WD 質量分布の巾が広くなり過ぎる。質量の中央値は Mi - Mf 関係の低質量側、つまり 1 M๏ の星が残す WD 質量、に大きく影響 される。観測との比較は、上の関係が1 M๏ 付近で、低 WD 質量, かつ平坦な勾配であることを支持している。

表１　仮定した４つの Mi - Mf 関係から導かれる WD 質量分布　





図２ (a)　実線＝ＮＰＮの観測質量分布(Schonberner 1982)。
　　　　　鎖線＝ DA型 WD の観測質量分布(Koester,Schulz,Weidemann 1079)
　　　(b) 図１の Mi - Mf 関係を使ったＷＤの理論的質量分布。
　　　　　点線＝Iben, Renzini の (η, b) = (1/3, 1), (2, 1)
　　　　　鎖線＝本論文のケースＡ，Ｂ



　６．議論と結論　

若い星団　NGC 2316 の意義　

　NGC 2316 の観測は次の事実を疑いなく確立した。

（１）．若い星団には重い白色矮星が存在する。　
（２）．8 M๏ まで白色矮星形成が伸びている。

　初めの点は、重い母星ほど重い WD を生むということを確定したで重要である。 この仮説を支持する証拠は今までプレアデスと NGC 2422 中のそれぞれ一個の WD だけであった。

　NGC 2516 のサンプル数の統計から、現在のターンオフ質量 4.75 M๏ と MWD = 8 M๏ の間で、予測された死亡星 の数と観測された WD の数の一致は完全で、この質量区間でその上超新星事象を 付け加える余地はない。

平坦な Mi - Mf 関係　

　第５章のモデル計算だけでも、現在観測されている WD 質量分布の鋭いピークを 説明するには、平坦な Mi - Mf 関係と高い MWD が必要となる。Koester, Weideman 1979 では急勾配の Mi - Mf 関係から、狭い WD 質量分布を説明したが、 その時には指数関数型の星形成史が仮定されていて、その場合には銀河系初期に 生まれた多数の小質量星に大きな重みがかかるのである。現在支持されている 星形成率一定のモデルに急勾配の Mi - Mf 関係を適用するとどうしても巾が広く なってしまうのである。

高度スケールの増加　

　第５章で採用した高度スケール増加の拡散メカニズムが正しいかどうかにも疑問 視は可能である。しかし、生まれた星を母星質量ー高度スケール関係にしたがって 薄めるだけで、メカニズムがどうであろうと定性的には同様の結果が得られる。

WD 質量分布の限界 　

　WD 質量分布には高質量側にテールが伸びているかもしれない。表面重力の高そうな WD 例えば、EG5, EG155, Gr+70°8247、の視差決定は非常に重要である。同様に 下限が本当に理論値、 0.45 M๏ であるかの確認も重要である。

惑星状星雲中心星 　

　NPN に対しては、 WD の場合と同様以下の点が大事であろう。

（１）距離決定の精度を上げる(Pottasch 1982, 1983)
（２）低光度 PN, NPN の観測を増やし、近傍サンプルの完全度を高める。

　タイプＩ PN (Peimbert, Torres-Peimbert 1982) の中に高質量 NPN があるのでは ないかという意見がある。ただ、それら　29 天体の中の 10 天体を調べた限りでは、 7 天体は M < 0.58 M๏, 2 天体が 0.62, 0.64 M๏, NGC 6537 だけが多分高質量であった。もしかすると、高質量 NPN は中心星が隠さ れているような PN に存在しているのかも知れない。その場合、既存の NPN リスト には載っていないわけである。



 ＬＭＣの高光度惑星状星雲中心星 　

　Stecher et al. 1982 はＬＭＣ内に ∼ 1 M๏ の NPN を 発見したと主張している。これは、Mbol ∼ -6.5 と Mcore - L 関係に基づいて いる。一般には、NPN の光度低下タイムスケールは質量に大きく依存し、したがって 非常に明るい NPN を見る確率はとても低いと思われていた。しかし、ＬＭＣのように 総質量が大きいと数個はあるのかも知れない。

　一方では、Flower 1981 が調べた NGC 1866 内の非常に明るい巨星の結果では、 大部分の星は AGB を離れる時 3.4 < log L/L๏ < 3.9 であり、これは Mcore = 0.55 - 0.65 M๏ に対応する。
（NGC 1866 の場合に限定？）
この星団は若い、9 × 107 yr, ので母星質量 ≈ 5 M๏ である。

ＰＮを経ない進化　

　Schonberner 1981 は NPN の下限が 0.55 M๏ 付近であるとした。 これは、逆のケースにあたる ハロー sdO星 RWT 152 が可視の星雲を伴わないが その温度 45,000 K は十分な電離放射を出している（Ebbets, Savage 1982）の 存在により支持される。RWT 152 は log L/L๏ = 3.25 であり、 Schonberner の進化経路上では M = 0.55 M๏ である。AGB 終了後 この位置までの時間が長すぎると放出ガスは散逸してしまった(Renzini 1981, 1982) 可能性がある。Schonberner 1983 の最近の計算では 0.546 M๏ 星が AGB から log Te = 4.5 まで移る時間は 、1.2 × 105 yr である。

　Sweigert et al. 1974 の計算では、0.51 M๏ の水平枝星は ABG に全く辿りつけない。低光度ままＰＮ放出なしにＷＤへ移行してしまうのである。 この問題の解明には、NPN の下限 0.55 M๏ を明確に定める 必要がある。現在のデータでは、表１、図２に見られるように PN 状態を経ないで WD になった星の数が 50 % （ NPN 下限 = 0.55 M๏ の場合) に達する。最終マスが 0.52 - 0.54 M๏ あたりに来る星の進化 計算も重要である。

　このように、Mi - Mf 関係で残された最大の問題は WD の下限である。

星間空間への寄与　

　こうして、Iben,Truran 1978, Renzini,Voli 1981 の進化スキームは変更が必要 であることが判った。星間空間に還流される質量は大幅に増加し、メタル量増加も 前の話とは変わるだろう。ただし、これまでの話は孤立星進化のみを考えてきた。 特にタイプI PN のような星は連星起源という説も強い。 まとめ　

（１）MWD ≈ 8 M๏

（２）Mi - Mf 関係は平坦である。

（３）低中質量星の大部分は ∼ 0.6 M๏ の　WD を残す。

（４）高質量 NPN, WD が存在するが極めて少ない。

（５）M < 0.55 M๏ （全体の50%）の　WD は PN を経てない。

（６）孤立星進化の話は上の拘束を考慮しなければならない。