IRAS Observations of OH/IR Stars. Determination of Absolute Luminosities and Mass Loss Rates

　アブストラクト　

　１．イントロダクション　

　２．距離　

　３．サンプル　

　５種のデータ源　

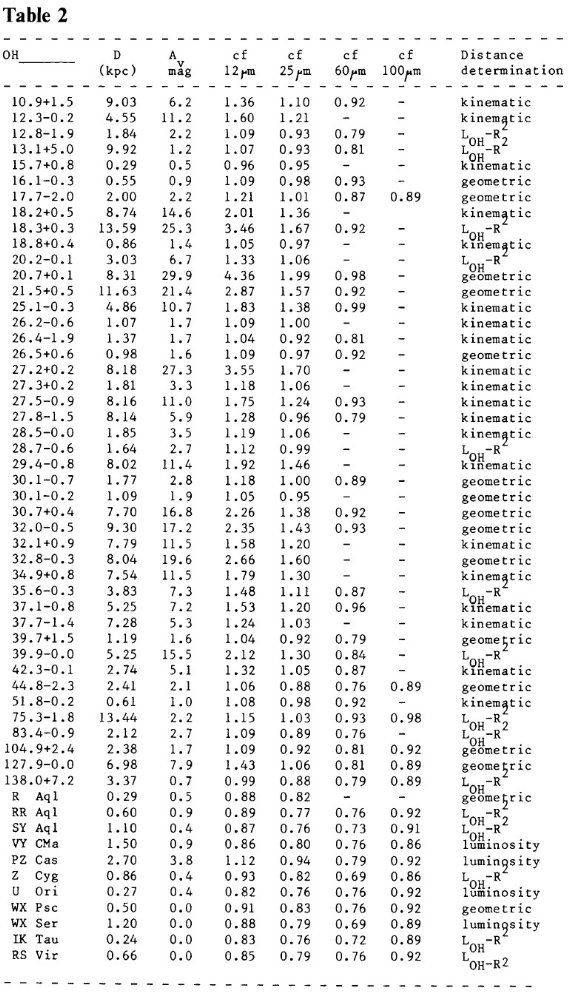
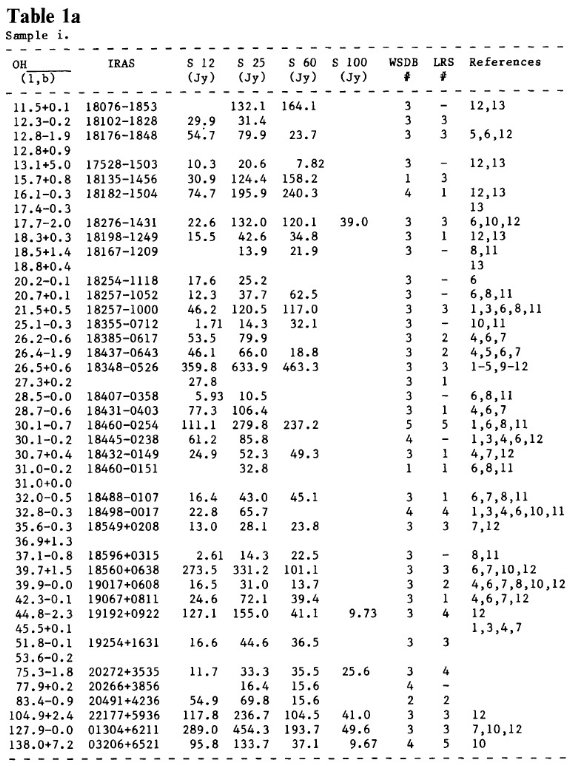
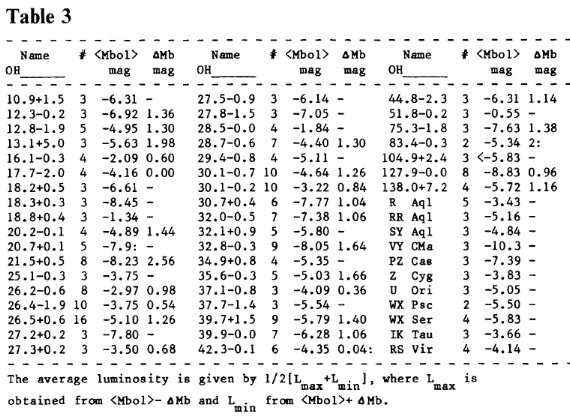
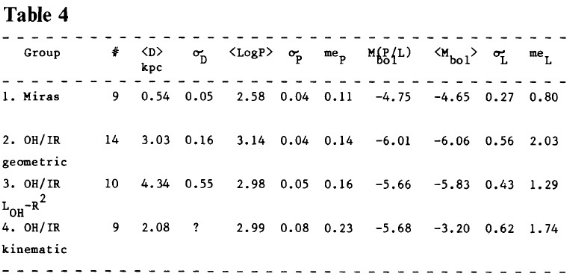
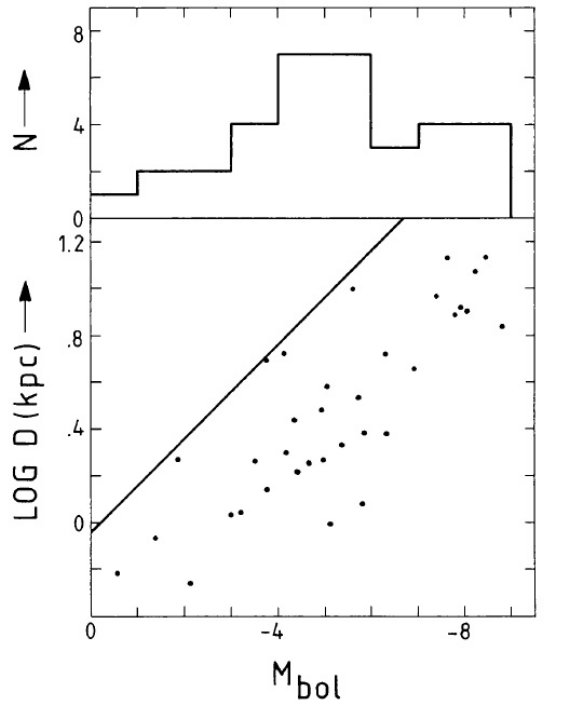
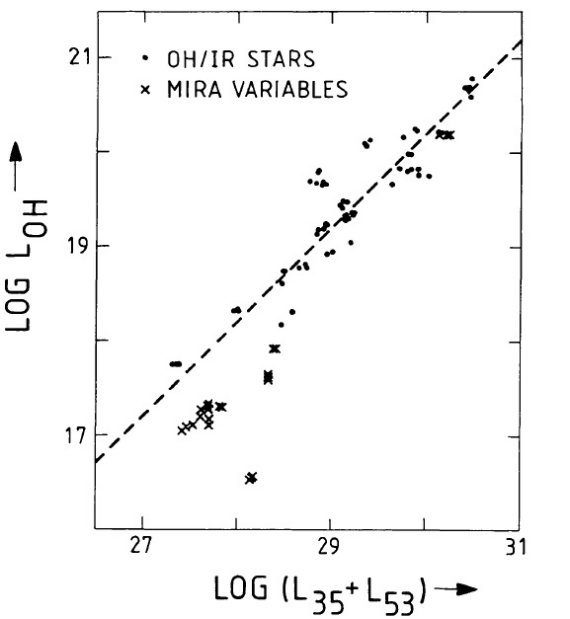
表１i．Baud et al.1979 のフラックスリミッテッドサンプルからの 45 星。 　サンプル主要部は Herman, Habing (1985a) で扱った Dwingeloo データである。それらは、 (i) Baud et al 1979 の サーベイ　　 　SOH > 4 Jy サーベイからの 45 天体。 14/45 星は VLA から 幾何学的距離が知れている。10/45 星は LOH - R2 距離が分かる。このグループの平均距離は 4.3 kpc である。弱くて近距離 (< 1 kpc) から非常に明るいが遠距離 (> 10 -12 kpc) まで幅が広い。 (ii) GC 天体　　 　３天体。距離を 9.2 kpc とする。 (iii) ミラ型星　 　９星。近傍 (< 1 kpc) にあり、まあまあのマスロスで弱いメーザー。 R Aql と WX Psc は幾何学距離、5/9 星は LOH - R2 距離。ミラシェルの半径は OH/IR 星の一桁小さいので、位相遅れ半径、敷い ては距離の精度は悪い。 　(iv)　超巨星　 　1612 MHz メーザーを出す 3 星。距離は文献から得た。

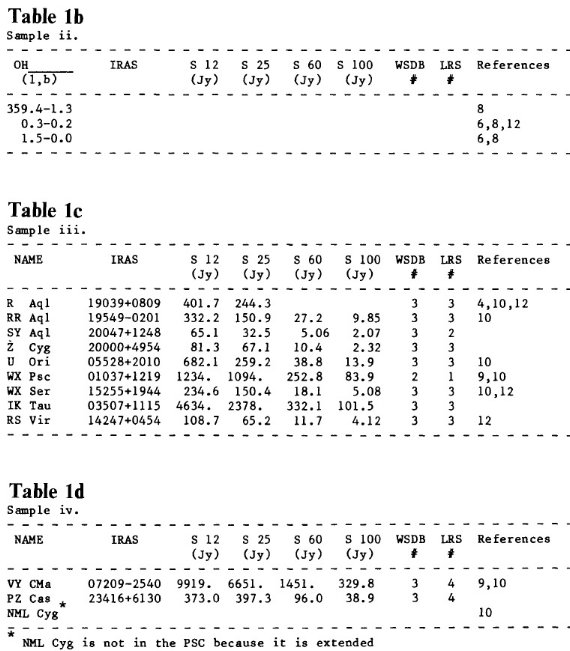
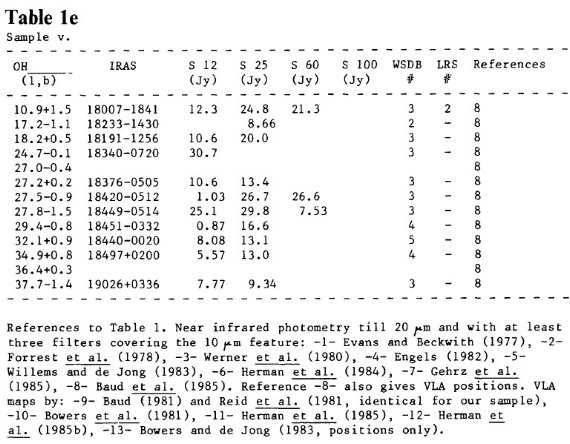
表１ii = ＧＣ付近, iii = ミラ型星, iv = 超巨星． 表１v．接線方向天体 　(v) 接点天体　 　Baud et al 1985 の、 SOH > 1 Jy で視線速度が大きい OH/IR 星。接点付近にいると看做される。平均距離は 8 kpc.

　フラックス　

図１b．WX Ser の地上近赤外、IRAS 測光、分光結果。 　図１＝赤外スペクトル　 　図１a の OH26.5+0.6 は典型的な OH/IR 星、 OH17.7-2.0 は珍しいタイプ の非変光 OH/IR 星の例である。図１b の WX Ser は可視ミラ型星である。 図１c の VY CMa はグループ (iv) の超巨星の一つである。 　フラックスの信頼度　 　QI = 3 で信頼できる IRAS フラックスのみを扱うので、 OH 45.5+0.1 のよう に AFGL カタログに載っていても混入の危険がある天体は外される。一方 GC 3 天体は同定が怪しいが距離は正確であろう。 　F25, F60 しか Q = 3 でない　 　OH 11.5+0.1, OH18.5+1.4, OH 77.9+0.2 は F25, F60 しか使えない。それらは OH 31.0-0.2 (Q2=3 だけ）と並び、OH17.7-0.2 と似ている。SED と LRS は似ていて、 どもうも全て非変光らしい。 　位置が不確かな 5 OH/IR 星　 　OH 12.8+0.9, OH 27.3+0.2, OH 31.0+0.0, OH 36.9+1.3, OH 53.6-0.2 の 位置は精度が低いため、赤外同定が怪しく IRAS フラックスが得られない。

図１a．OH 26.5+0.6 と OH 17.7+2.0 の地上近赤外、IRAS 測光、分光結果。 図１c．VY CMa の地上近赤外、IRAS 測光、分光結果。

　位置　

VLA 位置と IRAS 位置との比較　 　45 天体では VLA 観測が行われ、正確な位置が分かった。ただ、 OH 17.4-0.3, OH 18.8+0.4, OH 27.0-0.4, OH 36.4+0.3, OH 45.5+0.1 は HIIR と近いために位置が決まらない。VLA 位置と IRAS 位置との差の ヒストグラムを図２に示す。一致は良い。 RS Vir は固有運動が大きいために ズレが大きい。

図２．VLA 位置と IRAS 位置との差。

　カラー、星間減光の補正　

カラー補正　 　PSC では νF(ν) = 一定を仮定して補正したフラックスを載せている。 Explanatory Supplement VI C6 にはパワー則 SED に対する補正値が載 っている。そこで、各バンドでの SED 勾配を求めれば補正値が求まる。 ただし、F12 は 10μ シリケイトバンドの影響がある。8 - 15 μm の 平均勾配を使えばｍエラーは精々 7 % に押さえられる。IRAS 4 バンドでの 補正値は、ミラ型星で 5, 10m 15, 10 %, OH/IR 星で 5, 10, 15, 10 % である。 　星間減光　 　25 μm でも減光補正はファクター 2 に達する場合がある。減光量は 簡単なモデル de Jong 1983, Herman et al 1984 から求めた。60, 100 μ では減光より星間放射が影響するが、考慮しない。 　距離　 　表２には個々天体の距離を最終列の参考文献と共に示す。第４−７列には 表１のフラックスに施すべき補正ファクターを示す。以降ではフラックス は補正後の値を意味するとする。

表２．OH/IR 星のカラー、減光補正と距離。

　４．輻射等級　

図３．上：地上観測 [2, 20] μm から計算した C12 カラーの分布。 下； IRAS 観測による C12 カラーの分布。 斜枠＝ミラ型星。白枠＝ OH/IR 星。地上観測には観測しやすい青天体に バイアスが掛かる。 　図４のフィット線は 　　　I(0) = 0.147 C122 - 0.487 C12 + 0.419 　　　I(1) = 0.052 C122 + 0.276 C12 - 0.146 と表される。

図４．I(0) と I(1) の C12 による変化。 　　　I(0) =log[∫2μm12μmSνdν /(ν&12S&12)] 　　　I(1) =log[∫12μm100μmSνdν /(ν&12S&12)] 　OH/IR 星の赤外フラックスは F12 と F25 を知れば、 　　　F: = ν&12S&12[10**I(0) + 10**I(1)] で求まる。ミラ型星では星の < 2 μm 放射が多いので不正確となる。

　４．１．OH/IR 星の変光曲線　

図５．少なくとも４点の観測がある 17 OH/IR 星の輻射等級変光曲線。 変光周期とゼロ点は Dwigeloo モニターによる。 OH20.7+0.1 の第１点、 OH39.7+1.5 の φ 0.48 点でのみズレが大きい。 表３．17 OH/IR 星の輻射等級。

図６．(a): OH26.5+0.6 の 輻射等級と OH 等級の変光の比較。 (b): OH 32.8-0.3 での比較。 　近似変光曲線　 　f = 増光期間の割合、とすると、変光曲線は二つに分けた式で良く表現される。 0 < φ < (1-f) では 　Mbol = ⟨Mbol⟩ + ΔMbol cos[2π(1-φ)/2f] (1-f) < φ < 1 では 　Mbol = ⟨Mbol⟩ + ΔMbol cos[2πφ)/2(1-f)] 　輻射等級と OH 等級の比較　 　図６にあるように、両者の変化は良く合っている。

　４．２．周期光度関係　

表４．４グループの星の平均輻射等級と周期。 　 　Feast 1984 は LMC (DM=18.53) 非炭素星ミラに対し、 　　　Mbol = 1.03 - 2.242 log P 　　　Mbol = -2.5 log(L*/Lo) + 4.7 という関係を見出した。周期が非常に長い我々のサンプルもその関係 に従うことが図７から分かる。グループ１、２，３の平均値は LMC ミラの延長 とよく合う。グループ４は運動距離グループだが、 2.5 mag 落ちる。 ( 個々の星をプロットすべきだ。)

図７．４グループの星に対する平均輻射等級と周期の関係。 グループ１＝ OH メーザーありのミラ型星。グループ２＝幾何学距離 のある OH/IR 星。グループ３＝LOH - R2 距離 のある OH/IR 星。グループ４＝運動距離のある OH/IR 星。 破線＝ Feast 1984 の LMC ミラ。

　４．３．AGB 光度関数　

図８．距離と輻射等級。実線＝ OH 検出限界と LOH - L* 関係とからの限界線。 　N(Mbol) = OH/IR 星の光度関数　 　図８はサンプル(i)= Baud et al.1979 のフラックスリミッテッドサンプル からの 45 星の光度分布を示す。実線＝ OH 検出限界フラックス 4 Jy に 対応する。サーベイは銀河面の両側 4° 以内に限定された。Herman, Habing 1985b Phys.Rep. で求めたスケール高を採用し、更に図８下のサンプル領域の 変化を補正して、観測された光度分布を光度関数 N(Mbol) へと変換した。 図９に得られた光度関数 N(Mbol) を示す。

図９．AGB光度関数。破線＝ Miller, Scalo 1979 の主系列光度関数から導いた予測。 　モデルから求める OH/IR 光度関数　 　 Baud, Habing 1983 はシェル膨張速度 Ve が主系列質量と相関することを示した。その速度区間 11 - >20 km/s は Mms = 1.5 - 10 Mo に相当する。 Miller, Scalo 1979 は主系列星の質量関数と光度関数を与えた。彼らの光度関数と、我々の AGB 光度 関数の比較から、平均すると AGB 光度は主系列の 2.5 mag 明るいことが判る。 N(Mbol) = 単位銀河面当たりの OH/IR 星光度関数（星数/mag/kpc2)、 φ(Mbol) = 太陽近傍主系列星光度関数(星数/mag/kpc3)、 tms(Mbol) = ZAMS 寿命、H(Mbol) = スケール高、tOH = OH 期寿命、fOH = OH メーザーを持つ星の割合とおくと、 　　　N(Mbol) = 2H(mbol)φ(Mbol)tOHfOH/tms(Mbol) 　　　　　　　(5) ここに、φ(Mbol) = φ(Mv-2.5) (何を云おうとしているのか？ 上式の 2.5 が前に 述べられた主系列と AGB の等級差だろう。 φ(Mbol) は (Mbol+2.5) mag における 主系列星光度関数のつもりで使っている。輻射補正がカラーに依らず一定としてだが。 それなら、φ(Mbol+2.5) と書くべきと思う。)

　５．エネルギー分布の性質　

図１０．ポンプ光度 Lp = (L35+L53) と LOH の関係。破線＝ ポンプ効率 25 %. (L35, L53 の単位が本文にもない。 　Elitzer 1980 は 1612 MHz OH メーザーの励起が 35 μm と 53 μm 赤外光に依ることを示した。図１０は IRAS WSDB と同じ時期の メーザーモニター 観測値と Lp (内挿値？)の関係を示す。ミラ型星の変換効率が約ファクター２低い。 これは、 Bujarrabal et al 1980 により予言されていたことである。OH/IR 星に対してフィットすると、 　　　log LOH = log Lp - 9.76

図１１．ポンプ光度 Lp の総光度中比率　Lp/L*　と 赤外カラー C12 = 2.5 log(F25/F12) との関係。 　図１１には IRAS 赤外カラーが赤くなるほど、ポンプ周波数でのフォトン比率 が高くなることを示した。フィット式は、 　　　2.5log(L*/Lp) = 1/(0.19C122+0.81C12+0.22) 　　　(7) 後の使用のため、 X = 1/[2.5 log(L*/Lp]で C12 を表す。 　　　C12 = -0.125 X2 + 1.17 X - 0.23　　　　　　(7)'

図１２a．10μm シリケイト帯の深さ A10と C12 の関係。 A10 正は吸収。 A10 ＝ -2.5 log(F10/Fcont) 図１２b．20μm シリケイト帯の深さ A20と C12 の関係。 　可視ミラは 10, 20 μm の両方で放射帯を示す。OH/IR 星は、ほぼ確実に 10 μm 吸収と、非常に厚いシェルの場合は 20 μm 帯も吸収を示す。 A10 ＝ -2.5 log(F10/Fcont) で、Fcont は λ 8 μm と 12 μm の内挿値である。A20 も同様に定義される。 A10, A20 を決める地上赤外観測は IRAS と違う時期で、観測波長分解能が 10 程度で低いので、バンド強度は 0.32 程度過小評価で、またすこしずれている。 図１１a をフィットすると、 　　　A10(mag) = 2.57 C12 - 0.16　　　　　　　　　(8) と表せる。A20 の方は分散が大きく、はっきりした式が出ない。

図１３．OH 26.5+0.6 における、10 μm 帯深さ A10 と カラー C12 の変光 位相 φ による変化。実線＝ L* と LOH の差から予想された 変化。 φ = 0 が極大。 　以前に、総フラックスと OH フラックスの変光振幅が異なることが判り、 それは天体カラーが変光により変わるためと解釈された。 OH 26.5+0.6 は L* と LOH の変化が全位相に亘って観測されている唯一の星で ある。この星に対して、カラー C12 とシリケイト吸収強度 A10 の変化が 予言できる。 観測から、L* と LOH は位相 φ の関数として表される。 そこで、式 (6), (7)' から C12 が出て、式 (8) を使うと A10 が出る。 つまり、変光位相により LOH/L* が変化することを、赤外 SED ＝カラーの変化と看做し、そのカラー変化を吸収深度に変換するという訳で ある。 (図の実線を見ると、極大時に青くなり、 浅くなる。しかしこの予想曲線は観測点からは支持されない。観測点を見ると、 カラー変化に吸収深度が連動していない。うーむ。)

　６．マスロスとエンベロープパラメタ―　

この後の話は少しわずらわしいので略する。

図１４．rd = ダスト半径と ROH の関係。