| Olnon, Baud, Habing, de Jong, Harris, Pottasch (1984) による ミラ型星、OH/IR 星の IRAS 二色図は変光星が狭い系列を成すことを明らかにした。 ここでは、シリケイトダストシェルモデルを使い、この系列の解釈を与える。モデルは内径を ダスト形成温度 900 K で決め、光学的厚みを変えていく一次系列である。10 μm 吸収の 深い OH/IR 星にフィットするためには、吸収係数の形に以前使用されたものとは少し修正が 必要であった。それより薄い光学的深さの星では、マスロスに加速があると考えたモデルで 上手く合わせられた。 | 吸収係数が光学的厚みにより変化すると考える必要があった。光学的厚みが 大きい星では、 20 μm バンド強度の 10 μm バンドに対する比が大きく、 バンド幅が狭くなる。これは、吸収係数に温度依存性があるためであろう。 非変光 OH/IR 星はこのモデル系列のカラーでは再現できない。それらのダスト シェル内径は変光 OH/IR 星よりも大きい。これはマスロスの停止と解釈される。 そのような代表例 OH17.7-2.0 では、マスロスは突然止まったのでなく、 290 年掛けて、ファクター 6 104 下がったと思われる。その間に表面 温度は 現在の 15000 K にまで上がったらしい。 |
|
計算モデル Yorke 1977, 1980 の数値計算モデルを使い、入力パラメタ―は次のようにした。 (i) 中心星スペクトル R Cas 1 - 4 μm の位相 0.07, 0.46 SED (Strecker et al 1978)を使用。 λ > 4 μm には BB(3000K) を接続。レイリージーンズ領域なので もっと低温にしても差はない。非変光 OH/IR 星ではより高温の黒体を仮定する。 (ii) シェルの内径と外径 ダスト温度 Td = 凝結温度 Tc で内半径 rc を決める。図3では Tc = 1000 K を用いたが第3章での詳細フィットの結果からは Tc = 900 K の方が 良いようだ。 (iii) 密度分布 ここでは dM/dt を W と書き表す。速度非一定マスロスを考えているので、半径 r でのマスロス = W(r), 速度= u(r) と書く。密度分布は、
u(r) は重力と輻射圧のみを考えた運動方程式の近似解である。uc = 2 km/s = 1000 K ガスの音速、u∞ = 15 km/s とした。 (iV) シェル光学深さ ある波長でのダストシェル光学深さ。ここでは 10 μm ピークをとる。 |
(v) ダーティシリケイト吸収係数 Jones, Merrill (1976), Bedijn 1977 のダーティシリケイト、つまり κ(1μm) = κ(9.7μm)、 だが、少し修正を加え、SEDフィットを向上させた。 (a) 散乱 a = 0.1 μm 散乱は無視する。 Jones, Merrill (1976), は λ = 1 μm、ダスト半径 a = 0.1 μm で散乱効率を吸収の 30 %, レイリー散乱で ∝λ-4 としたが、光学的深さが小 さいシェルではスペクトルに差はなかった。テスト計算では、 τ9.7 = 4 の光学深さ中程度の場合、散乱を入れても λ > 2 μm での スペクトルに変化はない。ただし、λ = 1.5 μm で 20 %, 1 μm で 50 % の減少が起きる。τ9.7 = 30 という厚いシェルでは、 λ > 2.8 μm でのスペクトルに変化はないが、λ = 1.8 μm で 20 %, 1 μm で 90 % の減少が起きる。それより短波長側では、 散乱の光学的深さが 1 以上になるため、スペクトルは突然急になる。 (b) 散乱 a = 0.05 μm レイリー近似では単位質量当たり散乱 ∝ a3, 吸収一定、 であるから、a = 0.05 μm の場合、散乱強度は 1/8 に減少する。このため、 厚いダストシェルでも散乱の効果は無視してよい。 (c) λ ≤ 5 μm λ ≤ 5 μm では、κ ∝ λ-1.5 と 仮定する。すると、κ1.65/κ9.7 = 0.67 と なる。 (どうしてか不明。 ) これは、Jones,Merrill グレインに比べると、 κ1/κ9.7 で 1.1 倍、 κ1.65/κ9.7 で 1.37 倍、 κ3.5/κ9.7 で 1.86 倍小さい。 ミラと OH/IR 星のスペクトルへのベストフィットは、κ1.65/κ9.7 が 10 % くらい大きい値を示唆しているが、上述のモデルを使って、二色図上 のカラーを計算した。 (d) λ ≤ 0.3 μm λ ≤ 0.3 μm では一定値 κλ = 10 κ9.7 を採用する。この値自身は ミラ型星や OH/IR 星では放射の 弱い波長帯なので意味がない。ただし、中心星が高温になる非変光 OH/IR 星では より丁寧な扱いが必要となる。 (e)λ > 40 - 60 μ κ ∝ λ-1 を仮定。 (e)κ(20μm) と κ(10μm) κ(20μm)/κ(10μm)はフリーパラメタ―。 形は OH26.5+0.6 吸収帯にフィットさせた。他の星、 OH39.7+1.5(GL2290), OH104.9+2.4(GL2885), OH127.9+0.0(GL230) も似た狭い 10 μm バンドを示 す。しかし、Rowan-Robinson, Harris 1983 による低光学的深さの放射帯はより 広い幅の方が合う。 幅が二色図位置にどう影響するかは第4章で調べる。 |
|
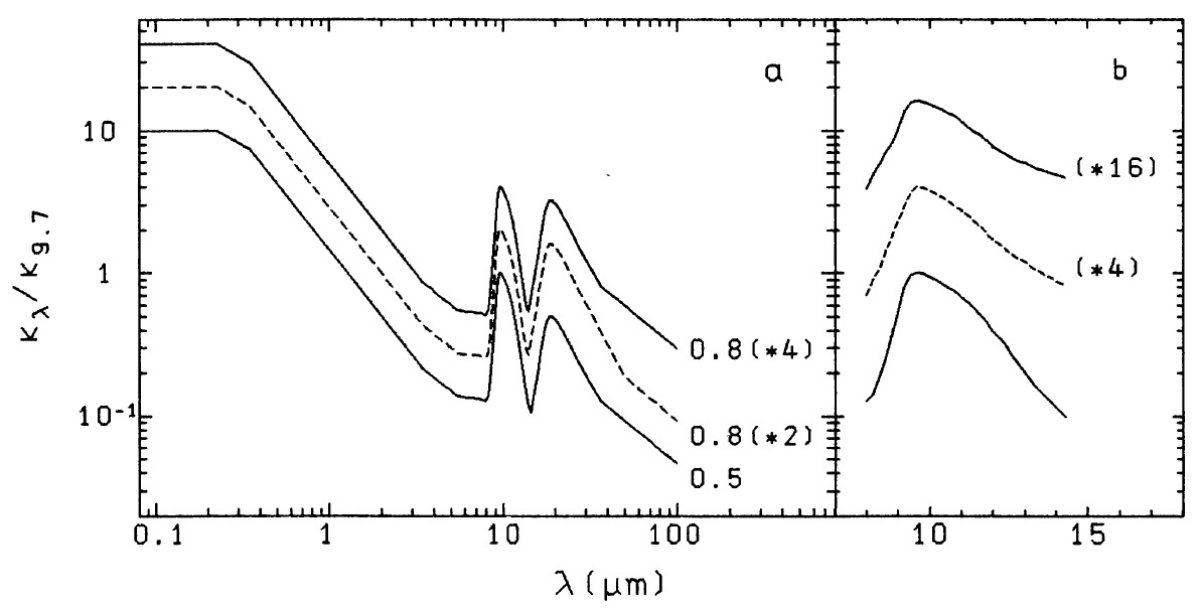
図1a = 3種類の吸収係数 図1a には、IRAS 二色図上の点の計算に用いた3種類の吸収係数を示す。 曲線横の数字は κ19/κ9.7 である。0.8 が付いている二つの曲線は、 破線が κ100/κ9.7 = 0.045, 実線が κ100/κ9.7 = 0.072 である。これ等の値は Rowan-Robinson, Harris 1982, 1983 が用いたダーティ シリケイトより大分大きいが、Day 1976a が測定した非晶質シリケイトの値に 近い。λ > 40 μm での波長依存性は Rowan-Robinson et al 1986 によっても独立に実証されている。 図1b = 3種の 10 μm バンド 図1b には、計算で用いた3種の 10 μm バンドを示す。 上の実線=低光学的深さ τ9.7 ≤ 1 のダストシェル、 中の破線=中間低光学的深さ τ9.7 ≈ 4, 下の実線=大きな光学的深さ τ9.7 ≥ 15 に適している。 |
バンドフラックスの計算 計算した SED を測光観測結果と比較するために、
ここに、Φλ = 感度曲線、 Fλ = モデルフラックス分布、 Fλa = 仮定したフラックス分布、 λo = バンド中心波長である。IRAS に対しては、 Neugebauer et al 1984 の Φλ を、UKIRT のバンド にはガウシャンプロファイルを用いた。 Fλa ∝ λ-4 = レイリー ジーンズテイルを仮定した。 (式3左辺の F はバンドフラックスの意味らしい。 ) |

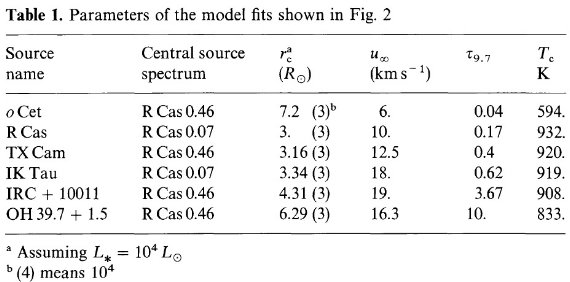 表1.図2でモデルフィットしたM-型ミラと OH/IR 星のパラメタ―。 OH26.5+0.6 OH26.5+0.6 は深い吸収を示す。 Forrest et al. (1978) は変光サイクルの同一位相における 2 - 40 μm 分光測光観測 がある唯一の星であり、κ(λ) の決定に使える。 他の天体では、同じ時期の測光データから SED を作ることは出来なかった。 しかし、バンドの形はフラックスの変化に比べると小さい。図6には 6 天体のスペクトルを示す。異なる記号は異なる時期を示す。例えば、 ο Cet, TX Cam, IK Tau, OH39.7+1.5 の小さい点は Merrill, Stein 1976a,b と Merrill 1977 の分光測光データを、R Cas では Puetter et al 1977 のデータを示す。図2での位相は ο Cet 0.7, R Cas 0.1, IK Tau 0.15, ITC+10011 0.3 と考えられる。 ベストフィット 図2の実線はベストフィットである。計算に用いたパラメタ―は表1に載せた。 ただし、 u∞ は OH, CO 観測からの値である。 10 μm バンドκλ の改訂 Schutte, Tielens 1985 は光学深さと共に 10 μm バンドの幅が狭くなることを 示した。本論文のモデルフィットでもそれが確認された。 (i) ο Cet, R Cas, TX Cam, IK Tau は 図1bの上曲線=幅広バンドを使用。 (ii) IRC+10011は 中間のバンド使用。 (iii) OH 26.5+0.6 は図1bの下曲線使用。 |
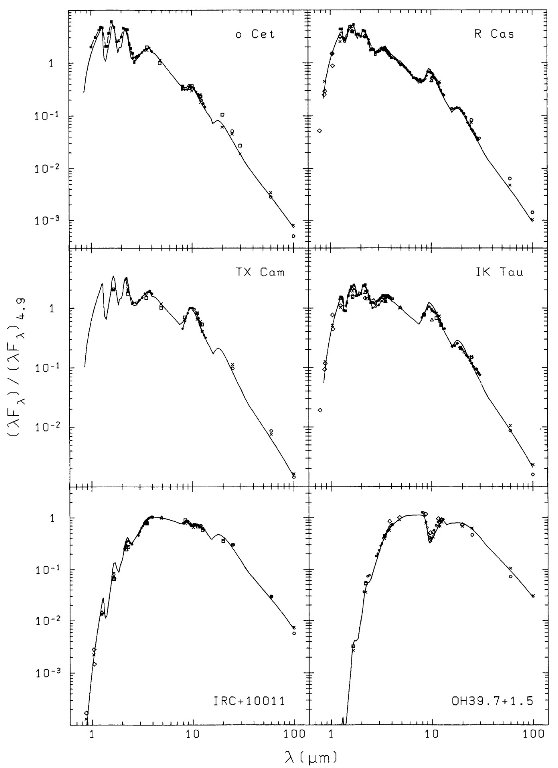 図2.M-型ミラと OH/IR 星へのモデルフィット。モデルパラメタ―は表1. バツ=計算したバンドフラックス。他の印=観測値。 |
|
κ1.65/κ9.7 OH39.7+1.5 を除き、κ1.65/κ9.7 は 10 % 程度大きい方がフィットが良い。ただし、λ < 8 μm では 図1a の実線0.5 を使用。これは吸収係数の温度効果と考えられる。 Tc 表1にフィットで決まる Tc = シェル内半径 rc での温度、を示す。 ο Cet を除き Tc = 900 K である。ただし、光学的に薄いモデルでは もう少し高い Tc でも同程度に良いフィットが得られる。ただし、 IRC+10011 と OH26.5+0.6 ではそうでない。現在の所、光学的深さが大きくなると Tc が 下がるという表1の結果が正しいのか、それとも光度極小時に Tc が低いのか、 はっきりしない。Tc に関しては様々な位相での全波長 SED を色々な光学的 深さのシェルに対して観測を集めることが望ましい。 伴星の影響? ο Cet で Tc が低いことは Rowan-Robunson, Harris 1983 も報告 している。 Gail, Seldmyer 1986 も参考にすると、これは伴星の影響で高温で のダスト形成が妨げられているのかも知れない。 Jones, Merrill モデル Jones, Merrill (1976) のダーティシリケイトは光学的にあまり厚くない r-2 密度分布 モデルに対して全体的にはベストフィットモデルを与える。しかし、IRC+10011 の λ = [8, 13] μm では、我々のモデルよりフィットが悪い。 ο Cet の干渉計観測 Sutton et al 1978 はスペックル干渉計により、ο Cet が位相 0.9 の時に、 11 μm で直径 0".62±0.08 と観測した。ここに直径=輝度 分布の 1/e に下がる点間の距離。この直径は、 位相 0.11 で 0."77±0".14, 位相 0.24 で 0."79±0".12 である。 |
総光度に対するダストシェル放射の割合は、位相 0.9 で 46 %, 0.11 で 60 %,
0.24 で 52 % である。我々のモデルによる値、L4.9/L*
= 559 cm-1、
Forrest et al. (1978)
による位相 0.15 (光度極大) 期の L4.9 を使うと, 表1にある
モデル rc は中心にあるダストなし空間の直径は 0".38 を意味する。
(全然分からない ) モデルでは総光度の 47 % がダスト放射である。 (τ9.7 = 0.03 でなぜ そんなに高い? ) IRC+10011 Zappala et al 1974 による IRC+10011 の 2.2 μm 月掩蔽観測は 一様円盤直径 0".013 から 2.2 μm 放射の 65 %, 一様円盤直径 0".065 から 2.2 μm 放射の 35 % と解釈された。 モデル値 L2.2/L* = 1060 cm-1 と 掩蔽時の観測値 F2.2 = 5.01 10-15W cm-2 μm-1 を使うと、表1の rc は内側シェル縁の角 直径が 0".049 であることを意味する。 (全然分からない ) モデルでは F2.2 の 30 % がダストシェルから放射され、それらは 1.3 rc = 0".064 以内に集中する。10 μm 観測は 2.2 μm 円盤の倍の直径の円盤、又は 36 % が 0".065 以内、全直径 0".13 の2成分 モデルで再現できる。0".2 以上外からの放射は 15 % 以下である。モデルは フラックスの 25 % が 0".065 以内、60 % が 0".13 以内、23 % は 0".2 より 外から来ると予言している。最後に 20 μm データは直径 0".27 の単一円盤 で説明できるが、2成分モデルも可能である。その場合、 フラックスの 63 % が 0".13 以内、全広がりは 0".27 である。 (ここも何を云おうとしているのか全然分からない ) 薄いダストシェルは急勾配モデルで説明できる 結論として、以上で光学的深さが薄いダストシェルはモデルで十分に説明で きることを実証した。これは、シェル内側付近で加速による r-2 密度分布より急な勾配を採用したためである。 |
|
標準モデルのパラメタ― IRAS WSDB を探ると、変光に伴うカラー変化があるらしい。一般には極小 付近で赤くなるようである。しかし、その揺れ幅は測光不定性の程度で小さい ので確認できない。モデル系列は 12 ダストシェルモデルに対し、光学的深さ を変えて行き得られた。中心星スペクトルは R Cas 位相 0.46 を用い、Tc = 1000 K とした。ただし、3章で述べたように Tc = 900 K の方が良い。吸収 係数には幅の狭い 10 μm バンドを採用したが、これはシェルの光学的深さ が浅い時には不適当である。u∞ = 15 km/s とした。 4.1.ダスト吸収係数表2=モデルパラメタ― batu 表2には 12 個のモデルに対するパラメタ―を示す。rc と dM/dt は L* = 104 を仮定した値で、L*1/2 でスケー リングされる。(dM/dt) は実際には rin(=rc) と τ9.7 に dM/dt = const.rinτ9.7 で繋がっているので、完全な自由パラメタ―ではない。 ダスト/ガス比は一定とする。 (その値が書いていない! ) 図3a = モデル系列 図3a にモデル系列を示す。実線 0.5, 0.8 は図1a の吸収係数 0.5 と 0.8 を用いた系列、破線 0.8 は同じく図1a の破線 0.8 を用いている。実際に 計算されたモデル点は白三角で示した。光学的深さ=マスロス率は左下から 右上にかけて増加する。 |
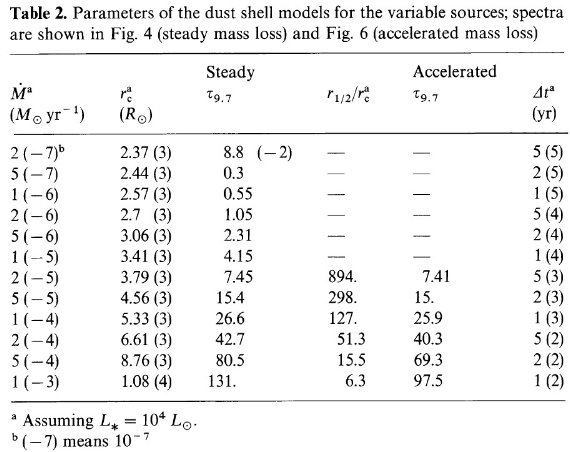 表2.様々な天体のモデルパラメタ―。定常マスロスのスペクトル は図4、加速流のスペクトルは図6に示す。 |
|
κ19/κ9.7 の変化 κ100/κ9.7 の値は実線 0.5 が κ9.7 ≤ 10 でよくフィットするように選んだ。と言うの は、個々天体の SED フィットは κ19/κ9.7 = 0.5 が適当であることを示しているからである。それにまた、F20/F10 - F10/F8 図に LRS の 10 μm 放射帯を持つ星をプロットすると、そのような κ19/κ9.7 のモデルでよくフィットする。 しかし、実線 0.8 の方は κ9.7 ≥ 20 の OH/IR 星の位置 を良く表す。それに、 OH26.5+0.6 の SED フィットも κ19/κ9.7 = 0.8 がベストフィットする。 この場合には明らかな 20 μm 帯の吸収を与えるが、 κ19/κ9.7 = 0.5 では僅かな吸収しか見 えない。 放射半径の変化 我々は κ19/κ9.7 のこの変化は吸収係 数の温度依存性によると考える。光学的に薄いシェルでは放射光は主にシェル 内側の高温ダストから来る。しかし、光学的深さが大きくなると、内側が隠さ れ、放射光は外側の冷たい領域から来るようになる。例えば、 (i)τ9.7 = 0.55 F10 の 50 % が r ≤ 1.7 rc (Td ≥ 753 K)から来る。 F19 の 50 % が r ≤ 3.1 rc (Td ≥ 536 K)から来る。 (ii)τ9.7 = 4.15 F10 の 50 % が r ≤ 2.7 rc (Td ≥ 424 K)から来る。 F19 の 50 % が r ≤ 4 rc (Td ≥ 370 K)から来る。 (iii)τ9.7 = 26.6 F10 の 50 % が r ≤ 5.6 rc (Td ≥ 261 K)から来る。 F19 の 50 % が r ≤ 10.5 rc (Td ≥ 181 K)から来る。 したがって、光学的に厚いシェルのスペクトルフィットに大きな κ19/κ9.7 が必要であるということは、 低温ダストの吸収率にそのような変化があることを意味する。 κ の温度依存性実験 実際、 Day 1976a, 1976b の実験では、κ9.7 も κ19 も低温になると増加し、かつ、 κ20/κ10 の 100 K での値は 380 K での 値の 1.55 倍になる。 κ10 は 1 - 2 割程度の変化だが、 それ以上に κ20 が大きく変化することがその原因である。 これに関し思い出して欲しいのは、光学的に薄いシェル (= 高温ダスト) では κ1.65/κ9.7 を 10 % 大きくするとフィッ トが良くなった。 λ < 8 μm で κλ が 変わらないとした場合、上の温度依存性は説明として良く合う。 |
κ100/κ19
は一定 図3a の破線 0.8 は長波長で吸収率をファクター 2 小さくした時の効果を 調べるための計算である。どうやら κ100/κ19 は変えない方がフィットがよい。 図4=モデルスペクトル 図4にはモデルスペクトルを示す。実線=中心星+ダストシェル。破線= シェルのみ。バツ=計算された広帯域等級フラックス。上の6スペクトルは κ19/κ9.7 = 0.5、下の6つは κ19/κ9.7 = 0.8 モデルである。 0.5 系列、下の6スペクトルは実線 0.8 系列に対応する。 図を見ると dM/dt = 10-6 Mo/yr で 10 μm 放射ピークが連続光 の2倍で極大値に達し、dM/dt = 10-5 Mo/yr で 10 μm 帯の 自己吸収が始まり、最後に深い吸収帯となることが判る。20 μm 帯は 5 10-5 Mo/yr で自己吸収が始まる。同様の系列を Merrill 1977 も示している。 吸収係数に温度依存性があるモデル 吸収係数に温度依存性があり、κ19/κ9.7 = 1 (T=100K), 1/1.55 (T=380) (Day 1976b) とした時のモデルを計算した。 単純化のため、κ9.7 自体は温度依存しない。図3b 破線は フィットのため κ100/κ19 を図1a 実線 0.5 の 25 % 下げた例。 温度依存吸収係数のモデルは τ9.7 ≤ 4 では τ19/τ9.7 = 0.5 モデルに、 τ9.7 ≥ 25 では τ19/τ9.7 = 0.8 モデルに似る。 τ9.7 = 26.6 スペクトルを見ると、0.5 モデルでは僅かな自己 吸収があるだけだが、0.8 モデルでははっきりした自己吸収を形成している。 一方温度依存モデルの 20 μm 自己吸収は 0.8 モデルより少し浅いくらい である。 パラメタ―の影響 (i) Tc = 700 K Tc = 1000 K から Tc = 700 K に変えた場合の IRAS 二色図は図3a と殆ど変 らない。 (ii) 10 μm 帯の巾 10 μm 帯の巾に図1b の上側曲線を使用した結果も2色図の変化は小さい。 (iii) u∞ u∞ = 5 km/s もほとんど影響はない。 |
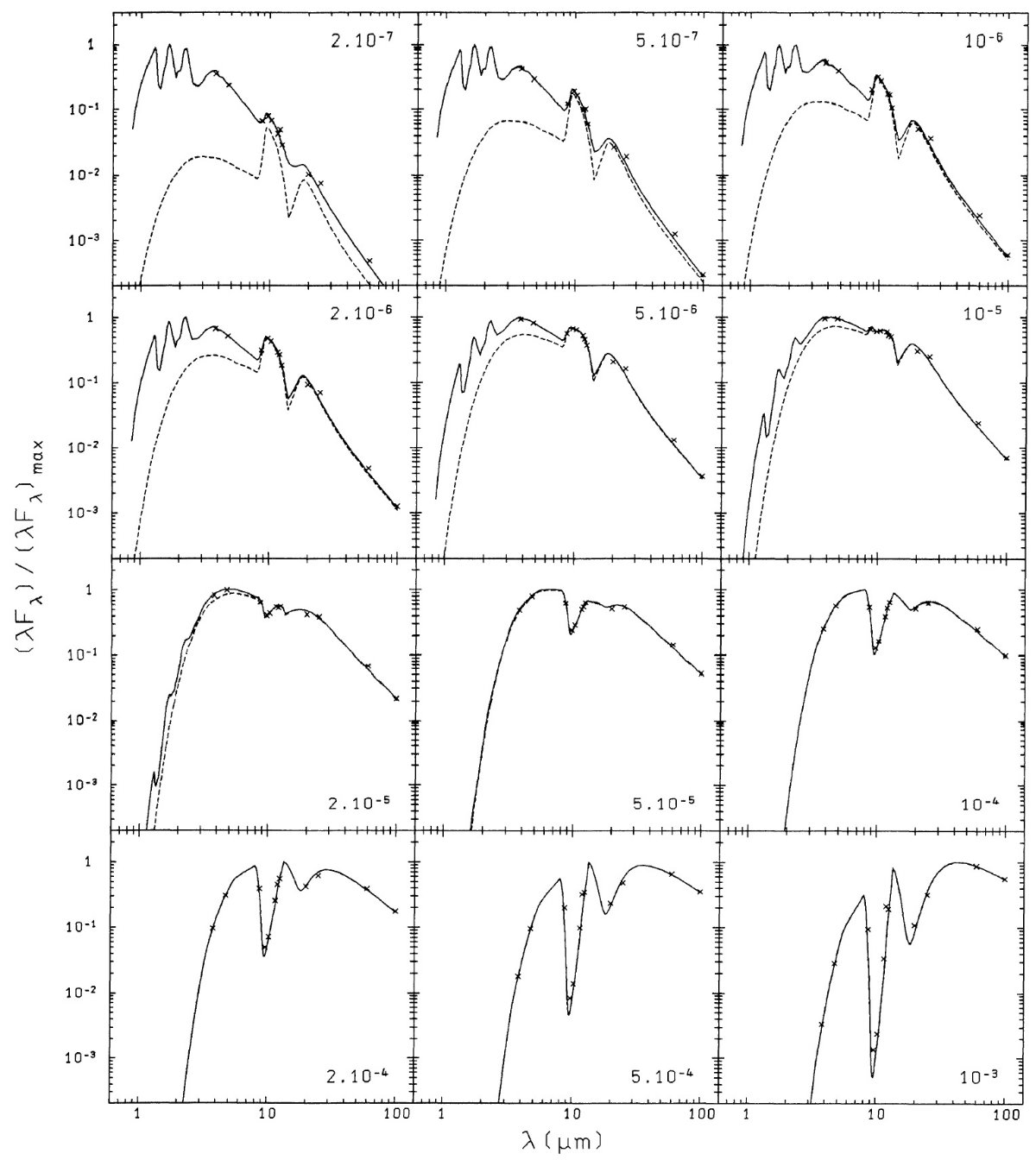
|
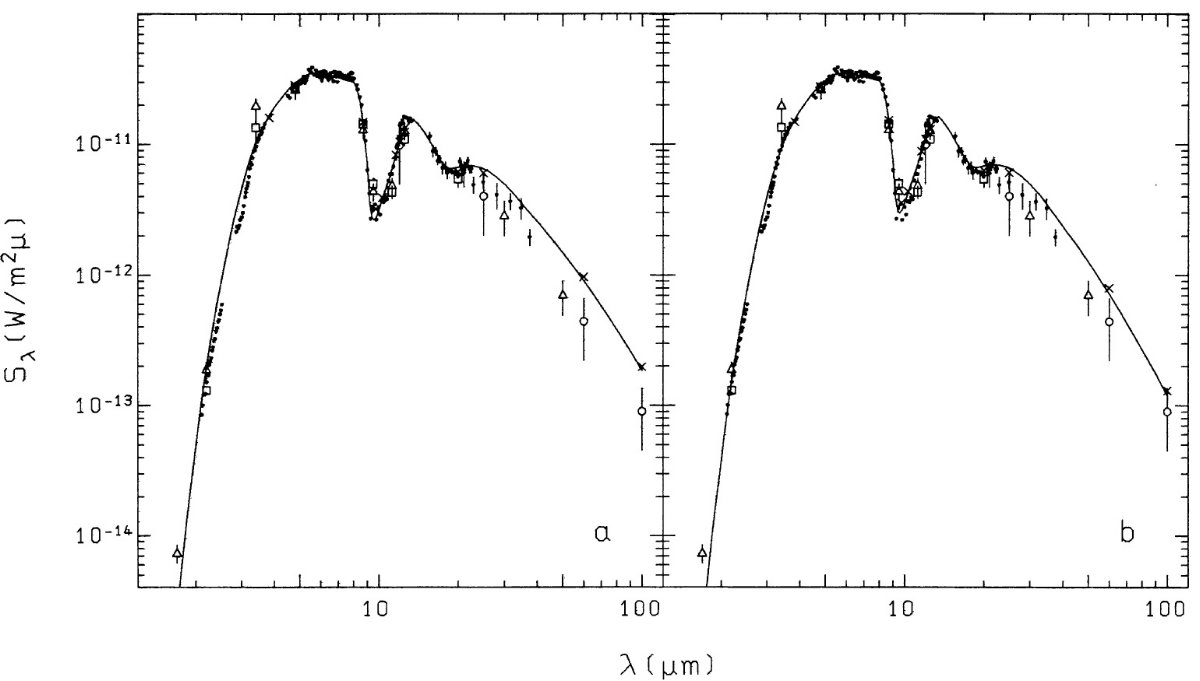
図5a = OH26.5*0.6 への定常流モデルフィット 図5a に OH26.5*0.6 のスペクトルフィットを示す。黒点= Forrest et al. (1978), 四角= Evans, Beckwith 1977, 三角= Werner et al 1980, 丸= IRAS である. 三角は黒点の半周期後(P = 1500 d)の観測である。また丸の位相は黒点の 1.6 - 1.9 周期後である。モデルスペクトルは図4の dM/dt = 10-4 Mo/yr である。図は Tc = 1000 K であるが、 Td = 900 K の方がフィットが 改善される。しかし、より低温 Tc = 790 K までのテスト計算では rc τ9.7 が一定である限り、結果は殆ど変わらない。 (スペクトルから τ9.7 が決まるわけではなく、rcτ9.7 が決まるというのは なぜか?) このように、光学的深さが大きいシェルでは Tc に関する情報は得られない。 これは、κ(λ) の形を調べるには最適な状況である。 遠赤外でモデルフラックスをどう下げるか? 図5a をよく見ると、 λ > 25 μm ではモデルフラックスが 1.4 - 2 倍大きいことが判る。しかし、短波長側と長波長側とでは変光位相が 異なり、OH26.5+0.6 の L* はファクター4変化することを考量する必要がある。 λ ≥ 30 μm で急勾配の κ(λ) を用いると、 λ ≥ 100 μm でのフィットが良くなるが、λ [30, 60] μm でのフィットが出来ない。もう一つの可能性は、 密度勾配をもっと急にすることである。少なくともシェルの外側=遠赤外光の出る 領域、の勾配を急にするとフィットが良くなる。その理由としては、マスロスが 時間と共に増加することが考えられる。この効果が表れるには、マスロス変化の タイムスケールが(赤外放射領域の大きさ/流速) と同程度である必要がある。 それが満たされるのは、超星風の段階であろう。 マスロス率の変化時間 C(r,t) = 半径 r, 時刻 t におけるマス流とする。 Baud, Habing (1983) は OH/IR 星の光度関数に基づき、マスロス率 C(rc, t) の進化を 次の式で表した。
t = 0 でのマスロス率 C(rc, t)=10-7 Mo/yr の程度である。 OH/IR 星は t = tOH5 yr) の特異点直前でマスロス が急増する時期に出現する。Bedijn 1986 はマスロス率のそのような進化は、マスロス により恒星質量が減少することによる外層構造の変化によるのではないかと提案した。 |
マスロスの時間変化をマス流の空間変化に直す C(r, t) = C(rc, tr) (5a) (C(r, t) = C(rc, t-tr)の間違い? ) tr = ∫rcru -1(r')dr' (5b) 式(5)は次のように書き換えられる。
ここに
r1/2 >> rc の時は、
自己流でやると、 C(rc,t) = C(rc,t-(r-rc)/u) = Co/[(tOH-t+(r-rc)/u)/tOH] = Co/[(tOH-t)/tOH]・1/{1+[(r-rc)/u]/(tOH-t)} = C(rc,t)/{1+[(r-rc)/u]/(tOH-t)} (r-rc)/u >> (tOH-t) の場合、つまり、特異点までの時間= 残された時間よりより、ダストがその点までに掛かった時間=ダストの年齢の方が長い場合、 C(r,t) = C(rc,t)・u(tOH-t)/(r-rc) さらに、r >> rc 領域では、 C(r,t) = C(rc,t)・u(tOH-t)/r = (Co tOH u)/r 以上から密度分布は r-2 より r-3 となる。 |
|
図5b = 増加していく星風モデルのフィット 図5b には増加していく星風モデルで OH26.5+0.6 をフィットした例を示す。 τ9.7 = 28.5, rc 5.6 103 Ro, r1/2 = 100 rc. 図5a と同じ吸収係数が用いられた。 つまり、図1a の 実線 0.8 である。これらのパラメタ―は C(rc, t) = 1.15 10-4 Mo/yr に相当する。 ( 式7b を書き直すと、 r1/2 = u∞ (tOH-t) しかし、この残された走路みたいな距離の物理意味は何だろ?) r1/2 の値は妥当に見える。u∞ = 14.5 km/s, t 加速モデルのフィット λ > 50 μm でのモデルフィットは図5a より向上しているが、 それより短波長側では著しい改善は見られない。光学的深さと、従ってマスロ ス率は加速モデルの方が幾分大きい。 (二つのスペクトルの差は逆に短波長側に しか認められない。変だな? ) |
加速モデルの特徴 加速モデルを使い、異なるマスロス進化段階にある 2 10-5 Mo/yr から 10-3 Mo/yr の6モデルを計算した。モデルパラメタ―は表2に 示す。吸収係数は図1a の実線 0.8 を使用した。表2には Δt = tOH-t の値も載せた。図3c と図3d に載せたスペクトルは、 OH26.5+0.6 の過去と未来を示すと考えてよい。特に高いマスロス率の時に 加速モデルでは [25-60] カラーが定常モデルよりずっと青いことに注意 せよ。 (定常モデルに比べ、低温外辺部の密度が 低いため、長波長フラックスが小さくなることを述べているのだろうが、どこに ) 系列は (log(λFλ(25)/λFλ(12), λFλ(60)/λFλ(25)) = (0.2, -0.2) 付近で終結するらしい。しかし、この最終点は r1/2 と C の関係に依存し、従って主系列質量に依るであろう。 |
|
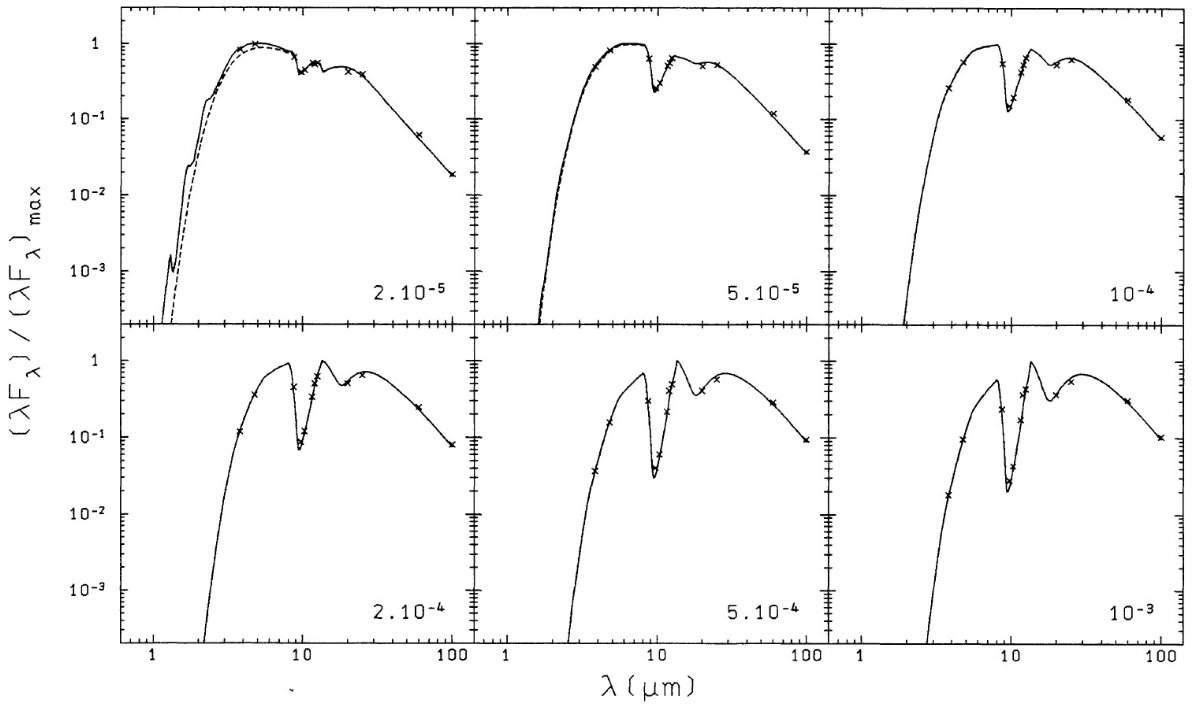
図6=加速マスロスのモデルスペクトル 加速マスロスのモデルスペクトルを図6に示す。dM/dt ≤ 10-4 Mo/yr では加速モデルと定常モデルのスペクトルの差は殆どない。長波長側 でフラックスが少し下がるくらいである。しかし、dM/dt ≥ 2 10-4 になると、スペクトルにはっきりした差が生じる。最大マスロスにかけて、 10, 20 μm 吸収深さは定常流ほど深くならないし、長波長カラーもそう赤くは ならない。加速マスロス 5 10-4 Mo/yr スペクトルの 10 μm 深さ 図6)が定常マスロス 2 10-4 Mo/yr (図4) と同程度である。 加速マスロスのスペクトルは短波長側で赤く、長波長側で青い傾向がある。 したがって、 OH26.5+0.6 よりも深い 10 μm を持つ LRS 天体を探して、 カラーを調べることは興味深い。ただし、星間減光の扱いが問題である。 2成分ダストシェルモデル Rowan-Robinson 1982 と Rowan-Robinson, Harris 1983 は単一シェルでは全体の カラーを合わせると、 10 μm 吸収の深さが不足することから、第2の冷たい シェルを加える必要性を指摘した。しかし、我々の単一シェルモデルは 10 μm 放射帯も吸収帯も同じように良く再現できた。それは、λ < 8 μm で彼らと異なる吸収率を用い、かつ密度分布が異なるからである。 κ1.65/κ9.7 でファクター 1.37 小さく、 κ3.5/κ9.7 でファクター 1.86 小さい。 光学的深さが浅いシェルで、κλ<8μm/κ 9.7 が 10 % 大きい必要があるということは、温度依存性の証拠と 考えられる。 |
スペックル干渉計によるシェル半径観測 スペックル干渉計観測値は 波長(μm) NS 軸 EW 軸 観測者 3.8 0".074 0".099 Dyck et al 1984 4.8 0".159 0".107 Dyck et al 1984 10. 0".32 0".3 Cobb, Fix 1985 我々のモデルでは、輝度分布が最高の 1/e に落ちるのは、 (3.8μm, 1.4rc), (4.8μm, 1.52rc), (10μm, 3.2rc) である。 rc = 0".07 に対しては、0".097, 0".11, 0".24 になる。 10 μm での値に関して、 Dyck et al は変光位相 0.2 で平均光度に近い 時に行われたが、 Cobb et al 観測は位相 0.7 で極小に近い時の値であることに 注意する必要がある。10 μm のスペックル観測を繰り返し行うことは 興味深いであろう。二重シェルでは 10 μm 吸収が冷たいシェルで行われ、 大きさが動かないが、単一シェルでは動きが大きいだろう。 |
|
非変光 OH/IR 星のスペクトル 非変光 OH/IR 星のダストシェルを以下のように特性化する。 (i)rin > rc (ii)C(rc, tstop) その時、時刻 t1, 半径 r1 における密度は、
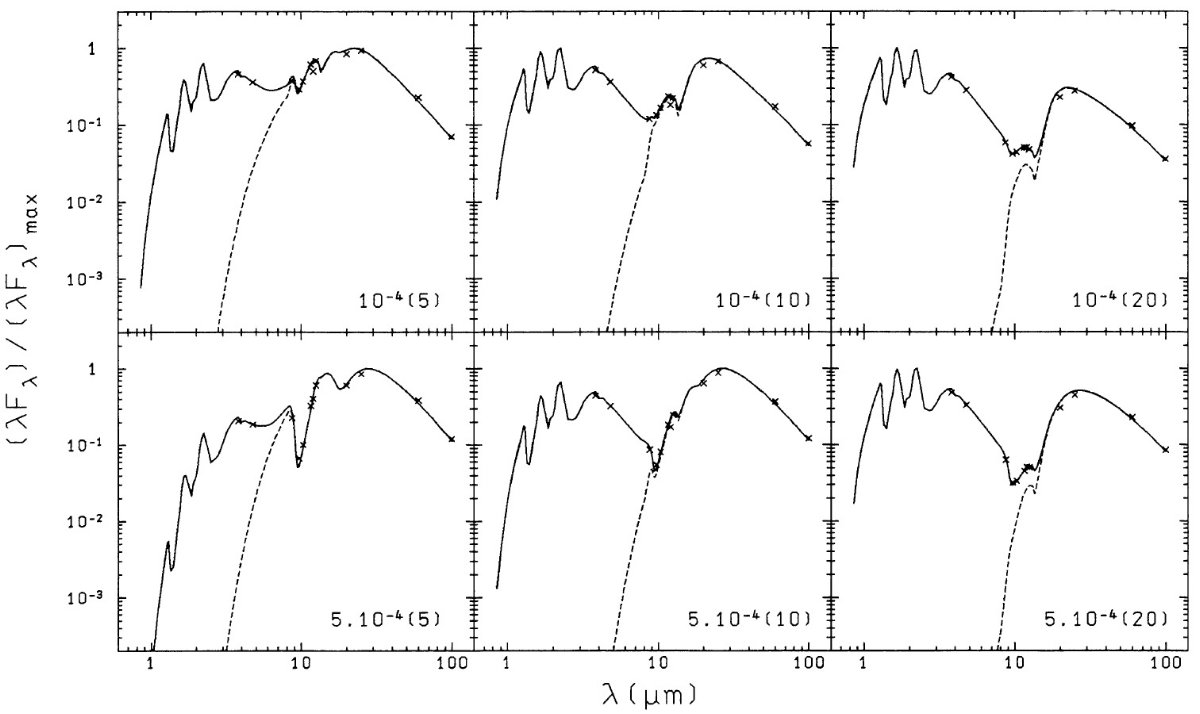
t1 = ∫rr1 u-1(r')dr' (9) ここに、t1 は当初 r にあったマスが r1 まで来た時刻。 C(r,0) はマスロスが停止した時のマス流の分布で、式6で表される。表3には、 スペクトルを計算したモデルのパラメタ―を吸収係数には図1の実線 0.8 を用いた。 二色図上の系列 計算したスペクトルから導いた IRAS 二色系列を定常マスロスの場合を図3b に、加速マスロスの場合を図3c に示す。 観測されない! しかし、図7のようなスペクトルが実際に観測された例はない。van der Veen et al 1986 で 15 天体の近赤外観測結果が報告された。明らかなショルダーは検出 されたが、図7に比べると何桁も低いレベルである。これは、モデルで中心星 を R Cas にとったためかも知れない。そこで、中心星スペクトルを 7000 K 黒体として計算を繰り返した結果を図3d と図8に示す。この場合でさえも、 中心星のレイリージーンズテイルは短波長赤外側で観測される。 van der Veen, Habing, Geballe (1986) の図5を見よ。 |
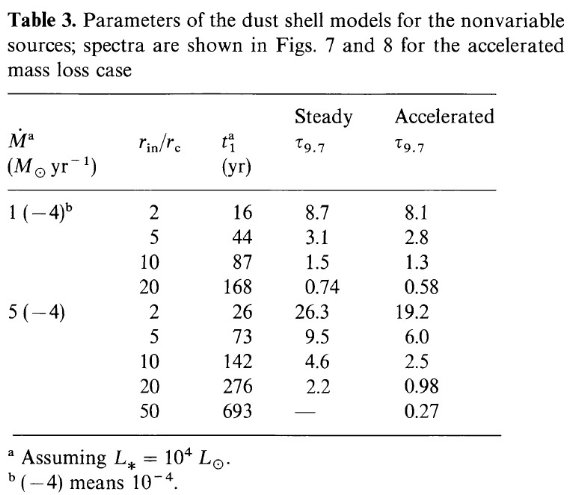 表3.非変光 OH/IR 星のダストシェルパラメタ―。スペクトルは図7、8に 示す。 |
|
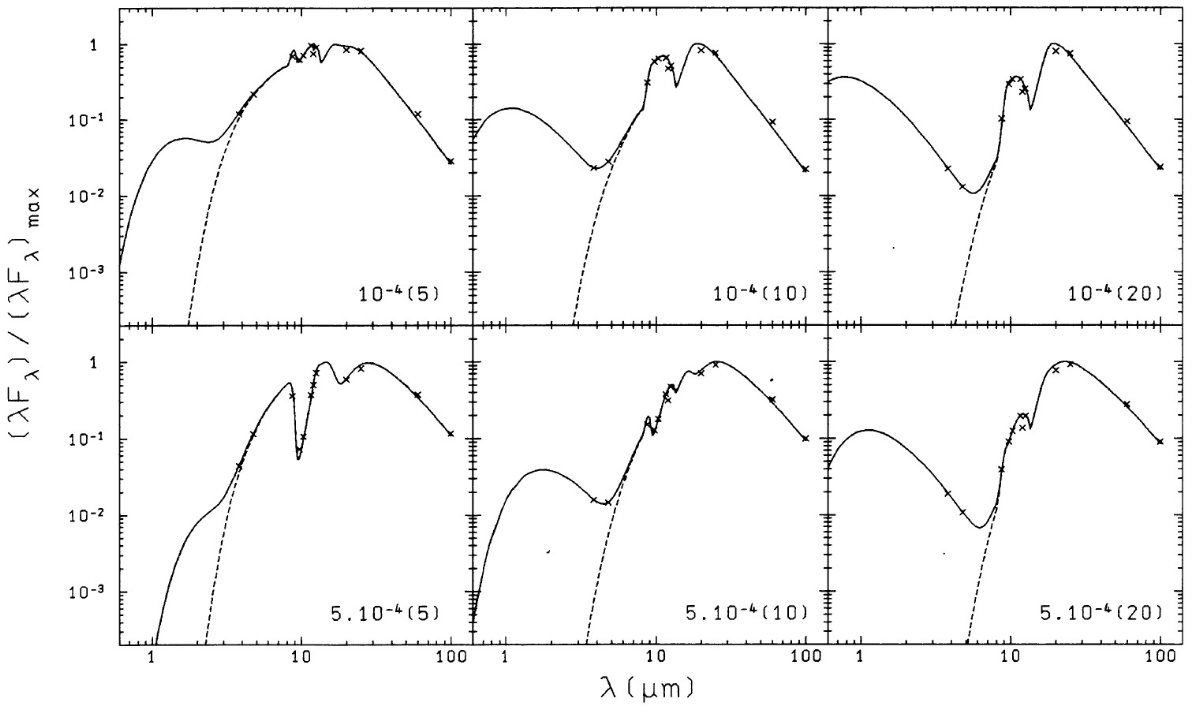
非変光 OH/IR 星スペクトルフィット 先に述べたモデルで非変光 OH/IR 星 OH 17.7-2.0 の λ ≥ 8 μm のスペクトルを綺麗にフィットできる。また、 1 - 2 μm の観測も高温の BB を中心に置くことで説明できる。しかし、 2 - 6 μm ではモデルフラッ クスは観測よりずっと低い。図9a にそれを示す。 dM/dt = 10-3 Mo/yr, rc = 1.08 104 Ro = マスロス停止時のダスト凝結半径。r1/2/rc = 6.3, rin/rc = 12, τ9.7 = 2.14, t1 = 208 yr, 中心星=BB(15,000 K), L* = 10.000 Lo. λ = 3.8 μm でモデルフラックスは観測に比べファクター7低く、 その大部分は中心星からの光である。 |
減衰マスロスモデル おそらく、rin 内側にダストが無いという仮定はまずいのだろう。 そこで、人為的であるが、 t = 0 の後、マスロスの減衰を次の式で表した。 C(rc, t) = C(rc,0)exp(-t/t1/2) (19) t = t1 の時の rin 内部でのダスト分布は次のようである。 C(r,t1) = C(rc,0)exp[-(t1-t2) /t1/2] (11) t2 = ∫rcr u-1(r')dr' (12) こうして作ったモデルのスペクトルを図9b に示す。t1/2 = 26.2 yr, t1 = 289 yr である。 |
|
1.ミラ - OH/IR 星の系列 ミラ - OH/IR 星の系列は単一シェルで説明可能である。モデル計算は Tc = 1000 K で行ったが、 Tc = 700 K でも同じくらい良く二色図観測にフィットする。 ミラ型星と OH/IR 星の SED フィットからは Tc = 900 K がベストであった。 定常マスロスも加速マスロスも同じくらい良く観測を説明する。 2.ダスト吸収係数 二色図と SED のフィットには Jones, Merrill (1976) のダーティシリケートへの修正が必要であった。λ ≤ 8 μm では 勾配を急にして、κ1.65/κ9.7 が彼らの モデルよりファクター 1.37 小さくした。λ ≥ 30 μm では波長 依存性がより緩やかにした。後者は Rowan-Robinson et al 1986 も見出した。 さらにシェルの光学深さが増大するにつれ 10 μm シリケート帯の幅は狭く なっていく。最後に、IRAS 二色図へのフィットはダスト吸収係数に温度依存 性があり、κ19/κ9.7 が低温で大きくなる ことを示唆する。これは実験結果とも合致する。 |
3.非変光 OH/IR 星 非変光 OH/IR 星は post-AGB 星の周りの残存ダストシェルにより説明される。 マスロス停止時の最高マスロス率は 10-4 - 10-3 Mo/yr で、主系列質量に依る。 4.減衰マスロス 非変光 OH/IR 星の SED フィットから、マスロスは突然停止するのではなく、 290 年の間にファクター 6 104 低下したことが判った。この期間に 星温度は 3000 K から 15000 K にまで上がった。 |