IRAS edge-on View if Our Galaxy I/ The Disk


Habing
1988 AA 200, 40 - 50



　アブストラクト

　IRAS F12=F25 天体
　IRAS PSC から F12 ∼ F25 の天体を選んで、銀河系の横向き像を得た。 そのほぼ全ては、大きな質量放出率を持つ長周期変光星である。星の数を銀経、 銀緯、フラックスの区分毎に数えた。どの方向でも、星の数はフラックスに対して 極めて平坦であった。星の数を、空間分布と光度関数の畳み込みとして解釈する。

二つの種族　
　その結果、二つの種族が含まれていることが判った。同じ光度関数を持つが異なる 空間分布をする二つの種族か、同じ平均光度を持つが空間分布が異なる二つか。 私が好むのは後者で、4/5 は薄い円盤に属す。その厚みは FWHM = 440 pc、動径 方向のスケール長 = 4.5 kpc, カットオフ = 9.5 kpc である。そのピーク光度は 4000 Lo である。 		厚い円盤　
　残りの 1/5 はもっと厚い成分で、厚みは 1.2 - 2.8 kpc, スケール長 6.5 kpc, カットオフ = 18 kpc である。この成分も平均光度 = 4000 Lo である。この厚い 種族はおそらく Gilmore, Reid 1983 が提唱した厚い円盤に属する。

　その他の結果　
　この他の結論は
（i）薄い円盤種族の光度分布はバルジと似ている。
（ii）光度から導いた星のコア質量分布は白色矮星のそれとよく似ている。

　１．イントロダクション　

　IRAS 点源の示す銀河系　　

　1984 年に IRAS の結果を調べて、我々は OH/IR 星のカラーを持つ天体を選ぶと、銀河系が くっきりと描かれる(Habing et al 1985)ことを発見した。図１にその画像を再現する。 この図には円盤とバルジがはっきりと現れている。したがって、銀河系を構成する 全く違う二つの要素を、このデータから新しく調べる可能性が生まれた。

　円盤は太陽付近で断ち切られている？　

　バルジ天体に関しては、既に Feast 1987, Habing 1986, Frogel 1986, Rowan- Robinson, Chester 1987 などで論じられている。ここでは円盤に集中する。 図１を見ると直ちに、 l = 90 と 270 で星の数が急落下することが判る。これは、 円盤が R = Ro 付近で断ち切られていることを示すものである。円盤の見かけ厚み FWHM = 0.1 Ro である。この論文ではその点を詳しく調べる。

これまでの銀河構造研究　

　"Galactic Structure" 中の Blaauw, Oort のレビューはヴァチカン会議 1957 以降の星種族研究のまとめである。最近、 Bahcall, Soneira 1980 は、現存の星計数データをまとめて、さらに精緻な銀河系モデルを構成した。1986 に開かれた研究会の成果が "the Galaxy" としてまとめられている。それが この論文のスタートである。 		　利点と欠点　

　しかし、いくつかの重要な情報がまだ欠けている。例えば、様々なタイプの 星毎に銀河面に垂直な方向の密度分布や運動が知られているが、銀河面の動径 方向については、主に星間減光のために、不明である。図１が示すように、 IRAS データはこの欠落部分の情報を与えてくれる。簡単に言うと、IRAS 12, 25 データには以下の利点と欠点がある：

利点
(a) 大部分が Mbol < -3 と明るく、比較的低質量　1 ≤ M ≤ 4.
(b) SED ピークが F12 付近にある。
(c) 星間減光が無視できる。
(d) 観測が全天で一様に行われた。
欠点
(a) 天体当たりの情報は測光値と変光指数で少ない。
(b) 進化時期が短いため、天体総数が２万程度で少ない。
(c) IRAS 分解能が悪いため、銀河面でコンフュージョンが生じる。


　解析法について　

　この論文では、主に天体の方向分布に基づいて解析を実施する。スケールの 導入には Ro = 8.5 kpc を使用する。

　２．天体の選択　

　領域選択基準＝コンフュージョン　

　銀河構造を調べることを目的にするので、調査は銀河面に沿った領域となる。 しかし、天体数が多すぎて、紛れ=source confusion を引き起こす領域は除いた。
(その結果が表１？)
表１に 12, 25 μm で天体の紛れが起きる領域の面積比率を示してある。 紛れの情報は IRAS-PSC 附属の 「天体数高密度ファイル」= "high source density file" から得た。領域１ではかなり高い。しかし、その影響は無視した。

　フラックス選択基準　

(a) FQ = flux quality = 3　
(b) 0.8 < C21 = f25/f12 < 3.8

次の量は意識的に使用しなかった。
(a) variability index. 暗い星で変光の検出が難しい。みかけ明るさでバイアスがかか る。 いずれにせよ質量放出星は変光星である。
(b)　銀河系背景放射のため、f60 の探査は浅い。これを入れると暗い星が多数落ちる。
このために、 HIIR や PN を含むサンプルになった。

HIIR, PN 混入の効果　

　混入効果を調べるため、サンプルを次の３つに分けた。
(1) 「星」：f25 > f60 または f25 > f60 上限値、または変光指数 > 90%
(2) "HP" : f25 < f60 で 変光指数 < 90 %
(3) "?" : 残り。

　領域９を除く全領域で "?" 天体の数は 10 % 以下なので今後は無視する。領域９では、 "HP" 天体と "?" 天体の割合は、 f12 > 4 Jy に対しては 10 % 以下である。しかし、 それ以下の二つのフラックス枠 f12 = [1, 2], [2, 4] Jy ではその二つが全体の半分以上 を占める。"HP" 天体は除去し、"?" 天体は残した。領域９になぜ多数の混入天体が存在 するかの理由は、多分銀経沿いに一様な分布を持ち、従って大きな領域では総数が増加 するからだろう。
( 割合の話になんで領域の「面積」？)
領域９にこの補正を施すと混入効果は無視できるレベルとなった。（ただ、後から考えると、 C21 > 2.0 天体は落としておくべきだった。そこに "HP" 天体の大部分が集中し、 一方「星」は僅かしか存在しなかったからである。）

　カラー選択 I. 1.0 < C21 < 3.8

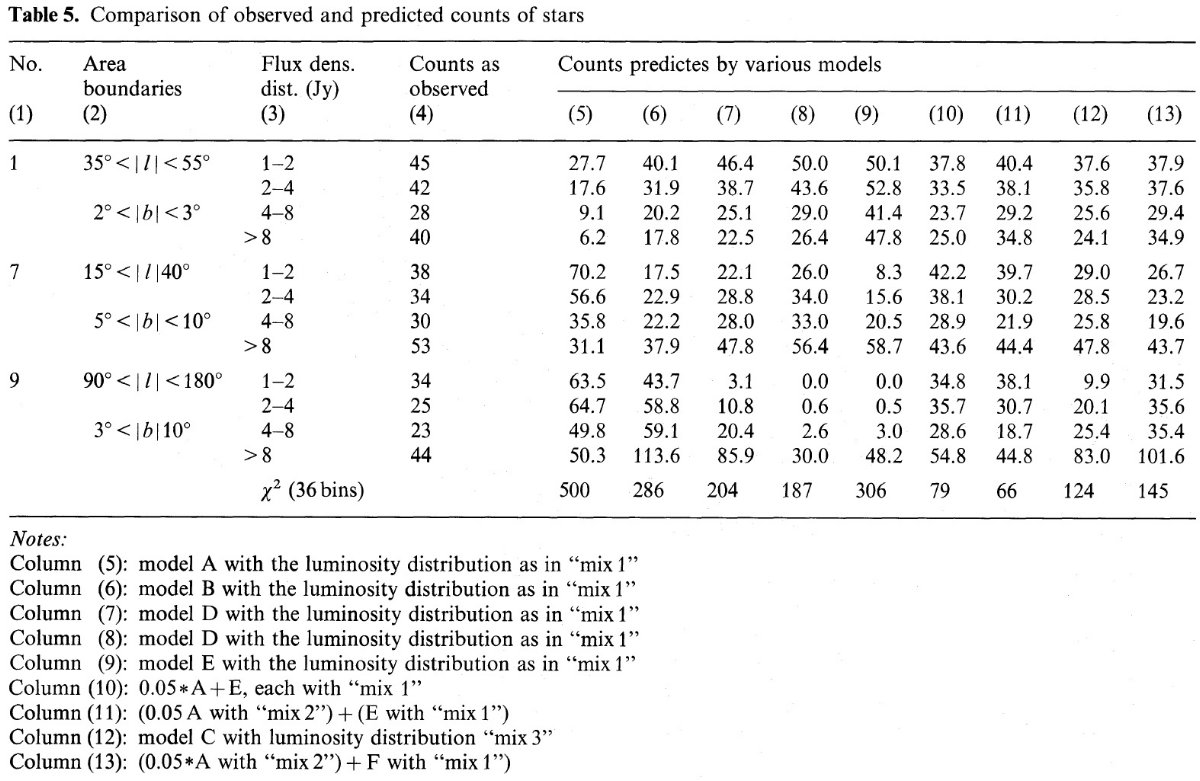
　５００個しか引っ掛からなかった。少なすぎる。フラックス区分＝４で９ 領域だと、計36区分で、これでは一区分当たり 14 個にしかならない。

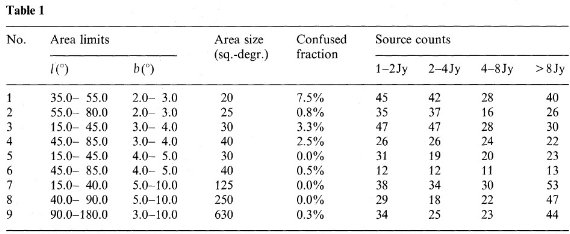
表１．サンプル領域のリスト。



　カラー選択 II. 0.82 < C21 < 3.8 　

　総数が　１０５７個に増えた。ここから "HP" をできる限り除いた。レフェリー Gilmore の示唆で 0.82 < C21 < 0.90, 0.90 < C21 < 1.15, 1.15 < C21 に区分し直して調べたがカラー区分間に差はなかった。

　AGB なのか？　

　この選択の天体が AGB 星であることは確実だろうか？半数以上は変光指数 p が 90 % 以上であった。これは実際上ほとんどの星が LPV で、したがって OH/IR 天体に関係することを意味する。
(だから、ここで使っている "OH/IR" 天体は 大質量かどうかは問うていない。)
それらが実際に OH メーザーを出しているかどうかは進行中のメーザーサーベイ の結果を待つ必要がある。大体 30 % くらいから OH メーザーが検出されるようである。

　60 μm 超過天体　

　サンプル中に　60 μm 超過天体が幾つか見つかった。Willems, van der Veen は マスロスが途中停止する時期があり、それらが以前のマスロス雲と考えている。ここでは 踏み込まない。

　結局　

　（１）９つの選択域
　（２）IQ(12), IQ(25) =3
　（３）f60 > f25 と分かったら撥ねる。
　（４） 0.82 < C21 < 3.8

　３．解析　

　３．１．解析の方法　

　基本方程式　

(l,b) 方向、立体角ΔΩ内でフラックスΔfν 内にある星の数Δn(fν)は次の式で与えられる。

　Δn(fν) = ΔfνΔΩ ∫dLν∫D2dDΨ(R,z,Lν) δ(Lν-4πD2fν)

ここに、δ はディラックのデルタ関数である。
( 上式は、 Δn(fν) = ΔfνΔΩ ∫D2dDΦ(R,z,4πD2fν) ?)

(そうなら間違っている。20150304 ノート)


　Ψ の分離　

　Ψ(R, z; Lν) = ρ(R, z)ψ(Lν) と仮定する。これは 後に正しくないことが判るが。さらに、ρ(R, z) と ψ(Lν) を 以下のように仮定する。

　　　ρ(R, z) = exp(-R/hR) sech2(z/hz) 　　　　(R < Rm)
　　　　　　　　 = 0　　　　　　　　　　　　　　　　　　　(R > Rm)

　　　ψ(Lν) = Σ Wi δ(Lν - Lν,i)

　銀河系中心 (R, z) = (0, 0) で ρ(R, z) = 1 と規格化した。Wi = 銀河中心における光度 Lν,i 星の数密度で、次元は kpc -3 である。

　星の期待数　

　天空の領域 Aj 内で、フラックスが f = [fk, fk+1] 間に期待される星の数は、
　　　　　Nj,kexp = ΣWiJj,k i

　　　　　Jj,ki = ∫∫Aj dΩ ∫Dk, iDk, i+1 D2ρ(R, z) dD

ここに、4πDk,i2fk = Lν, i
(∫Dk, iDk, i+1　は ∫Dk, iDk+1, i ではないか？)

図２．sech2(x) と exp(-|x|). sech2(x)の 半値点は x = 0.881 であり、 exp(-|x|) では x = 0.693 である。 また、質量の 半分は sech2(x) では (-0.537, +0.537) に、 exp(-|x|) では (-0.693, +0.693) に含まれる。




表２．分布モデルのパラメタ―

　sech2(x) と exp(-|x|)　

　ρ の関数形に　sech2(x) 型を採用したのは、 van der Kruit, Searle 1982 の横向き銀河の研究から、この形が良く合うと結論されたからである。
( Kent, Dame, Fazio 1991 は、sech2(x) より exp(-|x|) の方が合うと述べている。)
彼らの研究によると、hz は円盤上で一定である。z-方向の重力が R により かなり強く変化するから、hz もそうだろうと期待されるので、hz 一定と言う結果は意外である。

　最適パラメタ―の決定　

　hR, hz, Rlim,｛Wi｝は、 - χ2 最小の条件から決まる。計算手続きは、

（１） f12 を [1, 2], [2, 4], [4, 8], [8, ∞] Jy 区分に分ける。

（２） 8 個の領域 A1, A2,..., A8 を選択。

（３） Lν, 0 = 3.33 1014 W Hz-1; Lν, i+1 =2 Lν, i

（４） hR, hz, Rlim　を固定した。

（５） ｛Wi｝を変えて
　　　　　χ2 = Σj,k(Nj,kexp - Nj,kobs)2/Nj,kexp
　　　を最小にする。

（hR, hz, Rlim）の様々な組に対して、（５）を 繰り返した。表２には後で用いるモデルのパラメタ―を示す。 		光度関数 Ψ∗(L)

　hR, hz, Rlim,｛Wi｝が最適化 されたら、次の課題は Ψ(Lν) から Ψ∗(L) を求めることである。この問題は付録で議論してある。結論は簡単で、 Ψ(Lν) も Ψ∗(L) と同様｛Wi｝ から得られる。W1 は銀河中心で 1000 Lo の星の密度 (kpc-3) を表し、W2 は 2000 Lo の、W3 は 4000 Lo の、，，，の 密度を表す。

　多重光度関数　

　光度関数の導出法からも分かるように、総密度・光度関数が以下のような 形も可能である。

　　　　　Ψ = ρ1ψ1 + ρ2ψ2

そしてこの場合も、以下のような表現が得られる。

　　　　　Nj,kobs = Σ WiJj,ki

パラメタ―の数が増えるので、計算手続きは面倒になる。しかし、最終結果は 光度関数が場所に依らないという制限から脱却したものとなった。




表３．光度毎の星数の割合。効率 η = 0.33, f12 > 1.0 Jy




表４．L = 4000 Lo 星の分布。様々なフラックスに渡り η = 0.33.




表５．星計数の観測値とモデル値との比較

　３．２．結果：　入門編　

　結果の吟味　

　IRAS 天体の最も魅力的な特徴は、遠方まで見通せることである。星は光度が 大きくて Mbol < -3.5 , 12 μ 付近で SED ピークである。例えば、 L = 2000 Lo (Mbol = -3.5), η = 0.33 の星は D = 9.4 kpc で f12 = 1 Jy である。この節では表１の数字の意味を読者がそして著者もまた、「感じ取れる」 よう、結果の吟味を行う。

　問題１：　 f > 1 Jy となる星の割合　

　与えられたモデル分布に対して、ある (l, b) 方向で f > 1 Jy となる 星の割合はどのくらいだろうか？

　表３にその解答が載っている。モデルＡを見てみよう。 (l, b) = (17.5, 3.5) では、視線方向にならぶ L = 4000 Lo の星の 54 % は 1 Jy を越している。 表３をさらに見ると、銀河面から離れると IRAS が大きな割合で、しかし全てではない、 AGB 星を検出していることが判る。

　問題２：　ｆ１２分布　

　では次の問題として、フラックス分布はどうなるのか？

　表１を見ると分かるが、フラックス分布は調べた９つの領域を通じて全て 平坦であった。表４で表３の時と同じ列には L = 4000 Lo の星が色々なフラックス 区間で何割の寄与をしているかが示されている。
( 他の光度の話はなしなのは残念。)
最初に、外側銀河系 l = 137.5, 177.5 の方向を見よう。表からはモデル E が観測される 平坦なフラックス分布を説明できないこと、それに対しモデルＡはうまく、特に星が L ≤ 4000 Lo の場合なら、説明することがわかる。
(表４からどうして分かるのかが分からない。 )
反中心方向の星計数はしたがって、受け入れ可能なモデルは外側まで広がり、かつ主に L ≤ 4000 Lo の星から成るという結論に導く。
　次に内側銀河系 l = 17.5, 57.5 方向を見ると、表４からは平坦なフラックス 分布には明らかにモデルＥが好都合である。特に L > 4000 Lo の星が多いと そうである。このように、観測が示す平坦なフラックス分布は反中心方向と中心 方向とで逆のモデルを支持する。つまり、中心方向を説明するには高光度星が多 く密集型のモデルが、反中心方向には低光度星の拡散型モデルが好都合なので ある。この矛盾の解決が結合モデルである。

χ2　の計算　

　ミックス１は 1000, 2000, 4000, 8000, 16,000, 32,000 Lo の星が 3:4:4:2:1:0.2 で混ざっている。表１のように総計 1057 星に対し、表２パラメ タ―のモデルに対し、４フラックス×９領域＝３６枠での星数を計算した。 		そして、

　　　　　χ2 = Σ(Npred - Nobs) 2/Nobs

を計算した。表５には、領域１、７、９での４フラックス区分に対して、第４列に 観測星数、第５−１３列には様々なモデルでの予想星数を載せてある。


　ミックス１の χ2 　

　第５−９列はモデルＡーＥであるが、χ2 > 187 と なった。この値は大き過ぎ、モデルとして不適切である。
　次に、0.05(A + E)
( 0.05A + E の間違い？)
密度分布で光度関数はミックス１のモデルを第１１行に載せた。これは χ2 = 79 まで下がった。私は許容範囲を χ2 < 72, 枠毎で差が２個以下としているので、この結果はかなりそれに近い。

　Ａをミックス２にした２成分円盤　

　モデルＡは低光度星優位であるべきという示唆が得られていたので、ミック ス２は、1000, 2000, 4000, 8000, 16,000, 32,000 Lo の星を 1:2:1:0:0:0 で混ぜた。その結果が第１１行で、0.05Ａ(ミックス２)＋ Ｅ(ミックス１) での χ2 = 66 となった。つまり、 （１）厚く動径方向に広がり、低光度の星から成る円盤と、（２）薄く密集し、 光度分布が高い方まで伸びている円盤という２成分がある。光度分布のピーク は 2000 - 4000 Lo である。

　コメント１：光度関数をいじる　

　密度分布は単一円盤だが、光度関数が双峰的なものを考える。これは、 1000, 2000, 4000, 8000, 16,000, 32,000 Lo の星を　6:1:1:2:0.4:0.1 で 混ぜた。ミックス３と名付ける。第１２行はモデルＣとミックス３の組み合わせで 他の単一円盤モデル＝第５-９列よりよい結果を出した。
( なら、なぜ単一円盤で {Wi} を決める時ミックス３に辿りつかなかった？本当に極値を探したのか？)
私はしかし、これよりは２円盤の方が良いと思う。

　　コメント２：　小さい Rlim は嫌い　

　モデル E の Rlim が小さすぎて嫌な人も多いだろう。第１３列では 厚い円盤 A は以前と同じだが、薄い円盤 E はスケール長は小さいが限界半径はずっと 大きいモデル F で置き換わっている。しかし、これは大失敗で、反中心方向に 高ふっくす星が増えすぎてしまう。




表６．ベストフィットモデルのパラメタ―

　３．３．完全解析の結果　

　自動計算の手順　

（１）密度分布を選択する。
（２）{Wi}を決める。
（３） χ2 極小となる{Wi}を探す。
（４）最初は単成分円盤＋W1,W2,...W7 モデル
（５）各単成分モデルに対し、Nj,k = j-領域の k-フラックス区分 にある星数と Jj,ki = i-光度の星が j-領域の k-フラックス区分 に入る体積内の規格化（銀河中心で密度＝１）総星数の間の偏相関係数を計算しておく。
（６）偏相関係数は最適な単円盤モデルを素早く決めるのに有効である。
（７）単円盤モデルは皆、高銀緯で低フラックス星が少ない、という欠陥がある。
（８）２円盤モデルを考える。二つの円盤それぞれに対し、hR, hz, Rlim を決め、{Wi} を変化させて χ2 最小を探す。
（９）χν2 = χ2/μ, ここに ν はモデル自由度、により最終フィットの程度を調べる。モデル自由度 = 枠数 36 - 自由パラメタ―数(１０ か　１８）。
（１０）理想的には、χν2 = 1 である。統計学 教科書では　χν2 = 1.5 で満足するよう薦めている。
（１１）ベストモデルの表６を見ると、χν2 = 2.4 - 2.6 で完全に満足できる結果ではない。しかし、大体の特徴は捕えた。

　単円盤モデル　

　１０フリーパラメタ―を持つ単円盤モデルは表６で "I" と名付けられた。少し 驚いたのは光度関数が二つ山だったことである。 低光度の山は低フラックス枠を満たすために、高光度の山は高フラックス枠に 必要とされた。χν2 = 2.6 はまあまあでフィット と看做せる範囲だが、私はやや躊躇する。と言うのは、

（１）領域９＝反中心方向で高フラックス星が多過ぎ、低フラックス星が少な過ぎる。

（２）光度関数の二つ山は異なる二つの種族を指し示し、それらが同じ空間分布なのは 却って不自然。

　二円盤モデル　

　そこで、自由パラメタ―数１８と多いのが難だが、二円盤モデル II を考えた。 表６から分かる通り、χν2 = 2.4 で少ししか改善され ないが、上に述べた欠陥は消えている：領域９で観測とモデルの一致は良好になり、 各円盤成分の光度関数は二つ山ではなくなった。この解析から、大部分の星を含む 薄い円盤と高光度星を欠き多分古い種族の厚い円盤との二つの種族が現れてきた。 二円盤モデル II の結果は表７に載せた。

最良パラメタ―の吟味　

　表６のパラメタ―は最良ではあるが、ほんの僅か悪いだけのモデルが他に多数ある。 特に厚い円盤のパラメタ―は推定巾が広い。そのスケール高は 600 pc から 1200 pc の間のどれとも云える。しかし、hz(ΣWi) はあまり 変えられない。これは厚い円盤のコラム密度で、 6 ±1 kpc-2 である。厚い円盤の Rlim もあまり明確には決まらない。これは 14 kpc くらいまで下げても可であるが、一方無限大も可能である。ただし、はっきりして いることは、厚い円盤は薄い円盤より遠方に広がっていることである。可能性としては hR(厚い円盤) が hR(薄い円盤) と同じもありだが、計算結果 は hR(厚い円盤) が少し大きい。

　ΣWi　について　

　ΣWi は銀河系中心における全星密度である。将来の使用の ためここに再録すると、薄い円盤に対しては 220 kpc-3, 厚い円盤 に対しては 7 kpc-3 である。太陽付近では空間密度として、 33 kpc-3, 2.5 kpc-3 となる。

表７．最終解二円盤モデル II の予想星数と観測星数。

　４．他の研究との比較　

　Gilmore, Reid 1983 の厚い円盤　

　 Gilmore, Reid 1983 は南銀極 Mv ≥ 4 mag = F8V より晩期の主系列星 (M ≤ 1.2 Mo)の中に 一部（ 2 %）の星はスケール高が 1350 pc と残りの星の 300 pc より遥かに 大きいことを見出した。彼らはこの少数の星を中間種族 II であると考えた。 我々の厚い円盤をそれと同じであると考えたくなる。しかし、いくつか考慮 すべき点がある。

（１）我々のベスト解はスケール高 = 800 pc であり、1350 pc より小さい。 ただし、既に述べたようにスケール高はそうしっかり決まったわけでなく、 もっと大きくても差し支えない。
（２）表２（表６の間違い）からは、厚い円盤成分と薄い円盤成分の空間密度比は銀河系中心で 7/220 = 3 % である。太陽近傍ではこの比は 5.7 % となり、Gilmore, Reid の 2 % よりかなり大きい。ただし、これも前に述べたが hz と ΣWi のそれぞれがよく決まらなくても、その積はかなり 狭い範囲にある。したがって、もし hz を 0.8 kpc から 1.4 kpc へ 上げると、密度は 1.2 kpc-3, 密度比は 5.7×0.8/1.4 = 3.5 % と下がる。
(IRAS星/主系列星)が厚い円盤と薄い 円盤で異なる可能性がある。
（３）IRAS サンプルは Mbol = -3.5 (L = 2000 Lo) の AGB 星である。それらは M ≥ 1.0 Mo の主系列星が進化したものである。これは Gilmore, Reid が 厚い円盤は太陽より高質量の星を含むと述べていることと合致する。

以上をまとめると、この論文で現れた厚い円盤は Gilmore, Reid のそれと同じと 考える。

　パイオニア１０観測　

　Van der Kruit 1986 はパイオニア１０による表面測光を解析した。この データは |b| ≥ 10 以上で信頼できる。かれは hR/hz = 15.7 を得た。hz = 0.35 kpc (円盤の古い矮星)と仮定して、 彼は hR = 5.5±1 kpc を得た。私の得た　hｚ = 250 pc は矮星のそれではない。古い円盤巨星は 250 pc で良く合っている。 これは AGB 星がそのような巨星から進化したのでもっともである。 		Habing 1987b

　ここに示したデータを以前扱った際には、今回とは違う hz と hR を得た。その際には扱いがもっと粗く、光度を一定と考えたり、 反中心方向を抜かしたりしていた。そのため、高フラックスと低フラックスの比 やカットオフ半径の問題を見逃し、特に２成分円盤に気付かなかったのである。

　バルジの IRAS 星計数　

　Rowan-Robinson, Chester 1987 はバルジの IRAS 星係数を扱った。バルジ星は ほぼ等距離にあるので、彼らは光度関数を直接導いた。次に、彼らは円盤も 同じ光度関数を持つと仮定し、 hz = 0.25 kpc, hR = 6 kpc を得た。 内側銀河のみを扱ったので、カットオフ半径は無視された。 また、単円盤モデルであるが、ここでの薄い円盤に対応するものであろう。 エラーが示されていないので、彼らの hR = 6 kpc とこの論文の hR = 4.5 kpc との差が有意味かどうか不明である。彼らが 円盤に適用した光度関数は私が実際に薄い円盤に対して導いた 2000 - 4000 Lo に山を持つ光度関数と同一であった。僅かな違いは私の光度関数が 16,000 - 32,000 Lo へ伸びる弱いウイングを持つことである。

　気球観測　

　舞原その他 1978, 早川その他 1981 は気球望遠鏡により 2.4, 3.4 μm 銀河系表面測光を行った。早川その他のモデルは、軸比 5:1 で スケール長 2.05 kpc の指数関数密度分布を持つ薄い回転楕円体、 と渦状腕に対応する二つのリングからなる。リングは銀河面を離れると見えない。 従って、この回転楕円体はこの論文の薄い円盤に対応するが、定量的な 比較はまだ行われていない。

　５．まとめと議論　

　二円盤モデル　

　　0.82 < f25/f12 < 3.8 の IRAS 天体は質量放出星であり、二つの種族が 含まれる。第１解釈は表６のモデルＩで、二つの種族は同じ空間分布に従うというもの、 第２解釈のモデル II では二つの空間分布は異なる。それらはほぼ 4000 Lo に光度関数の山を持つ点は同じ、しかし、薄い円盤は 32,000 Lo まで伸びる高光度 成分を持つ。

　薄い円盤のカットオフ　

　厚い円盤(薄い円盤の間違い)はカットオフ半径 9.5 kpc を持つ。太陽は このカットオフのギリギリ内側にいる。このカットオフは反中心方向での星計数が 小さいことから要請され、３．２．節で論じたように、短い hR の採用 では解決されない。この構造が意味するのは、R-Ro = 1 kpc 付近から星密度の 急激な低下が始まるということである。この低下は晩期 M 型星や長周期変光星 において、V > 12 または K > 6 の数の減少として検出可能である。
　 McCuskey 1969 は 反中心　(l, b) = (186, +1) 方向の M 型巨星の計数を解析した。彼は星 密度が非常に急勾配で低下することを示した。彼の図が示す局所スケール長は 1.5 kpc である。さらに、その密度低下が 2 kpc 先からは緩くなり、星の分布 がこの低レベルのまま遠方まで伸びることを示唆している。彼の結果は 早川その他 1978 による 2.4 μm 半中心方向の表面輝度観測で確認された。 市川 1981 は (l, b) = (120.8, -1.8) 方向での M 型巨星の分布を調べ、 D = 3 kpc (R = 9.2 kpc) で同じ密度現象が見られることを見出した。残念ながら、 McCurkey も 市川も扱ったサンプル数が少なかった。
　惑星状星雲の数にも R > 9.5 kpc の密度急落 が現れている。距離決定の困難さからデータの信頼度は低い。しかし、 Pottasch 1984 は銀緯分布がカットオフと合致することを示した。

　ＣＯ円盤との対比　

　薄い円盤の性質は R > 5 kpc での CO 円盤と似ている。 R > 5 kpc での CO 光度は exp(-R/4.5kpc) でよく近似される。Burton 1988 の 図７．１５を見よ。外側銀河系でも分子雲は存在するが、R = 12 kpc を越すと、 雲は小さくなり、HIIR も小さく、低励起となる。

　星円盤に穴があるか？　

　もし星円盤が CO 円盤と R > 5 kpc で比例しているなら、R < 5 kpc でもそうであろう。つまり、星円盤には穴が空いているのだろうか？これは 重要な質問であるが、現在使えるデータでは答えられないと感じる。紛れ効果 のために内側部分のカタログが不完全だからである。 		星の総数　

　３．１．節で与えた密度分布にしたがう星の数は、
Ntot = (ΣWi)4πhR2hz [ 1 - exp ( - Rlim ) ( 1 + Rlim ) ]
hR hR

この値は薄い円盤で 8800, 厚い円盤で 2230 個となる。この値は表１にあるサンプル 1100 個から導かれたものである。つまり銀河面に沿ってと内側銀河系円盤は 推測値である。
( バルジも丸抜け)


　太陽近傍の局所密度　

　太陽近傍の局所密度は、薄い円盤で 33 kpc-3、厚い円盤は 2.5 kpc-3 である。Pottasch 1984 によると、ＰＮの局所密度は 50 kpc-3 である。 Wood, Cahn 1977 はミラ型星の局所密度を 250 kpc-3 とした。一方、 　 Gilmore, Reid 1983 は主系列星の局所密度を求め、1.0 Mo より大きい星に対して 5.6 106kpc-3, 1.26 Mo より大きい星に対して 3.2 106kpc-3 という値を得た。これらの星はいずれ AGB 星へ進化すると考えられる。（全ての？）ミラ型星は OH/IR 星の前駆 天体で、
( 激しい質量放出星＝OH/IR という定義？)


　寿命推定値　

（全ての）ＰＮは OH/IR 星から進化してきたと考えられている。様々な タイプの恒星の数は各時期の寿命の相対比を表す。もしＰＮ寿命を 2 10 4 yr とするなら、ミラは 105 yr, IRAS 天体に対しては 1.5 104 yr となる。このミラ寿命は Wood, Cahn 1977 の得た 7 105 yr より大幅に短いが、彼らの使用した質量放出率は 低すぎるので、再解析すると一致は良くなるだろう。

　スケール高　

　ＰＮ　のスケール高に関し、 Cahn, Wyatt 1976 は 150 pc, それに対し Pottasch 1984 は 250 pc を与えた。 Wood, Cahn 1977 が与えたミラ型星のスケール高は 310 pc である。これらの値の不一致は 決定精度の問題であり、私の薄い円盤のスケール高 250 pc もその範囲と考えてよい。

Mcore 分布　

　L = 59,000(Mcore-0.495) から求めた Mcore 分布と PN 中心星の質量 分布は IRAS が 0.53 Mo, PN が 0.58 Mo でよい一致を示す。

　

　Wyse, Gilmore 1986 は厚い円盤が非対称ドリフトが 100 km/s で、内部運動 のディスパージョンは 70 km/s であると述べた。これに関連して興味深いのは OH/IR 星の速度が銀河回転から大きく外れる例が多数観測されている。

　光度分布　

　最後に注目したいのはバルジの光度関数と薄い円盤の光度関数が似ている ことである。これは両者の年齢が近いことを意味する。

　付録：　

　変数　

　 Ψ(Lν) = Lν 分布関数。
　 Ψ∗(L) = L 分布関数。
　 L = η(νLν)
　C21 = F25/F12
　 f(C21 |L) = ある L での C21 の分布関数。
とする。

　Ψ(Lν)の表現　

　dN = Ψ(Lν)dLν
　dN = Ψ∗(L)f(C21 |L)dLdC21
　　 = Ψ∗(L)f(C21 |L) ∂(L,C21)/∂(Lν,C21) dLνdC21 　　= Ψ∗(L)f(C21 |L)(ν/η)dLν dC21

から、

　　Ψ(Lν) = ∫Ψ∗(L)f(C21 |L) (ν/η)dC21
 Ψ(Lν) と Ψ∗(L) が同じ形になるわけ

　η の変動が小さい C21 範囲を選ぶと、 　　Ψ(Lν) = Ψ∗(L) ν⟨1/η⟩∫f(C21 |L)dC21

Ψ(Lν)　は Ψ∗(L)と同じ形だが、 ファクター倍違う。このファクターは、ＡＧＢ期のうち星が高質量放出を 行い、カラーがC21範囲にある割合であることがよく考えるとわかる。