Wang14

Universality of the Near-Infrared Extinction Law on the APOGEE Survey

Wang, Jiang

2014 Astro-ph

　アブストラクト

　APOGEE H バンド分光サーベイ（SDSSIII)から多数の巨星の表面温度、そして固有カラーが求められた。5942 個の K-型巨星を用いて NIR 減光則を再検証した。
( 個々の星毎に固有カラーを決めて赤化を求めているのは斬新である。)
E(J-H)/E(J-Ks) には E(J-Ks) = 0.3 - 4.0 の範囲で色超過依存性が認められなかった。

　これは星間空間の希薄領域と濃密領域とで減光則が一定であることを示す。その一定値 E(J-H)/E(J-Ks) = 0.64 はべき乗指数　n = 1.95 に対応する。他の比は E(H-Ks)/E(J-Ks) = 0.36 と E(J-H)/E(H-Ks) = 1.78 であった。以上の結果は MNR ダストサイズ分布に合致する。

　1. イントロ　

　A_λ ∝ λ^-α

　Draine 1989 は NIR 減光則がべき乗型ではないかと指摘した。ただし、その指数は研究者により 1.61( Rieke, Lebofsky 1998 ), 1.70 (Whittet 1988), 1.75 (Draine 1989), 1.8 (Martin, Whittet 1990), 1.8 (Whittet et al 1993)　に散らばる。しかし散らばりの小ささは UV-Opt にかけての Rv が 2 - 6 に大きく変化する事情と対照的である。

21 世紀のべき乗則　

　21 世紀に入ってからの研究結果は明らかに前世紀と異なる結果を示した。例えば、 1.9 (Messineo et al 2005), 1.99 ( Nishiyama et al 2006 ), 2.07 (Straizys, Laugalys 2008), 2.64 ( Gosling et al 2009 ), 2.23 ( Nishiyama et al 2009 ), 2.14 (Stead, Hoare 2009), 2.26 ( Zasowski et al 2009 ), 2.21 ( Schoedel et al 2009 ), 2.11 (Fritz et al 2011) なのである。唯一の例外は Indebetouw et al 2006 が与えた 1.65 である。我々 Wang et al 2013 が石炭袋の 5 個所を調べた結果は, 半透明または濃い雲で α = 2.1, 希薄な領域では 1.73 であった。

サンプルの選択の問題　

　α の決定にはいくつか不確かな個所がある。赤外光度が高い個々の星を用いると、スペクトル型の不定性、変光などによる固有カラーの不定性に悩まされる。一方、カラー情報に基づいて集めた星の集団を統計的に処理した時には混入してくる類似カラーの他種星の影響を被る。

　有効波長　

　問題をさらに複雑にするのは Stead, Hoare 2009 が指摘した、選択した星のスペクトル型により有効波長が変化するという問題である。

　APOGEE 　

　SDSS DR10 データ公開(2013) により、APOGEE サーベイは多くの巨星の固有色指数を決めることを可能とした。この研究では個々の星の固有カラーを決めるという利点と多数のサンプルを統計的に処理する利点の二つを結びつける。

　２． K 型巨星固有カラーの決定　

　２．１．APOGEE データ　
　APOGEE は SDSS-III の４つのプロジェクトの一つで、銀河系恒星の近赤外分光サーベイである。約１０万の巨星を H = 13 mag まで選び、 S/N > 100 のデータを撮る。APOGEE では Teff を 150 K, log g を 0.2 dex, Z を 0.1 dex 精度で決定する。
　２．２．APOGEE K-型巨星の Te - カラー関係　
　観測から直接固有カラーを決める　

　Johnson 1966 は 100 pc 以内の星のカラーを決めた。その際赤化を無視したので、導かれた固有カラーは実際より少し赤い。Ducati et al 2001 は Gezari et al 1999 の Catalog of Infrared Observation に入っている > 64,000 個の星の 396,000 観測値を使い、カタログ中にあるスペクトル型の星のカラーで最も青い値をそのタイプの固有カラーと定めた。しかし、低温の星ではサンプル数が減ることと、カラーの散らばりが増加することのために固有カラーの不定性が大きい。

　Ducati 法の改良　

　観測カラーは 2MASS を使用する。APOGEE から星のパラメタ―, 例えば Te、を決定する。こうして得た Te - カラー図上で Ducati et al 2001 と同じく青側の縁を固有カラーとする。この手法はどんなタイプの星にも適用可能だが、ここでは APOGEE で K-型巨星とされた星のみを扱う。それにより Te の巾が狭まり、固有カラーの値の信頼度が向上するからである。
(サンプルに複数の種族が含まれていると、その中で最も青い種族だけが取り出されてしまう。)
K-型巨星は E_JKs = 4 （Av = 24) まで浸透可能である。これに対し、図１の青点で示した G 型巨星は E_JKs = 1.5 までしか到達しない。また、M-型巨星のモデルは信頼度が低い。

　サンプル基準　

　図１を見ると、APOGEE で巨星とされた星は Te = [4800, 5000] で G-型と K-型が重なっている。
( よく理解できない。初めに吸収線などで G-型、K-型という分類がなされていて、2MASS のカラーもあり、それらを APOGEE 観測から Te を決めたら重なったということか？それとも、G-型、K-型も APOGEE から出したがそれでも重複が生じたのか？)
　我々は K-型の高温側境界を Te ≤ 4800 K で定める。これは、 Bessell、Brett 1988 の境界と一致する。低温側境界は APOGEE カタログの 3500 K と一致するが、実際にはこれは 3600 K で生じる。
( ここも " Te agrees with the APOGEE catalog, 3500 K," がよく理解できない。その先の、 " this occurs at 3600 K" も分からない。)
この値は古典的な K-型巨星境界よりも低い。 Bessell、Brett 1988 は K-型巨星の低温側境界を 3800 K とし、 3600 K は M4 に対応させた。これら早期 M 型の可能性もある星も対象に含めたが、それはこれらの星がよく定義された Te - カラー関係に従っているからであり、もっと重要なのはそれらが深い減光域にまで入っていくからである。表面重力は log g ≤ 3.0 であり APOGEE カタログの巨星基準を満たしている。さらに対象星は測光エラーが ≤ 0.05 mag であることを要求される。銀河面減光を調べるので |b| ≤ 5° とした。また Z ≥ -1 とした。以上から、

(1) Te = [3500, 4800]

(2) log g ≤ 3.0

(3) σ_J,H,Ks ≤ 0.05

(4) |b| ≤ 5°

(5) Z > -1

これらを満たすサンプル数は 6074 個であった。

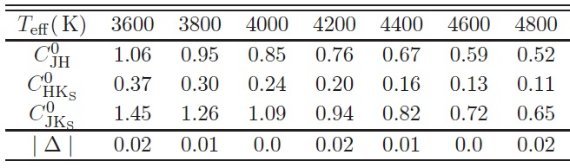
表１．G-, K-型巨星の表面温度と固有カラーの関係。

青い縁＝固有カラー　

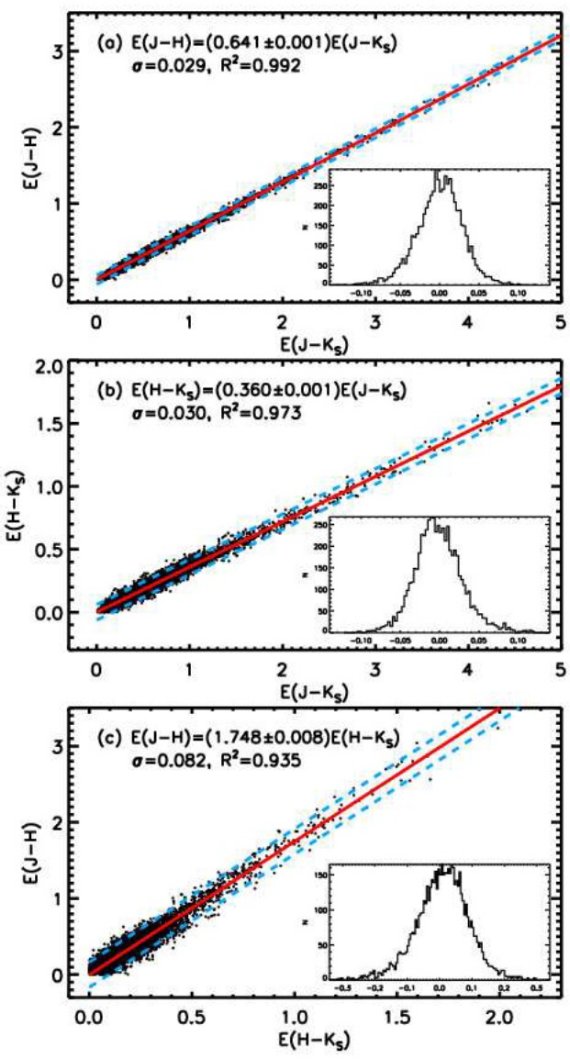
　図１は　K-型巨星と G-型巨星の CI - Te 関係である。ある Te に対応する CI の最も小さい値は無視できるほど小さい減光を受けており、固有カラーと看做しても構わない。このアイデアは Ducati et al 2001 と同じであるが、縁の決め方は少し変えた。図１に示される通り、まず δTe = 50 K の区画内で最も青い星を選ぶ。次にそれらを２次式で近似する。結果は T₃ = (Te/1000K)　として、

　　　C_JH = 4.37 - 1.27 T₃ + 0.098 T₃²

　　　C_HKs = 3.35 - 1.29 T₃ + 0.128 T₃²

　　　C_JKs = 9.19 - 3.26 T₃ + 0.309 T₃²

　考慮すべき問題点　

　次の二つが問題となる：
（１）カラーの観測エラー。測光エラーを 0.05 mag として、カラーのエラーは最大 0.1 mag となる。これは、縁をぼかすばかりでなく、観測された最も青いカラーは真の固有カラーよりも青いということになる。これを補償するため、視察して C_JH は 0.02, C_HKs は 0.03 足した。
（２）三つのカラーの間の噛み合い。表１の値を見ると、|Δ| = |C_JH + C_HKs - C_JKs| < 0.02 mag である。
　カラー値は Bessell、Brett 1988 や Wainscoat et al 1992 と良く合う。Te = 3600 K でのカラーは Bessell、Brett 1988 より 0.1 赤い。しかし、補正は行わなかった。図１を見ると Te = 3600 K でのカラーが過大評価されている兆候は見えなかったからである。

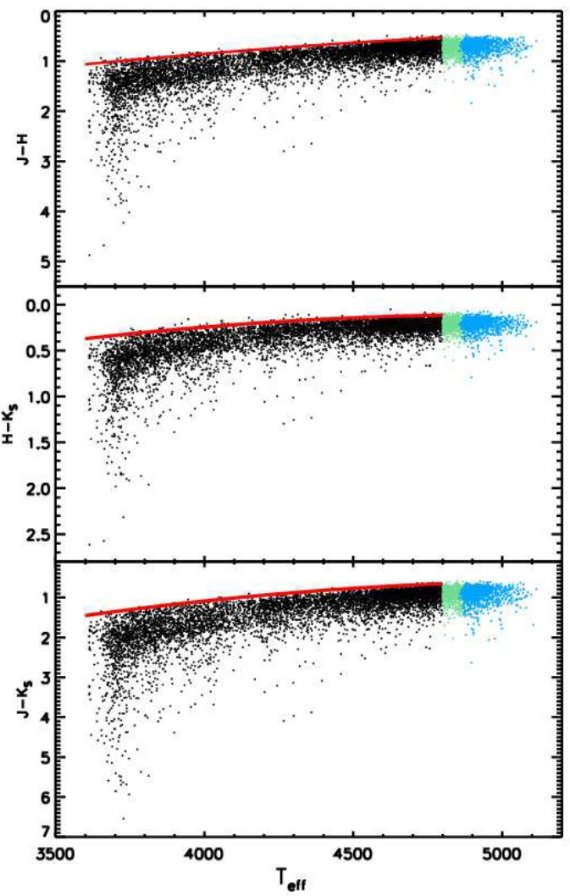
図１．固有カラー C_JH, C_HKs, C_JKs と表面温度の関係。黒点＝ 6074 K-型巨星、青点＝ G-型巨星、緑点＝多分 G-型巨星と混同された K-型巨星。赤線＝フィットした固有カラー線

　２．３．レッドクランプ星　　

　レッドクランプ星は光度とカラーの分散が小さいことで有名である。スペクトル型は K2III で、絶対等級は M_K = -1.61 ( Alves 2000 ) である。固有カラーの中心値は、C_JKs = 0.75 (Wainscoat 1992), または = 0.65 (Gonzalez-Fernandez et al 2014) である。Te - log g 図上でレッドクランプ星は Te = [4550, 4800], log g = [2.5, 2.9] の塊りとして見える。これは Puzeras et al 2010 が得た Te = 4750 ±160 K, log g = 2.41 ±0.26 と一致する。先に述べた Te - カラー関係に基づくと、レッドクランプ星の固有カラーは 0.52 ≤ C_JH ≤ 0.61, 0.11 ≤ C_HKs ≤ 0.14, 0.65 ≤ C_JKs ≤ 0.75 となる。

(前にもコメントしたが、レッドクランプが複数の種族から成っている場合、最も青い種族の Te - カラー関係が使われる。 )
これから判断すると、Wainscoat 1992 はカラー範囲の上限値を、 Gonzalez-Fernandez et al 2014 は下限値を与えている。
( スペクトルから有効温度や log g まで分かるなら、なぜ固有カラーが出せないのか？)

　３．近赤外減光則　

　測光システム間の有効波長の違いに起因するべき乗指数の不確定性は色超過比を採用すると小さくなる。なぜなら、測光は広い波長幅で実行されるからである。
( この理由付けは理解できない。)

　３．１．色超過比　
個々の星から減光則も可能　

　132 星では色超過が負になったので落とした。残った 5942 星を解析した。原理的には個々の星に対して、３つの色超過 E(J-H), E(H-Ks), E(J-Ks) を求め、近赤外減光則の指標として用いることが可能である。しかし、個々の星の解析に付随する不定性を大幅に低減するため統計的手法を用いる。

　色超過の原点　

　色超過間の線形関係を求める際に、切片の値は重要である。物理的にはある色超過がゼロの時には、他の色超過もゼロになるべきである。以前の研究ではこの点に注意してこなかった。

　

　図２には色超過間の関係をプロットした。上に述べたようにフィット直線が原点を通るという制限を課して求めた関係は、

　　　　　E(J-H)/E(J-Ks) = 0.641 ±0.001

　　　　　E(H-Ks)/E(J-Ks) = 0.360 ±0.001

　　　　　E(J-H)/E(H-Ks) = 1.748 ±0.008

であった。挿入したのは残差ヒストグラムで標準偏差は 0.029, 0.030, 0.082 である。３つの比は独立に求められたが、E(J-H)/E(J-Ks) + E(H-Ks)/E(J-Ks) = 1.78 で E(J-H)/E(H-Ks) = 1.748 とよい一致を示している。３つの内で E(J-H)/E(J-Ks) は波長間隔が広く、安定しているので、べき乗則の指標として調べる。過去の研究では E(H-Ks) が減光則の研究で用いられた、それは表２に示すようにべき乗則指数の変動に対して敏感だからであろう。
(表２のどの部分を指すのか？ )

図２．5942 K-型巨星の色超過間の関係。赤線＝原点を通るフィット。枠内は残差ヒストグラム。

表２．結果のまとめと過去の研究との比較。

　３．２．E(J-H)/E(J-Ks) の E(J-Ks) 依存性　　

　E(J-H)/E(J-Ks) 対 E(J-Ks)　

　本研究では l = [0, 220] APOGEE サンプルの星を用いた。図３(a)では E(J-H)/E(J-Ks) 対 E(J-Ks) をプロットした。赤線は図２のフィットから求めた E(J-H)/E(J-Ks) = 0.641 である。E(J-H)/E(J-Ks) が E(J-Ks) に依存する傾向は認められない。小さな E(J-Ks) で示唆される希薄星間空間と大きな E(J-Ks) が表す濃い領域との間に E(J-H)/E(J-Ks) の差は認められない。ピアソン相関係数は 0.03 で無相関を強く示唆する。一方 E(J-H)/E(J-Ks) の散らばりは大きく、小さな E(J-Ks) では特に大きくなる。

　E(J-H)/E(J-Ks) のエラー　

　E(J-H)/E(J-Ks) のエラーには幾つかの原因がある。
まず　APOGEE が与える有効温度には 100 K の誤差がある。この誤差は、有効温度 - 固有カラー関係を通じて (J-H)o, (H-Ks)o, (J-Ks)o に 0.05, 0.02, 0.07 の誤差を与える。
( d(J-H)/dT3=-1.27 + 0.196*T3 だから、 T3= 4.5, dT3=0.1 として、d(J-H)=0.04 だからまあいいか。)
　測光誤差 σ_JHKs < 0.05 という条件で与えられる平均測光誤差は 0.02 である。よって、観測カラーの誤差は平均で 0.04 程度である。
　観測カラーと固有カラーの誤差を結ぶと、E(J-H) には 0.09, E(H-Ks) には 0.06, E(J-Ks) には 0.11 の誤差がある。
( ただ足すのは誤差の伝播則と違う。観測カラーの平均誤差は0.02*1.4=0.03, E(J-H), E(H-Ks), E(J-Ks) の平均誤差は 0.06, 0.04, 0.08 である。)
　これらの誤差を色超過に入れると、色超過比のエラーは誤差の伝搬則に従って計算される。この方法で個々の星毎に計算した誤差が図３の下側に示されている。誤差の大きさは上側の色超過比の散らばりをよく説明する。

図３．(a) E(J-H)/E(J-Ks) 対 E(J-Ks) (b) E(J-H)/E(H-Ks)対 E(J-Ks).
　　　赤線＝図２で決めた色超過比。下はエラー。

依存性はない　

　このように、色超過比には色超過の大きさに対する依存性が存在しない。従って我々は近赤外減光則は場所に依らず一定であると結論する。

　４．議論　

　色超過比に対するべき乗指数　

　有効波長を 1.25(J), 1.65(H), 2.15(Ks) として、求めた色超過比からべき乗則指数を計算した。

　　　　　α(E(J-H)/E(J-Ks)=0.641 ±0.001) = 1.95 ^+0.02_-0.01

　　　　　α(E(H-Ks)/E(J-Ks)=0.360 ±0.001) = 1.95 ^+0.02_-0.02

　　　　　α(E(J-H)/E(H-Ks)=1.748 ±0.008) = 1.88 ^+0.02_-0.01

　べき乗指数と色超過比

　次に過去の研究で出されたべき乗指数から色超過比、または色超過比からべき乗指数を計算した。その際有効波長として２MASS の λ_eff を使用した。表２では太字はその文献で使用された値、細字は我々が変換して求めた値である。我々の α = 1.95 は 1980 年代に求められた 1.6 - 1.8 より大きく、2000 年代の値に近い。その原因の一部はジョンソンシステムの λ(K) と 2MASS システムの λ(Ks) との差にある。与えられた A(J)/A(Ks) (=2.88) に対して、２MASS システムは大きな α を導く。λ_eff が　２MASS の 2.15 μm からジョンソンの 2.22 μm へ移ると α は 1.95 から 1.84 に変わる。
(馬鹿げた論理に聞こえる。 )
　もう一つの可能な原因は isophotal wavelength λ_iso を λ_eff の代わりに使用することである。２MASS に関しては λ_iso = 1.24(J), 1.66(H), 2.16(Ks) μm となる。すると、E(J-H)/E(J-Ks) = 0.64 に対して α = 1.65, A(J)/A(Ks) = 2.51 を与え、 λ_iso を採用した Indebetouw et al 2006 が与えた小さな α の説明が可能となる。

　メタル量効果　

　 Gao et al 2013 は LMC で E(J-H)/E(H-Ks) = 1.25 という値を得た。これはそれまでの研究結果と一致するが、銀河系での値より著しく低い。一方で彼らの　E(J-H)/E(J-Ks) = 0.64 は我々の銀河系の値と良く合う。APOGEE サンプルから取った低メタル（Z < -1) の 735 巨星は大部分がハローにあり、小さな減光 E(J-Ks) < 1 であった。　このサンプルに同じ処理を施した結果は、 E(J-H)/E(J-Ks) = 0.73, E(H-Ks)/E(J-Ks) = 0.36 でつまり E(J-H)/E(H-Ks) = 2.03 であった。この変化は Gao et al 2013 とは逆方向である。しかし、サンプル数が不足してメタル効果をどう評価すべきかは不明である。

　Weingartner, Draine 2001 のダストモデルは表２に示すように、 Rv = 3.1 - 5.5 の変化に対して α = 1.60 - 1.62 と殆ど変らない。これは近赤外減光則の普遍性を説明するものかも知れない。しかも、サイズ分布を NMR モデルのべき乗則指数 3.5 とすると、E(J-H)/E(J-Ks) = 0.65 となり、われわれの結果と一致する。

　５．まとめ　

　APOGEE NIR 分光サーベイに基づき、K-型巨星サンプルを選び、固有カラーと有効温度の関係を導いた。

　固有カラーから個々星の色超過を導き近赤外色超過比を計算した。その値は色超過の大きさに依存しなかった。その値はべき乗指数 α = 1.95 に対応する。