Modeling the IR Extinction toward the GC

　アブストラクト

　１．イントロ　

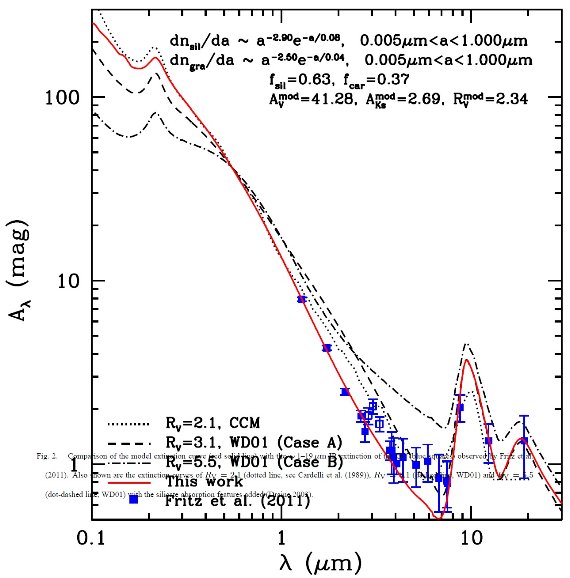
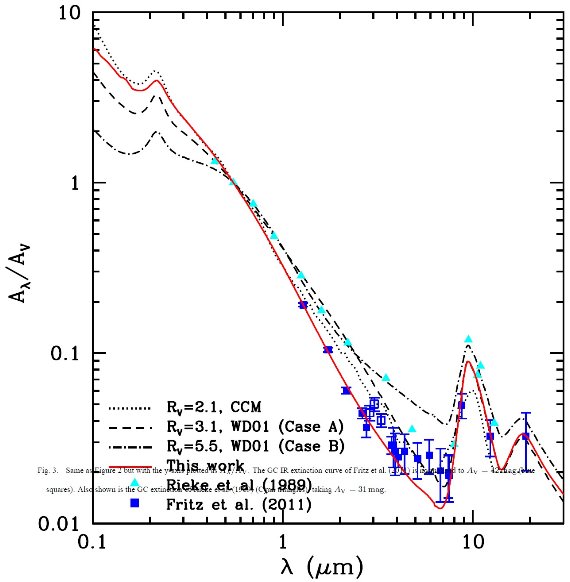
紫外・可視減光曲線と Rv　 　紫外・可視減光曲線は視線方向により、Rv の値に伴って 変化する (Cardelli et al. 1989) ことが知られている。一般には濃い星間雲では Rv > 4 が、希薄な星間媒質 に対しては Rv = 3.1 が典型的な値である。この差はダスト粒子のサイズ分布が 雲の中では大きい方に傾くためであろうとされている。 　赤外減光曲線　 　赤外減光曲線も視線方向により変化する。しかし、単純に Rv を変えただけでは その変化は表現されない。最近の Fitzpatrick, Massa 2009, Gao et al 2009, Zasowski et al. 2009 の研究は、普遍的赤外減光曲線というものは存在しないことを示している。 中間赤外減光曲線は平坦で Draine 1989 のモデルで予言された深い 7 μm の 谷は見当たらない。興味深いことに、平坦な中間赤外減光曲線は標準的な シリケイト・グラファイトモデル (Weingartner,Draine 2001) の Rv=5.5 ケース と良く合っていることで、これはこれは Rv = 3.1 の場合より大きなダストサイズ を支持する。 (平坦部が Rv5.5 モデルで指示される と言うが、実際に中間赤外の観測が得られた方向の Rv はどうなのか？ または、Rv = 3.3 の方向での中間赤外減光曲線は平坦部を示さないのか？ ただ、希薄星間媒質の中間赤外減光は測定できない？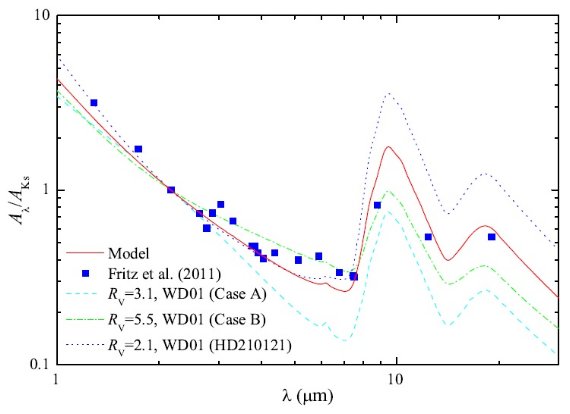 ) 　Fritz et al 2011 の 1 - 19 μm 減光曲線　 　Fritz et al 2011 は ISO-SWS と SINFONI を用いて、銀河中心ミニスパイラルの 水素輝線を観測し、そこから 1 - 19 μm 減光曲線を導いた。　その近赤外減光曲線は Nishiyama et al. 2006, Nishiyama et al. 2009 の結果と一致する急な勾配を示した。中間赤外部は他の研究と同じく平坦であった。 この結果は Rieke, Lebofsky 1985 や Rieke et al 1989 とは合致しない。Fritz et al 2011 は GC 方向で Av = 59 mag. という値を得た。ただしこの値は N(H)/Av に仮定する値で変動する。この値は Rieke, Lebofsky 1985 が得た Av = 31 よりずっと大きい。 　標準グレインモデル　 　この論文では、 Draine,Lee 1984 のグラファイト＋シリケイト標準グレインモデルを Fritz et al 2011 の GC 方向 減光曲線にフィットする。

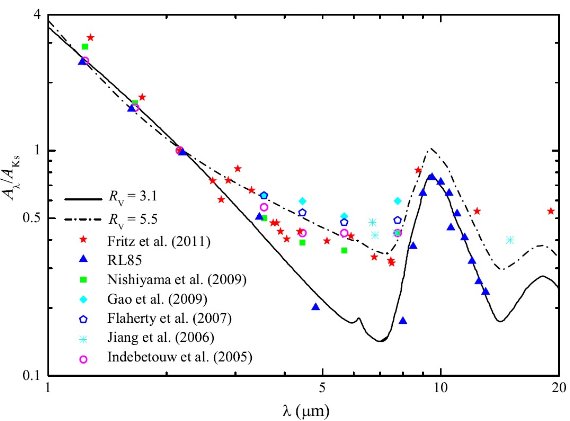
図１．赤外減光曲線。 赤星：GC 方向星 H ラインによる。(Fritz et al 2011) 青三角：GC 付近の赤色巨星、 Rieke, Lebofsky 1985 緑四角：赤色巨星枝を用いた推定レッドクランプ Nishiyama et al 2009。 シアン菱形：|l| < 5, |b| < 2 平均減光(Gao 2009)。 他の３種類は　ＧＣ　から外れた方向。 実線：Weingartner, Draine 2001 モデル、Rv=3.1. 一点鎖線：同上。Rv=5.5

　２．ダストモデル　　

　３．モデルフィット　

標準減光曲線をフィット　 　モデルをテストするため、まず Rv=3.1 の標準減光曲線をフィットしてみた。 非晶質シリケイトは dn/da ∝ a-3.5 exp(-a/0.14), グラファイトは dn/da ∝ a-3.1 exp(-a/0.11) として、 モデルは Rv = 3.1 減光曲線をよく再現した。 　Fritz 減光曲線フィットに失敗　 　Fritz 減光曲線をフィットする際に、最初はシリケイト、グラファイト同じ形の サイズ分布を仮定してフィットした。次に両者が違う形をしてもよいとしてフィット した。結果は表１に示した。同じサイズ分布でも異なるとしてもほとんど差はなかった。 結局、どれも平坦な中間赤外減光曲線を生み出すことに成功しなかった。ただ、ケースＢ は比較的良かった。 　フィット曲線の検討　 　図２には、異なるサイズ分布を仮定してのケースＢベストフィットを示す。 観測と比べると、モデルは 2.166 バンドで高過ぎ、7 μm では低すぎる。 αC = -2.5, ab,C = 0.04 μm のグラファイトサイズ 分布は急な近赤外減光を再現したが、それが 7 μm に極小部を作る原因となった。 サイズのカットオフ ab,C を 0.04 μm という小さな値にしたことは、 つまりモデルが小さなグラファイト粒子に富んでいることを意味し、そのためこの モデル減光曲線は UV で Rv = 2.1 減光曲線によく似る。 αsi = -2.9, ab,si = 0.08 μm のシリケイトサイズ 分布は 9.7 μm の強い吸収バンドを生み出した。 図２．青四角：Fritz et al 2011 の観測減光 Aλ。赤実線： モデル。点線： 　 Cardelli et al 1989 の Rv=2.1 減光曲線。 破線：Weingartner, Draine 2001 の Rv=3.1 減光曲線。 一点破線：Weingartner, Draine 2001 の Rv=5.5 減光曲線にシリケイト吸収付加。

モデルの改善策　 　中間赤外の平坦部を作るには 0.5 μm かもっと大きなサイズのダストを取り 入れる必要がある。シリケイト吸収帯の面倒を避けるため、われわれは観測との フィットを 1 - 7 μm に限定した。 　3 - 19 μm フィット　 　3 - 19 μm に限定するとうまくフィットできる。しかし、その場合は 1 - 3 μm がうまく合わない。結局 1 - 19 μm 全体を合わせることはできなかった。 グラファイトを非晶質炭素で置き換えたが同様の結果に終わった。 　近赤外減光曲線の急な勾配　 　 Rieke, Lebofsky 1985 は β = -1.6、Rieke et al 1989 は β = -1.8 に対し、 Nishiyama et al. 2009 と Fritz et al 2011 は β = -2.0 を与えた。 　Rieke et al 1989 のフィット　　 　αsi = -2.1, ab,si = 0.08 μm αC = -3.0, ab,C = 0.28 μm は Rieke et al 1989 のフィットに成功した。これは実際には Rv=3.1 減光曲線である。 図３にはその結果を示した。 　３種混合減光曲線？　 　結局、UV-NIR は Rv = 2.1, 平坦 MIR は Rv = 5.5, それに Rv = 3.1 の強い シリケイト的特徴の混合なので、３種類のサイズ分布が必要である。 図３．図２と同じだが、縦軸を Aλ/Av にした。 青四角： GC で Av = 42 mag に取った Fritz et al 2011 減光曲線。 シアン三角：Av = 31 mag の Rieke et al 1989 GC 減光曲線。

　４．議論　

　５．まとめ　　

多成分モデルは尤もらしいではないか。

図４．青四角： Fritz et al 2011 の銀河中心減光曲線。 　　　赤実線： ３成分モデル。点線:Rv=2.1(28%)。破線：Rv=3.1(39%)。 一点鎖線：Rv=5.5(33%)。緑三角：西山(2009) の減光。