JHKLM Photometry : Standard Systems, Passbands, and Intrinsic Colors

　アブストラクト　

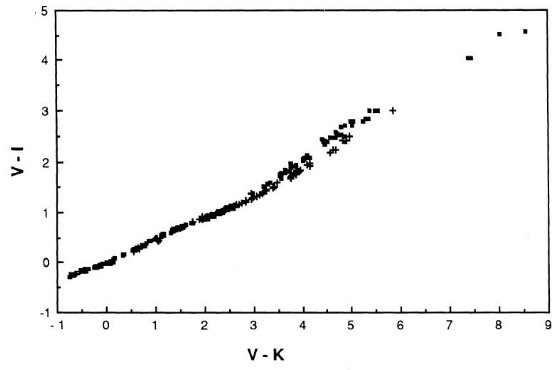
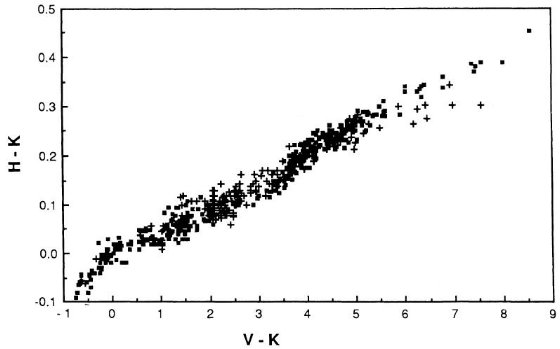
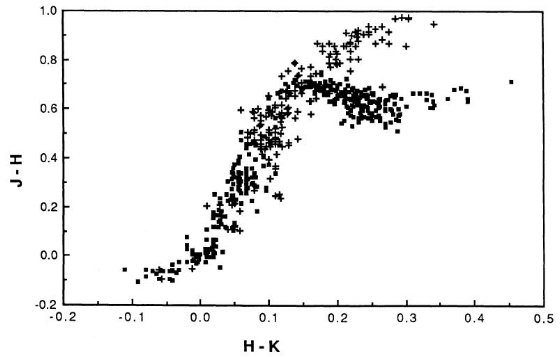
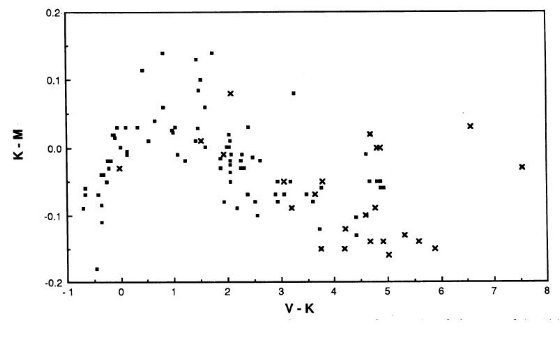
SAAO, ESO, CIT/CTIO, MSO, AAO, Arizona の JHKL システムのカラーの関係を 調べ、カラー変換を一次式で表わした。均質化システム、基本的には Johnson - Glass システム、を提案し、その絶対等級は Bell の α Lyr 大気フラックスモデルに 基づいて導いた。標準星の均質化カラーを用いて、 B7V - M6V と G7III - M5III の 固有カラーを定めた。 　MSO IR システムの JHKL パスバンドを用いて、太陽を含む幾つかの星の相対的な 絶対フラックスから合成カラーを計算した。 図１. (V-K) 対 (V-I) 関係。十字＝巨星と超巨星。黒四角＝矮星。 図３.(H-K) 対 (V-K) 関係。十字＝巨星と超巨星。黒四角＝矮星。 図５. 図７. 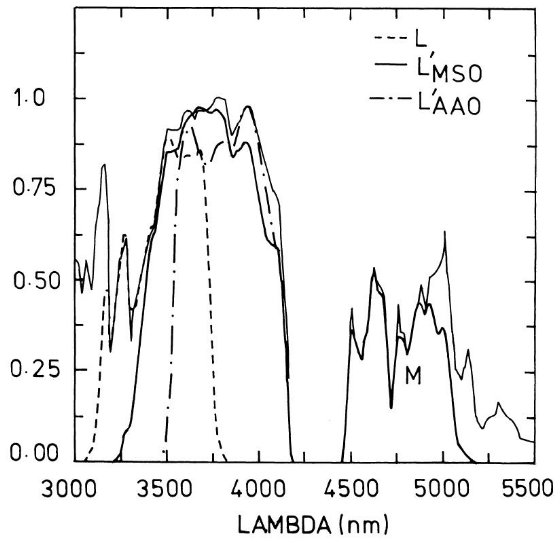(K-M) 対 (V-K) Engels et al 1981, Wamstecker 1981, Thomas et al 1973 図９. 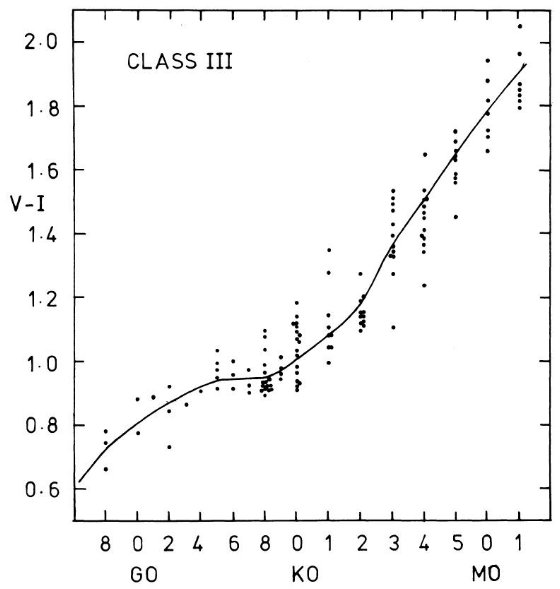3 - 5.5 μm 大気透過率と L, L' M 図Ａ２.巨星の (V-I) 対 MK スペクトル型。

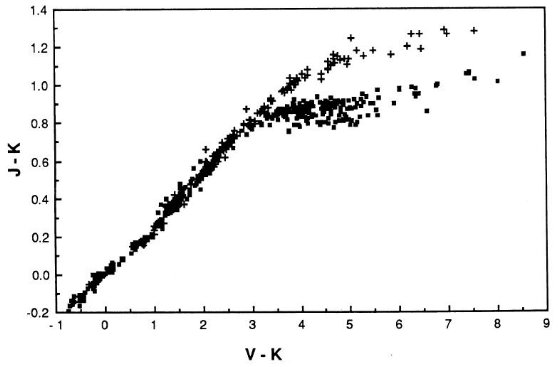
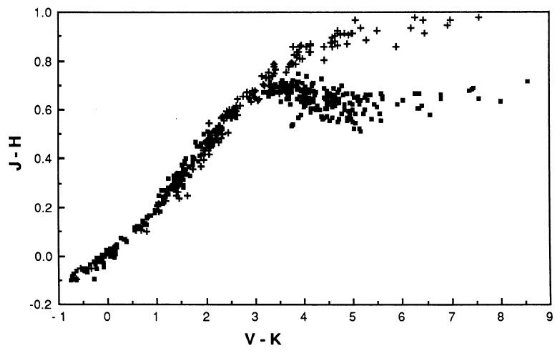
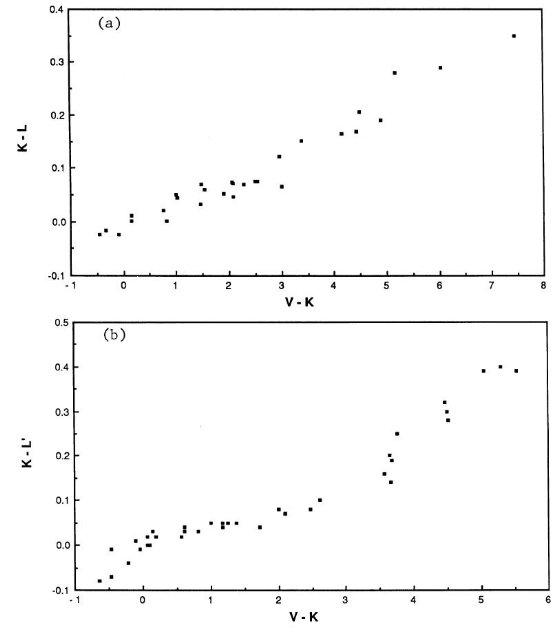
標準化（？）された JHKL カラーとの 一致がよいことから MSO パスバンドを均質化システムを代表するものとして採用 し、理論的または観測フラックスから赤外カラーを計算できることが判った。 　他の赤外システムのパスバンドは公表データを用いて同様に評価された。 こうして得たこれらのパスバンドは、次に、システム間の観測的な関係と一致 するように波長を調整された。こうして異なるナチュラルシステムの有効波長 を評価できた。非常に赤い星の分光測光が得られれば、有効波長の決定はさらに 改善されるであろう。 図２.(J-K) 対 (V-K) 関係。十字＝巨星と超巨星。黒四角＝矮星。 図４.(J-H) 対 (V-K) 関係。十字＝巨星と超巨星。黒四角＝矮星。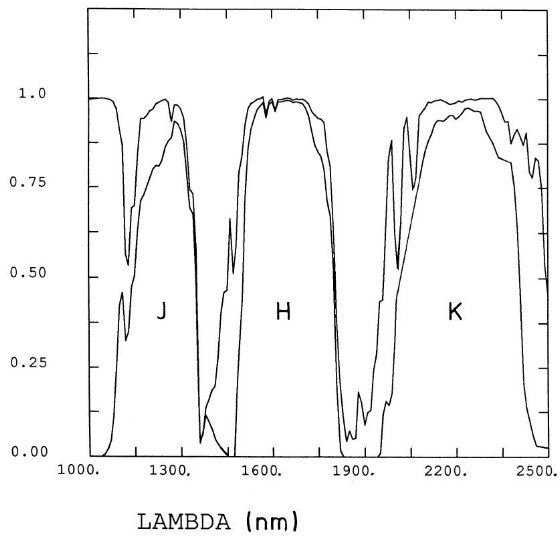 図６.(a) Elias et al 1982 星の (K-L) 対 (V-K) 　　　(b) Allen, Cragg 1983 の(K-L') 対 (V-K) 図８. 1 - 2.5 μm 大気透過曲線と採用した(MSO?)フィルター透過率。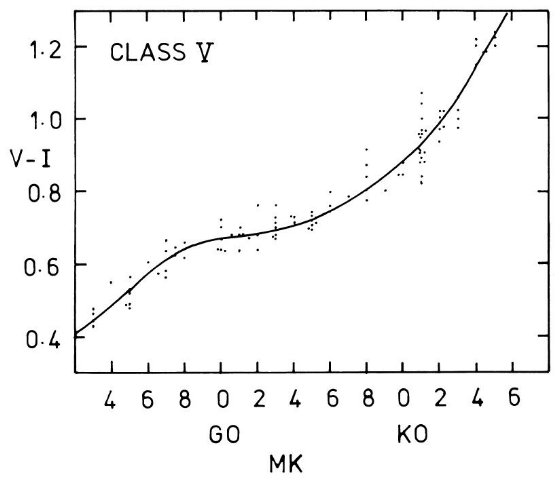 図Ａ１. 矮星の (V-I) 対 MK スペクトル型。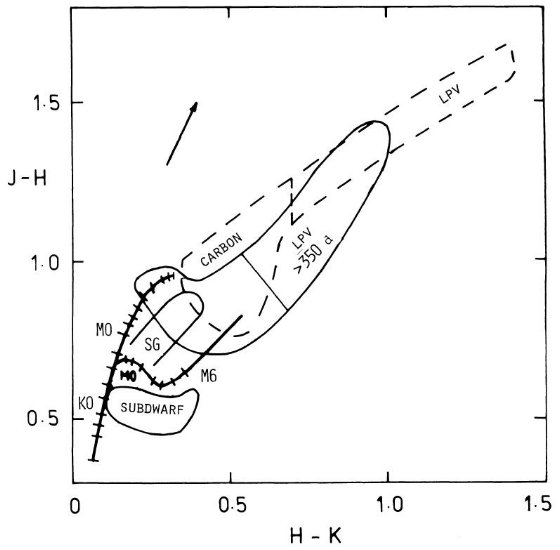 図Ａ３.矮星と巨星の赤外二色図上の位置。