Galactic Structure from the SPACELAB Infrared Telescope. II. Luminosity Models of the Milky Way

　アブストラクト

　１．イントロダクション　

　２．放射とダストのモデル　

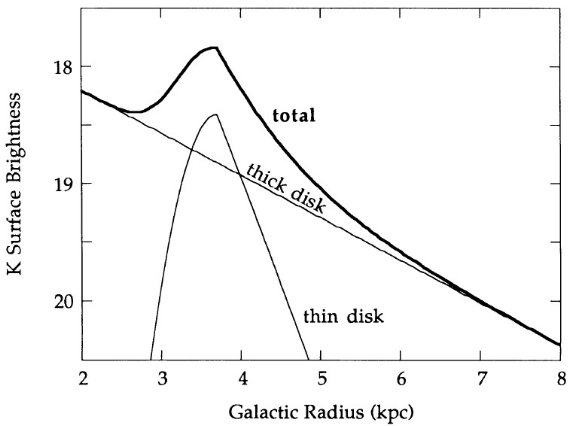
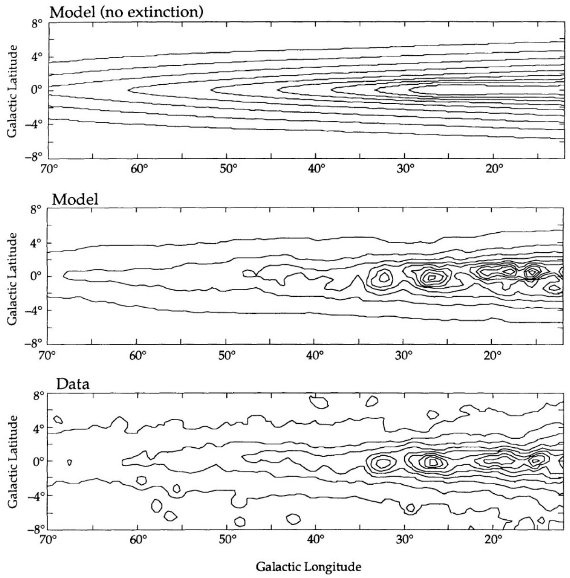
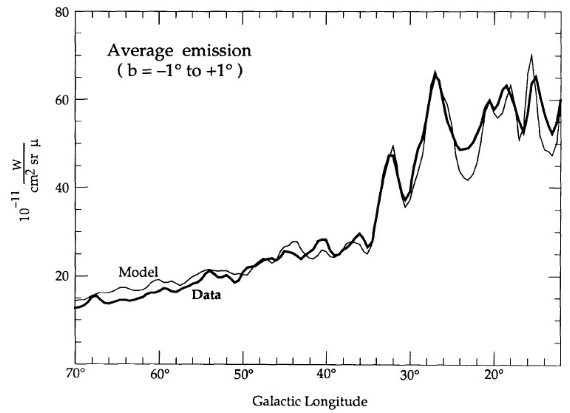
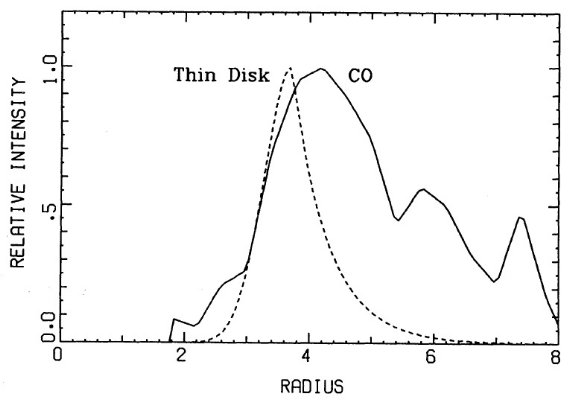
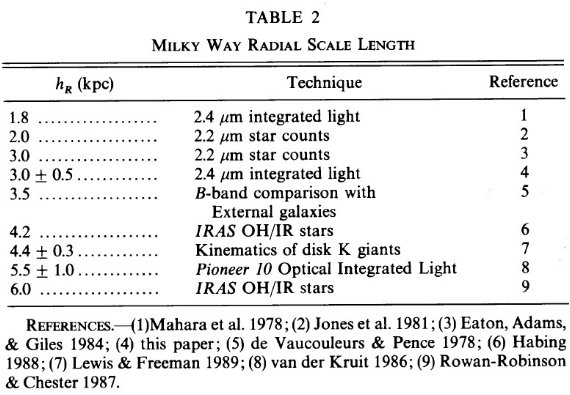
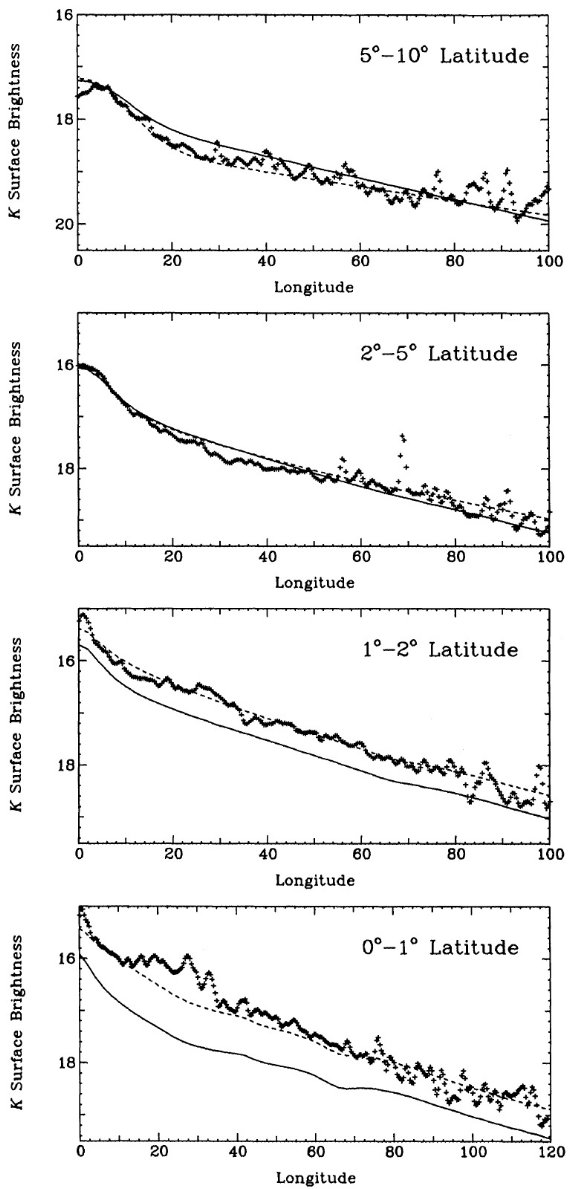
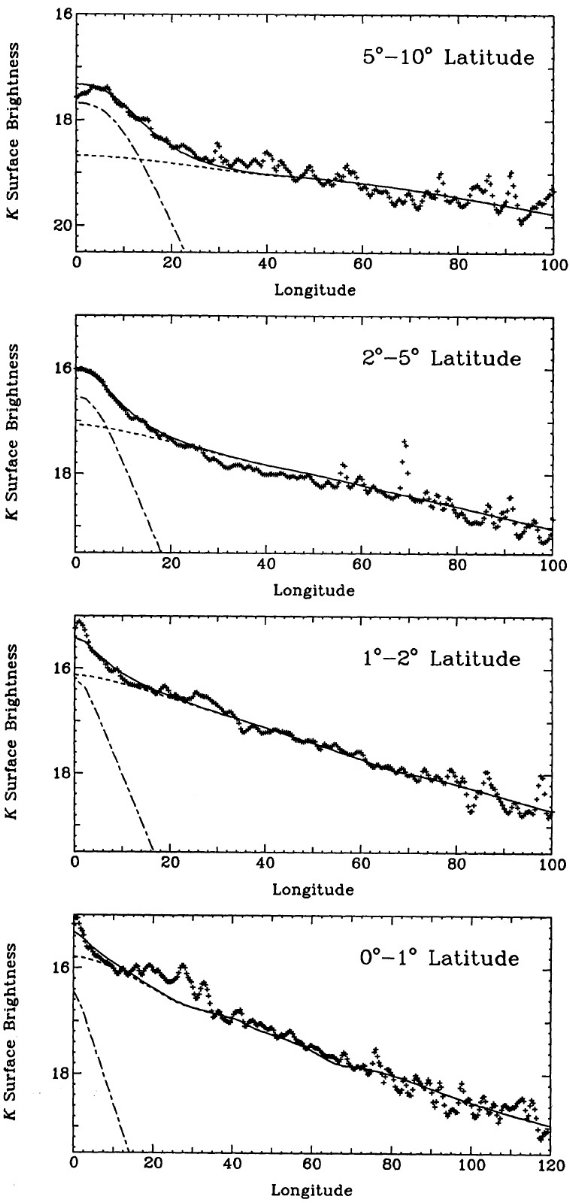
垂直方向の密度分布　 　銀河系＝円盤＋バルジでモデル化を試みる。円盤は、 　　　ν(r, z) = μDexp(-r/hr)g(z/hz)/hz 　　　　　（１） ここに、(r, z) は円筒座標、ν は体積放射率、μD は円盤 中心で垂直に積分した表面輝度、hr はスケール長＝一定値、 、hr はスケール高＝ r の関数。∫g(x)dx = 1 と規格化した。 g(x) として二種類考えた。 　　　　　g(x) = (1/4)sech2(x/2)　　　　　　　　(2) 　　　　　g(x) = (1/2) exp(-|x|)　　　　　　　　　　(3) 式（２）は自己重力等温膜面の密度分布で、van der Kruit, Searle 1981 により、 横向き銀河の垂直プロファイルを良く表すモデルとして提案された。ファクター２は 遠方で式が exp(-|x|) に収れんするために含ませた。しかし、Pritchet 1983 は 単純な指数関数型の方が銀河系の星計数データに良く合うことを見出した。また、 Wainscoat, Freeman, Hyland 1989 は横向き銀河 IC2531 の赤外測光による面に 垂直方向の輝度輪郭は sech2 型より尖がっていることを発見した。 Van der Kruit 1988 は sech 型が最も良く合うとした。ここでは、指数関数と sech2 型の二つを試す。 　楕円体成分は無視　 　de Vaucouleurs, Pence 1978 は銀河系楕円体を r1/4 則で表した。 しかし、図１からも分かるように、この関数をバルジ領域に外挿すると短軸沿いの フィットが悪い。半径 10° 以内ではスケール長 2.7° = 378 pc の 指数関数型の方が良く合う。実際、内側バルジと外側楕円体が一つの成分である 必要はない。横向き銀河 NGC 4565 では　Kormendy 1980 による短軸プロファイル はバルジと楕円体を単一の関数でフィットすることは不可能であった。Frankston, Schild 1976 は NGC 4565 の内側バルジは指数関数型で、 50″ より外側ではべき乗型になることを示した。ここでは内側バルジを扱うので楕円体 成分は考えない。 　箱型バルジ　 　バルジの形は低光度バルジに多く見慣れる特徴として箱型である。そこで、バルジの 放射密度として、

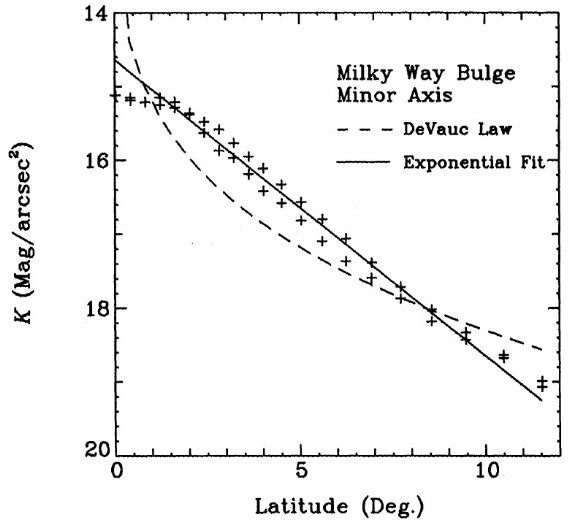
図１．バルジ短軸沿いの輪郭を指数関数フィットとドボークルー・ペンスのモデル で合わせた。後者は V - K = 3.2 を仮定。 　　　　　ν(s) = (μ0/πhB)Ko(s/hB) 　　　　（４） ここに ν = 放射密度、μ0 = 中心での投影表面輝度、hB = 主軸スケール長、εB = バルジ楕円率、Ko = 修正ベッセル関数 である。動軸座標 s は s4 = R4 + [Z/(1-εB) ]4 で与えられる。この式は箱型の投影を生み出す。強調しておきたいのは このバルジモデルは 1° - 10° 範囲のバルジに合わせる目的で使われ、外側の 楕円体も、 Becklin, Neugebauer 1968 が見出した中心部の尖がりも無視している。

　３．銀河系のパラメタ―　　

図２．2.4 μm 輝度の銀経沿い輪郭を二種類のフィットを行った。各 銀緯区分は銀緯正負の平均。実線＝銀河系の標準パラメタ―使用。破線 ＝パラメタ―は最少二乗平均で調整。 　表面輝度の比較　 　放射密度分布のパラメタ―が与えられれば、太陽から見た表面輝度分布を 計算できる。 Kent et al 1992 の観測データと比較するために、銀河赤道と平行な次の４つの帯の平均輝度 輪郭を計算した：|b| < 1, 1 < |b| < 2, 2 < |b| < 5, 5 < |b| < 10。 フィッティングに際して、次の領域のデータは無視した。 （１）銀河系中心から 4° 以内。減光が不確定だから。 （２）10 < l < 35, |b| < 1. コブ部分。 （３）明るい星の周り、数か所。 変動する背景光の問題により、 Kent et al 1992 では、 (l, b) = (66, -21) で I = 0 として輻射強度を決めた。モデルも このシステムにあうようにした。 　図２＝標準モデル　 　標準的な円盤モデルのパラメタ―は、hR = 3.5 kpc, hz = 250 pc, それに sech2 垂直分布を仮定した。 バルジの短軸方向スケール長 = hB = 378 pc とし、楕円率 ε = 0.35 とした。ベストフィット解は図２に示す。垂直方向の規格化には 2 - 5° カットにもっと見良く合うように定めた。銀河面上でのフィットは 悲惨で、実際よりうんと低いレベルを予想している。 　図２＝最少二乗フィット　 　次に円盤パラメタ―(hR, hz, μD)と、 バルジパラメタ―(hB, εB, μB)を 調整して、最少二乗解をやはり図２に示した。モデルパラメタ―を表１に示す。 省略したデータ部分以外でフィットはずっと良くなった。ただ、0° - 1° 帯では依然としてフィットが不十分である。もっと混乱させられるのは、垂直 スケール高の 122 pc が期待された値の半分以下であったことである。 　sech2 を exp 型に　 　sech2 垂直分布型を指数関数型に変えてみた。その結果はここに 示さないが、あまり改善されなかった。スケール高は 204 pc になったが、依然 太陽近傍での値に比べるとずっと小さい。そこで、最後の手として、指数関数形 でスケール高を半径により変化させた。色々な関数形を試したが、最後に辿りついた のは、 　　　　　hz = hmin　　　　　　　　　　　(R < Rmin) 　　　　　　　= hmin + a(R - Rmin)　　 (R > Rmin) この形でフィットした結果を図３に示す。今回は改善が目覚ましく、太陽近傍での スケール高も 427 pc と期待値に大分近づいた。そこで、このモデルを標準 モデルと呼ぶことにする。このモデルのパラメタ―を表１に示す。 　バルジ　 　短軸沿い表面輝度分布を直接フィットした結果のスケール高は 378 pc である。 しかし、モデル予想値は 407 pc で大分大きい。その理由は図３を見ると分かる。 上パネル、5 - 10 帯の観測輪郭は l = 0 付近でへこみが生じている。箱型バルジ モデルでさえも中心を窪ませることはできなかった。この窪みが本当かどうか、 はっきりしないが、COBE の図にも同様の窪みが見えている。いずれにせよ、 より正確なバルジモデルでは等密度面の形が距離により変化するものとなるだろう。

図３．図２と同じ 2.4 μm 輝度の銀経沿い輪郭の二種類のフィット。 ただし、垂直方向にスケール高が変化する指数関数型分布を仮定。 バルジと円盤成分をそれぞれ示す。 表１．天の川銀河のモデルパラメタ― 　光度と放射率　 　円盤の光度＝ 5.5 × 1010 Lo, バルジの光度＝ 1.2 × 1010 Lo を得た。モデルは、太陽近傍での 2.2 μm 放射率 = 2.8 × 1024W μm-1 pc-3, 表面フラックス = 1.4 × 1027W μm-1 pc -2 を予想する。石田、三上 1982 の得た値は、それぞれ 3 × 1024、2.2 × 1027 である。 前者は良く合っているが、後者はややずれがある。おそらく、石田、三上 のスケール高がここでの値より大きいためでああろう。

　４．ダスト/ガス　比の較正　

コブは HIIR か 低減光か？　 　図２，３の |b| < 1 帯のプロファイルを見ると、滑らかな背景の上に 幾つかの個別天体が乗っている。Melnick et al 1987, 早川その他 1981 は それらを HIIR と渦状腕とした。一方、奥田その他 1981 はそれらのコブと CO 強度に逆相関があることから低減光領域と看做した。我々は減光変化を 調べて、後者の解釈が正しいことを見出した。 　薄いリング　 　2.4 μm マップ第１象限に見られる強度デコボコを再現するため、太陽円 内側での放射とダストの密度分布のモデル化を考える。つまり、第３章のモデル より詳しいモデルを。早川その他 1981 に従い、放射密度分布を厚い円盤 （第３章で使ったパラメタ―の円盤）と薄い円盤（実際には円環）の重ね合わせ と考える。薄い円盤は l = [10, 35] の輝度超過を表現するためのものである。 薄い円盤は、垂直方向には z 厚み = 112 pc のガウシャンで、ピークは R = 3.7 kpc にあり、それより内側ではガウシャンで落ち、外側は指数関数型で落下 していく。この関数形は第１象限を最もよく表現するように選ばれた。 　この薄いリングは R = 4.2 kpc でピークに達する分子雲の集中に伴う若い星 の集まりかも知れない。図４には銀河系を真上から見た時の円盤輝度分布を 示した。 図４．モデルに使用した厚い円盤と薄い円盤の表面輝度

電波ーー＞ガス分布 = ダスト分布　 　 Dame et al 1987 の CO 観測、Weaver, Williams 1973 の HI 21 cm 観測を用いて、ガスの３次元 分布を作った。ガスまでの距離は視線速度と銀河系回転曲線から導く。運動距離 には "near" と "far" の二つがあるので、|b| < 1.5 で Vr が端末速度の 15 km/s 以内にある放射は近距離と遠距離の双方に等しく分ける。残りの放射は 全て近距離に付ける。と言うのは、この解析での分解能 0.5° では遠距離の 放射からの寄与は無視できるほどに小さいからである。CO と HI 放射率は第３章 で述べた方法でダスト吸収率に変換される。 　３次元分布から 2.4 μm 表面輝度マップへ　 　放射と減光の３次元モデルから、2.4 μm マップを計算した。図５には 計算した輝度分布を、 Kent et al 1992 の観測マップと比較した。細かいデコボコまでが良く再現されている。 ( 減光＝ガスの３次元分布は銀河赤道に対して 対称ではない。それが 2.4 μm マップに反映。) 図５．上：ダスト減光なし、薄い円盤は含む 2.4 μm 放射モデル。中： 上と同じだが、ダストの３次元分布を含むモデル。下：IRT実験で観測した 2.4 μm 輝度分布。下の二つでは等高線は 18.2 mag arcsec-2 間隔。

図６．実線＝ 2.4 μm 放射観測値。薄線＝図５モデル。双方共に b = [-1, +1] の平均値。 　図６＝銀河赤道に沿った輝度分布　 　図６は b = [-1, +1] の平均輝度分布をモデルと観測とで比較したものである。 モデルのパラメタ―はベストフィットを目指して決めたが、デコボコはダストモデ ルの正しさに依存する。特に、 l = [10, 35] 領域のダストモデルの正確さは影響 が大きい。モデルと観測との間でのズレ最大は l = 23 で生じているが、これは 遠距離　 (Dame et al 1986) にあることが知られている M = 5 × 106 Mo の巨大分子雲複合 の存在が原因と考えられる。

図７．CO 分布と 2.4 μm 超過放射の比較。ピーク半径のずれが顕著。 　図７の解説　 　図７では我々のモデル薄い円盤からの放射分布を北半球銀河面の CO 分布と 比較した。光分布は CO に較べ著しく幅が狭い。そして放射ピーク位置は CO に較べ半径 0.5 kpc 内側にある。このズレは本物のように見える。

　５．他の研究との比較　

スケール長　 　指数関数型分布のスケール長に関してはこれまで多数の研究があった。表２には 最近の幾つかを挙げた。 舞原その他 1978, Jones et al 1981, Eaton et al 1984　hR < 3 kpc 　近赤外面輝度分布または近赤外星計数から 　放射密度変化を回転楕円体モデルのスケール長に直しているので指数型と違う。 ドボークルーとPence 1978　3.5 kpc 　星計数から太陽近傍での垂直積分表面輝度を決定。それを系外銀河と較べ、 銀河系中心表面輝度は　B で 21.65 mag arcsec-2 と仮定し て上の値を求めた。 　 Lewis, Freeman 1989　　　　4.4 kpc　 　円盤 K 巨星の速度分散が銀河中心距離に応じてどう変わるかを観測し、 σ ∝ exp(-R/2h) を仮定して決定した。 (この論理はよく分からない。 ) 　円盤星の速度分散は円盤からの高度に依らず一定、スケール高は銀河系半径に依存しない、 速度分布非等方性も不変と仮定している。しかし、銀河面垂直方向の分布が指数型だと 最初の仮定は間違い(van der Kruit 1988)である。 van de Kruit 1986　　　　　6.5 kpc　 　Pioneer 10 Background Experiment で測った |b| > 20 での、星の積分光、 バンドは可視の赤と青、の l 変化から。 　近傍の表面輝度勾配から局所スケール長しか出ないはず。 Habing 1988, Rowan-Robinson, Chester 1987 　4 - 6 kpc 　IRAS が発見した OH/IR 星。 　Habing は |b| < 2° の天体を撥ねた。 表２．天の川銀河のスケール長

どうして、こんなに違うのか？　 （１）正当化されていない仮定の存在 　 　　　個々の研究にコメントしてある。 （２）銀河系を構成する成分毎に異なるスケール長を持つ。 　 　　　例えば系外銀河では、赤外スケール長は可視光でのスケール長の 0.85 倍。 　IRT 観測の利点　 　IRT は 早川その他 1981 以外ではどれよりも広い銀経範囲をカバーしている。 銀河面を含んでいるのも、銀河半径勾配の検出には大事である。2.4 μm では 古い円盤の K, M 巨星を測るので、若い星の存在やメタル量勾配の影響は小さい だろう。星形成域に付随する赤色超巨星の効果が不確定である。我々のマップには 良く知られた HIIR からの強い 2.4 μm 放射は記録されていないが、 R = 4 kpc の放射のコブは分子雲密度最高位置に一致する。Sera, Puget, Ryter 1980, 奥田 1981, 川良その他 1982 はそれを活発な星形成に伴う盛り上がりと解釈した。 　スケール高の問題　 　我々のモデルではスケール高が半径 5 kpc から先で線形に増加していく。もし 4 kpc のコブもモデルに組み入れるとスケール高の変化は一層激しくなる。 van der Kruit,Searle 1981 は横向き銀河でスケール高が半径に依らず一定という 結果を得ているが、我々のモデルはそれと矛盾する。我々がスケール高を変化させた 一番の理由は、一定モデルだと hz = 2-4 pc で小さくなり過ぎるため である。van der Kruit, Searle 1981 の観測は減光の影響を少なくするため 銀河面高度が大きいところでスケール高を決めているが、これは古い円盤種族の 速度分散の大きい星のスケール高になっている可能性がある。一方我々は そういう区別なくまぜこぜに測っていて、そのため銀河中心方向では スケール高の小さな若い星の影響が大きく出たのかも知れない。 van der Kruit, Searle 1981 はまた、フレアリング＝円盤の縁方向でスケール高が大きくなること、 を注意している。太陽は丁度その位置にいる可能性もある。

　６．IRAS バルジとの比較　

　７．結論