The Universe at Faint Magnitudes
I. Models for the Galaxy and the Predicted Star Count


Bahcall, J.N., Soneira, R.M.
1980 ApJS 44, 73 - 110



　アブストラクト

２成分モデル　

　指数型円盤＋ドヴォークルー回転楕円体の銀河系モデルを構成した。スターカウ ントを使って銀河系構造パラメターを決める方法を実演し、ハロー成分を検出する 可能性を論じた。光度関数とスケール高は太陽近傍の値を使う。楕円体の光度関数 は +4 > Mv > 12 では円盤光度関数と同じ形であることが分かった。

　楕円体成分の密度は太陽近傍で円盤の 1/800 である。楕円体にドヴォークルー 則を使ったスターカウント計算は観測と合うが、ハッブル則では合わない。

等級、カラー変化の意味　

　モデル星数分布の見かけ等級、銀緯、銀経による変化はデータが揃っている +4 > mV > 22 の範囲で観測とよく合う。モデルカラー分布も観測 と合う。カラーデータから mV = 22 でのクエーサーの混入は数％に過ぎ ないことが分かった。

 スターカウント総数　

　楕円体成分の形はほぼ球形であることが分かった。モデルのスケール長、総光度、 M/L 比は Sbc 銀河の観測値と合う。銀河系形状を更によく決めるために何処を観測 すべきかの提言を行った。

　２成分モデルによるスターカウントの予言をスペーステレスコープの到達等級 m = 28 までで銀極方向では１平方度あたり 104 と予言した。この 数字はパラメターにあまり影響されないが、光度関数に大きな変化があれば別である。

回転曲線　

円盤と楕円体のみの銀河系モデルから計算した回転曲線は 10 kpc の先で低下し 始める。太陽付近で 0.01 M๏ pc-3 程度の低密度の ハローでも回転曲線を平坦に持ちあげられる。このハロー成分を担う恒星が Mv ≤ 19 mag ならばスペーステレスコープで検出されるであろう。

　本文ではＶ等級に関する結果を述べ、Ｂ等級に関する話は付録Ａに回した。スター カウントのモデル予測は付録Ｂに載せた。

　1.イントロ　

以前のモデルとの違い　

　この論文はＳＴカメラが観測すべき領域を指し示す目的で書かれるシリーズの 最初の論文である。この論文が以前の Schmidt 1965, Innanen 1973, de Vaucouleurs, Pence 1978, Ostriker Caldwell 1978 と異なる点は、物質や放射の分布を求める だけでなく、銀緯、銀経の関数として予想されるスターカウントを求めた所にある。 光度関数とスケール高は近傍の観測値を使った。銀河全体の密度分布は他の銀河の 観測で決まる関数を用いた。

今回のモデル　

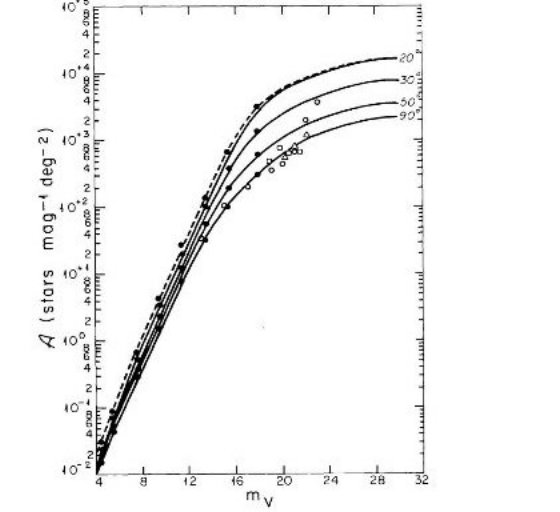
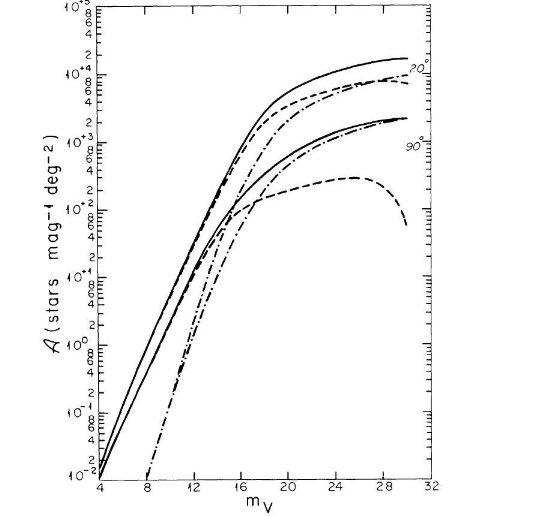
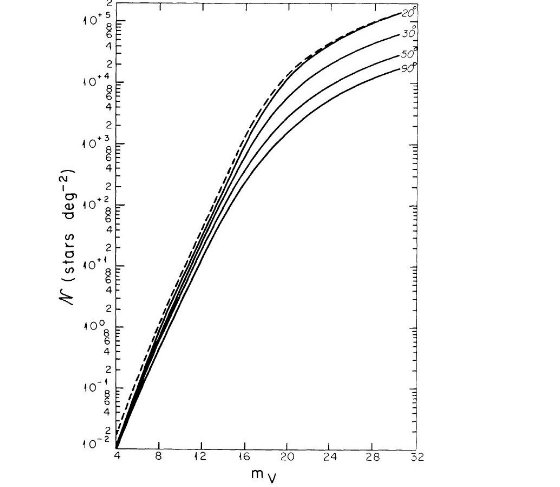
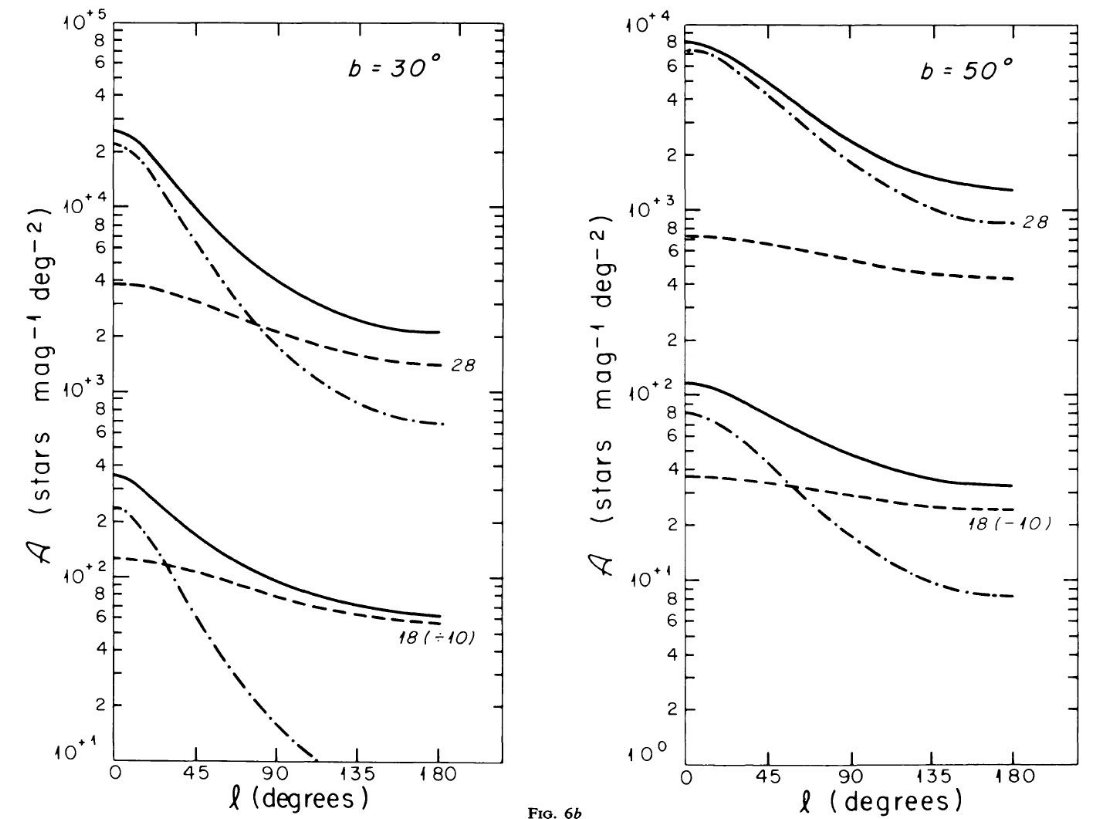
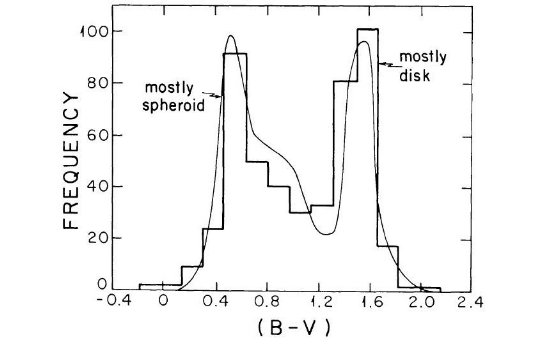
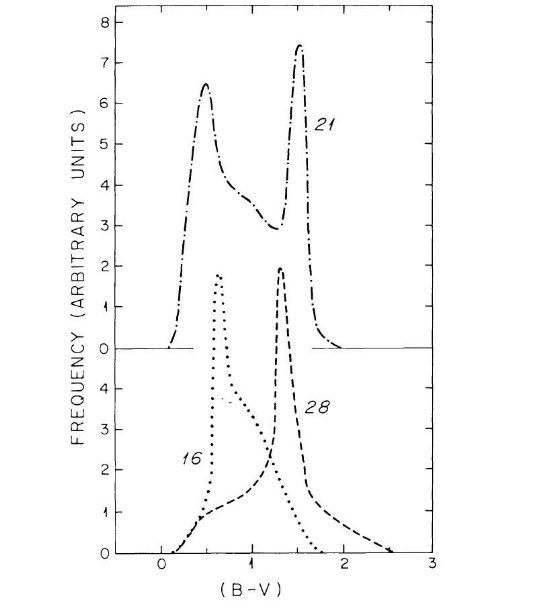
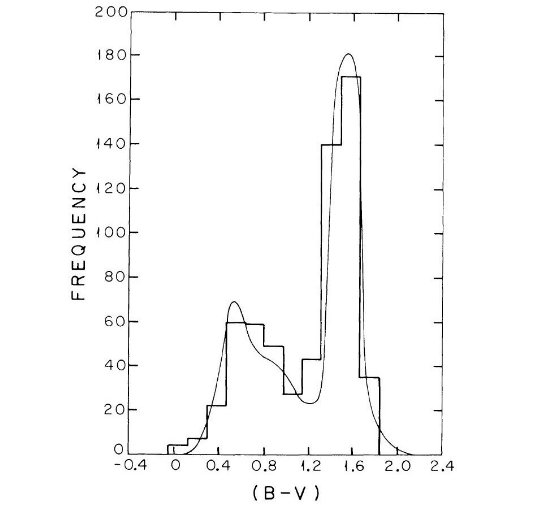
　ここでは、古典的な可視域のスターカウントが 4 ≤ mV ≤ 22 で 単純な２成分モデルと合致することを示した。モデルから計算した mV =　 21 等でのカラー (B-V) 分布は２個所から得たデータとよく合った。

　今回は V, B について述べ、 R, I バンドは今後の報告にする。

　２.銀河系のモデル　

仮定　

　　（１）銀河は円盤＋回転楕円体と考える。
　　（２）光度関数とスケール高は位置に依らない。近傍データを使う。
　　（３）回転楕円成分は高速度星からなり、種族II である。
　　（４）円盤は極端種族I から種族II までの広い巾の種族から構成される。

　回転楕円体成分は時にバルジとかハローと呼ばれる。我々はハローの名を後に出てくる 第３成分のために取っておく。

２．１．円盤　

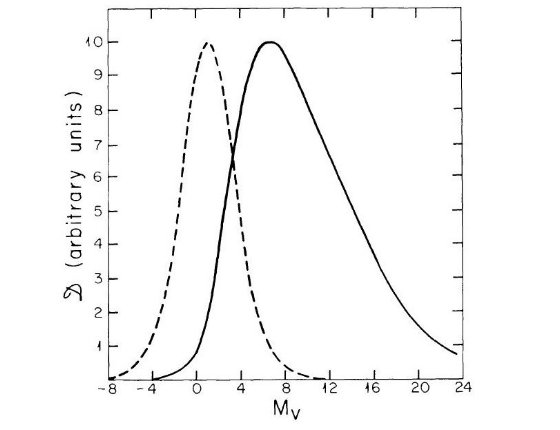
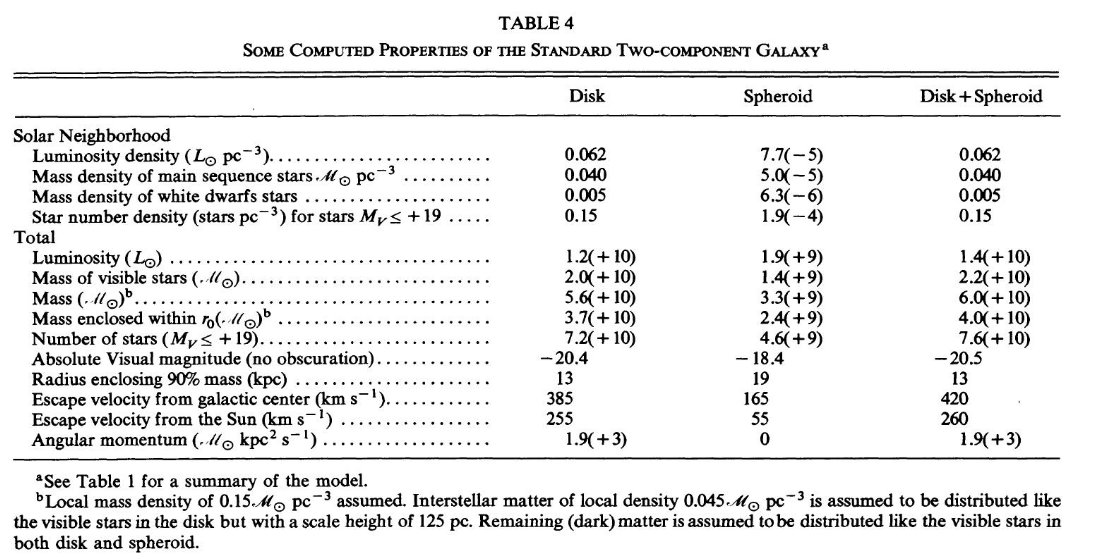
光度関数の範囲　 　近傍星は円盤に属すると看做して差し支えない。その光度関数はスターカウントと 距離決定から定められ、Luyten 1938 から Wielen 1974 に至るまで大きな変化はない。 図１は、 McCuskey 1966, Luyten 1968, Wielen 1974 の光度関数である。Mv = 7 付近の窪みは統計的に有意でなく、全ての観測に見られるわけでもない。Mv = 14 付近の 反りかえりまたは平坦化は実在するようだ。Mv ≤ -3 での光度関数はサンプル数が 少なすぎて不確かになる。多くの様々な手法の研究結果が一致することから円盤種族の 光度関数はよく確立していると言える。図１の最も暗い星は 0.1 M๏ であり恒星となり得る最低質量に近い。最も明るい星は非常に若い星団で見つかる星に 対応している。以下では　Mv ≤ -3、 Mv ≥ +16 での不定性が及ぼす影響を考える。

光度関数の解析表示　 　簡単のため、光度関数を以下の解析表示で表わす。(Tremaine, Ostriker,Spitzer 1975, Soneira 1980)

φ(M) = n∗10β(M - M∗) ,　　( Mb ≤ M ≤ 15 ),
[ 1 + 10-(α - β)δ(M-M∗ ]1/δ


　　　　　　　= φ(15),　　　　　　　　　　　　　　　 　　　　　( 15 ≤ M ≤ Md)

　　　　　　　= 0,　　　　　　　　　　　　　　　 　　　　　　　　( M ≤ Mb, or M ≥ Md)

ここに、n∗ = 4.03 × 10-3, M∗ = +1.28, Mb = -6, Md = +19
　α = 0.74, β = 0.04, (1/δ) = 3.40
この関数は図１の実線で示されている。この関数を使用した結果は良好であった。

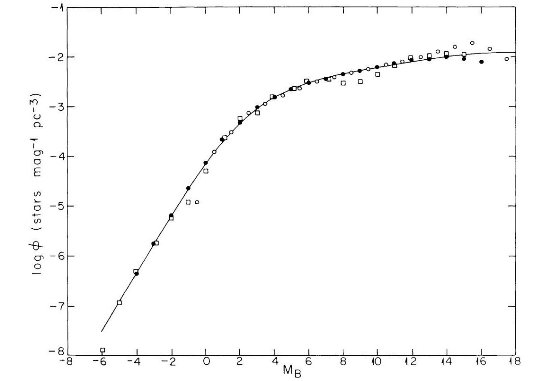
スケール高　 　円盤星密度のスケール長は質量（主系列等級 M ）により以下のように変化する。

　　　　　ρ(z,M) = ρ(z=0,M) exp[ - z/H(M)]　　　　(2a)

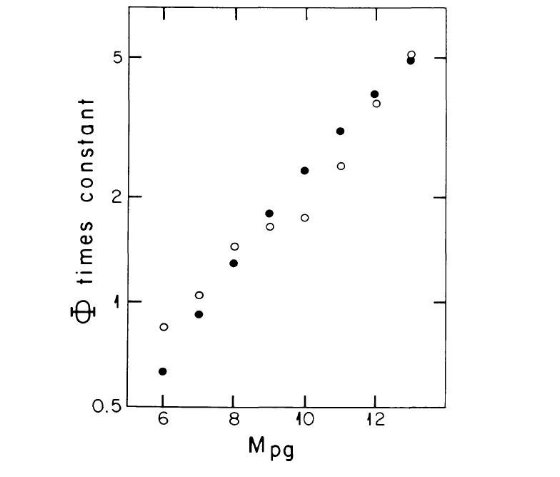
図２はスケール高 H の光度による変化を示している。暗い方 Mv ≥ +8 は外挿 である。Faber et al 1976 は　M 矮星の Mv = +13 にまで、指数関数型スケール高 が約 300 pc であることを見出した。図の実線がここで採用する関係である。

　進化の進んだ星はスケール高が大きくなるだろうから、白色矮星に対しては H = 325 pc を仮定した。mV = 15 より暗い所のスターカウントには巨星 のスケール高不定性の影響はない。晩期型巨星 (Mv ≈ +1) RC より下？ のスケール高の評価には大きなばら つきがある。もっともらしいのは 250 pc (Oort 1960) だが、150 pc (Elvius 1965), 225 pc (Hill 1960), 300 pc (van Rhijn 1956) などもある。非円盤星の影響が強まる とこれらの見積もりは過大になりがちである。数スケール高を過ぎると、巨星密度 の低下が緩むのはこのためだろう。

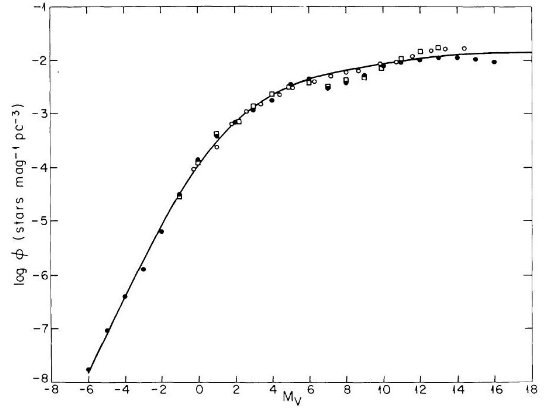
図１　円盤星のＶバンド光度関数。黒丸=McCuskey, 黒丸=Luyten, 四角=Wielen




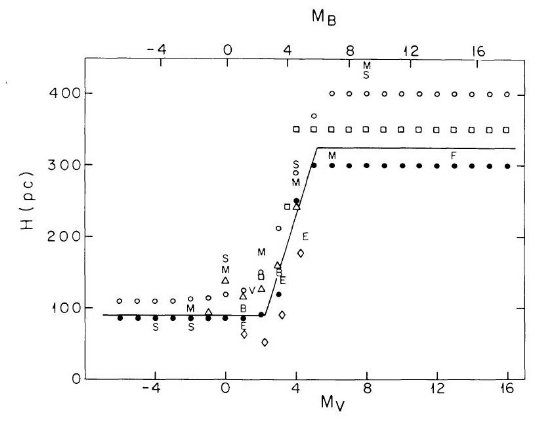
図２　絶対等級によるスケール高変化。Schmidt 1959 データ使用。白丸=Schmidt
, 黒丸=Oort, 三角=Upgren, 四角=McCuskey, ダイア=Becker





巨星スケール高の違いは無視　 　結局、我々は図２の関係を全ての星に適用する。巨星や準巨星のスケール高が 250 pc の大きさであったとしても、銀極方向のスターカウントで mV ≤ 12 での増加は 20 % 以下であろうし、 mV ≥ 15 では何の 影響もないだろう。

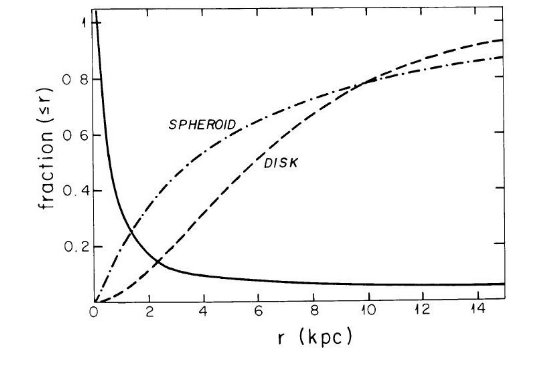
動径方向密度変化　 　回転軸からの距離 x による密度変化は、

　　　　　ρD(x) ∝ exp [ -(x-r0)/h],　　　　　　(2b)

で表わされる。r0 = 太陽銀河中心距離である。スケール長 h は de Vaucouleurs Pence 1978 に倣って 3.5 kpc とする。

円盤の密度変化　 　と言う訳で

　　　ρD = exp[-z/H(M) - (x-r0)/h],　　　　(2c)

になるが、勿論軸付近では良い表現でない (Kormendy 1977)。しかし、本論文の結果は 軸付近の正確さにはあまり影響されない。 円盤星のスターカウント　 　光度関数と密度分布が決まるので、視線方向に積分すれば、円盤成分のスター カウントは完全に決定される。


２．２．回転楕円体　

de Vaucouleurs の 1/4 乗則　 　回転楕円体成分の恒星分布は楕円銀河のそれとよく似ている。投影輝度分布は de Vaucouleurs により次の式で与えられた。

log10 I(θ) = -3.3307 [( θ ) 1/4 - 1 ]
I(θe) θe


ここに、θ は中心からの角距離、θe は光度の半分が収まる 角距離である。投影輝度分布が上式となる３次元空間密度は Poveda 1960 により与え られた。(r/re) ≥ 0.2 での漸近式は Young 1976 により与えられた。

ρS(r) = C exp[-7.669 (r/re)1/4]
(r/re)7/8


ここに、 re は θe に対応する実距離である。de Vaucouleurs, Buta 1978 に 依ると、銀河系の場合 re ≈ r0/3 である。

他の表現　 　他にも、King 1966, Abell,Mihalas 1966, Oemler 1976 などがあるが、Hubble 1930 の表式は次のようである。

I(θ) = I(0)
[1 + (θ/a)]2


このハッブル則は無限に積分すると光度が発散する。そのため多くの改定案が 提出された。

　しかし、今回は球状の楕円体を採用する。つぶれた形については第４章で検討する。

光度関数　 　回転楕円成分の光度関数 φ は Schmidt 1975 が計算した。彼は視差の求まった 111 個の高固有運動星 ( ≥ 1."3/yr) を用い、直交速度 > 250 km/s の 高速度星１８個を選び出した。250 km/s は RR Lyr 星の速度の中間値である。それで Schmidt は統計を取る時はサンプル数を２倍にして落とされた分の補正とした。 彼は i 番目の星に、 Vi = その星の等級で検出可能な体積を付与し、 　密度 = Σi [1/Vi] とした。



図３　白丸=Schmidt1975の累積光度関数。黒丸=Luytenの円盤光度関数。
　　　　二つは観測の共通範囲では同じ形と看做せる。


図３には累積光度関数

Φ(≤M) = ∫ M φ(M) dM
+6


を、楕円体星（黒丸）と円盤星（白丸）で較べた。規格化は任意である。データ 精度の範囲で両者は同じ形と言える。

楕円体と円盤の密度比　 　円盤と楕円体の密度比は 800:1 である。

　３．円盤と回転楕円体の恒星分布　

　３．１．基本関係式　

表面数密度　C(m1, m2, l, b)

　表面数密度　C(m1, m2, l, b)は、等級 m が m1 ≤ m ≤ m2 にあり, (l, b) 方向の単位立体角に存在する星の 数である。その表式は

Ci(m1, m2, l, b) = ∫ m2 dm ∫ ∞ dR R2 ρi (r,M) φ(M)
m1 0


ここに、i はS(pheroidal) か D(isk) で、C = CD + CS である。

M = m - 5 log R - A(R) + 5,　　　

R = 太陽からの距離、 r = 銀河中心からの距離、r0 = 太陽銀河中心距離、
x = 軸からの距離、z = 銀河面からの高さなので、

　　　　　z = R sin b, 　　　　　r = [x2 + z2]1/2
　　　　　x = [ r02 + R2cos2b - 2 R r0 cos b cos l ]1/2

減光　A

　減光Ａに関しては、(1)ゼロ減光、（２）cosecant モデル、（３）Sandageモデル、 の３種類を考えた。どのモデルでも b ≤ 30° では実視等級で 0.3 等以下 と小さい。

減光はまだらである。これは小さなダスト雲がスケール高 100 pc 程度 で出鱈目に分布していることに由来する。銀河中心から数度の所でさえ、「バーデの 窓」のように減光が 1.4 等という低さのところが存在するほどである。このため、 スターカウントに乱れが生じ、単純な減光モデルを導出する障害となっている。

　一様な減光板による減光則は以下の式で与えられる。

　　　　　A∞(b) = A∞(90°) csc b

A∞(90°) は実視等級で 0.15 等で、Av = 0.75 AB である。(de Vaucouleurs, de Vaucouleurs, Corwin 1976) 		　Sandage 1972 は高銀緯での小さな減光を考慮して、次の式を導いた。

　　　　　A∞(b) = 0.165 (1.192 - tan b ) csc b, 　　　 b ≤ 50°
　　　　　　　　　　= 0 　　　　　　　　　　　　　　　　　　　　b > 50°


しかし、この式の妥当性はまだ確認されていない。　

　密度 ρ の銀河面高度 z 依存性を、 ρ = ρ0 exp( -z/H ), H = 100 pc, と仮定すると、

　　　　　A = A∞[ 1 - e(-sin b/H)R ]

もし、ダスト雲密度が星と同様銀河中心距離により指数関数型の変化をしていると、 b ≤ 10° では上式に大きな影響がある。しかし、そのような低銀緯では、 減光のまだらさが意味あるスターカウントを不可能にしているので考えなくてもよい。

標準モデルの特性

　標準モデルの特性を表１に載せた。円盤、楕円体の星の数を計算するのに用いた パラメターも表中にある。



　３．２．観測スターカウント　

　Seares のスターカウント　

　単一システムで総合的な星密度の観測は現在でも、Seares et al 1925 が唯一で ある。彼らは主にウィルソン山選択領域カタログから選んだ 105 個の 星に基づき、スターカウントを実施した。このカタログは 139 選択領域からなり、 各自は(1/3)° × (1/3)° の大きさである。等級は mV = 13 - 18 等に渡っている。13 等より明るい星に対して Seares は既存カタログ から引用した。カウントのゆれを滑らかにするため、彼らは３次関数での表示を 用いた。スターカウントの結果は銀経全体で平均化し、銀緯の関数として表わされた。 銀経変化は後に Seares, Joyner 1928 が研究した。 　カウントは国際写真等級 mipg を実視等級 mV に変換 してから行われた。ちょっと省略。

　最近のスターカウント　

　最近、銀河を測定限界までカタログ化するため、乾板の自動測定が進んだ。その 副産物として暗い星のカウントが進んだ。

　バークレイカウント　 　Kron 1978 は b = 86° 付近で ∼ 103.4 のカウントを行った。

ベル研カウント　 　Tyson, Javis 1979 は ∼ 104.3 のカウントを行った。

b ≥ 74 ° の３箇所は 25° < |b| < 45° の５箇所と mJ まで 同じ平均カウントを示す。従ってベル研データを銀極モデルカウントと比較する際、 スケーリングは施さなかった。何のことか？

ＡＡＴカウント　 　Peterson et al 1979 は b = 65° だが、銀河中心から 90° それた方向で、 ∼ 102.9 のカウントを行った。

　バンド変換　 　ベル研とＡＡＴデータは J-バンド( B と V の間)、バークレイは F バンド ( V と R の間 ) と J バンドなので、Kron 1978 の変換式に従い、

　　　　　mV = mJ - 0.75

　　　　　mV =( mJ + mF )/2 - 0.20

　　　　　(B - V) ≡ ( mB - mV ) = 1.0

この最後の (B - V) は晩期型矮星が多いことから予期した値で、また　Kron が 見出した平均値でもある。

　ここに述べた３つのサーベイは全て暗い方は mJ = 24 まで伸びているが 我々はバークレイとＡＡＴデータは 22.5 等までしか使わなかった。それより暗い方 では、ノイズや銀河のコンタミで等級スケールがひずんでいるからである。

　３．３．観測とモデルの比較　



図４(a) 銀緯によるスターカウントの変化　

　図４(a) にはモデルスターカウントを銀経で平均したものを示す。モデルのパラメター は表１にある通りである。b = 20°, 30° については A∞ (90°) = 0.15 mag. の　cosec 則減光を仮定した。b = 20° の破線は減光＝０ を仮定した時のモデルカウントである。

減光の効果 δm　 　減光の効果 δm を、C( m + δm )Extinction = C( m )No Extinction で定義する。　図を見ると、 δm ( b = 20° ) ≈ 0.3 である。。b = 50°, 90° については減光ゼロで モデルを計算した。

m ≥ 22　で急上昇は本当？　 　観測値は図４(a) でモデルと較べられた。高銀緯ではモデルと観測は m = 22 まで 良く合っている。m ≥ 22 になると、ベル研カウントはモデルよりずっと急激に 上る。この急な上昇はハロー成分かも知れないし、急に増える QSO のせいかも知れない。 ＡＡＴとバークレイデータには急な上昇は見られないので更なる観測的検証が必要で ある。



図４(a) b = 20°, 30°, 50°, 90°, での銀経で平均した 星数/mag/deg2。
　　　　 b = 20° に対する破線は減光＝０を仮定。
　　　　 b = 20°, 30° の実線はcosec 減光を仮定。
　　　　 b = 50°, 90° の実線はゼロ減光を仮定。
　　　　 黒丸＝Seares。三角＝Kron。白丸＝Tyson,Javis。四角=Peterson etal 		Brown の観測　 　Brown 1979 は b > 70° １２領域でスターカウントを行った。かれの サンプルは 104.0 星を含んでいる。

b = 20° での差　 　図４(a) の　b = 20° を見ると、cosec 減光則のモデルと Seares データ の間には 0.3 等のずれがあることが分かる。却ってゼロ減光のモデルがよくフィット する。色々な理由が考えられるが、最も簡単な説明は高銀緯と低銀緯で等級の較正 スケールにズレがあるというものだ。その他減光を大きく見積もりすぎた、モデルの パラメターが適切でなかった、円盤のスケール長を h = 3 kpc にすると合う、等 がある。しかし、現在のところどれとは断定できない。


図４(b)　円盤と楕円体の寄与の比較　

　図４(b) は円盤と楕円体の寄与を比較している。銀極では微分カウントは m ≤ 16 では円盤星、 m ≥ 19 では楕円体成分星が支配的である。両者の寄与は m = 17 で 等しい。円盤密度が高度につれて指数関数的に薄くなる影響は m ≥ 17 で明らかに なる。26 等を越えると円盤モデルの微分スターカウントは下がってくる。これは、 光度関数 φ を　M ≥ MD = 19 でゼロにしているためである。 このため、有効円盤厚みの距離指標 = 7 とすると、円盤の端で M = 19 の星は見かけ 等級 = 26 となり、それより暗く見える星はなくなってしまう。 b = 20 ° では 銀極より 4 等暗いところまで、円盤星が占める。



図４(b) 実線: b = 20°(cosec 減光則), 90°(ゼロ減光)のスター カウント(/deg2/mag)
　　　　破線＝円盤成分、一点鎖線＝回転楕円体成分

図４(c)　累積スターカウント　

　図４(c) には累積スターカウントを b = 20°, 30°, 50°, 90° で示した。減光は図４(a) と同じである。28 等までの予想星数(/deg2) は 銀極方向での 1 × 104 から、 b = 20° での 1 × 105 まで変化する。他の方向での累積スターカウントは 付録Ｂに表として載せた。



図４(c) 累積星数密度。破線： b = 20° のゼロ減光モデル。
　　　　実線(20°,30°)：銀極で A=0.15のcosec減光。
　　　　実線(50°,90°)：ゼロ減光 		図５　微分スターカウントの銀緯による変化　

　図５には、銀経で平均した微分スターカウントの銀緯による変化を b ≥ 20° について示した。全てのモデルはcosec 減光モデル、A∞(90°) = 0.15 を採用している。



図５　与えられたmV 毎の微分スターカウントの銀緯による変化。
　　　cosec 減光モデル、A∞(90°) = 0.15 採用。


図５　微分スターカウントの銀経による変化　

変化のモデル計算　 　スターカウントは銀経により大きく変化する。図６(a) には、スターカウントの銀経に よる変化を、b=20°, 30°, 50°, 70° での等級毎の微分星数密度 として表示した。減光の扱いは前に同じ。星数密度の変化は低銀緯で暗い等級ほど大きい。 b=20°, m = 28 では　15 倍の変動がある。

　図６(b) には円盤と楕円体に分けて、b = 30°, 50°, m = 18, 28 の経度場合 を図示した。変化の大部分は楕円体成分に起因することが分かる。この強い経度変化 は楕円体の密度変化をより正確に測るのに使える。b = 50°, 18 ≤ mV ≤ 22 でのスターカウントは特に有用である。

銀経変化の観測　 　観測による微分星数密度の経度変化はモデル計算よりずっと雑音が多い。観測では 北と南半球でさえ差が大きいし、まだらな星間吸収、星の分布自体の集合化による 変動、サンプル数の制限がある。

表２：　観測とモデルの比較　 　そこで、銀経範囲を 45° と広くとり揺らぎの効果を減らして観測とモデルを 比較した。表２には、銀経巾 45° での総数と巾銀経全体での平均値との差、 Δ = log N - ⟨ log N ⟩、 を、b = 60°, 20°, m = 12, 18 について示した。一致はよい。






図６(a) b=20°, 30°, 50°, 70° での等級毎の微分星数密度の銀経変化。 減光は前に同じ。





図６(b)　b=30°, 50°, m = 18, 28 での 星数密度の銀経変化。 破線＝円盤、一点鎖線＝楕円体の寄与。m = 18 の星数は 1/10 にして表示。

　３．４．スターカウントによる楕円体光度関数の決定　



観測の方向と等級範囲　

　楕円体光度関数は mV = 18 - 22、 銀極方向でのスターカウントから 観測的に求めることができる。この範囲では、標準モデルによると、楕円体成分の 寄与は 70 % である。

決定方法　

　光度関数を、φ(M) = 10γM と仮定すると、スターカウント は密度分布に関係なく、 C(m) ∝ 10γm となる。
両側に無限に続けばね。または、M-5logR が重なる m の範囲。
もし光度関数が M= 3 - 9 (ここが考えているスターカウントで効くところ)の範囲外 で滑らかに低下すれば、上の観測結果は保持される。銀極方向、mV = 18 - 22 の範囲での観測結果から、標準モデルでの円盤成分を差し引き、 残りのカウントから γ = 0.145 ± 0.035 と求めた。この値は、 Schmidt 1975 が求めた γ = 0.130 とよく合う。

楕円成分星質量関数の傾き　

　質量関数 dF/dM = C M-α の勾配 α は γ と 質量光度関係から決まる。
主系列だけ考えている。なぜ？

　実際上、主系列星と白色矮星しかカウントに効いてこないので、後に出る 主系列の質量光度関係（１７式）を用いて、α = 2.55 ± 0.37 を 得る。この値は円盤星の質量関数の傾き、α = 2.40 (M = 4 - 8 mag)と 近い。Schmidt 1975 が得た値は 2 ± 0.5 であった。

　３．５．円盤星スターカウントの近似的振る舞い　



　円盤星スターカウントの銀緯、銀経による変化は暗い領域、m ≥ 20, と 明るい領域、m ≤ 12、では比較的単純である。この領域はそれぞれが、 光度関数 φ の暗い端と明るい端で支配されている。簡単のため、光度関 数を &@hi; ∝ 10γM と仮定し、平均スケール高 = H とすると、

CDisk ∝ 10γm
{sin b [1-(H/h) cot b cos l]} 3-5γ


明るい端　 mV ≤ 12 では C は MV ≤ 4 の星が支配的である。 図１を見ると、γ ≈ 0.4, 図２から H ≈ 100 pc である。

暗い端　 mV ≥ 20 では C は MV ≥ 4 の星が支配的である。 図１を見ると、γ ≈ 0.04, 図２から H ≈ 300 pc である。

円盤スケール長　 　円盤スケール長をスターカウント A から決めるには式 (13a) を使う。見かけ等級 が明るい方では、A ∝ cosec b であり、スターカウントへの銀経 l による影響 は小さい。しかし、暗い端では、A ∝ cosec3 b であり、スター カウントへの銀経 l による影響は９倍くらい大きい。したがって、円盤スケール長は mV ≥ 20 で決めるのがよい。方向としては、20° ≤ b ≤ 40°, l ≥ 120° がよい。

　３．６．楕円体星スターカウントの近似的振る舞い　



　楕円体スターカウント A の銀緯、銀経による変化もまた比較的簡単な式で表現できる。 光度関数が &@hi; ∝ 10γM と仮定し、Md = ∞ とし、 更に密度分布を ρ ∝ r-ν と仮定すると、 方程式（５）から、
ASpheroid ≈ C 10γm
{sin b [1-cos b cos l]} (ν-1)/2


この式は、ν = 4 (γ=0.0-0.3) から ν = 3 (γ=0.1-0.2) にかけて 有効である。

ハッブル密度式とドボークルー密度式　 　ハッブルとドボークルーの楕円体の式はどちらも、太陽から観測する範囲内では, 太陽中心距離＝ｒとして、r-ν の形に近似できる。ハッブル式では ここで扱う l ≥ 20%deg; では　ν = 3 である。銀河中心から 50° 以上 離れたところでは、ドボークルーの式は　ν = 3.8 でよい。それより近距離に なると、ドボークルーの式は ν = 3.0 に近づく。

光度関数の勾配 γの決定　 　式(13b) の主な制限は、光度関数の勾配 γ が絶対等級の全領域にわたって 一定ではないことから来る。このため、我々は式（５）の数値積分から γ を 導かざるを得ない。我々は銀極方向のスターカウントから近似的に γ を 定めた。ベル研データの m > 22 での急な立ち上がりは他のデータに見られない ので考慮しなかった。

νの決定: ドボークルー楕円体を支持　 　スターカウントから、モデル円盤カウントを引き、フィットした結果、ν = 4.0 ± 0.3 が得られた。ハッブル分布則は合わなかった。ドボークルー則は 合う。

銀河中心から 40° の役割　 　詳しい計算によると、銀河中心から 40° 離れた方向では、スターカウントは ν の値に影響されない。それは、ν 大だと r < r0 で密度 が上がり r > r0 で急に下がり、ν 小だとその傾向が ゆるいが、スターカウントでは 40° のとき両者の効果が大体打ち消し合うので ある。したがって、規格化定数 C を決めるのに最善の方向は l = 0°, b = 40° である。

　３．７．距離、絶対等級の分布　

平均距離　 　図７は 21, 28 等で我々がどのくらい遠くを見ているかを示す。円盤では 0.6 kpc, 楕円体では 7 kpc のあたりを見ていることが分かる。同じ見かけ等級でも、楕円体 星は円盤星より一桁遠くを見ていることが分かる。数密度の低下が見かけ等級を 上げても透視深度をあまり向上させないことが分かる。見かけ等級を 21 から 28 等 にしても、平均距離は円盤で 10 %, 楕円体で 50 % しか伸びない。

実際に見ている絶対等級　 　図８(a) は等級限界サンプルが与えられた時、光度関数のどの部分が研究できるかを 示している。Mv = 9 等より明るい星は 21 等でも 28 等でも同じである。同様に、 Mv = +4 より明るい星の数は 21 等と 28 等の間で変わらない。円盤の急な密度低下 は暗い星に有利に働き、観測される典型的な楕円体星は円盤星に較べ　6 等明るい。

　図８(a) は円盤と楕円体光度関数のどの部分が観測されるかを示す。







図８(a) m = 21, 28 等での銀極方向の絶対等級分布。
　　　　破線＝円盤、一点鎖線＝楕円体


図７　銀極方向、m = 21, 28 等より明るいの星の、太陽からの距離の分布（モデル）。
　　　左：　円盤成分、　右：楕円体成分星。

　３．８．(B - V)カラーの分布　

絶対等級からカラーへ　

　図８(a) の絶対等級分布は、絶対等級からカラーへの変換により、 カラー分布に導かれる。変換には HR 図を使う。詳しくは 付録Ｃを見よ。

銀極方向のカラー分布　

　図８(b) は銀極方向、mV = 16, 21, 28 でのモデルカラー分布である。 mV = 16 では分布は円盤の青い星、B - V ≈ 0.75、が支配的である。 mV = 28 では分布は楕円体の赤い星、B - V ≈ 1.5、が支配的である。 mV = 21 では分布は双耳峰的となり、楕円体の青い星、B - V ≈ 0.5、 と円盤の赤い星、B - V ≈ 1.5、の二つが並ぶ。

双耳峰的カラー分布　

　双耳峰的カラー分布が見えるのは限られた見かけ等級、方向においてである。 双耳峰性が強い、 18 ≤ mV ≤ 24 においては、二つのピークを カラーのみで円盤星と楕円体星に分けることが可能である。 mV = 21 では (B - V) ≥ 1.2 の星の　85 % 以上が円盤星で、 (B - V) ≤ 1.2 の星の　 99 % 以上が楕円体星である。このように、固有のカラー分布は円盤と楕円体とで おなじにしてあるのだが、等級限界サンプルをとると、円盤星の平均カラーは 楕円体星に較べかなり赤くなる。これは、視線に沿っての密度低下の勾配が異なっ ているためである。

　低銀緯になると、双耳峰型の分離は悪くなる。これは、視線に沿っては円盤成分 の密度勾配が緩くなるからである。特に、反中心側では楕円体成分のピークが 大きく低下する。双耳峰の特徴が最も強く現れるのは銀極方向、mV ≈ 21 である。

カラー分布の観測　

　図８(c) は Kron 1978 による SA 57(b=86°) のカラー分布である。元データ はＪ，Ｆバンドであり、カラー変換は (B-V) = 0.75 (J-F) とした。図 に載せたカラーは、mV = 19.75 - 22.0 の星が対象である。19.75 は Kron が定めた探査の最高光度で、22.0 はこれより暗いとノイズの影響が大きく なり過ぎるのである。

　モデル分布はデータと同じ 1080 平方分で計算した。観測との一致は素晴らしい。 この結果はまた、円盤と楕円体の中間のスケール高を有する成分が無いことを 示している。二つの峰の間の窪みは、+4 ≤ Mv ≤ +8 に相当する。

カラー分布の観測　

　図８(b) で (B-V) ≤ 1.2 の星の割合は、観測値で 0.56、 モデルで 0.66 で ある。モデルによると、このカラー範囲の星は殆どが楕円体から来ている。この結 果は２−２節で行った、Schmidt 1975 の太陽近傍高速度星データに基づく楕円体成 分の規格化の正しさを確認する。



図８(c) (B - V)カラーの分布。銀極方向、mV = 16, 21, 28 より明るい星
　　　　曲線は標準モデルの予想。ゼロ減光。



図８(b) (B - V)カラーの分布。銀極方向、mV = 19.75 - 22.0
　　　　曲線は標準モデルの予想。ゼロ減光。ヒストグラムは Kron データ




図８(d) SA 68 方向 ( l = 111°, b = -46°) の (B - V) 分布。

　３．９．ＱＳＯ数密度への制限　

　カラー分布の観測とモデルが一致したことは、ＱＳＯの進化に大きな制約を かける。Bohuski, Weedman 1979 はＱＳＯ等級分布を mV = 19 から 22 へ外挿すると、 恒星状天体の殆どすべてはＱＳＯで占められると予想した。 彼らは同時に、 22 等でのＱＳＯカウントがＱＳＯ進化の理解に非常に重要な 意味を持つことを指摘した。Kron のデータは 22 等の恒星状天体の殆どが 星であることを示している。

　これまでに見つかったＱＳＯの殆どは(B-V) ≤ 0.40 で、暗い円盤または 楕円体星より青い。主に電波でみつかったＱＳＯのカタログ中 60 % は (B-V) ≤ 0.30 である。Kron データ22 等より明るいＱＳＯのうち,

(B-V) ≤ 0.30 はわずかに 3 % である。22 等より明るいＱＳＯの 60 ％ が (B-V) ≤ 0.30 と仮定すると、22 等より明るいＱＳＯの数は ≤ 65 deg -2 である。白色矮星の多くはこのカラー帯に存在することを考慮 するとこの上限値は更に下がる。この値は mV = 16 - 20 の ＱＳＯ等級分布を外挿した予想値の１−２桁低い。我々の上限値はこれまでに 得られた実測値 13 QSOs deg-2 に近い。

　固有運動も静止天体の選別に使える。Chiu 1980 は SA 57 0.09 deg 2 領域で固有運動を観測し、 mV = 21.25 まで完全な データを得た。その中に検出限界以下の天体が 6 個あった。これは 66 deg -2 に相当する。　

　４．光度関数と空間分布の不定性　

　４．１．光度関数の不定性　

光度関数両端の影響　

　光度関数の明るい端では関数はべき乗則より急速に低下し有効最大光度に 達する。暗い端では増加が止まり、低下の兆候も見られる。我々は、光度関数の 明るい側の端の光度 Mb 暗い側の端の光度 Md を幾つか取ってその影響を見た。

円盤カウントへの影響　 円盤に関しては、 Md を 18 から 28 等に変えた時、見かけ等級 28 等より明るい星の数は 10 % 以下しか 変化せず、円盤＋楕円体の総カウントでは 2 % 以下である。 Mb を +3 から -10 へと変えても、 m > 10 のカウントには 1 % 以下の影響しかない。

楕円体カウントへの影響　 　楕円体成分の光度関数は +4 等から +12 等という比較的狭い巾で使われた。 楕円体の Md を　13 から 28 に変化させた時、見かけ等級 28 等以上の 星の総数の変化は 10 % 以下である。Mb を　+3 から -10 に変化させた時、 見かけ等級 10 等以下の星の総数の変化は 5 % 以下である。 したがって、楕円体光度関数の明るい端、暗い端の不定性は 28 等より明るいスター カウントには殆ど影響しないと言える。

観測範囲外での効果　

光度関数が暗い方で急上昇したら　 　光度関数を、 φ(M) ≈ 10αM と仮定する。すると 累積星数密度 N(≤m) ∼ 10αM である。したがって、 暗い側での N(≤m) の表式は光度関数 φ(M) と同じである。円盤星の N(≤m) に見られる　m = 16 での「ひざ」(図４) は、光度に伴う指数関数 的密度低下と光度関数の暗い端での傾きの平坦化が一緒になって起きた効果である。 この「ひざ」は、もし

光度関数がある絶対等級 Me から勾配が十分に急になれば 起きない。M ≥ Me で φ(M) ∝ 10σM と仮定する。

カウント増加比の計算　 　カウントの増加比を以下のように定義しよう。

ΔN/N = NMe, σ(≤m) - N(≤m) 　　　　　(14)
N(≤m)


受け入れやすい値 σ = 0.2 と、極端な値 σ = 0.4 について、 mV = 28 での ΔN/N を計算した。注意しておくが、図１の 光度関数は Mv = -6 から 0 の間で、 勾配＝0.6, +2 と +8 の間で 0.1 で ある。
円盤の計算結果　 　計算結果は、 σ = 0.2 の時、 Me = +16 に対して (ΔN/N)Disk = 0.9, Me = +20 では (ΔN/N)Disk = 0.1, 一方、 σ = 0.4 の時、 Me = +16 に対して (ΔN/N)Disk = 8, Me = +20 では (ΔN/N)Disk = 0.2 であった。総数の変化はその約 (1/5) である。 Me = 16 は丁度データが切れた先から光度関数が急上昇することを意味する。 Me = +16, σ = 0.4 では「ひざ」は消失する。その上、m = 28 において円盤 星の数は楕円体の星よりずっと多くなる。それにも関らず、スターカウントの総数は 適当なパラメターが選ばれればあまり変わらない。

楕円体の計算結果　 　楕円体に関して、、 σ = 0.2 の時、 Me = +12 に対して (ΔN/N) Spheroid = 0.1, 一方、 σ = 0.4 の時、 Me = +12 に対して (ΔN/N)Spheroid = 0.6, Me = +16 では (ΔN/N) Spheroid ≤ 0.01 であった。したがって、Me ≤ 16, &sigama ≥ 0.2 であれば、20 % 以上の増加を検出できる可能性がある。

　４．２．密度分布の変動　

円盤スケール高の影響　 　円盤光度関数の明るい端が変化してもスターカウントには殆ど影響がない。 明るい星のスケール高が小さいからである。したがって、カウントはそれら 明るい星の空間分布の不定性と独立である。もしも、明るい、Mv ≤ +3、円盤星の スケール高が 70 pc から 100 pc へと変わっても mV ≥ 10 での スターカウントへの効果は 1 % 以下である。暗い、Mv ≥ +5、星のスケール高が 275 pc から 375 pc に変わると円盤カウントは 50 % 上がる。しかし、総カウント は 15 ％しか変化しない。

太陽銀河中心距離の影響　 　太陽銀河中心距離が 7 kpc から 9kpc へ変わると、カウント総数は 25 % 変化する。

　４．３．銀緯、銀経変化への制限　

　表１の標準モデルパラメターを大きく変えた時にスターカウントがどう変わるかを 調べた。太陽銀河中心距離 r0、円盤スケール長 h、楕円体特性長 re を変えた時の N'/N0 が表３に掲げてある。

　N0 は標準モデルでの累積スターカウント、N' は変化パラメターでの 結果である。br>
　表３を見ると、パラメター変化の影響は銀緯に沿っての変化にも銀経に沿っての 変化にも同じように現れることが分かる。

　４．４．回転楕円体の扁平率　

何だか分からない　

　球状星団の分布はほぼ球状である。一方、銀河系の中心付近は扁平であることが 赤外観測(Maihara et al 1978)から知られている。

　z' = κz という変換は回転楕円体を軸比 κ, 楕円率 ε = (1 - κ) の回転の楕円に変える。何のことだ？全然 分からん。　それに伴い、回転楕円体の特性長は rex と rez になり、

　　　　　rex rez = re2 = (2.67 kpc)2

となる。

スターカウントにから軸比へ　

　スターカウントは軸比に強い制限をかける。V = 21 でのスターカウントデータ ３つの値は 705 ± 110 mag-1 deg-2 を与える。 モデルの予想する極方向 mV = 21 での値は、ASpheroid (b=90°) は、ε = 0 の時の値と較べ、ε = 0.25 で (1/1.9)、 ε = 0.5 で (1/4.6) である。総数では (1/1.5) と (1/2.25) である。 これらの減少は極方向で密度勾配が急になるためである。Schmidt 1975 の規格化 を採用して、極方向 mV = 21 での値に最もよく合うのは ε = 0.05 のときである。

　もし、Schmidt 1975 の規格化のエラーを認めるなら、それぞれの楕円率にあった 規格化を採用すれば極方向 mV = 21 での値には合わせることができる。 その場合、楕円率は銀緯、銀経、カラーの変化から決めるべきである。

楕円率決定に最適な方向　

　楕円体成分の変動が最も大きいのは反中心方向である。 l = 180°, b = 20° 方向では ε = 0 と 0.25 でのカウントの比は 2:1 である。しかし、 この方向は円盤成分が 10 倍くらいある。 しかし、l = 180°, b = 60° では円盤成分は 全体の半分である。 銀河中心方向では b = 40° の時に ε の変化に対するカウントの変動が最も大きい。この方向では、ε を 0.25 と 0.5 で、ε = 0 の時に較べ mV = 21 で 32 %, 70 % 増加する。何で減少しないいんだ？　

l = 180°, b = 60° と l = 0°, b = 40° の２方向での観測はまだない。 　l = 90° - 270° 面はもう一つの重要な方向である。この面内での楕円体 成分のカウントは回転楕円体の ε を決める重要な情報を与える。ただし、 円盤の混入が大きいという問題がある。例えば、 l = 90°, b = 30° での 円盤対楕円体は m = 21 で 2.5 であり、極方向の６倍大きい。

カラー　

銀極と SA 68 での観測対モデルの比較　 　カラーにより円盤と楕円体成分を分離する方法は混入を防ぐよい方法である。 Kron 1978 は SA 68 (l = 111°, b = -46°) で J-, F- の観測を行った。 この方向は望ましい l = 90° 		方向に十分近い。 図８(d) には、mV = 19.75 - 22.0 の星の (B-V) カラー分布が、 球形の楕円体成分を持つ標準モデルの予想と共に示されている。楕円体成分カラー 分布の中央値はいくらか楕円率に依存する。ε = 0.5 に対しては、(B-V) は 0.15 等赤い方に動く。しかし、モデルとの一致は良い。(B-V) ≤ 1.1 の星 (99 % は楕円体星）のモデル（ε = 0）数は観測より 5 % 下回るだけである。銀極 方向では(B-V) ≤ 1.1 の星の数はやや、30% , 観測より大きい。等級較正での 0.1 等程度のずれがその原因かも知れない。

楕円率によるズレの説明　 　上に述べた食い違いに対するもう一つの説明は、楕円体成分が扁平であるという ものである。 SA 57 (b = 86° で銀極に近い) には (B-V) &le: 1.1 の星が248 星、SA 68 には 228 星が存在する。楕円率を評価するため、まず銀極方向で　248 星となるモデルを作り、それがSA 68 方向で 228 星を与える ε を探った。 その結果、 サンデージ減光モデルとcosec 減光モデルのどちらに対しても、 ε = 0.15 ± 0.07 を得た。ε = 0.15 の場合、楕円体成分 星のSchmidt規格化は 12 % 増加させる必要があるがこれは、ポアソン誤差の範囲内 である。このモデルでの円盤＋楕円体の星のカウントは標準モデルのそれと同じくらい である。両モデルの差は暗い等級になると大きくなり、mV = 30 で、 ≤ 25 % である。

ハッブル楕円体モデル　

　以上の検討はドボークルー楕円体の場合なので、ハッブル楕円体（第３章で 却下されたが）も ε を変えて調べた。しかし、観測に合うパラメター の組み合わせは依然として見いだせなかった。

地上観測の重要性　

　地上望遠鏡により、幾つかの方向で、正確なカラー (B-V) の分別を mV = 21 まで行えば、ε を精密に決定できる。それらは、(l = 0°, b = 40°), それに l = 0° - 90° 面上の数点である。ポアソン誤差を 下げるため領域は 1 deg2 以上は必要である。 mV = 21 から 28 等までは ε に対して感度の向上は無いので、地上観測は重要であり、 かつ十分なのである。　

　４．５．銀河中心付近の恒星密度　

　Kormendy 1977 の示唆に従い、円盤の密度分布に次のような変形が加えられた とする。

ρDisk' = ρDisk { exp [ -(rc/x)3 + (rc/r0)3 ], 　　x ≤r0
1,　　　　　　　　　　x > r0


ここに ρDisk は変形なしの密度分布であり、rc は あるカットオフ半径でその内側で密度が急低下する。

　恒星の穴の半径 rc を 3 kpc とした時、 l = 0 °, b = 20 ° でのカウントの変化は 8 % であった。 rc を 5 kpc とした時でさえ 15 % しか変化が認められない。したがって、観測スターカウントは銀河中心 付近の構造に鈍いと言える。


　５．標準銀河モデルの特性　

　５．１．恒星密度分布　

５．１．１．太陽近傍の諸密度　

密度の表式　 　近傍の光度密度 DL、質量密度 DMass、恒星数密度 DN は以下のように積分計算で求まる。
DL = ∫ +∞ 10-(M-M๏) /2.5 φ(M) dM 　　(L๏ pc-3)
-∞


DMass = Σi ∫ +∞ Massi(M) fi(M) φ(M) dM 　　(M๏ pc-3)
-∞


DN = ∫ +∞ φ(M) dM 　　(stars pc-3)
-∞


　ここで fi(M) は i 種の星の光度質量関係、fi(M) は i 種の星の割合である。ここでは、主系列と白色矮星のみを考える。

主系列星と白色矮星　 　主系列星に対しては以下の等級質量関係を考える。

log MMS = { -0.09289 MV + 0.448,　　　Mv ≥ 0
-0.2710 MV + 0.448,　　　 Mv ≤ 0


　白色矮星の割合は白色矮星の光度関数を用いて計算される。Mv ≤ 15 は Sion, Liebert 1977, Mv ≥ 15 は Liebert 1979 がある。太陽近傍の白色矮星数密度 は上のデータから 0.008 pc-3 と見積もられる。対応する質量密度は 0.005 pc-3 である。他の研究者は Mv ≤ 15 で Liebert より緩い 光度関数を使っているので、質量密度を大きく見積もっている。

　以上から主系列星の割合は、

　　　　　fMS(Mv) = 1 - 0.15 × 10-0.25|Mv - 15|

各光度毎の寄与　 　これらの式から計算した太陽近傍の様々な密度は表４にまとめた。
図９には円盤と 楕円体の主系列星からの光度と質量への寄与を絶対等級の関数として示した。光度 への寄与と質量への寄与は異なる等級に分かれていることに注意。


図９　円盤と楕円体主系列星の等級別の寄与。
　　　破線＝光度密度。実線＝質量密度。

５．１．２．総量　

　星の光度、質量、数などの量Ｆの総量 ＴF は次の式で計算される。

　　　　　ＴF = ∫F(M)ρ(r,M)dMdv　　　　　　　　　(19)

　円盤に対してはまず表面密度 σ を計算するのがよい。太陽近傍では、

　　　　　 σL = 16.0 L๏ pc-2
　　　　　 σMass = 27.0 M๏ pc-2
　　　　　 σN = 95 stars pc-2 　　(Mv < 19)

円盤全体の積分の結果は、

　　　　　ＴF, Disk = 2 π h2 σF (r0) exp (r0/h)

ここに h = スケール長である。

　表４には、総光度、総質量、Mv & le; 19 の星の総数が円盤、楕円体、その和で 載せてある。実視総等級は減光なしで -20.5 等である。この値は Sbc 銀河の平均値 -20.3 等に近い。円盤対楕円体の光度比は６である。これも Sbc 銀河の値と合う。

　５．２．総質量と M/L 比　

近傍密度　

　円盤を離れた星の運動から推測される円盤密度は 0.15 M๏ pc -3 , Oort 1960, である。その内、0.045 M๏ pc -3は表４にあるように可視の星であり、0.045 M๏ pc -3　(本当？)　が星間物質である。 残りの 0.06 M๏ pc-3 が「失われた」暗黒物質 である。

暗黒物質　

太陽近傍の暗黒物質比率　 星間物質は星と同じスケール長を持ち、スケール高は 125 pc である。ここで、 我々は暗黒物質が円盤、楕円体双方で可視の物質密度に比例して存在すると考える。 すると、（可視星＋暗黒）/（可視星）= 2.3 となる。　 (楕円体には星間物質がないから？) 　この値は太陽半径内の総質量、銀河系総質量の評価に利用される。

楕円体成分に付随する暗黒物質　 　太陽近傍では楕円体成分は総密度（暗黒物質も含めて）の５％以下である。 もし、局所総質量の５％が楕円体に属すると、太陽半径以内に含まれる質量は 標準モデルの値より約４倍に増加する。すると、太陽の回転速度は 350 km/s 以上 という受け入れがたい値になる。楕円率 ε ≤ 0.5 の扁平回転楕円体では 楕円体質量密度は 10% 以下である。これは、暗黒物質の大部分が円盤成分に付随して いることを意味する。

M/L 比　

　円盤の M/L 比は 5 である。この値は、ハッブル定数 100 km/s /Mpc で Roberts 1975 が 80 渦状銀河に対して求めた平均値に近い。しかし、この 値の分散は平均値そのものと同じくらいに大きい。したがって、ハッブル定数 50 km/s /Mpc でも 1 σ 以内である。
図１０．半径 r 内に含まれる質量、光度の割合。実線＝（楕円体/円盤）質量比



　標準モデルでは、円盤の M/L は銀河中心からの距離に依らないが、銀河面からの 光度に伴って増加する。z = 0 では M/L = 2.5 であるが、 z = 1 kpc になると M/L = 15 である。楕円体では M/L = 1,7 であり、球状星団の平均値 1.6 に近い。

　図１０には、銀河中心からの距離 r により、r 内部の質量の割合がどう変化するかを 示す。実線は楕円体対円盤の比である。楕円体は質量の 6%, 光度の 14 % を占める。

　５．３．回転曲線　

２成分銀河モデルによる回転曲線の計算　

　２成分標準モデルで回転曲線を計算した。次章ではハローを入れた場合を検討する。 ２成分モデル回転曲線は Freeman 1970 が見出した無限に薄い指数型円盤の回転と球 対称な分布の周りのニュートン的な回転の組み合わせから計算される。

　　vrot(r) = (G/r)1/2{Ms(≤r) + 4 Md s3[I0(s)K0(s) - I1(s) K1(s)]}1/2

ここに、　s = r/2h, Ms(≤r)は半径 r 内の楕円体質量、 Md は円盤総質量、
I, K は変形ベッセル関数、 h はスケール長である。

　回転曲線は図１１に示した。太陽回転速度は 170 km/s であり、観測値の 235 km/s よりかなり低い。また、このモデルのオールト定数は A = 11.1, B = -9.8 である。 これも、Oort, Plaut 1975 の A = 16.9, B = -9.0 と異なる。

脱出速度　

　脱出速度は次の式から計算でき、
Vesc2 = 2 ∫ ∞ Vrot2 dR
r R


表４に載せてある。この値はハローによる増加分は入っていない。

図１１．実線＝２成分標準モデルによる回転曲線。
　　　　点線＝ハローを入れた時の回転曲線

観測との差　

　回転曲線の形は他の銀河での観測と較べるべきである。それによると、穏やかな 立ち上がりが 235 km/s 付近まであり、その後小さな窪みその先は平坦または 緩やかな増加が 30 kpc 付近まで続く。銀河系において、Gunn et al は 25 kpc まで平坦な回転曲線が伸びている。このような特徴は２成分モデルでは作り出せない。

　６．ハロー　

　６．１．第３成分の認識　

６．１．１．ハローの密度分布　

　銀河団のビリアル運動(Zwicky 1933)や銀河回転(Roberts 1976) の研究は銀河に 第３の成分（Oort 1965, Truran,Cameron 1970, Ostriker,Peebles,Yahil 1974）が あるのではないかという考えを起こさせた。この成分はしばしば「重いハロー」と 呼ばれる。第５-３節の結果はこの示唆と整合する。

　ハロー密度を下のように仮定する。

ρH(r) = ρH(r0) 　　　　　　　　　　　　(22)
1 + (r/a)2


　６．２．力学的効果　

ハローによる回転速度　 　ハロー質量だけを考えた時の回転速度は、

　　　　　VH(r) = V(∞)(r/√3 a),　　　　　　r≪a,
　　　　　　　　　= V(∞),　　　　　　　　　　　r≫a,
ここに、V(∞) = [4 π G ρH(0) a2] 1/2 である。

回転速度漸近値によるハロー密度の制限　 　ρH(0) a2 はハローの漸近速度が 176 km/s から 350 km/s の間にあるという要請から定まる。この制限は次の不等式と同等である。

0.6 ≤ [( ρH(r0) )( r02 + a2 )] ≤ 2.3,　　　　　(24)
0.01 M๏ pc-3 100 kpc2
ここで、計算の都合上太陽近傍の量で表現した。すると、

　　　　　ρH(r0) ≤ 0.035 M๏ pc-3

この値は太陽付近での総質量密度 0.15 M๏ pc-3 より 大幅に小さい。この値はダークマターの密度 0.06 M๏ pc-3 と較べても小さい。ハローパラメターの ρH, a は太陽位置での 回転定数が観測値と一致するように決める。

３種類のハローモデルを加えた回転曲線　 　図１１には重いハローを加えたモデル計算を３つ示した。破線は ρH(r0) = 0.011 M๏ pc-3 で a = 0 の場合、点線は ρH(r0) = 0.017 M๏ pc-3 で a = 2 kpcの場合、一点鎖線は ρH () = 0.010 M๏ pc-3 で a = 2 kpc の場合 である。太陽近傍の星とダークマターの量は双密度を 0.15 M๏ pc-3 に保つよう調整される。

ハローを加えたモデルの回転定数　 　回転定数は a = 0 の場合、A = 16.1 km/s /kpc, B = -15.4 km/s /kpc, A r0 = 130 km/s, 太陽回転速度 = 250 km/s である。a = 2 kpc では、 回転定数は ρH(r0) = 0.011 の時、 13.3, -14.7, 105, 225 であり、 ρH(r0) = 0.017 の時、 14.4, -17.7, 115, 250 となる。これらのモデルは観測と誤差の範囲で合っている。

ハロー質量　 　ハローの密度は太陽位置でが総密度の約 10 % を占めている。 ρH (r0) > 0.010 の時、太陽半径 r0 の内側ではハロー質量が 全体の 2/3 を占める。 ρH(r0) = 0.010 ではこの値は 1/2 となる。このように大きなハローは円盤のバーモード不安定性に対して(Ostriker, Peebles 1973) 安定化に働く。

円盤スケール長 h とハロー質量　 　ハローパラメターは円盤スケール長に影響を受ける。例えば、h = 2.75 kpc では ρH(r0) = 0.025, a = 25 kpc （？）のハローは 15.8, -11.7, 125, 220 という許容範囲内の値を与える。このハロー成分は r0 の内側質量の 10 % しか占めない。h = 2.75 kpc では殆どの a に対し、観測と合うモデルを作れる。しかし、 h = 3.5 kpc になるとそれは 難しい。

　６．３．ハローのスターカウント　

銀極方向でのハロー星　

m ≤ 21 でのハロー星の寄与　 　次に「重いハロー」が銀極方向のスターカウントにどう影響するかを考えよう。 (22)式の密度則ではハロー密度は 10 kpc 以内ではファクター２以内で一定と看做せる。 したがってハロー星のスターカウントは、ハローには Mbright より明るい 星があまりないという想定で、 m ≤ 15 + Mbright の範囲では 10 0.6m で増加する。このハロー星の増加は円盤や楕円体に較べるとずっと 急である。もしある等級でハローがカウントで有意な割合を占めればそれより暗い 方ではハローがずっと支配的になる。　

しかし、この急激な増加は mV ≤ 21 では見出されない。(Tyson Jarvis 1979 は mV ≥ 21 で急増 するとしているが他の報告では確認されない。 Kron 1978 も mV ≥ 22.5 で増加するが銀河の混入がある。) したがって、ハローは mV ≤ 21 で は僅かな寄与しかない。

ハロー星のスターカウント　 　例示目的で、ρ ∝ r-2 でのハロー星の１平方度あたり、 m 等以下の星の数は次の式で与えられる。簡単のため、ハロー星の絶対等級は 一定でM0とする。

NH(≤m) = 1.0 × 10-4 ρH(r0) zmax3[3 (x0 - arctan x0/x03)]
Mass(M0)


ここに、x0 = zmax/r0,　 log (zmax /10 pc) = 0.2 (m - M0)　である。括弧の中の量は zmax ≤ 10 kpc (m - M ≤ 15) に対して、 0.5 - 1.0 である。

ハロー星光度の見積もり　 　ハロー星の密度は mV ≤ 21 までは観測星数の一桁下である。なぜなら 急なカウントの増加が見られないからである。この観測的制限がハロー星の絶対等級に 次の制限を課す。

　　　　　MvMS ≥ 12.5　　　　　　　　　　(27a)
　　　　　MvWD ≥ 12.5　　　　　　　　　　(27a)

この式を出すにあたり、仮定として ρ(r0) = 0.011 Mํ pc-3, a = 0 さらに、MMS(Mv=12.5) = 0.2 M ํ とした。しかし、ハロー星の光度を出すにはさらに観測が必要 である。

ハロー星の種族　

　ハロー星は円盤や楕円体星と大きく異なる種族かも知れない。


　７．議論と結論　

まとめ　

（１）標準モデルは円盤と楕円体の特性パラメターを与える。
　　　それらは、密度、光度の変化、脱出速度、太陽から各方向への密度
　　　変化、カラー分布などである。
　　　計算された M/L 比、光度、スケール長は Sbc 銀河と合う。

（２）スターカウントの銀経、銀緯変化は観測と合う。
　　　　銀極方向で mV ≤ 28 の星数は 104 deg-2 である。

（３）楕円体成分の楕円率 ε ≤ 0.15 である。
　　　　楕円体の観測によいのは l = 0° - 180°, l = 90° - 270° である。
　　　　銀緯では b = 90°, 45°

（４）円盤のスケール長は l ≥ 120°, 20 ≤ mV ≤ 23 で の地上観測が有効。
　　　　銀緯では b = 30° がよい。 		（７）観測データは次の仮定と合致する。
　　　(a) 中間スケール高(H≥1kpc)の種族は存在しない。
　　　(b) 光度関数は場所によらない。

（８）暗い（mB≈23）での(B-V)分布はQSO数が明るい側から の外挿値より
　　　　ずっと低いことを示す。

（９）２成分モデルから計算される回転曲線は遠距離で平坦にならない。
　　　ハローの導入で平坦化が達成される。

課題　

（１）ＳＴによる mV = 28 までの観測はもしハロー星が Mv ≤ 19 の 主系列星であるならその検出に成功するだろう。

（２）21 ≤ mV ≤ 23 での地上観測によりカウントの勾配変化が あるかを確定することは重要である。

　付録Ａ　Ｂバンドでのスターカウント


図１２．円盤のＢバンド光度関数。
　　　黒丸 = McCuskey 1966, 白丸 = Luyten 1966, 四角 = van Rhijn 1936。


図１４．Ｂバンド星数密度の銀緯変化。減光A∞(90°)=0.2

図１３．（左）銀経で平均したＢバンド星数密度 NB。減光A∞ (90°)=0.2　　　　　　　　 　　　　（右）銀経で平均した累積星数




図１５．銀経、銀緯の関数としてのＢバンド星数密度



　付録Ｂ　Ｂバンドでのスターカウント　

星数密度等を等級、銀緯、銀経の関数として簡単に計算する近似式の紹介。

表５，６は微分および累積星数密度関数を、適当な銀経・銀緯・等級に対して 示したものである。Ｖ，Ｂバンドが載っている。


表５．微分星数密度




表５．累積星数密度。　　なぜか表がない。



　付録Ｃ　色等級関係　

　円盤星に対しては、主系列星のカラー等級関係を使用し、巨星(Mv≤+4)は無視した。 なぜなら、ここで考えている見かけ等級巾では彼らの寄与は無視できるからである。

　楕円体星に対しては、主系列が青い方に少しずれる。Δ(B-V) = -0.15 をすべて の楕円体星に適用した。楕円体巨星は mV ≤ 19 で大きな寄与がある。 巨星枝に対しては M67 のデータ Johnson,Sandage 1955 を使った。